Reversible Image Fragile Watermarking with Dual Tampering Detection
Abstract
1. Introduction
2. Preliminaries
2.1. Arnold Algorithm for Scrambling
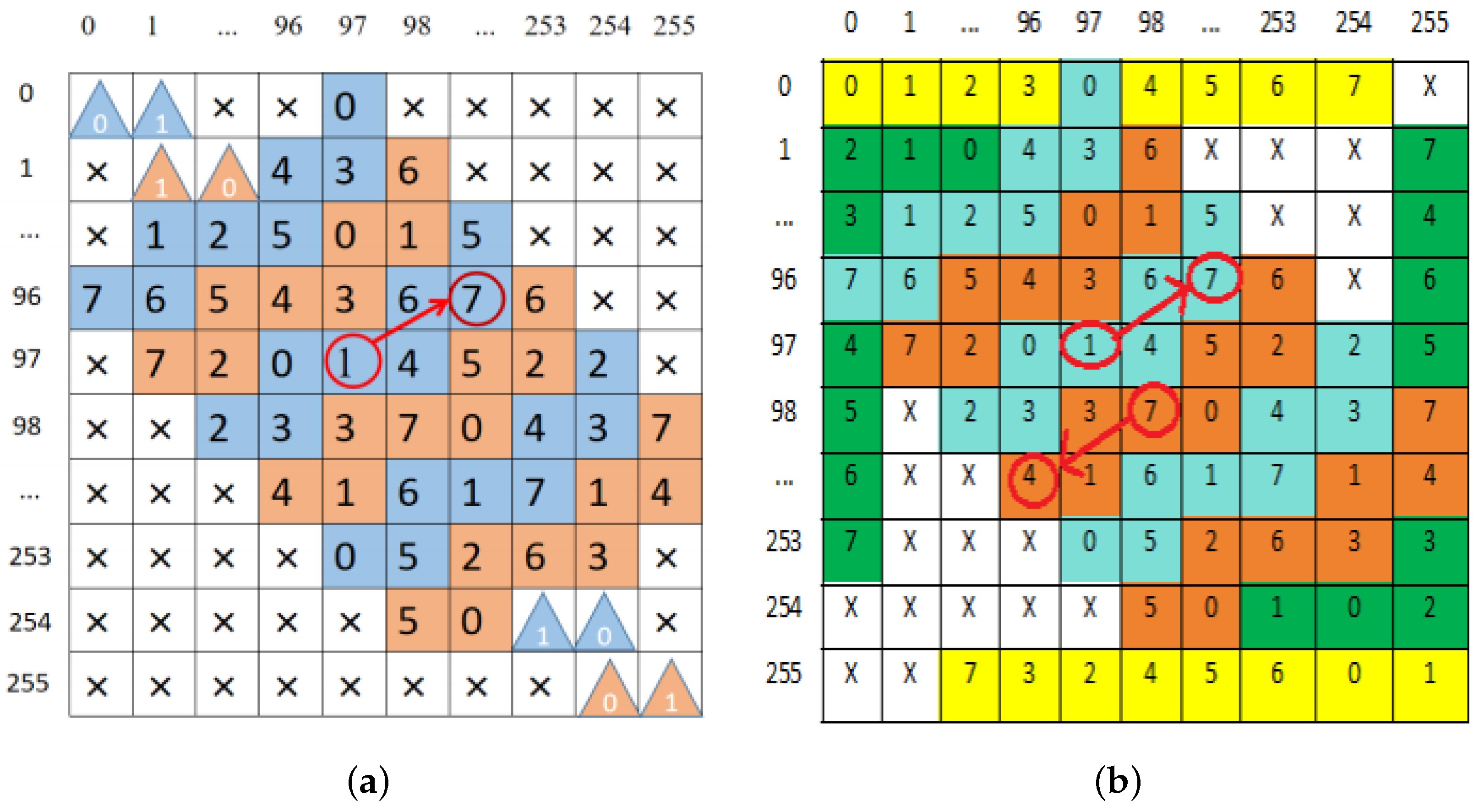
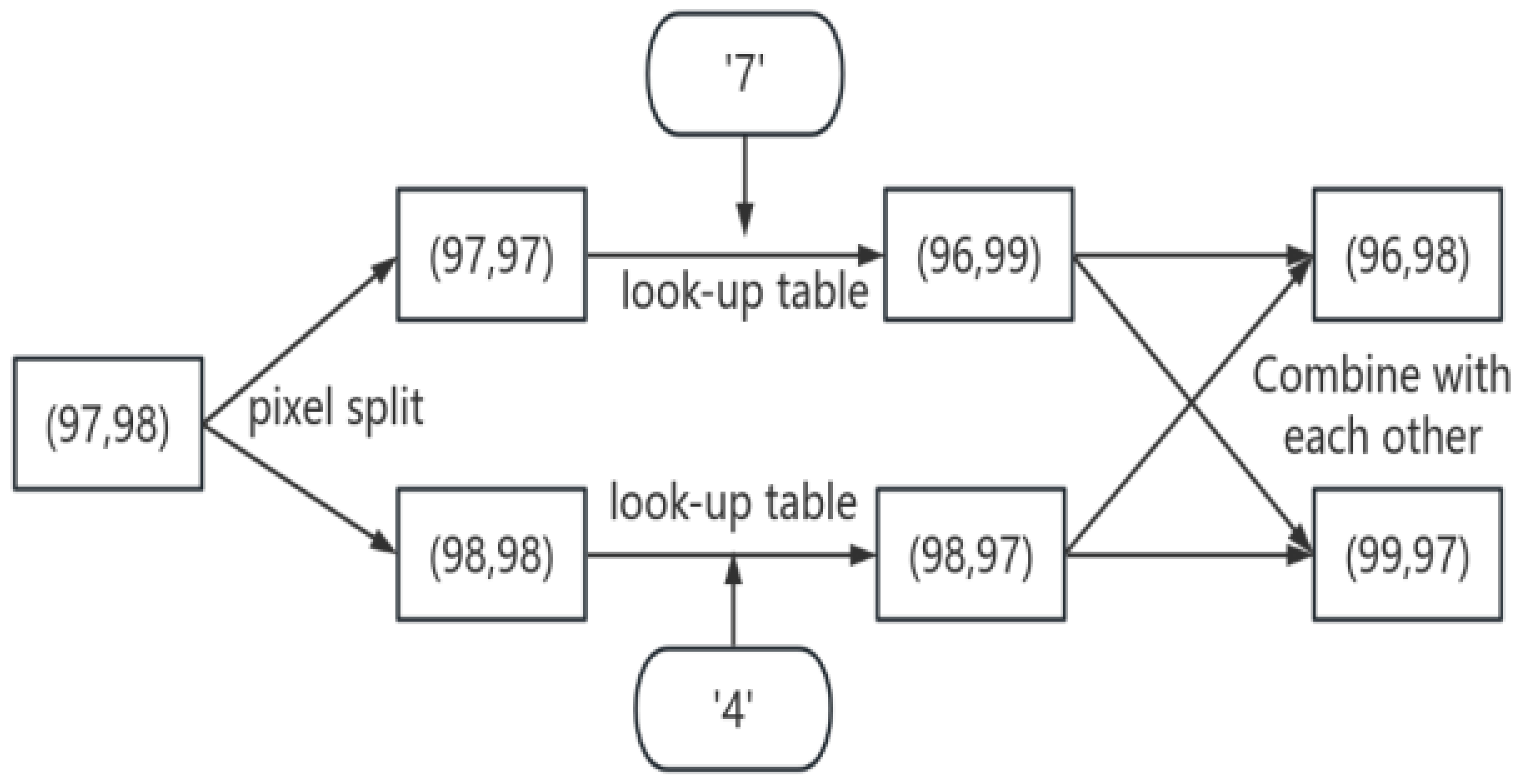
2.2. Insect Matrix for Embedding Algorithm
| Algorithm 1: Turtle shell embedding algorithm. |
Original pixel: (6, 7). Secret information: ‘100’. 1. Find the pixel position in the matrix: (6, 7) → 7. 2. Make the turtle shell matrix: With (6, 7) as the vertex, make three turtle shells. 3. Convert secret information to an octal number: ‘100’→ 4. 4. Find the value of 4 in the turtle shell and the position closest to the pixel pair (6, 7): (5, 6). 5. Output the final pixel pair: (5, 6). |
3. Proposed Method
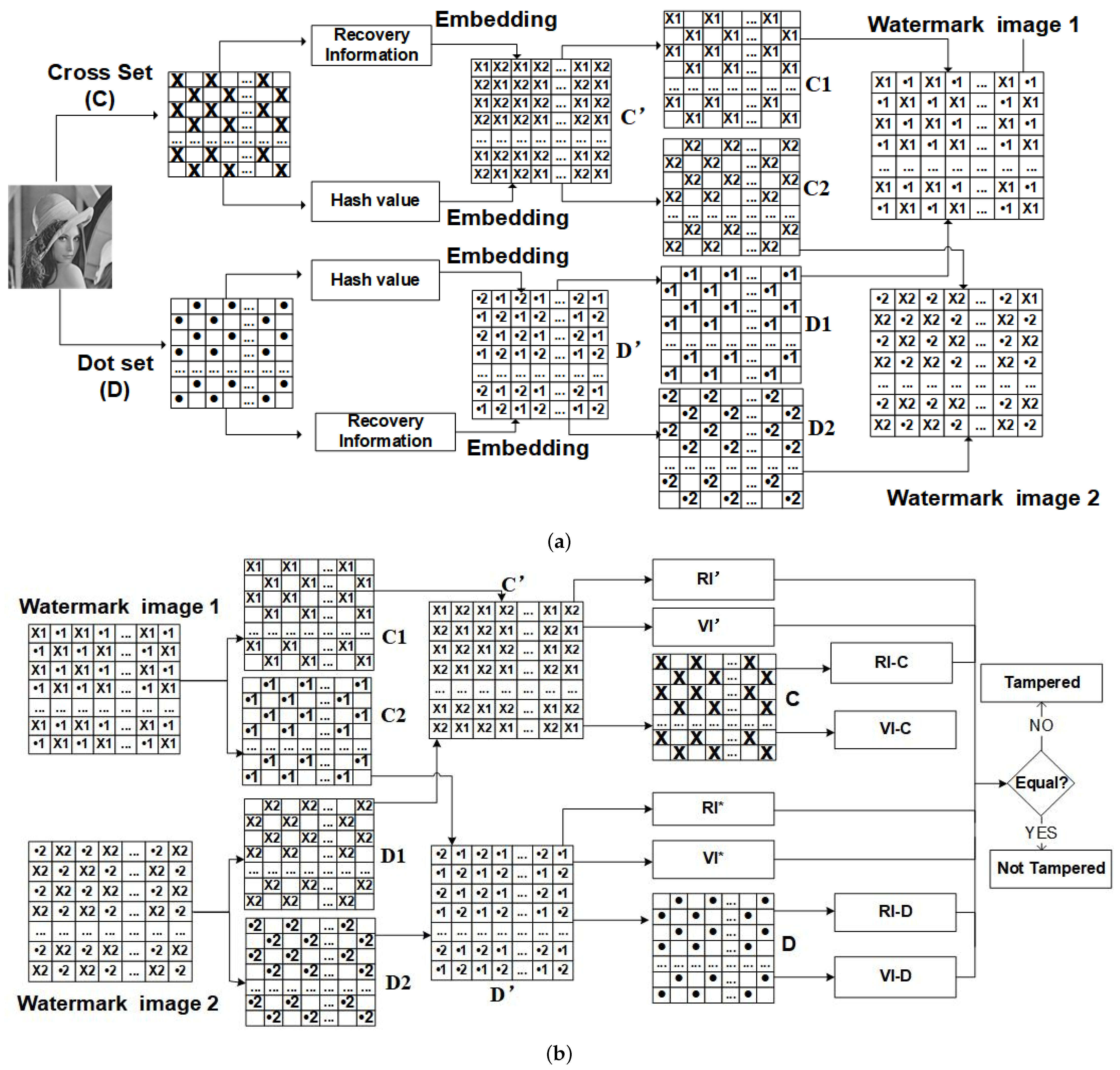
3.1. Watermark Generation
3.2. Watermark Embeddings
3.3. Tampering Detection
| Algorithm 2: Second tampering detection process. |
Input: Block1, Block2, Block3. Output: Is Block1 tampered with? 1. Extract the recovery information RI2 from Block1. 2. Recalculate the recovery information RI2’ from Block2. 3. Extract the recovery information RI1 from Block3. 4. Recalculate the recovery information RI1’ from Block1. 5. Determine whether Block1 is tampered with: If RI2 = RI2’ and RI1 = RI1’: Output Block1 is not tampered with. Else: Output Block1 is tampered with. |
3.4. Tampering Recovery
4. Experiments
4.1. Evaluation Criteria
4.2. Threshold for Supplemental Judgment
4.3. Tampering Detection and Recovery
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panchikkil, S.; Vegesana, S.P.; Manikandan, V.M.; Donta, P.K.; Maddikunta, P.K.; Gadekallu, T.R. An ensemble learning approach for reversible data hiding in encrypted images with fibonacci transform. Electronics 2023, 12, 450. [Google Scholar] [CrossRef]
- Chi, H.X.; Chang, C.C.; Wang, X.; Lin, C.C. Hiding and extracting important information in encrypted images by using the transformation of all possible permutations and VQ codebook. Electronics 2022, 11, 3475. [Google Scholar] [CrossRef]
- Zhou, N.R.; Tong, L.J.; Zou, W.P. Multi-image encryption scheme with quaternion discrete fractional Tchebyshev moment transform and cross-coupling operation. Signal Process. 2023, 211, 109107. [Google Scholar] [CrossRef]
- Zhou, N.R.; Hu, L.L.; Huang, Z.W.; Wang, M.M.; Luo, G.S. Novel multiple color images encryption and decryption scheme based on a bit-level extension algorithm. Expert Syst. Appl. 2024, 238, 122052. [Google Scholar] [CrossRef]
- Serrano, D.; Ruíz, J.F.; Muñoz, A.; Maña, A.; Armenteros, A.; Crespo, B.G. Development of applications based on security patterns. In Proceedings of the 2009 Second International Conference on Dependability, Athens, Greece, 18–23 June 2009. [Google Scholar]
- Feng, Q.; Leng, L.; Chang, C.C.; Horng, J.H.; Wu, M. Reversible data hiding in encrypted images with extended parametric binary tree labeling. Appl. Sci. 2023, 13, 2458. [Google Scholar] [CrossRef]
- Fridrich, J. Protection of digital images using self-embedding. In Proceedings of the Symposium on Content Security and Data Hiding in Digital Media, Newark, NJ, USA, 9–12 May 1999; New Jersey Institute of Technology: Newark, NJ, USA, 1999. [Google Scholar]
- Lee, T.Y.; Lin, S.D. Dual watermark for image tamper detection and recovery. Pattern Recognit. 2008, 41, 3497–3506. [Google Scholar] [CrossRef]
- Chang, Y.F.; Tai, W.L. A block-based watermarking scheme for image tamper detection and self-recovery. Opto-Electron. Rev. 2013, 21, 182–190. [Google Scholar] [CrossRef]
- Sinhal, R.; Ansari, I.A.; Ahn, C.W. Blind image watermarking for localization and restoration of color images. IEEE Access 2020, 8, 200157–200169. [Google Scholar] [CrossRef]
- Su, G.-D.; Chang, C.-C.; Lin, C.-C. High-precision authentication scheme based on matrix encoding for AMBTC-compressed images. Symmetry 2019, 11, 996. [Google Scholar] [CrossRef]
- Singh, D.; Singh, S.K. Effective self-embedding watermarking scheme for image tampered detection and localization with recovery capability. J. Vis. Commun. Image Represent. 2016, 38, 775–789. [Google Scholar] [CrossRef]
- Tohidi, F.; Paul, M.; Hooshmandasl, M.R. Detection and recovery of higher tampered images using novel feature and compression strategy. IEEE Access 2021, 9, 57510–57528. [Google Scholar] [CrossRef]
- Shehab, A.; Elhoseny, M.; Muhammad, K.; Sangaiah, A.K.; Yang, P.; Huang, H.; Hou, G. Secure and robust fragile watermarking scheme for medical images. IEEE Access 2018, 6, 10269–10278. [Google Scholar] [CrossRef]
- Hemida, O.; He, H. A self-recovery watermarking scheme based on block truncation coding and quantum chaos map. Multimed. Tools Appl. 2020, 79, 18695–18725. [Google Scholar] [CrossRef]
- Lin, C.-C.; He, S.-L.; Chang, C.-C. Pixel P Air-Wise Fragile Image Watermarking Based on HC-Based Absolute Moment Block Truncation Coding. Electronics 2021, 10, 690. [Google Scholar] [CrossRef]
- Aminuddin, A.; Ernawan, F. AuSR1: Authentication and self-recovery using a new image inpainting technique with LSB shifting in fragile image watermarking. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 5822–5840. [Google Scholar] [CrossRef]
- Su, G.D.; Chang, C.C.; Lin, C.C. Effective self-recovery and tampering localization fragile watermarking for medical images. IEEE Access 2020, 8, 160840–160857. [Google Scholar] [CrossRef]
- Renklier, A.; Öztürk, S. Image authentication and recovery: Sudoku puzzle and MD5 hash algorithm based self-embedding fragile image watermarking method. Multimed. Tools Appl. 2024, 83, 13929–13951. [Google Scholar] [CrossRef]
- Molina-Garcia, J.; Reyes-Reyes, R.; Ponomaryov, V.; Cruz-Ramos, C. Watermarking algorithm for authentication and self-recovery of tampered images using DWT. In Proceedings of the 2016 9th International Kharkiv Symposium on Physics and Engineering of Microwaves, Millimeter and Submillimeter Waves (MSMW), Kharkiv, Ukraine, 20–24 June 2016. [Google Scholar]
- Haghighi, B.B.; Taherinia, A.H.; Mohajerzadeh, A.H. TRLG: Fragile blind quad watermarking for image tamper detection and recovery by providing compact digests with optimized quality using LWT and GA. Inf. Sci. 2019, 486, 204–230. [Google Scholar] [CrossRef]
- Rhayma, H.; Makhloufi, A.; Hamam, H.; Hamida, A.B. Semi-fragile self-recovery watermarking scheme based on data representation through combination. Multimed. Tools Appl. 2019, 78, 14067–14089. [Google Scholar] [CrossRef]
- Molina-Garcia, J.; Garcia-Salgado, B.P.; Ponomaryov, V.; Reyes-Reyes, R.; Sadovnychiy, S.; Cruz-Ramos, C. An effective fragile watermarking scheme for color image tampering detection and self-recovery. Signal Process. Image Commun. 2020, 81, 115725. [Google Scholar] [CrossRef]
- Al-Otum, H.M.; Ellubani, A.A. Secure and effective color image tampering detection and self restoration using a dual watermarking approach✩. Optik 2022, 262, 169280. [Google Scholar] [CrossRef]
- Haghighi, B.B.; Taherinia, A.H.; Harati, A. TRLH: Fragile and blind dual watermarking for image tamper detection and self-recovery based on lifting wavelet transform and halftoning technique. J. Vis. Commun. Image Represent. 2018, 50, 49–64. [Google Scholar] [CrossRef]
- Li, Y.; Song, W.; Zhao, X.; Wang, J.; Zhao, L. A novel image tamper detection and self-recovery algorithm based on watermarking and chaotic system. Mathematics 2019, 7, 955. [Google Scholar] [CrossRef]
- Sinhal, R.; Ansari, I.A. Multipurpose image watermarking: Ownership check, tamper detection and self-recovery. Circuits Syst. Signal Process. 2022, 41, 3199–3221. [Google Scholar] [CrossRef]
- Kang, H.; Leng, L.; Chang, C.C. Overlapped (7, 4) hamming code for large-capacity and low-loss data hiding. Multimed. Tools Appl. 2023, 82, 30345–30374. [Google Scholar] [CrossRef]
- Huang, C.T.; Shongwe, N.S.; Weng, C.Y. Enhanced Embedding Capacity for Data Hiding Approach Based on Pixel Value Differencing and Pixel Shifting Technology. Electronics 2023, 12, 1200. [Google Scholar] [CrossRef]
- Kang, H.-Y.; Leng, L.; Kim, B.-G. Data hiding of multicompressed images based on Shamir threshold sharing. Appl. Sci. 2022, 12, 9629. [Google Scholar] [CrossRef]
- Qureshi, M.A.; Deriche, M.; Beghdadi, A.; Amin, A. A critical survey of state-of-the-art image inpainting quality assessment metrics. J. Vis. Commun. Image Represent. 2017, 49, 177–191. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Y.-P.; Zhang, L.-F. Dynamic selection network for image inpainting. IEEE Trans. Image Process. 2021, 30, 1784–1798. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Lin, Z.; Yang, J.; Shen, X.; Lu, X.; Huang, T.S. Generative image inpainting with contextual attention. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Bugeau, A.; Bertalmío, M.; Caselles, V.; Sapiro, G. A comprehensive framework for image inpainting. IEEE Trans. Image Process. 2010, 19, 2634–2645. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhang, J.; Deng, W.; He, D. Arnold transformation algorithm and anti-Arnold transformation algorithm. In Proceedings of the 2009 First International Conference on Information Science and Engineering, Nanjing, China, 26–28 December 2009. [Google Scholar]
- Liu, Y.; Chang, C.C. A turtle shell-based visual secret sharing scheme with reversibility and authentication. Multimed. Tools Appl. 2018, 77, 25295–25310. [Google Scholar] [CrossRef]
- Gao, K.; Horng, J.H.; Liu, Y.; Chang, C.C. A reversible secret image sharing scheme based on stick insect matrix. IEEE Access 2020, 8, 130405–130416. [Google Scholar] [CrossRef]








| Method | PSNR (dB) | |||||
|---|---|---|---|---|---|---|
| Barbara | Lena | Peppers | Baboon | Average | ||
| [13] | 44.17 | 44.11 | 44.1 | 44.29 | 44.17 | |
| [17] | 45.69 | 45.71 | 45.66 | 45.7 | 45.69 | |
| [19] | 44.32 | 44.27 | 44.39 | 44.22 | 44.24 | |
| [25] | 44.16 | 44.17 | 44.16 | 44.15 | 44.16 | |
| [26] | 40.71 | 40.72 | 40.71 | 40.7 | 40.71 | |
| [27] | 41.16 | 41.17 | 41.01 | 40.2 | 40.89 | |
| Proposed | Watermark Image 1 | 46.37 | 46.36 | 46.35 | 46.39 | 46.37 |
| Watermark Image 2 | 46.36 | 46.36 | 46.36 | 46.38 | 46.37 | |
| Method | SSIM | |||||
|---|---|---|---|---|---|---|
| Barbara | Lena | Peppers | Baboon | Average | ||
| [13] | 0.9867 | 0.9821 | 0.9827 | 0.9945 | 0.9865 | |
| [17] | 0.9967 | 0.9993 | 0.9889 | 0.9900 | 0.9937 | |
| [19] | 0.9878 | 0.9814 | 0.9881 | 0.9922 | 0.9874 | |
| [25] | 0.9851 | 0.9835 | 0.9817 | 0.9937 | 0.9860 | |
| [26] | 0.9785 | 0.9687 | 0.9722 | 0.9900 | 0.9774 | |
| [27] | 0.9734 | 0.9667 | 0.9650 | 0.9823 | 0.9719 | |
| Proposed | Watermark Image 1 | 0.9947 | 0.9963 | 0.9893 | 0.9966 | 0.9942 |
| Watermark Image 2 | 0.9947 | 0.9963 | 0.9893 | 0.9966 | 0.9942 | |
| Method | Tampering Rate | |||||
|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | ||
| [13] | Recall | 99.50% | 99.25% | 99.44% | 98.75% | 99.12% |
| Precision | 100% | 100% | 100% | 100% | 100% | |
| [17] | Recall | 100% | 100% | 100% | 100% | 100% |
| Precision | 99.50% | 99.18% | 99.25% | 100% | 100% | |
| [25] | Recall | 99.95% | 100% | 100% | 100% | 99.99% |
| Precision | 100% | 100% | 100% | 100% | 100% | |
| [26] | Recall | 99.83% | 99.95% | 99.99% | 100% | 100% |
| Precision | 100% | 100% | 100% | 100% | 100% | |
| [27] | Recall | 99.88% | 99.88% | 99.99% | 99.95% | 100% |
| Precision | 100% | 100% | 100% | 100% | 100% | |
| Proposed | Recall | 100% | 99.65% | 100% | 100% | 100% |
| Precision | 100% | 100% | 100% | 100% | 100% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, C.; Leng, L.; Chang, C.-C.; Horng, J.-H. Reversible Image Fragile Watermarking with Dual Tampering Detection. Electronics 2024, 13, 1884. https://doi.org/10.3390/electronics13101884
Zhan C, Leng L, Chang C-C, Horng J-H. Reversible Image Fragile Watermarking with Dual Tampering Detection. Electronics. 2024; 13(10):1884. https://doi.org/10.3390/electronics13101884
Chicago/Turabian StyleZhan, Cai, Lu Leng, Chin-Chen Chang, and Ji-Hwei Horng. 2024. "Reversible Image Fragile Watermarking with Dual Tampering Detection" Electronics 13, no. 10: 1884. https://doi.org/10.3390/electronics13101884
APA StyleZhan, C., Leng, L., Chang, C.-C., & Horng, J.-H. (2024). Reversible Image Fragile Watermarking with Dual Tampering Detection. Electronics, 13(10), 1884. https://doi.org/10.3390/electronics13101884









