Abstract
Digital chaotic systems used in various applications such as signal processing, artificial intelligence, and communications often suffer from the issue of dynamical degradation. This paper proposes a solution to address this problem in the digital tent map. Our proposed method includes a simple and optimized hardware architecture, along with a hardware-efficient perturbation method, to create a high-performance computing system that retains its chaotic properties. We implemented our proposed architecture using an FPGA (Field-Programmable Gate Array) and the 1’s complement fixed-point format. Our results demonstrate that the implemented digital circuit reduces logical resource consumption compared to state-of-the-art references and exhibits pseudo-random nature, as confirmed by various statistical tests. We validated our proposed pseudo-random number generator in a hardware architecture for particle swarm optimization, demonstrating its effectiveness.
1. Introduction
In recent years, the use of digital chaotic systems has been extensively explored in various digital applications, including chaos synchronization, signal, and image encryption, and pseudo-random number generation [1,2,3,4,5,6,7,8,9,10,11]. For example, pseudo-random number generators (PRNGs) are of significant importance in many areas, such as system identification and cryptography [12,13,14].
However, the use of chaotic systems in finite-precision environments, such as computers, is impacted by a phenomenon known as dynamical degradation. This occurs when the chaotic dynamics of the system cannot be preserved and results in short cycle lengths [15]. To mitigate this issue, various strategies have been proposed, such as using high finite precision, cascading/coupling multiple chaotic systems, switching multiple chaotic systems, and pseudo-randomly perturbing the chaotic system [16].
Despite significant progress in countering dynamical degradation, the current approaches tend to be overly complex. For instance, the authors in [17] introduced a parameter perturbation method for the tent map based on the Lyapunov exponent, which has proven to be an effective way to preserve its chaotic features. However, this solution did not address hardware efficiency. While there has been a lot of work in representing chaotic maps on digital circuits [1,3,18], little attention has been paid to optimizing their hardware [19]. In other words, few studies focus on designing chaotic systems with as few components as possible while also counteracting dynamical degradation. However, creating efficient and simple digital chaotic systems is a crucial issue that has been prompted by the increasing use of chaos in various fields.
The simplicity of digital chaotic systems is related to the number of arithmetic operations [19]. The authors in [19] used the logistic map to create a minimal digital chaotic system. An alternative to the logistic map is the tent map [20], especially with the bifurcation parameter , which only requires shift operations for multiplication. In this article, we present the design of a straightforward digital chaotic tent map based on the 1’s complement fixed-point format. This numerical representation reduces hardware and power consumption, improving execution time. To counteract dynamical degradation, we also introduce a clear-cut perturbation method that involves disturbing only the two least significant bits of the digital tent map using an XOR gate. Our main contribution is demonstrated by reducing logical resource consumption per bit while preserving the chaotic properties of the map and countering the dynamical degradation. Compared to other state-of-the-art articles in the literature [3,21,22,23], our proposed tent map demonstrates a reduction in resource consumption per bit of at least .
To validate the chaotic and statistical features of the digital map, we estimate the largest Lyapunov exponent [24] and show its return map, time series, histogram plot, and autocorrelation function. Furthermore, to evaluate the randomness of the digital tent map, we apply the Kolmogorov–Smirnov test, Runs test, and ENT test suite. After verifying the randomness, we use the tent map as a source of pseudo-random number generation in a hardware implementation for particle swarm optimization [25].
In summary, the main novelties and contributions of this paper are
- A simple and efficient method to counteract the dynamical degradation of the digital tent map, using an XOR gate to disturb each iteration of this chaotic map.
- A hardware architecture design for the tent map that consumes few logical resources and maintains the chaotic properties.
- An application of this hardware architecture in optimization problems.
This paper is organized as follows: Section 2 describes the tent map concepts and the methods used to synthesize them while avoiding dynamical degradation. The main results and application in optimization problems are presented in Section 3. The conclusion and final considerations are shown in Section 4.
2. Design of the Digital Tent Map
2.1. Tent Map
The tent map [20] is described by:
where the bifurcation parameter , is the nth state of the system, and . The model of this system is simple yet exhibits chaotic behavior, which is highly sensitive to initial conditions. As one of our objectives is to design a hardware architecture for a chaotic map that consumes fewer logical resources while maintaining its chaotic properties, it is crucial to select a map that requires minimal mathematical operations. As aforementioned, the simplicity of digital chaotic systems is directly related to the number of arithmetic operations involved. Hence, opting for the tent map over other chaotic maps is a judicious decision. Additionally, the tent map has been successfully applied in various fields, including radar design [26], image encryption [17,27], and metaheuristic optimization algorithms [28]. These applications demonstrate the importance of creating a simple and efficient hardware architecture for this chaotic system. Finally, as presented in [29], the analysis of the tent map can be simplified using binary representations, which further highlights its advantages for digital circuit applications.
2.2. Method
In this section, we show a method to decrease the number of arithmetic operations and a perturbation approach to perform Equation (1). Here, we use a fixed-point representation since it has higher hardware performance, is less flexible, and is used to represent a more limited range of values than floating-point arithmetic. Moreover, since we work with a chaotic map with and we intend to implement a digital-chaotic system with as few logical resources as possible, the use of floating-point arithmetic is unnecessary in this case.
As , using a fixed-point representation, the fractional binary number is represented by:
where is a decimal number, is its respective binary number, 0 is the hidden bit, and represents the kth bit. In this paper, we investigate representations with , where also indicates the resolution.
In such a way, considering 1’s complement [30]:
where M is the complementation constant and is the unit in the last place.
Let be a binary number and its respective bitwise complement. Hence:
Note that . Thus, as long as and , the can be neglected:
Inasmuch as the subtraction only occurs when (seen in Equation (1)), the first step must confirm such a condition. Because , the most significant bit is the only bit needed to verify the aforesaid condition. Therefore, when , , no subtraction is required. Otherwise, when , the complement operation is necessary, according to Equation (5). These conditions can be easily computed by
where is the binary number of the nth state. Note it is clear that XOR gates can be used in such cases.
To simplify Equation (1), we use , because it allows us to perform arithmetic multiplication using shift operations. However, the tent map displays dynamical degradation when , resulting in a periodic function. Indeed, orbits of binary shift chaotic maps eventually converge to zero [23]. In this way, we apply an XOR gate between the least two significant bits. Thus, in the digital domain, the tent map with the perturbation method can be represented as
- Tent map:
- Perturbation method:
It is important to explain that we use an XOR gate since it has a chance of outputting logical high or low level. This operation is sufficient to cause a disturbance and reduce the degradation phenomenon caused by the reduction of precision in digital circuits [15,17], as will be seen in Section 3.
Table 1 compares the many existing methods to counteract such an issue in the tent map. We can observe that many approaches are more complex to implement in hardware than our perturbation at a logic-gate level. If such techniques were conceived as a hardware architecture, they would certainly consume many logical resources.

Table 1.
Approaches for counteracting the dynamical degradation in the tent map.
Ultimately, Figure 1 shows the flowchart representation of the digital tent map. Note the small number of blocks and operations that can still generate chaotic orbits. This is due that 1’s complement fixed-point numerical representation allows the replacement of arithmetic operations using a few logic gates.
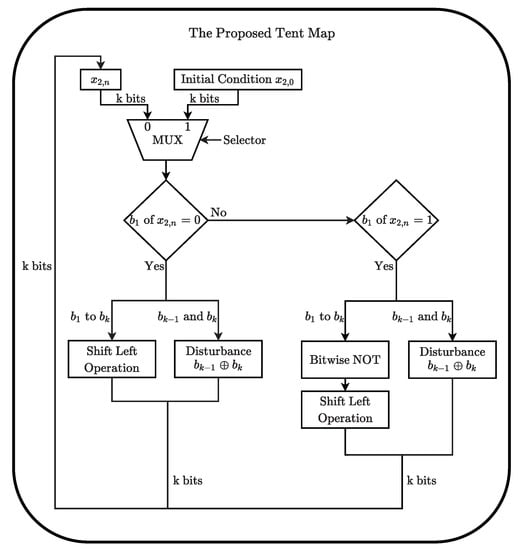
Figure 1.
Flowchart representation of the digital tent map.
3. Results and Discussion
3.1. Hardware Performance
The designed circuit was implemented using the VHDL (VHSIC Hardware Description Language) in the Xilinx Vivado 2019.1 design tool, and its operation was simulated in ModelSim—Mentor Graphics. We adopted the low-cost FPGA device Artix 7 XC7A100TFGG676-3 to embed such a chaotic system. This choice is based on the fact that this semiconductor device is commonly used for prototyping digital circuits. Moreover, FPGA offers several advantages, including flexibility, reliability, robustness, and fast processing [22].
The tent map was implemented using three different fixed-point numerical precision formats: 16-bit, 32-bit, and 64-bit. These formats were chosen due to their common usage in many designs. One advantage of this circuit is its ability to adapt to different precision requirements based on the specific application it will be used for.
To demonstrate this result, we present the 16-bit implementation of the tent map in Figure 2. This digital circuit presents chaotic behavior, yet contains only a small number of logical components and has a latency of one clock cycle. In the figure, the block labeled “&” represents the concatenation operation. The first fifteen XOR gates determine which condition for the tent map is satisfied in the nth iteration and perform the complement operation if necessary. To save FPGA resources, we avoid using an XOR gate to execute , since the resultant bit is always zero and will be discarded after a shift left operation. Additionally, note that the perturbation process is performed by the rightmost XOR gate, since .
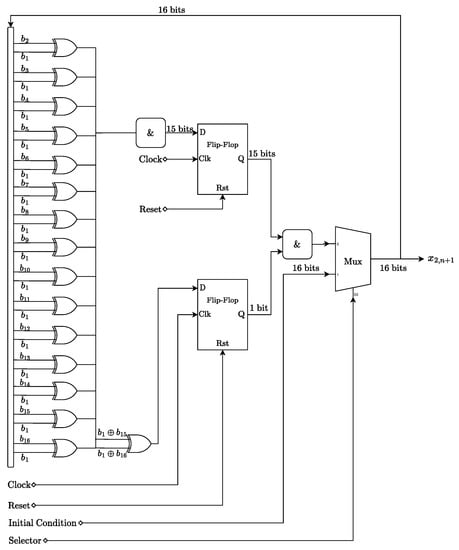
Figure 2.
A digital representation of the tent map.
Table 2 shows which components are used to represent the tent map. Since there are many synthesis and implementation strategies in the Xilinx Vivado design tool, we chose to optimize the area of the implemented digital circuit as much as possible. The proposed scheme is compared to [19], which also focuses on minimizing hardware. Note that the proposed circuit contains fewer logical resources, consumes less than of the available capacity in the FPGA, does not use DSP (Digital Signal Processing) resources, and has a superior operating frequency.

Table 2.
List of components used in the digital representation of the tent map with different resolutions, in comparison with the proposed design using the logistic map in [19].
Although Xilinx and Intel produce FPGAs with different architectures, it is relevant to mention that the proposed tent map presents the same results concerning Logic Utilization and Registers as the LUTs and FFs indicated in Table 2 when using the Cyclone V device. Therefore, the proposed hardware architecture remains superior to the one shown in [19].
Additionally, Table 3 compares the logical resource consumption among other tent-map-based works as well as discrete chaotic maps. The sixth column shows the ratio between the total number of logical resources used and the number of bits. This is an objective way to measure the simplicity of a chaotic system since many of these papers do not clarify which components were used. Notice that the number of components used in this proposed digital circuit is lower than the other ones, reducing the number of components by at least .

Table 3.
Comparing logical components of chaotic maps across approaches.
To emphasize the chaotic nature of the proposed digital tent map and that the perturbation method works, the largest Lyapunov exponent () was estimated using Wolf’s method [24,35]. This calculation was performed on a decimal representation converted from the generated binary data produced by ModelSim. The reported in the literature is and, as can be seen in Table 4, the estimated values are in good agreement with the expected value. Moreover, as the largest Lyapunov exponent is positive, this can be considered evidence of the chaotic properties present in the proposed digital circuit. Furthermore, the return map and two-time series with slightly different initial conditions were plotted, as shown in Figure 3. By Figure 3, it is possible to note that the digital circuit preserves the tent shape of the map, and the chaotic orbits diverge over time periods, indicating its sensitivity to initial conditions.

Table 4.
Quantitative results to show the chaotic nature and randomness of the proposed digital circuit.
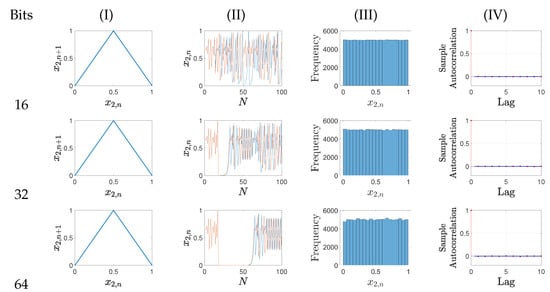
Figure 3.
The results achieved by the proposed chaotic circuit and perturbation method. Column (I) shows the return map. Column (II) shows two chaotic time series with initial conditions (blue line) and (brown line), respectively. The x-axis is the number of iterations (N) and the y-axis is the decimal converted value of the digital chaotic system—. Ultimately, columns (III) and (IV) show the histogram and the autocorrelation function, respectively.
The tent map, a type of 1D piecewise linear map, is required to have a specific correlation function and probability distribution [36]. As shown in Figure 3, the histogram and the autocorrelation function for all bit precision formats of the proposed digital tent map are presented. The histograms show a uniform distribution, indicating that all values of are equally likely to be the circuit output. Additionally, the lack of correlation in the generated orbits indicates that the samples are independent of each other. These results align with previous findings in the literature.
The pseudorandom properties of the tent map can be observed through the p-values obtained from one-sample Kolmogorov–Smirnov and Runs statistical tests, as well as the ENT test suite analysis. The Kolmogorov–Smirnov test compares the sample distribution with a theoretical uniform distribution, while the Runs test examines the sequence for randomness. Table 4 shows the p-value obtained for each bit precision. Since all p-values are greater than or equal to the significance level of , the sequence generated by the digital circuit passes these tests.
The ENT test suite [37] is a tool that has been extensively used [38,39]. By running six different statistical tests, the tool provides a reliable measure of quality for compression algorithms, pseudo-random number generators for use in statistical sampling, and encryption applications. The six tests include Entropy, Optimum compression, distribution, Arithmetic mean, Monte Carlo value for , and Serial correlation coefficient tests. The results obtained are shown in Table 5. Since the bit-stream of the map passed all tests for different precision formats, we concluded that the map could generate pseudo-random numbers.

Table 5.
The results of the ENT test suite for our digital tent map. The value in brackets is the expected value in each test.
Thus, the digital chaotic circuit can serve as a PRNG. As Herring and Palmore [40] demonstrated, PRNGs are chaotic systems and vice versa. Since the circuit can function as a pseudo-random number generator, we will demonstrate a simple application of our digital circuit for a statistical sampling in a particle swarm optimization hardware architecture.
3.2. Hardware Architecture for Particle Swarm Optimization
Optimization techniques have been employed over the years, as shown by [41,42,43,44,45,46,47,48]. Such a topic is important in engineering and computer science since the technique allows the best location of resources [49,50,51]. The mono-objective optimization problems rely on finding a point, in a space of innumerable optimization variables, in which the objective function achieves its minimum solution [49].
A mono-objective optimization problem can be stated as
where is the optimum point of the fitness function , and and are the constraints.
One approach to solve optimization problems are metaheuristic algorithms. Particularly, such algorithms can solve many complex problems. Moreover, they are practical since they can find approximately optimal solutions in reasonable times [52].
A classical metaheuristic algorithm is particle swarm optimization (PSO) [53]. PSO is a method that uses a population of candidate solutions, namely particles, where each particle i moves in the search space to find the most promising area. Such an algorithm uses a velocity vector to update the position of each particle. The position of each particle is updated based on population social behavior, i.e., the swarm of particles [51]. From iteration to iteration, each particle i advances in the direction of its previous local best () and the best global position () of the swarm.
The velocity and position of each particle i are updated by Equations (10) and (11), respectively [54]:
where j is the current iteration, is the inertia weight, and are acceleration coefficients, and are two independently uniform random numbers within range of , and P is the total number of particles. Algorithm 1 summarizes the steps performed in a particle swarm optimization.
One topic that has been discussed is the utilization of chaos theory on PSO [55,56,57]. There are several ways to apply chaos on PSO to improve the local search in the algorithm [58]. In this case, the chaotic properties of the proposed digital tent map are used for generating pseudo-random numbers. For such a task, a well-known hardware architecture of the parallel PSO is employed based on [25].
| Algorithm 1: Particle Swarm Optimization |
 |
Figure 4a shows the general hardware architecture used. This architecture was assembled in a parallel approach to improve running speed. It uses floating-point arithmetic to obtain a dynamic range for representing large and small numbers and is divided into five components: the FSM (Finite State Machine), the swarm unit, the evaluation unit, and the individual and global best detection units. While the FSM synchronizes the hardware operation, the swarm unit is responsible for updating the velocity and the position of each particle, according to Equations (10) and (11). Figure 4b illustrates how the velocity and position of the particle are updated. The architecture is executed in five states, and in each state, all the operations are computed simultaneously. The architecture comprises just one floating-point multiplier, one floating-point adder/subtractor, and our digital tent map. To avoid using two more multipliers, instead of the tent map generating uniform random numbers within a range of , the digital circuit generates uniform random numbers within a range of and . Additionally, as the proposed digital tent map performs the operations using fixed-point arithmetic, a fixed-to-float converter is applied to match the specified conditions of the hardware architecture for particle swarm optimization.
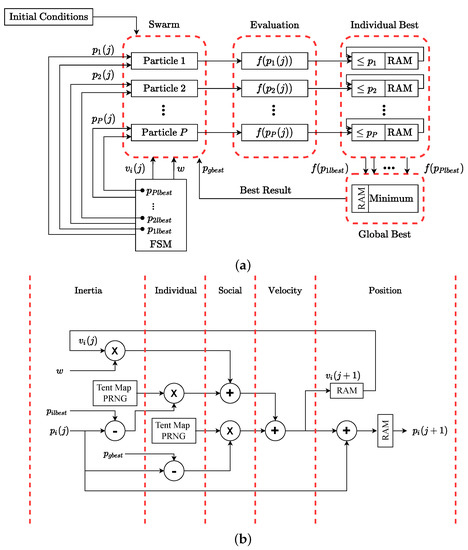
Figure 4.
Implemented architecture. (a) Hardware architecture for particle swarm optimization. (b) Particle architecture which uses our digital tent map. Adapted with permission from ref. [25]. 2023, IEEE.
The evaluation unit carries out the fitness function evaluation. In this task, the hardware architecture was tested using benchmark functions applied in the literature. The chosen ones are the Sphere and Rosenbrock functions, where each one imposes different scenarios also found in real problems. The Sphere function is a unimodal and convex one, its domain is , for all , and the global minimum is at the position . The Sphere function is defined as [59]
The Rosenbrock function is a typical non-convex and a multimodal function, its domain is , for all , and the global minimum is at the position . The Rosenbrock function is defined as [60]
The best individual unit is responsible to determine if the current fitness value of each particle is lower than its respective best fitness value. Thus, if , the best particle position of the particle i is updated and stored in RAM.
Lastly, the global best unit concludes what the minimum value among all the P best fitness values is. Hence, if , the best global position is updated and stored in RAM. It is important to note that these values are not effectively stored in a Block RAM (BRAM). The RAMs shown in Figure 4a,b are based on Flip-Flops.
We implemented the hardware architecture using the IEEE standard for floating-point arithmetic (IEEE 754) [61] with a bit-width of 27 bits. This bit-width consists of 1 bit for the signal, 8 bits for the biased exponent, and 18 bits for the mantissa. Our digital tent map was configured to generate pseudorandom numbers with a bit-width of 20 bits. We based this configuration on the same guidelines the authors in [25] used since this architecture presents the best trade-off between the FPGA resources used and the PSO algorithm’s response. Moreover, it is important to highlight that the digital tent map produces a pseudo-random number at every clock cycle, so it has no impact on the latency of the proposed particle architecture [25]. Using the proposed digital chaotic map as PRNG improves the performance of the PSO algorithm since previously an LFSR (Linear-Feedback Shift Register) was used as a source for generating random numbers, a technique that has serious drawbacks such as self-correlation and the possibility to reconstruct the parameters from a sequence of outputs [62].
Table 6 shows the synthesis results of the implemented hardware for particle swarm optimization. Using the low-cost Artix 7—XC7A100TFGG676-3, we can embed this optimization technique efficiently.

Table 6.
Implementation results in the PSO design.
The hardware architecture for particle swarm optimization using our digital tent map as a source of pseudo-random numbers was validated using particles to optimize problems with dimensions. Table 7 exhibits the parameter set used in the experiment. Note the linear decrease in the inertia weight, which aims to refine the final solution and improve the convergence results. We also chose the initial and maximum velocities so that they did not cause the particle to leave the search space.

Table 7.
Parameters used in the experiment to validate the proposed digital tent map as a pseudo-random number generator in a hardware architecture for particle swarm optimization.
All the benchmark functions were optimized 16 times, with each run using distinct initial particle positions. This design ensured the preservation of swarm diversity, convergence, and quality of results, as it allowed us to estimate the global minimum of these benchmark functions in each run. Table 8 summarizes the results obtained.

Table 8.
Convergence results in the PSO design.
Ultimately, it is certainly important to mention that a crucial point of this application is the numerical conversion of the random number generated in fixed-point to floating-point format. As there is a nonlinearity present in such conversion, the numbers generated by the tent map could lose their random characteristics. However, this is not the case. After the fixed to float-point conversion, we applied just the Kolmogorov–Smirnov and Runs tests to ensure the generated sequence is pseudo-random and uniform. The p-values obtained for each test are and , respectively, for . Thus, as , the proposed digital tent map kept its uniform distribution and pseudorandom feature after conversion, as well as helped the PSO hardware performance.
4. Conclusions
This paper presents a hardware-efficient perturbation method for a simple digital tent map. By adopting the 1’s complement fixed-point numerical representation, a straightforward and flexible digital chaotic map architecture was designed and implemented on an FPGA. Only 33 components (16 XOR gates, 1 multiplexer, and 16 D-type flip-flops) were required to implement the 16-bit precision version, resulting in a significant reduction of at least 60% compared to the state-of-the-art references. To the best of the authors’ knowledge, there is no other digital chaotic map that requires fewer components. The perturbation method used at the logic-gate level is less demanding from a hardware perspective, and the use of an XOR gate is sufficient to prevent the dynamical degradation of the digital tent map. Results indicate that the chaotic and statistical properties of the system are preserved, as demonstrated by the largest Lyapunov exponent, return map, time series, histogram plot, and autocorrelation function.
Furthermore, the validation of the digital tent map as a pseudo-random number generator was confirmed through the one-sample Kolmogorov–Smirnov test, Runs test, and ENT test suite. This article showcases the practical application of the digital chaotic system in generating pseudo-random numbers, utilizing chaos as an effective tool in the hardware architecture for particle swarm optimization.
Looking ahead, the authors aim to continue exploring new and innovative avenues in the field of digital chaos. Specifically, we plan to study new maps and perturbation methods that can be designed as efficient hardware architectures similar to what has been done in [63]. Additionally, we will investigate the scalability of the digital map and seek out new optimization techniques that can be integrated into the system. Through these efforts, the authors aim to push the boundaries of what is possible in the realm of digital chaotic systems and contribute to the ongoing development of this exciting and rapidly evolving field.
Author Contributions
Conceptualization, L.N., E.N. and J.A.-G.; data curation, L.N. and D.M.; formal analysis, E.N., D.M., D.B. and J.A.-G.; funding acquisition, L.N., E.N. and D.B.; investigation, L.N.; methodology, L.N., E.N., D.B. and J.A.-G.; project administration, J.A.-G.; resources, D.M., D.B. and J.A.-G.; software, L.N. and D.M.; supervision, E.N. and J.A.-G.; validation, E.N. and J.A.-G.; writing—original draft, L.N.; writing—review and editing, E.N., D.M., D.B. and J.A.-G. All authors have read and agreed to the published version of the manuscript.
Funding
Lucas Nardo was partly supported by FAPEMIG and by the Coordination for the Improvement of Higher Education Personnel—Brazil (CAPES)—Finance Code 001. Erivelton Nepomuceno, Ph.D., was supported by Brazilian Research Agencies, including CNPq (Grant Nos. 465704/2014-0, 425509/2018-4 and 311321/2020-8) and FAPEMIG (Grant No. APQ-00870-17). Denis Butusov, Ph.D., was supported by Russian Science Foundation (Grant No. 22-19-00573).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author. Alternatively, the reader can access all the algorithms and routines used in this paper in https://osf.io/xt5wj/(accessed on 17 April 2023).
Acknowledgments
The authors would like to thank the Xilinx University Program (XUP) for the software licenses provided, Lucas J. C. Carvalho and Roberto M. P. Júnior for their valuable advice about optimization problems, and Iain McLeod for his pertinent comments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 1D | One-Dimensional |
| BRAM | Block RAM |
| DSP | Digital Signal Processing |
| FF | Flip-Flop |
| FPGA | Field-Programmable Gate Array |
| FSM | Finite State Machine |
| IEEE | Institute of Electrical and Electronics Engineers |
| LFSR | Linear-Feedback Shift Register |
| LUT | Look-Up Table |
| PRNG | Pseudo-Random Number Generator |
| PSO | Particle Swarm Optimization |
| RAM | Random-Access Memory |
| VHDL | VHSIC Hardware Description Language |
| VHSIC | Very High-Speed Integrated Circuit |
References
- Wang, Q.; Yu, S.; Li, C.; Lu, J.; Fang, X.; Guyeux, C.; Bahi, J.M. Theoretical design and FPGA-based implementation of higher-dimensional digital chaotic systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 401–412. [Google Scholar] [CrossRef]
- de la Fraga, L.G.; Torres-Pérez, E.; Tlelo-Cuautle, E.; Mancillas-López, C. Hardware implementation of pseudo-random number generators based on chaotic maps. Nonlinear Dyn. 2017, 90, 1661–1670. [Google Scholar] [CrossRef]
- Sreenath, H.; Narayanan, G. FPGA implementation of pseudo chaos-signal generator for secure communication systems. In Proceedings of the 2018 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Bangalore, India, 19–22 September 2018; pp. 804–807. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Arias-Garcia, J.; Butusov, D.N. Image encryption using finite-precision error. Chaos Solitons Fractals 2019, 123, 69–78. [Google Scholar] [CrossRef]
- Souza, C.E.C.; Pimentel, C.; Chaves, D.P.B. A symbolic dynamics approach to trellis-coded chaotic modulation. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2189–2193. [Google Scholar] [CrossRef]
- Dridi, F.; Assad, S.E.; Youssef, W.E.H.; Machhout, M.; Lozi, R. The design and FPGA-based implementation of a stream cipher based on a secure chaotic generator. Appl. Sci. 2021, 11, 625. [Google Scholar] [CrossRef]
- Lin, C.H.; Hu, G.H.; Chan, C.Y.; Yan, J.J. Chaos-based synchronized dynamic keys and their application to image encryption with an improved AES algorithm. Appl. Sci. 2021, 11, 1329. [Google Scholar] [CrossRef]
- Cardoso, M.B.R.; da Silva, S.S.; Nardo, L.G.; Passos, R.M.; Nepomuceno, E.G.; Arias-Garcia, J. A new PRNG hardware architecture based on an exponential chaotic map. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Korea, 22–28 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Bastos, G.T.; Santos, T.A.; Butusov, D.N.; Arias-Garcia, J. A reliable chaos-based cryptography using Galois field. Chaos 2021, 31, 091101. [Google Scholar] [CrossRef]
- Salunke, S.; Shrivastava, A.K.; Hashmi, M.F.; Ahuja, B.; Bokde, N.D. Quad key-secured 3D Gauss encryption compression system with Lyapunov exponent validation for digital images. Appl. Sci. 2023, 13, 1616. [Google Scholar] [CrossRef]
- da Silva, S.S.; Cardoso, M.; Nardo, L.; Nepomuceno, E.; Hubner, M.; Arias-Garcia, J. A new chaos-based PRNG hardware architecture using the HUB fixed-point format. IEEE Trans. Instrum. Meas. 2023, 72, 1–8. [Google Scholar] [CrossRef]
- Yao, L.; Zhao, J.; Qian, J. An improved pseudo-random binary sequence design for multivariable system identification (A16-395). In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; pp. 1768–1772. [Google Scholar] [CrossRef]
- Ismail, S.M.; Said, L.A.; Radwan, A.G.; Madian, A.H.; Abu-Elyazeed, M.F. Generalized double-humped logistic map-based medical image encryption. J. Adv. Res. 2018, 10, 85–98. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C.; Tan, W.; Li, L. A novel chaos-based image encryption scheme by using randomly DNA encode and plaintext related permutation. Appl. Sci. 2020, 10, 7469. [Google Scholar] [CrossRef]
- Li, S.; Chen, G.; Mou, X. On the dynamical degradation of digital piecewise linear chaotic maps. Int. J. Bifurc. Chaos 2005, 15, 3119–3151. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, Y.; Song, S.; Cao, L.; Liu, J.; Harkin, J. Counteracting dynamical degradation of digital chaotic Chebyshev map via perturbation. Int. J. Bifurc. Chaos 2017, 27, 1750033. [Google Scholar] [CrossRef]
- Cao, L.C.; Luo, Y.L.; Qiu, S.H.; Liu, J.X. A perturbation method to the tent map based on Lyapunov exponent and its application. Chin. Phys. B 2015, 24, 100501. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Banerjee, S. A Route to Chaos Using FPGAs; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Nepomuceno, E.G.; Lima, A.M.; Arias-García, J.; Perc, M.; Repnik, R. Minimal digital chaotic system. Chaos Solitons Fractals 2019, 120, 62–66. [Google Scholar] [CrossRef]
- Brock, W. Distinguishing random and deterministic systems: Abridged version. J. Econ. Theory 1986, 40, 168–195. [Google Scholar] [CrossRef]
- Khani, F.; Ahmadi, A. Digital realization of twisted tent map and ship map with LFSR as a pseudo-chaos generator. In Proceedings of the ICCKE 2013, Mashhad, Iran, 31 October–1 November 2013; pp. 207–212. [Google Scholar] [CrossRef]
- Wang, H.; Song, B.; Liu, Q.; Pan, J.; Ding, Q. FPGA design and applicable analysis of discrete chaotic maps. Int. J. Bifurc. Chaos 2014, 24, 1450054. [Google Scholar] [CrossRef]
- Öztürk, I.; Kılıç, R. Digitally generating true orbits of binary shift chaotic maps and their conjugates. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 395–408. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Arboleda, D.M.M.; Llanos, C.H.; dos S. Coelho, L.; Ayala-Rincón, M. Hardware architecture for particle swarm optimization using floating-point arithmetic. In Proceedings of the 2009 Ninth International Conference on Intelligent Systems Design and Applications, Pisa, Italy, 30 November–2 December 2009; pp. 243–248. [CrossRef]
- Garcés, H.; Flores, B.C. Statistical analysis of Bernoulli, logistic, and tent maps with applications to radar signal design. In Proceedings of the Radar Sensor Technology X. SPIE, Orlando, FL, USA, 8 May 2006; pp. 152–161. [Google Scholar]
- Li, C.; Luo, G.; Qin, K.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Kaur, G.; Arora, S. Chaotic whale optimization algorithm. J. Comput. Des. Eng. 2018, 5, 275–284. [Google Scholar] [CrossRef]
- Crampin, M.; Heal, B. On the chaotic behaviour of the tent map. Teach. Math. Appl. 1994, 13, 83–89. [Google Scholar] [CrossRef]
- Parhami, B. Computer Arithmetic: Algorithms and Hardware Designs; Oxford University Press, Inc.: Oxford, UK, 1999. [Google Scholar]
- Wang, X.Y.; Wang, L.L. A new perturbation method to the tent map and its application. Chin. Phys. B 2011, 20, 050509. [Google Scholar] [CrossRef]
- Jeoti, V.; Khan, M.A. On the enlargement of robust region of chaotic tent map for the use in key based substitution-box (S-Box). J. Comput. Sci. 2015, 11, 517–525. [Google Scholar] [CrossRef][Green Version]
- Jallouli, O.; Assad, S.E.; Chetto, M.; Lozi, R.; Caragata, D. A novel chaotic generator based on weakly-coupled discrete skewtent maps. In Proceedings of the 2015 10th International Conference for Internet Technology and Secured Transactions (ICITST), London, UK, 14–16 December 2015; pp. 38–43. [Google Scholar] [CrossRef]
- Sankpal, P.R.; Vijaya, P.A. Fusion implementation of security mechanisms for secured transmission of images. In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Kodba, S.; Perc, M.; Marhl, M. Detecting chaos from a time series. Eur. J. Phys. 2005, 26, 205–215. [Google Scholar] [CrossRef]
- Baranovsky, A.; Daems, D. Design of one-dimensional chaotic maps with prescribed statistical properties. Int. J. Bifurc. Chaos 1995, 5, 1585–1598. [Google Scholar] [CrossRef]
- Walker, J. ENT: A Pseudorandom Number Sequence Test Program. 2008. Available online: https://www.fourmilab.ch/random/ (accessed on 17 April 2023).
- Stoyanov, B.; Kordov, K. Novel image encryption scheme based on Chebyshev polynomial and Duffing map. Sci. World J. 2014, 2014, 283639. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Qian, S.; Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Deng, Z.; Li, Y.; Du, S. Pseudorandom number generator based on three kinds of four-wing memristive hyperchaotic system and its application in image encryption. Complexity 2020, 2020, 8274685. [Google Scholar] [CrossRef]
- Herring, C.; Palmore, J.I. Random number generators are chaotic. ACM SIGPLAN Not. 1989, 24, 76–79. [Google Scholar] [CrossRef]
- Censor, Y. Pareto optimality in multiobjective problems. Appl. Math. Optim. 1977, 4, 41–59. [Google Scholar] [CrossRef]
- Sakawa, M. Multiobjective reliability and redundancy optimization of a series-parallel system by the Surrogate Worth Trade-off method. Microelectron. Reliab. 1978, 17, 465–467. [Google Scholar] [CrossRef]
- Yi, W.; Zhang, Y.; Zhao, Z.; Huang, Y. Multiobjective robust scheduling for smart distribution grids: Considering renewable energy and demand response uncertainty. IEEE Access 2018, 6, 45715–45723. [Google Scholar] [CrossRef]
- Chen, J.; Du, T.; Xiao, G. A multi-objective optimization for resource allocation of emergent demands in cloud computing. J. Cloud Comput. 2021, 10, 20. [Google Scholar] [CrossRef]
- Qin, X.; Liu, Z.; Liu, Y.; Liu, S.; Yang, B.; Yin, L.; Liu, M.; Zheng, W. User OCEAN personality model construction method using a BP neural network. Electronics 2022, 11, 3022. [Google Scholar] [CrossRef]
- Sun, R.; Fu, L.; Cheng, Q.; Chiang, K.W.; Chen, W. Resilient pseudorange error prediction and correction for GNSS positioning in urban areas. IEEE Internet of Things J. 2023, 1–11. [Google Scholar] [CrossRef]
- Liu, M.; Gu, Q.; Yang, B.; Yin, Z.; Liu, S.; Yin, L.; Zheng, W. Kinematics model optimization algorithm for six degrees of freedom parallel platform. Appl. Sci. 2023, 13, 3082. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Y.; Wang, H.; Xu, K. ASRO-DIO: Active subspace random optimization based depth inertial odometry. IEEE Trans. Robot. 2023, 39, 1496–1508. [Google Scholar] [CrossRef]
- Carrano, E.; Soares, L.; Takahashi, R.; Saldanha, R.; Neto, O. Electric distribution network multiobjective design using a problem-specific genetic algorithm. IEEE Trans. Power Deliv. 2006, 21, 995–1005. [Google Scholar] [CrossRef]
- Liu, L.; Chang, Z.; Guo, X.; Mao, S.; Ristaniemi, T. Multiobjective optimization for computation offloading in fog computing. IEEE Internet Things J. 2018, 5, 283–294. [Google Scholar] [CrossRef]
- Costa, A.L.X.D.; Silva, C.A.D.; Torquato, M.F.; Fernandes, M.A.C. Parallel implementation of particle swarm optimization on FPGA. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1875–1879. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Dong, N.; Fang, X.; guo Wu, A. A novel chaotic particle swarm optimization algorithm for parking space guidance. Math. Probl. Eng. 2016, 2016, 5126808. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, L.; Wang, B.; Wang, Z.; Shafie-khan, M.; Catalão, J. Modified chaos particle swarm optimization-based optimized operation model for stand-alone CCHP microgrid. Appl. Sci. 2017, 7, 754. [Google Scholar] [CrossRef]
- Zhu, T.; Zheng, H.; Ma, Z. A chaotic particle swarm optimization algorithm for solving optimal power system problem of electric vehicle. Adv. Mech. Eng. 2019, 11, 168781401983350. [Google Scholar] [CrossRef]
- Liu, B.; Wang, L.; Jin, Y.H.; Tang, F.; Huang, D.X. Improved particle swarm optimization combined with chaos. Chaos Solitons Fractals 2005, 25, 1261–1271. [Google Scholar] [CrossRef]
- Stacey, A.; Jancic, M.; Grundy, I. Particle swarm optimization with mutation. In Proceedings of the 2003 Congress on Evolutionary Computation (CEC ’03), Canberra, ACT, Australia, 8–12 December 2003; Volume 2, pp. 1425–1430. [Google Scholar] [CrossRef]
- Dixon, L.C.W.; Mills, D.J. Effect of rounding errors on the variable metric method. J. Optim. Theory Appl. 1994, 80, 175–179. [Google Scholar] [CrossRef]
- IEEE Std 754-2019 (Revision of IEEE 754-2008); IEEE Standard for Floating-Point Arithmetic. Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2019; pp. 1–84. [CrossRef]
- Singh, S.K.; Gupta, M.D.; Mani, S.; Chauhan, R.K. Design of LFSR circuit based on high performance XOR gate. In Proceedings of the 2020 International Conference on Electrical and Electronics Engineering (ICE3), Gorakhpur, India, 14–15 February 2020; pp. 656–660. [Google Scholar] [CrossRef]
- Liu, J.; Liang, Z.; Luo, Y.; Cao, L.; Zhang, S.; Wang, Y.; Yang, S. A hardware pseudo-random number generator using stochastic computing and logistic map. Micromachines 2020, 12, 31. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).