The Impact of Data Quality on Software Testing Effort Prediction
Abstract
1. Introduction
- RP1: The performance of particular models for testing effort prediction—This involved creating a ranking of models based on a comparison of prediction accuracy between the models, both for each data variant and across all of them. In addition, the performance of models for various conditions reflected in training data variants was explored.
- RP1A: The stability of performance of models across passes—As a follow-up to the RP1, this was motivated by previous analyses that investigated a different outcome attribute [18], and which revealed the fluctuating performance of most predictive models depends on a particular iteration of data split into CV and test subset.
- RP2: Identification of good and poor data variants for particular models for testing effort prediction—This involved ranking data variants, based on comparing prediction accuracy achieved with various training data variants for each predictive model.
- RP2A: The stability of performance of data variants for particular models between CV and test data subsets—As a follow-up to the RP2, this involved investigating whether the data variants that delivered predictions at the specific rank (accurate or inaccurate) for particular models in the cross-validation subphase also delivered a similar rank of predictive accuracy on the test data subset. This was investigated for each model in each pass.
- RP3: Identification of the best combinations of models and data variants— Investigation of the previous RPs delivered partial answers, as they focused on identifying the best-performing models for given data variants and best-performing data variants for given models. For a complete picture, it was also necessary to identify the best combinations of models and data variants.
2. Materials and Methods
2.1. Overview of the Research Process
- Data preprocessing—Section 2.2; the outcome of this phase, i.e., a prepared dataset—Section 2.3;
- Preparation of the environment—Section 2.4; the outcomes of this phase, i.e., the definitions of data variants–Section 2.5, predictive models—Section 2.6, hyperparameter tuning grids—Section 2.7;
- Model training and evaluation—Section 2.8;
- Analysis of results—Section 2.9.
2.2. Data Preprocessing

- Effort Test > 0—the outcome value for prediction must be known;
- Resource Level = 1—only development team effort was included for effort-related attributes;
- Count Approach = ‘IFPUG 4+’—projects in which size was estimated using IFPUG 4+ technique;
- Adjusted Function Points != NA—projects with no missing values for Adjusted Function Points, because it was not reasonable to predict effort without data on project size.
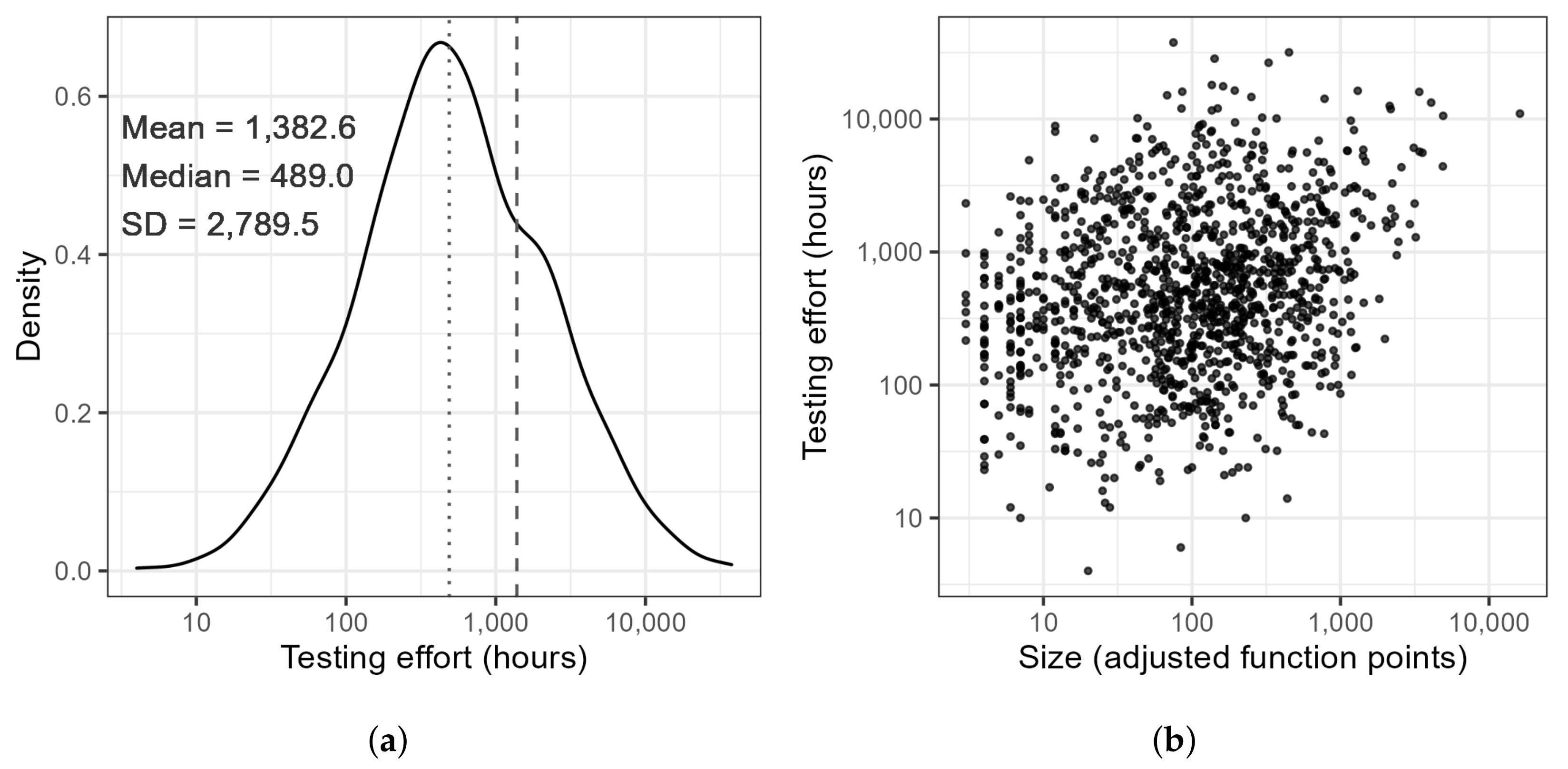
2.3. Prepared ISBSG Dataset
2.4. Preparation of the Environment
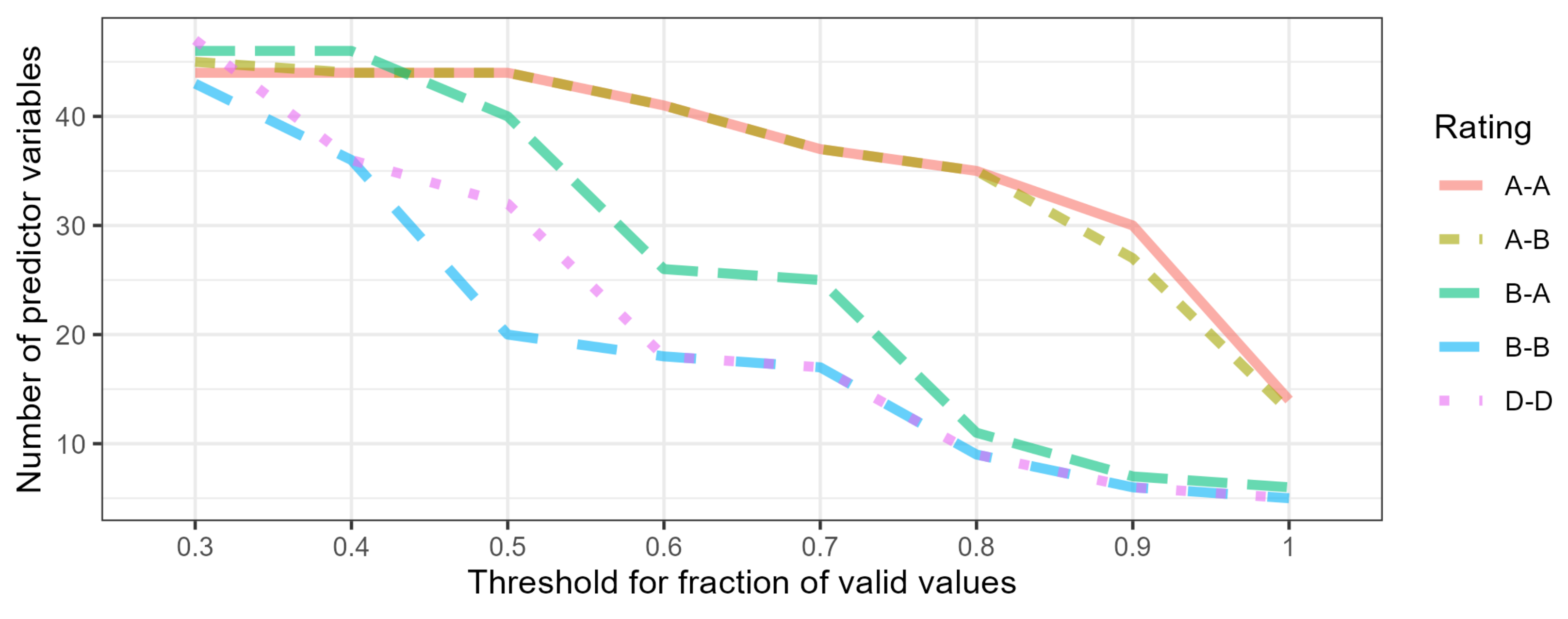
2.5. Data Variants
- A-A: ,
- A-B: ,
- B-A: ,
- B-B: ,
- D-D: .
2.6. Predictive Models
| Model | Description | Data Type | Log Outcome | Log Predictors 1 | Impute by Mode 2 | Impute by Median 3 | Normalize | PCA 4 |
|---|---|---|---|---|---|---|---|---|
| bMean | baseline model predicting | regular | + | – | – | – | – | – |
| bMed | baseline model predicting | regular | + | – | – | – | – | – |
| bR | baseline model predicting a random value from | regular | – | – | – | – | – | – |
| bRU | baseline model predicting a random value from | regular | + | – | – | – | – | – |
| enet | elastic net [34] | numeric | + | + | + | + | + | – |
| gbm | generalized boosted regression [35] | numeric | – | + | + | + | + | + |
| glmnet | generalized linear regression with convex penalties [36] | numeric | – | + | + | + | + | – |
| knn | k-nearest neighbour regression [37] | numeric | – | + | + | + | + | + |
| lm | linear regression [38] | numeric | + | + | + | + | + | + |
| lmStepAIC | linear regression model with stepwise feature selection [39] | numeric | + | + | + | + | + | – |
| M5 | model trees and rule learner [40,41] | numeric | – | + | + | + | + | + |
| nnet | neural network with one hidden layer [42] | numeric | + | + | + | + | + | – |
| ranger | random forest [43] | regular | – | + | + | + | – | – |
| rpart2 | recursive partitioning and regression tree [44] | regular | – | + | + | + | – | – |
| svm | support vector machines [45] | numeric | + | + | + | + | + | + |
| xgbTree | extreme gradient boosting [46] | numeric | – | + | – | – | – | – |
2.7. Hyperparameter Tuning Grids
2.8. Model Training and Evaluation
- filter training data by Data Quality Rating and UFP Rating, according to the current data variant;
- remove attributes not meeting the threshold according to the current data variant;
- apply missing value imputation by median (according to the current model definition);
- apply missing value imputation by mode (according to the current model definition);
- group together least frequent states ( i.e., states with frequency < 0.03 of all cases) of nominal predictors as state ’other’;
- convert nominal attributes to dummy attributes (if the current model requires numeric data);
- remove attributes with zero variance;
- log-transform outcome attribute (according to the current model definition);
- log-transform numeric predictors (according to the current model definition);
- normalize numeric attributes (according to the current model definition);
- apply PCA transformation (according to the current model definition);
- prepare the model;
- save data preparation definitions;
- generate hyperparameter grid.
2.9. Analysis of Results
3. Results
3.1. RP1: The Performance of Particular Models for Testing Effort Prediction
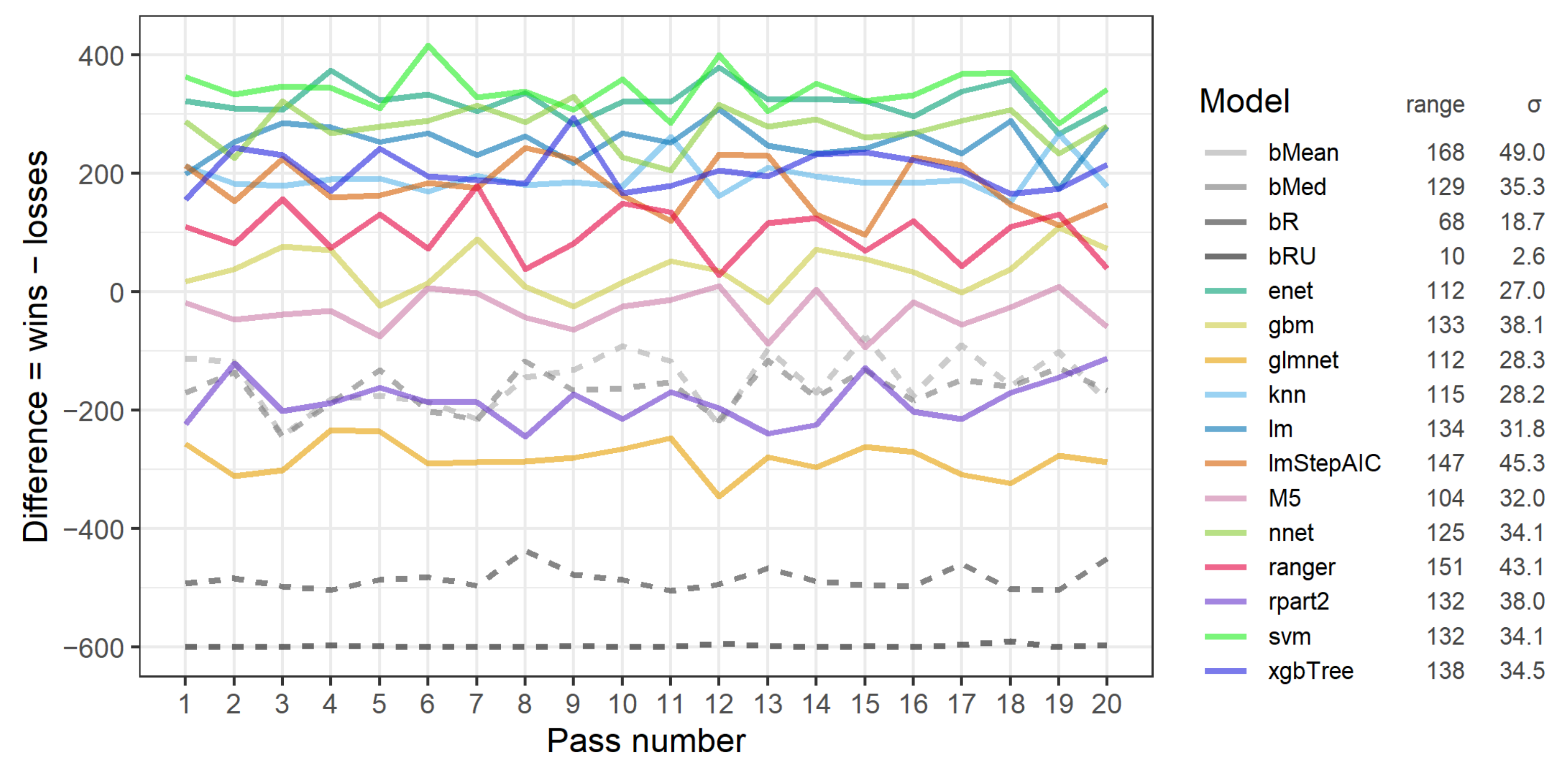
3.2. RP1A: The Stability of Performance of Models across Passes
3.3. RP2: Identification of Good and Poor Data Variants for Particular Models
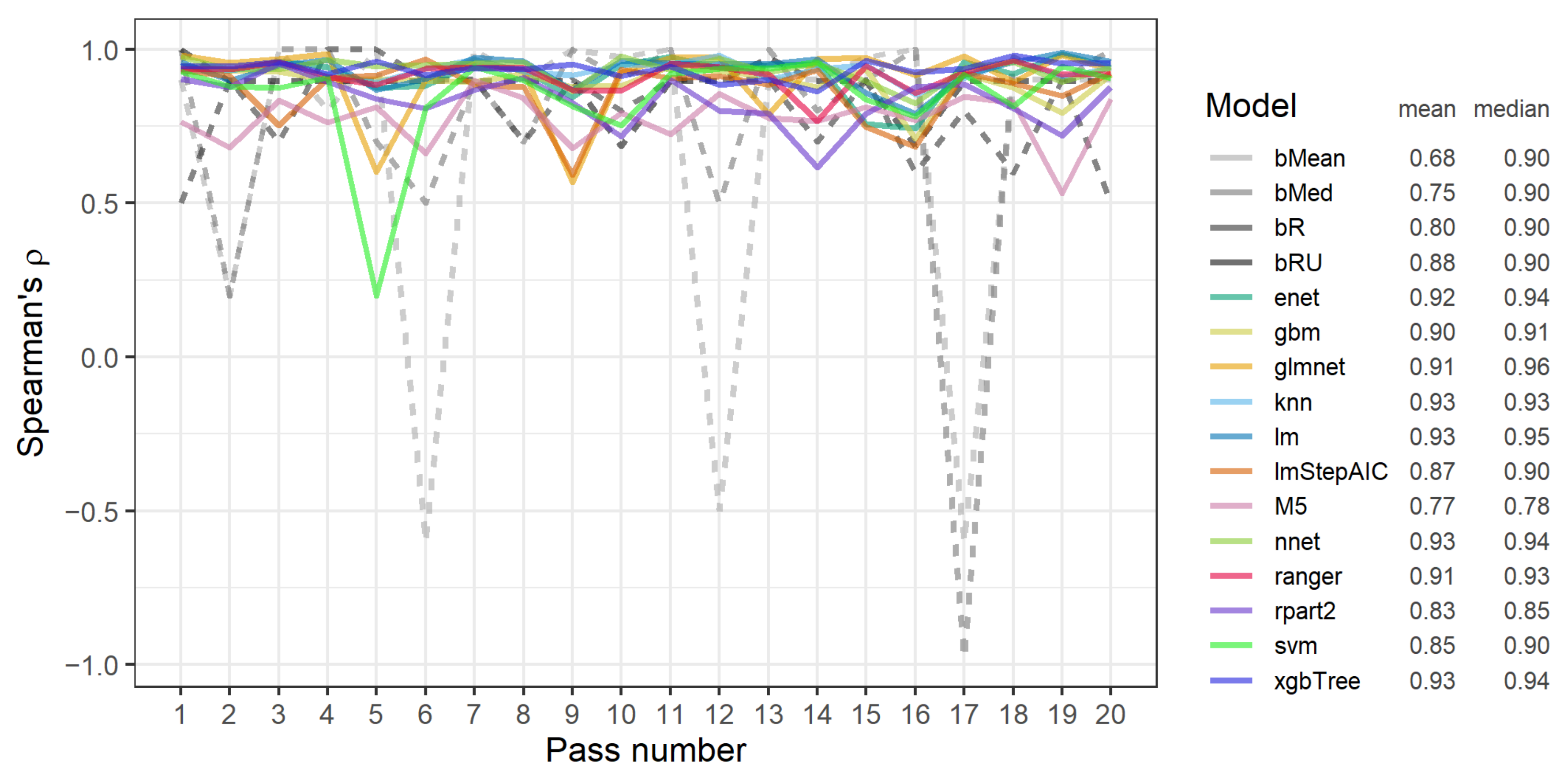
3.4. RP2A: The Stability of Performance of Data Variants between CV and Test Data Subsets
3.5. RP3: Identification of the Best Combinations of Models and Data Variants
4. Discussion
4.1. Experimental Results
4.2. Related Work
4.3. Utilizing the Results
4.4. Threats to Validity
4.5. Future Work
5. Conclusions
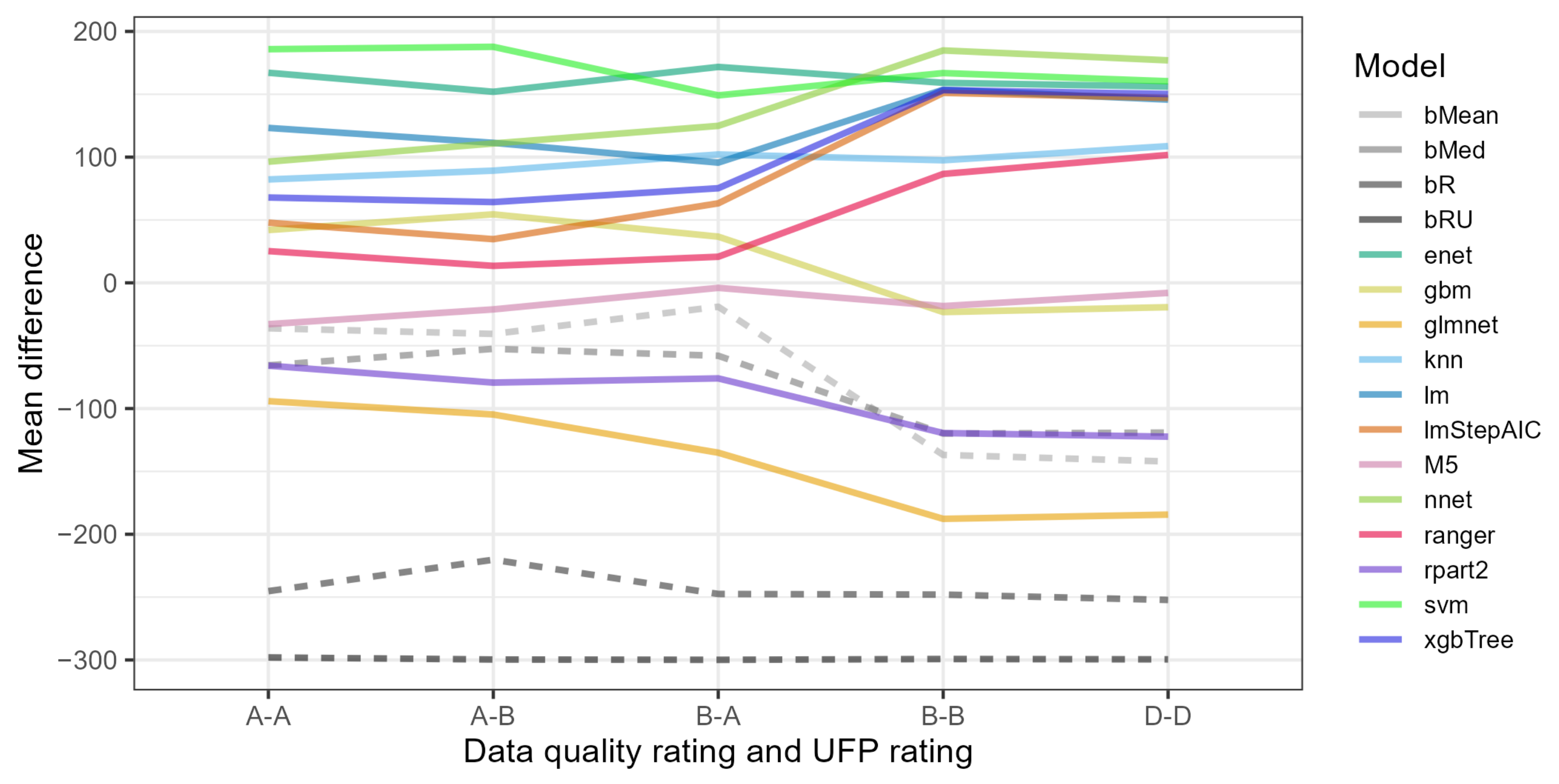
- Among the best three models overall, the svm (support vector machines) performed the best for the most restrictive ratings A-A and A-B, enet (elastic net) performed the best for ratings B-A, and nnet (neural network) performed the best for the least restrictive ratings B-B and D-D.
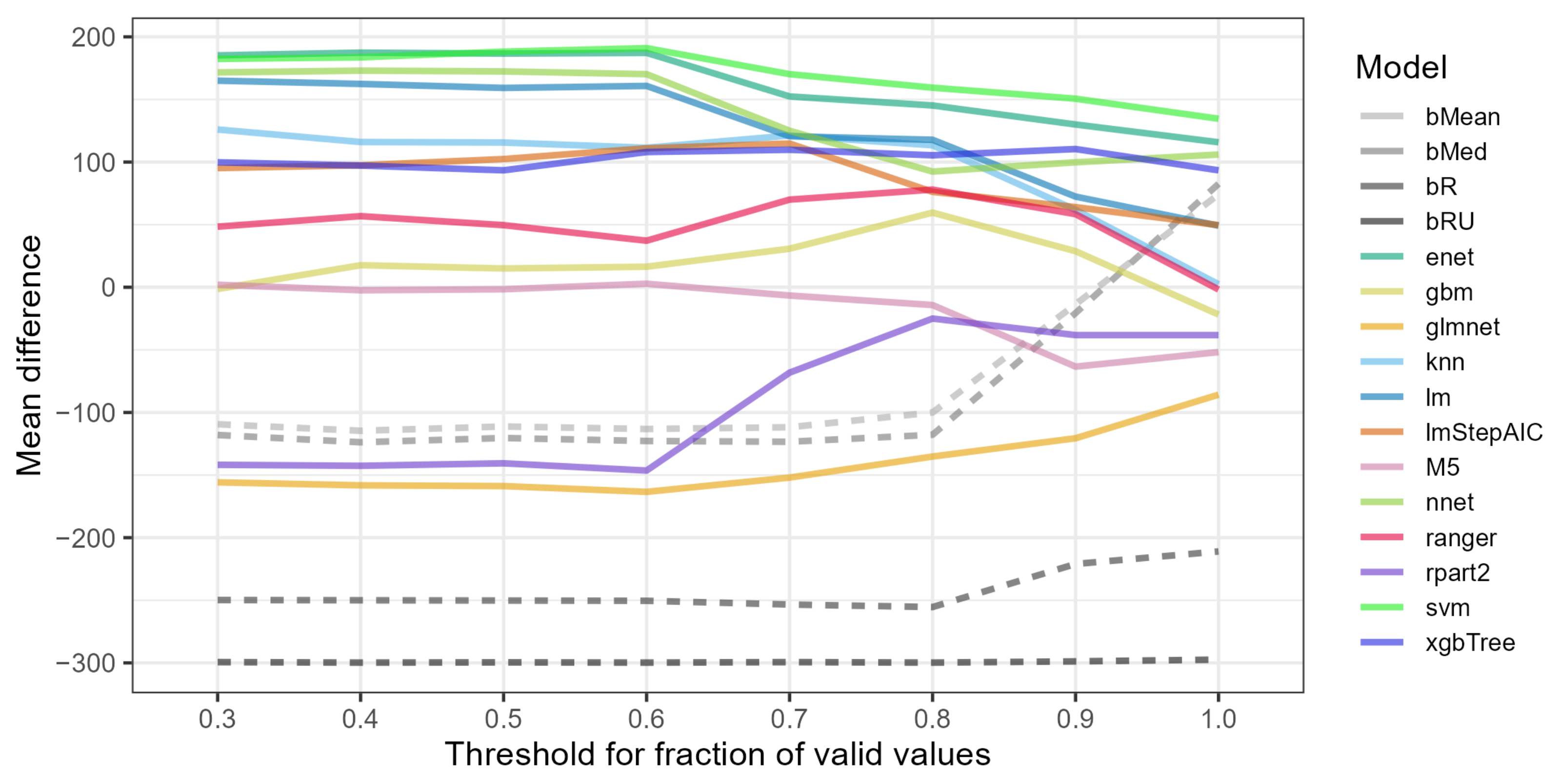
- Using restrictive data variants, i.e., involving ratings A-A, A-B or B-A that reduced the number of rows (projects) and high thresholds of valid values of 1.0 or 0.9, led to poor performance of most models.
- Most models, especially the most accurate, performed the best with data variants using ratings D-D. The performance of most models on data variants with ratings B-B was lower.
- No global optimum threshold of valid values common for all models was detected as it was specific for a particular model.
- The relative rank of models for particular groups of data variants, including only particular data ratings or only thresholds of valid values, was quite stable.
- Performance of data variants for most models and most passes, excluding less than ten exceptions, was stable between CV and test subsets.
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wen, J.; Li, S.; Lin, Z.; Hu, Y.; Huang, C. Systematic literature review of machine learning based software development effort estimation models. Inf. Softw. Technol. 2012, 54, 41–59. [Google Scholar] [CrossRef]
- Jorgensen, M.; Shepperd, M. A Systematic Review of Software Development Cost Estimation Studies. IEEE Trans. Softw. Eng. 2007, 33, 33–53. [Google Scholar] [CrossRef]
- Ali, A.; Gravino, C. A systematic literature review of software effort prediction using machine learning methods. J. Softw. Evol. Process. 2019, 31, e2211. [Google Scholar] [CrossRef]
- Eduardo Carbonera, C.; Farias, K.; Bischoff, V. Software development effort estimation: A systematic mapping study. IET Softw. 2020, 14, 328–344. [Google Scholar] [CrossRef]
- Mahmood, Y.; Kama, N.; Azmi, A.; Khan, A.S.; Ali, M. Software effort estimation accuracy prediction of machine learning techniques: A systematic performance evaluation. Softw. Pract. Exp. 2022, 52, 39–65. [Google Scholar] [CrossRef]
- Bluemke, I.; Malanowska, A. Software Testing Effort Estimation and Related Problems: A Systematic Literature Review. ACM Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- López-Martín, C. Machine learning techniques for software testing effort prediction. Softw. Qual. J. 2022, 30, 65–100. [Google Scholar] [CrossRef]
- ISBSG. ISBSG Repository Data Release 2020 R1; International Software Benchmarking Standards Group: Melbourne, Australia, 2020. [Google Scholar]
- ISBSG. Guidelines for Use of the ISBSG Data; International Software Benchmarking Standards Group: Melbourne, Australia, 2020. [Google Scholar]
- López-Martín, C. Predictive accuracy comparison between neural networks and statistical regression for development effort of software projects. Appl. Soft Comput. 2015, 27, 434–449. [Google Scholar] [CrossRef]
- Mendes, E.; Lokan, C.; Harrison, R.; Triggs, C. A Replicated Comparison of Cross-Company and Within-Company Effort Estimation Models Using the ISBSG Database. In Proceedings of the 11th IEEE International Software Metrics Symposium (METRICS’05), Como, Italy, 19–22 September 2005; IEEE: Piscataway, NJ, USA, 2005; p. 36. [Google Scholar] [CrossRef]
- Huijgens, H.; van Deursen, A.; Minku, L.L.; Lokan, C. Effort and Cost in Software Engineering: A Comparison of Two Industrial Data Sets. In Proceedings of the 21st International Conference on Evaluation and Assessment in Software Engineering, Karlskrona, Sweden, 15–16 June 2017; ACM: New York, NY, USA, 2017; pp. 51–60. [Google Scholar] [CrossRef]
- Gencel, C.; Heldal, R.; Lind, K. On the Relationship between Different Size Measures in the Software Life Cycle. In Proceedings of the 2009 16th Asia-Pacific Software Engineering Conference, Batu Ferringhi, Malaysia, 1–3 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 19–26. [Google Scholar] [CrossRef]
- Seo, Y.S.; Bae, D.H. On the value of outlier elimination on software effort estimation research. Empir. Softw. Eng. 2013, 18, 659–698. [Google Scholar] [CrossRef]
- Ono, K.; Tsunoda, M.; Monden, A.; Matsumoto, K. Influence of Outliers on Estimation Accuracy of Software Development Effort. IEICE Trans. Inf. Syst. 2021, E104.D, 91–105. [Google Scholar] [CrossRef]
- Mittas, N.; Angelis, L. Ranking and Clustering Software Cost Estimation Models through a Multiple Comparisons Algorithm. IEEE Trans. Softw. Eng. 2013, 39, 537–551. [Google Scholar] [CrossRef]
- Murillo-Morera, J.; Quesada-López, C.; Castro-Herrera, C.; Jenkins, M. A genetic algorithm based framework for software effort prediction. J. Softw. Eng. Res. Dev. 2017, 5, 4. [Google Scholar] [CrossRef]
- Radlinski, L. Stability of user satisfaction prediction in software projects. Procedia Comput. Sci. 2020, 176, 2394–2403. [Google Scholar] [CrossRef]
- Mendes, E.; Lokan, C. Replicating studies on cross- vs. single-company effort models using the ISBSG Database. Empir. Softw. Eng. 2008, 13, 3–37. [Google Scholar] [CrossRef]
- Liebchen, G.A.; Shepperd, M. Data sets and data quality in software engineering. In Proceedings of the 4th International Workshop on Predictor Models in Software Engineering, Leipzig, Germany, 12–13 May 2008; ACM: New York, NY, USA, 2008; pp. 39–44. [Google Scholar] [CrossRef]
- Bosu, M.F.; Macdonell, S.G. Experience: Quality Benchmarking of Datasets Used in Software Effort Estimation. J. Data Inf. Qual. 2019, 11, 1–38. [Google Scholar] [CrossRef]
- Fernández-Diego, M.; González-Ladrón-de Guevara, F. Application of mutual information-based sequential feature selection to ISBSG mixed data. Softw. Qual. J. 2018, 26, 1299–1325. [Google Scholar] [CrossRef]
- Sarro, F.; Petrozziello, A. Linear Programming as a Baseline for Software Effort Estimation. ACM Trans. Softw. Eng. Methodol. 2018, 27, 1–28. [Google Scholar] [CrossRef]
- Whigham, P.A.; Owen, C.A.; Macdonell, S.G. A Baseline Model for Software Effort Estimation. ACM Trans. Softw. Eng. Methodol. 2015, 24, 1–11. [Google Scholar] [CrossRef]
- Fernández-Diego, M.; González-Ladrón-de Guevara, F. Potential and limitations of the ISBSG dataset in enhancing software engineering research: A mapping review. Inf. Softw. Technol. 2014, 56, 527–544. [Google Scholar] [CrossRef]
- Gautam, S.S.; Singh, V. Adaptive Discretization Using Golden Section to Aid Outlier Detection for Software Development Effort Estimation. IEEE Access 2022, 10, 90369–90387. [Google Scholar] [CrossRef]
- Xia, T.; Shu, R.; Shen, X.; Menzies, T. Sequential Model optimization for Software Effort Estimation. IEEE Trans. Softw. Eng. 2022, 48, 1994–2009. [Google Scholar] [CrossRef]
- Kuhn, M. caret: Classification and Regression Training, R Package Version 6.0-93; 2022. Available online: https://CRAN.R-project.org/package=caret (accessed on 21 October 2022).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 8 September 2022).
- Kitchenham, B.; Mendes, E. Why comparative effort prediction studies may be invalid. In Proceedings of the 5th International Conference on Predictor Models in Software Engineering, Vancouver, BC, Canada, 18–19 May 2009; ACM: New York, NY, USA, 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Radliński, Ł. Preliminary evaluation of schemes for predicting user satisfaction with the ability of system to meet stated objectives. J. Theor. Appl. Comput. Sci. 2015, 9, 32–50. [Google Scholar]
- Radliński, Ł. Predicting Aggregated User Satisfaction in Software Projects. Found. Comput. Decis. Sci. 2018, 43, 335–357. [Google Scholar] [CrossRef]
- Radliński, Ł. Predicting User Satisfaction in Software Projects using Machine Learning Techniques. In Proceedings of the 15th International Conference on Evaluation of Novel Approaches to Software Engineering, Prague, Czech Republic, 5–6 May 2020; Ali, R., Kaindl, H., Maciaszek, L., Eds.; SciTePress: Setubal, Portugal, 2020; Volume 1, pp. 374–381. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Wilkinson, G.N.; Rogers, C.E. Symbolic Description of Factorial Models for Analysis of Variance. Appl. Stat. 1973, 22, 392. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Statistics and Computing; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Wang, Y.; Witten, I.H. Induction of model trees for predicting continuous classes. In Proceedings of the Poster Papers of the European Conference on Machine Learning, Prague, Czech Republic, 23–25 April 1997; University of Economics, Faculty of Informatics and Statistics: Prague, Czech Republic, 1997. [Google Scholar]
- Witten, I.; Frank, E.; Hall, M. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R. Classification and Regression Trees; Chapman & Hall: Boca Raton, FL, USA, 1984. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining-KDD ’16, San Francisco, CA, USA, 13–17 August 2016; ACM Press: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Villalobos-Arias, L.; Quesada-López, C. Comparative study of random search hyper-parameter tuning for software effort estimation. In Proceedings of the 17th International Conference on Predictive Models and Data Analytics in Software Engineering, Athens, Greece, 19–20 August 2021; ACM: New York, NY, USA, 2021; pp. 21–29. [Google Scholar] [CrossRef]
- Luo, G. A review of automatic selection methods for machine learning algorithms and hyper-parameter values. Netw. Model. Anal. Health Inform. Bioinform. 2016, 5, 18. [Google Scholar] [CrossRef]
- Minku, L.L. A novel online supervised hyperparameter tuning procedure applied to cross-company software effort estimation. Empir. Softw. Eng. 2019, 24, 3153–3204. [Google Scholar] [CrossRef]
- Kocaguneli, E.; Menzies, T.; Bener, A.; Keung, J.W. Exploiting the Essential Assumptions of Analogy-Based Effort Estimation. IEEE Trans. Softw. Eng. 2012, 38, 425–438. [Google Scholar] [CrossRef]
- Shepperd, M.; MacDonell, S. Evaluating prediction systems in software project estimation. Inf. Softw. Technol. 2012, 54, 820–827. [Google Scholar] [CrossRef]
- Kocaguneli, E.; Menzies, T.; Keung, J.; Cok, D.; Madachy, R. Active learning and effort estimation: Finding the essential content of software effort estimation data. IEEE Trans. Softw. Eng. 2013, 39, 1040–1053. [Google Scholar] [CrossRef]
- Menzies, T.; Jalali, O.; Hihn, J.; Baker, D.; Lum, K. Stable rankings for different effort models. Autom. Softw. Eng. 2010, 17, 409–437. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Fernández-Diego, M.; Martínez-Gómez, M.; Torralba-Martínez, J.M. Sensitivity of results to different data quality meta-data criteria in the sample selection of projects from the ISBSG dataset. In Proceedings of the 6th International Conference on Predictive Models in Software Engineering-PROMISE ’10, Timisoara, Romania, 12–13 September 2010; ACM Press: New York, NY, USA, 2010; pp. 1–9. [Google Scholar] [CrossRef]
- Ceran, A.A.; Ar, Y.; Tanrıöver, Ö.Ö.; Seyrek Ceran, S. Prediction of software quality with Machine Learning-Based ensemble methods. Mater. Today Proc. 2022. [Google Scholar] [CrossRef]
- Minku, L.L.; Yao, X. An Analysis of Multi-objective Evolutionary Algorithms for Training Ensemble Models Based on Different Performance Measures in Software Effort Estimation. In Proceedings of the 9th International Conference on Predictive Models in Software Engineering, Baltimore, MD, USA, 9 October 2013; ACM: New York, NY, USA, 2013; pp. 8:1–8:10. [Google Scholar] [CrossRef]
- Bosu, M.F.; MacDonell, S.G. A Taxonomy of Data Quality Challenges in Empirical Software Engineering. In Proceedings of the 2013 22nd Australian Software Engineering Conference, Hawthorne, VIC, Australia, 4–7 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 97–106. [Google Scholar] [CrossRef]
- Rosli, M.M.; Tempero, E.; Luxton-Reilly, A. Evaluating the Quality of Datasets in Software Engineering. Adv. Sci. Lett. 2018, 24, 7232–7239. [Google Scholar] [CrossRef]
- Shepperd, M. Data quality: Cinderella at the software metrics ball? In Proceedings of the 2nd International Workshop on Emerging Trends in Software Metrics, Honolulu, HI, USA, 24 May 2011; ACM: New York, NY, USA, 2011; pp. 1–4. [Google Scholar] [CrossRef]
| Attribute | N | Mean | SD | Median | Min | Max | Skew |
|---|---|---|---|---|---|---|---|
| Year of Project | 1242 | 2005.0 | 6.4 | 2005.0 | 1992 | 2019 | 0.0 |
| Adjusted Function Points | 1242 | 267.6 | 645.1 | 106.0 | 3 | 16148 | 13.7 |
| Value Adjustment Factor | 714 | 1.0 | 0.1 | 1.0 | 0.7 | 1.4 | −0.3 |
| Effort Plan [hours] | 832 | 320.7 | 1042.8 | 94.5 | 0.0 | 17,668.0 | 11.1 |
| Effort Specify [hours] | 1072 | 602.7 | 1726.7 | 223.0 | 0.0 | 32,657.0 | 10.5 |
| Effort Design [hours] | 646 | 595.3 | 1139.3 | 225.5 | 0.0 | 10,759.0 | 4.6 |
| Effort Build [hours] | 1196 | 1820.9 | 3300.6 | 824.0 | 0.0 | 35,520.0 | 5.2 |
| Effort Test [hours] | 1242 | 1382.6 | 2789.5 | 489.0 | 4.0 | 37,615.0 | 6.0 |
| Max Team Size [# people] | 1073 | 26.9 | 37.0 | 12.0 | 0.5 | 468 | 3.7 |
| Attribute | N | Type 1 | # States | Mode |
|---|---|---|---|---|
| Data Quality Rating | 1242 | nominal | 4 | B |
| UFP Rating | 1242 | nominal | 4 | A |
| Industry Sector | 972 | nominal | 6 | Medical & Health Care |
| Application Group | 452 | nominal | 4 | Business Application |
| Development Type | 1242 | nominal | 3 | Enhancement |
| Development Platform | 480 | nominal | 4 | Mainframe |
| Language Type | 628 | nominal | 4 | 3GL |
| Primary Programming Language | 627 | nominal | 11 | COBOL |
| Team Size Group | 1073 | nominal | 14 | 5–8 |
| How Methodology Acquired | 381 | nominal | 2 | Developed In-house |
| Architecture | 422 | nominal | 3 | Stand alone |
| Used Methodology | 518 | logical | 2 | yes |
| Upper CASE Used | 385 | logical | 2 | no |
| Metrics Program | 533 | logical | 2 | yes |
| Organisation Type | 967 | multinominal | 7 | Medical and Health Care |
| Application Type | 473 | multinominal | 3 | Transaction/Production System |
| Project Activity Scope | 1242 | multinominal | 3 | Specification |
| 1st Language | 636 | multinominal | 10 | COBOL |
| 1st Data Base System | 389 | multinominal | 3 | DB2 |
| Functional Sizing Technique | 572 | multinominal | 2 | Manual supported by a tool |
| Data Quality | UFP Rating | Sum | |||
|---|---|---|---|---|---|
| Rating | A | B | C | D | |
| A | 288 | 52 | 0 | 0 | 340 |
| B | 317 | 489 | 7 | 0 | 813 |
| C | 23 | 8 | 1 | 0 | 32 |
| D | 42 | 12 | 0 | 3 | 57 |
| Sum | 670 | 561 | 8 | 3 | 1242 |
| Model | Wins | Ties | Losses | Difference |
|---|---|---|---|---|
| svm | 7274 | 4252 | 474 | 6800 |
| enet | 6842 | 4765 | 393 | 6449 |
| nnet | 6479 | 4594 | 927 | 5552 |
| lm | 6131 | 4775 | 1094 | 5037 |
| xgbTree | 5452 | 5183 | 1365 | 4087 |
| knn | 5164 | 5511 | 1325 | 3839 |
| lmStepAIC | 5343 | 4867 | 1790 | 3553 |
| ranger | 4469 | 5045 | 2486 | 1983 |
| gbm | 4186 | 4353 | 3461 | 725 |
| M5 | 3682 | 3960 | 4358 | −676 |
| bMean | 3133 | 2736 | 6131 | −2998 |
| bMed | 2972 | 2735 | 6293 | −3321 |
| rpart2 | 2510 | 3275 | 6215 | −3705 |
| glmnet | 1512 | 3327 | 7161 | −5649 |
| bR | 979 | 336 | 10,685 | −9706 |
| bRU | 7 | 16 | 11,977 | −11,970 |
| Data Variant | Model 1 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| svm | enet | nnet | lm | xgbT | knn | lmS | Ranger | gbm | M5 | bMean | bMed | rpart2 | glmnet | bR | bRU | |
| A-A-0.3 | 231 | 206 | 184 | 202 | 62 | 119 | 58 | −29 | 3 | 16 | −88 | −114 | −166 | −134 | −251 | −299 |
| A-A-0.4 | 222 | 208 | 188 | 209 | 49 | 86 | 63 | −1 | 44 | 17 | −97 | −126 | −170 | −142 | −251 | −299 |
| A-A-0.5 | 223 | 209 | 187 | 212 | 42 | 85 | 64 | −8 | 41 | 18 | −90 | −122 | −171 | −140 | −251 | −299 |
| A-A-0.6 | 218 | 213 | 191 | 206 | 49 | 94 | 68 | −13 | 27 | 2 | −85 | −115 | −166 | −141 | −249 | −299 |
| A-A-0.7 | 182 | 144 | 50 | 81 | 75 | 118 | 72 | 58 | 83 | −51 | −64 | −108 | 33 | −121 | −254 | −298 |
| A-A-0.8 | 166 | 118 | 1 | 80 | 110 | 126 | 2 | 91 | 96 | −49 | −58 | −98 | 69 | −97 | −258 | −299 |
| A-A-0.9 | 120 | 118 | −39 | −1 | 102 | 22 | 35 | 52 | 40 | −147 | 99 | 84 | 29 | 6 | −224 | −296 |
| A-A-1.0 | 125 | 121 | 9 | −3 | 54 | 8 | 21 | 52 | 2 | −69 | 94 | 74 | 15 | 16 | −224 | −295 |
| A-B-0.3 | 215 | 164 | 180 | 190 | 48 | 136 | 53 | −12 | 36 | 0 | −77 | −90 | −174 | −137 | −234 | −298 |
| A-B-0.4 | 229 | 168 | 178 | 189 | 25 | 134 | 45 | −7 | 82 | 3 | −89 | −104 | −177 | −141 | −235 | −300 |
| A-B-0.5 | 227 | 169 | 178 | 189 | 18 | 138 | 47 | −9 | 83 | 2 | −88 | −103 | −177 | −139 | −235 | −300 |
| A-B-0.6 | 220 | 186 | 163 | 172 | 76 | 124 | 68 | −21 | 58 | 11 | −87 | −100 | −178 | −155 | −237 | −300 |
| A-B-0.7 | 170 | 113 | 80 | 98 | 69 | 110 | 99 | 72 | 72 | −28 | −97 | −109 | 21 | −124 | −247 | −299 |
| A-B-0.8 | 177 | 140 | 56 | 90 | 62 | 103 | 12 | 54 | 93 | −22 | −76 | −95 | 56 | −99 | −251 | −300 |
| A-B-0.9 | 125 | 139 | 6 | −16 | 101 | −7 | −23 | 29 | 25 | −61 | 92 | 90 | −11 | −22 | −167 | −300 |
| A-B-1.0 | 139 | 137 | 46 | −21 | 115 | −24 | −23 | 2 | −13 | −74 | 97 | 91 | 5 | −21 | −156 | −300 |
| B-A-0.3 | 168 | 209 | 141 | 113 | 76 | 130 | 54 | 35 | 11 | 4 | −33 | −68 | −137 | −153 | −250 | −300 |
| B-A-0.4 | 167 | 211 | 142 | 113 | 77 | 130 | 52 | 34 | 18 | 3 | −35 | −68 | −139 | −155 | −250 | −300 |
| B-A-0.5 | 164 | 207 | 185 | 78 | 73 | 127 | 65 | −1 | 13 | 19 | −29 | −60 | −129 | −166 | −247 | −299 |
| B-A-0.6 | 187 | 197 | 146 | 103 | 89 | 121 | 101 | −4 | 35 | 14 | −42 | −77 | −147 | −177 | −246 | −300 |
| B-A-0.7 | 184 | 191 | 170 | 111 | 80 | 120 | 106 | 0 | 5 | 24 | −47 | −80 | −146 | −170 | −248 | −300 |
| B-A-0.8 | 132 | 169 | 102 | 121 | 53 | 72 | 68 | 19 | 78 | −40 | −13 | −76 | 0 | −135 | −250 | −300 |
| B-A-0.9 | 107 | 121 | 64 | 94 | 86 | 90 | 41 | 69 | 87 | −40 | −14 | −82 | 59 | −127 | −255 | −300 |
| B-A-1.0 | 84 | 69 | 49 | 32 | 68 | 27 | 19 | 14 | 47 | −16 | 61 | 47 | 31 | 2 | −234 | −300 |
| B-B-0.3 | 144 | 180 | 183 | 158 | 162 | 125 | 158 | 113 | −37 | −8 | −173 | −159 | −112 | −180 | −254 | −300 |
| B-B-0.4 | 156 | 172 | 173 | 156 | 160 | 123 | 160 | 124 | −30 | −11 | −176 | −161 | −112 | −180 | −254 | −300 |
| B-B-0.5 | 160 | 177 | 176 | 159 | 174 | 86 | 171 | 127 | −26 | −24 | −175 | −162 | −110 | −175 | −258 | −300 |
| B-B-0.6 | 171 | 176 | 178 | 167 | 173 | 94 | 167 | 100 | −27 | −14 | −176 | −163 | −116 | −170 | −260 | −300 |
| B-B-0.7 | 164 | 160 | 166 | 163 | 162 | 126 | 150 | 99 | 5 | −2 | −176 | −163 | −123 | −173 | −258 | −300 |
| B-B-0.8 | 166 | 152 | 156 | 148 | 151 | 135 | 154 | 107 | 22 | 1 | −176 | −161 | −123 | −174 | −258 | −300 |
| B-B-0.9 | 201 | 141 | 234 | 157 | 131 | 92 | 143 | 58 | −19 | −46 | −107 | −92 | −134 | −233 | −228 | −298 |
| B-B-1.0 | 173 | 115 | 213 | 121 | 113 | −1 | 106 | v35 | −74 | −44 | 64 | 102 | −126 | −217 | −214 | −296 |
| D-D-0.3 | 154 | 167 | 170 | 162 | 151 | 120 | 153 | 135 | −20 | −2 | −176 | −159 | −120 | −175 | −260 | −300 |
| D-D-0.4 | 144 | 178 | 184 | 145 | 175 | 107 | 167 | 134 | −26 | −24 | −176 | −160 | −115 | −173 | −260 | −300 |
| D-D-0.5 | 167 | 171 | 136 | 158 | 160 | 142 | 165 | 139 | −36 | −23 | −174 | −155 | −116 | −174 | −260 | −300 |
| D-D-0.6 | 159 | 164 | 173 | 156 | 153 | 124 | 151 | 124 | −11 | 1 | −176 | −159 | −125 | −174 | −260 | −300 |
| D-D-0.7 | 151 | 154 | 159 | 150 | 163 | 132 | 147 | 121 | −11 | 24 | −175 | −157 | −126 | −172 | −260 | −300 |
| D-D-0.8 | 156 | 147 | 147 | 150 | 151 | 131 | 145 | 119 | 9 | 39 | −177 | −159 | −127 | −171 | −260 | −300 |
| D-D-0.9 | 200 | 131 | 234 | 128 | 132 | 112 | 124 | 84 | 11 | −23 | −138 | −103 | −134 | −227 | −231 | −300 |
| D-D-1.0 | 152 | 137 | 213 | 117 | 117 | 2 | 125 | −42 | −71 | −56 | 55 | 99 | −116 | −209 | −227 | −296 |
| Mean | 170 | 161 | 139 | 126 | 102 | 96 | 89 | 50 | 18 | −17 | −75 | −83 | −93 | −141 | −243 | −299 |
| Data Variant | Model 1 | Mean | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bMean | bMed | bR | bRU | enet | gbm | glmnet | knn | lm | lmS | M5 | nnet | Ranger | rpart2 | svm | xgbT | ||
| D-D-0.3 | −72 | −48 | −136 | −464 | 501 | 277 | 109 | 371 | 468 | 530 | 310 | 410 | 584 | 269 | 317 | 521 | 247 |
| D-D-0.7 | −72 | -48 | −136 | −464 | 382 | 299 | 158 | 354 | 412 | 500 | 353 | 376 | 525 | 256 | 346 | 538 | 236 |
| D-D-0.6 | −72 | −48 | −136 | −464 | 401 | 311 | 152 | 342 | 456 | 476 | 326 | 339 | 544 | 257 | 340 | 468 | 231 |
| D-D-0.4 | −72 | −48 | −136 | −464 | 456 | 198 | 125 | 286 | 367 | 528 | 284 | 438 | 564 | 269 | 294 | 567 | 228 |
| D-D-0.5 | −72 | −48 | −136 | −464 | 443 | 194 | 134 | 312 | 425 | 532 | 271 | 330 | 565 | 269 | 313 | 512 | 224 |
| D-D-0.8 | −72 | −48 | −136 | −464 | 378 | 332 | 156 | 259 | 390 | 489 | 386 | 280 | 512 | 256 | 378 | 490 | 224 |
| B-B-0.7 | −176 | −120 | −96 | −464 | 326 | 323 | 105 | 308 | 342 | 514 | 319 | 323 | 461 | 271 | 376 | 491 | 206 |
| B-B-0.3 | −176 | −120 | −96 | −464 | 450 | 175 | −38 | 290 | 357 | 511 | 255 | 447 | 504 | 274 | 303 | 511 | 199 |
| B-B-0.4 | −176 | −120 | −96 | −464 | 436 | 188 | −51 | 283 | 341 | 524 | 269 | 421 | 505 | 274 | 271 | 493 | 194 |
| B-B-0.8 | −176 | −120 | −96 | −464 | 283 | 341 | 77 | 235 | 319 | 475 | 320 | 303 | 459 | 271 | 341 | 453 | 189 |
| B-B-0.6 | −176 | −120 | −96 | −464 | 321 | 218 | 75 | 273 | 344 | 489 | 268 | 329 | 447 | 270 | 293 | 484 | 185 |
| B-B-0.5 | −176 | −120 | −96 | −464 | 384 | 193 | 5 | 207 | 331 | 534 | 226 | 338 | 491 | 274 | 314 | 498 | 184 |
| B-A-0.7 | 256 | 192 | 64 | 176 | 163 | 65 | 245 | 188 | 76 | 208 | 241 | 177 | −48 | −1 | 176 | 67 | 140 |
| B-A-0.6 | 256 | 192 | 64 | 176 | 154 | 133 | 251 | 200 | 65 | 184 | 205 | 150 | −57 | −1 | 172 | 39 | 136 |
| A-A-0.6 | 8 | −16 | 88 | 496 | 265 | 98 | 251 | 217 | 331 | 15 | 133 | 175 | −119 | −207 | 261 | −95 | 119 |
| A-A-0.4 | 8 | −16 | 88 | 496 | 245 | 153 | 246 | 177 | 319 | −39 | 170 | 156 | −76 | −207 | 266 | −119 | 117 |
| A-A-0.5 | 8 | −16 | 88 | 496 | 245 | 141 | 246 | 177 | 319 | −39 | 150 | 153 | −97 | −207 | 266 | −115 | 113 |
| A-A-0.3 | 8 | −16 | 88 | 496 | 233 | 96 | 250 | 256 | 323 | −41 | 137 | 159 | −143 | −207 | 251 | −106 | 112 |
| B-A-0.5 | 256 | 192 | 64 | 176 | 137 | 90 | 249 | 177 | −95 | 42 | 154 | 178 | −87 | −1 | 37 | −8 | 98 |
| B-A-0.4 | 256 | 192 | 64 | 176 | 137 | 45 | 290 | 210 | −27 | −28 | 146 | 92 | −29 | −4 | 15 | −18 | 95 |
| B-A-0.3 | 256 | 192 | 64 | 176 | 140 | 34 | 290 | 202 | −34 | −41 | 147 | 86 | −7 | −4 | −3 | −17 | 93 |
| A-B-0.6 | −16 | −8 | 80 | 256 | 69 | 114 | 128 | 215 | 204 | −34 | 152 | 160 | −159 | −215 | 244 | −117 | 67 |
| A-B-0.4 | −16 | −8 | 80 | 256 | 51 | 163 | 128 | 194 | 219 | −71 | 76 | 196 | −116 | −215 | 200 | −197 | 59 |
| A-B-0.5 | −16 | −8 | 80 | 256 | 51 | 163 | 128 | 192 | 219 | −71 | 76 | 196 | −129 | −215 | 187 | −199 | 57 |
| A-B-0.3 | −16 | −8 | 80 | 256 | 25 | 32 | 128 | 221 | 219 | −69 | 49 | 149 | −181 | −215 | 174 | −146 | 44 |
| B-A-0.8 | 256 | 192 | 64 | 176 | −92 | 138 | 183 | −93 | −47 | −52 | −38 | −169 | −11 | 267 | −155 | −152 | 29 |
| B-A-0.9 | 256 | 192 | 64 | 176 | −315 | 96 | 207 | −211 | −335 | −320 | −98 | −424 | 25 | 418 | −415 | −165 | −53 |
| A-A-0.7 | 8 | −16 | 88 | 496 | −307 | 49 | 136 | −201 | −334 | −312 | −200 | −381 | −84 | 140 | −207 | −234 | −85 |
| A-B-0.7 | −16 | −8 | 80 | 256 | −346 | 4 | −75 | −181 | −358 | −232 | −165 | −321 | −84 | 216 | −283 | −262 | −111 |
| A-A-0.8 | 8 | −16 | 88 | 496 | −420 | 20 | 102 | −309 | −464 | −460 | −276 | −521 | −101 | 240 | −315 | −217 | −134 |
| D-D-0.9 | −72 | −48 | −136 | −464 | −289 | −103 | −571 | −99 | −140 | −50 | −87 | 68 | −101 | −98 | −63 | 15 | −140 |
| A-B-0.8 | −16 | −8 | 80 | 256 | −408 | 24 | −82 | −313 | −433 | −417 | −171 | −443 | −85 | 234 | −349 | −286 | −151 |
| B-B-0.9 | −176 | −120 | −96 | −464 | −311 | −230 | −621 | −141 | −106 | −115 | −127 | 45 | −138 | −188 | −95 | −34 | −182 |
| B-A-1.0 | 256 | 192 | 64 | 176 | −423 | −473 | −154 | −638 | −585 | −555 | −568 | −568 | −513 | −158 | −475 | −465 | −305 |
| A-A-0.9 | 8 | −16 | 88 | 496 | −619 | −551 | −294 | −641 | −680 | −620 | −653 | −712 | −583 | −225 | −610 | −543 | −385 |
| A-A-1.0 | 8 | −16 | 88 | 496 | −618 | −659 | −287 | −654 | −681 | −600 | −603 | −645 | −560 | −352 | −635 | −548 | −392 |
| A-B-0.9 | −16 | −8 | 80 | 256 | −638 | −609 | −464 | −671 | −691 | −625 | −593 | −646 | −625 | −415 | −623 | −510 | −425 |
| A-B-1.0 | −16 | −8 | 80 | 256 | −631 | −677 | −465 | −679 | −684 | −660 | −635 | −567 | −678 | −413 | −658 | −464 | −431 |
| D-D-1.0 | −72 | −48 | −136 | −464 | −632 | −708 | −711 | −661 | −567 | −542 | −617 | −537 | −698 | −599 | −631 | −553 | −511 |
| B-B-1.0 | −176 | −120 | −96 | −464 | −627 | −697 | −741 | −654 | −585 | −558 | −592 | −540 | −677 | −578 | −618 | −577 | −519 |
| Rank | Model | Data Variant 1 | Wins | Ties | Losses | Difference |
|---|---|---|---|---|---|---|
| 1 | enet | D-D-0.3 | 10,869 | 1812 | 99 | 10,770 |
| 2 | nnet | D-D-0.4 | 10,888 | 1681 | 211 | 10,677 |
| 3 | enet | B-B-0.3 | 10,789 | 1840 | 151 | 10,638 |
| 4 | enet | D-D-0.4 | 10,742 | 1896 | 142 | 10,600 |
| 5 | enet | D-D-0.5 | 10,758 | 1859 | 163 | 10,595 |
| 6 | nnet | B-B-0.3 | 10,795 | 1769 | 216 | 10,579 |
| 7 | enet | B-B-0.4 | 10,708 | 1897 | 175 | 10,533 |
| 8 | nnet | B-B-0.4 | 10,689 | 1922 | 169 | 10,520 |
| 9 | nnet | D-D-0.3 | 10,657 | 1879 | 244 | 10,413 |
| 10 | lmStepAIC | D-D-0.4 | 10,441 | 2216 | 123 | 10,318 |
| 11 | enet | D-D-0.6 | 10,407 | 2220 | 153 | 10,254 |
| 12 | lm | D-D-0.3 | 10,542 | 1944 | 294 | 10,248 |
| 13 | xgbTree | D-D-0.7 | 10,388 | 2205 | 187 | 10,201 |
| 14 | lmStepAIC | B-B-0.5 | 10,290 | 2387 | 103 | 10,187 |
| 15 | lmStepAIC | D-D-0.5 | 10,392 | 2177 | 211 | 10,181 |
| 16 | enet | B-B-0.5 | 10,335 | 2283 | 162 | 10,173 |
| 17 | enet | D-D-0.7 | 10,333 | 2273 | 174 | 10,159 |
| 18 | lm | D-D-0.6 | 10,286 | 2360 | 134 | 10,152 |
| 19 | lmStepAIC | B-B-0.4 | 10,285 | 2348 | 147 | 10,138 |
| 20 | xgbTree | D-D-0.4 | 10,364 | 2187 | 229 | 10,135 |
| 23 | svm | D-D-0.8 | 10,233 | 2354 | 193 | 10,040 |
| 78 | knn | D-D-0.3 | 9136 | 3302 | 342 | 8794 |
| 85 | ranger | D-D-0.4 | 8967 | 3412 | 401 | 8566 |
| 155 | M5 | D-D-0.8 | 7388 | 3967 | 1425 | 5963 |
| 168 | gbm | D-D-0.8 | 7150 | 3797 | 1833 | 5317 |
| 272 | rpart2 | B-A-0.9 | 5791 | 2663 | 4326 | 1465 |
| 322 | bMean | B-A-* | 4656 | 3186 | 4938 | −282 |
| 340 | bMed | B-A-* | 4160 | 3290 | 5330 | −1170 |
| 423 | glmnet | A-A-0.3 | 2389 | 4173 | 6218 | −3829 |
| 559 | bR | A-B-* | 1196 | 1137 | 10,447 | −9251 |
| 601 | bRU | A-A-* | 607 | 298 | 11,875 | −11,268 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radliński, Ł. The Impact of Data Quality on Software Testing Effort Prediction. Electronics 2023, 12, 1656. https://doi.org/10.3390/electronics12071656
Radliński Ł. The Impact of Data Quality on Software Testing Effort Prediction. Electronics. 2023; 12(7):1656. https://doi.org/10.3390/electronics12071656
Chicago/Turabian StyleRadliński, Łukasz. 2023. "The Impact of Data Quality on Software Testing Effort Prediction" Electronics 12, no. 7: 1656. https://doi.org/10.3390/electronics12071656
APA StyleRadliński, Ł. (2023). The Impact of Data Quality on Software Testing Effort Prediction. Electronics, 12(7), 1656. https://doi.org/10.3390/electronics12071656








