A Novel Denoising Algorithm Based on Wavelet and Non-Local Moment Mean Filtering

Abstract

Denoising is the basis and premise of image processing and an important part of image preprocessing. Denoising can effectively improve image quality, which contributes to subsequent image processing such as image segmentation, feature extraction, and so on. In this paper, we propose a novel image denoising method based on wavelet transform and nonlocal moment mean filtering approach (NMM). The noisy image is firstly denoised by a wavelet-based soft-thresholding denoising technique and NMM is then utilized to further eliminate the rest noises. Meanwhile, the fusion of moment invariants increases the robustness of our denoising algorithm due to the invariance of image scaling, translation, and rotation of color moments. Experiments show that our algorithm achieves a better denoising effect compared with some other denoising approaches.

1. Introduction

Image is often disturbed by random noise signals in the process of acquisition or transmission. Common image noises include salt and pepper noise, Gauss noise, Poisson noise, and so on. These noises reduce the quality of the images, which seriously hinders the subsequent image processing such as edge extraction, image segmentation, feature extraction, and so on. For example, Gaussian noise is a kind of noise whose probability density function obeys Gaussian distribution (i.e., normal distribution). If the amplitude distribution of noise is Gaussian, and its power spectral density is uniformly distributed, it is called Gaussian white noise. The effect of Gaussian noise on the image is random, which is a common noise in the image. The causes of this kind of noise mainly include: the light not being bright enough or uniform enough when the images are taken; the noise and interaction of circuit components; the temperature being too high because the sensor works for a long time. In the image, Gaussian noise is represented by the random change of pixel value, making the image become blurred or dotted with noise, which will lead to blurred or distorted details in the image, thus affecting the quality and subsequent image processing.

In order to obtain high-quality digital images, it is necessary to carry on the image noise reduction processing. Image denoising is a technology that uses context information of image sequence to remove noise and restore a clear image. It is one of the important research contents in the field of computer vision, that is, to maintain as much as possible the integrity of the original information (e.g., the main features) through a certain algorithm, but also to remove the useless information in the signal, so that the processed image is clearer. The quality of the image denoising algorithm is directly related to the effect of subsequent image processing.

Wavelet transform is a local transform of time and frequency domain, so it can extract information from signal effectively, and carry out a multi-scale detailed analysis of function or signal through operation functions such as scaling and shifting. It is widely used in image denoising. Meanwhile, the non-local Means (NLM) algorithm is one of the most popular image-denoising algorithms. It uses the redundancy of the natural image itself to restore the image polluted by noises and takes into account as much similarity-structure information as possible. At the same time, the denoising method based on the whole block information can better preserve the image edge and texture features.

In order to make full use of the advantages of the wavelet denoising and NLM method and improve the denoising effect, a novel hybrid filtering algorithm combining wavelet-based denoising technique (W) with a nonlocal mean moment filtering approach (NMM) is proposed (named W-NMM) in this paper. The technique can effectively remove noises while still retaining enough detailed information.

The remainder of this article is organized as follows: the relevant work is described in Section 2. Section 3 presents a detailed description of our W-NMM model. The experiments are displayed in Section 4 and the key issues of this paper are discussed in Section 5. In Section 6, we make a brief conclusion. A group of abbreviations and the corresponding nomenclature is shown in Table A1.

2. Related Work

The existence of noise reduces the image quality and hinders the subsequent processing of the image. In order to remove noise and improve image quality, many scholars have proposed a variety of image denoising methods including traditional techniques and neural network-based techniques as shown in Table 1.

The traditional image denoising methods can be divided into two categories: spatial denoising and frequency denoising. The former includes morphology filtering, mean filtering, Gauss filtering, morphological filtering, local filtering, non-local filtering, and so on [1]. The latter includes Wiener filtering, wavelet threshold denoising [2], and so on. For example, Chen et al. [3] proposed a multi-structural element auto-adapted determination weight algorithm combining morphology filter of opening and closing operations. According to the different characteristics of images contaminated by different kinds of noises, a hybrid denoising method was proposed by Guan et al. [4]. Firstly, the local threshold was used to classify the pixels as those polluted by Gauss noise and salt and pepper noise. Mean and median filtering approaches were used to denoise them. Hu et al. [5] analyzed mean filtering, median filtering, and wavelet transform, which are three conventional methods for image denoising processing. Because median filtering usually results in image blur, Zhao et al. [6] improved median filtering and put forward a weighted fast median filtering algorithm and a weighted adaptive median filtering algorithm. Aiming at the shortcomings of classical soft and hard thresholding methods in denoising, Yin et al. [7] presented an improved new threshold function, which could satisfy the continuous input-output curve while the decomposed wavelet coefficients were kept unchanged. Traditional soft and hard thresholding methods cannot effectively express energy distribution, so it is necessary to find a balance between denoising and edge information preserving. Zhang et al. [8] presented an improved threshold function integrating the advantages of the classical wavelet threshold function and other improved methods. Wang et al. [9] used a wavelet thresholding method to denoise the COVID-19 CT image, where the threshold function was obtained by the improved particle swarm optimization. Kazuaki et al. [10] removed quantum noise from the STEM image with a total variation denoising algorithm, where they defined an entropy of the STEM image that corresponds to the image contrast and then determined a hyperparameter to maximize the entropy. Guo et al. [11] presented a median filtering algorithm based on an adaptive two-stage threshold to improve the accuracy of CT image noise detection. In the method, an adaptive weighted median filter image denoising method was put forward based on a hybrid genetic algorithm. Yuan et al. [12] put forward an edge-preserving median filter and weighted coding with sparse nonlocal regularization for low-dose CT image denoising. In addition, the classical filtering algorithm also includes anisotropic diffusion [13], bilateral filtering [14], kernel singular value decomposition (K-SVD) [15], sparse 3-D transform-domain collaborative filtering [16], and so on.

Deep learning, especially convolutional neural network (CNN), has achieved good results in image recognition and other fields. In recent years, image denoising methods based on deep learning have also been developed. Wang et al. [17] proposed a multi-scale feature-extraction-based normalized attention neural network for image denoising. In the model, they employed a multi-scale feature extraction block to extract and combine features at distinct scales of the noisy image, and a normalized attention network was applied to learn the relationships between channels. Ahmed et al. [18] proposed a medical image denoising system based on the stacked convolutional autoencoder technique. Huang et al. [19] presented an unsupervised learning approach incorporating a pseudo-siamese network for image processing, where two independent branches of the network utilize different filling strategies, namely zero filling and adjacent pixel filling. Wang et al. [20] used an optimized denoising convolutional neural networks method based on sub-region processing and transfer learning to denoise the images. Usui et al. [21] compared the dose-dependent properties of a CNN-based denoising method for low-dose CT with those of other noise reduction methods on unique CT noise simulation images. They observed that the CNN model can eliminate noise and maintain image sharpness at these dose levels. Rajesh et al. [22] developed a differential evolution-based automatic network evolution model by exploring the fittest parameters. Furthermore, they adopted a transfer learning technique to accelerate the training process.

Table 1. A list of the literature on denoising methods.

Classification	Year	Author	Methods
Traditional image denoising methods	2003	Chen et al. [3]	Mathematics morphology
	2005	Guan et al. [4]	Mean and median filtering approaches
	2007	Hu et al. [5]	Mean filtering, median filtering, and wavelet transform
	2011	Zhao et al. [6]	Improved median filtering
	2018	Yin et al. [7]	Improved wavelet threshold
	2017	Zhang et al. [8]	Threshold with wavelet transform
	2022	Wang et al. [9]	Wavelet transform combined with improved PSO
	2022	Kazuaki et al. [10]	Total variation regularization
	2022	Guo et al. [11]	Adaptive threshold and optimized weighted median filter
	2021	Yuan et al. [12]	Edge-Preserving Median Filter and Weighted Coding with Sparse Nonlocal Regularization
	1990	Perona et al. [13]	Anisotropic diffusion
	1998	Tomasi [14]	Bilateral filtering
	2005	Aharon et al. [15]	K-SVD
	2007	Kostadin et al. [16]	Sparse 3-D transform-domain collaborative filtering
Deep learning approaches	2021	Wang et al. [17]	Attention neural network
	2021	Ahmed et al. [18]	Stacked convolutional autoencoder
	2021	Huang et al. [19]	Unsupervised pseudo-siamese network
	2021	Wang et al. [20]	Convolutional neural network
	2021	Usui et al. [21]	Convolutional neural network
	2022	Rajesh et al. [22]	An evolutionary block-based network

Table 1. A list of the literature on denoising methods.

Classification	Year	Author	Methods
Traditional image denoising methods	2003	Chen et al. [3]	Mathematics morphology
	2005	Guan et al. [4]	Mean and median filtering approaches
	2007	Hu et al. [5]	Mean filtering, median filtering, and wavelet transform
	2011	Zhao et al. [6]	Improved median filtering
	2018	Yin et al. [7]	Improved wavelet threshold
	2017	Zhang et al. [8]	Threshold with wavelet transform
	2022	Wang et al. [9]	Wavelet transform combined with improved PSO
	2022	Kazuaki et al. [10]	Total variation regularization
	2022	Guo et al. [11]	Adaptive threshold and optimized weighted median filter
	2021	Yuan et al. [12]	Edge-Preserving Median Filter and Weighted Coding with Sparse Nonlocal Regularization
	1990	Perona et al. [13]	Anisotropic diffusion
	1998	Tomasi [14]	Bilateral filtering
	2005	Aharon et al. [15]	K-SVD
	2007	Kostadin et al. [16]	Sparse 3-D transform-domain collaborative filtering
Deep learning approaches	2021	Wang et al. [17]	Attention neural network
	2021	Ahmed et al. [18]	Stacked convolutional autoencoder
	2021	Huang et al. [19]	Unsupervised pseudo-siamese network
	2021	Wang et al. [20]	Convolutional neural network
	2021	Usui et al. [21]	Convolutional neural network
	2022	Rajesh et al. [22]	An evolutionary block-based network

Although the traditional denoising method is simple, it also has many limitations. For example, the morphology method, neighborhood average method, and median filtering can suppress the noise, but also easily cause the image blur phenomenon, which is not suitable for the image with more details of points, lines, and peaks. The neural network–based techniques require a large number of training samples, and it is difficult to obtain all kinds of natural noise samples for training. Based on this, this paper aimed to propose a novel filtering algorithm based on wavelet and non-local moment mean filtering.

3. Methodology

The algorithm in this paper mainly includes two steps: multi-scale decomposition denoising and non-local moment mean filtering.

3.1. Multi-Scale Decomposition Denoising

Wavelet transform (see Figure 1 for a reference) [23] is a time-frequency localization analysis method in which the size of the window is fixed but its time window and frequency window can be changed. That is, the low-frequency part has a low time resolution and a high-frequency resolution, and the high-frequency part has a high time resolution and a low-frequency resolution, which is suitable for the analysis of non-stationary signals such as images and the extraction of local features from such signals.

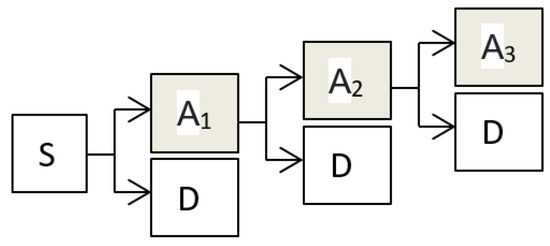
Figure 1. Image decomposition with wavelet transform.

Wavelet transform is to move a mother wavelet with a displacement $\tau$, and then do the inner product with the analytic signal $x(t)$ at different scales $a$.

$$W^{\prime }{\mathtt{T}}_x(a,\tau )=\frac{\sqrt{a}}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }X}(\omega ){\phi }^{*}(a\omega )e^{+j\omega \pi }d\omega$$

(1)

$a$ is a scale factor and $a>0$. $\tau$ reflects displacement. In the frequency domain, it is expressed as

$$W{T}_x(a,\tau )=\frac{1}{\sqrt{a}}{\displaystyle {\int }_{-\infty }^{\infty }x}(t){\psi }^{*}\left(\frac{t-\tau }{a}\right)dt$$

(2)

Discrete Wavelet Transform (DWT) discretizes scale parameters according to power series, which is often used in multi-resolution analysis and signal decomposition and reconstruction.

$$DWTx(m,n)\le x(t),{\psi }_{m,n}(t)\ge 2^{-\frac{m}{2}}{\displaystyle {\int }_{R}x}(t)\psi \left(2^{-m}t-n\right)dt$$

(3)

where the wavelet function is

$${\psi }_{jk}(t)=2^{-\frac{j}{2}}\psi \left(2^{-j}t-k\right)$$

(4)

In multi-resolution analysis, for example, orthogonal wavelet transform can be equivalent to a set of mirror filtering processes, i.e., signal $\mathrm{S}$ is decomposed through a high-pass filter and a low-pass filter. The high-frequency component, $D_i$, of the corresponding signal is called the detail component. The output of the low-pass filter corresponds to the relative signal $A_i$, which is called the approximate component, see Figure 1 for a reference.

In the wavelet domain, coefficients corresponding to the effective signal are usually very large, while those corresponding to noises are very small. At present, the commonly used threshold-based methods include hard threshold, soft threshold, and so on. The wavelet coefficients obtained by the soft threshold method have good continuity and no discontinuity. Here, we adopted the soft-threshold-based method to remove Gaussian noises.

When the absolute value of the wavelet coefficients is less than a given threshold value, it is zero; when the wavelet coefficients are larger than the threshold value, the threshold value is subtracted from the wavelet coefficients.

$$w_{\lambda }=\{\begin{array}{cc}[\mathrm{sgn}(w)](|w|-\lambda )& \left|w\right|\ge \lambda \\ 0& \left|w\right|<\lambda \end{array}$$

(5)

where sgn(x) returns “+1” if x is a positive value and “−1” otherwise cases. $\lambda$ is calculated with [24].

$$\lambda =\sigma \sqrt{2\ln N}$$

(6)

here, σ = M/0.6745, and M is the median absolute deviation of detail coefficients at high-frequency sub-images. N is the length of the signal.

Figure 2 shows several denoising results with the soft threshold-based wavelet denoising method. From Figure 2, we can find that the noisy image was denoised well.

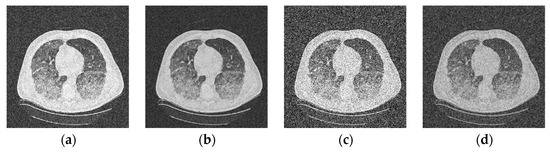
Figure 2. Image denoising with wavelet transform. (a,c) are noisy images with Gaussian noise variance = 0.02 and variance = 0.1, respectively. (b,d) are the denoising results of (a,c), respectively.

3.2. Non-Local Moment Mean Filtering

Non-local mean filtering uses all the pixels in the image, and these pixels are weighted according to some kind of similarity. After filtering, the image clarity is high, and the details are not lost, so the structural information of the image is better protected [25]. If we take the noise image v(i) as the sum of the image $u(i)$ and the noise $n(i)$ whose mean value is 0 without noise contamination, $v(i)$ can be expressed as

$$v(i)=u(i)+n(i)$$

(7)

For a given pixel $i$ in an image $v$, the image block $N(i)$ sized $n\times n$ is an image block with $i$ as the block center and $N(j)$ is an image block in the neighborhood of $N(i)$. The similarity between $i$ and $j$ is measured by Gaussian weighted Euclidean distance between the image blocks $N(i)$ and $N(j)$. The smaller the distance between $N(j)$ and $N(i)$ is, the more similar the pixel $j$ is to the pixel $i$, and the greater the weight given by the pixel $j$ in cumulative restoration.

Assuming that the denoised image is $I(i)$, for a pixel $i$, the NLM calculation is as follows

$$I(i)=\frac{{\displaystyle \sum _{j\in v}W}(i,j)v(j)}{{\displaystyle \sum _{j\in v}w}(i,j)}$$

(8)

We define $v\left(N_i\right)$ as a rectangular neighborhood centered on $i$, and the similarity coefficient $w(i,j)$ of the pixels $i$ and $j$ in the image $v$ is as follows:

$$w(i,j)=\mathit{exp}\left(-\frac{{\Vert v\left(N_i\right)-v\left(N_j\right)\Vert }_{2,\alpha }^2}{h^2}\right)$$

(9)

where $\alpha$ is the standard deviation of the Gaussian kernel function, ${\Vert v\left(N_i\right)-v\left(N_j\right)\Vert }_{2,\alpha }^2$ represents the weighted Euclidean distance between two image blocks; $h$ is a filtering parameter to control the smoothness

$$\Vert V(N_i)-V(N_j){\Vert }^2=\frac{1}{d^2}{\displaystyle \sum _{i+z\in N_i,j+z\in N_j}\Vert v(}i+z)-v(j+z){\Vert }^2$$

(10)

The non-local mean filtering algorithm makes full use of the block information of the image and can keep the texture and edge of the image well. The filtering effect is better [26]. However, similarity measurement lacks robustness. In this paper, we replace the gray difference with the moment the difference in the weighted Euclidean distance between two image blocks and produce a novel denoising method, called the non-local moment mean denoising method, abbreviated as NMM.

Moments and the related invariants have been extensively analyzed to characterize the patterns of images in a variety of applications [27].

$$m_{pq}={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{x}^p}}f(x,y)dxdy,p,q=0,1,2,\cdots$$

(11)

Hu [24] introduced seven-moment invariants $M=\{{\varphi }_1,{\varphi }_2,{\varphi }_3,{\varphi }_4,{\varphi }_5,{\varphi }_6,{\varphi }_7\}$

$${\varphi }_1={\eta }_{20}+{\eta }_{02}$$

(12)

$${\varphi }_2={\left({\eta }_{20}-{\eta }_{02}\right)}^2+4{\eta }_{11}^2$$

(13)

$${\varphi }_3={\left({\eta }_{30}-3{\eta }_{12}\right)}^2+{\left(3{\eta }_{21}-{\eta }_{03}\right)}^2$$

(14)

$${\varphi }_4={\left({\eta }_{30}+{\eta }_{12}\right)}^2+{\left({\eta }_{21}+{\eta }_{03}\right)}^2$$

(15)

$$\begin{array}{l}{\varphi }_5=\left({\eta }_{30}-3{\eta }_{12}\right)\left({\eta }_{30}+{\eta }_{12}\right)\left[{\left({\eta }_{30}+{\eta }_{12}\right)}^2-3{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]\\ +\left(3{\eta }_{21}-{\eta }_{03}\right)\left({\eta }_{21}+{\eta }_{03}\right)\left[3{\left({\eta }_{30}+{\eta }_{12}\right)}^2-{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]\end{array}$$

(16)

$${\varphi }_6=\left({\eta }_{20}-{\eta }_{02}\right)\left[{\left({\eta }_{30}+{\eta }_{12}\right)}^2-{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]+4{\eta }_{11}\left({\eta }_{30}+{\eta }_{12}\right)+\left({\eta }_{21}+{\eta }_{03}\right)$$

(17)

$$\begin{array}{l}{\varphi }_7=\left(3{\eta }_{21}-{\eta }_{03}\right)\left({\eta }_{30}+{\eta }_{12}\right)\left[{\left({\eta }_{30}+{\eta }_{12}\right)}^2-3{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]\\ -\left({\eta }_{30}-3{\eta }_{12}\right)\left({\eta }_{21}+{\eta }_{03}\right)\left[3{\left({\eta }_{30}+{\eta }_{12}\right)}^2-{\left({\eta }_{21}+{\eta }_{03}\right)}^2\right]\end{array}$$

(18)

Moment invariants are useful properties of being unchanged under image scaling, translation, and rotation. In the end, the weighted Euclidean distance between two image blocks is

$$\Vert V(N_i)-V(N_j){\Vert }^2=\frac{1}{d^2}{\displaystyle \sum _{}\Vert v(}{N}_{i,M})-v(N_{j,M}){\Vert }^2$$

(19)

where $N_{i,M}$ is the moment value of the image block $N_i$ and $N_{j,M}$ is the moment value of the image block $N_j$.

Combined with wavelet-based denoising (W) and non-local moment mean filtering (NMM), the algorithm W-NMM is described as Algorithm 1.

Algorithm 1: W-NMM filtering

Input: image I to be filtered t: radio of search window f: radio of similarity window h: degree of filtering 1. Take sym8 as the wavelet basis function to decompose the image in two layers. 2. Calculate the soft threshold according to Equation (6) on the high-frequency domains. 3. Denoise image I according to Equation (5) and obtained I’. 4. Symmetric padding I’; 5. For each pixel in I’(i,j) (i = f:M − f, j = f:N − f): i1 $\Leftarrow$ i + f; j1 $\Leftarrow$ j + f; Create objective window: W1= I’(i1 − f:i1 + f, j1 − f:j1 + f); 6. Set the borders of the neighboring window: rmin$\Leftarrow$max(i1 − t, f + 1); rmax$\Leftarrow$min(i1 + t, m + f); smin$\Leftarrow$max(j1 − t, f + 1); smax$\Leftarrow$min(j1 + t, n + f); 7. For each pixel in W2(r,s):        Set neighboring window: W2 = input2(r − f:r + f, s − f:s + f); 8.   Calculate the moments of W1 and W2: n1 = hu_moments(W1);           n2 = hu_moments(W2); 9. Calculate the similarity of W1 and W2 according to n1 and n2. 10. Calculate the Gaussian weight: w$\Leftarrow$exp − d/h); 11. Find the maximum of w: wmax.         sweight$\Leftarrow$sweight + w;         average$\Leftarrow$average + w × I’(r,s);      end 12. Calculate the accumulation of       average = average + wmax × I’(i,j);       sweight = sweight + wmax; 13. Calculate denoised image Iout:       if sweight > 0         Iout’(i,j) = average/sweight;       else         Iout’(i,j) = I’(i,j);       end 14. end 15. Extract the image Iout with the size same to I from Iout’.

4. Experiment

In order to evaluate the performance of our algorithm, we test it on a set of noisy images and several examples. The following metrics are utilized for evaluating the performance of image processing approaches Peak Signal to Noise Ratio (PSNR) [28] and Structural Similarity Index (SSIM) [29].

PSNR is widely used to evaluate image quality and is defined as

$$\mathrm{PSNR}=10\cdot {\log }_{10}\left(\frac{MA{X}_I^2}{\mathrm{MSE}}\right)=20\cdot {\log }_{10}\left(\frac{MA{X}_I}{\sqrt{\mathrm{MSE}}}\right)$$

(20)

where $MA{X}_I$ is the maximum value of an image $I$, MSE is Mean Square Error, and expressed as

$$\mathrm{MSE}=\frac{1}{mn}{\displaystyle \sum _{i=0}^{m-1}{\displaystyle \sum _{j=0}^{n-1}\Vert I(}}i,j)-K(i,j){\Vert }^2$$

(21)

Where $I$ and $K$ can be taken as the denoised image and original image, respectively.

The smaller the MSE and the bigger the PSNR, the better the image quality.

SSIM is one of the indicators to measure image quality. Given two images $I$ and K, their SSIM can be defined as:

$$\mathrm{SSIM}=\frac{(2{\mu }_I{\mu }_K+c_1)(2{\sigma }_{IK}+c_2)}{({\mu }_I^2+{\mu }_K^2+c_1)({\sigma }_I^2+{\sigma }_K^2+c_2)}$$

(22)

where, ${\mu }_I$ and ${\mu }_K$ are the means of $I$ and $K$, respectively. ${\sigma }_I^2$ and ${\sigma }_K^2$ are variances of $I$ and $K$, respectively. ${\sigma }_{IK}$ is the covariance of $I$ and $K$. $c_1={(k_{1}L)}^2$ and $c_2={(k_{2}L)}^2$ are constants keeping things stable. $L$ is the dynamic range of the image pixel value, $k_1=0.01$, $k_2=0.03$.

The range of SSIM is [0, 1]. The larger the SSIM is, the better the image quality is. Figure 3 shows the denoising result with our W-NMM algorithm. In Figure 3a–d there are images with Gaussian white noise with variances 0.01, 0.02, 0.04, and 0.06, respectively. The first two lines are the corresponding noisy images with their partial histograms, and the last two lines are the denoised images with their partial histograms. It can be seen the algorithm removed the noises well. Figure 4 and Figure 5 show the denoising results on the original noisy image and the corresponding ones after rotation, scaling, and translation. It can be seen that the results were similar, which shows the robustness of the method.

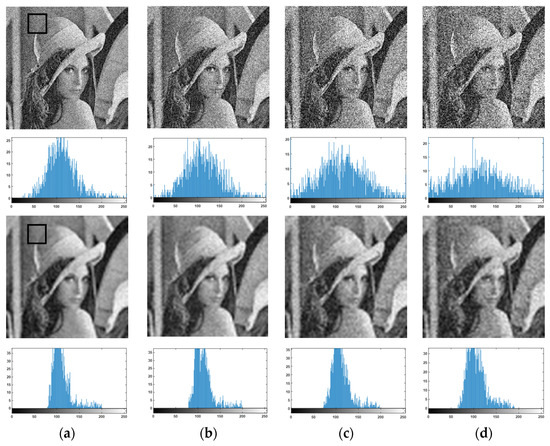
Figure 3. The denoising result with W-NMM algorithm. (a–d) are images added Gaussian white noise of variance 0.01, 0.02, 0.04, and 0.06, respectively. The first two lines are the corresponding noisy images with their partial histograms, and the last two lines are the denoised images with their partial histograms.

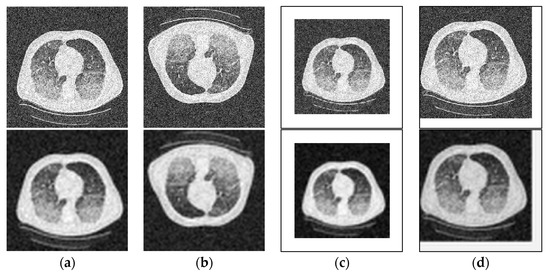
Figure 4. The denoising results of the (a) original noisy image, (b) rotated image, (c) scaled image, and (d) translated image.

Figure 5. The evaluation of the denoising results of Figure 4 in terms of PSNR and SSIM. a~d refter to the images a–d in Figure 4.

We compare our W-NMM algorithm with the anisotropic diffusion filter (AD) [13], bilateral filter (BF) [14], Kernel Singular Value Decomposition (KSVD) [15], and block Matching and 3D collaborative filtering (BM3D) [16] on a group of CT images [30]. The visual results are shown in Figure 6, where the noisy CT images are added Gaussian white noise of variance = 0.02 as shown in Figure 6a–f) are the corresponding denoised results with AD, BF, KSVD, BM3D, and W-NMM. From Figure 6, we can find that the W-NMM algorithm has a better effect on Gaussian noise denoising. Compared with the other denoising methods, our algorithm can produce better results on noisy image denoising. The three-dimensional (3D) visualizations of the denoising effectiveness are exhibited in Figure 6 where two images are randomly selected from Figure 7 and their 3D visualizations are depicted before and after denoising with the proposed method. (a) are the noisy images and (b) are the corresponding denoised images with W-NMM. It can be observed that the proposed method removed the sharp noises, and the image regions become smooth while keeping the edges.

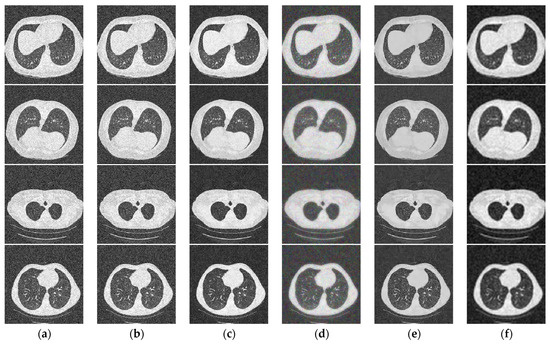
Figure 6. Comparison of different denoising methods on four images. (a) are noisy images. (b–f) are the denoised images with AD, BF, KSVD, BM3D, and our W-NMM method, respectively.

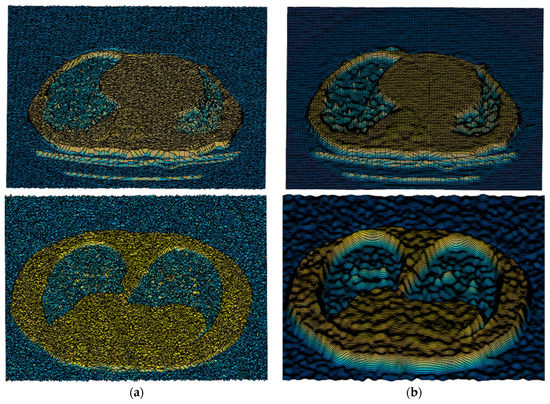
Figure 7. The 3D visualization of the denoising results of two images in Figure 6 with the WM-NLM method. (a) show the noisy images with Gaussian white noise, and (b) are the corresponding denoised results.

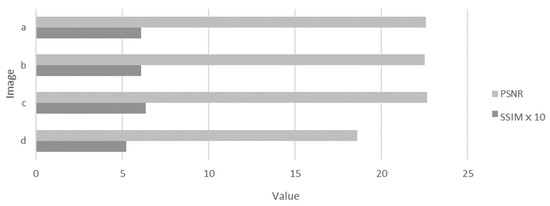
We evaluated the denoising methods (AD, BF, NLM, BM3D, and W-NMM) on the images in Figure 6 in terms of PSNR and SSIM. The results are shown in Table 2. We can find that our method achieved higher PSNR and SSIM than other methods. We test the methods on a group of medical images and compare their denoising effect, and the average results in terms of PSNR and SSIM are displayed in Figure 8. It can be observed that the W-NMM method is superior to the compared methods.

Table 2. Comparison of different denoising methods evaluated with PSNR and SSIM (The best results are shown in bold).

Image	I1		I2		I3		I4
Metrics	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
AD	18.48	0.2964	18.38	0.2407	18.42	0.2352	18.27	0.3298
BF	20.37	0.3593	19.95	0.3004	20.21	0.2965	19.71	0.3731
KSVD	22.61	0.5578	22.49	0.3787	23.34	0.5512	22.67	0.5660
BM3D	20.66	0.5479	23.63	0.5736	22.80	0.4603	21.15	0.4830
W-NMM	22.67	0.6219	24.20	0.6798	23.62	0.6557	22.43	0.6714

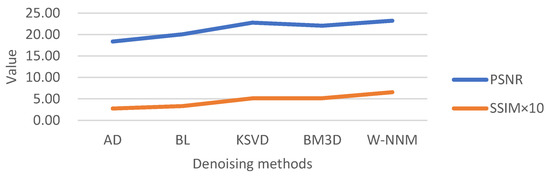
Figure 8. Comparison of the denoising performance with different denoising methods in terms of PSNR, and SSIM.

In order to test the validity of the two stages of filtering, we made an ablation experiment and the result is shown in Figure 9. S1 represents the result in the first stage, that is the corresponding image is denoised with wavelet filtering. S2 is the result in the second stage, that is the corresponding image was denoised with the NMM filter. It can be found that the SSIM was improved after the NMM filtering in the S2 stage.

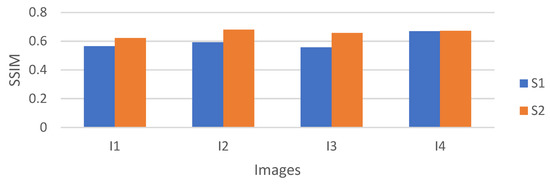
Figure 9. Ablation experiment of the W-NMM algorithm.

5. Discussion

In the process of digital image digitization and transmission, it is often affected by the noise of imaging equipment and the external environment, so that the image quality will be degraded. Image denoising is the process of reducing the noise in the digital image. The commonly used image denoising methods are suitable for processing images with low requirements on image details, that is to say, the loss of tiny details has little impact on the subsequent processing of image denoising. However, when dealing with medical images, such small mistakes are not allowed, because every small mistake in medical diagnosis or treatment can affect the doctor’s treatment and even threaten the patient’s life. So, we need good denoising techniques that can effectively remove noise while still preserving enough detail. It can be seen from the experiment that the algorithm proposed in this paper can effectively smooth the noise information in the image and keep the details of the image. Effective image denoising can not only help doctors diagnose the condition, but also be very conducive to the subsequent image segmentation, e.g., lung segmentation, providing help for computer-aided diagnosis.

Our algorithm achieved good performance on image denoising. However, the cost time is sometimes high, and the time efficiency is low due to the fusion of moments and the NLM approach. Our algorithm can generate the highest denoising effect with low time efficiency while the anisotropic diffusion filter has the highest time efficiency with the lowest PNSR. Accordingly, we can select suitable methods for different applications.

6. Conclusions

In this paper, we denoised the images with a wavelet-based non-local moment mean denoising algorithm. The proposed W-NMM algorithm combined frequency domain denoising with spatial domain denoising, and the introduction of moments increased the robustness of the denoising algorithm. The average of PSNR and SSIM achieved 23.3 and 0.66, respectively. In addition, it showed a better-denoised effect compared with several classical image denoising methods. It contributes to the subsequent image processing, such as image segmentation, 3D reconstruction, and so on. Nevertheless, the time cost was high because of the NLM operation. In the future, we will improve the time efficiency of our algorithm.