Abstract
Wireless medical sensor networks (WMSNs), a type of wireless sensor network (WSN), have enabled medical professionals to identify patients’ health information in real time to identify and diagnose their conditions. However, since wireless communication is performed through an open channel, an attacker can steal or manipulate the transmitted and received information. Because these attacks are directly related to the patients’ lives, it is necessary to prevent these attacks upfront by providing the security of WMSN communication. Although authentication protocols are continuously developed to establish the security of WMSN communication, they are still vulnerable to attacks. Recently, Yuanbing et al. proposed a secure authentication scheme for WMSN. They emphasized that their protocol is able to resist various attacks and can ensure mutual authentication. Unfortunately, this paper demonstrates that Yuanbing et al.’s protocol is vulnerable to smart card stolen attacks, ID/password guessing attacks, and sensor node capture attacks. In order to overcome the weaknesses and effectiveness of existing studies and to ensure secure communication and user anonymity of WMSN, we propose a secure and anonymous authentication protocol. The proposed protocol can prevent sensor capture, guessing, and man-in-the-middle attacks. To demonstrate the security of the proposed protocol, we perform various formal and informal analyses using AVISPA tools, ROR models, and BAN logic. Additionally, we compare the security aspects with related protocols to prove that the proposed protocol has excellent security. We also prove the effectiveness of our proposed protocol compared with related protocols in computation and communication costs. Our protocol has low or comparable computation and communication costs compared to related protocols. Thus, our protocol can provide services in the WMSN environment.
1. Introduction
With the development of wireless internet technology, the Internet of Things (IoT) has experienced rapid expansion, with a large number of sensors being deployed in IoT devices. Wireless Sensor Network (WSN) is an essential IoT technology that enables data collection, monitoring, and exchange in diverse environments, e.g., smart grid monitoring and smart healthcare using WSN [1,2,3]. Applying WSN to a smart healthcare environment and using it for medical monitoring is called Wireless Medical Sensor Networks (WMSNs).
Based on WMSN, medical personnel, such as doctors and nurses, can continuously monitor the health of patients. These healthcare systems collect various medical factors, such as pulse, blood pressure, ECG, and body temperature by medical sensors attached to the patient [4]. By continuously monitoring this information, medical personnel can quickly diagnose a patient. WMSNs, similar to typical WSNs, comprise of users, gateways, and medical sensor nodes. The user (medical professional) and the medical sensor node register their respective information in the gateway node, and the users is able to obtain the patient’s bio-information through the medical sensor node. However, since devices equipped with medical sensors have limited capabilities (e.g, transmission range, calculation, and storage capabilities), protocols that use heavy computations may cause communication failure of the system [4]. In addition, because WMSN exchanges information through wireless open channels vulnerable to attack, if an attacker obtains the information shared on the wireless channel, the attacker can obtain the patient’s medical information or deliver incorrect medical information to the user [5]. Thus, a communication failure of the system and manipulation of medical information by an attacker may result in a situation in which the patient’s condition cannot be determined. Since this is directly related to the patients’ lives, lightweight authentication among users, gateways, and sensor nodes based on a predetermined session key is essential for secure information exchange.
Therefore, in order to provide secure services using WMSN, researchers have proposed two-factor authentication protocols by adopting passwords and smart cards. However, the typical two-factor authentication protocol is not secure against guessing attacks and smartcard stolen attacks. Additionally, some researchers have argued that it is possible for attackers to guess ID/password pairs since users generate easy-to-remember ID/password pairs for their convenience [6,7,8].
In 2021, Yuanbing et al. [9] proposed an authentication scheme for smart healthcare by applying a WMSN. They argued that their protocol can resist against smartcard stolen, off-line guessing, and man-in-the-middle (MITM) attacks. They also said that their scheme can ensure mutual authentication and session key security. Unfortunately, we figure out that Yuanbing et al.’s scheme is not secure against off-line guessing, impersonation, sensor node capture, and MITM attacks. Furthermore, we discover that their scheme cannot provide session key security and mutual authentication. Our research contributions, motivations, and methodologies are discussed in Section 1.1.
1.1. Research Contributions, Motivations, and Methodology
Yuanbing et al. [9] analyzed Farash et al.’s protocol for secure authentication in smart healthcare systems and suggested an enhanced protocol. However, we identify security vulnerabilities in Yuanbing et al.’s protocol. Their protocol is vulnerable to offline ID/password pair guessing, impersonation, sensor capture, sensor impersonation, and MITM attacks over an WMSN, and does not guarantee essential security features. In addition, their protocol adopts elliptic curve cryptography (ECC), so the computation cost is high.
To overcome these problems, we propose a secure authentication protocol for smart healthcare based on WMSN. We adopt three-factor using the user’s biometrics, as well as smart card adoption to defend against ID/password pair guessing attacks. We also introduce Physical Unclonable Function (PUF) [10] technology to defend against sensor node physical capture attacks.
To prove the security of our protocol, we conduct formal and informal (non-mathematical) security analysis. We use the widely adopted Real-Or-Random (ROR) model [11] and Burrows Abadi Needham (BAN) logic [12] to perform formal analysis. Furthermore, we use the AVISPA [13] for proving that the proposed protocol can be secure against replay and MITM attacks. By comparing the proposed protocol with other authentication protocols, the efficiency is analyzed in terms of security, communication costs, and computational costs.
1.2. Organization of the Paper
The rest of this paper is structured as follows: In Section 2, we review diverse authentication protocols using WMSN. We briefly describe the protocol’s system model, adversary model, PUF, and fuzzy extraction in Section 3. We review the protocol of Yuanbing et al. in Section 4. We present a cryptographic analysis of the protocol in Section 5. Section 6 explains our proposed protocol and there is a security analysis in Section 7. We analyze the computation and communication costs of the protocol in Section 8. Finally, the work is summarized in Section 9.
2. Related Works
Research on authentication protocol for the WSN environment has been continued since Lamport [14] proposed a password-based authentication protocol for various network environments in 1981. We briefly review authentication protocols related to WMSN and wearable devices in the WSN environment. In 2012, Kumar et al. [15] suggested a new authentication protocol in the WMSN environment. They explained that the proposed protocol using only symmetric encryption and hash functions is effective to protect communication security. However, He et al. [6] found that the scheme of Kumar et al. was not secure against offline password guessing attacks, which could lead to guessing the user’s identity. To overcome this security vulnerability, He et al. proposed an improved authentication protocol for resource-limited sensors. Unfortunately, Li et al. [16] pointed out that He et al.’s protocol is wrong in the protocol in the authentication and session key agreement phase. Li et al. proposed an authentication scheme using biometrics. Das et al. [17] found that Li et al.’s scheme is vulnerable to privileged insider attacks, smart device physical capture attacks, and fails to maintain the anonymity of users and smart devices. In 2018, Amin et al. [18] suggested a lightweight two-factor authentication protocol for protecting data transmitted in the WMSN environment. However, Jiang et al. [19] discovered that their protocol is vulnerable to mobile device loss attacks due to failed delivery, sensor key exposure, and desynchronization attacks. Jan et al. [20] also found that security flaws of Amin et al.’s protocol. Then, Jan et al. introduced a two-factor-based authentication scheme for WMSN. In 2020, Fotouhi et al. [21] proposed a lightweight two-factor-based authentication protocol for healthcare monitoring systems. However, Nashwan [22] figured out that Fotouhi et al.’s scheme cannot support full mutual authentication. In 2021, Masud et al. [23] designed a lightweight and privacy-protected authentication protocol for IoT-based healthcare using the sensors of an IoT device carried out by a patient. However, Masud et al.’s protocol is also insecure against offline password guessing, user impersonation, and privileged insider attacks, and do not provide user anonymity [24].
Moreover, some researchers have pointed out that these traditional two-factor authentication protocols are vulnerable to ID/password simultaneous guess attacks [6,7,8]. Accordingly, a three-factor authentication protocol was proposed using the user’s biometric information.
In 2018, Ali et al. [25] discovered the problems of the protocol of Amin et al. [18] and introduced an authentication protocol based on three factors to solve the problem. However, their proposed protocol also cannot protect against desynchronization attacks or achieve full forward secrecy [26]. Shuai et al.’s protocol [26] uses a pseudonymous identification method to ensure forward secrecy, provide user anonymity, and resist desynchronization attacks. However, Nashwan [22] discovered that Shuai et al.’s protocol is not able to support the sensor node’s anonymous service and cannot protect against sensor node impersonation attacks. Mo et al. [27] also found that Shuai et al.’s protocol has a flaw at the password change phase. Then, Mo et al. proposed an enhanced protocol for WMSN. Li et al. [28] suggested an authentication scheme that guarantees perfect forward secrecy in the WMSN environment by using a three-factor method. However, their protocol also cannot guarantee the security of the sensor node and is vulnerable to sensor node spoofing attacks [29].
Since the three-factor-based authentication protocol for the WMSN-based medical system is also vulnerable to sensor node vulnerabilities and sensor node spoofing attacks, an improved system is designed according to a new technology called PUF. In 2018, Gope and Sikdar [30] designed a two-factor authentication scheme using PUF technology in the IoT environment. However, their protocol cannot resist ephemeral secret leakage (ESL) attacks and desynchronization attacks [31].
Authentication protocols using technologies such as multi-factor and PUF have been continuously proposed for the WMSN environment, but security vulnerabilities still exist. When security vulnerabilities occur in the WMSN environment, the patient’s medical information can be manipulated or leaked by a malicious attacker. The recently proposed protocol of Yuanbing et al. [9] is not safe against ID/password pair guessing attacks and spoofing attacks, and the security of sensor nodes cannot be guaranteed either. In this paper, we not only analyze the security vulnerabilities of Yuanbing et al.’s protocol, but also the proposed protocol, which can solve the security vulnerabilities that can occur even when using three-factor and PUF technology.
3. Preliminaries
We introduce the system model of the proposed protocol and the adversary model for protocol security analysis. In addition, the security technologies adopted by the proposed protocol, PUF, and fuzzy extraction will be briefly described. The symbols used in this paper are given in Abbreviations.
3.1. System Model of Our Protocol
The proposed system model is shown in Figure 1. Our proposed protocol consists of the following entities:
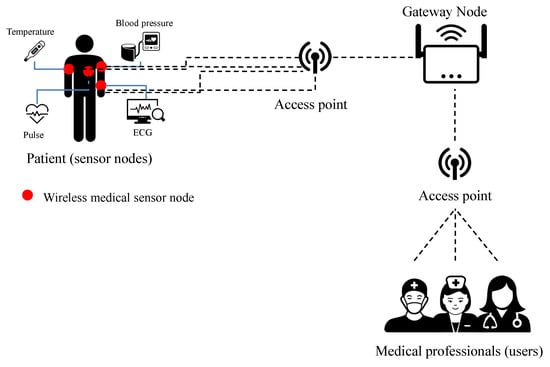
Figure 1.
The proposed system model.
- User (Medical Professional): The user obtains the patient’s sensor node information by requesting communication to the gateway. To this end, users register their information with the gateway and agree on a session key with the sensor node. In the future, only registered users can request communication to the gateway and use secure services through the session key.
- Sensor node (patient): The sensor node that the patient is equipped with collects various health information of the patient (e.g., body temperature, blood pressure, pulse, and ECG). The patient’s sensor nodes transmit the collected information to the user through the session key. Through this, the user can identify and diagnose the patient’s condition. Sensor nodes are resource-limited devices.
- Gateway node: A gateway is a trusted entity that performs registration and authentication processes, and regulates the authentication of users and sensor nodes. All users and sensor nodes must be registered with the gateway to acquire session keys and to communicate.
- Access point: The access point is a wireless connection between the patient’s sensor node and the gateway and between the user and the gateway. The communication between each access point and each entity is considered securely authenticated.
Sensor nodes and users must first register through the gateway. When sensor nodes and users request registration, the gateway stores their related registration information and controls communication between the users and sensor nodes. The users and relevant sensor nodes agree on a session key through the gateway, and secure communication can be achieved later through the agreed session key. The proposed protocol is composed of registration, login and authentication, and password and biometric update phases. At the registration phase, sensor nodes and users register their information through the gateway. Users, gateways, and sensor nodes perform mutual authentication at the login and authentication phase, and they agree on a session key for communication. At this time, our protocol uses the user’s biometric information to defend against malicious attacker’s ID/password pair guessing attack. In addition, the sensor node has a built-in PUF technology that guarantees security against physical capture attacks. Later, the user is able to safely collect the sensor node information by using the session key, and can manage the patient’s health based on this. At the password and biometric update phase, users are able to update passwords and biometrics.
3.2. Physical Unclonable Function
To securely store secret values and identity information in sensor nodes, we adopt PUF technology. PUF is able to be portrayed as “the representation of the instance-specific functionality, non-replicable, and unique of a physical entity” [10]. The uncertainty and randomity of the integrated circuit manufacturing are less likely to generate a duplicate value, so the PUF attracts more attention. A PUF receives challenge C and then obtains the response R through the physical properties of integrated chip and C. The allowed C and the generated R can be represented by the string of the bit. This operation can be expressed as Equation (1).
and this is like the nature of a one-way function. Ideally, there is a one-to-one correspondence between the PUF and the C/R pair. Furthermore, if the same PUF is challenged multiple times, responses will be the same, but the responses obtained for different PUFs will be different when given the same challenge. Additional characteristics of PUF are:
- It is not possible to clone a PUF to generate the same sensors or devices [32].
- If an attacker tries to change the sensor or device that the PUF is mounted on, the sensor or device will change the behavior of the PUF and destroy the PUF [33].
- In practical circuit manufacturing, the differences in input and output function mapping are fixed and unpredictable [34].
However, in a realistic situation, due to environmental and circuit noise, it is difficult for a PUF to always return the same R because of the small margin of error of C. To solve this, PUF has been applied together with fuzzy extraction technology [35].
3.3. Fuzzy Extraction
Fuzzy extraction [35] can be used to solve noise problems that may occur in biometric inputs. Furthermore, fuzzy extraction can also help with noisy PUF. The fuzzy extractor can get the same value by removing the noise through the function and the algorithm.
The algorithm generates key information that can respond to input values such as C of PUF or of biometric information. In other words, if the data is used as an input to the algorithm, the secret key data is output, and it is a uniform random string. At the same time that is output, the fuzzy extractor outputs the to help recover the key values and remove noise. This algorithm could be presented as Equation (2).
The algorithm can restore the secret key from and the entered C and values. First, input data such as C or and helper strings are input to the algorithm. This can cause noise in data . In this case, helps remove noise and restore data to output the correct . The metric spatial distance between and must be within the specified tolerance for the fuzzy extractor to recover a matching . This algorithm could be presented as Equation (3).
3.4. Adversary Model
We use the “Dolev–Yao (DY) adversary model [36]” to conduct the security analysis of the protocol proposed by Yuanbing et al. To this end, we first discuss the attack potential of attackers according to the DY model.
- According to the DY model, attackers have full control and learning of the messages exchanged on open wireless channels that are vulnerable to attack. They can then modify, remove, or insert legitimate messages.
- Attackers can obtain or steal users’ legitimate smart cards. After that, they can obtain the secret information stored on the smartcard by performing power analysis attacks [37,38].
- After obtaining the secret information of the smart card or sensor node, the attacker can try potential attacks such as offline identity guessing attacks, impersonation, and so on [39,40].
- Attackers can guess a user’s identity and password pairs in polynomial time.
In addition to the DY model, we also adopt the “Canetti–Krawczyk (CK) adversary model” [41]. The CK model is a more practical attacker model compared to the DY model. According to the CK model, for the consensus session key to be secure, the key exchange protocol must minimize the impact of long-term or short-term secret leaks.
4. Review of Yuanbing et al.’s Protocol
This section briefly presents the Yuanbing et al.’s authentication protocol for a smart healthcare system based on WMSN.
4.1. Pre-Deployment Phase
In this phase, a system administrator adopts that only the knows in offline mode, and predefined , which is the ID of each sensor node . The system administrator also sets a pre-shared key for each with the associated . The protocol of Yuanbing et al. uses the shared key at the sensor node registration phase. It is important to note the password is deleted from ’s memory once is successfully registered.
4.2. Sensor Node Registration Phase
registers its information in at this phase. The detailed steps are as follows.
Step 1: chooses a random nonce , and calculates and . After that, transmits to the gateway.
Step 2: checks the timestamp. If the condition holds, calculates . Then, computes and checks if . If it is the same, computes , , , and . Then, sends to .
Step 3: checks the timestamp. If the condition is correct, calculates and checks if . If it is correct, computes . stores in its memory. Then, deletes the and sends a respond message to .
Step 4: Upon receiving the response message, removes .
4.3. User Registration Phase
Users (such as nurses and doctors) must first register with the when they want to obtain the patient’s medical data at this phase. The detailed steps are as follows.
Step 1: The user selects their and , . Then, calculates , , and . After that, sends to .
Step 2: calculates , , , and . Then, stores into and issues it to .
Step 3: computes and stores into .
4.4. Login and Authentication Phase
At this phase, agrees on a session key by conducting mutual authentication with before accessing the patient’s medical information. The detailed steps are shown in Figure 2 and described below.

Figure 2.
Login and authentication phase.
Step 1: The user inserts , and inputs and . computes , , , and . Then, checks if . If it corrects, generates random nonce a and c, and computes , . also calculates , , , , and . Then, sends to through an open channel.
Step 2: checks . If this condition holds, generates timestamp and random nonce b. computes , , and . After that, transmits to through an open channel.
Step 3: After receiving the message, checks . If this condition holds, computes and . Then, checks . If it holds, computes and . checks . If it is correct, computes , , and . Then, sends to .
Step 4: Upon receiving the message, checks . If this condition holds, checks . If these values are the same, computes , , and . Finally, sends to .
Step 5: Upon receiving the message, checks . If this condition holds, computes , , and . After that, checks . If it corrects, and shares the same at the end.
5. Security Analysis of Yuanbing et al.’s Protocol
We conduct the security analysis proposed by Yuanbing et al. [9] in this section. Yuanbing et al. demonstrated the ability of their protocol to resist diverse types of attacks. They also claimed that it is capable of providing anonymity. However, we contend that their protocol is vulnerable to smartcard theft, impersonation, sensor node capture attacks, and so on. Further, we prove that it fails to provide user anonymity in some cases.
5.1. Off-Line Guessing Attacks
A malicious attacker is able to acquire secret credentials stored in the smartcard, as discussed at Section 3.4. Furthermore, can also obtain transmitted messages over insecure channels. Finally, is able to guess the ID and password pair. The detailed steps are as follows:
Step 1: can obtain the stored values from the smartcard through power analysis attacks, and selects the guessing ID/password pair .
Step 2: computes , , , and . Then, checks if .
Step 3: If these values match, is considered to have successfully guessed the legitimate user’s ID and password pair. If they do not match, repeats Step 1 and 2 again to guess .
5.2. Impersonation Attacks
If can successfully guess the legitimate identity and password pair of a user through Section 5.1, computes a valid to perform user impersonation attacks. The detailed steps of user impersonation attacks are as follows.
Step 1: If succeeds in guessing the ID/password pair of , then can compute a valid . Then, can calculate using the values and stored in the ’s smartcard. can also compute using stored values in the smartcard.
Step 2: After that, chooses random nonces and and timestamp . Subsequently, can compute , , , , and . Thus, can compute the login request message . Therefore, can conduct successful impersonation attacks.
5.3. Sensor Node Impersonation Attacks
can obtain the stored in through sensor node capture attacks. can then use the obtained values to compute a valid message and impersonate it as a valid . After the sensor node capture attacks, can perform sensor node impersonation attacks as follows:
Step 1: can acquire the values stored in through the sensor node capture attack. Then, chooses random nonces and . Subsequently, calculates .
Step 2: can obtain the values through the message sent to insecure channels. can calculate , , . chooses a random nonce and timestamp . Subsequently, can compute , , . Then, sends the message to . Thus, we can say that can impersonate the sensor node.
5.4. MITM Attacks
After sensor node impersonation attacks, can conduct MITM attacks using . The detailed steps are as follows:
Step 1: When receives the message , computes using obtained through sensor node capture attacks.
Step 2: Then, can compute the fake session key . also computes . Finally, sends the message to .
5.5. Fail to Ensure Anonymity and Mutual Authentication
Yuanbing et al. argued that the proposed protocol guarantees anonymity and provides mutual authentication. However, according to Section 5.1, is able to obtain the legitimate user’s real ID . Furthermore, according to Section 5.2 and Section 5.3, can impersonate the user or sensor node. In particular, according to Section 5.4, can interfere with mutual authentication by performing a man-in-the-middle attack. Therefore, Yuanbing et al.’s protocol fails to ensure user anonymity and mutual authentication.
6. Proposed Protocol
We propose a secure authentication protocol to overcome the problems of Yuanbing et al.’s proposed protocol. It utilizes the user’s biometrics to prevent off-line guessing attacks of ID/password pairs. We also introduce PUF technology to prevent capture attacks of sensor nodes. Therefore, the proposed protocol is found to be secure against various attacks. Additionally, the proposed protocol is a lightweight protocol to take into account the resource limitations of sensor nodes.
6.1. User Registration Phase
A user who wants to communicate with a specific must register with . The detailed steps are shown in Figure 3 and explained below.
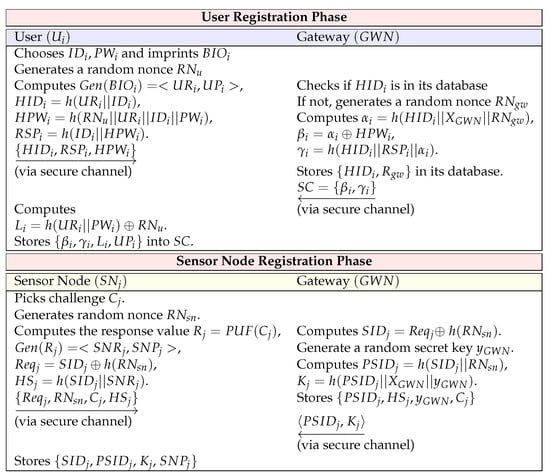
Figure 3.
Registration phase.
Step URP1: User chooses identity and password , and imprints their biometrics . generates a random nonce . Then, computes , , , and . Subsequently, sends to through a secure channel.
Step URP2: Upon receiving the message , checks if is in its database. If not, creates a random nonce . calculates , , and . Subsequently, saves in its database and also stores in . Then, issues to via a closed channel.
Step URP3: After receiving from , computes and stores and in . Finally, stores .
6.2. Sensor Node Registration Phase
is assigned an ID by the system administrator before being deployed. To register in , selects the PUF’s challenge and computes and the registration request message. After receives the registration request message, calculates and sends the values required for authentication to . The proposed protocol considers the data load for sensor nodes with limited capabilities. The sensor node stores only . Assuming that the ID and hash values are 160 bits, the value stored by the sensor node is only 640 bits. The sensor node registration steps are as follows and shown in Figure 3.
Step SRP1: chooses challenge value , and generates random nonces . Then, computes the response value . Furthermore, computes , , and . sends to via a closed channel.
Step SPR2: When receives the message , computes . creates a random secret key , and calculates and . stores in its database and sends to .
Step SPR3: Upon receiving the message , stores in its secure memory.
6.3. Login and Authentication Phase
In the login and authentication phase, a session key is generated for to communicate with a specific . All entities perform mutual authentication through message verification, and when mutual authentication is successful, a session key for future communication is agreed upon. In the proposed protocol, the user manually selects a new pseudo ID . When authentication is complete, the user updates the and values associated with . It is assumed that the IEEE 802.15.4 protocol is used for communication between the sensor node and the , and the IEEE 802.11 protocol is used for communication between the and the user [42]. The detailed steps are shown in Figure 4 and are described in detail below.

Figure 4.
Login and authentication phase.
Step AP1: inserts and inputs . computes , , , , , and . Then, checks . If it holds, generates a random nonce and timestamp . computes and . picks new pseudo identity and computes . Then, sends to through insecure channels.
Step AP2: Upon receiving the message , checks . If it holds, retrieves from its database and calculates , , and . checks . If it is not correct, then terminates the session. Otherwise, calculates . Then, fetches corresponding to . generates a random nonce and timestamp . computes , , , and . After that, sends to through an open channel.
Step AP3: After receiving the message from , checks . If it holds, computes , , , , , and . checks . If it corrects, generates a timestamp and calculates . computes and sends to .
Step AP4: When receives the message , checks . If it holds, computes the session key , and computes . Then, checks . If they are same, computes , , , and . sends the message . If session key agreement is successful, updates to . Otherwise, keeps .
Step AP5: When receives the message , calculates , and computes , and . checks . If they are same, computes and . Then, updates and . Finally, , , and agrees the same session key .
6.4. User’s Password and Biometrics Update Phase
may want to change their password and biometrics. To reduce computation and communication costs, we propose this phase to be executed locally without additional connections with .
Step 1: inserts their and inputs , , and biometrics . Then, computes , , , , , and . checks . If it corrects, asks to input a new biometrics and a new password .
Step 2: inputs a new biometrics and a new password . proceeds to compute parameters , , , , , and . Then, replaces with .
7. Security Analysis
This section analyzes the security of the proposed protocol. We prove that session key agreement and mutual authentication of our protocol can be securely achieved through the commonly used ROR model and BAN logic. Through AVISPA simulation tools, we show that the protocol is secure against replay and MITM attacks. At last, through informal security analysis, we demonstrate that the proposed protocol is secure against a variety of attacks.
7.1. ROR Model
Thorugh the ROR model, we demonstrate the session key security of the proposed protocol [43,44,45]. We present the brief explanation of the ROR model. In the ROR model of our protocol, there are three participants , which are user node , gateway node , and sensor node . , , and are the instances for , , and , respectively. We assume that can intercept, eavesdrop, delete, or modify messages exchanged via an open wireless channel. Additionally, can conduct security attacks through various queries, such as , , , , and . Detailed descriptions of these queries are as follows.
- : can conduct this query for obtaining transmitted messages via public channels between , , and .
- : indicates that the adversary can extract secret data stored in of .
- : is able to reveal the current session key between , , and by executing this query. is safe if fails to reveal using this query.
- : Using the query, an adversary is able to send a message to participants and receive response messages.
- : An unbiased coin is flipped to start the game, and the result is only known to . uses this result to determine the . When runs the query, returns for = 1 or a random number for = 0. Otherwise, it returns a null (⊥).
must distinguish the result value after conducts query over . checks the consistency of the random bit using results of the query. is able to win the game if the guessed bit equals . Additionally, has access to the collision-resistant cryptographic one-way hash function , which is modeled as a random oracle, .
Security Proof
Theorem 1.
An adversary attempts to calculate in polynomial time. Let be the advantage that can break the session key security of the proposed protocol. Then, we obtain the following.
and indicate that they are the span spaces of the function and the hash function , respectively. , , and are the number of , , and queries, respectively. In addition, is the number of bits in biometric of , and C and s denote Zipf’s parameters.
Proof.
The five games, , where , are conducted to prove the security of of the proposed protocol. indicates the event in which wins by guessing the random bit correctly. We represent the probability that wins the game as . This is followed by the description of each game.
- : executes a real attack to our protocol. chooses a random bit at the beginning of . The following advantage of is about this game.
- : executes the query and eavesdrops messages , , , and . After that, performs and queries to verify whether the derived is real. In the proposed protocol, is made up of long-term and short-term secrets. To derive , needs to know the identities and random nonces of , , and . As a result, cannot increase the winning probability of . Therefore, the probabilities of and are indistinguishable.
- : In this game, executes and queries to obtain the session key. attempts to attack by modifying the exchanged message. However, all messages are masked with one-way hash function , random nonces, and secret credentials. cannot derive any information due to a computationally infeasible problem of . Hence, using the birthday paradox, we can get the following equation.
- : This game is performed in analogy as described in . executes and queries. However, the probability obtained by the query is similar with the query since the physical function has security properties mentioned in Section 3.2. Therefore, we are able to acquire the following equation.
- : In the final game , tries to get with the query. With query, is able to extract sensitive values stored in the smart card of , which are expressed as , , and . For computing , should guess these parameters from the extracted values since has no knowledge of identity , password , and biometric . However, it is a computationally infeasible task for to guess , , and simultaneously. In conclusion, and are indistinguishable. We can derive the following result by utilizing Zipf’s law.
After all games are completed, must guess the to win the game. Therefore, we obtain the following equation.
Finally, the desired result can be obtained by multiplying both sides of Equation (10) by two.
Therefore, we prove Theorem 1. □
7.2. BAN Logic
BAN logic is a widely used mathematical proof method for demonstrating mutual authentication in security schemes [46,47]. With BAN logic, we prove that the proposed protocol can ensure mutual authentication. The notations of BAN logic are described in Table 1.

Table 1.
BAN Logic Notation.
7.2.1. Rules
The rules used in BAN logic are as follows.
- Nonce verification rule ():
- Message meaning rule ():
- Jurisdiction rule ():
- Freshness rule ():
- Belief rule ():
7.2.2. Goals for Mutual Authentication
To prove that the proposed protocol provides mutual authentication, we present the following goals.
- Goal 1:
- Goal 2:
- Goal 3:
- Goal 4:
- Goal 5:
- Goal 6:
- Goal 7:
- Goal 8:
7.2.3. Idealized Form of Exchanged Messages
We describe the idealized form of BAN logic as the message exchanged in the authentication phase as follows.
- :
- :
- :
- :
7.2.4. BAN Logic Initial State Assumptions
We construct all the considered assumptions as follows.
- :
- :
- :
- :
- :
- :
- :
- :
- :
- :
- :
- :
7.2.5. Proof of Providing Mutual Authentication
We will now prove that our protocol can guarantee mutual authentication with an idealized form, predefined BAN logic rules, and assumptions. The proof process is as follows.
- Step 1:
- is obtained from .
- Step 2:
- is obtained from the using and .
- Step 3:
- can be gained from the with and .
- Step 4:
- can be acquired by applying the with and .
- Step 5:
- is obtained from .
- Step 6:
- is gained from using and .
- Step 7:
- can be obtained by applying with and .
- Step 8:
- can be obtained from with and .
- Step 9:
- From , is obtained.
- Step 10:
- is gained from with and .
- Step 11:
- can be obtained by applying with and , since .
- Step 12:
- can be obtained from with and .
- Step 13:
- is obtained from .
- Step 14:
- is obtained from with and .
- Step 15:
- can be obtained from with and , since .
- Step 16:
- can be obtained by using on and .
- Step 17:
- and can be obtained from and since .
- Step 18:
- and can be obtained from with , , , and .
- Step 19:
- and can be obtained from and since .
- Step 20:
- and can be obtained by applying from , , , and .
We prove that the proposed scheme meets all the goals in Section 7.2.2. Therefore, the proposed protocol ensures secure mutual authentication.
7.3. AVISPA Simulation Analysis
We use the “AVISPA Simulation Tool” [13] in this section to validate our proposed system security against man-in-the-middle and replay attacks.
In AVISPA, there are four backends: “Tree Automata based on Automatic Approximations for “Tree Automata based on Automatic Approximations for Analysis of Security Protocols (TA4SP)”, “SAT based model checker (SATMC)”, “On-the-fly-mode-checker (OFMC)”, and “Const- raint-logic-based Attack Searcher” (CL-AtSe)”. Among these, SATMC and TA4SP backends can not aid “bitwise exclusive OR (XOR)”. However, since our system has an XOR operation, two backends are not suitable for analysis. Therefore, we adopt two backends, OFMC and CL-AtSe, which support XOR operations, and use them for analysis. In the proposed system, “High-Level Protocol Specification Language (HLPSL)”, a language supported by AVISPA, is used to implement the basic roles of , and . Figure 5 shows the HLPSL implementation of the role user.

Figure 5.
HLPSL specification for user.
At transition 1, sends the request message to using the operation and , which means the secure channel. The declaration means that the password and biometrics is only known to . The declaration means that is only known to and .
At transition 2, receives the smartcard. In login and authentication phase, sends the message to through insecure channels. The declaration means that generates a random nonce for .
At transition 3, receives the message from . The declaration specifies the request to the for checking the value of .
The HLPSL of the gateway node and sensor node is implemented similarly to the user’s HLPSL. In addition, it implements the “composite roles and goals for sessions and environment” of the proposed system through HLPSL. In the sessions and environment, it specifies whether secret maintenance and authentication of each value are successfully performed through , , and declared in the HLPSL of each entity. AVISPA used in this section is a security validation simulation based on the DY model [37].
Figure 6 is a screen showing the intruder simulation step-by-step according to the HLPSL configured in the CL-AtSe mode. It is a simulation in which knowledge is leaked to the intruder one-by-one for each step. In addition, the intruder knows the message transmitted through the wireless channel. Although this information is leaked to the intruder, we can see that our protocol is safe, as shown in Figure 7. Therefore, for replay attack inspection, AVIPA backends (such as OFMC and CL-AtSe) first verify that a legitimate agent can execute a specific protocol. It then provides the intruder’s knowledge of some legitimate sessions between legitimate agents. In addition, the DY model ensures that OFMC and CL-AtSe backends are capable of MITM attacks by intruders. Figure 7 gives the analysis results performed on the CL-ATse and OFMC backends. The results are shown in Figure 7 show that the proposed protocol is “safe” on the backends, which proves that our protocol is secure against replay and MITM attacks.
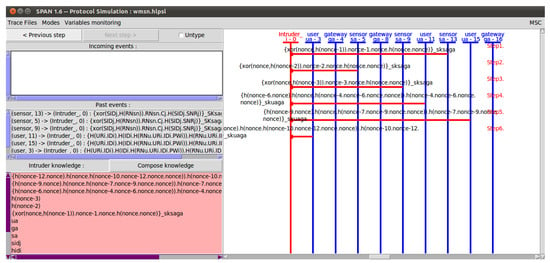
Figure 6.
AVISPA implementation results.

Figure 7.
AVISPA simulation results.
7.4. Informal Security Analysis
We demonstrate through informal security analysis that the proposed protocol can provide various security features are secure against various attacks.
7.4.1. Offline Guessing Attack
Adversary attempts to guess the user’s identity or password from the values contained in the user’s smartcard or messages on public channels. can obtain sensitive information through the guessed ID/password. However, our protocol is secure against offline guessing attacks. is able to obtain stored in through smartcard stolen attack. needs to compute to guess the ID/password of a valid . However, consists of and . In order for to calculate , it needs to know the user’s biometric key and the user’s ID. Furthermore, in order for to figure out , must have the biometric key , as well as valid , and random nonce . Therefore, cannot compute the user’s and according to the “computational infeasible problem”. Therefore, since cannot guess the user’s ID and password, the proposed protocol can guarantee the resilience of offline guessing attacks.
7.4.2. Privacy Preserving and Anonymity
may trace the use of services of through an identity or pseudonymous ID or intercept personal information. However, our protocol guarantees privacy by preserving and can provide anonymity. tries to obtain ’s real identity information through ’s information or transmitted messages. However, cannot obtain the real identity or pseudo identity because these values are hidden in the hash function and . Although pseudo identity is transmitted via an open channel, is updated when the authentication and key agree. Moreover, is masked by . Therefore, is always updated in every session. Therefore, the proposed protocol can preserve ’s privacy and anonymity property.
7.4.3. Impersonation Attack
attempts to impersonate , , and to obtain valid information. To obatin valid information, must be able to calculate messages sent via wireless channels. However, messages sent to the public channel change every session due to the , , and timestamp values. Furthermore, cannot compute a valid message because is also updated to upon successful authentication. Therefore, our protocol is security from impersonation attacks.
7.4.4. Sensor Node Physical Capture Attack
performs sensor node physical attack to acquire stored in . However, cannot compute the correct session key even if it gets the stored values. For to compute the session key, needs to be calculated. However, in the sensor node registration phase, the valid and cannot be obtained because the sensor randomly generates , which is different from the value of each sensor. Because is a value that generates, it cannot be physically replicated. Furthermore, the compromise in does not help compute the session key between and any other uncompromised medical sensor. Therefore, the proposed protocol is used to secure the sensor node’s physical capture attack.
7.4.5. Replay and MITM Attack
is able to obtain the information stored in and of valid and can acquire messages sent to the public channel. However, cannot count valid messages generated by and , as mentioned in Section 7.4.3 and Section 7.4.4. In addition, every message changes every session because of the and timestamp values. Therefore, it can be said that our protocol is safe to replay MITM attacks.
7.4.6. Desynchronization Attack
An attacker could delay the updating of , thereby interrupting the entity from being authenticated. These attacks are called desynchronization attacks. In our protocol, picks up a new during the login and authentication phase and passes it to the . After that, updates and with and upon successful authentication, and transmits the related values to . At this time, maintains if authentication is not successful. Moreover, if does not succeed in authentication, the existing is kept, and the login and authentication phase is performed again. Therefore, even if the login and authentication phase is blocked by , and can keep the original . Therefore, the proposed technique can resist desynchronization attacks.
7.4.7. Stolen Verifier Attack
Even if the information in the verfier table stored in the gateway is leaked to , must not be able to impersonate the user and sensor, and must also be unable to calculate the session key. Assume that obtains ’s verification tables and to perform impersonation attacks or compute the . However, cannot compute and without ’s secret key . Furthermore, owing to the nature of the , could not calculate . Thus, cannot perform impersonation attack and compute . Therefore, the proposed protocol can be said to be resistant against a stolen verifier attack.
7.4.8. Perfect Forward Secrecy
Even if the private key of is leaked to , should not be able to compute the session key of the previous session. Assuming that the private key of is leaked by , attempts to calculate a valid using the obtained . However, in the registration phase of and , and are masked with and is randomly generated by . Therefore, cannot compute valid and , so it is impossible to compute valid . Therefore, our protocol can guarantee complete forward secrecy.
7.4.9. Session-Specific Random Number Leakage Attack
Assume that , a random nonce generated in the session, is leaked to . Using this value, will help compute . However, is not able to calculate the valid . To calculate a valid , needs to calculate and . In order to calculate and , need to compute or obtain the values of , , and , but it is impossible. Therefore, the proposed protocol is secure against session-specific random number leak attacks.
7.4.10. Ephmeral Secret Leakage Attack
According to the CK attack model, when long-term or short-term secrets are leaked to , can calculate a valid session key. In our protocol, has acquired long-term secrets (e.g., and ). In this way, the session key = includes and as well as is also included. cannot calculate the correct without knowing these values. Furthermore, according to Section 7.4.9, even if a short-term secret value is leaked, cannot compute . Therefore, our method is resistant to ESL attacks.
7.4.11. Session Key Security and Mutual Authentication
computes to obtain sensitive information or attempts mutual authentication by disguising itself as a valid entity. However, as discussed in Section 7.4.7–Section 7.4.10, cannot compute a valid because of a “computationally infeasible problem”. Additionally, in our proposed protocol, all entities verify each message and mutually authenticate each other. At this time, messages are changed every session due to random number and timestamp and are encrypted with long-term key and short-term key. Therefore, an attacker cannot impersonate a valid entity. Therefore, the proposed protocol guarantees secure session key security and mutual authentication.
8. Efficiency Analysis
We compare communication and computation costs, and security aspect with related protocols for showing the efficiency of our proposed protocol.
8.1. Functionality and Security Features Comparison
This section compares the proposed protocol to related protocols in replay and MITM, guessing, impersonation, device or sensor capture, and desynchronization attacks. We also compare the provision of security features such as forward secrecy and anonymity. Table 2 indicates that the proposed protocol meets all essential security for communication in a WMSN, whereas existing protocols do not satisfy all security requirements.

Table 2.
Security and functional properties comparison.
8.2. Computation Costs Comparison
The cryptographic computation costs in [30,48] are used for comparative analysis of the computational costs. For the computation cost of cryptographic functions, except PUF and fuzzy extractor, the PBC library (version 0.5.12) built in the GMP library is used on a personal computer environment with Intel Pentium Dual CPU E2200 2.20 GHz processor, 2048 MB RAM, and Ubuntu 12.04.1 LTS 32-bit operating system [48]. The computational costs of PUF and fuzzy functions are obtained in the environment of a single-core 798 MHz CPU with 256 MB RAM, adopting a code offset mechanism using BCH, assuming a 128-bit arbiter PUF [30]. Accordingly, we assumed the times for the notation of the cryptographic function and the computational cost of the function as follows: , , , , , , and denote hash function, point multiplication, encryption, decryption, fuzzy extraction, PUF function, and random nonce generation. The execution time for , , , , , , and are 0.23 ms, 2.226 ms, 3.85 ms, 3.85 ms, 2.68 ms, 12 ms, and 53.9 ms. Table 3 provides an overview of the comparison results.

Table 3.
Computation costs at login and authentication phase.
8.3. Communication Costs Comparison
In this secion, we compare the communication costs of our protocol and related protocols at the login and authentication phases. For comparison, assume that the hash value, entity ID, random nonce, and symmetric encryption value are 160 bits and the ECC value is 320 bits at the 160 bit security level of Fp, AES, and SHA1 [49]. We also assume that the timestamp value is 32 bits [50]. Based on these assumptions, the communication cost of our protocol is analyzed. Message , , , and have (160 + 160 + 160 + 160 + 160 + 32 = 832), (160 + 160 + 160 + 32 = 512), (160 + 32 = 192), and (160 + 160 + 160 = 480) bits are required. The total communication cost is bits. Table 4 shows an analysis of communication costs of related protocols.

Table 4.
Communication costs at login and authentication phase.
8.4. Results of Comparative Analysis
The results of the comparative analysis of the proposed protocol and other studies are as follows. Our proposed protocol has higher computation and communication costs than Ali et al.’s protocol [25]. However, in terms of security, Ali et al.’s protocol is vulnerable to sensor capture and desynchronization attacks and does not guarantee perfect forward secrecy, but the proposed protocol is safe against various attacks and guarantees perfect forward secrecy. In addition, our protocol has a computation cost of 132.98 ms, which is lighter than other papers except for the protocol of Ali et al. Furthermore, the communication cost of our protocol is 2016 bits, which is higher than that of Ali et al., 1952 bits, but there is no big difference. In other papers, the communication cost of the proposed protocol is low. Moreover, from a security perspective, our proposed protocol is secure to replay, MITM, impersonation, smartcard stolen, and desynchronization attacks. PUF and three-factor can be used to provide security against ID/password pair guessing and sensor node capture attacks. Therefore, the proposed protocol can provide secure services to users in a WMSN environment and is a lightweight protocol that considers the resource limitations of sensor nodes.
9. Conclusions
With the development of WSN, patient status identification and medical diagnostic services using WMSNs, a type of WSN, have become common. However, since WMSN exchanges information through an open channel, it is vulnerable to attacks by attackers, and this vulnerability is an important security problem directly related to the patient’s life. Therefore, in order to provide a secure WMSN service, an authentication protocol is required. In this study, we identify the problems of various authentication protocols using two-factor, three-factor, and PUF, and analyze the security vulnerabilities of Yuanbing et al.’s protocol in 2021. To address security vulnerabilities in these protocols, in this paper, we propose a secure authentication protocol applied with three-factor and PUF technology. To prove that the proposed protocol is secure against various attacks and provides security functions, formal verification and informal verification were performed through the ROR model, BAN logic, and AVISPA tool. In addition, through a comparative analysis of protocols, it was found that the calculation and communication costs were lower than those of the related protocols, and provide a more secure service in WMSN environments. Therefore, our proposed protocol can be secure against guessing, replay, MITM, impersonation, and sensor capture attacks and can provide anonymity, perfect forward secrecy, and secure mutual authentication. Our protocol also solves the problem of the sensor node, which has resource limitation, and ultimately can be applied to the actual WMSN environment. In the future, we plan to develop a better protocol by constructing and applying the proposed protocol to a practical testbed.
Author Contributions
Conceptualization, J.L.; formal analysis, J.L. and J.O.; methodology, J.L. and Y.P.; software J.L. and J.O.; validation, J.L. and Y.P.; writing—original draft, J.L.; writing—review and editing, J.O. and Y.P.; supervision, Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Research Foundation of Korea (NRF) funded by the Ministry of Education under grant 2020R1I1A3058605.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Sample Availability
Samples of the compounds are available from the authors.
Abbreviations
The following abbreviations are used in this manuscript:
| Symbols | Meanings |
| i-th user (medical professional) | |
| j-th sensor node | |
| Gateway node | |
| Physical Unclonable Function | |
| The challenge/response pair | |
| , | Identity of and |
| Password of | |
| Biometrics of | |
| Fuzzy extractor’s generation and reproduction algorithm | |
| Secret key of | |
| , | Random nonces |
| Timestamps | |
| Pseudo identity of and | |
| Session key | |
| Collision resistant one-way hash function | |
| ⊕ | Bitwise exclusive-or operator |
References
- Rashid, B.; Rehmani, M.H. Applications of wireless sensor networks for urban areas: A survey. J. Netw. Comput. Appl. 2016, 60, 192–219. [Google Scholar] [CrossRef]
- Pierce, F.J.; Elliott, T.V. Regional and on-farm wireless sensor networks for agricultural systems in Eastern Washington. Comput. Electron. Agric. 2008, 61, 32–43. [Google Scholar] [CrossRef]
- Ryu, J.; Oh, J.; Kwon, D.; Son, S.; Lee, J.; Park, Y.; Park, Y. Secure ECC-based three-factor mutual authentication protocol for telecare medical information system. IEEE Access 2022, 10, 11511–11526. [Google Scholar] [CrossRef]
- Bahache, A.N.; Chikouche, N.; Mezrag, F. Authentication Schemes for Healthcare Applications Using Wireless Medical Sensor Networks: A Survey. SN Comput. Sci. 2022, 3, 382. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Tang, S.; Luo, H. Privacy protection for e-health systems by means of dynamic authentication and three-factor key agreement. IEEE Trans. Indust. Elec. 2017, 65, 2795–2805. [Google Scholar] [CrossRef]
- He, D.; Kumar, N.; Chen, J.; Lee, C.-C.; Chilamkurti, N.; Yeo, S.-S. Robust anonymous authentication protocol for health-care applications using wireless medical sensor networks. Multimed. Syst. 2015, 21, 49–60. [Google Scholar] [CrossRef]
- Wu, F.; Xu, L.; Kumari, S.; Li, X. An improved and anonymous two factor authentication protocol for health-care applications with wireless medical sensor networks. Multimed. Syst. 2017, 23, 195–205. [Google Scholar] [CrossRef]
- Wang, C.; Xu, G.; Li, W. A secure and anonymous two-factor authentication protocol in multiserver environment. Secur. Commun. Netw. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Yuanbing, W.; Wanrong, L.; Bin, L. An Improved Authentication Protocol for Smart Healthcare System Using Wireless Medical Sensor Network. IEEE Access 2021, 9, 105101–105117. [Google Scholar] [CrossRef]
- Maes, R. Physically unclonable functions: Properties. In Physically Unclonable Functions; Springer: Berlin/Heidelberg, Germany, 2013; pp. 49–80. [Google Scholar]
- Abdalla, M.; Fouque, P. -A.; Pointcheval, D. Password-based authenticated key exchange in the three-party setting. In Lecture Notes in Computer Science, Proceedings of the 8th International Workshop on Theory and Practice in Public Key Cryptography (PKC’05), Les Diablerets, Switzerland, 23–26 January 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 65–84. [Google Scholar]
- Burrows, M.; Abadi, M.; Needham, R. A logic of authentication. ACM Trans. Comput. Syst. 1990, 8, 18–36. [Google Scholar] [CrossRef]
- AVISPA. Automated Validation of Internet Security Protocols and Applications. Available online: http://www.avispa-project.org/ (accessed on 21 September 2022).
- Lamport, L. Password authentication with insecure communication. Commun. ACM 1981, 24, 770–772. [Google Scholar] [CrossRef]
- Kumar, P.; Lee, S.-G.; Lee, H.-J. E-SAP: Efficient-strong authentication protocol for healthcare applications using wireless medical sensor networks. Sensors 2012, 12, 1625–1647. [Google Scholar] [CrossRef]
- Li, X.; Niu, J.; Kumari, S.; Liao, J.; Liang, W.; Khan, M.K. A new authentication protocol for healthcare applications using wireless medical sensor networks with user anonymity. Secur. Commun. Netw. 2016, 9, 2643–2655. [Google Scholar] [CrossRef]
- Das, A.K.; Sutrala, A.K.; Odelu, V.; Goswami, A. A secure smartcard-based anonymous user authentication scheme for healthcare applications using wireless medical sensor networks. Wirel. Pers. Commun. 2017, 94, 1899–1933. [Google Scholar] [CrossRef]
- Amin, R.; Islam, S.H.; Biswas, G.P.; Khan, M.K.; Kumar, N. A robust and anonymous patient monitoring system using wireless medical sensor networks. Future Gener. Comput. Syst. 2018, 80, 483–495. [Google Scholar] [CrossRef]
- Jiang, Q.; Ma, J.; Yang, C.; Ma, X.; Shen, J.; Chaudhry, S.A. Efficient end-to-end authentication protocol for wearable health monitoring systems. Comput. Electr. Eng. 2017, 63, 182–195. [Google Scholar] [CrossRef]
- Jan, S.U.; Ali, S.; Abbasi, I.A.; Mosleh, M.A.; Alsanad, A.; Khattak, H. Secure patient authentication framework in the healthcare system using wireless medical sensor networks. J. Healthc. Engin. 2021, 2021, 9954089. [Google Scholar] [CrossRef]
- Fotouhi, M.; Bayat, M.; Das, A.K.; Far, H.A.N.; Pournaghi, S.M.; Doostari, M.A. A lightweight and secure two-factor authentication scheme for wireless body area networks in health-care IoT. Comput. Netw. 2020, 177, 107333. [Google Scholar] [CrossRef]
- Nashwan, S. An end-to-end authentication scheme for healthcare IoT systems using WMSN. Comput. Mater. Contin. 2018, 68, 607–642. [Google Scholar] [CrossRef]
- Masud, M.; Gaba, G.S.; Choudhary, K.; Hossain, M.S.; Alhamid, M.F.; Muhammad, G. Lightweight and anonymity-preserving user authentication scheme for IoT-based healthcare. IEEE Internet Things J. 2021, 9, 2649–2656. [Google Scholar] [CrossRef]
- Kwon, D.; Park, Y.; Park, Y. Provably Secure Three-Factor-Based Mutual Authentication Scheme with PUF for Wireless Medical Sensor Networks. Sensors 2021, 21, 6039. [Google Scholar] [CrossRef]
- Ali, R.; Pal, A.K.; Kumari, S.; Sangaiah, A.K.; Li, X.; Wu, F. An enhanced three factor based authentication protocol using wireless medical sensor networks for healthcare monitoring. J. Ambient. Intell. Humani. Comput. 2018, 1–22. [Google Scholar] [CrossRef]
- Shuai, M.; Liu, B.; Yu, N.; Xiong, L. Lightweight and secure three-factor authentication scheme for remote patient monitoring using on-body wireless networks. Secur. Commun. Netw. 2019, 2019, 8145087. [Google Scholar] [CrossRef]
- Mo, J.; Hu, Z.; Lin, Y. Cryptanalysis and security improvement of two authentication schemes for healthcare systems using wireless medical sensor networks. Secur. Commun. Netw. 2020, 2020, 5047379. [Google Scholar] [CrossRef]
- Li, X.; Peng, J.; Obaidat, M.S.; Wu, F.; Khan, M.K.; Chen, C. A secure three-factor user authentication protocol with forward secrecy for wireless medical sensor network systems. IEEE Syst. J. 2019, 14, 39–50. [Google Scholar] [CrossRef]
- Saleem, M.A.; Shamshad, S.; Ahmed, S.; Ghaffar, Z.; Mahmood, K. Security analysis on “A secure three-factor user authentication protocol with forward secrecy for wireless medical sensor network systems”. IEEE Syst. J. 2021, 15, 5557–5559. [Google Scholar] [CrossRef]
- Gope, P.; Sikdar, B. Lightweight and privacy-preserving two-factor authentication scheme for IoT devices. IEEE Internet Things J. 2018, 6, 580–589. [Google Scholar] [CrossRef]
- Chen, C.M.; Li, X.; Liu, S.; Wu, M.E.; Kumari, S. Enhanced authentication protocol for the Internet of Things environment. Secur. Commu. Netw. 2022, 2022, 8543894. [Google Scholar] [CrossRef]
- Aman, M.N.; Chua, K.C.; Sikdar, B. Mutual authentication in IoT systems using physical unclonable functions. IEEE Internet Things J. 2017, 4, 1327–1340. [Google Scholar] [CrossRef]
- Frikken, K.B.; Blantonm, M.; Atallahm, M.J. Robust authentication using physically unclonable functions. In International Conference on Information Security; Springer: Berlin/Heidelberg, Germany, 2009; pp. 262–277. [Google Scholar]
- Chatterjee, U.; Chakraborty, R.S.; Mukhopadhyay, D. A PUF-based secure communication protocol for IoT. ACM Trans. Embedded Comput. Syst. 2017, 16, 1–25. [Google Scholar] [CrossRef]
- Dodis, Y.; Reyzin, L.; Smith, A. Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. In Lecture Notes in Computer Science, Proceedings of the International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 523–540. [Google Scholar]
- Dolev, D.; Yao, A. On the security of public key protocols. IEEE Trans. Inf. Theory 1983, 29, 198–208. [Google Scholar] [CrossRef]
- Kocher, P.; Jaffe, J.; Jun, B. Differential power analysis. In Advances in Cryptology; Springer Science and Business Media: Berlin, Germany; New York, NY, USA, 1999; pp. 388–397. [Google Scholar]
- Messerges, T.S.; Dabbish, E.A.; Sloan, R.H. Examining smart-card security under the threat of power analysis attacks. IEEE Trans. Comput. 2002, 51, 541–552. [Google Scholar] [CrossRef]
- Lee, J.; Kim, G.; Das, A.K.; Park, Y. Secure and efficient honey list-based authentication protocol for vehicular ad hoc networks. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2412–2425. [Google Scholar] [CrossRef]
- Son, S.; Lee, J.; Park, Y.; Park, Y.; Das, A.K. Design of blockchain-based lightweight V2I handover authentication protocol for VANET. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1346–1358. [Google Scholar] [CrossRef]
- Canetti, R.; Krawczyk, H. Universally composable notions of key exchange and secure channels. In International Conference on the Theory and Applications of Cryptographic Thechniques (EUROCRYPT’02); Springer: Amsterdam, The Netherlands, 2002; pp. 337–351. [Google Scholar]
- Li, J.; Su, Z.; Guo, D.; Choo, K.K.R.; Ji, Y. PSL-MAAKA: Provably secure and lightweight mutual authentication and key agreement protocol for fully public channels in internet of medical things. IEEE Internet Things J. 2021, 8, 13183–13195. [Google Scholar] [CrossRef]
- Park, K.; Lee, J.; Das, A.K.; Park, Y. BPPS: Blockchain-Enabled Privacy-Preserving Scheme for Demand-Response Management in Smart Grid Environments. IEEE Trans. Depend. Secur. Comput. 2022. [Google Scholar] [CrossRef]
- Kim, M.; Lee, J.; Oh, J.; Park, K.; Park, Y.; Park, K. Blockchain based energy trading scheme for vehicle-to-vehicle using decentralized identifiers. Appl. Energy 2022, 322, 119445. [Google Scholar] [CrossRef]
- Yu, S.; Das, A.K.; Park, Y.; Lorenz, P. SLAP-IoD: Secure and Lightweight Authentication Protocol Using Physical Unclonable Functions for Internet of Drones in Smart City Environments. IEEE Trans. Veh. Technol. 2022, 71, 10374–10388. [Google Scholar] [CrossRef]
- Cho, Y.; Oh, J.; Kwon, D.; Son, S.; Yu, S.; Park, Y.; Park, Y. A Secure Three-Factor Authentication Protocol for E-Governance System Based on Multiserver Environments. IEEE Access 2022, 10, 74351–74365. [Google Scholar] [CrossRef]
- Oh, J.; Lee, J.; Kim, M.; Park, Y.; Park, K.; Noh, S. A Secure Data Sharing Based on Key Aggregate Searchable Encryption in Fog-Enabled IoT Environment. IEEE Trans. Netw. Sci. Eng. 2022, 9, 4468–4481. [Google Scholar] [CrossRef]
- Kilinc, H.H.; Yanik, T. A survey of SIP authentication and key agreement schemes. IEEE Commun. Surv. Tutor. 2013, 16, 1005–1023. [Google Scholar] [CrossRef]
- Wu, F.; Xu, L.; Kumari, S.; Li, X. A new and secure authentication scheme for wireless sensor networks with formal proof. Peer-to-Peer Netw. Appl. 2017, 10, 16–30. [Google Scholar] [CrossRef]
- He, D.; Zeadally, S.; Xu, B.; Huang, X. An efficient identity-based conditional privacy-preserving authentication scheme for vehicular ad hoc networks. IEEE Trans. Inf. For. Secur. 2015, 10, 2681–2691. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).