Mathematical Channel Modeling of Electromagnetic Waves in Biological Tissues for Wireless Body Communication
Abstract
1. Introduction
2. Proposed Model
2.1. Characteristics of Human Tissue
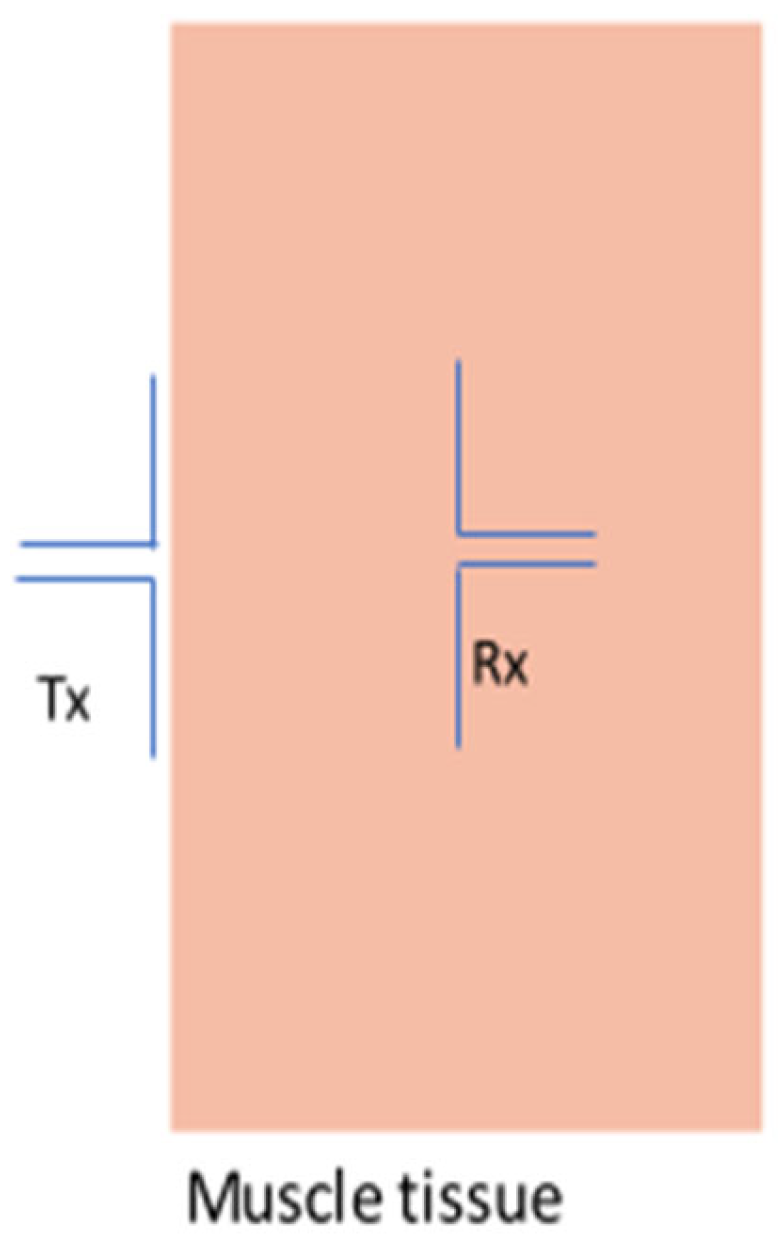
2.2. Lossy to Lossy Medium: Fat to Muscle Human Tissue
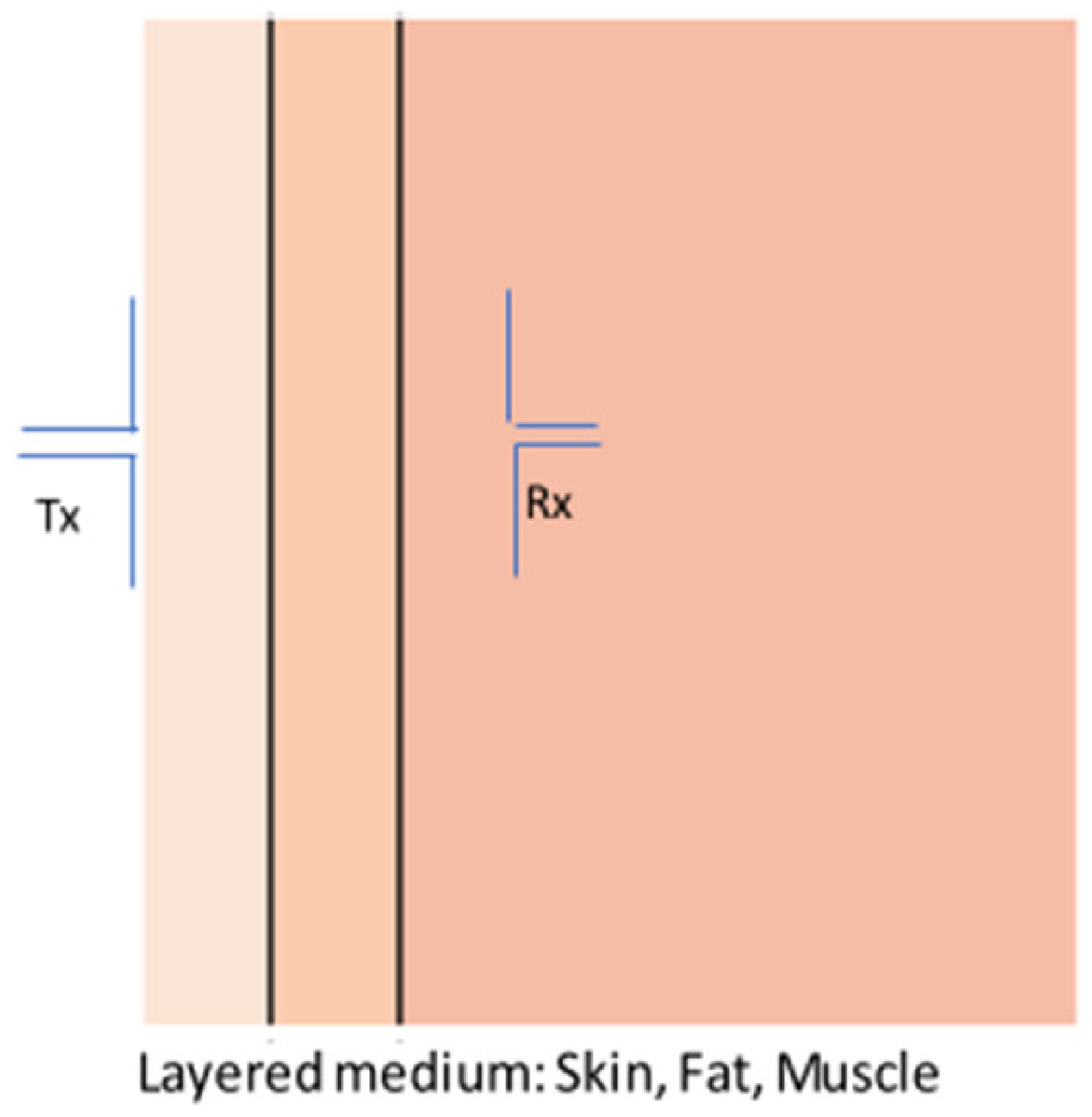
2.3. Lossless to Lossy Medium: Air to Layers Equivalent to Human Tissue
3. Mathematical Formulation
3.1. Selection Method
- MoM is most useful for unbounded problems related to radiation elements. It is efficient in terms of performance, precision, and execution time;
- FEM is based on the large-volume configuration for analysis. It is useful for large problems with complex, inhomogeneous configurations. Nevertheless, it does not support unbounded conditions;
- FDTD is a time-domain technique and is the most efficient for transient analysis problems. It is effective for complex, unbounded, and inhomogeneous problems. The disadvantage of FDTD is the complexity of the analysis, which requires more execution time.
3.2. MoM Formulation
3.2.1. TE Case
3.2.2. TM Case
3.3. Loss in the Medium
3.4. Simulation Settings
- In-body to on-body (IB2OB) communication;
- On-body to in-body (OB2IB) communication.
4. Results and Discussion
4.1. Communication Scenarios
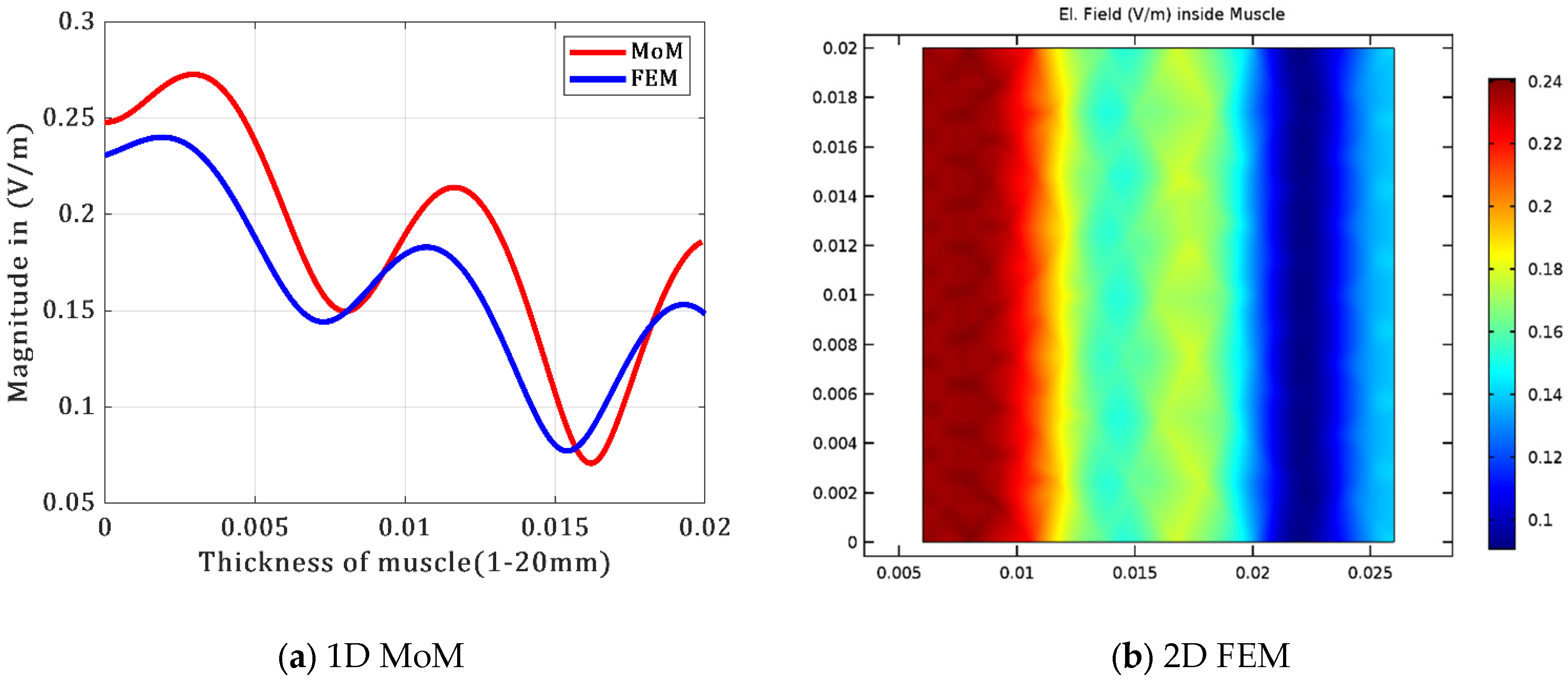
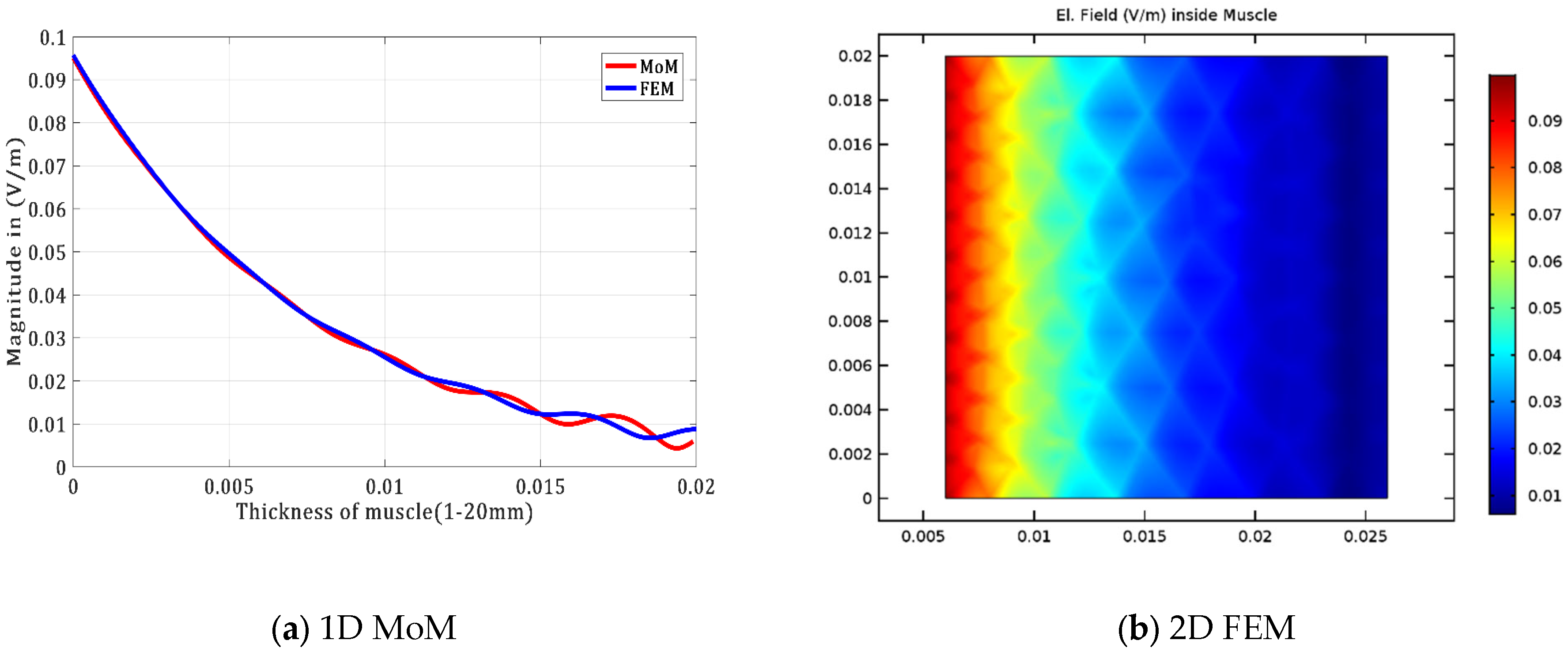
4.1.1. Communication inside Muscle Tissue
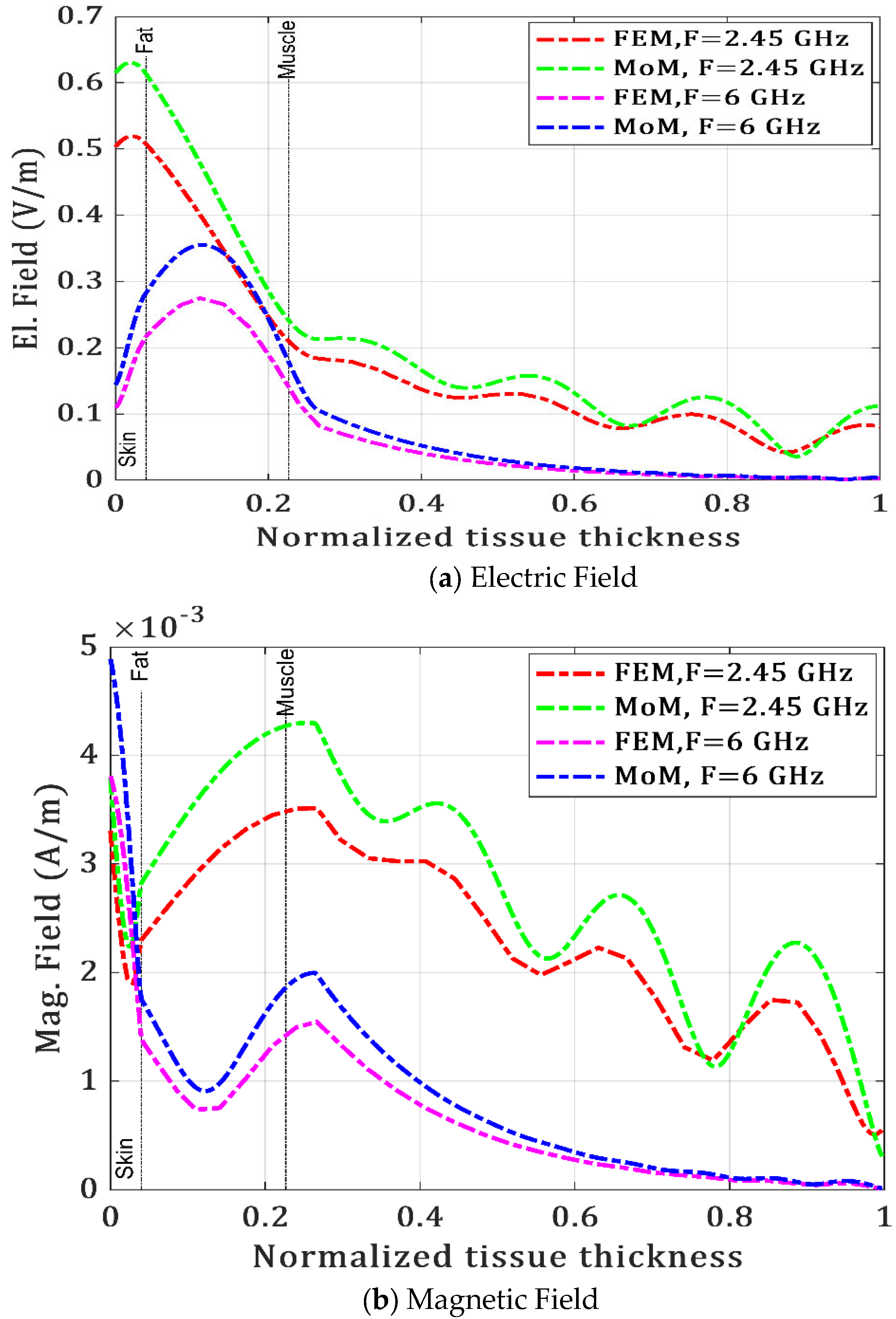
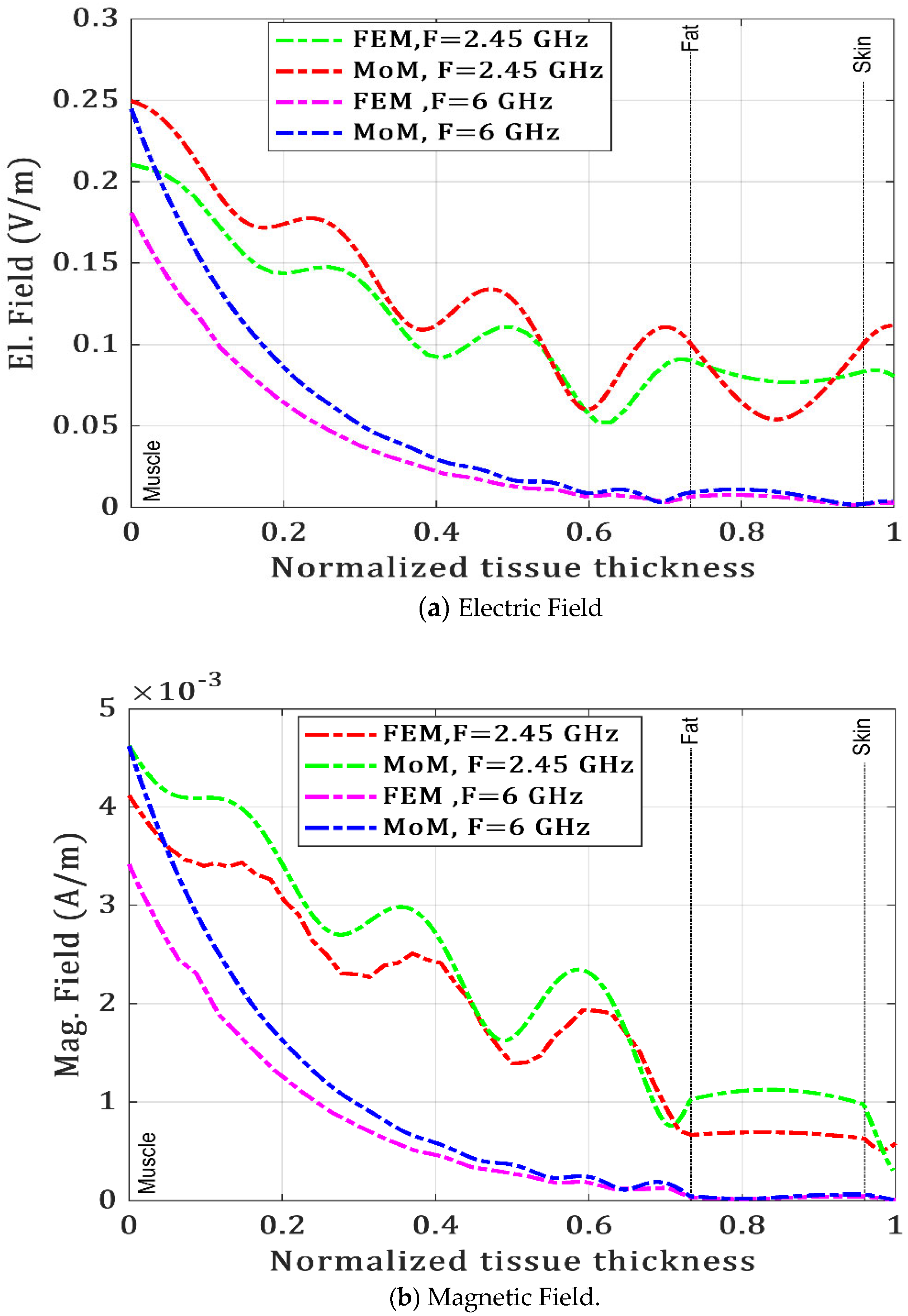
4.1.2. Communication in Inhomogeneous Human Body
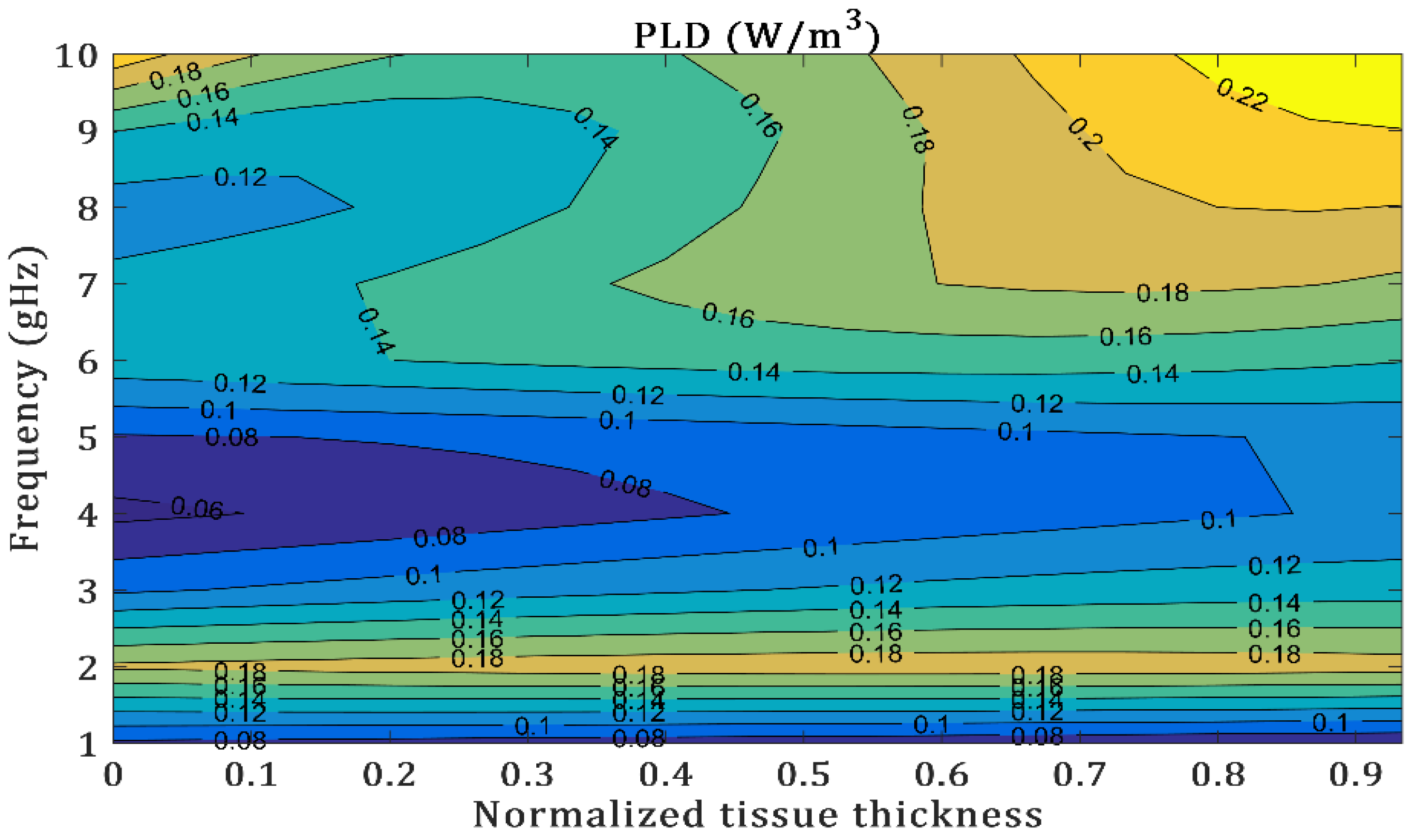
4.2. Path Loss Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nusrat, T.; Dawod, F.S.; Islam, T.; Kunkolienker, P.; Roy, S.; Rahman, M.; Ghosh, S.; Dey, S.; Mitra, D.; Braaten, B.D. A Comprehensive Study on Next-Generation Electromagnetics Devices and Techniques for Internet of Everything (IoE). Electronics 2022, 11, 3341. [Google Scholar] [CrossRef]
- Costanzo, S.; Qureshi, A.M. Compact and Wideband PIFA Design for Wireless Body Area Sensor Networks. Electronics 2021, 10, 2576. [Google Scholar] [CrossRef]
- Li, E.; Li, X.J.; Seet, B.-C. A Triband Slot Patch Antenna for Conformal and Wearable Applications. Electronics 2021, 10, 3155. [Google Scholar] [CrossRef]
- Jabbar, A.; Zubair, M.; Naveed, M.A.; Mehmood, M.Q.; Massoud, Y. A photopaper-based low-cost, wideband wearable antenna for wireless body area network applications. IET Microw. Antennas Propag. 2022, 16, 962–970. [Google Scholar] [CrossRef]
- Movassaghi, S.; Abolhasan, M.; Lipman, J.; Smith, D.; Jamalipour, A. Wireless Body Area Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 1658–1686. [Google Scholar] [CrossRef]
- Li, J.; Nie, Z.; Liu, Y.; Wang, L. Modeling and characterization of different channels based on human body communication. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Republic of Korea, 11–15 July 2017; pp. 702–705. [Google Scholar] [CrossRef]
- Ben Saada, A.; Ben Mbarek, S.; Choubani, F. Antenna Polarization Impact on Electromagnetic Power Density for an Off-Body to In-Body Communication Scenario. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1430–1433. [Google Scholar] [CrossRef]
- Ben Saada, A.; Ben Mbarek, S.; Choubani, F. Whole-Body Exposure to Far-Field Using Infinite Cylindrical Model for 5G FR1 Frequencies. In Advanced Information Networking and Applications; Lecture Notes in Networks and Systems; Barolli, L., Hussain, F., Enokido, T., Eds.; Springer: Cham, Switzerland, 2022; Volume 449, pp. 471–478. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, X.; Lin, F.; Gong, Z. Far-field characterization of wave oblique incidence on body channel for implant communication by using an analytical model. J. Electromagn. Waves Appl. 2021, 35, 1922–1938. [Google Scholar] [CrossRef]
- Mercier, P.P.; Chandrakasan, A.P. (Eds.) Ultra-Low-Power Short-Range Radios; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Kumpuniemi, T.; Tuovinen, T.; Hämäläinen, M.; Yazdandoost, K.Y.; Vuohtoniemi, R.; Iinatti, J. Measurement-based on-body path loss modelling for UWB WBAN communications. In Proceedings of the 2013 7th International Symposium on Medical Information and Communication Technology (ISMICT), Tokyo, Japan, 6–8 March 2013; pp. 233–237. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Gao, Y.M.; Du, M. Propagation characteristics of electromagnetic wave on multiple tissue interfaces in wireless deep implant communication. IET Microw. Antennas Propag. 2018, 12, 2034–2040. [Google Scholar] [CrossRef]
- Christ, A.; Klingenbock, A.; Samaras, T.; Goiceanu, C.; Kuster, N. The dependence of electromagnetic far-field absorption on body tissue composition in the frequency range from 300 MHz to 6 GHz. IEEE Trans. Microw. Theory Tech. 2006, 54, 2188–2195. [Google Scholar] [CrossRef]
- Khalaj-Amirhosseini, M. Analysis of Lossy Inhomogeneous Planar Layers Using the Method of Moments. J. Electromagn. Waves Appl. 2007, 21, 1925–1937. [Google Scholar] [CrossRef]
- Rothwell, E.J. Natural-mode Representation for the Field Reflected by an Inhomogeneous Conductor-backed Material Layer—TM Case. J. Electromagn. Waves Appl. 2007, 21, 569–584. [Google Scholar] [CrossRef]
- Sullivan, D.M. Electromagnetic Simulation Using the FDTD Method; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Ben Mbarek, S.; Choubani, F. FDTD modeling and experiments of microfabricated coplanar waveguide probes for electromagnetic compatibility applications. J. Electromagn. Waves Appl. 2020, 35, 634–646. [Google Scholar] [CrossRef]
- Krimi, I.; Ben Mbarek, S.; Hattab, H.; Choubani, F. Electromagnetic near-field study of electric probes for EMC applications. In Innovative and Intelligent Technology-Based Services for Smart Environments Smart Sensing and Artificial Intelligence; CRC Press: Boca Raton, FL, USA, 2021; pp. 45–50. [Google Scholar] [CrossRef]
- Carter, R. The Method of Moments in Electromagnetics, by W.C. Gibson. Contemp. Phys. 2010, 51, 183–184. [Google Scholar] [CrossRef]
- Happ, F.; Schröder, A.; Brüns, H.D.; Gronwald, F. A method for the calculation of electromagnetic fields in the presence of thin anisotropic conductive layers using the method of moments. In Proceedings of the 2013 International Symposium on Electromagnetic Compatibility, Brugge, Belgium, 2–6 September 2013; pp. 579–582. [Google Scholar]
- Sarestoniemi, M.; Hamalainen, M.; Iinatti, J. An Overview of the Electromagnetic Simulation-Based Channel Modeling Techniques for Wireless Body Area Network Applications. IEEE Access 2017, 5, 10622–10632. [Google Scholar] [CrossRef]
- Pellegrini, A.; Brizzi, A.; Zhang, L.; Ali, K.; Hao, Y.; Wu, X.; Constantinou, C.C.; Nechayev, Y.; Hall, P.S.; Chahat, N.; et al. Antennas and Propagation for Body-Centric Wireless Communications at Millimeter-Wave Frequencies: A Review [Wireless Corner]. IEEE Antennas Propag. Mag. 2013, 55, 262–287. [Google Scholar] [CrossRef]
- Carrara, N. Dielectric Properties of Body Tissues. Institute for Applied Physics; IFAC. Available online: http://niremf.ifac.cnr.it/tissprop/ (accessed on 1 December 2022).
- Kang, G.; Gandhi, O. Effect of Dielectric Properties on the Peak1-and 10-g SAR for 802.11 a/b/g Frequencies 2.45 and 5.15 to 5.85 GHz. IEEE Trans. Electromagn. Compat. 2004, 46, 268–274. [Google Scholar] [CrossRef]
- Abbasi, Q.H.; Sani, A.; Alomainy, A.; Hao, Y. Numerical characterization and modeling of subject-specific ultrawideband body-centric radio channels and systems for healthcare applications. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 221–227. [Google Scholar] [CrossRef] [PubMed]
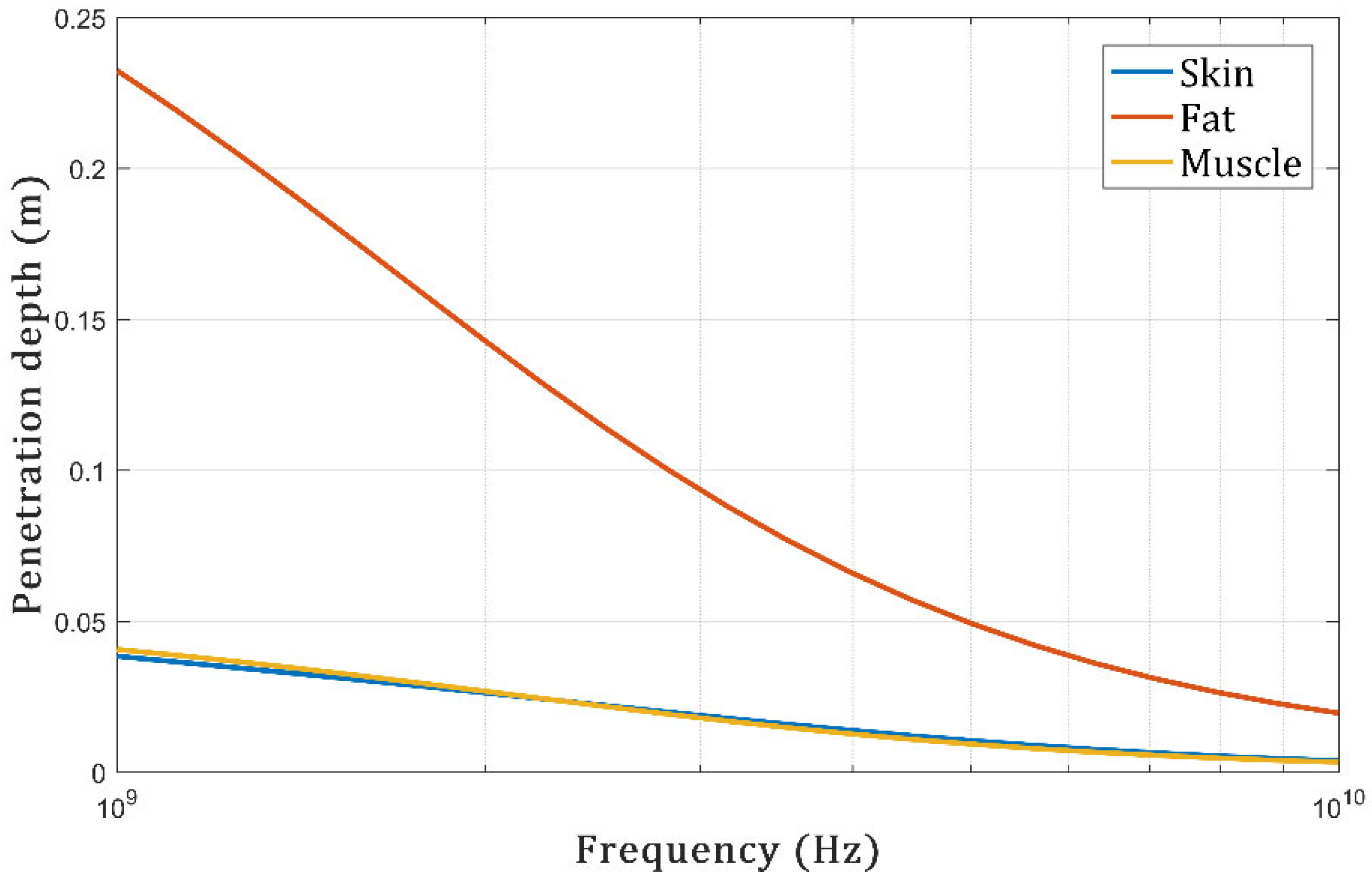



| Frequency | Tissue Parameters | Skin | Fat | Muscle |
|---|---|---|---|---|
| 915 MHz | ε Pd (mm) | 41.33 0.87 39.95 | 5.45 0.05 242.3 | 54.99 0.94 42.1 |
| 2.45 GHz | ε Pd (mm) | 38 1.46 22.57 | 5.28 0.1 117.02 | 52.73 1.73 22.33 |
| 5.8 GHz | ε Pd (mm) | 35.11 3.71 8.57 | 4.95 0.29 40.48 | 48.48 4.96 7.54 |
| Depth (mm) | 3 | 6 | 9 | 11 | 14 | 17 |
|---|---|---|---|---|---|---|
| 915 MHz | ||||||
| MoM | 0.23 | 0.18 | 0.20 | 0.24 | 0.27 | 0.28 |
| FEM | 0.22 | 0.17 | 0.16 | 0.21 | 0.23 | 0.24 |
| 2.45 GHz | ||||||
| MoM | 0.27 | 0.20 | 0.16 | 0.20 | 0.15 | 0.089 |
| FEM | 0.23 | 0.19 | 0.15 | 0.19 | 0.13 | 0.1 |
| 5.8 GHz | ||||||
| MoM | 0.06 | 0.043 | 0.028 | 0.02 | 0.016 | 0.011 |
| FEM | 0.058 | 0.047 | 0.033 | 0.02 | 0.015 | 0.012 |
| Communication Scenario | Physics Quantity | Calculation Result | Simulation Result | Reference |
|---|---|---|---|---|
| OB2IB | E (V/m) | 0.6144 | 0.5033 | Our work |
| 0.59746 | 0.59853 | Reference [12] | ||
| H (A/m) | 3.3 × 10−3 | 3.8× 10−3 | Our work | |
| 4 × 10−3 | 4.02 × 10−3 | Reference [12] | ||
| PL (dB) | 47.63 | 46.29 | Our work | |
| IB2OB | E (V/m) | 0.2495 | 0.2105 | Our work |
| H (A/m) | 4.1 × 10−3 | 4.6 × 10−3 | Our work | |
| PL (dB) | 33.01 | 33.15 | Our work |
| Communication Scenario (dB) | 2.45 GHz | 6 GHz |
|---|---|---|
| OB2IB in a different muscle position 5 mm; 20 mm | 35.29; 41.35 | 45.75; 63.87 |
| IB2OB on the interface of the skin | 47.67 | 76.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krimi, I.; Ben Mbarek, S.; Amara, S.; Choubani, F.; Massoud, Y. Mathematical Channel Modeling of Electromagnetic Waves in Biological Tissues for Wireless Body Communication. Electronics 2023, 12, 1282. https://doi.org/10.3390/electronics12061282
Krimi I, Ben Mbarek S, Amara S, Choubani F, Massoud Y. Mathematical Channel Modeling of Electromagnetic Waves in Biological Tissues for Wireless Body Communication. Electronics. 2023; 12(6):1282. https://doi.org/10.3390/electronics12061282
Chicago/Turabian StyleKrimi, Intissar, Sofiane Ben Mbarek, Selma Amara, Fethi Choubani, and Yehia Massoud. 2023. "Mathematical Channel Modeling of Electromagnetic Waves in Biological Tissues for Wireless Body Communication" Electronics 12, no. 6: 1282. https://doi.org/10.3390/electronics12061282
APA StyleKrimi, I., Ben Mbarek, S., Amara, S., Choubani, F., & Massoud, Y. (2023). Mathematical Channel Modeling of Electromagnetic Waves in Biological Tissues for Wireless Body Communication. Electronics, 12(6), 1282. https://doi.org/10.3390/electronics12061282






