A Model of Thermally Activated Molecular Transport: Implementation in a Massive FPGA Cluster
Abstract
1. Introduction
- The introduction of molecular bonds with excluded volume between elements must involve the BONDS mechanism, which is responsible for movement restriction related to the length-constant unbreakable bonds.
- The mechanisms BOND_BINDS and BOND_BREAKS are used when one wants to simulate the macromolecular polymerization and degradation processes, respectively.
- A growing macromolecule (in the case of polymerization, where new elements are joined to the molecule with some probability) can be terminated randomly using the TERMINATION mechanism.
- Chemical reactions of different orders can also be modeled with the REACTION mechanism, where elements can change their type with a given probability.
- Local trapping can be modeled with the MOBILITY mechanism, where movement of a given element can be restricted (e.g., due to its spatial position in the simulation box).
- Vector fields can be modeled using the VECTOR and REORIENTATION mechanisms.
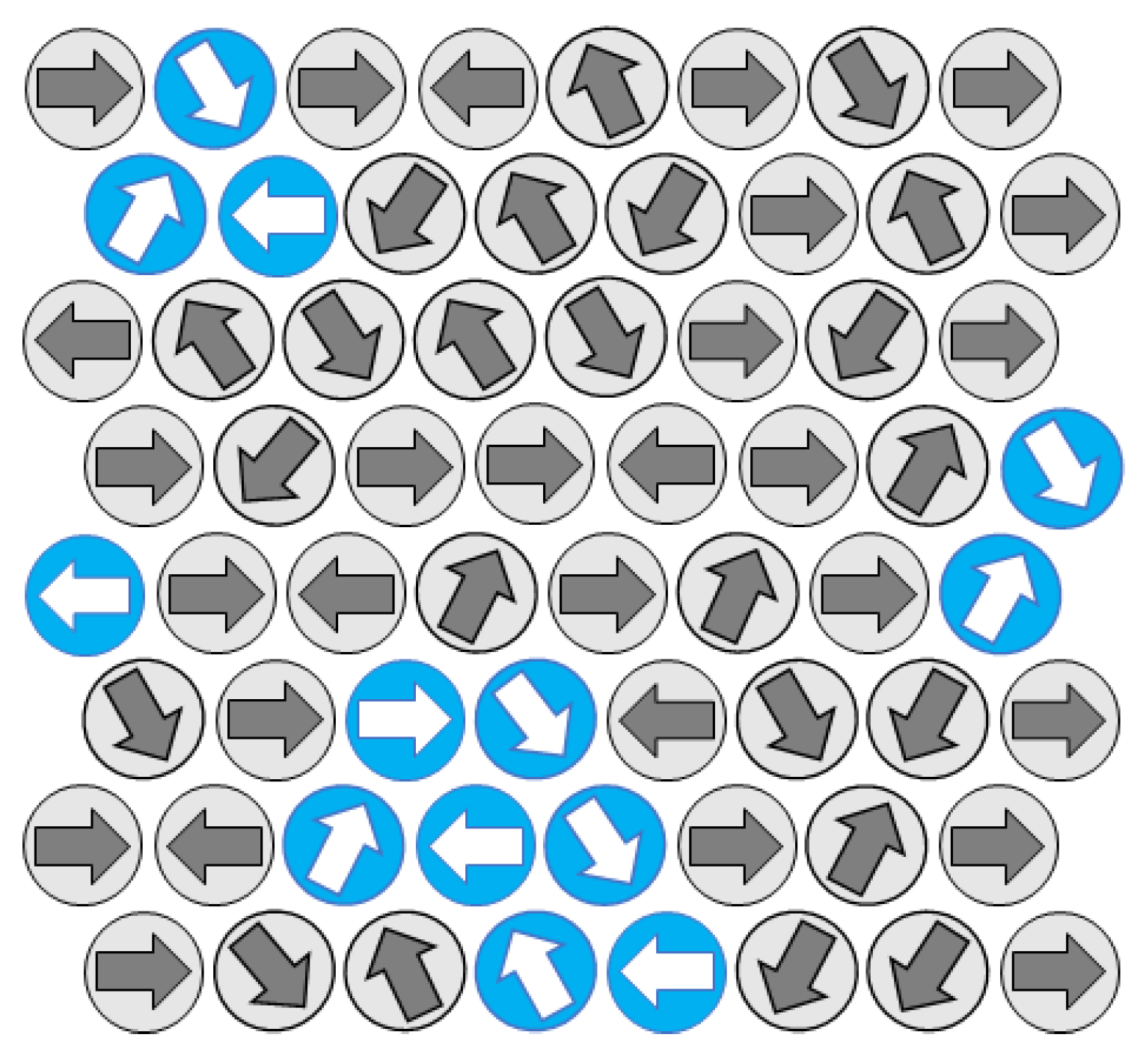
- In the case where vacancies are present, the WAYS mechanism is used to model cooperative motion involving empty lattice nodes, forming a cooperative set of elements (chain-like and not necessarily a loop).
- The APERIODIC mechanism is used to build immobile obstacles such as walls.
- Thermal noise can be reduced in simulations by lowering the temperature with the ENERGY mechanism (introducing potential energy barriers).
2. The ARUZ Simulator
3. Thermally Activated Diffusion Model
- T is the absolute temperature, and is the Boltzmann constant.
- is the interaction energy of the type X with the external field and can depend on the spatial position to model, for example, the temperature gradient.
- is the interaction energy of the pair and is position-independent. In the presented model, always equals .
4. Implementation Requirements
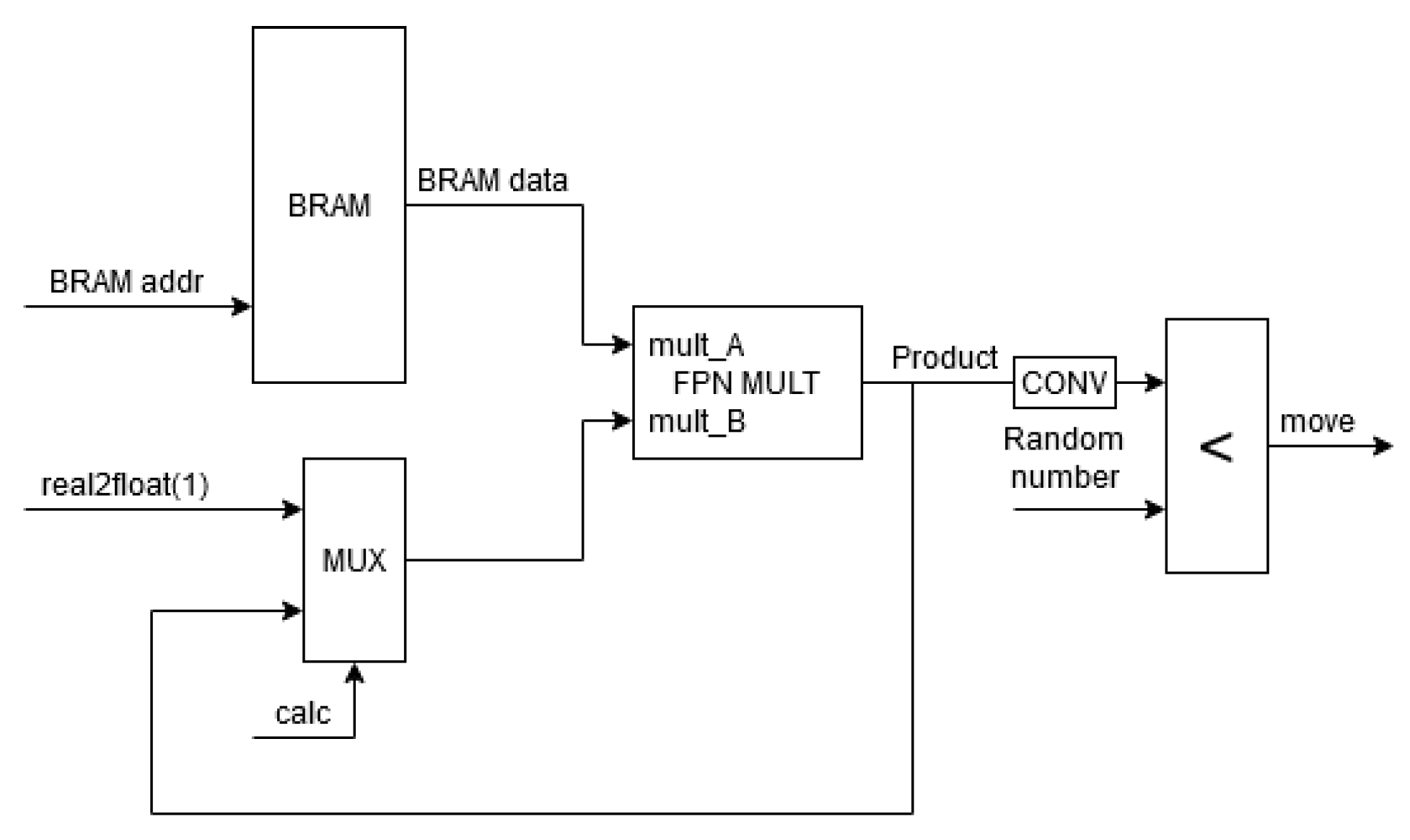
5. Implementation on FPGA
- An “e_offset” bit indicating parts of the memory storing and ;
- A vector representing the type of a neighbor element “other_type”;
- A vector representing the type of the considered element “my_type” (occupying the right-most bits).
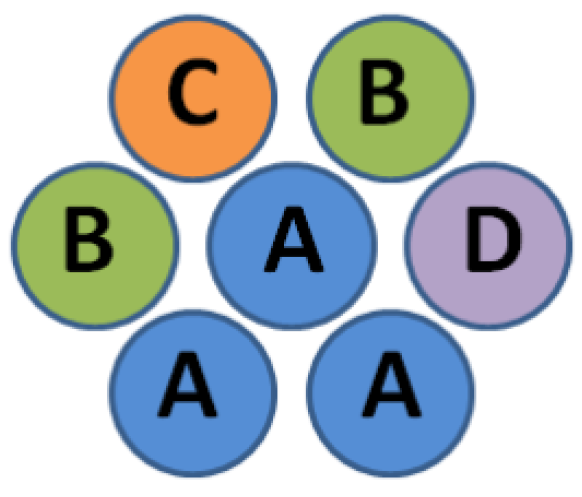
- Example 1: Four element types are used (types A, B, C, and D coded by a two-bit vector: A = 00, B = 01, C = 10, and D = 11). The address of an appropriate is a concatenation of the ”e_offset” bit set to 0, and two two-bit vectors (representing the type of the considered element and a neighbor, respectively). The address of is the concatenation of a constant coded by a three-bit vector (taking bits of ”e_offset” and ”other_type” vectors) and a two-bit vector representing the type of element considered. In this example, all memory locations are used, and 16 of them are needed for and 4 for , leading to a total of 20.
- Example 2: Three element types are used (types A, B, and C coded by a two-bit vector: A = 00, B = 01, and C = 10). The addresses of the appropriate coefficients and are determined in the same way as in the previous example. Only gray-colored memory locations are used, but the required number of memory locations is still 20.
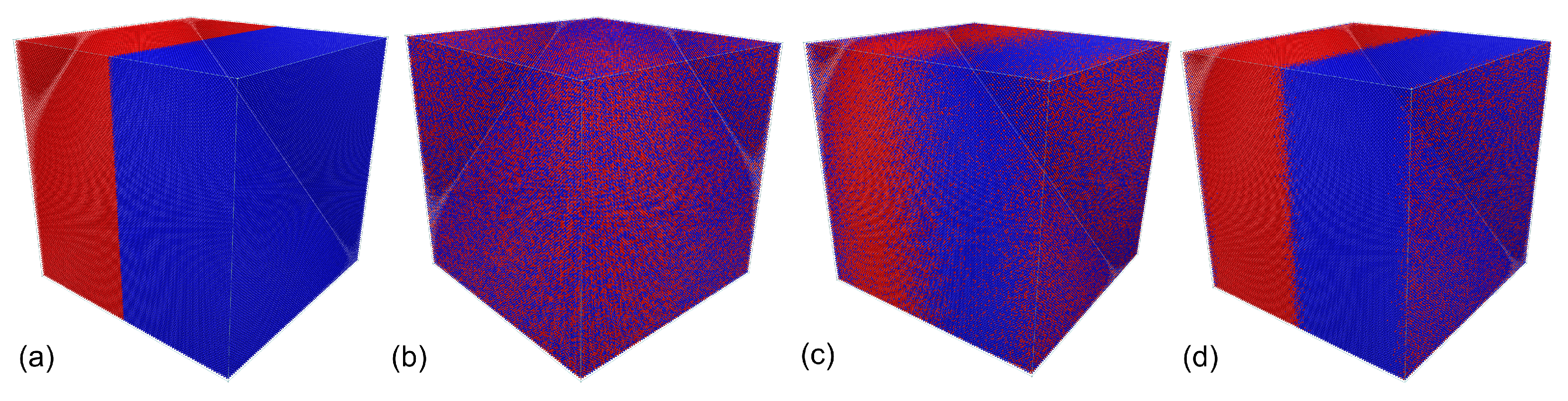
6. Example Simulation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARUZ | Analyzer of Real Complex Systems |
| (in Polish: Analizator Rzeczywistych Układów Złożonych) | |
| BRAM | Block random access memory |
| DLL | Dynamic Lattice Liquid |
| FCC | Face-centered cubic |
| FPGA | Field-programmable gate array |
| LUPS | Latice updates per second |
| TAUR | Technology of Real Word Analyzers |
| (in Polish: Technologia Analizatorów Układów Rzeczywistych) |
References
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Cahn, J.W. On Spinodal Decomposition. Acta Metall. 1961, 9, 795–801. [Google Scholar] [CrossRef]
- Binder, K.; Ciccotti, G. Monte Carlo and Molecular Dynamics of Condensed Matter; Società Italiana di Fisica: Bologna, Italy, 1996. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equations of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Binder, K.; Heerman, D.W. Monte Carlo Simulation in Statistical Physics. An Introduction, 4th ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Pakuła, T.; Teichmann, J. Model for Relaxation in Supercooled Liquids and Polymer Melts; MRS Online Proceedings Library: Berlin/Heidelberg, Germany, 1996; Volume 455, p. 211. [Google Scholar] [CrossRef]
- Polanowski, P.; Jeszka, J.K.; Matyjaszewski, K. Polymer brushes in pores by ATRP: Monte Carlo simulations. Polymer 2020, 211, 123124. [Google Scholar] [CrossRef]
- Kozanecki, M.; Halagan, K.; Saramak, J.; Matyjaszewski, K. Diffusive properties of solvent molecules in the neighborhood of a polymer chain as seen by Monte-Carlo simulations. Soft Matter 2016, 12, 5519–5528. [Google Scholar] [CrossRef]
- Pakula, T. Simulation on the completely occupied lattices. In Simulation Methods for Polymers; Marcel Dekker: New York, NY, USA; Basel, Switzerland, 2004. [Google Scholar]
- Kiełbik, R.; Hałagan, K.; Zatorski, W.; Jung, J.; Ulański, J.; Napieralski, A.; Rudnicki, K.; Amrozik, P.; Jabłoński, G.; Stożek, D.; et al. ARUZ—Large-scale, massively parallel FPGA-based analyzer of real complex systems. Comput. Phys. Commun. 2018, 232, 22–34. [Google Scholar] [CrossRef]
- Jabłoński, G.; Amrozik, P.; Hałagan, K. Molecular Simulations Using Boltzmann’s Thermally Activated Diffusion—Implementation on ARUZ—Massively-parallel FPGA-based Machine. In Proceedings of the 2021 28th International Conference on Mixed Design of Integrated Circuits and System, Lodz, Poland, 24–26 June 2021; pp. 128–131. [Google Scholar] [CrossRef]
- Kawasaki, K.; Ohta, T. Theory of Early Stage Spinodal Decomposition in Fluids near the Critical Point. II. Prog. Theor. Phys. 1978, 59, 362–374. [Google Scholar] [CrossRef]
- Yaldram, K.; Binder, K. Spinodal decomposition of a two-dimensional model alloy with mobile vacancies. Acta Metall. Mater. 1991, 39, 707–717. [Google Scholar] [CrossRef]
- Jung, J.; Kiełbik, R.; Hałagan, K.; Polanowski, P.; Sikorski, A. Technology of Real-World Analyzers (TAUR) and its practical application. Comput. Methods Sci. Technol. 2020, 26, 69–75. [Google Scholar]
- Polanowski, P.; Jung, J.; Kielbik, R. Special Purpose Parallel Computer for Modelling Supramolecular Systems based on the Dynamic Lattice Liquid Model. Comput. Methods Sci. Technol. 2010, 16, 147–153. [Google Scholar] [CrossRef]
- Pakula, T.; Cervinka, L. Modeling of medium-range order in glasses. J. Non-Cryst. Solids 1998, 232–234, 619–626. [Google Scholar] [CrossRef]
- Halagan, K.; Polanowski, P. Kinetics of spinodal decomposition in the Ising model with Dynamic Lattice Liquid (DLL) dynamics. J. Non-Cryst. Solids 2009, 355, 1318–1324. [Google Scholar] [CrossRef]
- Halagan, K.; Polanowski, P. Order-disorder transition in 2D conserved spin system with cooperative dynamics. J. Non-Cryst. Solids 2015, 127, 585–587. [Google Scholar] [CrossRef]
- Glauber, R.J. Time-Dependent Statistics of the Ising Model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar] [CrossRef]
- Pakula, T. Collective dynamics in simple supercooled and polymer liquids. J. Mol. Liq. 2000, 86, 109–121. [Google Scholar] [CrossRef]
- Hałagan, K. Investigation of Phase Separation and Spinodal Decomposition Phenomena with Cooperative Dynamics. Ph.D. Thesis, Lodz University of Technology, Łódź, Poland, 2013. [Google Scholar]
- Kiełbik, R.; Hałagan, K.; Rudnicki, K.; Jabłoński, G.; Polanowski, P.; Jung, J. Simulation of diffusion in dense molecular systems on ARUZ—Massively-parallel FPGA-based machine. Comput. Phys. Commun. 2023, 283, 108591. [Google Scholar] [CrossRef]
- Polanowski, P.; Pakula, T. Studies of mobility, interdiffusion, and self-diffusion in two-component mixtures using the dynamic lattice liquid model. J. Chem. Phys. 2003, 118, 11139–11146. [Google Scholar] [CrossRef]
- Migacz, S.; Dutka, K.; Gumienny, P.; Marchwiany, M.; Gront, D.; Rudnicki, W.R. Parallel Implementation of a Sequential Markov Chain in Monte Carlo Simulations of Physical Systems with Pairwise Interactions. J. Chem. Theory Comput. 2019, 15, 2797–2806. [Google Scholar] [CrossRef]
- 7 Series FPGAs Configurable Logic Block. Available online: https://docs.xilinx.com/v/u/en-US/ug474_7Series_CLB (accessed on 17 January 2023).
- 7 Series FPGA Memory Resources User Guide. Available online: https://docs.xilinx.com/v/u/en-US/ug473_7Series_Memory_Resources (accessed on 17 January 2023).
- 7 Series DSP48E1 Slice User Guide. Available online: https://docs.xilinx.com/v/u/en-US/ug479_7Series_DSP48E1 (accessed on 17 January 2023).
- 7 Series Product Selection Guide. Available online: https://www.xilinx.com/content/dam/xilinx/support/documents/selection-guides/7-series-product-selection-guide.pdf (accessed on 17 January 2023).
- Floating–Point Operator v7.1 LogiCore IP Product Guide. Available online: https://www.xilinx.com/content/dam/xilinx/support/documents/ip_documentation/floating_point/v7_1/pg060-floating-point.pdf (accessed on 17 January 2023).
- Newman, M.E.J.; Barkema, G.T. Monte Carlo Methods in Statistical Physics; Clarendon Press: Oxford, UK, 1999. [Google Scholar]
- Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Physik 1924, 31, 253. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1877, 49, 435. [Google Scholar] [CrossRef]
- Marko, J.F.; Barkema, G.T. Phase ordering in the Ising model with conserved spin. Phys. Rev. E 1995, 52, 2522. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.J.; Fisher, M.E. The three-dimensional Ising model revisited numerically. Physica A 1989, 156, 35–76. [Google Scholar] [CrossRef]
- Yu, U. Critical temperature of the Ising ferromagnet on the FCC, HCP, and DHCP lattices. Physica A 2015, 419, 75–79. [Google Scholar] [CrossRef]
- Gaulin, B.; Spooner, S.; Morii, Y. Kinetics of phase separation in Mn0.67Cu0.33. Phys. Rev. Lett. 1987, 59, 668. [Google Scholar] [CrossRef]
- Wagner, R. Chapter 5 in Phase Transformations in Materials; Wiley-VCH: Weinheimd, Germany, 2001. [Google Scholar]
- Wong, N.; Knobler, C. Light-Scattering Studies of Phase Separation in Isobutyric Acid + Water Mixtures. 2. Test of Scaling. J. Phys. Chem. 1981, 85, 1972–1976. [Google Scholar]
- Mauri, R.; Shinnar, R.; Triantafyllou, G. Spinodal decomposition in binary mixtures. Phys. Rev. E 1996, 53, 2613. [Google Scholar] [CrossRef]
- Bates, F.; Wiltzius, P. Spinodal decomposition of a symmetric critical mixture of deuterated and protonated polymer. J. Chem. Phys. 1989, 91, 3258–3274. [Google Scholar] [CrossRef]
- Demyanchuk, I.; Wieczorek, A.; Hołyst, R. Percolation-to-droplets transition during spinodal decomposition in polymer blends, morphology analysis. J. Chem. Phys. 2004, 121, 1141–1147. [Google Scholar] [CrossRef]


| Address | Data |
|---|---|
| (e_offset & other_type & my_type) | |
| 0 & 00 & 00 | |
| 0 & 00 & 01 | |
| 0 & 00 & 10 | |
| 0 & 00 & 11 | |
| 0 & 01 & 00 | |
| 0 & 01 & 01 | |
| 0 & 01 & 10 | |
| 0 & 01 & 11 | |
| 0 & 10 & 00 | |
| 0 & 10 & 01 | |
| 0 & 10 & 10 | |
| 0 & 10 & 11 | |
| 0 & 11 & 00 | |
| 0 & 11 & 01 | |
| 0 & 11 & 10 | |
| 0 & 11 & 11 | |
| 1 & 00 & 00 | |
| 1 & 00 & 01 | |
| 1 & 00 & 10 | |
| 1 & 00 & 11 |
| Nodes per Chip | Mechanisms | Multiplier Parameters | LUTs (%) | FFs (%) | BRAMs (%) | DSPs (%) |
|---|---|---|---|---|---|---|
| 200 | LOOPS | N/A | 58.01 | 29.21 | 0.00 | 0.00 |
| 288 | LOOPS | N/A | 81.52 | 40.98 | 0.00 | 0.00 |
| 128 | LOOPS, ENERGY | latency 3, no DSP | 80.09 | 34.93 | 0.00 | 35.07 |
| 200 | LOOPS, ENERGY | latency 3, full DSP | 79.17 | 47.90 | 27.03 | 54.79 |
| 200 | LOOPS, ENERGY | latency 3, max DSP | 76.56 | 48.05 | 54.05 | 54.79 |
| 200 | LOOPS, ENERGY | latency 4, max DSP | 77.58 | 48.95 | 54.05 | 54.79 |
| 200 | LOOPS, ENERGY | latency 8, max DSP | 78.24 | 50.87 | 54.05 | 54.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabłoński, G.; Amrozik, P.; Hałagan, K. A Model of Thermally Activated Molecular Transport: Implementation in a Massive FPGA Cluster. Electronics 2023, 12, 1198. https://doi.org/10.3390/electronics12051198
Jabłoński G, Amrozik P, Hałagan K. A Model of Thermally Activated Molecular Transport: Implementation in a Massive FPGA Cluster. Electronics. 2023; 12(5):1198. https://doi.org/10.3390/electronics12051198
Chicago/Turabian StyleJabłoński, Grzegorz, Piotr Amrozik, and Krzysztof Hałagan. 2023. "A Model of Thermally Activated Molecular Transport: Implementation in a Massive FPGA Cluster" Electronics 12, no. 5: 1198. https://doi.org/10.3390/electronics12051198
APA StyleJabłoński, G., Amrozik, P., & Hałagan, K. (2023). A Model of Thermally Activated Molecular Transport: Implementation in a Massive FPGA Cluster. Electronics, 12(5), 1198. https://doi.org/10.3390/electronics12051198









