Abstract
In this paper, a tensor-based approach to blind despreading of long-code multiuser DSSS signals is proposed. We aim to generalize the tensor-based methods originally developed for blind separation of short-code multiuser DSSS signals to long-code cases. Firstly, we model the intercepted long-code multiuser DSSS signals with an antenna-array receiver as a three-order tensor with missing values, and then, the blind separation problem can be formulated as a canonical or parallel factor (CANDECOMP/PARAFAC) decomposition problem of the missing-data tensor, which can be solved using optimum methods. Secondly, a constrained Cramér–Rao Bound (CRB) is also derived to provide a performance benchmark for the proposed approach. Simulation results verify the feasibility of our proposed approach in the case of low signal-to-noise (SNR) conditions.
1. Introduction
Direct sequence spread spectrum (DSSS) signals which multiply low-rate data signals by high-rate pseudo-noise (PN) sequences to expand bandwidth and reduce power spectral density (PSD) have been widely used in recent decades for secure communication due to their low probability of intercept (LPI) and anti-jamming characteristics [1,2]. Now, it is further used in radar, satellite communications, mobile communications, speed and distance measurement, navigation and tracking, and many other fields [3,4,5,6]. The combination of DSSS signals and other modulation techniques, such as Multi-carrier DSSS and M-ary DSSS, can further enhance communication performance [7,8,9].
For non-cooperative applications such as spectrum monitoring and cognitive radio, the PN sequence and other parameters are typically unknown to the non-cooperative receiver. The non-cooperative receiver has to deal with the intercepted signals in a blind manner. This brings great challenges to the detection and parameter estimation of the signals. Blind parameter estimation for DSSS signals has been extensively studied in the past decades. When the receiver is equipped with a single antenna element, many second-order statistics-based blind estimation techniques have been proposed for short-code DSSS systems [10,11,12,13,14,15] and long-code systems [16,17,18,19,20]. With the development of multilinear algebra, a recent trend for blind separation of multiuser DSSS signals is to exploit the tensor-based methods, where a tensor rather than a matrix represents the intercepted multiuser DSSS signals. A remarkable feature of tensor-based approaches is that they have the significant advantages of recovering the information-bearing signals of interest without requiring knowledge of spreading waveforms, DOA, array calibration information, or statistical independence. The intercepted multiuser DSSS signals can be naturally modeled as a third-order tensor, so that the blind separation problem can be solved with the canonical or parallel factor (CANDECOMP/PARAFAC) decomposition method.
There have been many studies using tensor-based techniques to estimate the DSSS signals. In [21], a blind parallel factor (PARAFAC) receiver has been proposed based on the tensor model. Such a receiver resorts to the identifiability of low-rank tensor decomposition and is able to separate the information of each user uniquely. For asynchronous uplink DSSS signals under a multipath environment in which inter-symbol interference (ISI) exists, a low-rank tensor decomposition can also be used for signal estimation [22]. In [23], a Bayesian blind identification algorithm was proposed for CDMA system with multiple antennas at the receiver. It uses the Markov chain Monte Carlo (MCMC) method to improve the performance of PARAFAC. In [24], the ISI was taken into consideration with the tensor model, and the blind separation was performed based on a Rank-(1,L,L) term decomposition. In addition, the authors of [24] derived the Cramér–Rao bound as a theoretical lower bound for performance evaluation.
The aforementioned tensor-based methods are specially developed for blind separation of short-code multiuser DSSS signals and cannot be adopted directly for long-code signals, because the spreading waveform period is a non-integer time of the symbol duration, which makes the signal model much more complicated [19]. In this paper, we are going to exploit the missing tensor model for representing the long-code multiuser DSSS signals. With such representation, the combination of the standard canonical or parallel factor (CANDECOMP/PARAFAC) and alternating least squares (ALS) algorithm is used to separate the information of each user uniquely.
This paper provides the following main contributions:
- -
- We exploit the missing-data tensor model to represent the long-code multiuser DSSS signals, which provides a new idea for developing tensor-based blind separation methods to estimate parameters of long-code multiuser DSSS signals. Then, we reformulate the blind separation problem into the CANDECOMP/PARAFAC decomposition problem for a missing tensor and discuss the identifiability of decomposition under this missing tensor model.
- -
- We derive the constrained CRB, which can be applied as a meaningful benchmark to asses the performance of blind separation techniques. Simulation results verify the feasibility of the proposed approach, and show that the estimated performance is close to the constrained CRB.
The rest of the paper is organized as follows. In the next section, the long-code multiuser signals received by multiple antennas are modeled in the discrete-time framework, whereas in Section 3, we introduce the basic concept of a tensor and model the long-code multiuser DSSS signal as missing tensor model, and then propose our blind despreading algorithm. In Section 4, we discuss the discriminability conditions for the general tensor model and the missing tensor model, providing theoretical feasibility for the algorithm proposed in Section 3. In Section 5, a constrained CRB is derived to provide a performance benchmark for the proposed approach. Some illustrative simulation results are presented in Section 6 and Section 7 is the conclusion.
2. Background
2.1. Notation
In this paper, scalars, column vectors, matrices, and tensors are denoted by lowercase (e.g., a), boldface lowercase (e.g., ), boldface uppercase (e.g., ), and calligraphic uppercase letters (e.g., ), respectively. The vector represents the ith column of matrix . The operations , denote the transpose and the Moore–Penrose pseudo-inverse, respectively. The symbols ∘, ⊗, *, ⊙, , , , , and represent outer product, Kronecker product, Hadamard (element-wise) product, Khatri–Rao product, ceiling function, floor function, Frobenius norm, trace, expectation, and the modulo n of L, respectively.
2.2. Problem Formulation
Consider an intercepted long-code multiuser DSSS signal with R users received by an array of I antennas. The received signals of each antenna are matched filtered and sampled to obtain N sampling points. The intercepted baseband long-code multiuser DSSS signals for n-th sample (for ) from the i-th (for ) antenna can be represented as [19]
where is the signal gain of the ith antenna receiving user r, is the Gaussian noise with variance , is the rectangular function with length G (i.e., when and otherwise), and thus, G can be used to represent the symbol duration of the binary phase-shift keying (BPSK) symbol sequence , i.e., . The spreading waveform with period is the convolution of spreading sequence and channel response , i.e., . and are the number of symbols and the number of repetitions of the spreading waveform, respectively. R denotes the number of users.
Similar to [21,25], the signal model denoted via (1) only considers the case without inter-symbol-interference (ISI). We assume that the signals have been synchronized at the symbol level. In this paper, the radio is generally not an integer [17,18,19]. Moreover, the number of users R, the period of the spreading waveform L, and the spreading gain G are assumed to be known or have been estimated. Please notice that such an assumption is reasonable due to the fact that the parameters R, G, and L can be obtained with some well-known operations [26,27,28]. Let , and denote spreading waveforms, symbols, and antenna gain matrix, respectively. With the aforementioned consideration, this paper aims to joint estimation of these three parameters.
3. Proposed Approach
In this section, we construct a missing tensor model for long-code multiuser DSSS signals and reformulate the blind separation problem as the CANDECOMP/PARAFAC decomposition problem for the missing tensor. Then, an approach based on single imputation (SI) combined with alternating least squares (ALS) is proposed to estimate the spreading waveform and symbol sequence .
3.1. Tensor Preliminaries
A tensor is an array of data consisting of three or more indexes. In this paper, we consider the third-order tensor which is defined as and indexed by with elements , where is the number field used to denote either the real field or complex field . For the given factor matrix , , , any tensor can be realized as a sum of three-way outer products
This is the polyadic decomposition (PD) of the third-order tensor. Similar to the rank of a matrix, we can define the tensor rank as the smallest F needed to synthesize . Then, F is called tensor rank and this kind of decomposition is known as classic canonical polyadic decomposition (CPD) or parallel factor analysis (PARAFAC). A tensor model of rank 3 is shown in Figure 1. Note that the multiuser DSSS signals can be naturally modeled using a third-order tensor, with the spreading sequence, symbol sequence, and antenna gain making up each factor matrix. A third-order tensor can be fully represented by its factor matrix and we use the notation to represent the tensor. The motivation to use a tensor is that the CPD is essentially unique under mild conditions. This will be illustrated in subsequent sections.
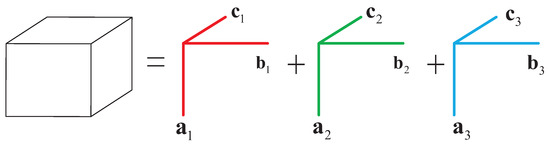
Figure 1.
Illustration of a rank 3 tensor.
Our problem is usually to estimate from observed data . Using the least squares criterion, the problem can be expressed as
Alternating least squares (ALS) is a commonly used algorithm to compute approximate low-rank models of tensor data. To achieve this, we need to transform the tensor into a matrix. For example, fixing the third subscript k of the tensor, iterating through the data of the other subscripts yields a matrix . It can be expressed as
where is a diagonal matrix formed by . By parallel stacking of the vectorized matrix , we can get
For a more concise form of expression, we use
Similarly, by fixing other subscripts, we can obtain the matrix of other two transformations
and
respectively.
By fixing two of three factor matrices, the iterative process of ALS can be expressed as
By updating at each step, when the iterative process converges, we get the estimation of the factor matrix.
3.2. Missing Tensor Model
Let represent the sample vector of received signals from the i-th antenna, which is further detailed as
where , , and denote the vectors of ones having a length of G and M, respectively. Then, the missing tensor model for blind separation is constructed via the following steps:
- -
- Divide the signal received by the i-th () antenna into sub-vectors of length G, each sub-vector corresponds to a fragment spreading waveform;
- -
- Define a matrix with size where each column represents a transmitted symbol; then, the -th symbol occupies to rows if ; otherwise, it occupies the to L and 1 to rows;
- -
- All received signals from I antennas are stacked in a similar way to construct a partially missing tensor . Define an incomplete tensor . For and , the -th raw and -th column element of the i-th slice of is 1, and other elements are missing entries denoted by zeros for simplicity.
The process of constructing the missing tensor model is depicted in Figure 2. Then, we have the tensor of the received signal as
where can be seen as an equivalent short-code signal with the same spreading waveforms, symbols, and antenna gains as long-code cases (1). As it can be seen in [21], admits an essentially unique CANDECOMP/PARAFAC decomposition
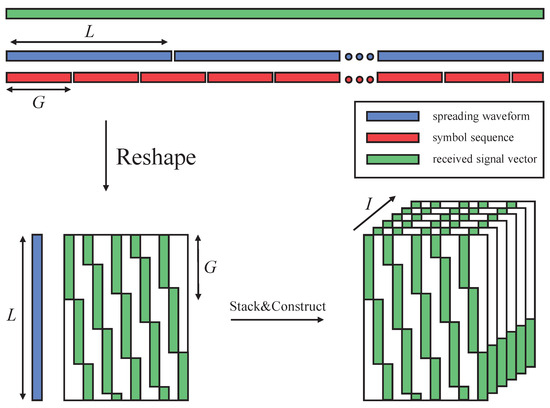
Figure 2.
Illustration of the missing tensor model for long-code multiuser DSSS signals.
3.3. Solution
In this subsection, we present an ALS-SI-based algorithm [30] to solve the optimization problem defined by (12). To be more specific, let us start with the standard alternating least squares for the short-code multiuser DSSS model, i.e., the original observation tensor is complete, and the elements of are all equal to one. By iterative steps, it can be shown that
where s denotes the number of iterations, the initial values are and . is the matrix transformed by as described in the previous section (for ).
We can define the following error function
If the value of decreases with iteration to a given value (the convergence condition), the algorithm then converges; otherwise, it continues to the next iteration until the maximum number of iterations is reached.
Considering long-code cases, i.e., is a part missing tensor, the ALS algorithm above cannot be used directly in the case of missing data, and some adjustments need to be made. Equations (13a) and (13b) are applied, instead of the mode-n unfolding (recall that ), to a complete matrix defined as
where is the mode-n unfolding of tensor computed by
at the s-th iteration, is a matrix with all elements of 1 and the same dimension as , and is the mode-n unfolding of the tensor . contains no missing entries, and thus, the standard CANDECOMP/PARAFAC-ALS algorithm is allowed to estimate the model parameters. It should also be pointed out that in order to avoid the convergence to local optima, the multiple initialization strategy can be adopted.
4. Identifiability of Decomposition
The most significant advantage of the low-rank decomposition of third-order tensors in comparison to the low-rank decomposition of matrices is the unique decomposition of tensors under mild conditions, whereas the decomposition of matrices is never essentially unique due to the unitary ambiguity between matrices.
Given a tensor of rank F, its CPD is essentially unique if the rank-1 terms of F in its decomposition are unique. If , then essential uniqueness as we mentioned before means that are unique up to a common permutation and scaling/counter-scaling of columns, meaning that if , then there exist a permutation matrix and diagonal scaling matrices such that
For ordinary tensor decomposition, the following theorem is used to ensure tensor identifiability.
Theorem 1.
Given , with , if , then and the decomposition of is essentially unique [29].
Note that the Kruskal rank of factor matrices is the largest integer k making any k columns of the matrix linearly independent. In addition, the generic of version of Kruskal’s condition also ensures the uniqueness of tensor decomposition and can be expressed as
For the missing tensor model, it is equivalent to sampling the complete tensor. For long-code signals as described before, it is equivalent to partially sampling the short-code signals to construct the missing data model. A sampling pattern is defined as a subset of rows and columns for which every point belongs to the pattern. Generally, this sampling pattern requires the following conditions to be met
where , D is the number of sampling pattern. After sampling, we get D sub-tensors
Finally, the generic identifiability of this sampling pattern is established in the following theorem.
Theorem 2.
Let be the original tensor signal with CPD of rank F. Assume that , and are drawn from some joint absolutely continuous distribution with respect to the Lebesgue measure in , and that satisfy the equations in (18). Then, recovers the ground-truth almost surely if [31]:
For the DSSS signal model, is the spreading gain and is the number of information source sequence, K is the number of antenna. Generally, are much larger than K and the number of users F. for each sampling pattern; thus, we get
or
For example, let . We only need to ensure that the number of users to satisfy the identification condition.
5. The Constrained Cramér–Rao Bound
Suppose the transmitted symbols are independent and identically distributed (i.i.d) and uncorrelated between each user, the noise is zero-mean Gaussian with a standard deviation equal to . Stacking the received signal vectors from all I antennas as a long vector , then, we have
where , denotes the i-th unit coordinate vector. Define the unknown parameter vector:
Based on (21), the log-likelihood function can be written as
with . The Fisher Information Matrix (FIM) associated with the estimates of these parameters is given by
where denotes the i-th element of vector . Because is subject to Gaussian distribution, i.e., , (24) can be given by [32]
in which and . Taking the partial derivatives of with respect to , and , we obtain
A delicate point in the derivation of the CRB is the inherent permutation and scale ambiguity of tensor decomposition, which may cause the FIM to be singular. As a result, the CRB, defined as the inverse of the FIM, has no analytical solution. To obtain a meaningful lower bound, we impose constraints on the parameters and get a constrained CRB [33,34]. Assume that the entries on the first row of , , and are known, i.e.,
for , where denotes the estimate of unknown parameters. Although considering the entries on the first row of , , and to be known is less appealing in a blind setting, and the extra information makes CRB somewhat harder to reach. However, it is worth noting that this method of adding constraints is intended to resolve the FIM singularity and ultimately to provide a performance assessment of the estimated parameters. Define the constrained vector
and the Jacobian matrix of the constrained vector as , i.e.,
Then, the constrained CRB of is given by
where returns the column vector of the main diagonal elements of matrix. In particular, the denotes the average constrained CRB of the estimated symbols , is given by
where represents the vector made up by m-th to n-th element of . To assess the performance of our proposed approach, a lower bound on the bit error rate (BER) is more meaningful than a lower bound on the variance of the estimated symbols due to the finite set property of the symbols. Assuming that the estimation errors of the symbols can be modeled as a zero-mean Gaussian random variable with variance equal to , the corresponding probability of error after detection for BPSK signals can be expressed as [24]:
where is the complementary error function.
6. Simulation Results
In this section, we assess the performance of proposed algorithm via simulation experiments. We compare the BER against the corresponding lower BER bound of the constrained CRB provided by (32). Our results are obtained from 1000 independent Monte Carlo trials, wherein for each Monte Carlo run, the antenna gains and the spreading waveforms are redrawn from an i.i.d. real Gaussian generator with zero mean and unit variance. Note that the spreading waveform can actually be represented as the convolution of the spread spectrum sequence and channel response, and the effects of transmit and multipath should be considered in the response. The focus of this paper is on the joint estimation of each user spreading waveform and message sequence. It is possible to disregard the details of specific channels, so it is reasonable to represent the spreading waveform with a Gaussian random sequence. The noise is zero-mean white (in all dimensions) Gaussian, with variance for all antennas. The observed tensor is given by , where is the noise-free missing tensor and is the noise tensor. The SNR at the input of the receiver is defined as follows:
In an independent experiment, the estimation of the spread spectrum waveform is shown in Figure 3, where the length of the spreading sequence , the spreading gain , the number of users , the number of symbols , the symbols are modulated using BPSK, the antenna number , and the signal-to-noise ratio dB. From Figure 3, we can observe that the estimated accuracy of the spread spectrum waveform is different for each user. This is due to the randomly generated user waveform amplitude, which causes the SNR to be different between each user, so users with small SNR will have larger spreading waveform estimation errors. For a practical communication scenario, this case corresponds to a multiuser uplink, where signal synchronization at the receiver side results in superimposed user waveforms of different amplitudes. We use the normalized mean squared error (NMSE) to measure the estimated error of spreading waveforms. NMSE is defined as follows:
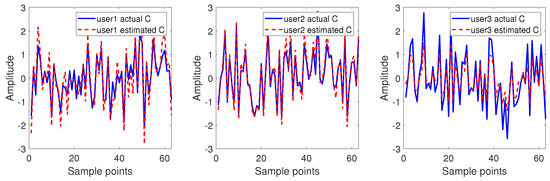
Figure 3.
Estimation of spreading waveforms.
By varying the number of antennas, spreading gain, number of users, and number of symbols, we obtain the curve of the NMSE of the spreading waveform estimation and the BER of the message sequence variation with the SNR. The experimental results are shown as follows.
As discussed earlier, the different SNR between each user can lead to variations in the spreading waveform estimation errors. Therefore, a large difference in SNR between users will inevitably occur in the Monte Carlo simulation process. These outlier points with large differences from the mean value are removed in our experiments. From the simulation results, it can be seen that the estimation error decreases as the number of antennas increases. This is due to the gain from multiple antenna diversity, as shown in Figure 4. We also note from Figure 5 that with a fixed length of the spreading sequence, the estimation error decreases as the spreading gain increases. This can be explained in two ways: for long-code DSSS signals, the increase of spreading gain results in a lower missing rate of segmented signals, which leads to a better estimation of the spreading waveform; also, the increase of spreading gain makes the BER of the message sequence lower, which is consistent with the typical spread spectrum communication system. As the number of users increases, the estimation error increases due to the inter-user interference, as shown in Figure 6. Therefore, in practical communication scenarios, we expect to use more antennas to reduce the losses caused by inter-user interference, as shown in Figure 7. Increasing the number of symbols will also result in lower estimation errors, but at high SNR, this gain will be less pronounced after a certain number of symbols is reached, as shown in Figure 8.
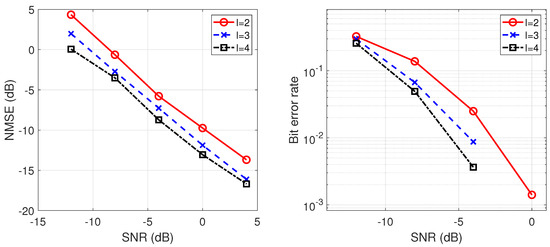
Figure 4.
NMSE of estimated spreading waveform and BER of information sequence (, , , ).
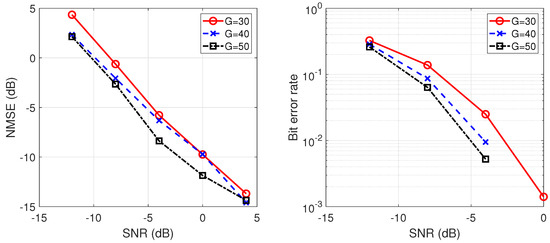
Figure 5.
NMSE of estimated spreading waveform and BER of information sequence (, , , ).
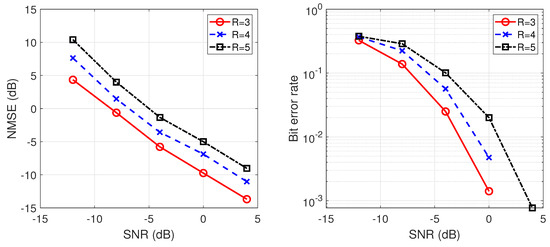
Figure 6.
NMSE of estimated spreading waveform and BER of information sequence (, , , ).
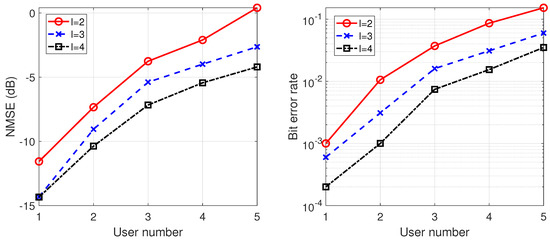
Figure 7.
NMSE of estimated spreading waveform and BER of information sequence (, , , dB).
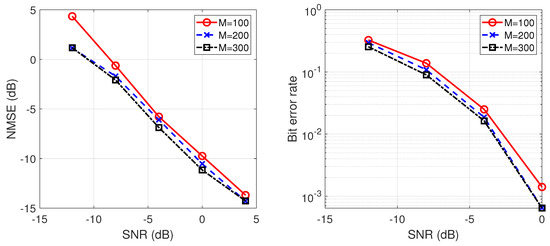
Figure 8.
NMSE of estimated spreading waveform and BER of information sequence (, , , ).
Finally, to verify the effectiveness of our algorithm, we compare the BER with the lower bound of the theoretical BER. As shown in Figure 9, the BER of the estimated message sequence is close to the lower bound of the theoretical BER. It shows that our algorithm has good blind despreading performance at low SNR.
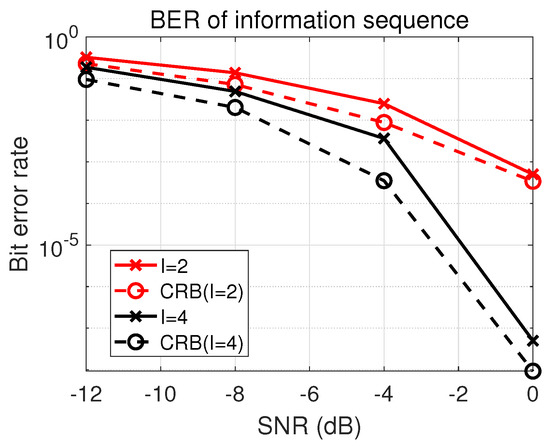
Figure 9.
Comparison of BER and CRB (, , , ).
7. Conclusions
We have presented a novel approach to blind separation of long-code multiuser DSSS signals. The proposed approach exploits the structure of long-code signals and reformulates the blind separation into the CANDECOMP/PARAFAC decomposition problem for a missing tensor. The constrained CRB is also derived to demonstrate the feasibility of our approach. Simulation results show that the proposed algorithm can estimate the spread spectrum waveform accurately and has good blind despreading performance at low SNR. They also verify the feasibility of the proposed algorithm and show that the estimated performance is close to the constrained CRB.
Author Contributions
Conceptualization, H.Z.; formal analysis, L.L., T.L., H.Z. and S.D.; investigation, L.L., T.L., H.Z. and S.D.; methodology, T.L. and H.Z.; project administration, H.Z.; software, L.L. and T.L.; supervision, H.Z. and L.G.; validation, L.L. and T.L.; writing—original draft, L.L., T.L. and H.Z.; writing—review and editing, L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under grant no. 61971103.
Acknowledgments
The authors thank the anonymous reviewers and editor whose valuable comments and suggestions have improved the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pickholtz, R.; Schilling, D.; Milstein, L. Theory of spread-spectrum communications—A tutorial. IEEE Trans. Commun. 1982, 30, 855–884. [Google Scholar] [CrossRef]
- Krisshna, P.A.; Aswini, B.; Nair, S.S.; Gopika, P.A.; Narayanan, G. Implementation of spread spectrum modulation schemes for secure communications. In Proceedings of the International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019; pp. 1397–1401. [Google Scholar]
- Bellili, A.M.F.; Affes, S.; Ghrayeb, A. Maximum likelihood time delay estimation from single and multi-carrier DSSS multipath MIMO transmissions for future 5G networks. IEEE Trans. Wirel. Commun. 2017, 16, 4851–4865. [Google Scholar]
- Neinavaie, M.; Khalife, J.; Kassas, Z.M. Blind Doppler tracking and beacon detection for opportunistic navigation with LEO satellite signals. In Proceedings of the IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; pp. 1–8. [Google Scholar]
- Khalife, J.; Shamaei, K.; Kassas, Z.M. Navigation with cellular CDMA signals—Part I: Signal modeling and software-defined receiver design. IEEE Trans. Signal Process. 2018, 66, 2191–2203. [Google Scholar] [CrossRef]
- Toru, I.; Yasuda, Y.; Sato, S.; Izumi, S.; Kawaguchi, H. Millimeter-precision ultrasonic DSSS positioning technique with geometric triangle constraint. IEEE Sens. J. 2022, 22, 16202–16211. [Google Scholar] [CrossRef]
- Hara, S.; Prasad, R. Overview of multicarrier CDMA. IEEE Commun. Mag. 1997, 35, 126–133. [Google Scholar] [CrossRef]
- Haque, M.N.; Shil, M.K. Performance perusal of multiuser MC-CDMA system for Nakagami-m, Rayleigh and Rician fading channel with spreading codes. In Proceedings of the IEEE 9th International Conference on Information, Communication and Networks (ICICN), Xi’an, China, 19–22 August 2021; pp. 1–8. [Google Scholar]
- Pursley, M.B.; Royster, T.C. High-rate direct-sequence spread spectrum with error-control coding. IEEE Trans. Commun. 2006, 54, 1693–1702. [Google Scholar] [CrossRef]
- Bouder, C.; Azou, S.; Burel, G. Performance analysis of a spreading sequence estimator for spread spectrum transmissions. J. Frankl. Inst. Eng. Appl. Math. 2004, 341, 595–614. [Google Scholar] [CrossRef]
- Tsatsanis, M.K.; Giannakis, G.B. Blind estimation of direct sequence spread spectrum signals in multipath. IEEE Trans. Signal Process. 1997, 45, 1241–1252. [Google Scholar] [CrossRef]
- Mehboodi, S.; Jamshidi, A.; Farhang, M. Spreading sequence estimation algorithms based on ML detector in DSSS communication systems. IET Signal Process. 2018, 12, 802–809. [Google Scholar] [CrossRef]
- Sarcheshmeh, H.M.; Bizaki, H.K.; Alizadeh, S. PN sequence blind estimation in multiuser DS-CDMA systems with multipath channels based on successive subspace scheme. Int. J. Commun. Syst. 2018, 31, e3591. [Google Scholar] [CrossRef]
- Qiu, Z.; Peng, H.; Li, T. A blind despreading and demodulation method for QPSK-DSSS signal with unknown carrier offset based on matrix subspace analysis. IEEE Access 2019, 7, 125700–125710. [Google Scholar] [CrossRef]
- Choi, H.; Moon, H. Blind estimation of spreading sequence and data bits in direct-sequence spread spectrum communication systems. IEEE Access 2020, 8, 148066–148074. [Google Scholar] [CrossRef]
- Liu, Q.; Li, T.; Xu, M. Joint blind estimation of PN codes and channels for long-code DSSS signals in multiple paths at low SNR. In Proceedings of the 2020 IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 28–31 October 2020; pp. 1266–1270. [Google Scholar]
- Liang, J.-H.; Wang, X.; Wang, F.-H.; Huang, Z.-T. Blind spreading sequence estimation algorithm for long-code DS-CDMA signals in asynchronous multi-user systems. IET Signal Process. 2017, 11, 704–710. [Google Scholar] [CrossRef]
- Zhang, H.G.; Gan, L.; Liao, H.S.; Wei, P.; Li, L. Estimating spreading waveform of long-code direct sequence spread spectrum signals at a low signal-to-noise ratio. IET Signal Process. 2012, 6, 358–363. [Google Scholar] [CrossRef]
- Zhang, H.; Wei, P.; Mou, Q. A semidefinite relaxation approach to blind despreading of long-code DS-SS signal with carrier frequency offset. IEEE Signal Process. Lett. 2013, 20, 705–708. [Google Scholar] [CrossRef]
- Qiang, X.; Zhang, T. Estimation of spreading code in non-periodic long-code DSSS signal. In Proceedings of the Sixth International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 25–27 March 2021; pp. 162–165. [Google Scholar]
- Sidiropoulos, N.D.; Giannakis, G.B.; Bro, R. Blind PARAFAC receivers for DS-CDMA systems. IEEE Trans. Signal Process. 2000, 48, 810–823. [Google Scholar] [CrossRef]
- Sidiropoulos, N.D.; Dimic, G.Z. Blind multiuser detection in W-CDMA systems with large delay spread. IEEE Signal Process. Lett. 2001, 8, 87–89. [Google Scholar] [CrossRef]
- de Baynast, A.; Aazhang, B.; Declerq, D.; Lathauwer, L.D. Bayesian blind PARAFAC receivers for DS-CDMA systems. IEEE Workshop Stat. Signal Process. 2003, 2003, 323–326. [Google Scholar]
- Lathauwer, L.D.; de Baynast, A. Blind deconvolution of DS-CDMA signals by means of decomposition in Rank-(1,L,L) terms. IEEE Trans. Signal Process. 2008, 56, 1562–1571. [Google Scholar] [CrossRef]
- Lathauwer, L.D.; Castaing, J. Tensor-based techniques for the blind separation of DS-CDMA signals. Signal Process. 2007, 87, 322–336. [Google Scholar] [CrossRef]
- Huang, Z.-T.; Liang, J.-H.; Wang, X. Estimating symbol duration of long-code direct sequence spread spectrum signals at a low signal-to-noise ratio. Wirel. Pers. Commun. 2020, 114, 1887–1904. [Google Scholar] [CrossRef]
- Sheng, S.; Yang, W.; Hou, Y. An improved power spectrum reprocessing method for DS-SS signal on spreading code period estimation. In Proceedings of the 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 774–779. [Google Scholar]
- Mou, Q.; Wei, P.; Tai, H.-M. Invariant detection for QPSK DS-SS signals. In Proceedings of the MILCOM 2009 IEEE Military Communications Conference, Boston, MA, USA, 18–21 October 2009; pp. 1–6. [Google Scholar]
- Sidiropoulos, N.D.; Lathauwer, L.D.; Fu, X.; Huang, K.; Papalexakis, E.E.; Faloutsos, C. Tensor decomposition for signal processing and machine learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Tomasi, G.; Bro, R. PARAFAC and missing values. Chemom. Intell. Lab. Syst. 2005, 75, 163–180. [Google Scholar] [CrossRef]
- Kanatsoulis, C.I.; Fu, X.; Sidiropoulos, N.D.; Akçakaya, M. Tensor completion from regular sub-Nyquist samples. IEEE Trans. Signal Process. 2020, 68, 1–16. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing; Prentice Hall PTR: Hoboken, NJ, USA, 1993. [Google Scholar]
- de Carvalho, E.; Cioffi, J.; Slock, D. Cramér-Rao bounds for blind multichannel estimation. In Proceedings of the 2000 IEEE Global Telecommunications Conference, Kuala Lumpur, Malaysia, 4–8 December 2000; pp. 1036–1040. [Google Scholar]
- Stoica, P.; Ng, B.C. On the Cramér-Rao bound under parametric constraints. IEEE Signal Process. Lett. 1998, 5, 177–179. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).