Abstract
The significant role for a contemporary control algorithm in the position control of a permanent magnet linear motor (PMLM) system is highlighted by the rigorous standards for accuracy in many modern industrial and robotics applications. A robust predefined time convergent sliding mode controller (PreDSMC) is designed for the high precision position tracking of a permanent magnet linear motor (PMLM) system with external disturbance, and its convergence time is independent of the system’s initial value and model parameters. We verified theoretically that the performance function conditions are satisfied, the motor speed is steady and constrained, and the motor position tracking error converges to zero within the prescribed time. First, we designed a sliding mode (SM) surface with predetermined time convergence, which mathematically demonstrates that the tracking error converges to zero within the predefined time and shows that the position tracking accuracy is higher. Secondly, we developed a PreDSMC law that is independent of initial state and based on the predefined time convergence Lyapunov stability criterion. Finally, to prove the accuracy and higher precision of the proposed PreDSMC, comparative numerical simulations are performed for PMLM with compound disturbances. Simulation findings show that the suggested robust predefined control method considerably reduces the impacts of friction and external disturbances; consequently, it may increase the control performance when compared to the typical proportional integral derivative (PID) controller, the nonsingular fast terminal SMC, and the linear SMC.
1. Introduction
Today, permanent magnet linear motors (PMLM) have a significant role in civil, industrial, military, and other high-precision applications [1,2]. Especially, PMLM is widely used in the high-precision manufacturing industry because of its higher thrust density, higher acceleration, speed, and very high precision. As a result, PMLM research has recently received more prominent attention from researchers. However, the performance of these motors degrades due to external disturbances, force ripple, and friction effects [3]. Concerning high-precision motion control, it is always very critical to attain a fast-dynamic response, especially when increasing the tracking accuracy is a vital goal of the PMLM.
Numerous control algorithms for PMLM analysis and design focusing on various applications have been presented in the literature. For instance, a robust adaptive algorithm was developed in [4] for the compensation and control of PMLM displacement in the presence of force ripple and friction. The authors of [5] presented a water-cooled PMLM system that was designed for studying the temperature behavior under various work tasks. The performance of PMLM rate control based on flow-oriented primary control was studied in [6]. Sliding mode control (SMC) is a preferred method for managing control problems in nonlinear systems. It is widely used in practical applications for its insensitivity to parameter changes and perturbations [7,8,9,10,11,12,13]. Design of an adaptive 2-SMC method for a class of unknown nonlinear discrete systems with multiple inputs and multiple outputs (MIMO) was described in [14]. Stable pressure control for coke oven gas distributors was achieved by combining SMC and data-driven control (DDC) methods [15]. The traditional SMC ensures the asymptotic stability of the closed loop control only in the sliding mode phase, i.e., the system to the equilibrium point indefinitely. However, the finite-time terminal SMC-based PMLM system realizes uncertainties by balancing control performance and robustness. An efficient tactic that not only guarantees control quality but can also improve robustness is predictive interference compensation, presented in the literature [16,17,18]. The observer-based design method is proficient for estimating perturbations such as SMC [19,20,21] and the finite-time approach [22,23,24]. Owing to the supremacy of finite-time convergence [25,26,27], terminal sliding mode control (TSMC) has been presented in [28,29,30].
Nonlinear systems have become the topic of extensive study during the past few decades because such systems provide a more critical perspective of the available information on the qualities of memory and legacy [31,32,33]. Some examples of physical systems involving nonlinearities include electrical circuits containing supercapacitive elements which are vital in the design of batteries and fuel cells [34,35,36,37], mechanical systems containing viscoelastic materials [38,39], and biological systems [40,41]. Moreover, sophisticated control design can benefit from the reliability of fractional-order approaches. Sliding mode approaches [42,43,44] are amongst the most often used methods because of their effectiveness in reducing the impact of uncertainty in the control of nonlinear systems.
Dynamic characteristics involve enforcing sliding motion with finite and fixed-time convergence [45,46,47]. Recent publications have investigated sliding mode and fixed-time tools, elaborating on the remarkable qualities of these uncertain systems [48]. Moreover, the time at which the sliding action is imposed (the settling-time function) is unbounded with respect to the initial condition. Nevertheless, sliding mode methods ensure finite-time convergence of the sliding function.
Recent research has established the concept of fixed-time stability to address the issue of an unbounded settling-time function. When starting from this state, the work in question enforces a sliding mode within a uniformly defined time. Designing appropriate controllers for nonlinear systems has been studied using the predefined time-stability approach [49,50,51,52,53]. Therefore, in the case of a second-order nonlinear system based on the Lyapunov stability criterion, predefined time SMCs have been proposed. These works differ from prior research as they suggest auxiliary controllers through a suitable dynamic extension. This research was influenced by adaptive predefined time stability.
The robustness of perturbations is rarely explored for predefined settling-time strategies, especially for autonomous systems [54,55,56]. The controller proposed in [57] could only mitigate the disturbances if the system’s initial states are known. In [53] and [55], complementary random time convergence is accomplished by changing the sliding phase solely; moreover, simulations presume that the reaching time of SMC is predictable. Additionally, [56] used a time-changing piecewise controller to discard matching instabilities and attain preset time by altering system parameters. The authors in [58,59] addressed this problem by developing unique terminal sliding surface-based control in a combined predetermined settling period for the category of nonlinear second-order systems containing coupled disturbances.
In [60,61,62], nonsingular terminal SMC is used to evaluate the overall effectiveness of a fixed-time control mechanism with mismatched disturbances. It is pertinent to mention that the constraints on the settling time were too conservative and required a significant amount of control effort. In [63], the authors extended this work and demonstrated the ultimate boundedness with predetermined temporal stability. Moreover, it is believed that the predetermined time in [59,63,64] is a factor of the system’s starting states and characteristics.
Research in [65] proposed a back-stepping strategy to establish fixed-time stability for higher-order systems with rigorous feedback. In [66], predetermined time stability is attained for dynamical systems with distributed order in the context of uncertainty. In addition, a recent study [44] designed a unique SMC that leads to preset time convergence. Further, nonsingular terminal SMC is being proposed to avoid singularities and it has been implemented in some practical control systems [67,68,69,70,71]. Despite this, inner discontinuities appear as never before in previous terminal SMC schematics. As a result, some effective techniques have been used to overcome the chattering problem resulting from internal discontinuities. In particular, the finite-time terminal SMC can achieve fast state convergence to improve tracking accuracy and limit the jitter problem of phase. In this article, motivated by the advantages of the finite-time terminal SMC, we designed a predefined time control method for the PMLM system.
A permanent magnet linear motor (PML) not only has advantages of high force density, low heat loss, and high precision and accuracy, but also has simple mechanical structure [72], so it is the first choice for motor motion control systems involving high strength, speed, and high precision [3]. Today, PML has been widely used in the precision manufacturing industry. Compared with traditional rotary motors [73,74,75,76], linear motors do not require indirect coupling mechanisms such as gear boxes, chains, and screw couplings, which greatly reduces contact-type nonlinearity and mechanical interference such as friction and recoiling [77,78,79]. As a result, PML can meet the growing demand for high performance servo system applications and has been successfully used in machine tools, semiconductor manufacturing systems, etc. Since PML is not equipped with a transport mechanism, the realizable performance of PML, such as the ability to reduce uncertainty and the influence of external interference, is inevitably lost to some extent. Therefore, it is very important to reduce these interference effects through appropriate mechanical design or control scheme. With new methods of mechanical design, the effect can be maintained at the allowable level, but this method is more expensive. The controller design based on a PML system is an economical and feasible method to suppress these effects.
The available literature not only ignores the impact of predefined stability and disturbances, but assumes that the predefined settling time is a factor of the initial states. Moreover, the convergence rate conventions are extra cautious and require a significant control effort. To the best of our knowledge, predefined time convergence for nonlinear systems containing uncertainties and unknown initial conditions remains an unsolved topic. The contributions of our paper are summarized below:
- A predefined time sliding surface of the tracking error is designed, and we also theoretically prove that the tracking error found at the sliding surface converges to the equilibrium point within a prescribed time. Furthermore, its derivative is bounded, which gives the tracking error superior information. A Lyapunov-based stability criterion with predefined time convergence is elaborated and proved theoretically. The results depict the predefined convergence time, which is independent of the initial value and the parameters of the controlled system.
- A robust predefined SMC law is designed and proven theoretically. We utilize the predefined sliding function to capture the control input variables, which simplifies the complexity of the designed controller. It is shown that the trajectory tracking error of the closed-loop system has a convergent nature within a predefined time. Moreover, the trajectory satisfies the performance, and it is worth noting that its derivative is bounded.
- We have designed a predefined robust control law to approximate the uncertain part of the PMLM, i.e., friction and ripple forces. The presented scheme in this paper has a wide range of applications. Our proposed PreDSMC only needs the trajectory tracking error of the PMLM and its derivative information to realize the high-precision trajectory tracking control of the system. It is independent of the initial conditions and model parameters of the system, which is why it is called a robust controller.
This study is organized into the following sections: Section 2 presents the mathematical model and control objective of the PMLM. Section 3 presents the linearization method of nonlinear parts and the variation method for the tracking error performance based on the predefined criterion of the sliding function. Moreover, the sliding mode surface with a predefined time for tracking error convergence and the Lyapunov stability criterion for convergence are presented in the same section. Section 4 presents the proposed PreDSMC control law. To verify the robustness of the proposed PreDSMC control algorithm, simulation results for various cases are presented in Section 5. Lastly, our study is concluded in Section 6.
2. Problem Formulation
In general, the second-order nonlinear dynamic system can be mathematically expressed as
where and are the internal parameter variables. Mass and are smooth continuous functions and N includes some nonlinearities such as Stribeck friction and ripple forces. Nomenclature is given in Table 1.

Table 1.
Parameters of the PMLM model.
PMLM Model Representation
Although a second-order system may frequently be used to illustrate the dynamics of a PMLM [27], owing to the low value of stator inductance relative to the resistance, we neglect it in this study along with loads and slight perturbations. A typical PMLM mathematical model is characterized as follows:
where the parameters are . Assuming the reference signal is denoted as and its first and second order derivatives, i.e., and are sequential and bounded, respectively. Consequently, position tracking error and speed tracking errors can be expressed as .
According to the model described above, the state-variable formulation of a PMLM is easily derivable. Additionally, the error dynamics equation can be described as:
The control goal of this article is to develop a robust controller that can accurately follow the reference position curve in the predefined time. The Stribeck curve in Figure 1 is a well-known tool for modeling the friction. It essentially indicates the relationship between the friction force and angular velocity for different values of friction. The Stribeck friction model can be expressed as in Equation (2). When the static friction is , with threshold, the dynamic friction can be given by the following piecewise expression:
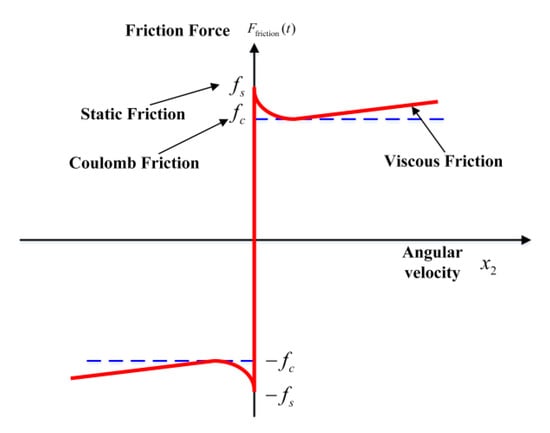
Figure 1.
Stribeck friction curve.
The Stribeck friction curve is a well-known model of the friction. It shows the relationship between the friction force and angular velocity for different values of the friction. A friction model can be expressed as in Equation (4). When the static friction is |θ ˙(t)| < α, with threshold, the dynamic friction can be given by (4). One can see that the static friction is |θ ˙(t)| > α, and can be given as above in which Fs denotes the driving force, Fc represents the maximum static friction force, and it is a small scaling factor.
where is the viscous friction coefficient, is the assumed measured lubrication parameter, is the minimum value of the Coulomb friction, and is the static friction. According to the cogging effect in the structure of the PMLM, the pulsating force generated by the reluctance is modeled as
where is the angular velocity and is the amplitude. The load disturbance torque is a constant value. The overall system is described as follows:
3. Predefined Time Sliding Surface Design
Definition 1: For the nonlinear system (2), if there is a predefined constant such that the condition is satisfied for any :
- (1)
- At the time , ;
- (2)
- When , and has , then the nonlinear system (2) is globally predefined time stable.
To take the full advantage of strong robustness of the sliding mode controller and ensure that the trajectory tracking error can converge to the equilibrium point within the predefined time , the sliding mode surface with the predefined time convergence is designed as follows:
where the parameter satisfies ; is the predefined time. For the sliding mode surface (7), Theorem 1 is given below.
3.1. Predefined Time Error Convergence Criterion
Theorem 1.
For any predefined timeand parameter, when the sliding mode surface (3) satisfies, the following holds true:
- (1)
- If the initial value of the tracking error is , then will converge to zero within the predefined time, and the convergence time
- (2)
- If the initial value of the tracking error is , then at that the time that converges to zero is , that is, when is the trajectory tracking error .
Proof of Theorem 1.
When , there is:
After transforming (8), we obtain
The following measures were taken to ease the integration:
Assuming that the tracking error converges to zero at time , i.e., , integrating both sides of Equation (10) on gives
Simplifying with the help of the steps given in Equations (12) and (13), we obtain
When and represent constant , it means that when the sliding surface , the tracking error is also equal to zero and hence the theorem is proved. □
3.2. Predefined Time Convergence Stability
Theorem 2.
For nonlinear system, for any predefined time, and parameter, if there is a radially unbounded and positive definite Lyapunov functionthat satisfies
then
- (1)
- If , the system is stable at the global predefined time and converges to the equilibrium point.
- (2)
- If , then and it indicates that the system state is always at the equilibrium point.
Proof of Theorem 2.
Let , then
After transforming (15) and taking the differential, we have
Let us assume that at time . Next, integrate both sides of Equation (16). Since, , then , we obtain:
After simplification, we have
□
4. Design of Predefined Time Control Law
First, take the Lyapunov function as , and derive it with respect to :
After simplification, we obtain
The controller is designed as: where
then
Therefore,
Among them , according to Theorem 2, it can be known that system (2) is globally stable at predefined time, and the sliding mode surface will converge to zero within the predefined time; the convergence time is .
Remarks.
In SMC, the usage of the signum function often results in a chattering phenomenon. Therefore, we must define a special function in order to mitigate this chattering effect. We can now define a continuous function, i.e., sat (s), for the compensation of chattering in the linear SMC (LSMC) control signal such that:
whereis taken as a positive constant. Its value can be chosen so that the control action and chattering effect are not compromised. For practical applications, any random but positive value can be set.
Here, the system states are ; denotes the displacement and represents the velocity of the PMLM. From this equation, we can set the sliding surface as: . In accumulation, the LSMC is taken as:
The renowned PID control law is given as: .
To compare with the finite control method, we can select the nonsingular fast terminal SMC (NFTSMC), which is given as follows:
In this formula, is the main control law. For nonsingularity, there is a compensation technique that provides a control law to compensate for disturbances. The following control is our proposed PreDSMC input control law:
According to Theorem 2, based on the proposed PreDSMC in Equation (25), a closed-loop system is able to converge to a defined surface within a predefined time . When the system state reaches and stabilizes in the sliding mode surface, (please refer to Equation (21), i.e., ), then according to Theorem 1, a tracking error will always converge to the equilibrium point within a predefined time . Thus, the system also converges to its origin to the respective predefined time . According to the conclusion of Theorem 1, the system tracking error and its derivative are bounded.
5. Numerical Simulation Analysis
5.1. PMLM Simulation
Taking the PMLM mathematical model as the simulation target [80,81,82], the relevant parameters of the PMLM model are set as given in Table 1. Additionally, the overall proposed robust control structure is shown in Figure 2.
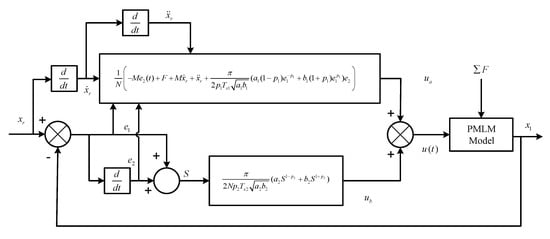
Figure 2.
Structure of the proposed PreDSMC.
PreDSMC is a robust controller that is particularly designed for PMLM position tracking in this study. The main goal is to track the displacement within a predefined time with a higher accuracy for the PMLM model. Two cases have been considered to check the robust performance of the proposed control scheme. The first is step tracking, and the second is sinusoid tracking. The control parameters are chosen according to the PMLM system for higher performance and accuracy. Multiple control schemes are considered for the purpose of comparison analysis with the PreDSMC. The control gains are chosen accordingly to achieve higher accuracy and precision in both the step and sinusoid tracking. The numerical values of these parameters are listed in Table 2.

Table 2.
Parameters of the controllers.
5.2. Step Tracking Response of PMLM Displacement
We chose the step signal as a reference to simulate the displacement of the PMLM, and the load is set to = 0 N. The step response of NFTSMC, LSMC, PID, and our proposed PreDSMC control is shown in Figure 3a, and the respective error curve is given in Figure 3b. The predefined time for our proposed controller is set to 0.5 s. The convergence of PID, LSMC, and NFTSMC is very slow as compared to our proposed PreDSMC. Owing to the steady state error, the convergence time of the other three controllers is about 1 s. Thus, the proposed control strategy has a good convergence time, which is settled before 0.5 s. The error tracking results in Figure 3b depict that our proposed control strategy has a good convergence as compared to NFTSMC, LSMC, and PID control.
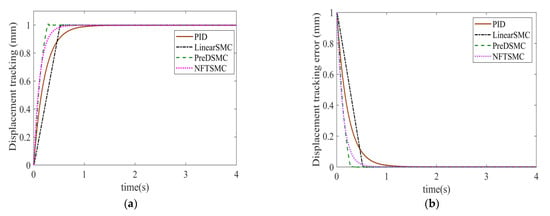
Figure 3.
(a) Comparative step tracking performance of displacement for all control laws. (b) The corresponding step tracking error of displacement.
To analyze the effectiveness of our proposed PreDSMC controller, we can compare the results of the derivative of the error signal as well as the control input. Figure 4a shows that the derivative error of our proposed controller is much less than that of LSMC, PID, and NFTSMC. Figure 4b depicts that our proposed controller needs less control effort as compared to NFTSMC, while NFTSMC has a chattering effect in the control input. It can clearly be seen that our proposed control does not have any chattering effect. The overall error convergence time and control response shows that the PreDSMC has priority over the PID, LSMC, and NFTSMC. To this end, we can summarize that the proposed PreDSMC control law has less steady state error, and the control effect is very impressive. It can precisely and accurately track the desired step signal, so we can conclude that the proposed controller is more robust as compared to the other three control algorithms.
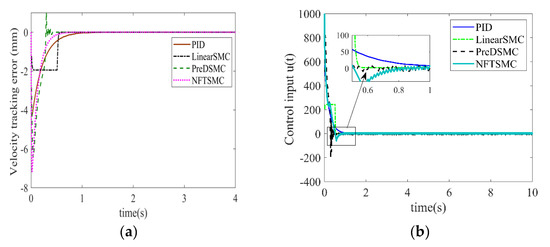
Figure 4.
(a) Comparison of velocity tracking error for the case of step response of displacement for all control laws. (b) Velocity tracking error for the corresponding step tracking of displacement.
5.3. Sinusoidal Tracking Response of PMLM Displacement
A sinusoidal displacement signal is taken as a reference, i.e., , with an amplitude of 5 mm and frequency of rad/s. Like the previous case of step response, is taken as 0 N. In the same manner, the predefined settling time PreDSMC in the sinusoidal case for the proposed controller is set to Ts = 0.5 s. It means we want the controller to settle before 0.5 s. It can be clearly observed from Figure 5a that our proposed controller convergence is very fast as compared to PID, LSMC, and NFTSMC. Moreover, the tracking accuracy of PreDSMC in the case of predefined time control is very high. The respective steady state error of the four controllers can be seen in Figure 5b. The steady state error in the case of PID is very large, about −0.3 to 0.3 mm, while for LSMC and NFTSMC it is almost −0.2 to 0.2 mm. Our proposed controller has a steady state error of almost 0.01 mm. It depicts that our proposed PreDSMC is more robust as compared to the simple PID, LSMC, and NFTSMC.
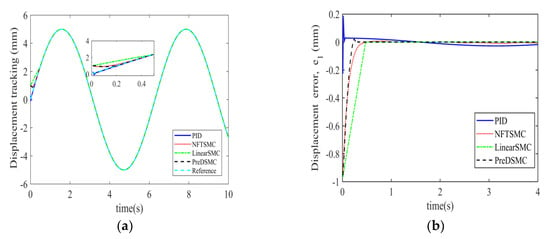
Figure 5.
(a) Sinusoidal tracking performance of displacement for all control laws. (b) The comparison of sinusoidal tracking error of displacement.
Figure 6a,b depict the derivative of the tracking error displacement and the control effort of the four control algorithms. It is clear from Figure 6a that the tracking error derivative in the case of PID and NFTSMC is much larger as compared to LSMC and the proposed PreDSMC control strategy. Moreover, we can analyze that the tracking error in the case of the proposed PreDSMC is less as compared to the other control laws. Figure 6b shows the control effort of these four control algorithms. The control effort of our proposed controller is much higher, and it is quite astonishing that PID has almost the same control effort but with a large steady state error.
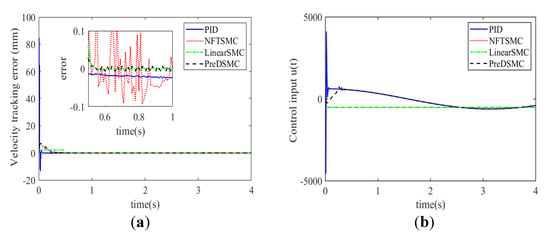
Figure 6.
(a) Comparison of sinusoid velocity tracking error displacement for all controllers. (b) Control input for different control algorithms.
To recapitulate, the proposed PreDSMC is robust and has the capability of high precision displacement tracking of PMLM. Furthermore, the proposed model can converge the error within the prescribed time. It is obvious from the simulation results given above that the proposed PreDSMC method is robust and able to obtain the fastest convergence within the predefined time and has smallest tracking errors. It also possesses preferable control features when compared with the PID, LSMC, and NFTSMC control laws.
6. Conclusions
In this article, a robust predefined time SMC control algorithm has been designed which has predefined convergent time characteristics. Predefined feature means its convergence time can be chosen in advance, which is especially designed for a PMLM with external compound disturbances, bounded state, and control saturation constraints. The designed predefined time SMC algorithm described in this paper not only ensures the position tracking error convergence of the PMLM within the predefined time, but also verifies that the velocity tracking error is bounded, and the control input meets the predefined boundedness requirements. Furthermore, the motor position can be tracked with high accuracy within the predefined performance function. The desired position is tracked with 10−4 order-of-magnitude accuracy within the chosen time to achieve a balance between the motor tracking accuracy and the tracking velocity. To recapitulate from the robustness point of view and the scope of application, it can also be used in future work for high-precision trajectory tracking control of nonlinear systems such as piezoelectric positioning, robotic arms, and other second-order nonlinear models. Future study may take into account other nonlinearities as PMLM servo system parameter uncertainty, gear backlash, and coupled frictional nonlinearity with external load variations.
Author Contributions
The following contributions reflect the role of individual authors in this study and manuscript. Conceptualization, S.R. and B.L.; methodology, S.R.; software, S.R.; validation, C.-W.Y., S.R. and B.L.; formal analysis, K.S.; investigation, R.Q.; resources, C.-W.Y.; data curation, C.-W.Y.; writing—original draft preparation, S.R.; writing—review and editing, B.L., K.S. and S.A.; visualization, R.Q.; supervision, R.Q. and B.L.; project administration, B.L.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been funded by the following agencies: (1) Science Foundation of Shaanxi Province for Outstanding Youth, 2022JC-32, and (2) Joint Key Project of Shaanxi Key R & D Program, 2021GXLH-01-14.
Data Availability Statement
Not applicable.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Nomenclature
| Notation | Description |
| Position and speed of PMLM | |
| Output of system | |
| Input voltage | |
| Resistance | |
| Motor mass | |
| Force constant | |
| Back electromotive force | |
| Friction force | |
| Ripple force | |
| Load | |
| Viscous friction coefficient | |
| Lubrication parameters | |
| Minimum value of Coulomb friction | |
| Static friction | |
| , | Angular velocity and amplitude of ripple force |
| Intermediate variable of system | |
| Reference trajectory | |
| Position error and speed error | |
| Sliding mode surface | |
| , | Predefined time |
| Parameter of sliding mode surface | |
| Convergence time | |
| Lyapunov function | |
| Parameters of Lyapunov function |
References
- Kim, J.; Choi, S.; Cho, K.; Nam, K. Position estimation using linear hall sensors for permanent magnet linear motor systems. IEEE Trans. Ind. Electron. 2016, 63, 7644–7652. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Q.; Zhen, S.; Zhao, H.; Li, C.; Chen, Y.-H. Robust constraint-following control for permanent magnet linear motor with optimal design: A fuzzy approach. Inf. Sci. 2022, 600, 362–376. [Google Scholar] [CrossRef]
- Chen, S.-L.; Tan, K.K.; Huang, S.; Teo, C.S. Modeling and compensation of ripples and friction in permanent-magnet linear motor using a hysteretic relay. IEEE/ASME Trans. Mechatron. 2009, 15, 586–594. [Google Scholar] [CrossRef]
- Tan, K.; Huang, S.; Lee, T. Robust adaptive numerical compensation for friction and force ripple in permanent-magnet linear motors. IEEE Trans. Magn. 2002, 38, 221–228. [Google Scholar] [CrossRef]
- Lu, Q.; Zhang, X.; Chen, Y.; Huang, X.; Ye, Y.; Zhu, Z. Modeling and investigation of thermal characteristics of a water-cooled permanent-magnet linear motor. IEEE Trans. Ind. Appl. 2014, 51, 2086–2096. [Google Scholar] [CrossRef]
- Cao, R.; Cheng, M.; Zhang, B. Speed control of complementary and modular linear flux-switching permanent-magnet motor. IEEE Trans. Ind. Electron. 2015, 62, 4056–4064. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Edwards, C.; Colet, E.F.; Fridman, L.; Colet, E.F.; Fridman, L.M. Advances in Variable Structure and Sliding Mode Control; Springer: Berlin/Heidelberg, Germany, 2006; Volume 334. [Google Scholar]
- Mou, F.; Wu, D.; Dong, Y. Disturbance rejection sliding mode control for robots and learning design. Intell. Serv. Robot. 2021, 14, 251–269. [Google Scholar] [CrossRef]
- Dong, H.; Yang, X.; Basin, M.V. Practical Tracking of Permanent Magnet Linear Motor Via Logarithmic Sliding Mode Control. IEEE/ASME Trans. Mechatron. 2022, 27, 4112–4121. [Google Scholar] [CrossRef]
- Cao, W.; Lan, Q.; Ma, T. Second-Order Sliding Mode Controller Design for Motion Control of PMLM System. In Advances in Guidance, Navigation and Control; Springer: Singapore, 2022; pp. 2097–2107. [Google Scholar]
- Sepestanaki, M.A.; Barhaghtalab, M.H.; Mobayen, S.; Jalilvand, A.; Fekih, A.; Skruch, P. Chattering-Free Terminal Sliding Mode Control Based on Adaptive Barrier Function for Chaotic Systems With Unknown Uncertainties. IEEE Access 2022, 10, 103469–103484. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Y.; Ye, M.; Zhang, J.; Cao, Z.; Zheng, J.; Man, Z. Real-Time Control Systems with Applications in Mechatronics. In Handbook of Real-Time Computing; Springer: Singapore, 2022; pp. 605–640. [Google Scholar]
- Hou, M.; Wang, Y.; Han, Y. Data-driven discrete terminal sliding mode decoupling control method with prescribed performance. J. Frankl. Inst. 2021, 358, 6612–6633. [Google Scholar] [CrossRef]
- Weng, Y.; Gao, X. Data-driven robust output tracking control for gas collector pressure system of coke ovens. IEEE Trans. Ind. Electron. 2016, 64, 4187–4198. [Google Scholar] [CrossRef]
- Chen, W.-H.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2015, 63, 1083–1095. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Y.; Wang, N. Nonlinear disturbance observer-based backstepping finite-time sliding mode tracking control of underwater vehicles with system uncertainties and external disturbances. Nonlinear Dyn. 2017, 88, 465–476. [Google Scholar] [CrossRef]
- Sun, H.; Li, S.; Sun, C. Finite time integral sliding mode control of hypersonic vehicles. Nonlinear Dyn. 2013, 73, 229–244. [Google Scholar] [CrossRef]
- Yang, Z.; Ding, Q.; Sun, X.; Lu, C.; Zhu, H. Speed sensorless control of a bearingless induction motor based on sliding mode observer and phase-locked loop. ISA Trans. 2022, 123, 346–356. [Google Scholar] [CrossRef]
- Zhou, M.; Cheng, S.; Xu, W.; Feng, Y.; Su, H. Control and Observation of Induction Motors Based on Full-Order Terminal Sliding-Mode Technique. In Advances in Control Techniques for Smart Grid Applications; Springer: Singapore, 2022; pp. 327–363. [Google Scholar]
- Liao, K.; Xu, W.; Bai, L.; Gong, Y.; Ismail, M.M.; Boldea, I. Improved Position Sensorless Piston Stroke Control Method for Linear Oscillatory Machine via an Hybrid Terminal Sliding-Mode Observer. IEEE Trans. Power Electron. 2022, 37, 14186–14197. [Google Scholar] [CrossRef]
- Du, H.; Qian, C.; Yang, S.; Li, S. Recursive design of finite-time convergent observers for a class of time-varying nonlinear systems. Automatica 2013, 49, 601–609. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Z.; Dang, Q.; Zhao, W.; Wang, G. Robust trajectory tracking control for a quadrotor using recursive sliding mode control and nonlinear extended state observer. Aerosp. Sci. Technol. 2022, 128, 107749. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, J. Continuous nonsingular terminal sliding mode control for nonlinear systems subject to mismatched terms. Asian J. Control 2022, 24, 885–894. [Google Scholar] [CrossRef]
- Chen, W.; Du, H.; Chen, C.-C. Stability and Robustness Analysis of Finite-Time Consensus Algorithm for Second-Order Multiagent Systems Under Sampled-Data Control. IEEE Trans. Syst. Man Cybern. Syst. 2022, 1–8. [Google Scholar] [CrossRef]
- Du, H.; Jiang, C.; Wen, G.; Zhu, W.; Cheng, Y. Current sharing control for parallel DC–DC buck converters based on finite-time control technique. IEEE Trans. Ind. Inform. 2018, 15, 2186–2198. [Google Scholar] [CrossRef]
- Du, H.; Zhai, J.; Chen, M.Z.; Zhu, W. Robustness analysis of a continuous higher order finite-time control system under sampled-data control. IEEE Trans. Autom. Control 2018, 64, 2488–2494. [Google Scholar] [CrossRef]
- Jin, M.; Lee, J.; Chang, P.H.; Choi, C. Practical nonsingular terminal sliding-mode control of robot manipulators for high-accuracy tracking control. IEEE Trans. Ind. Electron. 2009, 56, 3593–3601. [Google Scholar]
- Mobayen, S.; Alattas, K.A.; Assawinchaichote, W. Adaptive continuous barrier function terminal sliding mode control technique for disturbed robotic manipulator. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 4403–4412. [Google Scholar] [CrossRef]
- Sai, H.; Xu, Z.; Xia, C.; Sun, X. Approximate continuous fixed-time terminal sliding mode control with prescribed performance for uncertain robotic manipulators. Nonlinear Dyn. 2022, 110, 431–448. [Google Scholar] [CrossRef]
- Kaufmann, E.; Mboumi, E. Positive solutions of a boundary value problem for a nonlinear fractional differential equation. Electron. J. Qual. Theory Differ. Equ. 2008, 2008, 1–11. [Google Scholar] [CrossRef]
- Khan, A.; Nigar, U. Sliding mode disturbance observer control based on adaptive hybrid projective compound combination synchronization in fractional-order chaotic systems. J. Control Autom. Electr. Syst. 2020, 31, 885–899. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, L.; Niu, B.; Zhao, X.; Ahmad, A.M. Adaptive neural finite-time hierarchical sliding mode control of uncertain under-actuated switched nonlinear systems with backlash-like hysteresis. Inf. Sci. 2022, 599, 147–169. [Google Scholar] [CrossRef]
- Bertrand, N.; Sabatier, J.; Briat, O.; Vinassa, J.-M. Embedded fractional nonlinear supercapacitor model and its parametric estimation method. IEEE Trans. Ind. Electron. 2010, 57, 3991–4000. [Google Scholar]
- Martynyuk, V.; Ortigueira, M. Fractional model of an electrochemical capacitor. Signal Process. 2015, 107, 355–360. [Google Scholar] [CrossRef]
- Islam, M.M.; Siffat, S.A.; Ahmad, I.; Liaquat, M.; Khan, S.A. Adaptive nonlinear control of unified model of fuel cell, battery, ultracapacitor and induction motor based hybrid electric vehicles. IEEE Access 2021, 9, 57486–57509. [Google Scholar] [CrossRef]
- Thounthong, P.; Tricoli, P.; Davat, B. Performance investigation of linear and nonlinear controls for a fuel cell/supercapacitor hybrid power plant. Int. J. Electr. Power Energy Syst. 2014, 54, 454–464. [Google Scholar] [CrossRef]
- Penas, R.; Balmes, E.; Gaudin, A. A unified non-linear system model view of hyperelasticity, viscoelasticity and hysteresis exhibited by rubber. Mech. Syst. Signal Process. 2022, 170, 108793. [Google Scholar] [CrossRef]
- Şengül, Y. Nonlinear viscoelasticity of strain rate type: An overview. Proc. R. Soc. A 2021, 477, 20200715. [Google Scholar] [CrossRef]
- Bezerra, J.I.; Molter, A.; Rafikov, M.; Frighetto, D.F. Biological control of the chaotic sugarcane borer-parasitoid agroecosystem. Ecol. Model. 2021, 450, 109564. [Google Scholar] [CrossRef]
- Sabir, Z.; Baleanu, D.; Ali, M.R.; Sadat, R. A novel computing stochastic algorithm to solve the nonlinear singular periodic boundary value problems. Int. J. Comput. Math. 2022, 99, 2091–2104. [Google Scholar] [CrossRef]
- Aslmostafa, E.; Mirzaei, M.J.; Asadollahi, M.; Badamchizadeh, M.A. Stabilization problem for a class of nonlinear MIMO systems based on prescribed-time sliding mode control. Arab. J. Sci. Eng. 2022, 47, 15083–15094. [Google Scholar] [CrossRef]
- Liang, C.-D.; Ge, M.-F.; Liu, Z.-W.; Zhan, X.-S.; Park, J.H. Predefined-time stabilization of TS fuzzy systems: A novel integral sliding mode based approach. IEEE Trans. Fuzzy Syst. 2022, 30, 4423–4433. [Google Scholar] [CrossRef]
- Liang, C.-D.; Ge, M.-F.; Liu, Z.-W.; Ling, G.; Zhao, X.-W. A novel sliding surface design for predefined-time stabilization of Euler–Lagrange systems. Nonlinear Dyn. 2021, 106, 445–458. [Google Scholar] [CrossRef]
- Meng, X.; Gao, C.; Jiang, B.; Wu, Z. Finite-time Synchronization of Variable-order Fractional Uncertain Coupled Systems via Adaptive Sliding Mode Control. Int. J. Control Autom. Syst. 2022, 20, 1535–1543. [Google Scholar] [CrossRef]
- Aslmostafa, E.; Mirzaei, M.J.; Asadollahi, M.; Badamchizadeh, M.A. Synchronization problem for a class of multi-input multi-output systems with terminal sliding mode control based on finite-time disturbance observer: Application to chameleon chaotic system. Chaos Solitons Fractals 2021, 150, 111191. [Google Scholar] [CrossRef]
- Mobayen, S.; Tchier, F. Nonsingular fast terminal sliding-mode stabilizer for a class of uncertain nonlinear systems based on disturbance observer. Sci. Iranica. Trans. D Comput. Sci. Eng. Electr. 2017, 24, 1410–1418. [Google Scholar] [CrossRef]
- Roy, P.; Roy, B.K. Sliding mode control versus fractional-order sliding mode control: Applied to a magnetic levitation system. J. Control Autom. Electr. Syst. 2020, 31, 597–606. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X. Fractional order fixed-time nonsingular terminal sliding mode synchronization and control of fractional order chaotic systems. Nonlinear Dyn. 2017, 89, 2065–2083. [Google Scholar] [CrossRef]
- Tian, Y.; Cai, Y.; Deng, Y. A fast nonsingular terminal sliding mode control method for nonlinear systems with fixed-time stability guarantees. IEEE Access 2020, 8, 60444–60454. [Google Scholar] [CrossRef]
- Xie, S.; Chen, Q.; He, X. Predefined-time approximation-free attitude constraint control of rigid spacecraft. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Pan, Y.; Ji, W.; Liang, H. Adaptive Predefined-time Control for Lü Chaotic Systems via Backstepping Approach. IEEE Trans. Circuits Syst. Express Briefs 2022, 69, 5064–5068. [Google Scholar] [CrossRef]
- Mazhar, N.; Malik, F.M.; Raza, A.; Khan, R. Predefined-time control of nonlinear systems: A sigmoid function based sliding manifold design approach. Alex. Eng. J. 2022, 61, 6831–6841. [Google Scholar] [CrossRef]
- Abdel Hameed, M.; Hassaballah, M.; Hosney, M.E.; Alqahtani, A. An AI-Enabled Internet of Things Based Autism Care System for Improving Cognitive Ability of Children with Autism Spectrum Disorders. Comput. Intell. Neurosci. 2022, 2022, 2247675. [Google Scholar] [CrossRef]
- Xiong, X.; Pal, A.K.; Liu, Z.; Kamal, S.; Huang, R.; Lou, Y. Discrete-time adaptive super-twisting observer with predefined arbitrary convergence time. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 2057–2061. [Google Scholar] [CrossRef]
- Gómez-Gutiérrez, D. On the design of nonautonomous fixed-time controllers with a predefined upper bound of the settling time. Int. J. Robust Nonlinear Control 2020, 30, 3871–3885. [Google Scholar] [CrossRef]
- Pal, A.K.; Kamal, S.; Nagar, S.K.; Bandyopadhyay, B.; Fridman, L. Design of controllers with arbitrary convergence time. Automatica 2020, 112, 108710. [Google Scholar] [CrossRef]
- Sánchez-Torres, J.D.; Gómez-Gutiérrez, D.; López, E.; Loukianov, A.G. A class of predefined-time stable dynamical systems. IMA J. Math. Control Inf. 2018, 35, i1–i29. [Google Scholar] [CrossRef]
- Sánchez-Torres, J.D.; Muñoz-Vázquez, A.J.; Defoort, M.; Jiménez-Rodríguez, E.; Loukianov, A.G. A class of predefined-time controllers for uncertain second-order systems. Eur. J. Control 2020, 53, 52–58. [Google Scholar] [CrossRef]
- Moulay, E.; Léchappé, V.; Bernuau, E.; Defoort, M.; Plestan, F. Fixed-time sliding mode control with mismatched disturbances. Automatica 2022, 136, 110009. [Google Scholar] [CrossRef]
- Nian, W.; Chen, H.; Ding, D. A New Non-Singular Terminal Sliding Mode Control and Its Application to Chaos Suppression in Interconnected Power System. Int. J. Adv. Netw. Monit. Control. 2018, 3, 5–12. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Cao, J.; Hu, X. Fixed-time containment control for nonlinear multi-agent systems with external disturbances. IEEE Trans. Circuits Syst. II: Express Briefs 2021, 69, 459–463. [Google Scholar] [CrossRef]
- Jiménez-Rodríguez, E.; Muñoz-Vázquez, A.J.; Sánchez-Torres, J.D.; Defoort, M.; Loukianov, A.G. A Lyapunov-like characterization of predefined-time stability. IEEE Trans. Autom. Control 2020, 65, 4922–4927. [Google Scholar] [CrossRef]
- Sánchez-Torres, J.D.; Defoort, M.; Muñoz-Vázquez, A.J. Predefined-time stabilisation of a class of nonholonomic systems. Int. J. Control 2020, 93, 2941–2948. [Google Scholar] [CrossRef]
- Liu, B.; Hou, M.; Wu, C.; Wang, W.; Wu, Z.; Huang, B. Predefined-time backstepping control for a nonlinear strict-feedback system. Int. J. Robust Nonlinear Control 2021, 31, 3354–3372. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Fernández-Anaya, G.; Sánchez-Torres, J.D.; Meléndez-Vázquez, F. Predefined-time control of distributed-order systems. Nonlinear Dyn. 2021, 103, 2689–2700. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Jie, W.; Yudong, Z.; Yulong, B.; Kim, H.H.; Lee, M.C. Trajectory tracking control using fractional-order terminal sliding mode control with sliding perturbation observer for a 7-DOF robot manipulator. IEEE/ASME Trans. Mechatron. 2020, 25, 1886–1893. [Google Scholar] [CrossRef]
- Cruz-Ortiz, D.; Chairez, I.; Poznyak, A. Non-singular terminal sliding-mode control for a manipulator robot using a barrier Lyapunov function. ISA Trans. 2022, 121, 268–283. [Google Scholar] [CrossRef]
- Sun, G.; Wu, L.; Kuang, Z.; Ma, Z.; Liu, J. Practical tracking control of linear motor via fractional-order sliding mode. Automatica 2018, 94, 221–235. [Google Scholar] [CrossRef]
- Sun, G.; Ma, Z.; Yu, J. Discrete-time fractional order terminal sliding mode tracking control for linear motor. IEEE Trans. Ind. Electron. 2017, 65, 3386–3394. [Google Scholar] [CrossRef]
- Yang, C.; Che, Z.; Zhou, L. Composite feedforward compensation for force ripple in permanent magnet linear synchronous motors. J. Shanghai Jiaotong Univ. 2019, 24, 782–788. [Google Scholar] [CrossRef]
- Liu, W.; Chen, S.; Huang, H. Adaptive nonsingular fast terminal sliding mode control for permanent magnet synchronous motor based on disturbance observer. IEEE Access 2019, 7, 153791–153798. [Google Scholar] [CrossRef]
- Shengquan, L.; Juan, L.; Yongwei, T.; Yanqiu, S.; Wei, C. Model-based model predictive control for a direct-driven permanent magnet synchronous generator with internal and external disturbances. Trans. Inst. Meas. Control 2020, 42, 586–597. [Google Scholar] [CrossRef]
- Ting, C.S.; Chang, Y.N.; Shi, B.W.; Lieu, J.F. Adaptive backstepping control for permanent magnet linear synchronous motor servo drive. IET Electr. Power Appl. 2015, 9, 265–279. [Google Scholar] [CrossRef]
- Hui, Y.; Chi, R.; Huang, B.; Hou, Z. Extended state observer-based data-driven iterative learning control for permanent magnet linear motor with initial shifts and disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1881–1891. [Google Scholar] [CrossRef]
- Zhu, J.; Pan, Y.; Huang, T.; Luan, C.; Li, K. Research on Controlled Characteristic of the Novel Electromagnetic Recuperator. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; 2019; pp. 1980–1984. [Google Scholar]
- Zhao, Y.; Li, Y.; Lu, Q. An Accurate No-Load Analytical Model of Flat Linear Permanent Magnet Synchronous Machine Accounting for End Effects. IEEE Trans. Magn. 2022, 59, 8100111. [Google Scholar] [CrossRef]
- Du, H.; Chen, X.; Wen, G.; Yu, X.; Lü, J. Discrete-time fast terminal sliding mode control for permanent magnet linear motor. IEEE Trans. Ind. Electron. 2018, 65, 9916–9927. [Google Scholar] [CrossRef]
- Fu, D.; Zhao, X.; Zhu, J. A novel robust super-twisting nonsingular terminal sliding mode controller for permanent magnet linear synchronous motors. IEEE Trans. Power Electron. 2021, 37, 2936–2945. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, J.; Zheng, Z. Robust Speed Tracking Control of Permanent Magnet Synchronous Linear Motor Based on a Discrete-Time Sliding Mode Load Thrust Observer. IEEE Trans. Ind. Appl. 2022, 58, 4758–4767. [Google Scholar] [CrossRef]
- Li, J.; Du, H.; Cheng, Y.; Wen, G.; Chen, X.; Jiang, C. Position tracking control for permanent magnet linear motor via fast nonsingular terminal sliding mode control. Nonlinear Dyn. 2019, 97, 2595–2605. [Google Scholar] [CrossRef]
- Gao, W.; Chen, X.; Du, H.; Bai, S. Position tracking control for permanent magnet linear motor via continuous-time fast terminal sliding mode control. J. Control. Sci. Eng. 2018, 2018, 3813624. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Cao, Z.; Zheng, J.; Yu, M.; Yazdani, A.; Shahnia, F. Fast nonsingular terminal sliding mode control for permanent-magnet linear motor via ELM. Neural Comput. Appl. 2020, 32, 14447–14457. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).