A Direct Position Determination Method under Unknown Multi-Perturbation with Moving Distributed Arrays

Abstract

Distributed array manifold perturbation, which includes synchronization errors, amplitude-phase errors, and path attenuation, has seriously degraded the accuracy of existing direct position determination (DPD) methods. In this paper, a DPD method under unknown multi-perturbation with moving distributed coprime arrays is advocated for. Firstly, by means of array position interchange, the integrated signals received from distributed arrays can be fused, which contributes to multi-position fusion. Subsequently, by resorting to the orthogonality between the noise subspace and steering vector received via distributed arrays, a quadratic optimization problem is constructed. Finally, we realize multi-parameter decoupling and achieve localization regardless of unknown perturbations. The superiority of the advocated method is substantiated from simulation examples.

1. Introduction

Passive localization, whose main purpose is to determine source locations [1,2], is a Gordian technique in array signal processing, and is notably applied in communication, radars, seismic exploration, and other fields [3,4]. From the perspective of the procedures needed to implement localization, passive localization can be divided into two-step and one-step methods [5,6]. Traditionally, the two-step method first estimates the intermediate parameters of the acquired target data, such as the time difference of arrival (TDOA), the angle of arrival (AOA), the time of arrival (TOA), and the frequency difference of arrival (FDOA), after which it calculates positions by substituting them into the localization model [7,8,9]. Compared with conventional two-step methods, the one-step method realizes direct localization from signals to radiation sources, which is generally called direct position determination (DPD).

The original DPD algorithm, first proposed by Weiss, is a fixed multi-station algorithm [10]. In this algorithm, discrete Fourier transform (DFT) is applied to obtain the frequency domain data, after which a maximum likelihood (ML) estimation is used for data modeling in order to achieve direct localization. Amar and Sidi apply the DPD algorithm into a moving multi-station, from which a moving multi-station DPD algorithm based on Doppler is proposed [11,12]. A subspace data fusion DPD (SDF-DPD) method based on single-station motion is presented by M. Oispuu et al. The basic principle is using a moving array to receive signals at different locations, and that a fuse receives signals from multiple arrays to construct the loss function, such that the spatial position estimation of radiation sources can be obtained by a grid search [13]. DPD fuses target information into an array flow pattern, in which the pilot process can be omitted to improve the positioning accuracy.

In practical engineering, ubiquitous interference factors, such as mutual coupling, synchronization errors, amplitude-phase errors, and attenuation factors, inevitably perturb distributed array flow patterns, which degrade the estimation accuracy of the algorithms mentioned above [14,15,16]. Sparse arrays can significantly reduce the influence of mutual coupling through larger array spacing, but only increasing array spacing cannot avoid the influence of amplitude-phase errors, synchronization errors, and other factors. Therefore, array errors have become important thresholds for location techniques, from the stage of theoretical research to engineering applications. Active calibration is a feasible approach to alleviate the deficiency, which is executed by auxiliary sources with known locations [17]. Nevertheless, once the bias of auxiliary sources appears the estimation accuracy will be greatly reduced, such that it is tough to meet actual needs. Self-calibration, which depends on iteration operations to correct errors [18,19], is another calibration method. Specifically, the self-calibration method requires initial errors and tiny array disturbances. The instrumental sensor method (ISM), or so-called auxiliary element method, is introduced in [20]; it demands auxiliary elements more than the number of emitters. In [21], we propose a joint amplitude-phase error calibration and DPD method that relies on single-array movement to construct overall cost function and quadratic optimization, realizing the decoupling of amplitude-phase errors and positions. Nonetheless, synchronization errors and attenuation coefficients are not considered in these methods.

In this letter, a DPD algorithm with multi-perturbation that leverages the idea of array interchange is presented. The main contributions are as follows: (1) We take multiple errors into consideration, including synchronization errors, amplitude-phase errors, and path attenuation. Based on array position interchange, data information, including angle and transmission delay, is fused by different array permutations, from which we can separate interference terms and parameters to be estimated. (2) Without iteration, auxiliary sources, or auxiliary sensors, the proposed method can achieve multi-parameter decoupling and accurate localization under unknown stray errors. (3) Numerical simulations substantiate the viability of the proposed algorithm in the aspect of localization accuracy compared with existing methods.

The structure of this paper is as follows: we first generalize the research background and significance; secondly, we introduce the data model and theoretical basis; a DPD method under unknown multi-perturbation with distributed arrays is then proposed, and simulation results are shown to verify the feasibility of the proposal; and, finally, we provide a summary of our whole work.

2. Problem Formulation

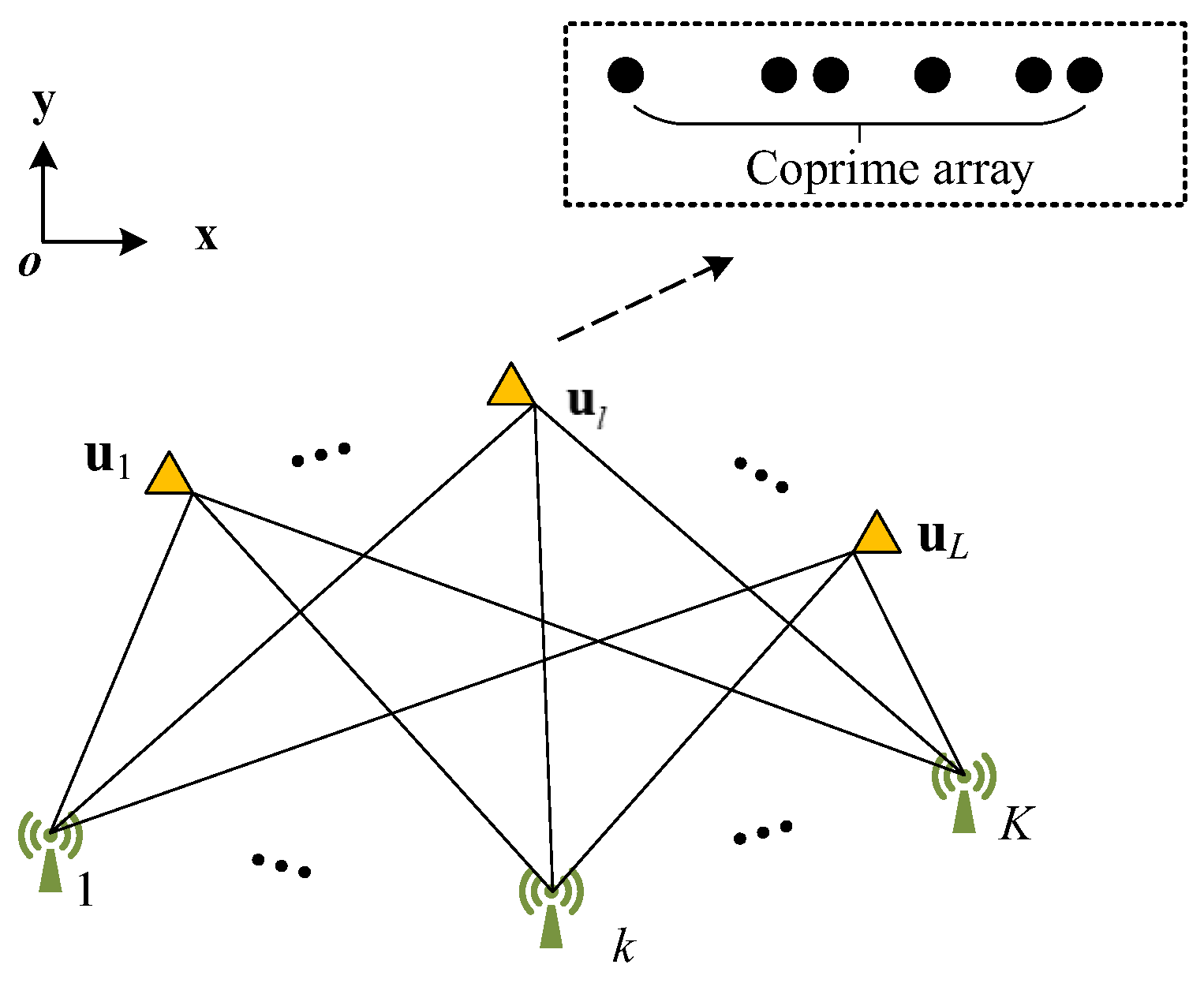
Assume that there are L arrays; the l^th array is a coprime array composed of M elements, $l\in [1,L]$. K unknown sources are placed in $p_k = {[p_{xk},p_{yk},p_{zk}]}^{\mathrm{T}},k\in [1,K]$, transmitting far-field narrowband signals continuously. Figure 1 depicts a localization scenario of multiple arrays. The l^th observation array, whose location is precisely known and denoted as $u_l = {[u_{xl},u_{yl},u_{zl}]}^{\mathrm{T}}$, intercepts the impinging signals.

The output of the l^th observation array in moment t can be represented as follows:

$$x_l(t) = {\displaystyle \sum _{k = 1}^K{\alpha }_{l,k}{G}_l{a}_l(p_k)s_{l,k}(t - {\beta }_l - {\tau }_l(p_k)) + n_l(t)}$$

(1)

where ${\alpha }_{l,k}$ denotes the attenuation coefficient; $n_l(t)$ denotes the Gaussian noise vector; $G_l = diag(g_l)$; $g_l = {\left[g_{l1},\dots ,g_{lM}\right]}^{\mathrm{T}}$; $g_{lm} = {\omega }_m\exp (j{\nu }_m)$; and ${\omega }_m$ and ${\nu }_m$ severally denote the amplitude error and phase error of the m^th element, in which $1\le m\le M$. ${\beta }_l$ represents the synchronization error of the l^th array relative to the first one, and is a complex scalar; $s_{l,k}(t)$ is the k^th radiation source signal incident to the l^th array; ${\tau }_l(p_k)$ represents the transmission delay from the k^th emitter to the l^th array. $a_l(p_k) = {[e^{j{k}_l^{\mathrm{T}}(p_k)d_1},\dots ,e^{j{k}_l^{\mathrm{T}}(p_k)d_M}]}^{\mathrm{T}}$ is the steering vector of the l^th observation array; $k_l(p_k)$ denotes the wavenumber vector at the observation position, $u_l$, which is expressed as follows:

$$k_l(p_k) = \frac{2\pi }{\lambda }\frac{p_k - u_l}{‖p_k - u_l‖}$$

(2)

in which $\lambda$ is the wavelength and $‖·‖$ denotes the Frobenius norm. $d_m$ is the position vector of the m^th sensor in respect of the reference one.

Since it is a narrowband signal assumption [19], the output of the l^th array can be obtained by rearranging Equation (1) as follows:

$$x_l(t) = G_l{A}_l(p){\Phi }_l{s}_l(t) + n_l(t)$$

(3)

where $A_l(p) = [a_l(p_1),\dots ,a_l(p_K)]$ denotes the array flow pattern matrix and $p = [p_1^{\mathrm{T}},\dots ,p_K^{\mathrm{T}}]$ represents the position vector composed of K sources’ position coordinates, $s_l(t) = {[s_{l,1}(t),\dots ,s_{l,K}(t)]}^{\mathrm{T}}$. ${\Phi }_l$ is a diagonal matrix consisting of an attenuation coefficient and transmission delay, which can be expressed as follows:

$${\Phi }_l = {\Lambda }_l{\mathrm{\Theta }}_l(p)$$

(4)

where ${\Lambda }_l = diag(e^{-jw{\beta }_l}{\alpha }_{l,1},e^{-jw{\beta }_l}{\alpha }_{l,2},\dots ,e^{-jw{\beta }_l}{\alpha }_{l,K})$ and ${\mathrm{\Theta }}_l(p) = diag(e^{-jw{\tau }_l(p_1)},e^{-jw{\tau }_l(p_2)},\dots ,e^{-jw{\tau }_l(p_K)})$.

The output data batch after collecting J snapshots can be expressed as follows:

$$X_l = [x_l(1),x_l(2),\dots ,x_l(J)] = G_l{A}_l(p){\Phi }_l{S}_l + N_l$$

(5)

where $S_l = {[s_{l,1},\dots ,s_{l,K}]}^{\mathrm{T}}$, $s_{l,k} = [s_{l,k}(1),\dots ,s_{l,k}(J)]$, $N_l = [n_l(1),n_l(2)\dots ,n_l(J)]$.

Integrating the received signals of all L observation arrays, the total output can be written as follows:

$$X = \tilde{B}(p,\alpha )S + N$$

(6)

where $\tilde{B}(p) = {[{\Phi }_1{A}_1^{\mathrm{T}}(p)G_1,\dots ,{\Phi }_L{A}_L^{\mathrm{T}}(p)G_L]}^{\mathrm{T}}$, $N = [N_1;\dots ;N_L]$.

3. The Proposed Algorithm

The approach advocated for in this paper is inspired by our previous work [22], in which multi-position fusion is considered to construct the overall cost function to achieve the separation of amplitude-phase errors and positions. To begin with, the covariance matrix of the measurements in Equation (6) is approximated via the following:

$$\widehat{R} = \frac{1}{J}{\displaystyle \sum _{j = 1}^{J}X\left(t_j\right)X^{\mathrm{H}}\left(t_j\right)}$$

(7)

By conducting eigenvalue decomposition on $\widehat{R}$, we can obtain the following:

$$\begin{array}{l}\widehat{R} = U\Sigma U = {\displaystyle \sum _{i = 1}^{ML}{\lambda }_i{e}_i{e}_i^{\mathrm{H}}}\\ U = [e_1,\dots ,e_{ML}]\\ \Sigma = diag\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{ML}\}\end{array}$$

(8)

where $U$ is a matrix composed of eigenvectors; $\Sigma$ is a diagonal matrix composed of eigenvalue ${\lambda }_i$; ${\lambda }_1 \ge {\lambda }_2 \ge \dots \ge {\lambda }_K \ge {\lambda }_{K + 1} = {\lambda }_{K + 2} = \dots = {\lambda }_{ML} = {\sigma }^2$; and $e_i$ is the eigenvector corresponding to ${\lambda }_i$. The noise subspace is as follows:

$$U_n = [e_{K + 1},\dots ,e_{ML}]$$

(9)

Take advantage of the orthogonal relation between $U_n$ and $\tilde{B}(p)$:

$$U_n^{\mathrm{H}}\tilde{b}(p_k) = 0, k = 1,2,\dots ,K$$

(10)

where $\tilde{b}(p_k)$ is the k^th row of the matrix $\tilde{B}(p)$. We can establish the cost function as follows:

$$\underset{p}{\min }{\tilde{b}}^H\left(p\right)U_n{U}_n^{\mathrm{H}}\tilde{b}\left(p\right)$$

(11)

It should be noted that, in the cost function of the above objectives, there are also multiple interference items, including synchronization errors, amplitude-phase errors, and attenuation coefficients, in which cases exact results cannot be obtained just by searching. Accordingly, we need to separate interference terms and position parameters. Expand $\tilde{b}(p)$ to obtain the following:

$$\begin{array}{l}\tilde{b}(p) = \left[\begin{array}{c}{G}_1{a}_1(p)e^{-jw{\tau }_1(p)}{\alpha }_1\\ ⋮\\ G_L{a}_L(p)e^{-jw{\tau }_L(p)}{\alpha }_L\end{array}\right] = \left[\begin{array}{c}diag(a_1(p)e^{-jw{\tau }_1(p)})g_1{e}^{-jw{\beta }_1}{\alpha }_1\\ ⋮\\ diag(a_L(p)e^{-jw{\tau }_L(p)})g_L{e}^{-jw{\beta }_L}{\alpha }_L\end{array}\right]\\ = diag\left(\left[\begin{array}{c}diag(a_1(p)e^{-jw{\tau }_1(p)})\\ ⋮\\ diag(a_L(p)e^{-jw{\tau }_L(p)})\end{array}\right]\right)\left[\begin{array}{c}{\alpha }_1{e}^{-jw{\beta }_1}{g}_1\\ ⋮\\ {\alpha }_L{e}^{-jw{\beta }_L}{g}_L\end{array}\right] = H_1(p)\gamma \end{array}$$

(12)

Consider eliminating trivial solutions with the constraint of $e_1^{\mathrm{H}}\gamma = 1$, in which $e_1 = {[1,0,\dots ,0]}^{\mathrm{T}}\in {ℝ}^{ML \times 1}$. Establish the quadratic optimization problem as follows:

$$\underset{p}{\min }{\gamma }^{\mathrm{H}}Q(p)\gamma ,s.t.e_1^{\mathrm{H}}\gamma = 1$$

(13)

where $Q(p) = H_1^{\mathrm{H}}(p)U_n{U}_n^{\mathrm{H}}{H}_1(p)$.

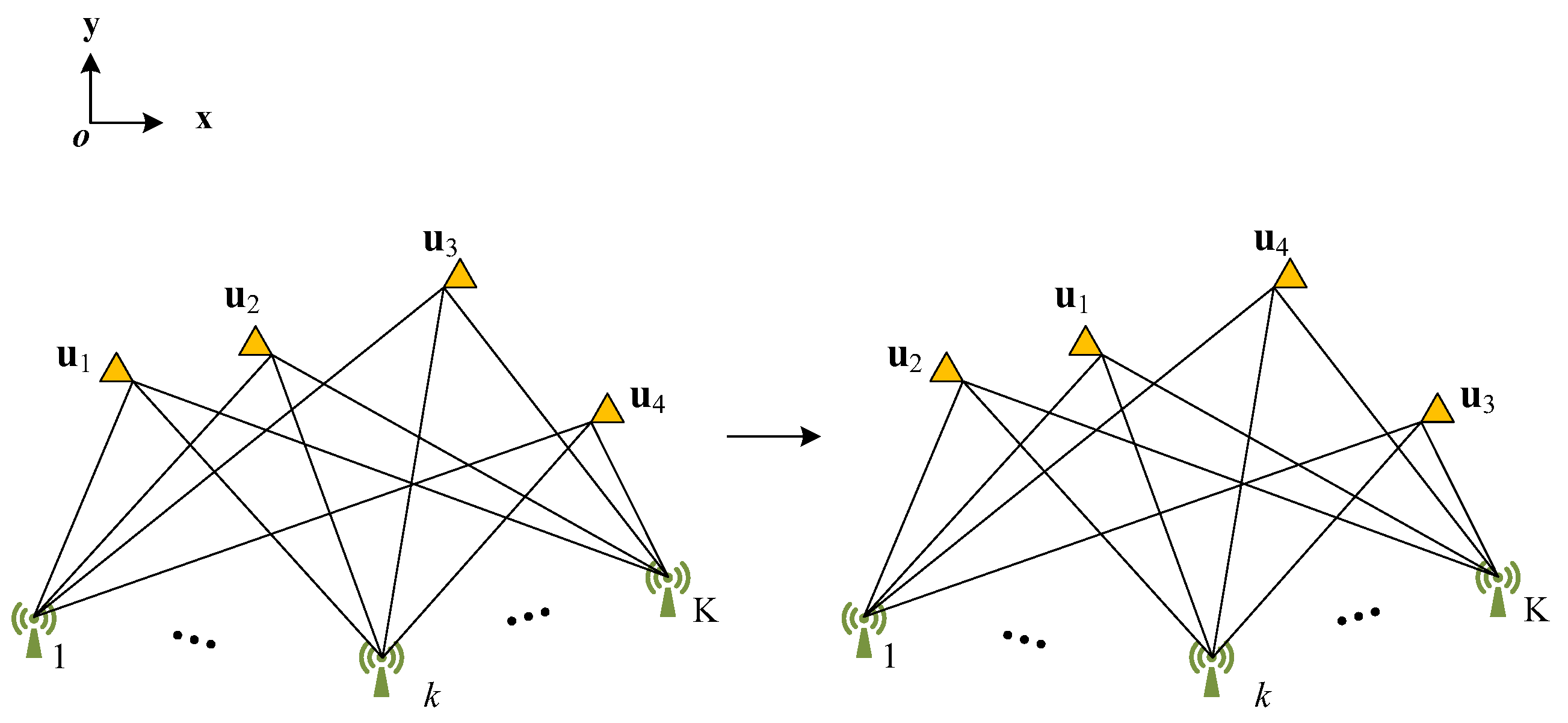
In this case, however, there is a problem of rank-defect. To accommodate this, we transform array positions to realize data fusion, as shown in Figure 2, in which interchanging positions between arrays does not change the attenuation coefficients.

Under the circumstance, $H_1(p)$ after interchange is expressed as follows:

$$H_2(p) = diag\left(\left[\begin{array}{c}diag(a_2(p)e^{-jw{\tau }_2(p)})\\ diag(a_1(p)e^{-jw{\tau }_1(p)})\\ diag(a_4(p)e^{-jw{\tau }_4(p)})\\ diag(a_3(p)e^{-jw{\tau }_3(p)})\end{array}\right]\right)$$

(14)

In general, the following equivalence relation exists between $H_1(p)$ and $H_2(p)$:

$$H_2(p) = W{H}_1(p)$$

(15)

where $W$ represents the interchange matrix, whose element distribution corresponds to the interchange of arrays. This being the case, Equation (12) can be rewritten as follows:

$$\underset{p}{\min }{\gamma }^{\mathrm{H}}{Q}_z(p)\gamma ,s.t.e_1^{\mathrm{H}}\gamma = 1$$

(16)

Notice that $Q_z(p)$ can be expressed as the sum of these two terms as $Q_z(p) = Q_1(p) + Q_2(p)$, where $Q_1(p)$ and $Q_2(p)$ respectively denote matrix $Q(p)$ before and after the array position transformation. Thus, the problem of rank-defect is solved.

For problems like this where we need to find an extreme value under a constraint, we can do so by using the Lagrange multiplier method. Construct the cost function as follows:

$$L\left(p,\gamma \right) = {\gamma }^H{Q}_z\left(p\right)\gamma - \lambda \left(e_1^H\gamma - 1\right)$$

(17)

in which $\lambda$ is a Lagrange multiplier. Taking the partial derivative of $L\left(p,\gamma \right)$, we obtain $\frac{\partial L\left(p,\gamma \right)}{\partial \left(\gamma \right)} = 2Q_z\left(p\right)\gamma + \lambda e_1 = 0$; combining this with $e_1^{\mathrm{H}}\gamma = 1$, we obtain parameter $\gamma$ with multiple errors, as follows:

$$\widehat{\gamma } = \frac{Q_z^{-1}\left(p\right)e_1}{e_1^{\mathrm{H}}{Q}_z^{-1}\left(p\right)e_1}$$

(18)

By substituting the expression of $\widehat{\gamma }$ into $\underset{p}{\min }{\gamma }^{\mathrm{H}}{Q}_z(p)\gamma$, the estimates of source position can be represented as follows:

$${\widehat{p}}_k = \arg \underset{p}{\min }\frac{1}{e_1^{\mathrm{H}}{Q}_z^{-1}\left(p\right)e_1} = \arg \underset{p}{\max }{e}_1^{\mathrm{H}}{Q}_z^{-1}\left(p\right)e_1$$

(19)

Although there are numerous stray parameters, including synchronization errors, amplitude-phase errors, and attenuation coefficients, the proposed approach, based on a dimension reduction process, requires only two-dimensional searching; DPD can be realized by obtaining the maximum value of the (1,1) element of $Q_z^{-1}\left(p\right)$. Therefore, based on a dimension reduction process, we can separate stray parameters from real positions, and we do not need to estimate interference items.

4. Numerical Examples

In this part, simulation experiments are performed to corroborate the feasibility and advantages of the advocated method.

The parameter search space for DPD is ${\rm P} = \{[x,y]|0 \le x \le 1000,0 \le y \le 1000\}$, and the search grid is 1 m × 1 m. Figure 3a,b manifests the location spectral peak diagram and contour map in terms of SNR = 10 dB and $J = 500$. The emitters are located in $p_1 = {(100,500)}^{\mathrm{T}}$, $p_2 = {(400,800)}^{\mathrm{T}}$, and $p_3 = {(700,500)}^{\mathrm{T}}$. The observation arrays are arranged in $u_1 = {(-500,0)}^{\mathrm{T}}$, $u_2 = {(1000,0)}^{\mathrm{T}}$, $u_3 = {(0,300)}^{\mathrm{T}}$, and $u_4 = {(0,700)}^{\mathrm{T}}$.

Three obvious spectral peaks can be seen from the simulation results. From the contour map, it can be seen that the position of the spectral peak corresponds to the real position of the target to be estimated, which indicates that the proposed algorithm can achieve multi-source simultaneous localization and have good location performance free from unknown multi-perturbation.

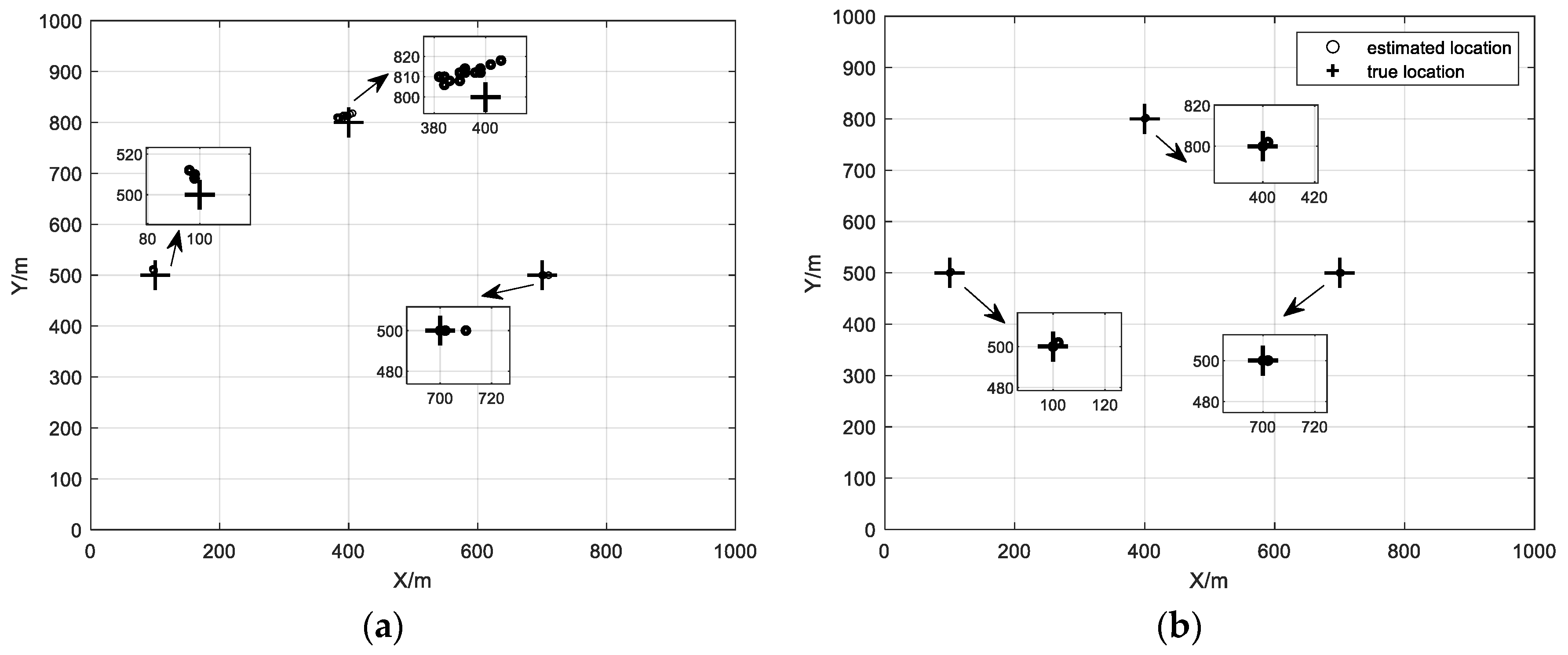
In this paper, the partial magnification of scatter plots shows a significant improvement in the proposed method. Figure 4a is the scatter diagram under multiple perturbations. It can be seen from Figure 4a that the estimated value differs somewhat from the true value. Figure 4b is the scatter diagram of DPD using the proposed method, which shows that the true value is in good agreement with the estimated value. Based on dimension reduction, the proposed algorithm realizes the separation of multiple parameters and source locations, achieving accurate localization without estimating attenuation coefficients, gain-phase errors, and synchronization errors.

Furthermore, root mean square error (RMSE), regarded as a benchmark, is used to assess the localization performance of different methods. The definition of RMSE is as follows:

$$RMS{E}_p = \sqrt{\frac{1}{NK}{{\displaystyle \sum _{n = 1}^N{\displaystyle \sum _{k = 1}^K‖p_k - {\widehat{p}}_{k,n}‖}}}^2}$$

(20)

where N denotes simulation times, whereas $p_k$ and ${\widehat{p}}_{k,n}$, respectively, denote true and theoretical values of the k^th source in the n^th simulation.

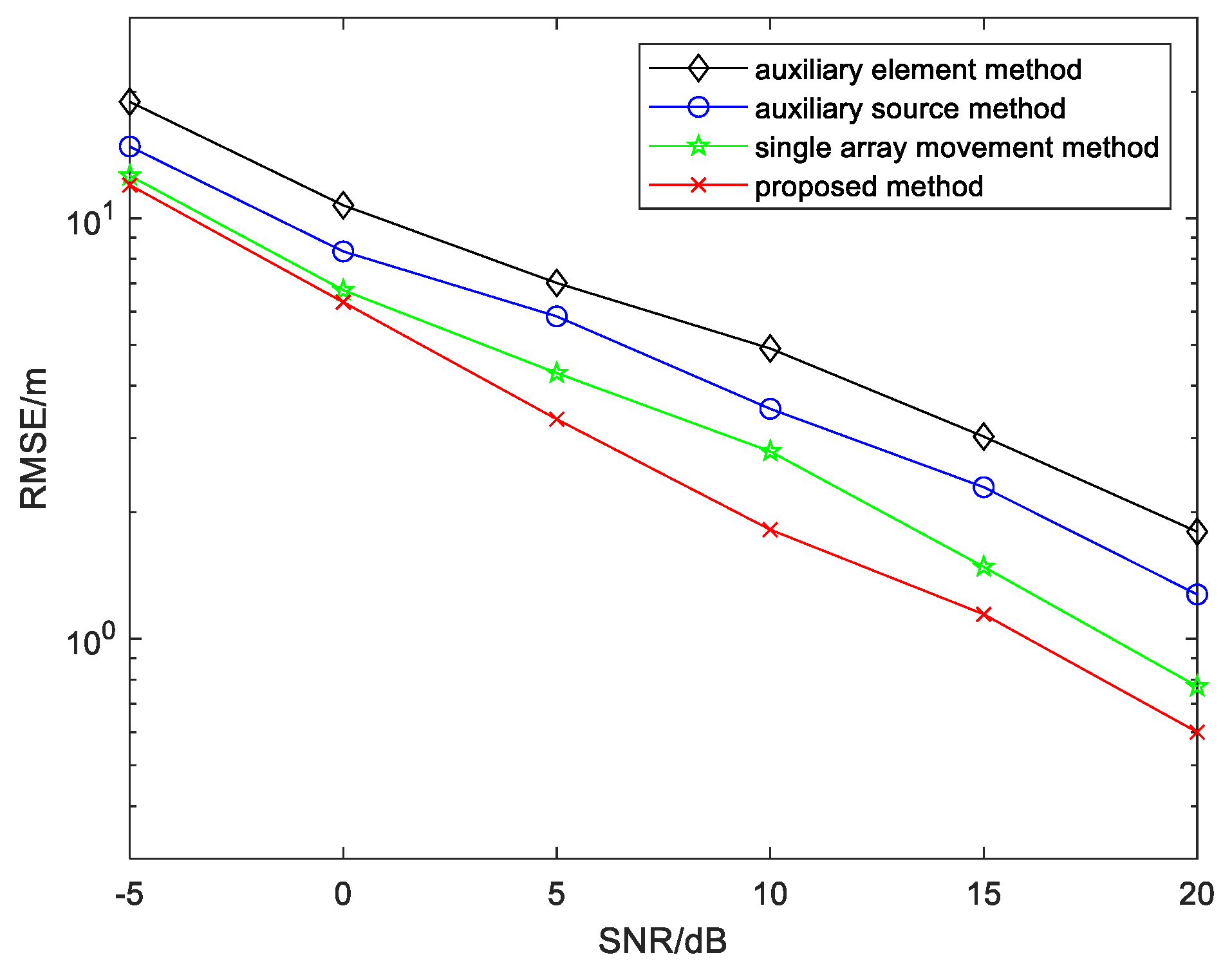
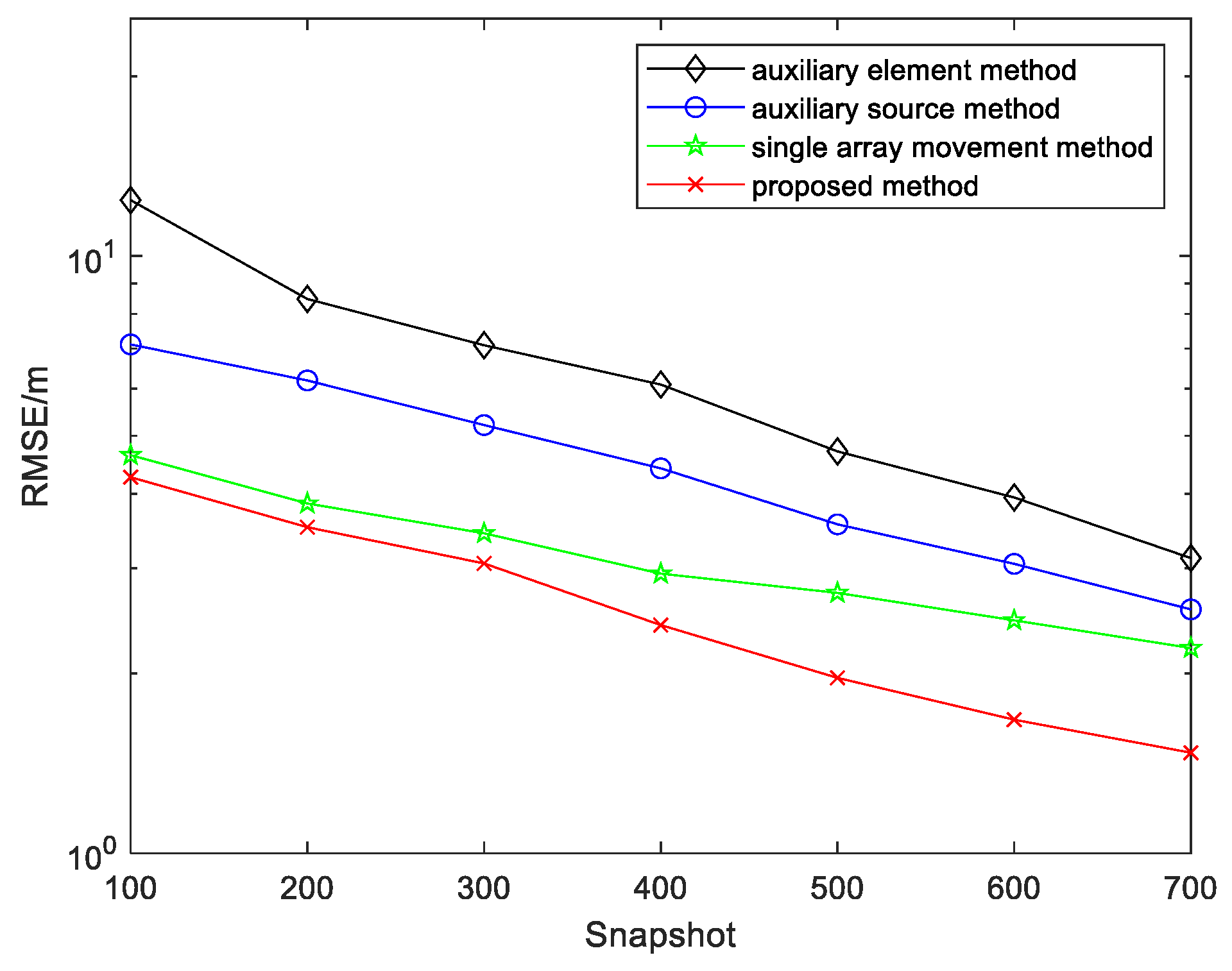
Figure 5 and Figure 6, respectively, exhibit the RMSE curves versus the SNR and snapshots, where M = 10, N = 100, K = 2, $p_1 = {(100,500)}^{\mathrm{T}}$, and $p_2 = {(700,400)}^{\mathrm{T}}$.

From the simulation results, it is vividly demonstrated that the positioning performance of these algorithms continues to improve with an increase in the SNR or snapshot. It can be concluded from Figure 5 that the performance of the proposed algorithm is superior to the auxiliary source approach [14], auxiliary element approach [15], and single-array movement approach [18]. Analogously, similar comparisons are carried out in Figure 6, the difference being that the SNR is fixed at 10 dB while snapshots change. As depicted in Figure 6, the proposed method has the best performance.

5. Discussion

The method advocated for in this paper takes the influence of attenuation coefficients, amplitude-phase errors, and synchronization errors into account in the objective function. Therefore, in a multi-source localization scenario, the location accuracy of the advocated approach precedes that of others. Because both existing methods and the proposed method require global search operations, the complexities are inevitably high; however, compared with the existing auxiliary source method and auxiliary element method, the proposed method needs no extra costs and is more feasible in reality. Meanwhile, the advocated method obtains superior positioning performance, which has been vividly shown in the scatter plots and RMSE comparison plots. The proposal can not only apply to finding a direction for wireless communication, but is also suitable for navigation and positioning, with strong practicability.

6. Conclusions

In this paper, the simultaneous localization of multiple sources in distributed arrays based on multi-error decoupling is discussed. It is considered that conventional DPD methods cannot meet the demand of high-precision estimation due to the influence of distributed array flow pattern disturbances, including attenuation coefficients, amplitude-phase errors, and synchronization errors. To accommodate this, we present a quadratic optimization problem to realize the separation of interference factors and position parameters, solving the problem of unsolvable equations caused by errors. The proposed algorithm makes use of distributed array interchange, which contributes to data fusion; thus, the position coordinates that are not affected by interference items can be obtained only through a spectral peak search. It is verified that high-precision position estimation can be obtained without auxiliary elements, auxiliary sources, or iterative calculations. Moreover, simulation results, including the performance comparison between the proposed algorithm and other algorithms, substantiate the superiority and effectiveness of the proposed algorithm in direct localization.