A Low-Loss Impedance Transformer-Less Fish-Tail-Shaped MS-to-WG Transition for K-/Ka-/Q-/U-Band Applications
Abstract
1. Introduction
2. Literature Survey
3. Materials and Methods
3.1. Transition Design Equations and Parameters
3.1.1. Microstrip Line Calculations
- w = width of the microstrip,
- h = height of the substrate
3.1.2. Rectangular Waveguide Calculations
- a = breadth (broadside) of the waveguide,
- b = width of the waveguide
3.1.3. Microstrip Patch Calculations
3.2. Field and Impedance Matching
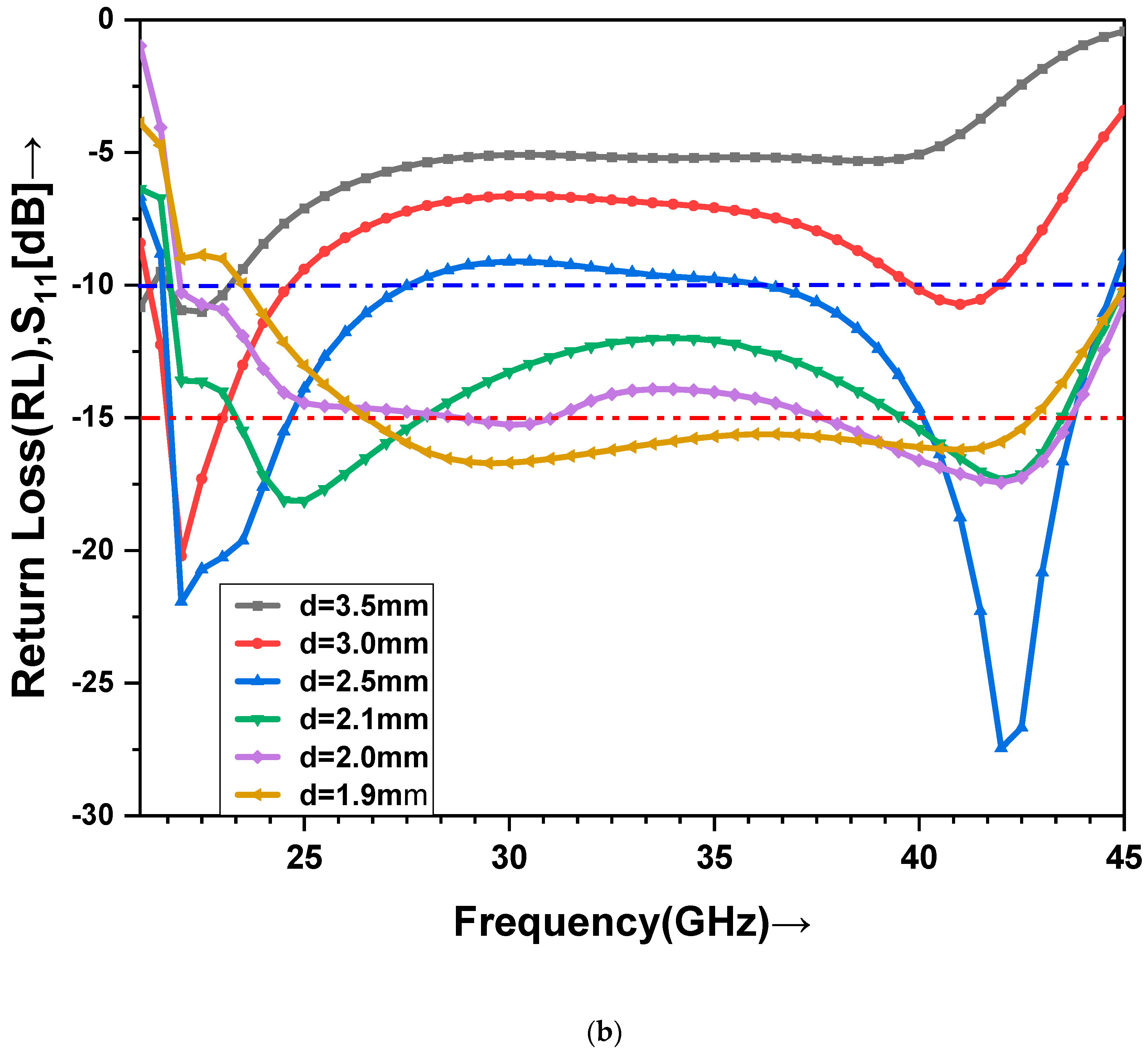
3.3. Optimization of the Back-Short Distance
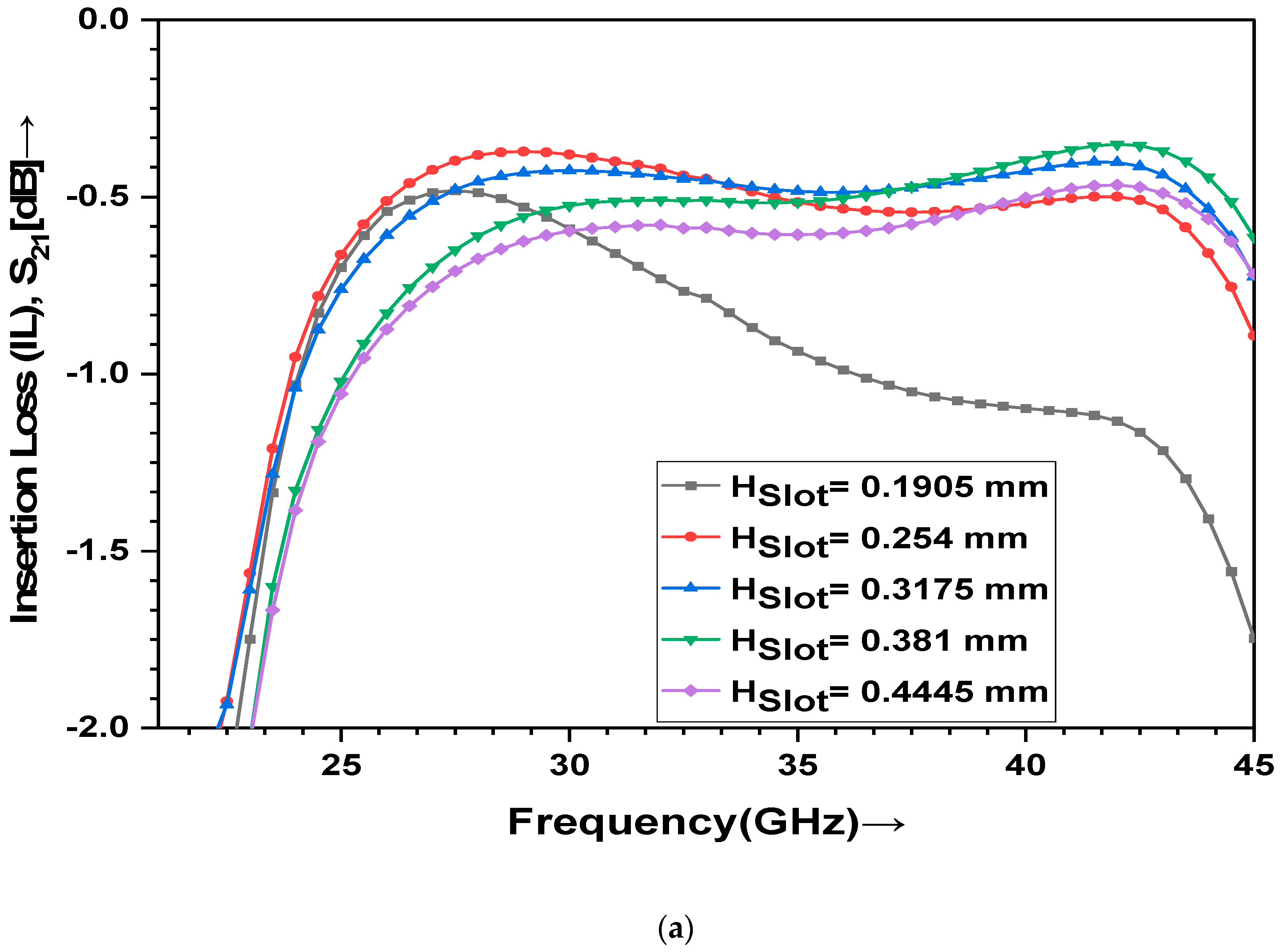
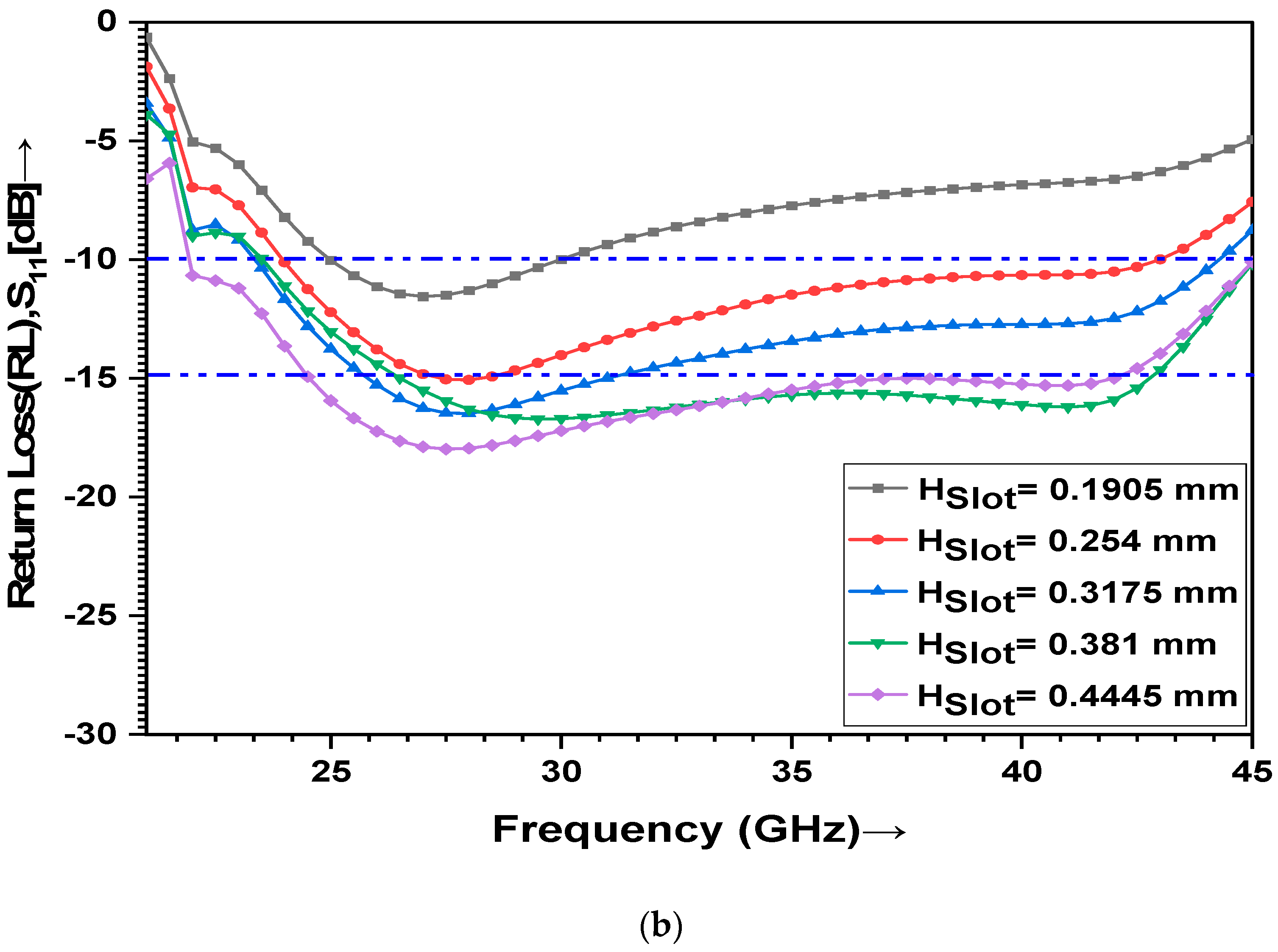
3.4. Optimization of Slot Height
3.5. Fishtail Probe Depth (LD) Optimization
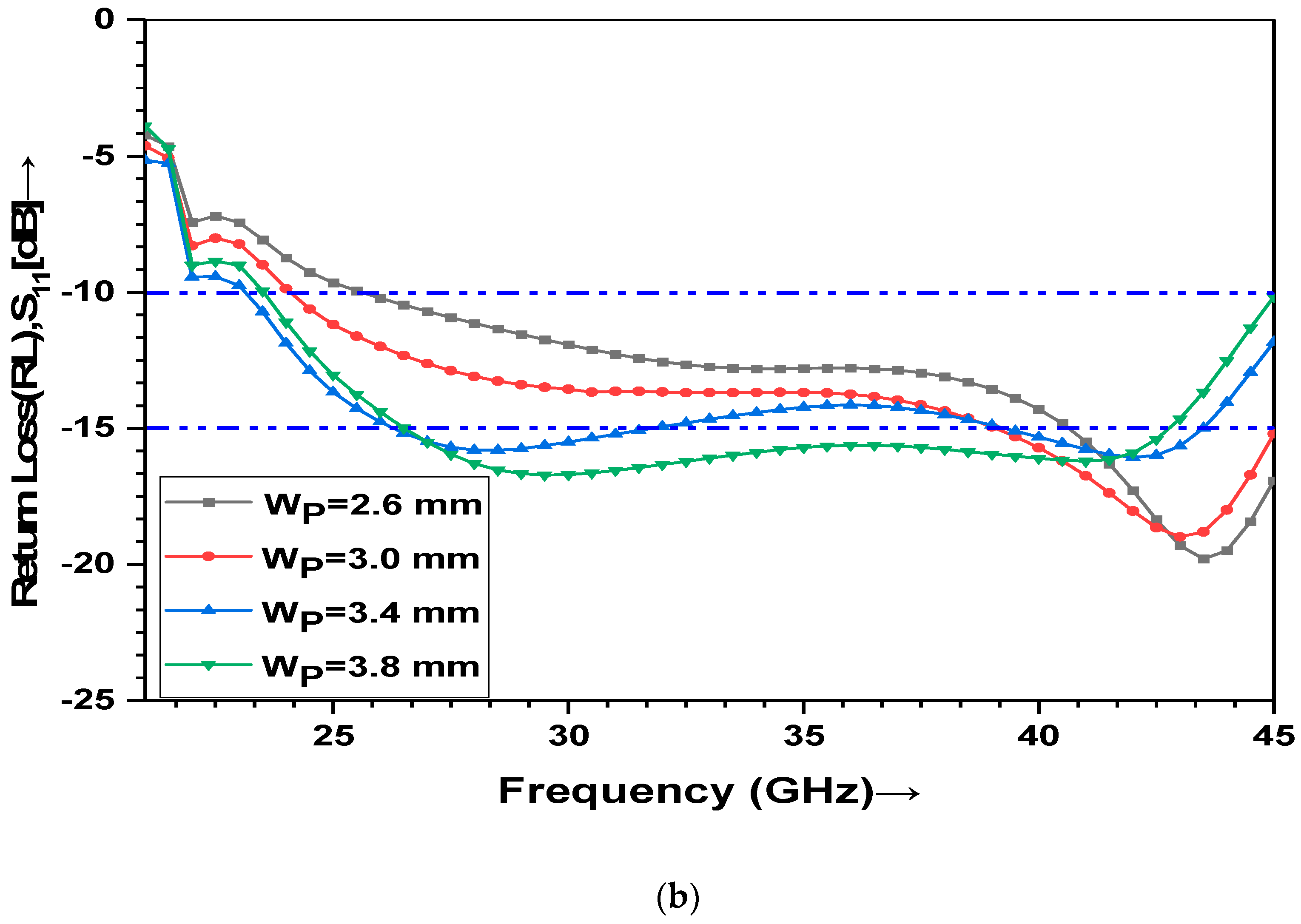
3.6. Fishtail Probe Width (WP) Optimization
4. Results and Discussion
4.1. Ka-Band RWG-to-Fish-Tail-Shaped MSL Design Model
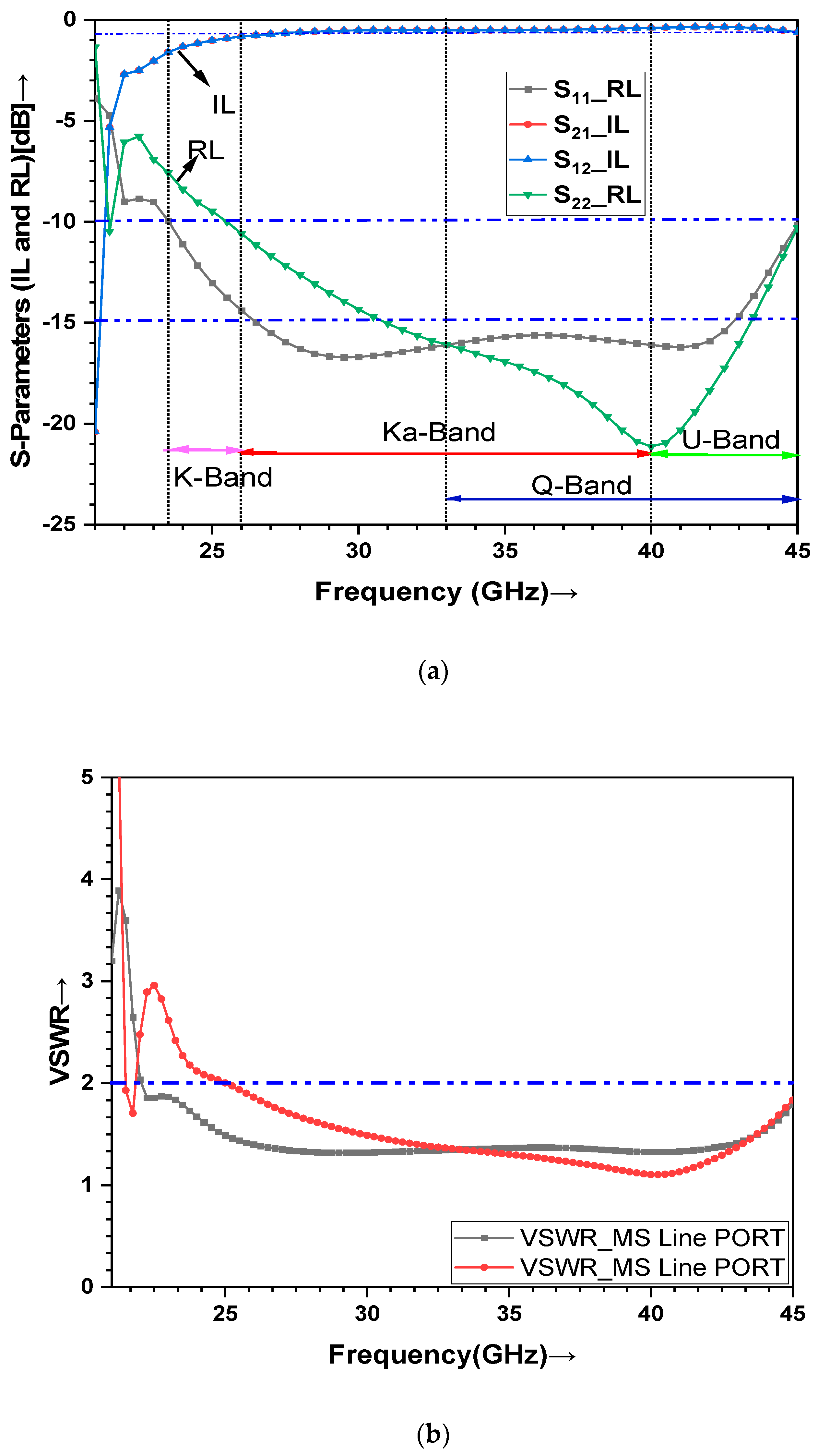
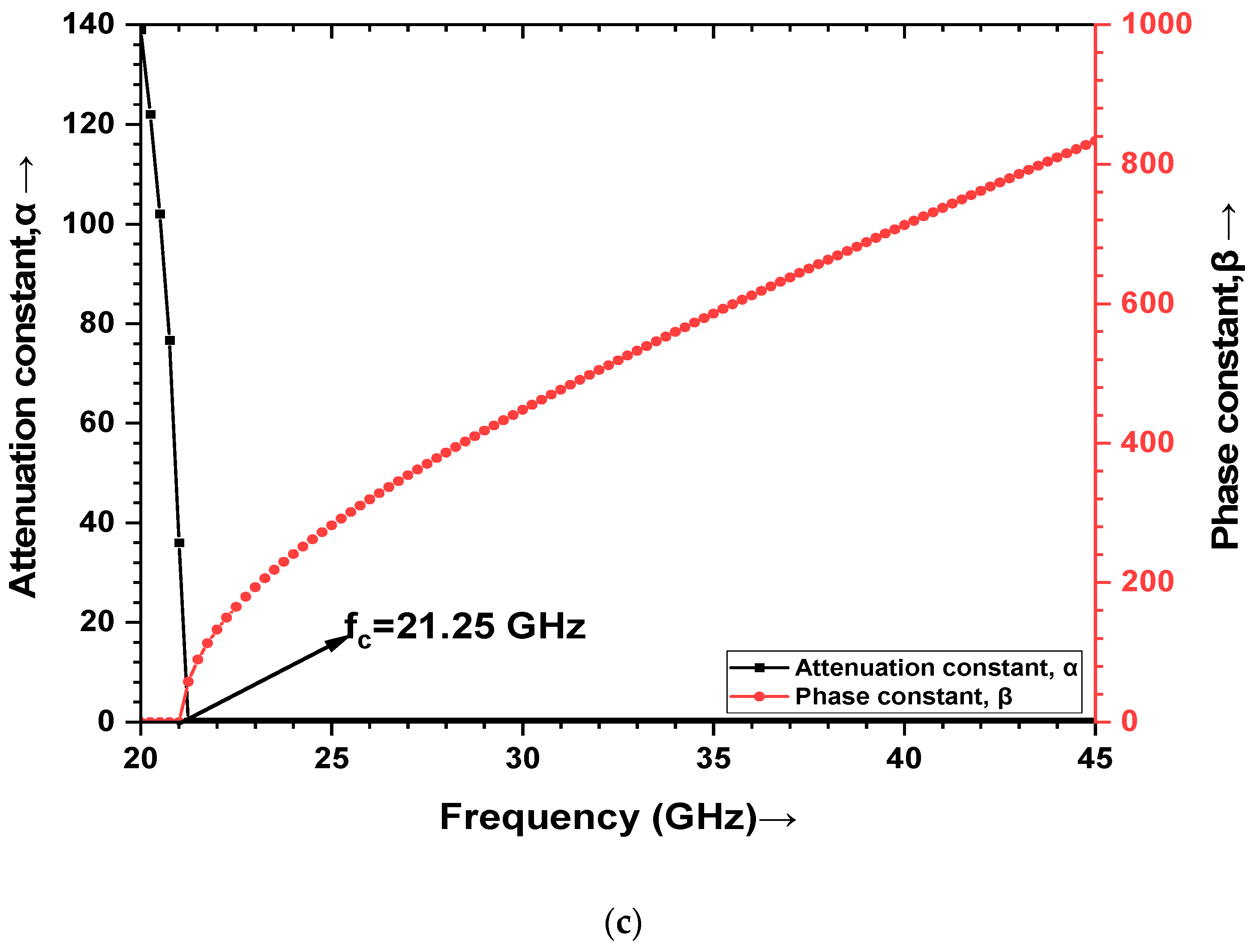
4.2. Optimized S-Parameters, VSWR, and Propagation Constant Plots of the Proposed Transition Model
4.3. Electric Field (E), Magnetic Field (H), and Surface Current Density (J) Distribution Inside the Designed Transition
4.4. RLC Electrical Equivalent Circuit of the Transition
4.5. Comparison of the Proposed Work with the Existing Ka-Band RWG-to-MSL Transitions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Varshney, A.; Sharma, V. A comparative study of microwave rectangular waveguide-to-microstrip line transition for millimeter wave, wireless communications, and radar applications. Microw. Rev. 2020, 26, 21–37. [Google Scholar]
- Iffat Naqvi, S.; Hussain, N.; Iqbal, A.; Rahman, M.; Forsat, M.; Mirjavadi, S.S.; Amin, Y. Integrated LTE and Millimeter-Wave 5G MIMO Antenna System for 4G/5G Wireless Terminals. Sensors 2020, 20, 3926. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Xu, J.; Fu, J.A. Full Ka-band microstrip to-waveguide transition using side-inserted magnetic coupling semicircular ring. In Proceedings of the Wamicon 2012 IEEE Wireless and Microwave Technology Conference, Cocoa Beach, FL, USA, 15–17 April 2012; pp. 1–6. [Google Scholar]
- Shih, Y.C.; Ton, T.N.; Bui, L.Q. Waveguide-to-microstrip transitions for mm-wave applications. IEEE MTT-S Int. Symp. Dig. 1988, 1, 473–475. [Google Scholar]
- Tomar, S.; Singh, S.K.; Suthar, L.; Singh, R.B.; Kumar, A. E-Plane waveguide to microstrip transition for wave applications. In Proceedings of the Conference ICMARS, Jodhpur, India, 14–17 December 2010; pp. 1–3. [Google Scholar]
- Varshney, A.K.; Rawat, G.S. A microwave rectangular waveguide-to-microstrip line transitions @ 30 GHz. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 563–568. [Google Scholar]
- Lou, Y.; Chan, C.H.; Xue, Q. An in-line waveguide-to-microstrip transition using a radial-shaped probe. IEEE Microw. Wirel. Compon. Lett. 2008, 18, 311–313. [Google Scholar] [CrossRef]
- Varshney, A.K.; Sharma, V. Using a reverse approach to obtain an efficient design for a wideband MS line-RWG hybrid transition. In Proceedings of the International Conference on Emerging Trends in Applied Sciences, Virtual, 28–29 October 2021. [Google Scholar]
- Tang, C.; Pan, X.; Cheng, F.; Lin, X.A. Broadband microstrip-to-waveguide end-wall probe transition and its application in Waveguide Termination. Prog. Electromag Res. Lett. 2020, 89, 99–104. [Google Scholar] [CrossRef]
- Li, C.L.; Jin, C.; Ma, H.Q.; Shi, X.W. An Inline Waveguide-to-Microstrip Transition for Wideband Millimeter-wave Applications. Microw. Opt. Technol. Lett. 2019, 62, 1516–1520. [Google Scholar] [CrossRef]
- Gupta, R.; Kumar, P.P. Improved Design of Ka-band Waveguide to Coaxial Right Angle Microwave Transition. In Proceedings of the URSI RCRS 2020, IIT (BHU), Varanasi, India, 12–14 February 2020. [Google Scholar]
- Simone, M.; Fanti, A.; Valente, G.; Montisci, G.; Ghiani, R.; Mazzarella, G. A Compact In-Line Waveguide-to-Microstrip Transition in the Q-Band for Radio Astronomy Applications. Electronics 2018, 7, 24. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Goh, Y.M.; Yoshida, M.; Bui, T.T.; Aoyagi, M.; Liu, C. 30-GHz High-Frequency Application of Screen Printed Interconnects on an Organic Substrate. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 1506–1515. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley Student Edition; John Wiley and Sons: Hoboken, NJ, USA, 2016; pp. 148–149. [Google Scholar]
- Liao, S.Y. Microwave Devices and Circuits, 3rd ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 2007; pp. 120–137. [Google Scholar]
- Chang, K. RF and Microwave Wireless Systems; John Wiley and Sons: Hoboken, NJ, USA, 2015; pp. 90–99. [Google Scholar]
- ESATCOM INC. WR-28 Waveguide Termination. 1995. Available online: https://esatcom.com/waveguideterminations/1360-WR-28-waveguidetermination.html (accessed on 26 May 2022).
- Varshney, A.; Cholake, N.; Sharma, V. Low-cost ELC UWB fan-shaped antenna using parasitic SRR triplet for ISM band and PCS applications. Int. J. Electron. Lett. 2021, 10, 391–402. [Google Scholar] [CrossRef]
- Varshney, A.; Sharma, V.; Arya, V. Tri-Blade Table Fan-Shaped Ultra-Wideband Microstrip Antenna Using Parasitic SRR Triplet. Australian Patent No. 2021101898, 19 May 2021. [Google Scholar]
- Choudhary, D.R. Networks and Systems, 12th ed.; New Age International Publishers: Delhi, India, 1999; pp. 432–484. [Google Scholar]
- Varshney, A.; Sharma, V.; Shrivastava, A. A Novel Simplified Equivalent Modeling for Microstrip Line Interconnects. Indian Patent No. 202111019468, 7 May 2021. [Google Scholar]
- Shireen, R.; Shi, S.; Prather, D.W. W-band microstrip-to-waveguide transition using via fences. Prog. Electromagn. Res. Lett. 2010, 16, 151–160. [Google Scholar] [CrossRef]
- Tong, Z.; Stelzer, A. A vertical transition between rectangular waveguide and coupled microstrip Lines. IEEE Microw. Wirel. Compon. Lett. 2012, 22, 251–253. [Google Scholar] [CrossRef]
- Varshney, A.; Sharma, V.; Elfergani, I.; Zebiri, C.; Vujicic, Z.; Rodriguez, J. An Inline V-Band WR-15 Transition Using Antipodal Dipole Antenna as RF Energy Launcher @ 60 GHz for Satellite Applications. Electronics 2022, 11, 3860. [Google Scholar] [CrossRef]
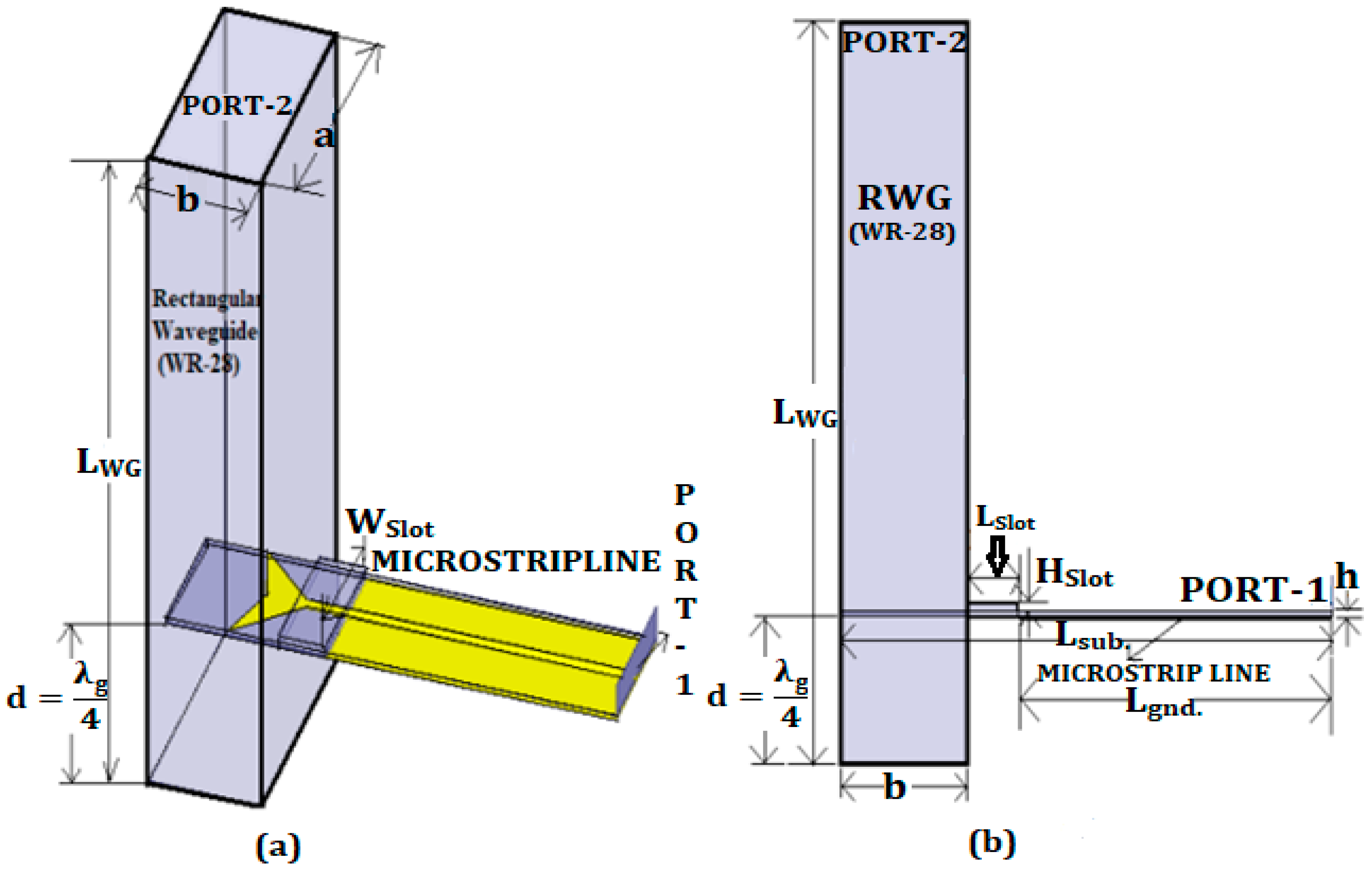








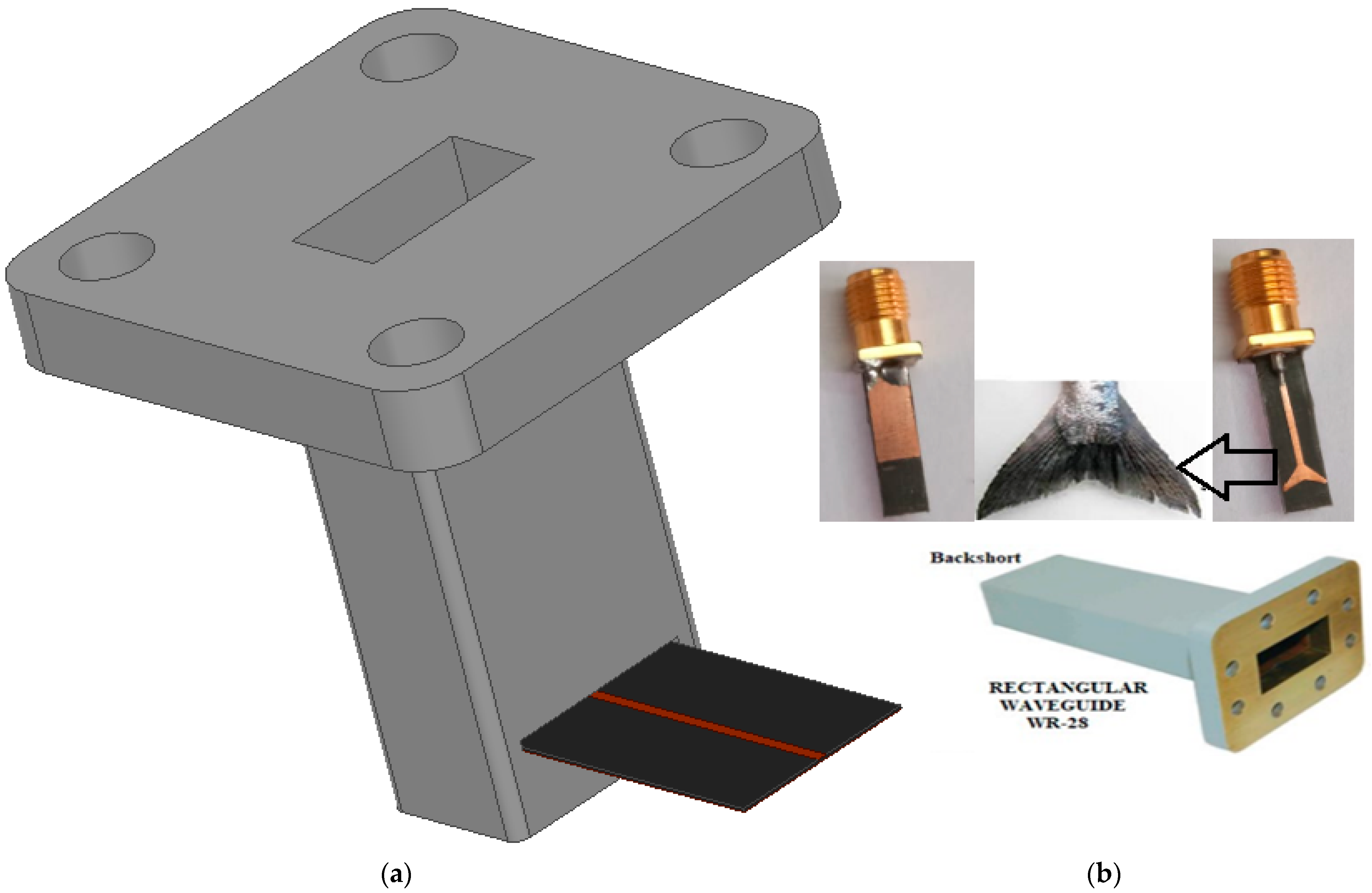


| Part Name | Dimension Designation | Dimension Values (mm) |
|---|---|---|
| Rectangular Waveguide (RWG) | Waveguide type | WR-28 |
| Dielectric | Air-filled PEC (Al) | |
| Broadside | a = 7.112 | |
| Narrow side | b = 3.556 | |
| Length | LWG = 19.9 | |
| Microstrip Line (MSL) | Material | Copper (Cu) |
| Width | w = 0.37 | |
| Length | Lstrip = 10.4 | |
| Thickness | t = 0.035 | |
| Fish-tail lengths (upper) | LFT1 = LFT4 = 2.414 | |
| Fish-tail lengths (lower) | LFT2 = LFT3 = 1.9416 | |
| E-plane 90° broadside Waveguide Slot | Dielectric | Air-filled |
| Width | WSlot = 7.0 | |
| Length | LSlot = 1.015 | |
| Height | HSlot = 0.381 | |
| Ground | Material | Copper (Cu) |
| Width | Wgnd. = 7.0 | |
| Length | Lgnd. = 9.629 | |
| Thickness | t = 0.035 | |
| Substrate | Material | Roger RT Duroid 5880 (tm) |
| Width | Wsub. = 7.0 | |
| Length | Lsub. = 14.2 | |
| Height | h = 0.127 | |
| Back Short | Back-short distance | d = λg/4 = 1.9 |
| Broadside | a = 7.112 | |
| Narrow side | b = 3.556 |
| Back-Short Distance d = λg/4 (mm) | Min. IL (dB) | RL (dB) | Resonance Frequency fr (GHz) | −10 dB Absolute BW (fL–fH) (GHz) |
|---|---|---|---|---|
| 3.5 | −1.91 | −10.98 | 22.68 | (21.68–23.19) |
| 3.0 | −1.64, −0.75 | −20.20, −10.68 | 22.05, 41.13 | (21.21–24.65), (39.83–41.97) |
| 2.5 | −1.78, −0.26 | −21.82, −42.06 | 22.05, 42.13 | (21.55–27.55), (36.19–44.75) |
| 2.0 | −0.36 | −15.26 | 30 | (21.97–45.0) |
| 2.1 | −0.32 | −18.12 | 25 | (21.74–45.0) |
| 1.9 | −0.36 | −16.72 | 29.75 | (23.52–45.0) |
| Slot Height, HSlot (mm) | Min. IL (dB) | RL (dB) | Resonance Frequency fr (GHz) | −10 dB Absolute BW (fL–fH) (GHz) |
|---|---|---|---|---|
| 1.5 h= 0.1905 | −0.48 | −11.51 | 27.35 | (24.98–29.98) |
| 2 h = 0.254 | −0.38 | −15.05 | 27.57 | (23.95–43.36) |
| 2.5 h = 0.3175 | −0.40 | −16.47 | 27.78 | (23.35–44.28) |
| 3 h = 0.381 | −0.36 | −16.72 | 29.75 | (23.52–45.0) |
| 3.5 h = 0.4445 | −0.47 | −17.98 | 27.51 | (21.93–45.0) |
| Depth of the Fish-Tail from the Substrate End, LD (mm) | Min. IL (dB) | RL (dB) | Resonance Frequency fr (GHz) | −10 dB Absolute BW (fL–fH) (GHz) |
|---|---|---|---|---|
| 1.9 | −0.50 | −18.22, −11.59 | 24.14, 43.07 | (21.79–33.87), (38.30–44.96) |
| 2.1 | −0.46 | −36.72 | 25.04 | (21.78–44.70) |
| 2.3 | −0.43 | −25.98 | 25.94 | (21.84–44.80) |
| 2.5 | −0.36 | −16.72 | 29.75 | (23.52–45.0) |
| Fish-Tail Probe Width, WP (mm) | Min. IL (dB) | RL (dB) | Resonance Frequency fr (GHz) | −10 dB Absolute BW (fL–fH) (GHz) |
|---|---|---|---|---|
| 2.6 | −0.25 | −19.76 | 43.56 | (25.60–45.0) |
| 3.0 | −0.29 | −18.94 | 43.11 | (24.09–45.0) |
| 3.4 | −0.35 | −15.79 | 27.96 | (23.13–45.0) |
| 3.8 | −0.36 | −16.72 | 29.75 | (23.52–45.0) |
| Ref. | Coupling Method | Type | Need of Impedance Transformer | IL (>dB) | RL (<dB) | FBW (%) | RLC Equivalent Circuit |
|---|---|---|---|---|---|---|---|
| [3] Li et al., 2012 | Narrow side wall (b) inserted, E-plane, side inserted magnetic coupling using semi-circular microstrip ring probe | Transverse | Yes (multi-section step transformer) | −0.95 | −10 | 33 | Not Given |
| [4] Shih et al., 1988 | Broadside wall (a) inserted, E- Plane (90°) | Transverse | Yes (multi-section step transformer) | −0.10 | −10 | 40 | Not Given |
| [5] S. Tomar et al., 2010 | Broadside wall probe insertion through aperture (E-plane), via-less | Transverse | Yes (single-step Impedance Transformer) | −0.30 | −45 | 14.54 | Not Given |
| [6] Varshney et al., 2013 | Broadside wall probe insertion, E-plane 90° transition, Uses rectangular probe | Transverse | Yes (two-section step) | −0.30 | −10 | 38 | Not Given |
| [7] Lou et al., 2008 | Inline E-plane (90°), radial-shaped probe with notch cut and extended ground | Inline | No | −0.30 | −10 | 69 | Not Given |
| [12] Simone et al., 2018 | Q-band transition uses a section of the ridged waveguide and Chebyshev impedance transformer, simple and planar structure, increases the ease of fabrication and the compactness, good return loss, via-less, broad BW | Inline | Yes (Chebyshev impedance transformer) | −0.26 | −24 | 40 | Not Given |
| [10] Long, C. et al., 2019 | Patch above a wedge-shaped cavity, low-cost, single-sided PCB, wideband compact structure and easy integration, high integration density | Inline | No | −0.40 | −13 | 71.43 | Not Given |
| [9] Tang et al., 2020 | Inline (90°) transition, 22 semi-circular ring probe | Inline | Yes (single step) | −0.13 | −10 | 48.3 | Not Given |
| [11] R.Gupta, P.P. Kumar, 2020 | 90° WG-to-coaxial transition, field matching, and Impedance matching were achieved through a ridged waveguide, customized coaxial probe, and back-short distance | Transverse | No | −0.47 | −23.4 | 38 | Not Given |
| [8] Varshney, 2021 | Broadside wall inserted, E-plane, 90°, reverse approach of microstrip insertion | Transverse | Yes | −0.10 | −10 | 72 | Given |
| This work | Broadside wall inserted, E-plane, 90°fishtail shaped probe insertion, compact, easy fabrication of PCB | Transverse | No | −0.50 | −10 | 66.5 | Given |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varshney, A.; Sharma, V.; Nayak, C.; Goyal, A.K.; Massoud, Y. A Low-Loss Impedance Transformer-Less Fish-Tail-Shaped MS-to-WG Transition for K-/Ka-/Q-/U-Band Applications. Electronics 2023, 12, 670. https://doi.org/10.3390/electronics12030670
Varshney A, Sharma V, Nayak C, Goyal AK, Massoud Y. A Low-Loss Impedance Transformer-Less Fish-Tail-Shaped MS-to-WG Transition for K-/Ka-/Q-/U-Band Applications. Electronics. 2023; 12(3):670. https://doi.org/10.3390/electronics12030670
Chicago/Turabian StyleVarshney, Atul, Vipul Sharma, Chittaranjan Nayak, Amit Kumar Goyal, and Yehia Massoud. 2023. "A Low-Loss Impedance Transformer-Less Fish-Tail-Shaped MS-to-WG Transition for K-/Ka-/Q-/U-Band Applications" Electronics 12, no. 3: 670. https://doi.org/10.3390/electronics12030670
APA StyleVarshney, A., Sharma, V., Nayak, C., Goyal, A. K., & Massoud, Y. (2023). A Low-Loss Impedance Transformer-Less Fish-Tail-Shaped MS-to-WG Transition for K-/Ka-/Q-/U-Band Applications. Electronics, 12(3), 670. https://doi.org/10.3390/electronics12030670








