A Kind of Optoelectronic Memristor Model and Its Applications in Multi-Valued Logic
Abstract
1. Introduction
2. Optoelectronic Memristor Model and Electrical Characteristics Analysis
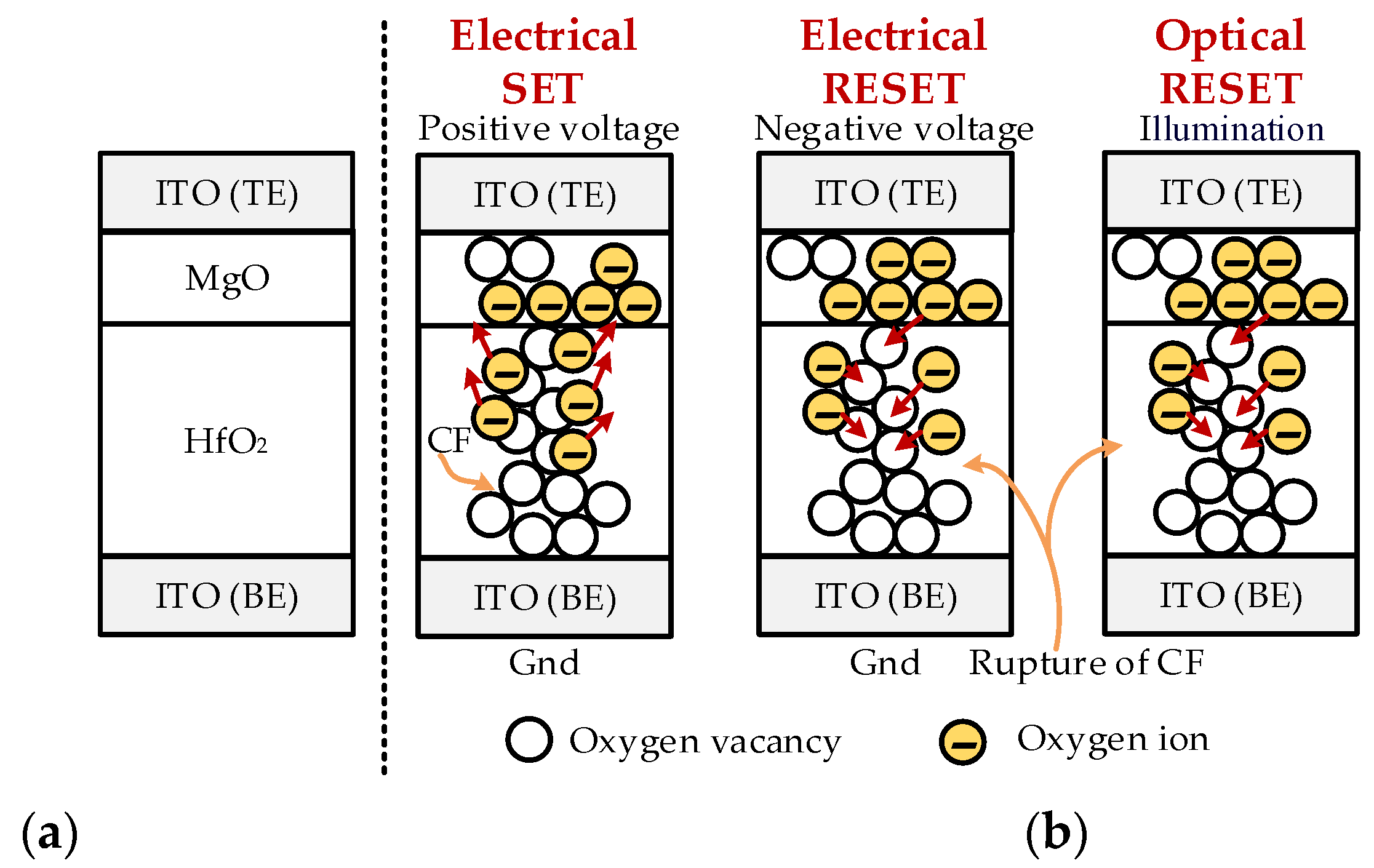
2.1. Background of Opoelectronic Memristor
2.2. Modelling of Opoelectronic Memristor
2.3. Electrical Characteristics Analysis
3. Rotation Mechanism Based Multi-Valued Logic
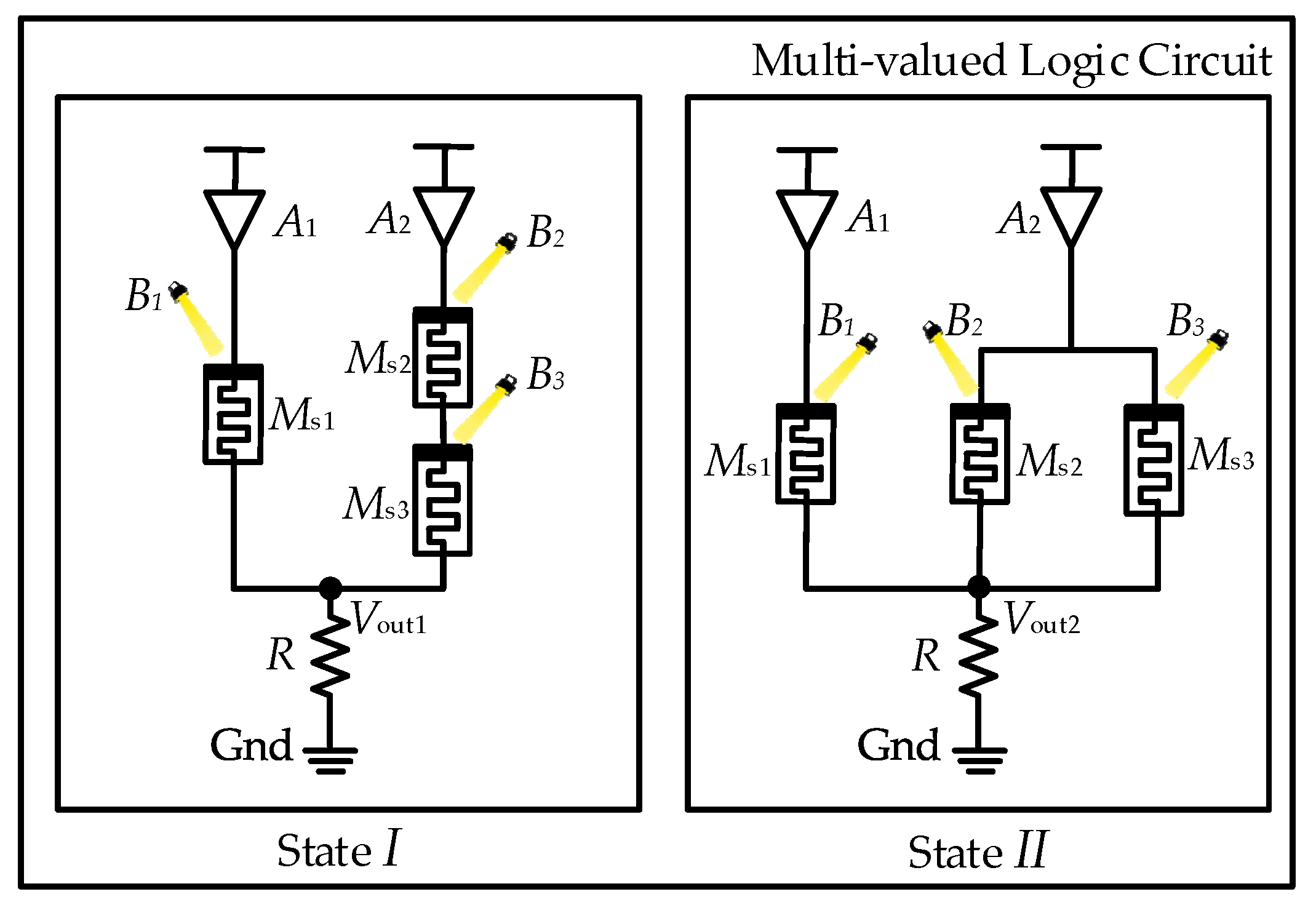
3.1. Rotation Mechanism Based Composite Circuit
3.2. Implementation of Multi-Valued Logic
3.2.1. State I for Multi-Valued Logic
- Case A: When B1 = B2 = B3 = Ipl, the node voltage Vout1 can be computed as:
- Case B: When B1 = Ipl, B2 = Ipl and B3 = Iph (or B1 = Ipl, B2 = Iph and B3 = Ipl), the node voltage Vout1 can be computed as:
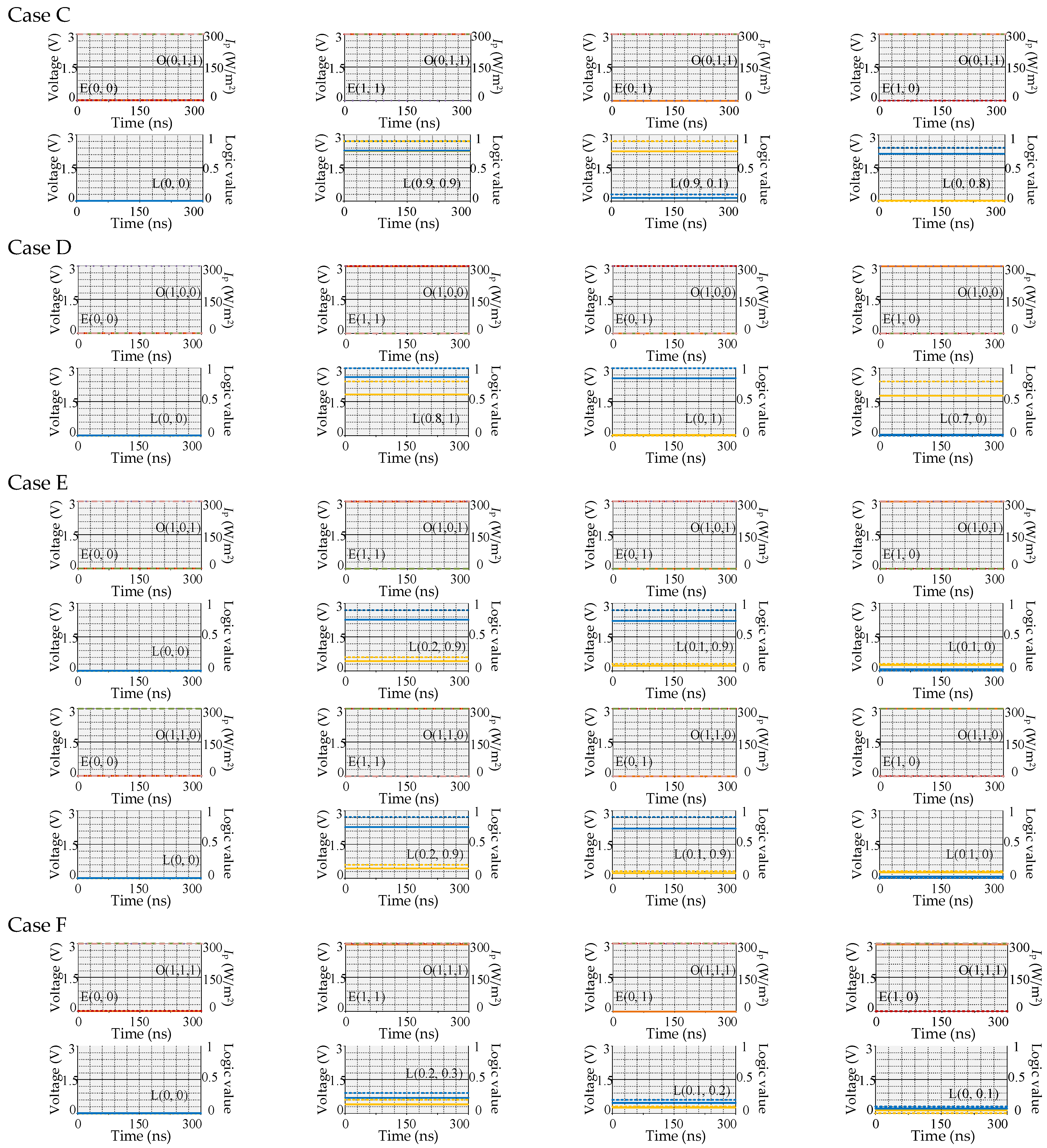
- Case C: When B1 = Ipl and B2 = B3 = Iph, the node voltage Vout1 can be computed as:
- Case D: When B1 = Iph and B2 = B3 = Ipl, the node voltage Vout1 can be computed as:
- Case E: When B1 = Iph, B2 = Ipl and B3 = Iph (or B1 = Iph, B2 = Iph and B3 = Ipl), the node voltage Vout1 can be computed as:
- Case F: When B1 = B2 = B3 = Iph, the node voltage Vout1 can be computed as:
3.2.2. State II for Multi-Valued Logic
- Case A: When B1 = B2 = B3 = Ipl, the variation of resistance Rs1, Rs2, and Rs3 is the same as that of Case A in state I, thus the node voltage Vout2 can be computed as:
- Case B: When B1 = Ipl, B2 = Ipl and B3 = Iph (or B1 = Ipl, B2 = Iph and B3 = Ipl), the variation of resistance Rs1, Rs2, and Rs3 is the same as that of Case B in state I, thus the node voltage Vout2 can be computed as:
- Case C: When B1 = Ipl and B2 = B3 = Iph, the variation of resistance Rs1, Rs2, and Rs3 is the same as that of Case C in state I, thus the node voltage Vout2 can be computed as:
- Case D: When B1 = Iph and B2 = B3 = Ipl, the variation of resistance Rs1, Rs2, and Rs3 is the same as that of Case D in state I, thus the node voltage Vout2 can be computed as:
- Case E: When B1 = Iph, B2 = Ipl and B3 = Iph (or B1 = Iph, B2 = Iph and B3 = Ipl), the variation of resistance Rs1, Rs2, and Rs3 is the same as that of Case E in state I, thus the node voltage Vout2 can be computed as:
- Case F: When B1 = B2 = B3 = Iph, the variation of resistance Rs1, Rs2, and Rs3 is the same as that of Case F in state I, thus the node voltage Vout2 can be computed as:
3.3. Circuit Smulations and Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, X.; Taylor, B.; Wu, A.; Chen, Y.; Chua, L.O. Research progress on memristor: From synapses to computing systems. IEEE Trans. Circuits Syst. I: Regul. Pap. 2022, 69, 1845–1857. [Google Scholar] [CrossRef]
- Ji, X.; Dong, Z.; Lai, C.S.; Qi, D. A brain-inspired in-memory computing system for neuronal communication via memristive circuits. IEEE Commun. Mag. 2022, 60, 100–106. [Google Scholar] [CrossRef]
- Zhong, Y.; Tang, J.; Li, X.; Liang, X.; Liu, Z.; Li, Y.; Xi, Y.; Yao, P.; Hao, Z.; Gao, B.; et al. A memristor-based analogue reservoir computing system for real- time and power-efficient signal processing. Nat. Electron. 2022, 5, 672–681. [Google Scholar] [CrossRef]
- Zhong, Y.; Tang, J.; Li, X.; Gao, B.; Qian, H.; Wu, H. Dynamic memristor-based reservoir computing for high-efficiency temporal signal processing. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Ji, X.; Zhou, G.; Gao, M.; Qi, D. Multimodal neuromorphic sensory-processing system with memristor circuits for smart home applications. IEEE Trans. Ind. Appl. 2022. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Liao, K.; Lei, P.; Tu, M.; Luo, S.; Jiang, T.; Jie, W.; Hao, J. Memristor based on inorganic and organic two-dimensional materials: Mechanisms, performance, and synaptic applications. ACS Appl. Mater. 2021, 13, 32606–32623. [Google Scholar] [CrossRef]
- Dong, Z.; Ji, X.; Lai, C.S.; Qi, D.; Zhou, G.; Lai, L.L. Memristor-based hierarchical attention network for multimodal affective computing in mental health monitoring. IEEE Consum. Electr. Mag. 2022. [Google Scholar] [CrossRef]
- Shen, Z.; Zhao, C.; Zhao, T.; Xu, W.; Liu, Y.; Qi, Y.; Mitrovic, I.Z.; Yang, L.; Zhao, C.Z. Artificial synaptic performance with learning behavior for memristor fabricated with stacked solution-processed switching layers. ACS Appl. Electron. Mater. 2021, 3, 1288–1300. [Google Scholar] [CrossRef]
- Ji, X.; Lai, C.S.; Zhou, G.; Dong, Z.; Qi, D.; Lai, L.L. A flexible memristor model with electronic resistive switching memory behavior and its application in spiking neural network. IEEE Trans. Nanobioscience 2022, 22, 52–62. [Google Scholar] [CrossRef]
- Ji, X.; Dong, Z.; Lai, C.S.; Zhou, G.; Qi, D. A physics-oriented memristor model with the coexistence of NDR effect and RS memory behavior for bio-inspired computing. Mater. Today Adv. 2022, 16, 100293. [Google Scholar] [CrossRef]
- Khalid, M. Review on various memristor models, characteristics, potential applications, and future works. Trans. Electr. Electron. Mater. 2019, 20, 289–298. [Google Scholar] [CrossRef]
- Li, J.; Dong, Z.; Luo, L.; Duan, S.; Wang, L. A novel versatile window function for memristor model with application in spiking neural network. Neurocomputing 2020, 405, 239–246. [Google Scholar] [CrossRef]
- Li, T.; Duan, S.; Liu, J.; Wang, L.; Huang, T. A spintronic memristor-based neural network with radial basis function for robotic manipulator control implementation. IEEE Trans. Syst. Man Cybern. Syst. 2015, 46, 582–588. [Google Scholar] [CrossRef]
- Kvatinsky, S.; Friedman, E.G.; Kolodny, A.; Weiser, U.C. TEAM: Threshold adaptive memristor model. IEEE Trans. Circuits Systems I Regul. Pap. 2012, 60, 211–221. [Google Scholar] [CrossRef]
- Kvatinsky, S.; Ramadan, M.; Friedman, E.G.; Kolodny, A. VTEAM: A general model for voltage- controlled memristors. IEEE Trans. Circuits Syst. II 2015, 62, 786–790. [Google Scholar] [CrossRef]
- Wang, X.; Li, P.; Jin, C.; Dong, Z.; Iu, H.H. General modeling method of threshold-type multivalued memristor and its application in digital logic circuits. Int. J. Bifurcat. Chaos 2021, 31, 2150248. [Google Scholar] [CrossRef]
- Dong, Z.; Ji, X.; Lai, C.S.; Qi, D. Design and implementation of a flexible neuromorphic computing system for affective communication via memristive circuits. IEEE Commun. Mag. 2022. [Google Scholar] [CrossRef]
- Dong, Z.; Qian, Z.; Zhou, G.; Ji, X.; Qi, D.; LAI, J. Memristor-based full-function pavlov associative memory circuit design, implementation and analysis. J. Electron. Inf. Techn 2021, 43, 1–13. [Google Scholar]
- Berco, D.; Ang, D.S.; Kalaga, P.S. Programmable photoelectric memristor gates for in situ image compression. Adv. Intell. Syst. 2020, 2, 2000079. [Google Scholar] [CrossRef]
- Zhou, J.; Li, W.; Chen, Y.; Lin, Y.-H.; Yi, M.; Li, J.; Qian, Y.; Guo, Y.; Cao, K.; Xie, L.; et al. A monochloro copper phthalocyanine memristor with high-temperature resilience for electronic synapse applications. Adv. Mater. 2021, 33, 2006201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhao, X.; Shan, X.; Shan, X.; Tian, Q.; Wang, Z.; Lin, Y.; Xu, H.; Liu, Y. Humidity effect on resistive switching characteristics of the CH3NH3PbI3 memristor. ACS Appl. Mater. Inter. 2021, 13, 28555–28563. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Zhang, X.; Cheng, H.; Qiu, J.; Liu, X.; Wang, M.; Liu, Q. Emerging dynamic memristors for neuromorphic reservoir computing. Nanoscale 2022, 14, 289–298. [Google Scholar] [CrossRef]
- Liu, G.; Shen, S.; Jin, P.; Wang, G.; Liang, Y. Design of memristor-based combinational logic circuits. Circ. Syst. Signal Pr. 2021, 40, 5825–5846. [Google Scholar] [CrossRef]
- Xu, N.; Park, T.; Yoon, K.J.; Hwang, C.S. In-memory stateful logic computing using memristors: Gate, calculation, and application. Phys. Status Solidi Rapid Res. Lett. 2021, 15, 2100208. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Verma, D.; Wang, L.A.; Liang, H.; Zhu, H.; Li, L.-J.; Hou, T.-H.; Lai, C.-S. Bi2O2Se-based memristor-aided logic. ACS Appl. Mater. Inter. 2021, 13, 15391–15398. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Wu, Q.; Wang, X.; Wang, C.; Miao, X. Two memristors-based XOR logic demonstrated with encryption/decryption. IEEE Electron Device Lett. 2021, 42, 1398–1401. [Google Scholar] [CrossRef]
- Sun, B.; Ngai, J.H.; Zhou, G.; Zhou, Y.; Li, Y. Voltage-controlled conversion from CDS to MDS in an azobenzene-based organic memristor for information storage and logic operations. ACS Appl. Mater. Inter. 2022, 14, 41304–41315. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Duan, S. Memristor ratioed logic crossbar-based delay and jump-key flip-flops design. Inter. J. Circuit Theory Appl. 2022, 50, 1353–1364.2. [Google Scholar] [CrossRef]
- Dong, Z.; Qi, D.; He, Y.; Xu, Z.; Hu, X.; Duan, S. Easily cascaded memristor-CMOS hybrid circuit for high-efficiency boolean logic implementation. Int. J. Bifurcat. Chaos 2018, 28, 1850149. [Google Scholar] [CrossRef]
- Jha, C.K.; Thangkhiew, P.L.; Datta, K.; Drechsler, R. IMAGIN: Library of IMPLY and MAGIC NOR based approximate adders for in-memory computing. IEEE J. Explor. Solid-St. Compu. Devices Circuits 2022, 8, 68–76. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Gao, M.; Luo, L.; Duan, S.; Dong, Z.; Lin, H. Implementation of unbalanced ternary logic gates with the combination of spintronic memristor and CMOS. Electronics 2020, 9, 542. [Google Scholar] [CrossRef]
- Wang, X.Y.; Dong, C.T.; Wu, Z.R.; Cheng, Z.Q. A review on the design of ternary logic circuits. Chin. Phys. B 2021, 30, 128402. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, A.; Li, C.; Liu, G.; Cheng, X. Mathematical analysis and circuit emulator design of the three-valued memristor. Integration 2022, 86, 74–83. [Google Scholar] [CrossRef]
- Yang, J.; Lee, H.; Jeong, J.H.; Kim, T.; Lee, S.H.; Song, T. Circuit-level exploration of ternary logic using memristors and MOSFETs. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 707–720. [Google Scholar] [CrossRef]
- Dong, Z.; Lai, C.S.; Qi, D.; Xu, Z.; Li, C.; Duan, S. A general memristor-based pulse coupled neural network with variable linking coefficient for multi-focus image fusion. Neurocomputing 2018, 308, 172–183. [Google Scholar] [CrossRef]






| Research Gaps | Contributions |
|---|---|
|
|
|
|
|
|
| * Optoelectronic Memristor Model |
|---|
| .SUBCKT optoelectronic memristor model Plus Minus PARAMS: + xon=0 xoff=3E−9 Alphaon=0.1 Alphaoff=0.1 Ron=100 Roff=3E3 kon=−1 koff=1 Ip=100 + Epsilon=0.6 Ipmax=500 p=1 Beta=6.6666E8 Vth1=2 Vth2=−2 xinit=3E−9 ******* Differential equation modelling******* Gx 0 x value={f(V(x), V(Plus, Minus), kon, koff, Alphaon, Alphaoff, Vth1, Vth2, Epsilon, + Beta, p, Ip, Ipmax)} Cx x 0 1 IC={xinit} R x 0 1 T **************************Ohm’s Law******************** Emem Plus Aux value={I(Emem)*(Roff-Ron)*(V(x)-xon)/(xoff-xon)} Rs aux Minus {Ron} Emx Mx 0 value={(Roff-Ron)*(V(x)-xon)/(xoff-xon)+Ron} **************************Functions************************ .func f(x, v, kon, koff, Alphaon, Alphaoff, Epsilon, Ip, Ipmax, Beta, p)= + {If(v>Vth1, f1(x, v, kon, Vth1, Alphaon, Epsilon, Ip, Beta, Ipmax, p), + If(v<Vth2, f2(x, v, koff, Vth2, Alphaoff, Epsilon, Ip, Beta, Ipmax, p), + f3(x, Epsilon, Ip, Beta, Ipmax, p))} .func f1(x, v, kon, Vth1, Alphaon, Epsilon, Ip, Beta, Ipmax, p)= + {(kon*(v/Vth1−1)^Alphaon+Ip/(Epsilon*Ipmax))*(1-(Beta*x−1)^(2*p))} .func f2(x, v, koff, Vth2, Alphaoff, Epsilon, Ip, Beta, Ipmax, p)= + {(koff*(v/Vth2−1)^Alphaoff+Ip/(Epsilon*Ipmax))*(1-(Beta*x−1)^(2*p))} .func f3(x, Epsilon, Ip, Beta, Ipmax, p)={Ip/(Epsilon*Ipmax)*(1-(Beta*x−1)^(2*p))} .ENDS optoelectronic memristor |
| Optical Power Density (W/m2) | Electrical Stimulation (V) | Initial Value of Memristor (kΩ) | |
|---|---|---|---|
| Figure 3a,b | Ip = 0 | V = 3 sin(107πt) | 3 |
| Figure 3c,d | Ip = 20 | V = 3 sin(t) | 3 |
| Figure 4a | Ip = 10, 50, 100, 200, 300, 500 | V = −3 | 0.01 |
| Figure 4b | V = 0 | 0.01 | |
| Figure 4c | V = 3 | 0.01 | |
| Figure 4d | V = 3 | 3 | |
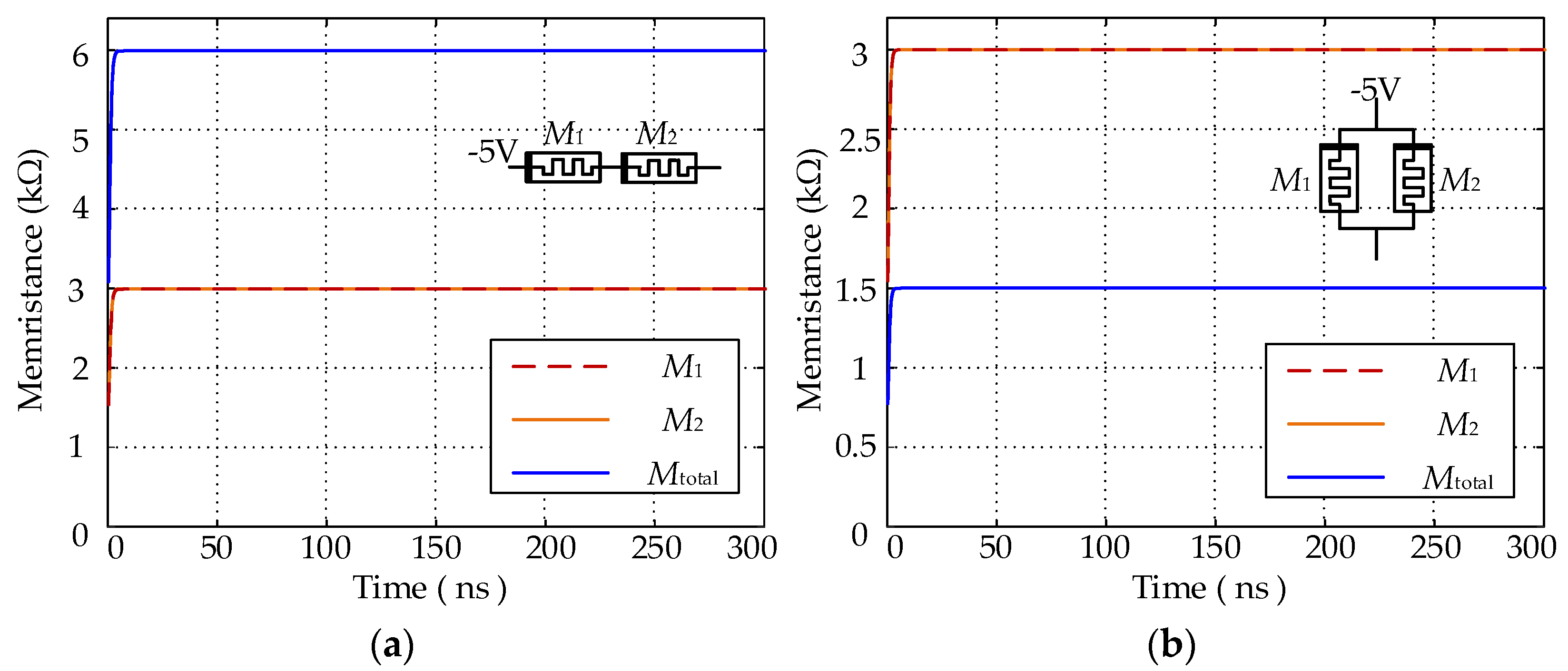
| Figure 5a | Ip = 100 | V = −5 | 1.5, 1.5 |
| Figure 5b | V = −5 | 1.5, 1.5 | |
| Figure 5c | V = 0 | 1.5, 1.5 | |
| Figure 5d | V = 0 | 1.5, 1.5 | |
| Figure 5e | V = 5 | 1.5, 1.5 | |
| Figure 5f | V = 5 | 1.5, 1.5 |
| Electronical Inputs | Optical Inputs | Output of state I | Output of state II | ||||
|---|---|---|---|---|---|---|---|
| A1 | A2 | Cases | B1 | B2 | B3 | Vout1 | Vout2 |
| 0 | 0 | - | × | × | × | 0 | 0 |
| 1 | 1 | Case A | 0 | 0 | 0 | 1 | 1 |
| Case B | 0 | 0/1 | 1/0 | 0.9 | 1 | ||
| Case C | 0 | 1 | 1 | 0.9 | 0.9 | ||
| Case D | 1 | 0 | 0 | 0.8 | 1 | ||
| Case E | 1 | 0/1 | 1/0 | 0.2 | 0.9 | ||
| Case F | 1 | 1 | 1 | 0.2 | 0.3 | ||
| 0 | 1 | Case A | 0 | 0 | 0 | 0.7 | 0.7 |
| Case B | 0 | 0/1 | 1/0 | 0.9 | 0.5 | ||
| Case C | 0 | 1 | 1 | 0.9 | 0.1 | ||
| Case D | 1 | 0 | 0 | 0 | 1 | ||
| Case E | 1 | 0/1 | 1/0 | 0.1 | 0.9 | ||
| Case F | 1 | 1 | 1 | 0.1 | 0.2 | ||
| 1 | 0 | Case A | 0 | 0 | 0 | 0.3 | 0.4 |
| Case B | 0 | 0/1 | 1/0 | 0 | 0.5 | ||
| Case C | 0 | 1 | 1 | 0 | 0.8 | ||
| Case D | 1 | 0 | 0 | 0.7 | 0 | ||
| Case E | 1 | 0/1 | 1/0 | 0.1 | 0 | ||
| Case F | 1 | 1 | 1 | 0 | 0.1 | ||
| Proposed Logic | Material Implication Logic | Memristor-Aided Logic | Memristor Ratioed Logic | Balanced Ternary Logic | Unbalanced Ternary Logic | |
|---|---|---|---|---|---|---|
| Input Variable | Voltage, illumination | M1 | M1 | Voltage | Voltage | Voltage |
| Output variable | Voltage | M1 | M1 | Voltage | Voltage | Voltage |
| Memristor type | Optoelectronic | HP | TEAM | VTEAM | VTEAM | Spintronic |
| Computation form | Parallel | Serial | Serial | Parallel | Parallel | Parallel |
| Need of resistors or transistors | √ | √ | × | √ | √ | √ |
| Initialization | √ | √ | √ | × | √ | √ |
| Cascading capacity | possible | difficult | difficult | possible | possible | possible |
| Logic values | Multi-valued | Binary | Binary | Binary | Ternary | Ternary |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Lin, Y.; Hu, C.; Zhou, S.; Gu, S.; Yang, M.; Ma, G.; Yan, Y. A Kind of Optoelectronic Memristor Model and Its Applications in Multi-Valued Logic. Electronics 2023, 12, 646. https://doi.org/10.3390/electronics12030646
Wang J, Lin Y, Hu C, Zhou S, Gu S, Yang M, Ma G, Yan Y. A Kind of Optoelectronic Memristor Model and Its Applications in Multi-Valued Logic. Electronics. 2023; 12(3):646. https://doi.org/10.3390/electronics12030646
Chicago/Turabian StyleWang, Jiayang, Yuzhe Lin, Chenhao Hu, Shiqi Zhou, Shenyu Gu, Mengjie Yang, Guojin Ma, and Yunfeng Yan. 2023. "A Kind of Optoelectronic Memristor Model and Its Applications in Multi-Valued Logic" Electronics 12, no. 3: 646. https://doi.org/10.3390/electronics12030646
APA StyleWang, J., Lin, Y., Hu, C., Zhou, S., Gu, S., Yang, M., Ma, G., & Yan, Y. (2023). A Kind of Optoelectronic Memristor Model and Its Applications in Multi-Valued Logic. Electronics, 12(3), 646. https://doi.org/10.3390/electronics12030646






