New Fixed-Frequency Digital Control to Improve the Light-Load Efficiency of an Isolated Regulated Converter
Abstract
:1. Introduction
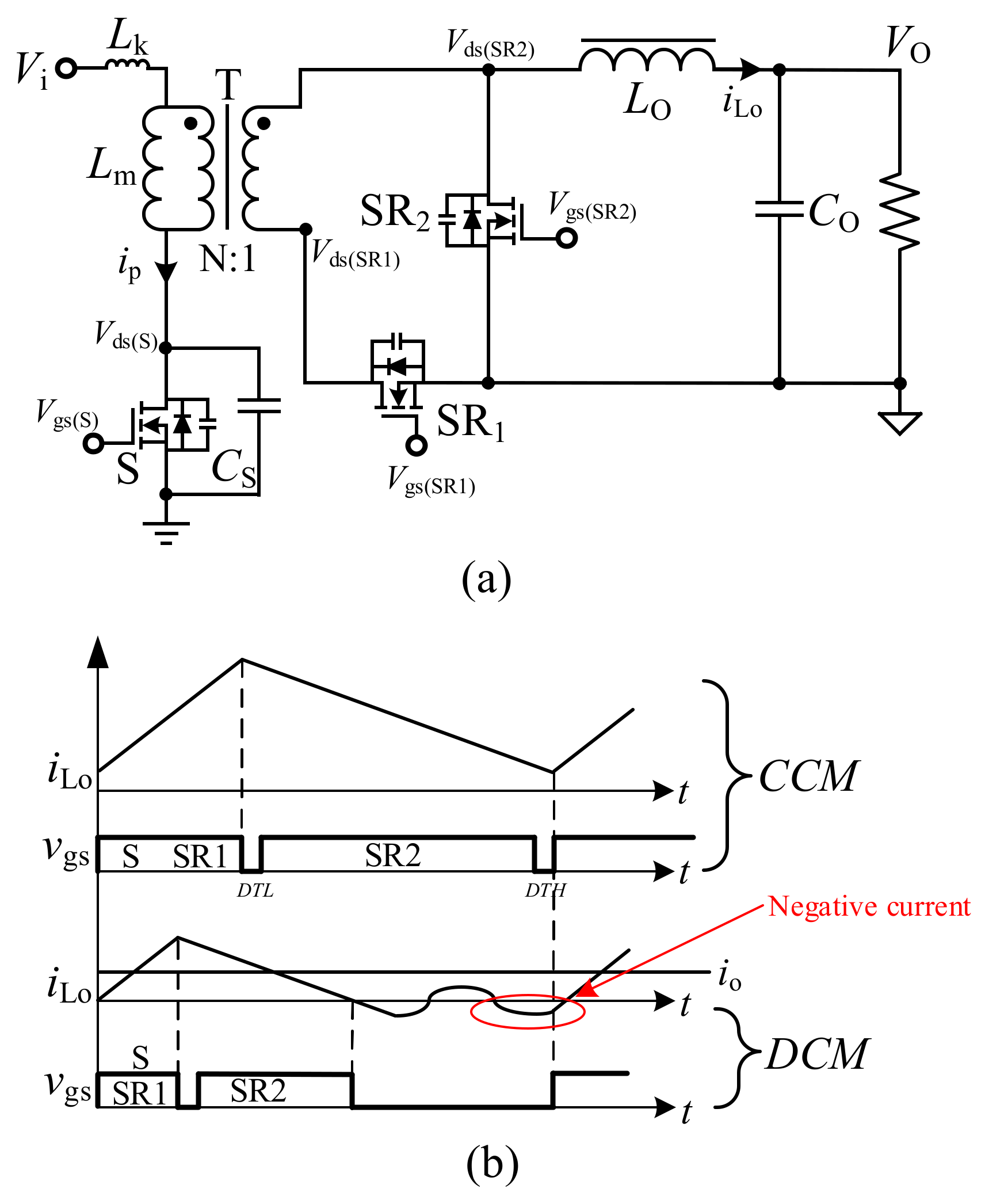
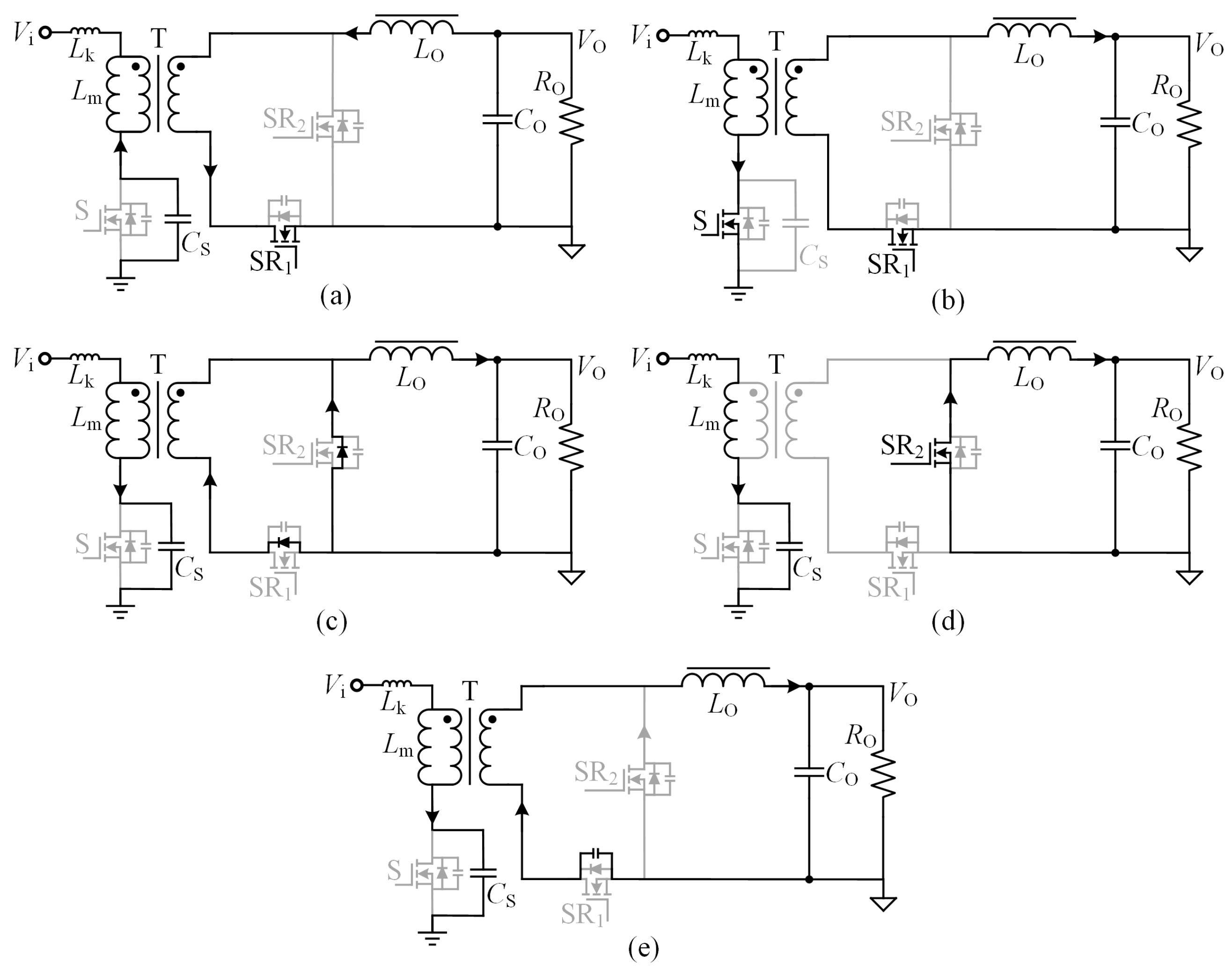
2. Working Principles in DCM
2.1. Soft-Switching of the Primary Switch
2.2. The Voltage–Second Balance Method
2.3. Operation Modes
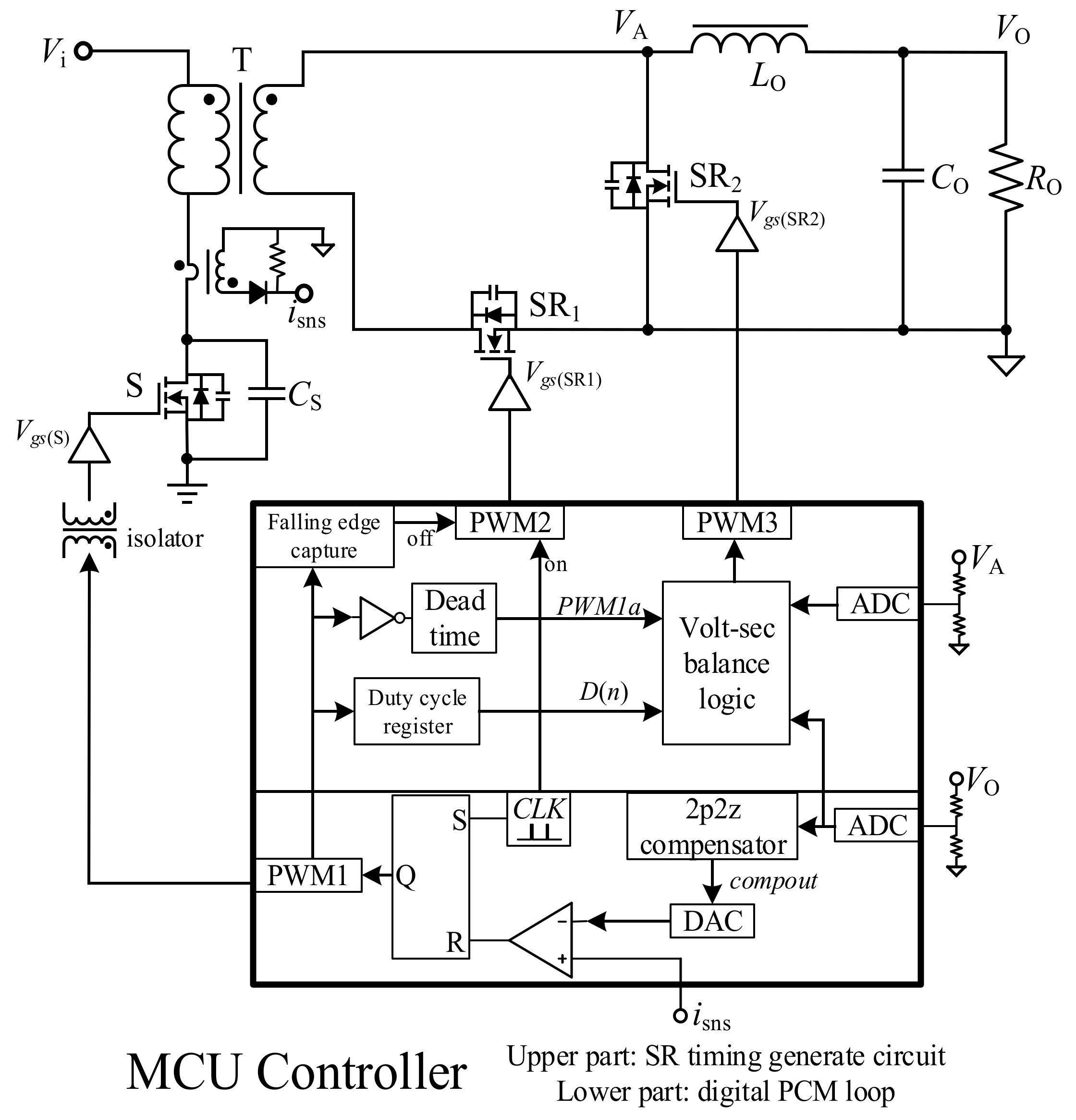
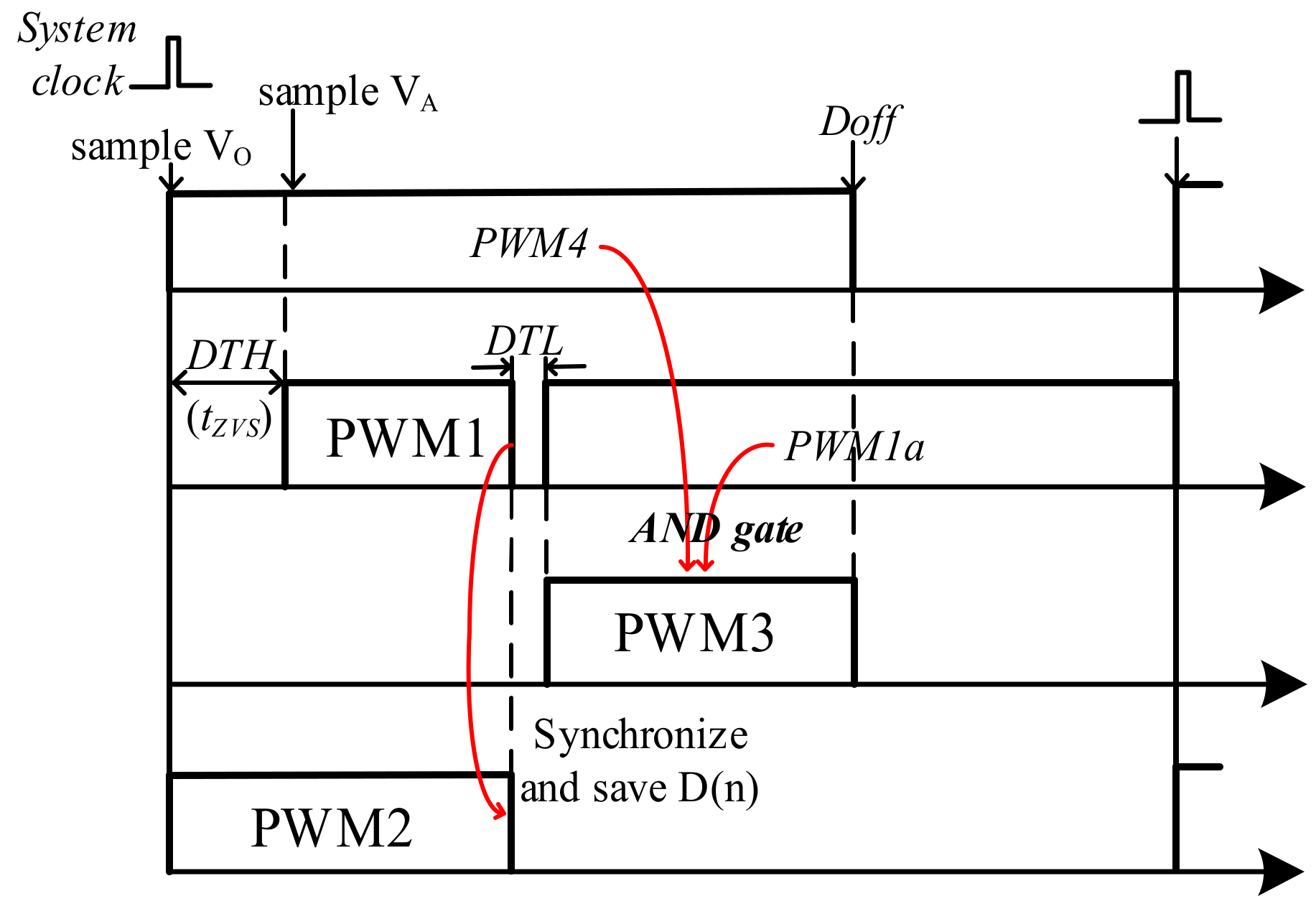
3. The Proposed Control Scheme
3.1. Control Diagram in DCM
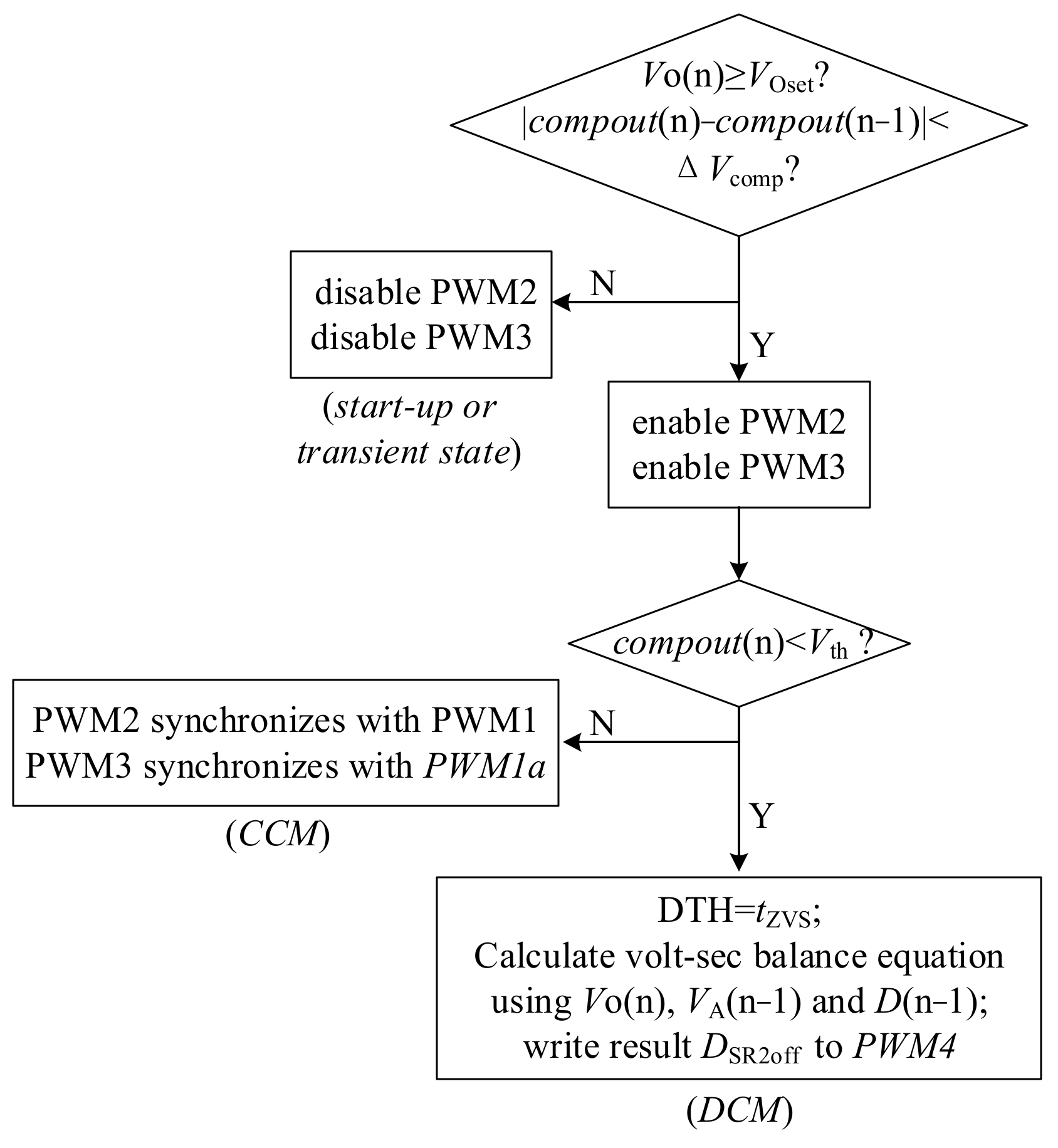
3.2. The Principle of Control Flow
3.3. Design Considerations
3.3.1. Dead Time in DCM
3.3.2. The Voltage Threshold of the Compout Signal
3.3.3. The Voltage Threshold of the Compout Variation Rate
3.3.4. Controller Selection and Comparison
4. Circuit Design
4.1. Hardware Parameters
4.2. Software Parameters
4.3. Power Loss, Ripple, and Regulation Estimation
5. Experimental Results
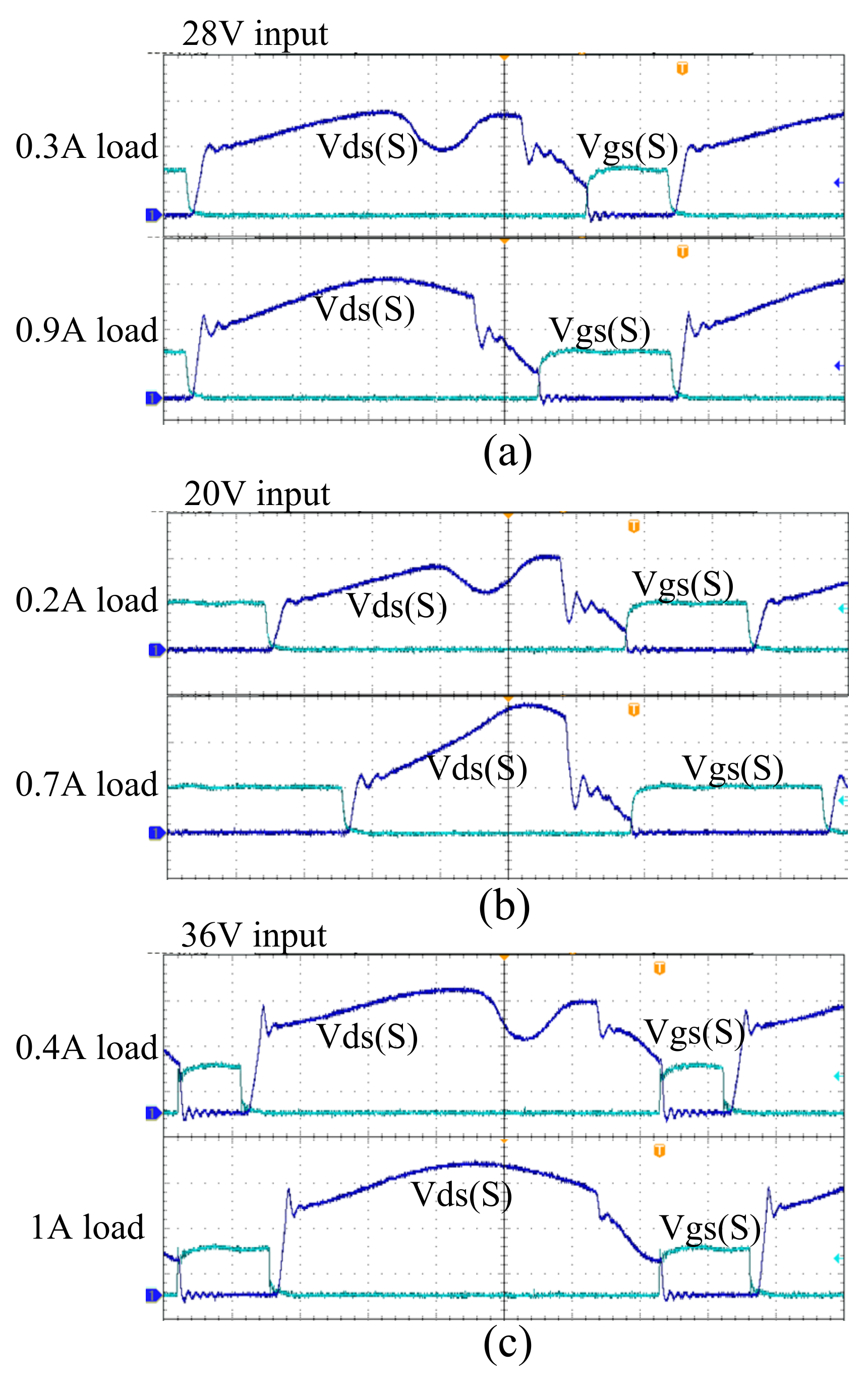
5.1. Waveforms in DCM
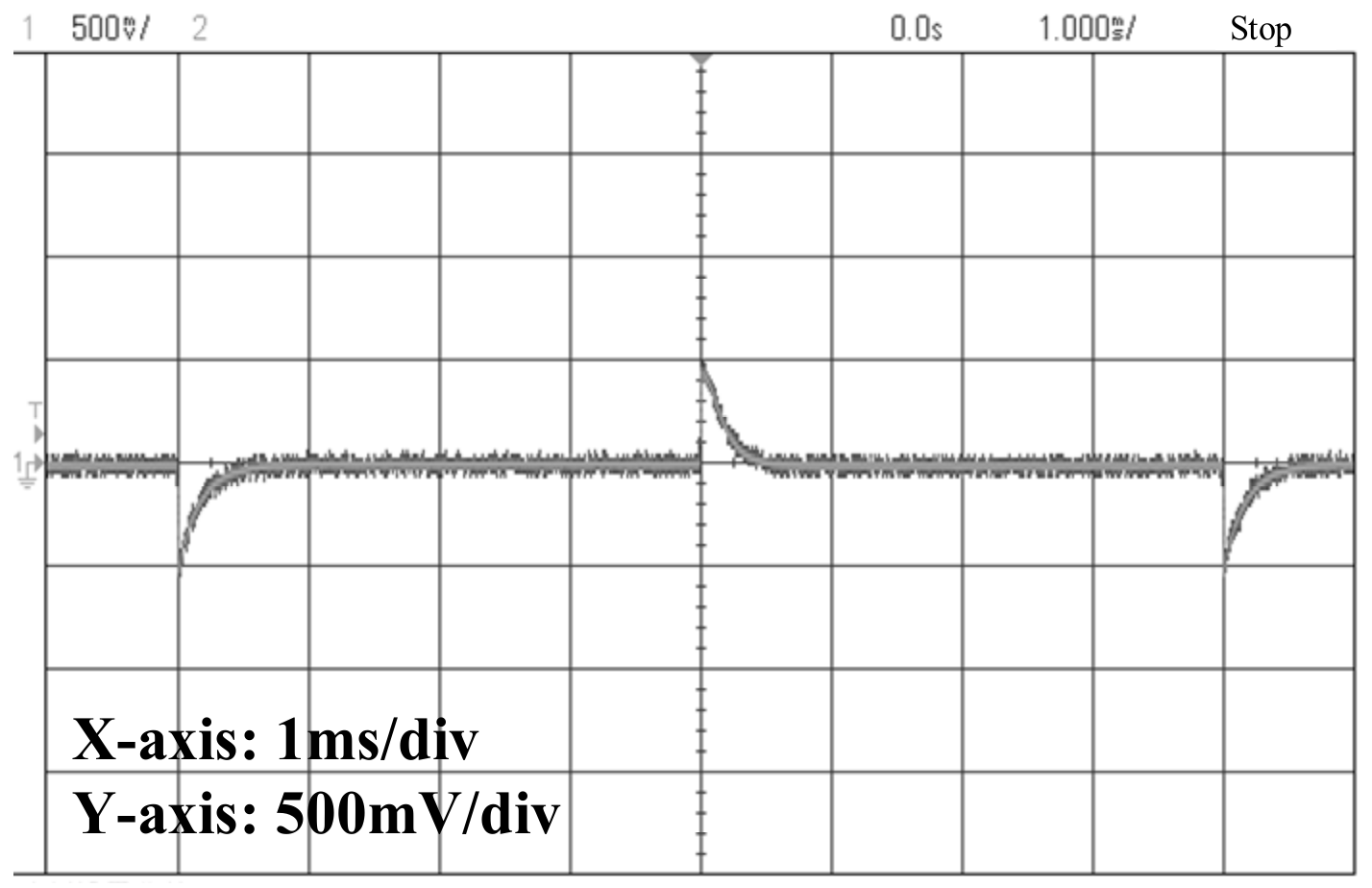
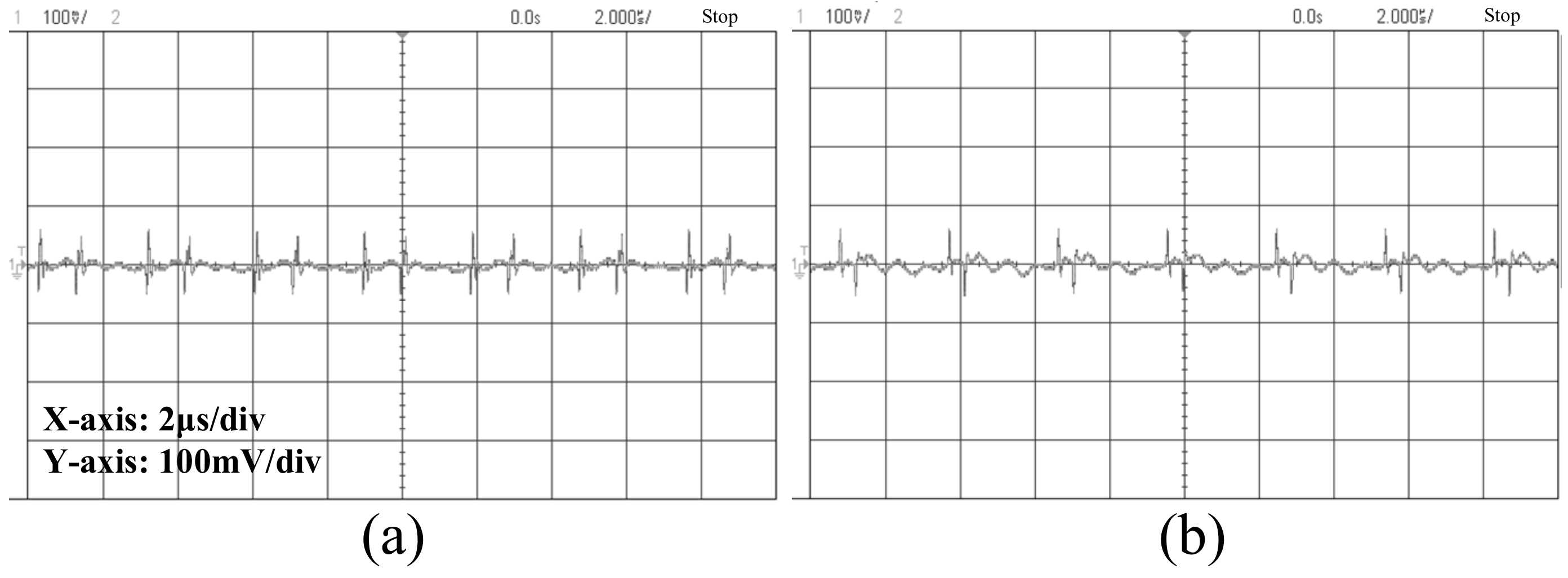
5.2. Transient, Ripple, and Regulation
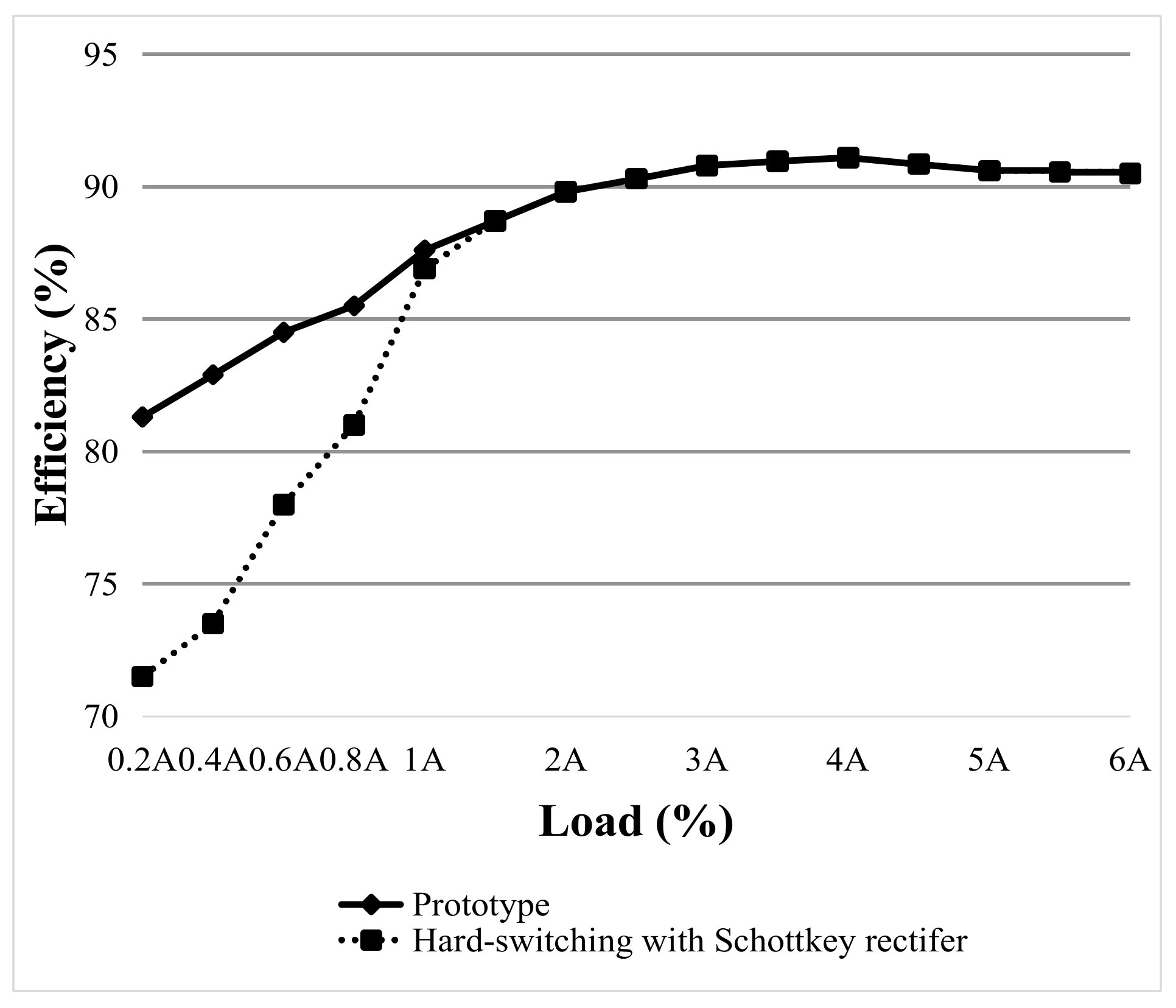
5.3. Efficiency Discussion and Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qahouq, J.A.; Abdel-Rahman, O.; Huang, L.; Batarseh, I. On Load Adaptive Control of Voltage Regulators for Power Managed Loads: Control Schemes to Improve Converter Efficiency and Performance. IEEE Trans. Power Electron. 2007, 22, 1806–1819. [Google Scholar] [CrossRef]
- Fu, D. Topology Investigation and System Optimization of Resonant Converters. Ph.D. Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 4 February 2010. [Google Scholar]
- ENERGY STAR Program Requirements for External Power Supplies (Version 2.0), U.S. Environmental Protection Agency. Available online: http://www.energystar.gov/ (accessed on 22 December 2022).
- Olivier, T.; Yue, W. A Survey of Light-Load Efficiency Improvement Techniques for Low-Power DC-DC Converters. In Proceedings of the International Conference on Power Electronics-ECCE Asia, Jeju, Republic of Korea, 30 May–3 June 2011. [Google Scholar]
- Jitaru, I. 99% efficiency DC-DC converter. In Proceedings of the IEEE International Telecom Energy Conference, Vancouver, BC, Canada, 28 September–2 October 2014. [Google Scholar]
- Zhou, X.W.; Donati, M. Improved Light-load Efficiency for Synchronous Rectifier Voltage Regulator Module. IEEE Trans. Power Electron. 2000, 15, 826–834. [Google Scholar] [CrossRef]
- Le, H.N.; Sato, D.; Orikawa, K.; Itoh, J.I. Efficiency Improvement at Light Load in Bidirectional DC-DC Converter by Utilizing Discontinuous Current Mode. In Proceedings of the European Conference on Power Electronics and Applications, Geneva, Switzerland, 8–10 September 2015. [Google Scholar]
- Geng, M.; Feng, Q. Design of A Synchronous Rectifier Controller for Limiting Reverse Current. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009. [Google Scholar]
- LT8311 Synchronous Rectifier Controller with Opto-Coupler Driver for Forward Converters, Analog Devices. Available online: https://www.analog.com/ (accessed on 20 December 2022).
- Chang, W.H.; Chen, Y.M.; Chen, C.J.; Wang, P.Y.; Lin, K.Y.; Lee, C.C.; Lo, L.D.; Lin, J.Y.; Yang, T.Y. Highly Integrated ZVS Flyback Converter ICs With Pulse Transformer to Optimize USB Power Delivery for Fast-Charging Mobile Devices. IEEE J. Solid-State Circuits 2020, 55, 3189–3199. [Google Scholar] [CrossRef]
- Vratislav, M. Inductor Current Zero-Crossing Detector and CCM/DCM Boundary Detector for Integrated High-Current Switched-Mode DC–DC Converters. IEEE Trans. Power Electron. 2014, 29, 5384–5391. [Google Scholar]
- Rodriguez, M.; Lamar, D.G. A Novel Adaptive Synchronous Rectification System for Low Output Voltage Isolated Converters. IEEE Trans. Ind. Electron. 2010, 58, 3511–3520. [Google Scholar] [CrossRef]
- UCC24636 Synchronous Rectifier (SR) Controller with Ultra-Low Standby Current, Texas Instruments. Available online: https://www.ti.com/ (accessed on 9 July 2022).
- XDPS21071 Forced Frequency Resonant Flyback Controller, Infineon Technologies. Available online: https://www.infineon.com/cms/en/ (accessed on 9 July 2022).
- Jitaru, I.; Savu, A.; Jitaru, B. Ideal Flyback Topology. In Proceedings of the International Exhibition and Conference for Power Electronics and Intelligent Motion, Nürnberg, Germany, 4–6 May 2021. [Google Scholar]
- Zhang, J.; Huang, X. A High Efficiency Flyback Converter With New Active Clamp Technique. IEEE Trans. Power Electron. 2010, 25, 1775–1785. [Google Scholar] [CrossRef]
- Tong, Q. A Soft-switching Step Down Converter for Point of Load Applications. In Proceedings of the IEEE International Conference on Electronics Technology, Chengdu, China, 8–12 May 2020. [Google Scholar]
- Ahn, M.; Park, J.H. An Optimal Control Method of Clamp Switch for ZVS Bi-directional DC-DC Converter. In Proceedings of the IEEE International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016. [Google Scholar]
- Knecht, O.; Bortis, D.; Kolar, J.W. ZVS Modulation Scheme for Reduced Complexity Clamp-Switch TCM DC-DC Boost Converter. IEEE Trans. Power Electron. 2018, 33, 4204–4214. [Google Scholar] [CrossRef]
- Ulrich, B. Analysis and Design of a ZVS Clamp-Switch SEPIC DC/DC Converter. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, New Orleans, LA, USA, 15–19 March 2020. [Google Scholar]
- Park, J.; Moon, Y.J.; Jeong, M.G.; Kang, J.G.; Kim, S.H.; Gong, J.C.; Yoo, C. Quasi-Resonant (QR) Controller with Adaptive Switching Frequency Reduction Scheme for Flyback Converter. IEEE Trans. Ind. Electron. 2016, 63, 3571–3581. [Google Scholar] [CrossRef]
- Khorasani, R.R.; Adib, E.; Farzanehfard, H. ZVT Resonant Core Reset Forward Converter With a Simple Auxiliary Circuit. IEEE Trans. Ind. Electron. 2018, 65, 242–250. [Google Scholar] [CrossRef]
- Soltanzadeh, K. Zero-current Transition Single-ended Forward Converter. IET Power Electron. 2020, 13, 1227–1235. [Google Scholar] [CrossRef]
- Chen, G.; Deng, Y.; Chen, L.; Hu, Y.; Jiang, L.; He, X.; Wang, Y. A Family of Zero-Voltage-Switching Magnetic Coupling Nonisolated Bidirectional DC–DC Converters. IEEE Trans. Ind. Electron. 2017, 64, 6223–6233. [Google Scholar] [CrossRef]





| Controller Type (Company) | Price (Source: DigiKey) | Released Year | Description |
|---|---|---|---|
| dsPIC33CK32MP502 (Microchip) | US$3.4 | 2018 | Twenty-Eight-Pin Digital Signal Controllers with High-Resolution PWM |
| LTC3726 (ADI) | US$5.8 | 2008 | Secondary-Side Synchronous Forward Controller |
| LTC3766 (ADI) | US$11 | 2016 | High Efficiency Secondary-Side Synchronous Forward Controller |
| SC4910A (Semtech) | US$2.5 | 2005 | Current-Mode PWM Controller with Complementary Output |
| Parameters | Value |
|---|---|
| Input voltage (Vi) | 20 V to 36 V (28 V typical) |
| Output voltage (VO) | 15 V |
| Maximum output power (PO) | 100 W |
| Switching frequency (fs) | 350 kHz |
| Transformer turns ratio (N) | 3:5 |
| Output inductance (LO) | 12 μH |
| Magnetizing inductance (Lm) | 33 μH |
| Output capacitance (CO) | 110 μF |
| Transformer leakage inductance (Lk) | 0.1 μH |
| Current transformer turns ratio (NS) | 100:1 |
| Sampling resistor (RS) | 22 Ω |
| Total Input Power (@ Load Current) | Power Board Loss | Control Board Loss | Total Efficiency |
|---|---|---|---|
| 3.7 W (0.2 A) | 0.4 W | 0.29 W | 81.3% |
| 7.3 W (0.4 A) | 0.94 W | 0.3 W | 82.9% |
| 10.7 W (0.6 A) | 1.34 W | 0.31 W | 84.5% |
| 14 W (0.8 A) | 1.73 W | 0.31 W | 85.5% |
| 17.1 W (1 A) | 1.81 W | 0.31 W | 87.6% |
| Author, Year | Topology | Additional Component Count | Light-Load Efficiency, (Load Range) | Maximum Output Power | Application Fields |
|---|---|---|---|---|---|
| This paper | SR forward | 0 | 81–87%, (0–20%) | 100 W | Industry, aerospace, military |
| [10], 2020 | Flyback | 0 | 82–88%, (0–30%) | 60 W | Fast-charging |
| [21], 2016 | Flyback | 0 | 84.9–87.4%, (8–25%) | 40 W | Fast-charging |
| [22], 2018 | Forward | >2, ZVT circuit | <86%, (<20%) | 150 W | Home appliances, industry |
| [23], 2020 | Forward | >3, ZCT circuit | <86%, (<20%) | 200 W | Medical, industry |
| [24], 2017 | Buck | >3, ZVS circuit | <91%, (<20%) | 500 W | Industry |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Wang, J.; Wang, K.; Long, B. New Fixed-Frequency Digital Control to Improve the Light-Load Efficiency of an Isolated Regulated Converter. Electronics 2023, 12, 575. https://doi.org/10.3390/electronics12030575
Ma C, Wang J, Wang K, Long B. New Fixed-Frequency Digital Control to Improve the Light-Load Efficiency of an Isolated Regulated Converter. Electronics. 2023; 12(3):575. https://doi.org/10.3390/electronics12030575
Chicago/Turabian StyleMa, Cong, Junfeng Wang, Kai Wang, and Baiguang Long. 2023. "New Fixed-Frequency Digital Control to Improve the Light-Load Efficiency of an Isolated Regulated Converter" Electronics 12, no. 3: 575. https://doi.org/10.3390/electronics12030575
APA StyleMa, C., Wang, J., Wang, K., & Long, B. (2023). New Fixed-Frequency Digital Control to Improve the Light-Load Efficiency of an Isolated Regulated Converter. Electronics, 12(3), 575. https://doi.org/10.3390/electronics12030575






