Agent-Based Models Assisted by Supervised Learning: A Proposal for Model Specification
Abstract
1. Introduction
2. Literature Review
2.1. Machine Learning in Agent-Based Modeling
2.2. Tax Evasion
3. Specification of Learning in Agent Based Modeling
3.1. Design of Agent-Based Models Assisted by Machine Learning
3.2. Validation and Analysis of Agent-Based Models Assisted by Machine Learning
3.3. Online Learning in ABM Assisted by Machine Learning
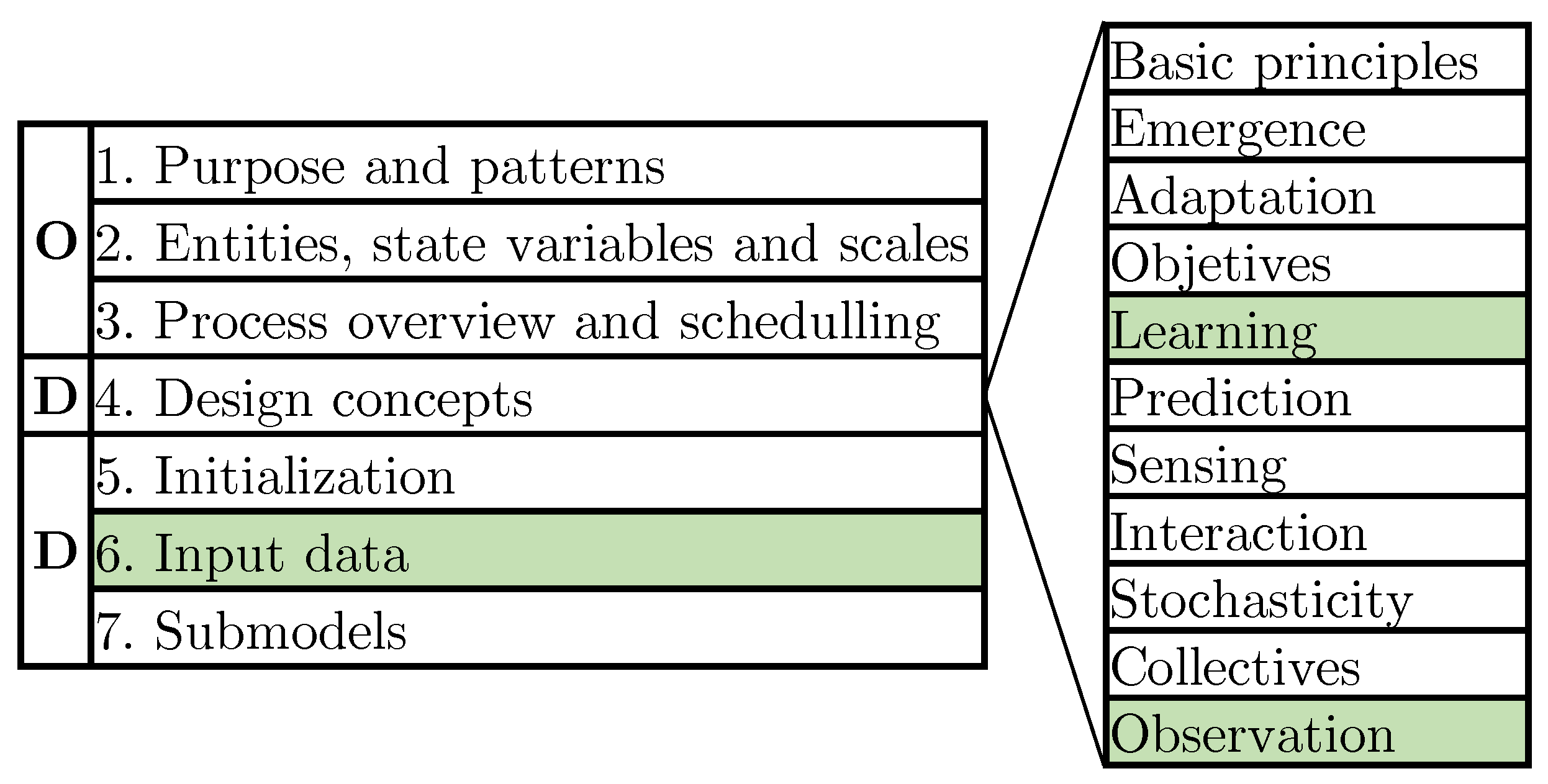
3.4. The Overview, Design Concepts and Details Protocol
- Overview.
- A general description of the model, including its purpose and its basic components, the agents and variables describing them and the environment, and the scales used in the model, e.g., time and space, as well as an overview of the processes and their scheduling.
- Design concepts.
- A brief description of the basic principles underlying the model’s design, e.g., rationality, emergence, adaptation, learning, etc.
- Details.
- Full definitions of the involved sub-models.
3.5. Proposal
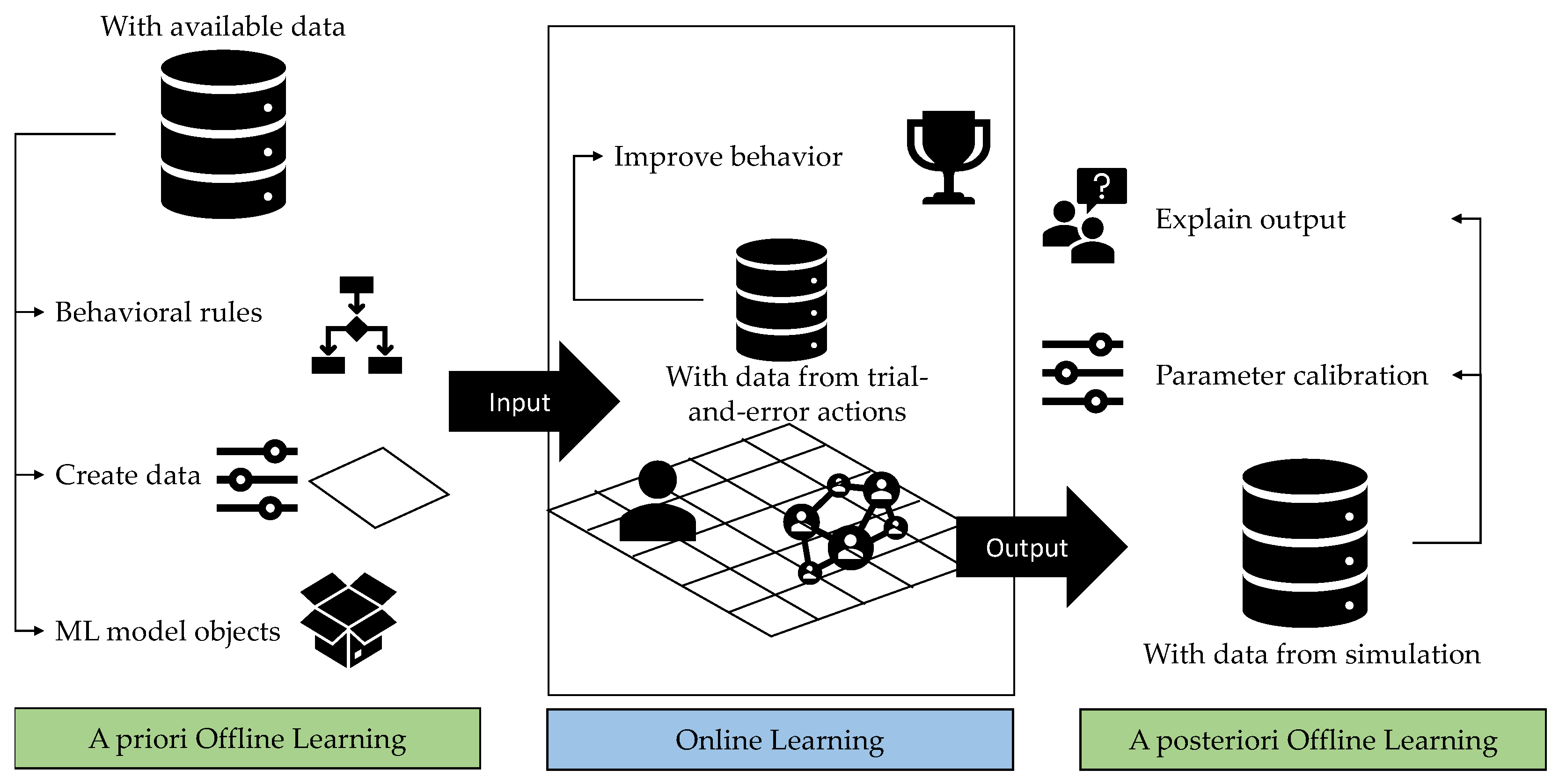
- What is the purpose of learning? Following the approach of the current ODD Protocol, as stated by Grimm et al. [13], a possible purpose of learning is to improve the performance of the agents during simulation based on their experience. Other equally valid purposes, as discussed above, include the following: generating data for simulations, inducing the rules defining the behavior of the agents from existing data, calibrating parameters of the model, and analyzing the results of the simulations.
- When is learning performed? According to its purpose, learning can take place at different moments. In the current ODD Protocol, learning is expected to occur during the simulation. It is also possible to learn before the simulation, to obtain models to generate synthetic data to be used during simulation, or the rules of the agents included in the ABM. It is also possible for the learning to occure after the simulation to calibrate parameters or to analyze the data produced by the simulation.
- What components of the ABM are affected by learning? In the current ODD Protocol, agents are the only components performing, and being affected by, learning. However, it is also possible that the environment exploits the use of ML methods, e.g., consuming synthetic data generated by learned models. It is also possible to learn the values of the parameters of the ABM to obtain some desired behavior of the whole system.
- How is learning computed? Finally, the type of algorithm used and its input data must be considered. Online learning requires incremental learning algorithms, such as those included in, but not limited to, RL. Supervised techniques can be used for offline learning, both before and after simulation. Evolutionary approaches are well suited for calibrating parameters. The preference for explainable methods versus black box techniques is also related to the purpose of learning.


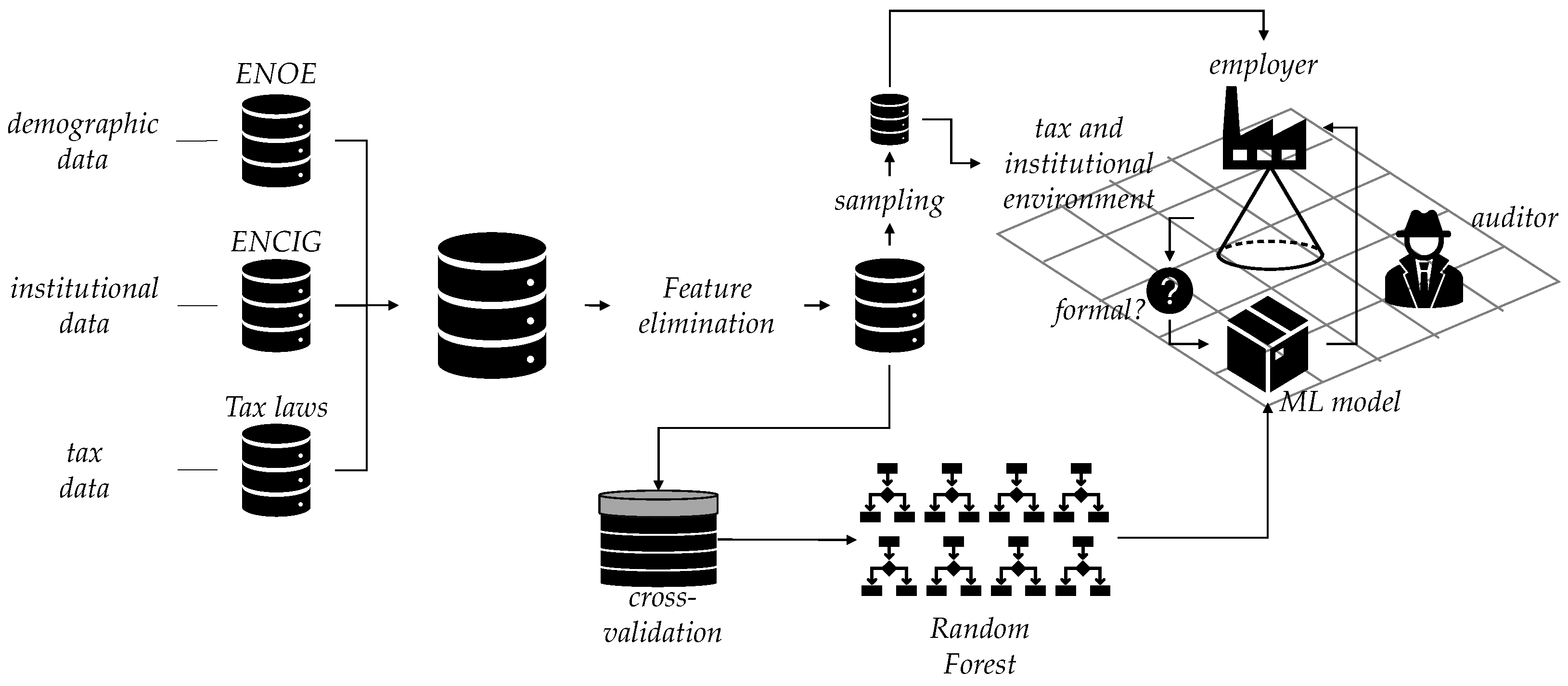
4. Case Study: The Payroll Tax Evasion Model
4.1. Overview
- Agents: Employers and tax authority.
- Environment: A Mexican state-level representation of the payroll tax system.
- Scales: Time is represented in discrete periods, each step representing a month, which corresponds to the tax collection period according to the current legislation. In order to have a margin of error less than 5% with a confidence interval of 99% in the selected sample, each employee agent in the model represents 2000 employers in the 2019 Mexican labor market.
- State variables: The attributes that characterize each agent are shown in Table 1 along with the method for initializing each variable.
- Employers decide in which market to, formally or informally, query a machine learning model.
- Informal employers are full evaders. Formal employers calculate the amount of taxes to report. If they calculate so as to report zero taxes, they also become full evaders. If they calculate to report all the tax, they become full taxpayers. In any other case, they become partial evaders.
- Tax authority collects the declared amount of taxes.
- The tax authority conducts audits on a random basis. If the audit is successful, then partial and full evaders must pay the evaded amount and a penalty for the undeclared amount.
- Every 12 months employers increase their age. With some probability, in each period, employers can die. If this happens, they are replaced by another employer with the same characteristics, except for age.
4.2. Design Concepts
4.3. Details
- After performing a pre-processing of the database, including a manual selection and a recursive feature elimination with resampling algorithm [97] available in R package “caret” [98], it was determined that the main variables that determined the employer’s sector were the size of the business (ambito2), education (anios_esc), economic activity (c_ocu11c), state (ent), size of the region (t_loc), and age (eda).
- A fast implementation of Random Forest in the R package “ranger” [99] was chosen to learn from data because it provides fast model fitting and evaluation, is robust to outliers, can deal with simple linear and complicated nonlinear associations, and produces competitive prediction accuracy [100]. To tune the hyperparameters and evaluate the performance of the model, cross-validation with folds was carried out. The final hyperparameter values were , , and . That setting provided an accuracy of 83.79%, which was considered good to avoid overfitting. The trained model was available to employers during the simulation.
- A Geographical Information System layer was loaded. Each polygon was a hexagonal tessellation of the corresponding Mexican state.
- employers were generated and initialized with information from the database and moved to their corresponding state.
- Auditors were generated and located in their assigned state.
- The a priori learned random forest model was loaded.
- Pareto-law values with the following distribution function were generated:
- Where was known as the Pareto exponent and estimated to be to characterize a capitalist economy [90].
- x are the values generated by a normal distribution function with a mean of 2 and a standard deviation of 0.2 for informal employers and 0.3 for formal ones.
- To assign a fixed monthly production value to each employer. Generated power law values were multiplied by 23 in the case of informal employers and 50 for the formal. Those quantities generated a perfectly mixed Pareto distribution according to the basic principles and preserved the participation of the informal economy in Mexican Gross Domestic Product (GDP) [101].
- For simplicity, it was assumed that each employer allocated 30 percent of the value of production to payroll W. The share of wages in Mexican GDP was between 30 and 40% [102].
- At the beginning of the simulation, it was assumed that non-informal employers declared all the tax, i.e., declared payroll .
- At the beginning declared tax by each employer was equal to the declared payroll multiplied by the tax rate in the employer’s state.
- Every 12 periods (months) employers increased their age, and they consulted the learned model to decide whether to opt for the formal or informal market, taking their internal attributes and perceived insecurity as a reference.
- Informal employers did not declare taxes.
- By social norm [26], employers modified their risk aversion according to their age, as follows:
- Let the perceived public goods efficiency, and the penalty rate.
- Let and the effectiveness of audit process and tax collection, respectively.
- Let the true audit probability and the subjective audit probability known to the employer.
- Let , the updating parameter for .
- If an employer was audited in a specific period, subjective audit probability became 1.
- In each period (if not audited again) decreased in amount until .
- In each period, employers calculated the amount of taxes to declare voluntarily , applying the expected utility maximization procedure adopted by Allingham and Sandmo [20]. Let lower bound be:
- And the upper bound be:
- If the subjective audit probability exceeded the upper limit in submodel 22, the employer became fully tax compliant, that is, , and when fell below the lower bound in submodel 21, the employer fully evaded, that is .
- For in the range for an inner solution, the employer voluntarily declared:
- The tax authority collected payroll taxes that employers voluntarily declared.
- The tax authority carried out audits with a random probability of and a level of effectiveness .
- If an evader was detected the undeclared tax was collected and a penalty rate applied over the undeclared tax.
- In each period, employers had a probability of dying, following a Weibull quantile derivation function:
- Where and are the scale and shape parameters, respectively.
- It was assumed that, when an employer died, someone else took their place with the same attributes, except for age, which was generated according to:
- At each time t, the observed output Extent of Tax Evasion (ETE) was calculated as follows:
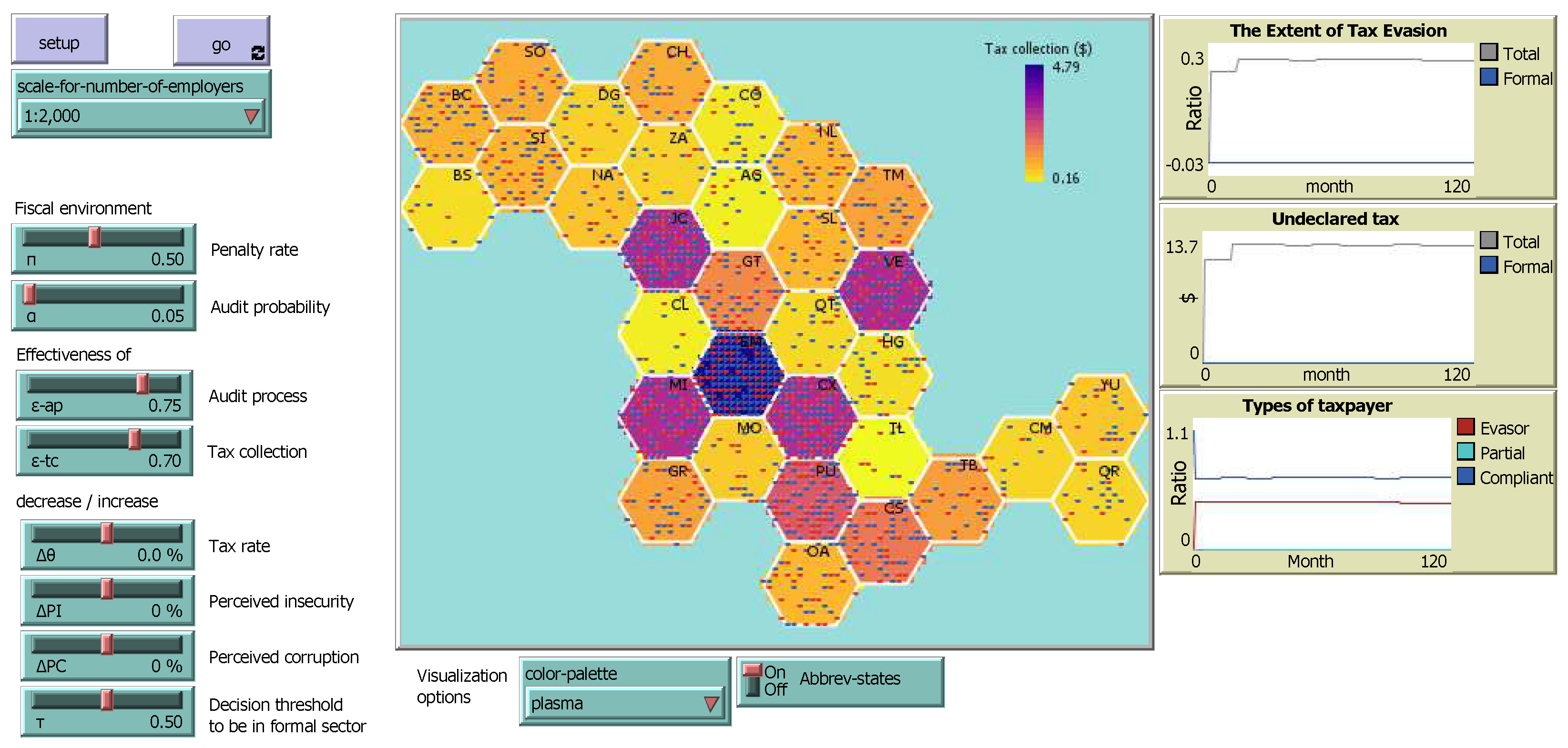
5. Results
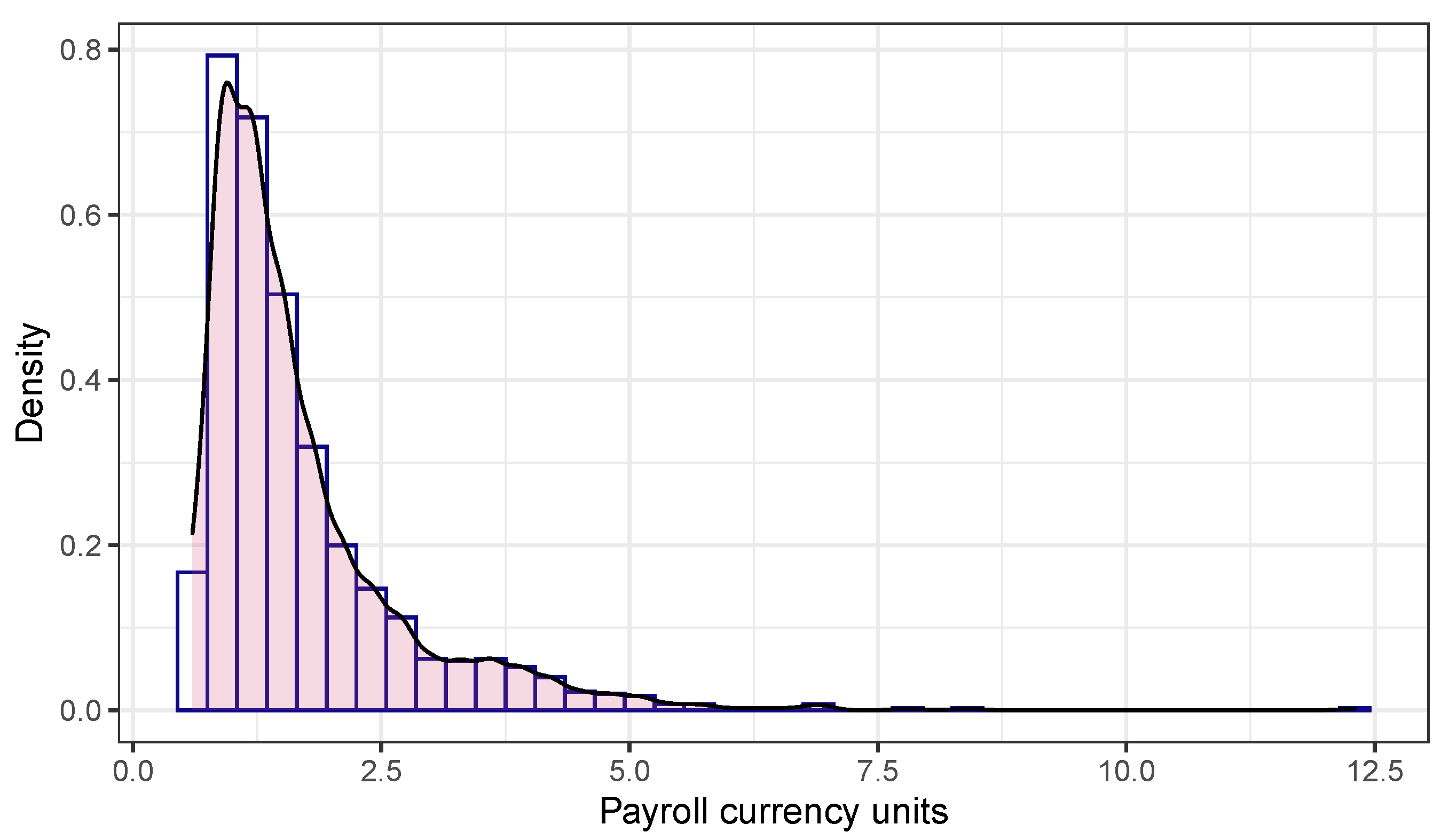
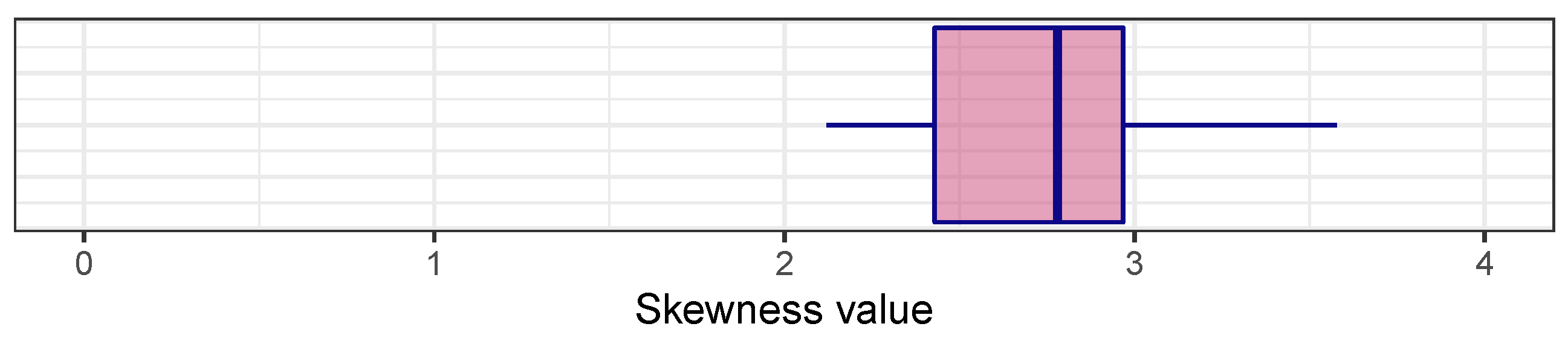
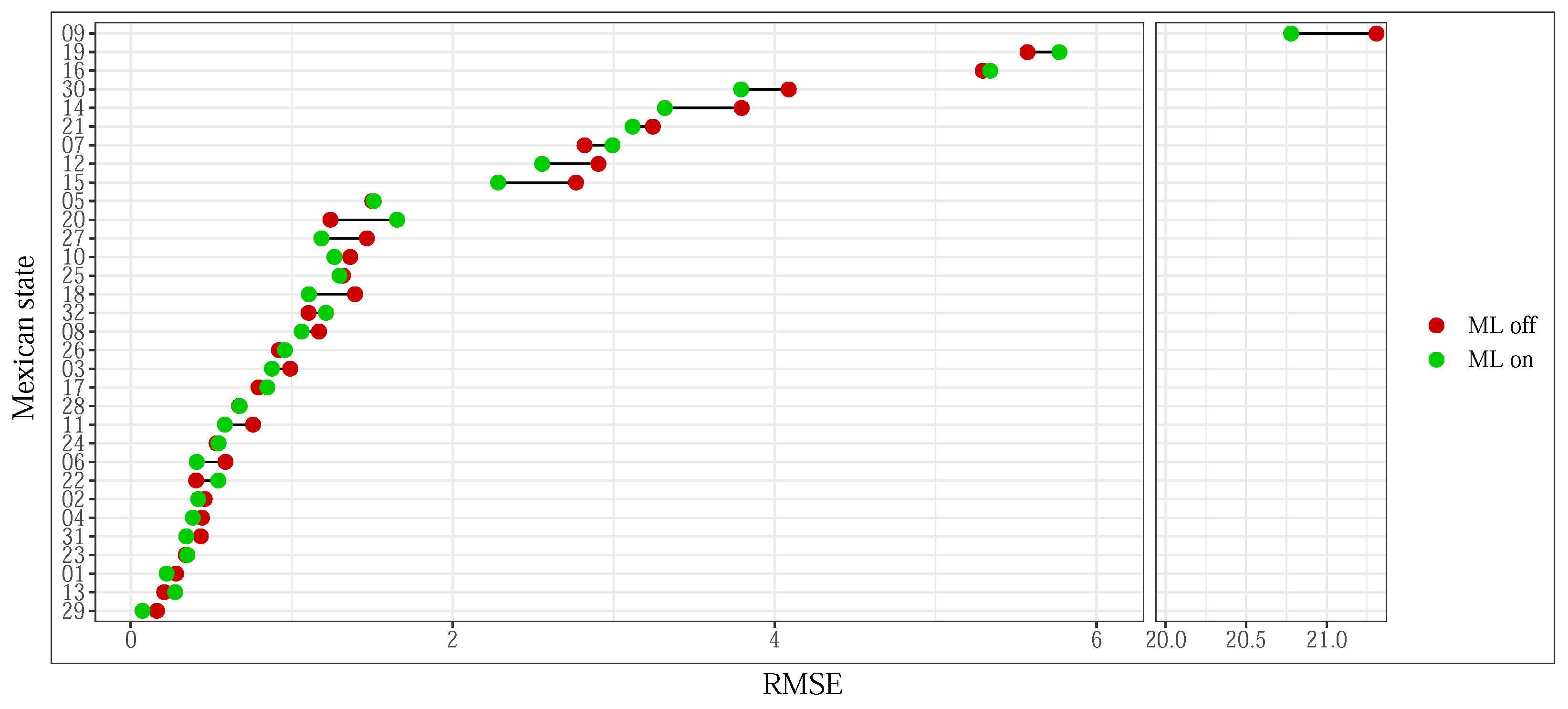
5.1. Validation
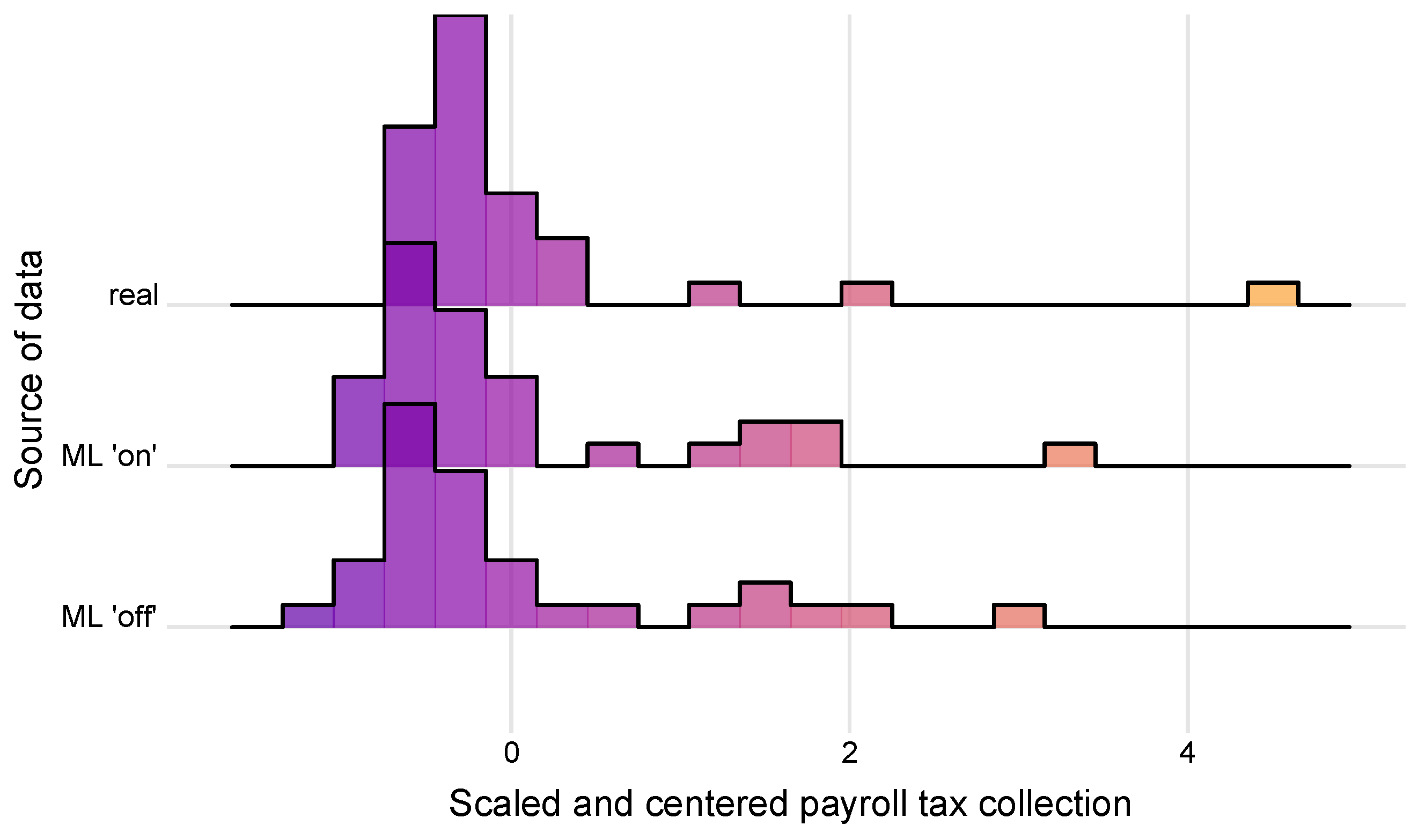
5.2. The Effect of Machine Learning in Simulation
6. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| ABM | Agent-Based Model |
| ODD | Overview, Design concepts, Details |
| RL | Reinforcement Learning |
| ANN | Artificial Neural Network |
| GDP | Gross Domestic Product |
| ETE | Extent of Tax Evasion |
References
- Schwarz, C.V.; Reiser, B.J.; Davis, E.A.; Kenyon, L.; Achér, A.; Fortus, D.; Shwartz, Y.; Hug, B.; Krajcik, J. Developing a learning progression for scientific modeling: Making scientific modeling accessible and meaningful for learners. J. Res. Sci. Teach. 2009, 46, 632–654. [Google Scholar] [CrossRef]
- Gilbert, N. Agent-Based Models; SAGE Publications, Inc.: Newbury Park, CA, USA, 2020. [Google Scholar] [CrossRef]
- Russell, S.; Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson series in artificial intelligence; Pearson: New York, NY, USA, 2020. [Google Scholar]
- Ghaffarian, S.; Roy, D.; Filatova, T.; Kerle, N. Agent-based modelling of post-disaster recovery with remote sensing data. Int. J. Disaster Risk Reduct. 2021, 60, 102285. [Google Scholar] [CrossRef]
- Yao, F.; Zhu, J.; Yu, J.; Chen, C.; Chen, X. Hybrid operations of human driving vehicles and automated vehicles with data-driven agent-based simulation. Transp. Res. Part D Transp. Environ. 2020, 86, 102469. [Google Scholar] [CrossRef]
- Augustijn, E.W.; Abdulkareem, S.; Sadiq, M.; Albabawat, A. Machine Learning to Derive Complex Behaviour in Agent-Based Modellzing. In Proceedings of the 2020 International Conference on Computer Science and Software Engineering (CSASE), Duhok, Iraq, 16–18 April 2020; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2020; pp. 284–289. [Google Scholar] [CrossRef]
- Chu, Z.; Yang, B.; Ha, C.; Ahn, K. Modeling GDP fluctuations with agent-based model. Phys. A Stat. Mech. Its Appl. 2018, 503, 572–581. [Google Scholar] [CrossRef]
- Lamperti, F.; Roventini, A.; Sani, A. Agent-based model calibration using machine learning surrogates. J. Econ. Dyn. Control 2018, 90, 366–389. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z.; Zhang, Y. Validation and Calibration of an Agent-Based Model: A Surrogate Approach. Discret. Dyn. Nat. Soc. 2020, 2020, 6946370. [Google Scholar] [CrossRef]
- Lakić, E.; Artač, G.; Gubina, A. Agent-based modeling of the demand-side system reserve provision. Electr. Power Syst. Res. 2015, 124, 85–91. [Google Scholar] [CrossRef]
- Jalalimanesh, A.; Shahabi Haghighi, H.; Ahmadi, A.; Soltani, M. Simulation-based optimization of radiotherapy: Agent-based modeling and reinforcement learning. Math. Comput. Simul. 2017, 133, 235–248. [Google Scholar] [CrossRef]
- Jalalimanesh, A.; Haghighi, H.; Ahmadi, A.; Hejazian, H.; Soltani, M. Multi-objective optimization of radiotherapy: Distributed Q-learning and agent-based simulation. J. Exp. Theor. Artif. Intell. 2017, 29, 1071–1086. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; DeAngelis, D.L.; Polhill, J.G.; Giske, J.; Railsback, S.F. The ODD protocol: A review and first update. Ecol. Model. 2010, 221, 2760–2768. [Google Scholar] [CrossRef]
- Grimm, V.; Railsback, S.F.; Vincenot, C.E.; Berger, U.; Gallagher, C.; DeAngelis, D.L.; Edmonds, B.; Ge, J.; Giske, J.; Groeneveld, J.; et al. The ODD Protocol for Describing Agent-Based and Other Simulation Models: A Second Update to Improve Clarity, Replication, and Structural Realism. J. Artif. Soc. Soc. Simul. 2020, 23, 7. [Google Scholar] [CrossRef]
- Müller, B.; Bohn, F.; Dreßler, G.; Groeneveld, J.; Klassert, C.; Martin, R.; Schlüter, M.; Schulze, J.; Weise, H.; Schwarz, N. Describing human decisions in agent-based models − ODD + D, an extension of the ODD protocol. Environ. Model. Softw. 2013, 48, 37–48. [Google Scholar] [CrossRef]
- Elbattah, M.; Molloy, O. ML-Aided Simulation. In Proceedings of the 2018 ACM SIGSIM Conference on Principles of Advanced Discrete Simulation, Rome, Italy, 23–25 May 2018; ACM: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Elbattah, M. How can Machine Learning Support the Practice of Modeling and Simulation?—A Review and Directions for Future Research. In Proceedings of the 2019 IEEE/ACM 23rd International Symposium on Distributed Simulation and Real Time Applications (DS-RT), Cosenza, Italy, 7–9 October 2019. [Google Scholar] [CrossRef]
- Zhang, W.; Valencia, A.; Chang, N.B. Synergistic Integration Between Machine Learning and Agent-Based Modeling: A Multidisciplinary Review. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–21. [Google Scholar] [CrossRef]
- Alm, J. Measuring, explaining, and controlling tax evasion: Lessons from theory, experiments, and field studies. Int. Tax Public Financ. 2011, 19, 54–77. [Google Scholar] [CrossRef]
- Allingham, M.G.; Sandmo, A. Income tax evasion: A theoretical analysis. J. Public Econ. 1972, 1, 323–338. [Google Scholar] [CrossRef]
- Becker, G.S. Crime and Punishment: An Economic Approach. J. Political Econ. 1968, 76, 169–217. [Google Scholar] [CrossRef]
- Slemrod, J.; Yitzhaki, S. Tax Avoidance, Evasion, and Administration. In Handbook of Public Economics; Elsevier: Amsterdam, The Netherlands, 2002; pp. 1423–1470. [Google Scholar] [CrossRef]
- Daude, C.; Gutiérrez, H.; Melguizo, Á. What Drives Tax Morale? 2012. Available online: https://www.oecd-ilibrary.org/development/what-drives-tax-morale_5k8zk8m61kzq-en (accessed on 2 June 2022).
- Mittone, L.; Patelli, P. Imitative Behaviour in Tax Evasion. In Advances in Computational Economics; Springer: New York, NY, USA, 2000; pp. 133–158. [Google Scholar] [CrossRef]
- Davis, J.S.; Hecht, G.; Perkins, J.D. Social Behaviors, Enforcement, and Tax Compliance Dynamics. Account. Rev. 2003, 78, 39–69. [Google Scholar] [CrossRef]
- Hokamp, S. Dynamics of tax evasion with back auditing, social norm updating, and public goods provision—An agent-based simulation. J. Econ. Psychol. 2014, 40, 187–199. [Google Scholar] [CrossRef]
- Charteris, P.; Golden, B.; Garrick, D.J. Livestock breeding industries as complex adaptive systems. In Proceedings of the Conference of the Association for the Advancement of Animal Breeding and Genetics, Townsville, Australia, 26–28 July 2001; Volume 14, pp. 461–464. [Google Scholar]
- Breckling, B. Individual-Based Modelling Potentials and Limitations. Sci. World J. 2002, 2, 1044–1062. [Google Scholar] [CrossRef]
- Ligmann, A.; Sun, L. Applying time-dependent variance-based global sensitivity analysis to represent the dynamics of an agent-based model of land use change. Int. J. Geogr. Inf. Sci. 2010, 24, 1829–1850. [Google Scholar] [CrossRef]
- Malleson, N.; Heppenstall, A.; See, L. Crime reduction through simulation: An agent-based model of burglary. Comput. Environ. Urban Syst. 2010, 34, 236–250. [Google Scholar] [CrossRef]
- Lengnick, M. Agent-based macroeconomics: A baseline model. J. Econ. Behav. Organ. 2013, 86, 102–120. [Google Scholar] [CrossRef]
- Conte, R.; Paolucci, M. On agent-based modeling and computational social science. Front. Psychol. 2014, 5, 668. [Google Scholar] [CrossRef]
- Ghorbani, A.; Dechesne, F.; Dignum, V.; Jonker, C. Enhancing ABM into an Inevitable Tool for Policy Analysis. J. Policy Complex Syst. 2014, 1, 61–76. [Google Scholar] [CrossRef]
- Siegfried, R. Modeling and Simulation of Complex Systems; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2014. [Google Scholar] [CrossRef]
- Tarvid, A. Complex Adaptive Systems and Agent-Based Modelling. In Agent-Based Modelling of Social Networks in Labour–Education Market System; Springer: Cham, Switzerland, 2016; pp. 23–38. [Google Scholar] [CrossRef]
- Li, X.; Mao, W.; Zeng, D.; Wang, F.Y. Agent-Based Social Simulation and Modeling in Social Computing. In Intelligence and Security Informatics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 401–412. [Google Scholar] [CrossRef]
- Baldwin, W.C.; Sauser, B.; Cloutier, R. Simulation Approaches for System of Systems: Events-based versus Agent Based Modeling. Procedia Comput. Sci. 2015, 44, 363–372. [Google Scholar] [CrossRef]
- Lee, J.S.; Filatova, T.; Ligmann-Zielinska, A.; Hassani-Mahmooei, B.; Stonedahl, F.; Lorscheid, I.; Voinov, A.; Polhill, J.G.; Sun, Z.; Parker, D.C. The Complexities of Agent-Based Modeling Output Analysis. J. Artif. Soc. Soc. Simul. 2015, 18, 4. [Google Scholar] [CrossRef]
- Axtell, R.L. Why Agents? On the Varied Motivations for Agent Computing in the Social Sciences. In Workshop on Agent Simulation: Applications, Models, and Tools; 2000; Available online: http://www.brook.edu/dybdocroot/es/dynamics/papers/agents/agents.htm (accessed on 2 June 2022).
- Nourqolipour, R.; Shariff, R. How agent based modeling (ABM) can be linked to GIS for modelling land use and land cover change. In Proceedings of the MRSS 6th International Remote Sensing and GIS Conference and Exhibition, Kuala Lumpur, Malaysia, 28–29 April 2010. [Google Scholar]
- Rand, W.; Rust, R.T. Agent-based modeling in marketing: Guidelines for rigor. Int. J. Res. Mark. 2011, 28, 181–193. [Google Scholar] [CrossRef]
- Miller, M.Z.; Griendling, K.; Mavris, D.N. Exploring human factors effects in the Smart Grid system of systems Demand Response. In Proceedings of the 2012 7th International Conference on System of Systems Engineering (SoSE), Genova, Italy, 16–19 July 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Kostadinov, F.; Holm, S.; Steubing, B.; Thees, O.; Lemm, R. Simulation of a Swiss wood fuel and roundwood market: An explorative study in agent-based modeling. For. Policy Econ. 2014, 38, 105–118. [Google Scholar] [CrossRef]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Broniec, W.; An, S.; Rugarber, S.; Goel, A.K. Guiding Parameter Estimation of Agent-Based Modeling through Knowledge-based Function Approximation. In Proceedings of the AAAI 2021 Spring Symposium on Combining Machine Learning and Knowledge Engineering (AAAI-MAKE 2021), Palo Alto, CA, USA, 22–24 March 2021. [Google Scholar]
- Tesfatsion, L. Agent-Based Computational Economics: Growing Economies From the Bottom Up. Artif. Life 2002, 8, 55–82. [Google Scholar] [CrossRef]
- Wang, C.; Hu, M.; Yang, L.; Zhao, Z. Prediction of air traffic delays: An agent-based model introducing refined parameter estimation methods. PLoS ONE 2021, 16, e0249754. [Google Scholar] [CrossRef]
- Saeedi, S. Integrating macro and micro scale approaches in the agent-based modeling of residential dynamics. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 214–229. [Google Scholar] [CrossRef]
- Sánchez-Maroño, N.; Alonso-Betanzos, A.; Fontenla-Romero, O.; Polhill, J.; Craig, T. Empirically-derived behavioral rules in agent-based models using decision trees learned from questionnaire data. In Understanding Complex Systems; Springer: Cham, Switzerland, 2017; pp. 53–76. [Google Scholar] [CrossRef]
- Pouladi, P.; Afshar, A.; Molajou, A.; Afshar, M. Socio-hydrological framework for investigating farmers’ activities affecting the shrinkage of Urmia Lake; hybrid data mining and agent-based modelling. Hydrol. Sci. J. 2020, 65, 1249–1261. [Google Scholar] [CrossRef]
- Jäger, G. Replacing rules by neural networks a framework for agent-based modelling. Big Data Cogn. Comput. 2019, 3, 51. [Google Scholar] [CrossRef]
- Romero-Mujalli, D.; Cappelletto, J.; Herrera, E.; Tárano, Z. The effect of social learning in a small population facing environmental change: An agent-based simulation. J. Ethol. 2017, 35, 61–73. [Google Scholar] [CrossRef]
- Wolf, I.; Schröder, T.; Neumann, J.; de Haan, G. Changing minds about electric cars: An empirically grounded agent-based modeling approach. Technol. Forecast. Soc. Chang. 2015, 94, 269–285. [Google Scholar] [CrossRef]
- van der Hoog, S. Surrogate Modelling in (and of) Agent-Based Models: A Prospectus. Comput. Econ. 2019, 53, 1245–1263. [Google Scholar] [CrossRef]
- Neri, F. Combining machine learning and agent based modeling for gold price prediction. Commun. Comput. Inf. Sci. 2019, 900, 91–100. [Google Scholar] [CrossRef]
- Cockrell, C.; An, G. Utilizing the Heterogeneity of Clinical Data for Model Refinement and Rule Discovery Through the Application of Genetic Algorithms to Calibrate a High-Dimensional Agent-Based Model of Systemic Inflammation. Front. Physiol. 2021, 12, 726. [Google Scholar] [CrossRef]
- Ye, P.; Chen, Y.; Zhu, F.; Lv, Y.; Lu, W.; Wang, F. Bridging the Micro and Macro: Calibration of Agent-Based Model Using Mean-Field Dynamics. IEEE Trans. Cybern. 2021, 52, 11397–11406. [Google Scholar] [CrossRef]
- Kim, D.; Yun, T.S.; Moon, I.C.; Bae, J. Automatic calibration of dynamic and heterogeneous parameters in agent-based models. Auton. Agents Multi-Agent Syst. 2021, 35, 1–66. [Google Scholar] [CrossRef]
- Rajabi, M.; Pilesjö, P.; Shirzadi, M.; Fadaei, R.; Mansourian, A. A spatially explicit agent-based modeling approach for the spread of Cutaneous Leishmaniasis disease in central Iran, Isfahan. Environ. Model. Softw. 2016, 82, 330–346. [Google Scholar] [CrossRef]
- Hayashi, S.; Prasasti, N.; Kanamori, K.; Ohwada, H. Improving behavior prediction accuracy by using machine learning for agent-based simulation. Lect. Notes Comput. Sci. (Incl. Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinform.) 2016, 9621, 280–289. [Google Scholar] [CrossRef]
- Vahdati, A.R.; Weissmann, J.; Timmermann, A.; Ponce de León, M.; Zollikofer, C. Drivers of Late Pleistocene human survival and dispersal: An agent-based modeling and machine learning approach. Quat. Sci. Rev. 2019, 221, 105867. [Google Scholar] [CrossRef]
- Ozik, J.; Collier, N.; Wozniak, J.; Macal, C.; An, G. Extreme-scale dynamic exploration of a distributed agent-based model with the EMEWS framework. IEEE Trans. Comput. Soc. Syst. 2018, 5, 884–895. [Google Scholar] [CrossRef]
- Chen, S.; Londoño-Larrea, P.; McGough, A.; Bible, A.; Gunaratne, C.; Araujo-Granda, P.; Morrell-Falvey, J.; Bhowmik, D.; Fuentes-Cabrera, M. Application of Machine Learning Techniques to an Agent-Based Model of Pantoea. Front. Microbiol. 2021, 12, 2638. [Google Scholar] [CrossRef]
- Perry, G.; O’Sullivan, D. Identifying Narrative Descriptions in Agent-Based Models Representing Past Human-Environment Interactions. J. Archaeol. Method Theory 2018, 25, 795–817. [Google Scholar] [CrossRef]
- Garg, A.; Yuen, S.; Seekhao, N.; Yu, G.; Karwowski, J.; Powell, M.; Sakata, J.; Mongeau, L.; JaJa, J.; Li-Jessen, N. Towards a physiological scale of vocal fold agent-based models of surgical injury and repair: Sensitivity analysis, calibration and verification. Appl. Sci. 2019, 9, 2974. [Google Scholar] [CrossRef]
- Edali, M.; Yücel, G. Exploring the behavior space of agent-based simulation models using random forest metamodels and sequential sampling. Simul. Model. Pract. Theory 2019, 92, 62–81. [Google Scholar] [CrossRef]
- Gursoy, F.; Badur, B. An Agent-Based Modeling Approach to Brain Drain. IEEE Trans. Comput. Soc. Syst. 2021, 9, 356–365. [Google Scholar] [CrossRef]
- Xu, T.; Gao, J.; Coco, G.; Wang, S. Urban expansion in Auckland, New Zealand: A GIS simulation via an intelligent self-adapting multiscale agent-based model. Int. J. Geogr. Inf. Sci. 2020, 34, 2136–2159. [Google Scholar] [CrossRef]
- Xiao, S.; Liu, R. Studies of covid-19 outbreak control using agent-based modeling. Complex Syst. 2021, 30, 297–321. [Google Scholar] [CrossRef]
- Zhang, Y.; Grignard, A.; Lyons, K.; Aubuchon, A.; Larson, K. Real-time machine learning prediction of an agent-based model for urban decision-making (extended abstract). In Proceedings of the AAMAS International Foundation for Autonomous Agents and Multiagent Systems (IFAAMAS), Stockholm, Sweden, 10–15 July 2018; Volume 3, pp. 2171–2173. [Google Scholar]
- Ten Broeke, G.; van Voorn, G.; Ligtenberg, A.; Molenaar, J. The Use of Surrogate Models to Analyse Agent-Based Models. J. Artif. Soc. Soc. Simul. 2021, 24, 3. [Google Scholar] [CrossRef]
- Janssen, S.; Sharpanskykh, A.; Curran, R.; Langendoen, K. Using causal discovery to analyze emergence in agent-based models. Simul. Model. Pract. Theory 2019, 96, 101940. [Google Scholar] [CrossRef]
- Nunes, A.; Zwick, M.; Wakeland, W. Sensitivity analysis of an agent-based simulation model using reconstructability analysis. Int. J. Gen. Syst. 2021, 50, 319–338. [Google Scholar] [CrossRef]
- Koda, H.; Arai, Z.; Matsuda, I. Agent-based simulation for reconstructing social structure by observing collective movements with special reference to single-file movement. PLoS ONE 2020, 15, e0243173. [Google Scholar] [CrossRef]
- Esmaeili Aliabadi, D.; Kaya, M.; Sahin, G. Competition, risk and learning in electricity markets: An agent-based simulation study. Appl. Energy 2017, 195, 1000–1011. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Hashem Nehrir, M.; Sheppard, J.; Kelly, N. Agent-Based Modeling of Retail Electrical Energy Markets with Demand Response. IEEE Trans. Smart Grid 2018, 9, 3465–3475. [Google Scholar] [CrossRef]
- Aghaie, A.; Heidary, M. Simulation-based optimization of a stochastic supply chain considering supplier disruption: Agent-based modeling and reinforcement learning. Sci. Iran. 2019, 26, 3780–3795. [Google Scholar] [CrossRef]
- Ibrahim, M.; Hashmi, U.; Nabeel, M.; Imran, A.; Ekin, S. Embracing Complexity: Agent-based Modeling for HetNets Design and Optimization via Concurrent Reinforcement Learning Algorithms. IEEE Trans. Netw. Serv. Manag. 2021, 18, 4042–4062. [Google Scholar] [CrossRef]
- Schauder, S.; Thomsen, M.; Nayga, R., Jr. Agent-based modeling insights into the optimal distribution of the Fresh Fruit and Vegetable Program. Prev. Med. Rep. 2020, 20, 101173. [Google Scholar] [CrossRef]
- Harati, S.; Perez, L.; Molowny-Horas, R. Promoting the emergence of behavior norms in a principal–agent problem—An agent-based modeling approach using reinforcement learning. Appl. Sci. 2021, 11, 8368. [Google Scholar] [CrossRef]
- Liang, Y.; Guo, C.; Ding, Z.; Hua, H. Agent-Based Modeling in Electricity Market Using Deep Deterministic Policy Gradient Algorithm. IEEE Trans. Power Syst. 2020, 35, 4180–4192. [Google Scholar] [CrossRef]
- Sert, E.; Bar-Yam, Y.; Morales, A. Segregation dynamics with reinforcement learning and agent based modeling. Sci. Rep. 2020, 10, 11771. [Google Scholar] [CrossRef]
- Jäger, G. Using Neural Networks for a Universal Framework for Agent-based Models. Math. Comput. Model. Dyn. Syst. 2021, 27, 162–178. [Google Scholar] [CrossRef]
- Salle, I. Modeling expectations in agent-based models - An application to central bank’s communication and monetary policy. Econ. Model. 2015, 46, 130–141. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, M.; Sheppard, J.; Kelly, N. Agent-Based Modeling in Electrical Energy Markets Using Dynamic Bayesian Networks. IEEE Trans. Power Syst. 2016, 31, 4744–4754. [Google Scholar] [CrossRef]
- Norman, M.; Koehler, M.; Kutarnia, J.; Silvey, P.; Tolk, A.; Tracy, B. Applying Complexity Science with Machine Learning, Agent-Based Models, and Game Engines: Towards Embodied Complex Systems Engineering. In Proceedings of the Unifying Themes in Complex Systems IX; Springer: Berlin/Heidelberg, Germany, 2018; pp. 173–183. [Google Scholar] [CrossRef]
- Fuller, D.; de Arruda, E.; Ferreira Filho, V. Learning-agent-based simulation for queue network systems. J. Oper. Res. Soc. 2020, 71, 1723–1739. [Google Scholar] [CrossRef]
- Cummings, P.; Crooks, A. Development of a Hybrid Machine Learning Agent Based Model for Optimization and Interpretability. In International Conference on Social Computing, Behavioral-Cultural Modeling and Prediction and Behavior Representation in Modeling and Simulation; Springer: Cham, Switzerland, 2020; pp. 151–160. [Google Scholar] [CrossRef]
- Grimm, V.; Berger, U.; Bastiansen, F.; Eliassen, S.; Ginot, V.; Giske, J.; Goss-Custard, J.; Grand, T.; Heinz, S.K.; Huse, G.; et al. A standard protocol for describing individual-based and agent-based models. Ecol. Model. 2006, 198, 115–126. [Google Scholar] [CrossRef]
- Chakraborti, A.; Patriarca, M. Gamma-distribution and wealth inequality. Pramana 2008, 71, 233–243. [Google Scholar] [CrossRef]
- Pinder, J.E.; Wiener, J.G.; Smith, M.H. The Weibull Distribution: A New Method of Summarizing Survivorship Data. Ecology 1978, 59, 175–179. [Google Scholar] [CrossRef]
- CONAPO. Datos Abiertos. Indicadores Demográficos 1950–2050. 2018. Available online: http://www.conapo.gob.mx/work/models/CONAPO/Datos_Abiertos/Proyecciones2018/ind_dem_proyecciones.csv (accessed on 21 October 2021).
- INEGI. Encuesta Nacional de Ocupación y Empleo (ENOE). 2019. Available online: https://www.inegi.org.mx/programas/enoe/15ymas/ (accessed on 27 September 2020).
- Bonet, J.A.; Rueda, F. Esfuerzo Fiscal en los Estados Mexicanos; IDB Publications (Working Papers) 3946; Inter-American Development Bank: Washington, DC, USA, 2012. [Google Scholar]
- Witten, I.; Frank, E.; Hall, M.; Pal, C. Data Mining: Practical Machine Learning Tools and Techniques; The Morgan Kaufmann Series in Data Management Systems; Elsevier Science: Amsterdam, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Lisic, J.; Cruze, N. Local Pivotal Methods for Large Surveys. In Proceedings of the International Conference on Establishment Surveys, Genev, Switzerland, 20–23 June 2016. [Google Scholar]
- Gościk, J.; Łukaszuk, T. Application of the recursive feature elimination and the relaxed linear separability feature selection algorithms to gene expression data analysis. Adv. Comput. Sci. Res. 2013, 10, 39–52. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Wright, M.N.; Ziegler, A. ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Han, S.; Kim, H. Optimal Feature Set Size in Random Forest Regression. Appl. Sci. 2021, 11, 3428. [Google Scholar] [CrossRef]
- INEGI. Medición de la Economía Informal. 2019. Available online: https://www.inegi.org.mx/temas/pibmed/ (accessed on 23 October 2021).
- Samaniego-Breach, N. La participación del trabajo en el ingreso nacional: El regreso a un tema olvidado. Econ. UNAM 2014, 11, 52–77. [Google Scholar] [CrossRef]
- Wilensky, U. NetLogo. Center for Connected Learning and Computer-Based Modeling. 1999. Available online: http://ccl.northwestern.edu/netlogo/ (accessed on 12 January 2022).
- Marks, R.E. Validation and model selection: Three similarity measures compared. Complex. Econ. 2013, 2, 41–61. [Google Scholar] [CrossRef]
- Fagiolo, G.; Guerini, M.; Lamperti, F.; Moneta, A.; Roventini, A. Validation of Agent-Based Models in Economics and Finance. In Simulation Foundations, Methods and Applications; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 763–787. [Google Scholar] [CrossRef]
- Windrum, P.; Fagiolo, G.; Moneta, A. Empirical Validation of Agent-Based Models: Alternatives and Prospects. J. Artif. Soc. Soc. Simul. 2007, 10, 8. [Google Scholar]
- Joanes, D.N.; Gill, C.A. Comparing Measures of Sample Skewness and Kurtosis. J. R. Stat. Society. Ser. D (Stat.) 1998, 47, 183–189. [Google Scholar] [CrossRef]
- INEGI. Finanzas Públicas Estatales y Municipales. 2019. Available online: https://www.inegi.org.mx/programas/finanzas/ (accessed on 13 September 2021).
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef]
- Xu, S.; Chen, M.; Feng, T.; Zhan, L.; Zhou, L.; Yu, G. Use ggbreak to Effectively Utilize Plotting Space to Deal With Large Datasets and Outliers. Front. Genet. 2021, 12, 2122. [Google Scholar] [CrossRef]

| Agent | Attributes | Type | Initialization | Value |
|---|---|---|---|---|
| Auditor | penalty-collected | Float | Deterministic | 0 |
| tax-collected | Float | 0 | ||
| my-employers | AgSet | Submodel 5 | ||
| ent-auditor | Int | Random | ||
| Employer | business-size (ambito2) | Int | Database | |
| education (anios_esc) | Int | |||
| economic-activity (c_ocu11c) | Int | |||
| age (eda) | Int | |||
| mexican-state (ent) | Int | |||
| income (ing7c) | Int | |||
| formal-or-informal (mh_col) | Int | |||
| size-of-region (t_loc) | Int | |||
| corruption | Float | |||
| insecurity | Float | |||
| tax | Float | |||
| audit? | Bool | Deterministic | false | |
| audited? | Bool | false | ||
| type-of-taxpayer | Int | 2 | ||
| declared-tax | Float | 0 | ||
| payroll | Float | Submodel 11 | ||
| payroll * | Float | Submodel 12 | ||
| risk-aversion- | Float | Submodel 16 | ||
| undeclared-payroll | Float | 0 | ||
| undeclared-tax | Float | 0 | ||
| -s | Float | 0.05 | ||
| Float | −0.1 | |||
| prob-formal | Float | Random | ||
| production | Float | Submodel 10 |
| Parameter | Description | Value | Initialization |
|---|---|---|---|
| Penalty rate | 0.75 | Database | |
| Audit probability | 0.05 | Experimentation | |
| Effectiveness of audit process | 0.75 | Experimentation | |
| Effectiveness of tax collection | 0.70 | Literature [94] | |
| Variation in tax rate | 0.00 | Database | |
| Variation in perceived insecurity | 0.00 | Database | |
| Variation in perceived corruption | 0.00 | Database | |
| Threshold for formal or informal sector choice | 0.50 | Literature [95] |
| Model | Year of Real Source | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |
| ML ‘off’ | 0.73 | 0.75 | 0.68 | 0.68 | 0.64 | 0.61 | 0.61 | 0.60 | 0.60 | 0.61 |
| ML ‘on’ | 0.71 | 0.73 | 0.68 | 0.68 | 0.65 | 0.62 | 0.60 | 0.60 | 0.60 | 0.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Platas-López, A.; Guerra-Hernández, A.; Quiroz-Castellanos, M.; Cruz-Ramírez, N. Agent-Based Models Assisted by Supervised Learning: A Proposal for Model Specification. Electronics 2023, 12, 495. https://doi.org/10.3390/electronics12030495
Platas-López A, Guerra-Hernández A, Quiroz-Castellanos M, Cruz-Ramírez N. Agent-Based Models Assisted by Supervised Learning: A Proposal for Model Specification. Electronics. 2023; 12(3):495. https://doi.org/10.3390/electronics12030495
Chicago/Turabian StylePlatas-López, Alejandro, Alejandro Guerra-Hernández, Marcela Quiroz-Castellanos, and Nicandro Cruz-Ramírez. 2023. "Agent-Based Models Assisted by Supervised Learning: A Proposal for Model Specification" Electronics 12, no. 3: 495. https://doi.org/10.3390/electronics12030495
APA StylePlatas-López, A., Guerra-Hernández, A., Quiroz-Castellanos, M., & Cruz-Ramírez, N. (2023). Agent-Based Models Assisted by Supervised Learning: A Proposal for Model Specification. Electronics, 12(3), 495. https://doi.org/10.3390/electronics12030495











