A Service Recommendation System Based on Dynamic User Groups and Reinforcement Learning
Abstract
:1. Introduction
- We proposed a joint-training method using deep reinforcement learning and dynamic user grouping to address issues related to changing user preferences and data sparsity.
- We introduced a user-grouping mechanism that classified users based on project features. By aggregating users through shared parameters, this approach effectively alleviated challenges posed by sparse data and cold-start problems.
- The proposed joint-training algorithm combined deep learning and reinforcement learning. By concurrently operating between embedding layers and the decision layer in reinforcement learning, it captured users’ evolving preferences and provided optimal recommendations based on current user preferences.
- The experimental results on large datasets, such as MovieLens and Amazon, demonstrated a significant performance improvement, as compared to baseline algorithms. The model particularly excelled at mitigating cold-start and data-sparsity challenges. Additionally, its predictive accuracy surpassed that of baseline algorithms.
2. Related Work
2.1. Matrix Factorization
2.2. Contextual Multi-Armed Bandit Algorithm
2.3. User-Based Collaborative Filtering
2.4. The Attention Mechanism
3. Preliminaries
3.1. Agent
3.2. States
3.3. Actions
3.4. Rewards
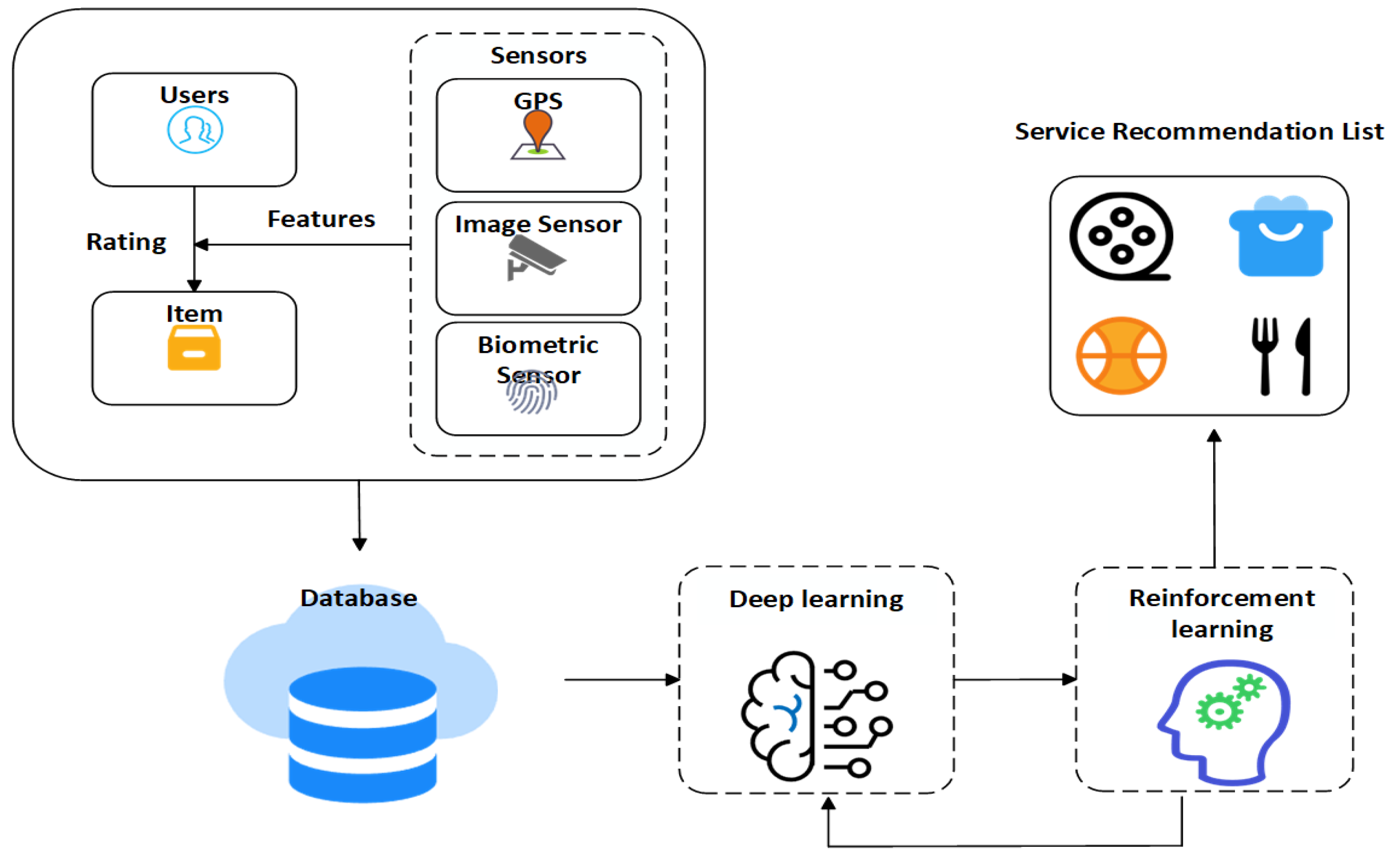
4. Proposed Method
4.1. Overview
| Algorithm 1 Dynamic User Groups and Reinforcement Learning |
|
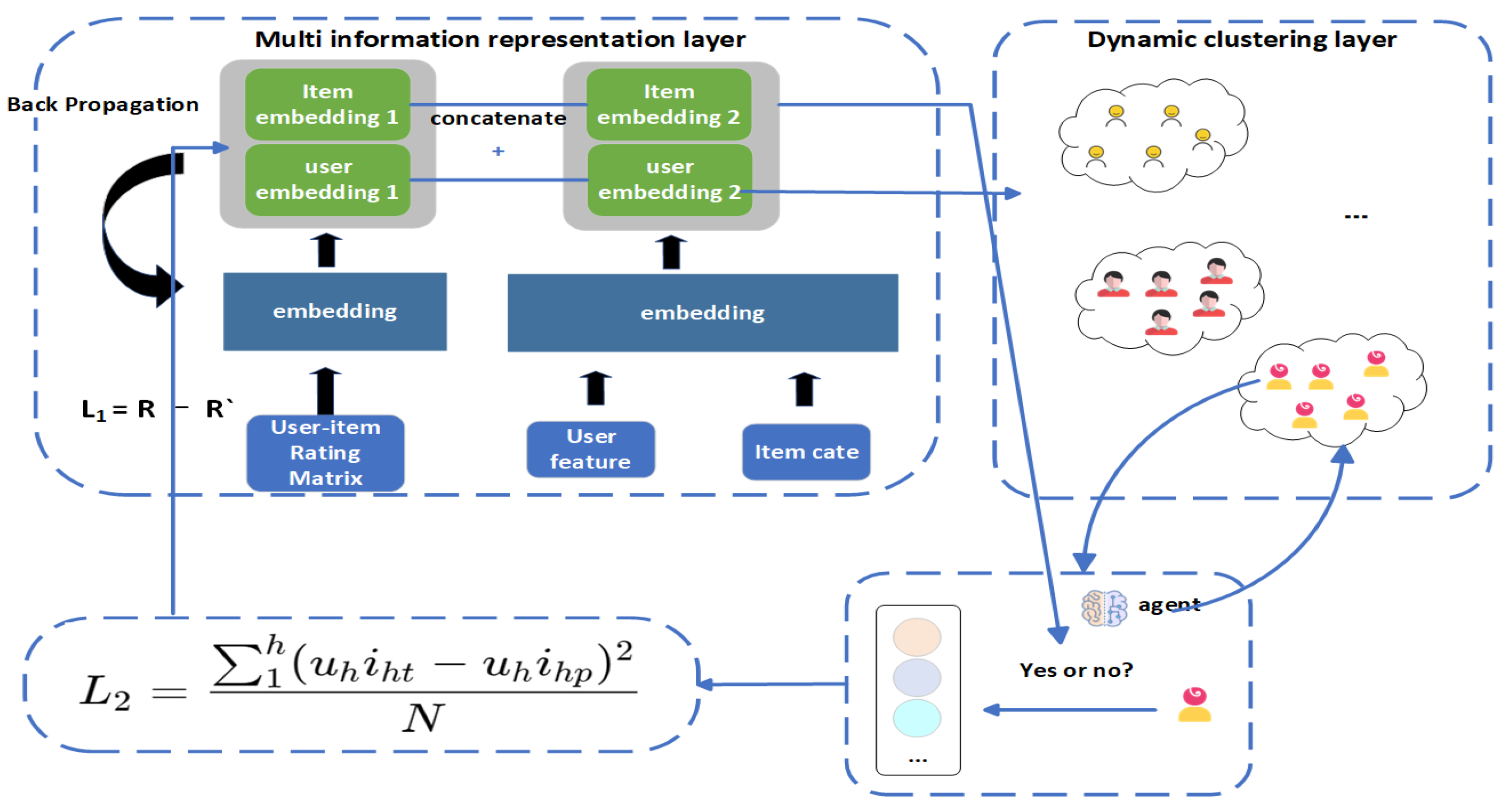
4.2. Multi-Information Representation
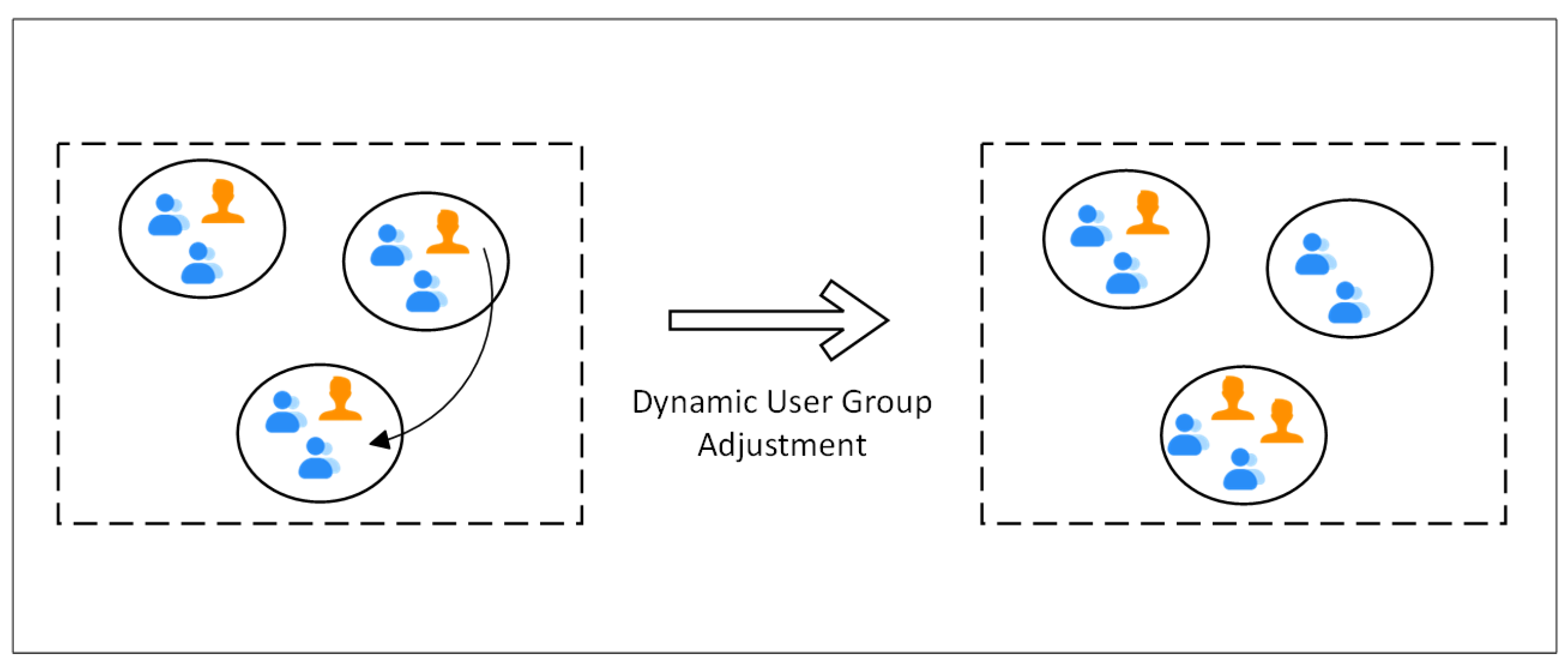
4.3. Dynamic Clustering
4.4. A Multi-Level Item-Filtering Module Based on Ratings
4.5. Joint Training
5. Experimental Results and Evaluation
5.1. Experimental Setup
5.1.1. Datasets
5.1.2. Evaluation Metrics
5.1.3. Baselines
- SVD [37]: SVD is a classic matrix factorization algorithm that decomposed the rating matrix into three matrices: the user matrix, the item matrix, and the singular value matrix.
- LFM [38]: LFM is a probability-based matrix factorization method that introduced latent variables (hidden factors) to model the relationships between users and items. By learning these latent factors, the model could make personalized recommendations. This was a probabilistic matrix factorization method that introduced latent variables (hidden factors) to model the relationships between users and items. By learning these latent factors, the model could make personalized recommendations.
- NCF [39]: Neural collaborative filtering is a recommendation system method that combined the characteristics of neural networks to enhance the recommendation algorithms and improve the accuracy of personalized recommendations. It utilized neural networks to capture the complex relationships between users and items, allowing for better predictions of user interest in items. Typically, this approach introduced neural network layers on top of collaborative filtering to enhance the recommendation precision and personalization.
- LinUCB [40]: LinUCB is an algorithm for multi-armed bandit problems. It was based on linear models and the concept of confidence intervals in order to make the best decisions within a limited time frame. The algorithm estimated potential rewards and uncertainties for each choice and selected the optimal action based on these estimates.
- TS [41]: Thompson sampling is a reinforcement-learning algorithm used in multi-armed bandit problems and recommendation systems. It made optimal choices based on Bayesian probability.
5.2. Comparison with Baseline Algorithms
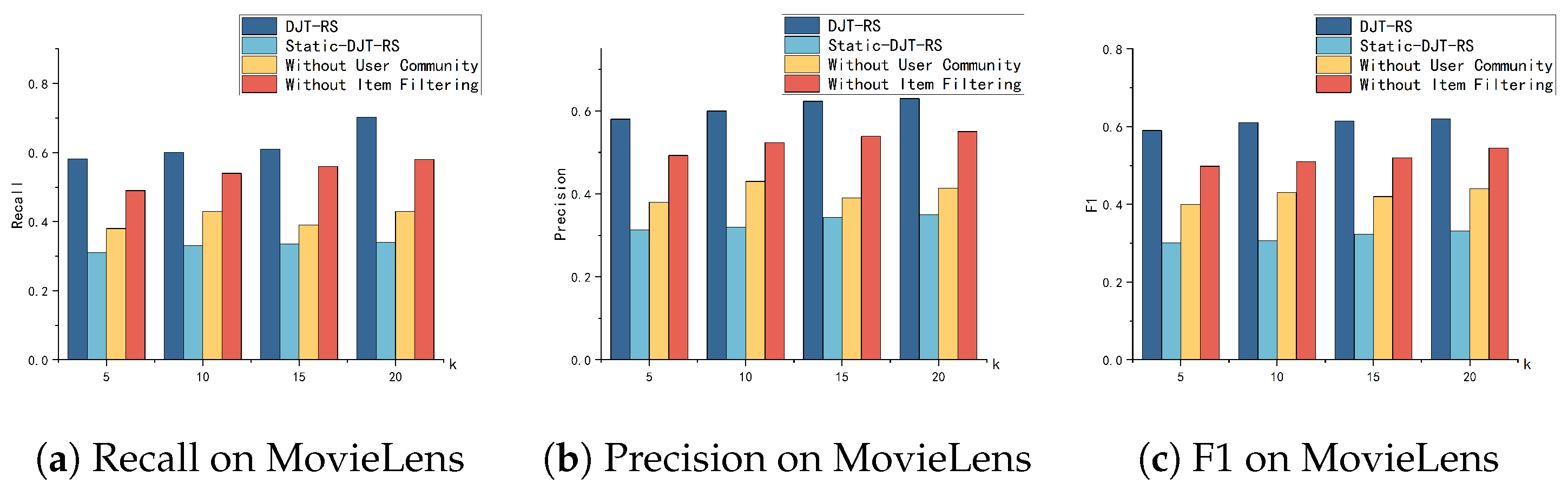
5.3. Ablation Study
5.3.1. Basic Ablation Study
5.3.2. Diversity Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Singh, J.; Sajid, M.; Yadav, C.S.; Singh, S.S.; Saini, M. A Novel Deep Neural-based Music Recommendation Method considering User and Song Data. In Proceedings of the 2022 6th International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 28–30 April 2022; pp. 1–7. [Google Scholar]
- Zha, D.; Feng, L.; Tan, Q.; Liu, Z.; Lai, K.H.; Bhushanam, B.; Tian, Y.; Kejariwal, A.; Hu, X. Dreamshard: Generalizable embedding table placement for recommender systems. Adv. Neural Inf. Process. Syst. 2022, 35, 15190–15203. [Google Scholar]
- Intayoad, W.; Kamyod, C.; Temdee, P. Reinforcement learning based on contextual bandits for personalized online learning recommendation systems. Wirel. Pers. Commun. 2020, 115, 2917–2932. [Google Scholar] [CrossRef]
- Sanz-Cruzado, J.; Castells, P.; López, E. A simple multi-armed nearest-neighbor bandit for interactive recommendation. In Proceedings of the 13th ACM Conference on Recommender Systems, Copenhagen, Denmark, 16–20 September 2019; pp. 358–362. [Google Scholar]
- Elena, G.; Milos, K.; Eugene, I. Survey of multiarmed bandit algorithms applied to recommendation systems. Int. J. Open Inf. Technol. 2021, 9, 12–27. [Google Scholar]
- Qin, L.; Chen, S.; Zhu, X. Contextual combinatorial bandit and its application on diversified online recommendation. In Proceedings of the 2014 SIAM International Conference on Data Mining, Philadelphia, PA, USA, 24–26 April 2014; pp. 461–469. [Google Scholar]
- Jiang, J.; Jiang, Y. Leader-following consensus of linear time-varying multi-agent systems under fixed and switching topologies. Automatica 2020, 113, 108804. [Google Scholar] [CrossRef]
- Li, S.; Lei, W.; Wu, Q.; He, X.; Jiang, P.; Chua, T.S. Seamlessly unifying attributes and items: Conversational recommendation for cold-start users. Acm Trans. Inf. Syst. (TOIS) 2021, 39, 1–29. [Google Scholar] [CrossRef]
- Aldayel, M.; Al-Nafjan, A.; Al-Nuwaiser, W.M.; Alrehaili, G.; Alyahya, G. Collaborative Filtering-Based Recommendation Systems for Touristic Businesses, Attractions, and Destinations. Electronics 2023, 12, 4047. [Google Scholar] [CrossRef]
- Lv, Z.; Tong, X. A Reinforcement Learning List Recommendation Model Fused with Graph Neural Networks. Electronics 2023, 12, 3748. [Google Scholar] [CrossRef]
- Ahmadian, S.; Ahmadian, M.; Jalili, M. A deep learning based trust-and tag-aware recommender system. Neurocomputing 2022, 488, 557–571. [Google Scholar] [CrossRef]
- Ahmadian, M.; Ahmadian, S.; Ahmadi, M. RDERL: Reliable deep ensemble reinforcement learning-based recommender system. Knowl.-Based Syst. 2023, 263, 110289. [Google Scholar] [CrossRef]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. arXiv 2012, arXiv:1205.2618. [Google Scholar]
- Guo, H.; Tang, R.; Ye, Y.; Li, Z.; He, X. DeepFM: A factorization-machine based neural network for CTR prediction. arXiv 2017, arXiv:1703.04247. [Google Scholar]
- Semenov, A.; Rysz, M.; Pandey, G.; Xu, G. Diversity in news recommendations using contextual bandits. Expert Syst. Appl. 2022, 195, 116478. [Google Scholar] [CrossRef]
- Kawale, J.; Bui, H.H.; Kveton, B.; Tran-Thanh, L.; Chawla, S. Efficient Thompson sampling for Online Matrix-Factorization Recommendation. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Volume 28. [Google Scholar]
- Gan, M.; Kwon, O.C. A knowledge-enhanced contextual bandit approach for personalized recommendation in dynamic domains. Knowl.-Based Syst. 2022, 251, 109158. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, L.; Wu, X. Achieving counterfactual fairness for causal bandit. Proc. AAAI Conf. Artif. Intell. 2022, 36, 6952–6959. [Google Scholar] [CrossRef]
- Setiowati, S.; Adji, T.B.; Ardiyanto, I. Point of Interest (POI) Recommendation System using Implicit Feedback Based on K-Means+ Clustering and User-Based Collaborative Filtering. Comput. Eng. Appl. J. 2022, 11, 73–88. [Google Scholar] [CrossRef]
- Yunanda, G.; Nurjanah, D.; Meliana, S. Recommendation system from microsoft news data using TF-IDF and cosine similarity methods. Build. Inform. Technol. Sci. (BITS) 2022, 4, 277–284. [Google Scholar] [CrossRef]
- van den Heuvel, E.; Zhan, Z. Myths about linear and monotonic associations: Pearson’s r, Spearman’s ρ, and Kendall’s τ. Am. Stat. 2022, 76, 44–52. [Google Scholar] [CrossRef]
- Jain, G.; Mahara, T.; Sharma, S.C.; Sangaiah, A.K. A cognitive similarity-based measure to enhance the performance of collaborative filtering-based recommendation system. IEEE Trans. Comput. Soc. Syst. 2022, 9, 1785–1793. [Google Scholar] [CrossRef]
- Linden, G.; Smith, B.; York, J. Amazon.com recommendations: Item-to-item collaborative filtering. IEEE Internet Comput. 2003, 7, 76–80. [Google Scholar] [CrossRef]
- Zhao, Z.D.; Shang, M.S. User-based collaborative-filtering recommendation algorithms on hadoop. In Proceedings of the 2010 Third International Conference on Knowledge Discovery and Data Mining, Phuket, Thailand, 9–10 January 2010; pp. 478–481. [Google Scholar]
- Hsieh, F.S. Trust-based recommendation for shared mobility systems based on a discrete self-adaptive neighborhood search differential evolution algorithm. Electronics 2022, 11, 776. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, H.; He, X.; Nie, L.; Liu, W.; Chua, T.S. Attentive collaborative filtering: Multimedia recommendation with item-and component-level attention. In Proceedings of the 40th International ACM SIGIR conference on Research and Development in Information Retrieval, Tokyo, Japan, 7–11 August 2017; pp. 335–344. [Google Scholar]
- Li, B. Optimisation of UCB algorithm based on cultural content orientation of film and television in the digital era. Int. J. Netw. Virtual Organ. 2023, 28, 265–280. [Google Scholar] [CrossRef]
- Wang, R.; Wu, Z.; Lou, J.; Jiang, Y. Attention-based dynamic user modeling and deep collaborative filtering recommendation. Expert Syst. Appl. 2022, 188, 116036. [Google Scholar] [CrossRef]
- Aramayo, N.; Schiappacasse, M.; Goic, M. A Multiarmed Bandit Approach for House Ads Recommendations. Mark. Sci. 2023, 42, 271–292. [Google Scholar] [CrossRef]
- Al-Ajlan, A.; Alshareef, N. Recommender System for Arabic Content Using Sentiment Analysis of User Reviews. Electronics 2023, 12, 2785. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-means clustering algorithms: A comprehensive review, variants analysis, and advances in the era of big data. Inf. Sci. 2022, 622, 178–210. [Google Scholar] [CrossRef]
- Dang, C.N.; Moreno-García, M.N.; Prieta, F.D. An approach to integrating sentiment analysis into recommender systems. Sensors 2021, 21, 5666. [Google Scholar] [CrossRef]
- Naeem, M.; Rizvi, S.T.H.; Coronato, A. A gentle introduction to reinforcement learning and its application in different fields. IEEE Access 2020, 8, 209320–209344. [Google Scholar] [CrossRef]
- Iacob, A.; Cautis, B.; Maniu, S. Contextual bandits for advertising campaigns: A diffusion-model independent approach. In Proceedings of the 2022 SIAM International Conference on Data Mining (SDM), Alexandria, VA, USA, 28–30 April 2022; pp. 513–521. [Google Scholar]
- Ding, Q.; Kang, Y.; Liu, Y.W.; Lee, T.C.M.; Hsieh, C.J.; Sharpnack, J. Syndicated bandits: A framework for auto tuning hyper-parameters in contextual bandit algorithms. Adv. Neural Inf. Process. Syst. 2022, 35, 1170–1181. [Google Scholar]
- London, B.; Joachims, T. Control Variate Diagnostics for Detecting Problems in Logged Bandit Feedback. 2022. Available online: https://www.amazon.science/publications/control-variate-diagnostics-for-detecting-problems-in-logged-bandit-feedback (accessed on 12 December 2023).
- Colace, F.; Conte, D.; De Santo, M.; Lombardi, M.; Santaniello, D.; Valentino, C. A content-based recommendation approach based on singular value decomposition. Connect. Sci. 2022, 34, 2158–2176. [Google Scholar] [CrossRef]
- Fang, H.; Bao, Y.; Zhang, J. Leveraging decomposed trust in probabilistic matrix factorization for effective recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014; Volume 28. [Google Scholar] [CrossRef]
- He, X.; Liao, L.; Zhang, H.; Nie, L.; Hu, X.; Chua, T.S. Neural collaborative filtering. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 173–182. [Google Scholar]
- Shi, Q.; Xiao, F.; Pickard, D.; Chen, I.; Chen, L. Deep Neural Network with LinUCB: A Contextual Bandit Approach for Personalized Recommendation. In Proceedings of the Companion Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023; pp. 778–782. [Google Scholar]
- Agrawal, S.; Goyal, N. Analysis of thompson sampling for the multi-armed bandit problem. In Proceedings of the Conference on Learning Theory, Lyon, France, 29–31 October 2012; JMLR Workshop and Conference Proceedings. pp. 39.1–39.26. [Google Scholar]



| Datasets | Models | k = 10 | k = 20 | k = 30 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Recall | Precision | F1 | Diversity | Recall | Precision | F1 | Diversity | Recall | Precision | F1 | Diversity | ||
| MovieLens | SVD | 0.3902 | 0.3213 | 0.3538 | 0.2863 | 0.4354 | 0.4031 | 0.4186 | 0.2765 | 0.3954 | 0.3643 | 0.3793 | 0.3065 |
| LFM | 0.4993 | 0.4214 | 0.4573 | 0.4658 | 0.4577 | 0.4003 | 0.4275 | 0.4895 | 0.5038 | 0.4357 | 0.4674 | 0.5268 | |
| NCF | 0.3894 | 0.3765 | 0.3829 | 0.4256 | 0.4038 | 0.3714 | 0.3872 | 0.4565 | 0.3953 | 0.3754 | 0.3852 | 0.6696 | |
| LinUCB | 0.5552 | 0.4662 | 0.5077 | 0.2659 | 0.6024 | 0.4721 | 0.5303 | 0.3596 | 0.5764 | 0.4921 | 0.5316 | 0.3985 | |
| TS | 0.5654 | 0.4532 | 0.5043 | 0.2685 | 0.5901 | 0.4601 | 0.5179 | 0.2985 | 0.6043 | 0.4945 | 0.5449 | 0.3698 | |
| DJT-RS | 0.6742 | 0.5364 | 0.5974 | 0.6859 | 0.7024 | 0.5572 | 0.6223 | 0.7596 | 0.6535 | 0.5313 | 0.5865 | 0.7776 | |
| Amazon | SVD | 0.4353 | 0.3532 | 0.3902 | 0.3986 | 0.4662 | 0.4736 | 0.4699 | 0.4265 | 0.4276 | 0.3829 | 0.4043 | 0.4586 |
| LFM | 0.5743 | 0.4564 | 0.5094 | 0.5463 | 0.4985 | 0.4355 | 0.4655 | 0.5796 | 0.5434 | 0.4875 | 0.5144 | 0.5593 | |
| NCF | 0.5432 | 0.4865 | 0.5139 | 0.5996 | 0.4576 | 0.4053 | 0.4301 | 0.6059 | 0.4363 | 0.3955 | 0.4148 | 0.6003 | |
| LinUCB | 0.6342 | 0.5334 | 0.5793 | 0.3236 | 0.6742 | 0.5623 | 0.6137 | 0.3363 | 0.5323 | 0.5231 | 0.5276 | 0.3238 | |
| TS | 0.6341 | 0.5962 | 0.6145 | 0.3696 | 0.6465 | 0.6041 | 0.6246 | 0.3889 | 0.5873 | 0.5437 | 0.5648 | 0.3826 | |
| DJT-RS | 0.6643 | 0.5923 | 0.6266 | 0.7652 | 0.6924 | 0.5963 | 0.6404 | 0.7966 | 0.6389 | 0.5212 | 0.5742 | 0.7652 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, E.; Ma, W.; Zhang, J.; Xia, X. A Service Recommendation System Based on Dynamic User Groups and Reinforcement Learning. Electronics 2023, 12, 5034. https://doi.org/10.3390/electronics12245034
Zhang E, Ma W, Zhang J, Xia X. A Service Recommendation System Based on Dynamic User Groups and Reinforcement Learning. Electronics. 2023; 12(24):5034. https://doi.org/10.3390/electronics12245034
Chicago/Turabian StyleZhang, En, Wenming Ma, Jinkai Zhang, and Xuchen Xia. 2023. "A Service Recommendation System Based on Dynamic User Groups and Reinforcement Learning" Electronics 12, no. 24: 5034. https://doi.org/10.3390/electronics12245034
APA StyleZhang, E., Ma, W., Zhang, J., & Xia, X. (2023). A Service Recommendation System Based on Dynamic User Groups and Reinforcement Learning. Electronics, 12(24), 5034. https://doi.org/10.3390/electronics12245034






