Abstract
This paper focuses on the problem of high-performance streaming random number generation in the range of uniform and normal distributions in FPGAs. Our work is focused on lightweight implementation, suitable for a wide range of FPGAs. First, we review the existing types of random generation modules. Next, in this paper we present the construction of the designed generator. We divide it into two sections: Stream Uniform Numbers Generator Implementation and Cumulative Distribution-Based Stream Gaussian Generator. Each design step was verified in the scope of the quality of the output data, especially regarding the produced distributions. The results obtained are compared with existing solutions. We mainly consider resource utilization and throughput. We also add our quality factor, which is an effective utilization of FPGAs. Despite quality results, our modules were implemented using a high-level synthesis language (C/C++), contrary to typical hardware description level (HDL) approaches. It provides the opportunity to implement the proposed algorithms on CPUs. It was tested with positive results, thus highlighting the versatility of the solution that is unavailable in terms of HDL implementations. Our designed generators were confirmed to stand out for their satisfactory performance while occupying low logical resources.
1. Introduction
A noticeable trend occurring in both scientific research approaches and industries is the increasing importance of simulation. This has a number of benefits: it allows reproducible results to be obtained regardless of the quality of the data collected, enables analysis of a certain narrower issue, and could predict certain defects in projects (e.g., silicon chips) even at the production stage. All these advantages are united by an additional one—cost savings. The only fundamental problem with this approach is that it requires time to implement appropriate software algorithms and access to high-performance computing systems capable of performing complex calculations. The distinctive cost-to-performance ratio is represented by FPGAs. In high-energy physics research, simulations based on Monte Carlo methods are particularly appreciated. They require access to huge amounts of random data.
The Monte Carlo methods are used in modeling and simulating complex problems where it is not possible to obtain solutions based on analytical approaches. Those methods are widely used in many scientific fields, exploited especially in applied mathematics and physics.
In high-energy physics, the MC methods enable obtaining the space-time characteristics of the system formed during the collision of heavy ions. Such relativistic collisions allow us to study the behavior of nuclear matter under conditions of high pressure and temperature, i.e., in conditions similar to the time shortly after the Big Bang. There are many different experimental methods to analyze this state of matter—one is correlation femtoscopy. The femtoscopy method is derived from intensity interferometry in astronomy—the Hanbury-Brown and Twiss effect [1,2]. Despite many analogies, the measurement method and the designated sizes are the main difference. In particle interferometry, energy and momentum correlations are measured to determine the spatiotemporal characteristics of microworld objects (sized m). The correlation function, , is then created and described by the following equation [3,4]:
where is the momentum of the first particle in the pair rest frame (PRF) system, is the source function, is the wave function of the pair, and is the relative difference between initial positions. There is no analytical formula describing the correlation function for pairs of nonidentical particles, such as and K mesons. The numerical procedure, based on MC methods, comes in handy, in which is determined using the squared wave function as the weight of each pair of particles. Then, it is compared with the experimental results using the statistical test (chi-squared test) [5]:
where is the number of observations of type i, is the expected (theoretical) number of observations of type i, and n is the number of types (here the number of points of the correlation function). This procedure shows excellent flexibility as it is not limited to analytically integrated source models.
The theoretical correlation function needs two sets of information to be calculated. The first set, the momenta of the particles of each pair, can be delivered from the experiment. The second set is formed of the relative positions of the emission points of two particles of each pair. These coordinates rely on the source model and pseudorandom numbers. For accurate results, the correlation function should be calculated for a large number of pairs for each bin in the fitting range.
The accuracy and precision of the results are directly dependent on the number of generated random numbers used to describe the problem. Therefore, obtaining satisfactory results depends on the quality of the used generator and the amount of numbers drawn, which significantly increases the calculation process. The second problem is particularly highlighted when using central processing units (CPUs) for calculations—their sequential mode of operation generates significant computational delays. A workaround for this problem is to parallelize calculations on multithreaded devices.
Most such calculations use the built-in pseudorandom generators provided by the operating system. An example would be /dev/random available on Linux. It is a high-quality generator that can be successfully used in cryptologic applications. Access to it is carried out in a blocking manner. It means that only one computation thread can receive a value from it at a given time. This strictly limits the data throughput and is a major drawback in high-performance applications. It is not noticeable in standard applications. However, in multithreaded computing using huge amounts of data (MC methods), a bottleneck is experienced. A workaround could be to use an external generator or to implement an independent one.
A field-programmable gate array (FPGA) is an alternative platform for the development of pseudorandom number generators (PRNG). A flexible architecture, dynamic reconfiguration, the possibility of pipelining, and true parallelism at low cost (for low-end devices) make it a good candidate for fast algorithms implementations. On top of that, the power consumption factor compared to CPUs or graphical processing units (GPUs) is at least a magnitude less. This is especially interesting on large experimental or computational infrastructures, where systems stay online all the time. However, this comes at the price of a long time and specific development of the software.
This paper describes a computation-effective implementation of the PRNG algorithm for FPGAs. It is focused mainly on maximum performance and lightweight implementation. Compared to the others, we are taking advantage of the currently intensively developing high-level synthesis (HLS) languages that significantly reduce implementation time. The main novelty is the approach of designing a high-quality PRNG module with normal and uniform distributions using modern HLS languages for FPGAs. We verify whether it is possible to achieve satisfactory results based on HLS compiler optimization algorithms. Therefore, we have also implemented the same PRNG version using the typical HDL language. The second achievement necessary to underline is excellent performance and hardware utilization properties. Compared to others, we can state that our design made in HLS language can produce good results with multiple-times-shortened development time. By using the HLS approach, we benefit from the following properties:
- Fast FPGA implementation by use of C/C++ languages;
- Compiler-level automatic optimizations;
- Ease of testbenching without using hardware;
- High-performance testbenching (opposite to HDL testbenches), suitable for integration with quality tests;
- Instant integration with currently existing complex algorithms (corrFit) for in-application verification of the quality of the results.
In this paper, we also provide a proof of concept that implementing high-performance PRNGs is possible to achieve using modern HLS languages for FPGAs. The unique features, like native C/C++, allow for integration with external PRNGs verification tools or already designed complex algorithms. The time-to-implementation ratio is much shorter than in HLD designs.
The article describes two pseudorandom generators generating random values with different distributions—uniform for the first generator and normal for the second generator. The motivation for creating both generators was a need to generate pseudorandom values for Monte Carlo simulations. So, that is their primary purpose. However, the range of possible applications of both generators is broader. They may be used as a high-performance source of noise waveforms to test data acquisition and processing systems. It should be noted that a solution accelerating the operation of the proposed uniformly distributed values generator may reduce its usefulness in cryptographic applications.
2. Pseudorandom Number Generation
Random number generation can be divided into two main branches: true random number generators (TRNGs) and pseudorandom number generators (PRNGs). The generation of truly random numbers in electronic circuits is a vast and complex problem. Security solutions impose very strict requirements on the randomness of the numbers used, for example, for generating encryption keys or for authentication protocols [6,7]. We can divide these types of generators into two main groups: analog and digital, with the latter being significantly more widely used. Digital TRNGs can, in turn, be divided into those based on ring oscillators (ROs) and those based on metastability [6].
The use of TRNGs is especially desired in the scope of security, e.g., cryptography algorithms. For most applications of Monte Carlo simulation, it is not necessary to use truly random numbers, and their substitution with pseudorandom numbers allows for a significant reduction in both time and design complexity.
A PRNG, unlike a TRNG, provides a strongly random sequence of numbers but with a definite (long) period and a predictable sequence [6,7]. There are many ways to implement these generators, and we distinguish between those based on hyperchaotic systems [8], linear congruential generators (based on modulo) [9], cellular automata [10], and linear feedback shift registers (LFSRs) [11]. In our algorithm, the generation of a homogeneous distribution in the range 0–1 was decided based on the latter—the LFSR. The LFSR is especially suitable for efficient FPGA implementation due to good representation in hardware: synchronous registers (flip-flops) and basic logic elements (AND, OR, XOR, etc.).
3. Generation of Normally Distributed Random Numbers
LFSRs may be used to generate normally distributed values. Summing up n uniformly distributed numbers, we can approximate the normal distribution (according to the central limit theorem), and the accuracy of such an approach will depend on the number n. In most cases, due to parallel computing on FPGAs, the LFSRs could be pipelined to obtain high throughput of pseudorandom values (uniform pseudorandom number—UPRN) every clock cycle. The required number of summed random values may be reduced if their distribution is similar to the normal distribution. It can be achieved through proper postprocessing of the generated random data.
For this purpose, one can use the cumulative distribution function of a known, well-defined normal distribution. To begin with, this function is defined for all real numbers, which makes it impossible to implement it on an FPGA. It must be trimmed to fit in the range, where a is an integer which can fit into memory of the device. In the case of CPUs, this is determined via the architecture of the chip, while in FPGAs, there is more flexibility in the choice. Then, the fact that this function is symmetric with respect to the mean value may be striking. It allows us to limit our considerations to half of this function, , while remembering to devote the most significant bit of the drawn vector to defining its sign (when it is equal to 0, the value is positive). With this procedure, it is possible to reduce hardware resources by almost half.
From the fundamental theorem of calculus, we know the relationship between the cumulative distribution function (CDF) ():
and the probability density function (PDF) ():
which, for the previously mentioned trimmed range, will be:
where —mean value; —standard deviation; and —Gauss error function.
This implies that the constant probability of finding a value in a given range/bin corresponds to the linear part of the function . The best linear approximation will be obtained for different bin widths. When considering half of the CDF function mentioned earlier, we can approximate it with a polyline. The number of comparators (C) used will depend on the number of bins (N) as follows: .
Knowing the positions of the bin, or more precisely, its start and end, we can define a function that maps the randomly generated value to the appropriate range:
where V—value in the bin; , —input range limits from polyline approximation of CDF (y values); and , —bin limits from polyline approximation of CDF (x values).
4. High-Level Synthesis Implementation of Stream Uniform Numbers Generator and Cumulative Distribution-Based Stream Gaussian Generator
The generators described earlier were initially implemented in a VHDL (very high-speed integrated circuit hardware description language). It is an common approach, since it gives the best timing control of the algorithm, and therefore, it is possible to optimize it on most low-level bases. On the other hand, the time to implement it is significantly higher, especially considering integration with other computation structures (algorithms). Also, it is difficult to integrate PRNGs into root algorithms, which are typically non-HDL.
Due to the constantly evolving high-level synthesis (HLS) environment for FPGAs and the benefits coming from it (short development time, simple integration, possible to use with legacy CPU codes) combined with the fact that the high-energy physics algorithms for which the generator was designed were developed in the C++ language, it was decided to reimplement the proposed solutions using HLS and the Xilinx Vitis environment. FPGA kernels were created from this code. All tests and implementations were carried out on an Alveo U50 Data Center Accelerator Card with Xilinx Vitis HLS 2021.1 edition. The accelerator card is part of a bigger computation infrastructure for the analysis of heavy ion collisions based on Monte Carlo algorithms.
4.1. Stream Uniform Numbers Generator Implementation (SUNG)
It was decided to use 167-bit and 125-bit vectors, initialized on device power-up with a static value different from zero. Exclusive or was used as a linear function to calculate the value of the input bit with respect to the state of the previous ones, so-called taps. The selection of these has a significant impact on the vectors drawn. Their combinations can lengthen or shorten the period, after which they will be repeated. The following taps positions were selected to obtain a SUNG with the longest possible interval: (161, 167) and (125, 124, 18, 17) [12]. A major problem of LFSR-based generators is the cross-correlation of bits in successive iterations of the generator. It is not possible to completely eliminate these relationships. However, the use of two vectors allows for effective concealment. Figure 1 shows an architecture overview of the implemented algorithm in term of final values generation. In Algorithm 1 is presented pseudocode that corresponds to the architecture overview on Figure 1. To begin with, vectors of a given length are defined along with the bits numbers to be used in the xor function. Then, the bits under the aforementioned numbers are checked and an exclusive or operation is performed in each iteration. The value is stored in the LSB variable. At the end, the vector is shift to left by one bit, and the value defined by LSB is appended at the lsb of given vector. Two 32-bit values are then extracted, one from the beginning of the longer shifted vector and the other from the end of the shorter vector. In the end, the generator performs an xor operation on these two values (with one of them additionally having an inverted bit order).
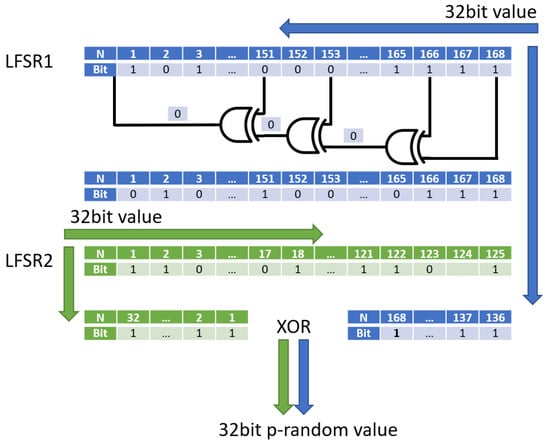
Figure 1.
Architecture of implemented SUNG algorithm.
In each clock cycle, the corresponding xor operations are performed with respect to the defined taps. The 32-bit values from each vector are then taken, with the bit order of one of the values reversed. Finally, a final bit-wise xor operation is performed, and a pseudorandom number is available on the output. Utilization of this algorithm is listed in Table 1. It can be noted that the resource consumption varies depending on the implementation approach. Nevertheless, the difference is small enough that the generators can be assumed to be uniform. In the pipelined variant, the generator is able to provide the output with a 32-bit random variable every clock cycle. Achieving such high performance is possible by using HLS pragmas which are then interpreted with the Vitis environment. In this particular case, they produce a complete pipeline of logical operations. It is then possible to create a kernel, that is, a single module with a given functionality, which can be used in other components—in this case, in the implementation of the CDBSGG generator.
| Algorithm 1 SUNG pseudocode |
|

Table 1.
Resource utilization of SUNG algorithm with comparison to examples of others.
Quality Tests of SUNG
The quality of the generator mentioned above was examined with a spectral test presented in Figure 2 on a -sample data set. The analysis was carried out using the ROOT framework [15]. The SUNG can provide 32-bit samples. These can be further scaled to integer or floating point type. In the case of this test, they were scaled to a range of . The spectral test is a two-dimensional histogram in which the value of n samples is marked on the x axis and the value of samples on the y axis. The histogram plotted in this way shows the randomness of the data obtained. The color map (Figure 2) illustrates the number of samples drawn from a given range. The smaller it is, the higher the quality of the generator.
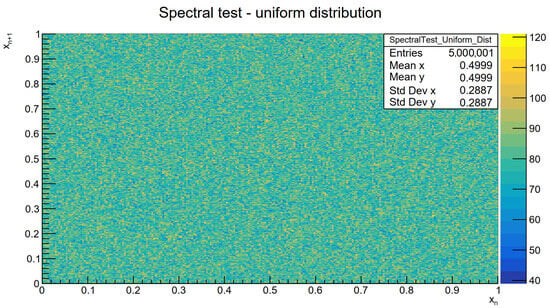
Figure 2.
Spectral test of SUNG. The histogram shows the relationship between the next drawn sample and the preceding one.
Analyzing Table 1, the proposed solution has the lowest consumption of FPGA logic resources. In addition, the spectral test (shown in Figure 2) does not show any specific shapes or patterns. The resulting generator is, therefore, efficient, takes few resources, and generates a strong sequence of pseudorandom numbers. However, its most significant advantage is the simplicity of implementation. It does not require the introduction of any formulas or equations, thus avoiding performing mathematical operations. The selection of a lower vector length and an appropriate sequence of taps could decrease resource consumption but will lower the quality of random numbers.
4.2. Cumulative Distribution-Based Stream Gaussian Generator Implementation
The implemented SUNG generator was then used to generate a normal distribution, as specified in Section 3. The generator consists of three stages (Figure 3). The first is to generate an unsigned number from a uniform distribution. The second step consists of assigning values to the appropriate bin based on the mapping function (approximating the CDF of the normal distribution with a set of linear functions) and obtaining the sign out of the MSB. It can be seen from Figure 4 that the drawn samples do not yet resemble a normal distribution. Only by going through stage 3 (i.e., adding up several numbers from stage 2) can it be made clear that the resulting values resemble a normal distribution (Figure 4). Detailed implementation of the CDBSGG generator was presented in Algorithm 2. As mentioned in Section 3, at the beginning, it is necessary to define the bin widths (limits) and the coefficients (a coeffs/b coeffs) of the linear functions that approximate half of the plot of the cumulative distribution function. The generation is performed by taking a random value from SUNG. The bin to which the drawn value belongs is then found. Value mapping is then performed according to Equation (6). In the next step, the sign of the processed variable is determined based on the MSB of the uniform value from SUNG. The output is chosen by selecting a 32-bit starting from the MSB of the processed variable. This flow describes CDBSGG stage 1, which is highlighted in Figure 3. At this point, the variables form the distribution marked on the left side of Figure 4. By conducting an addition of four consecutive process values, one obtains random variables that follow a normal distribution (seen on the right side of the same figure).
| Algorithm 2 CDBSGG pseudocode |
|
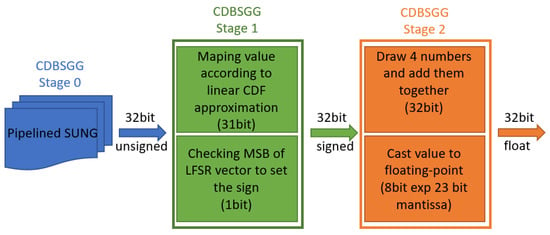
Figure 3.
Architecture of implemented CDBSGG algorithm.
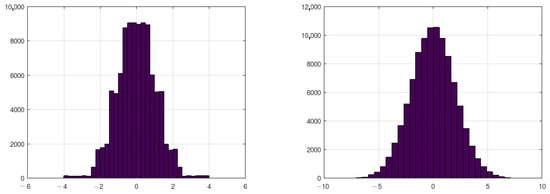
Figure 4.
(Left): an output of CDBSGG stage 1. (Right): an output of CDBSGG stage 2.
Quality Tests of CDBSGG
Similarly to SUNG, samples were generated and normalized to range (the normalization was carried out not in the FPGA, but in the test software), and a spectral test was carried out. In contrast to the test of the former generator, this time, a pattern similar to a two-dimensional Gaussian distribution was expected. The result of this test is presented in Figure 5. In addition, the same data were used to plot a projection of an x axis of the previous histogram (), and Figure 6 presents it with a fitted theoretical Gaussian distribution. Analysis carried out in this way makes it possible to confirm two things. It is important to note the high quality of the fit of the theoretical distribution to the drawn samples, allowing a clear conclusion that they come from a normal distribution. Despite the projection of only one dimension, when comparing the standard deviation and mean value of the fit to the spectral test (Figure 5), it is noticeable that in the second direction, we also obtain a normal distribution.
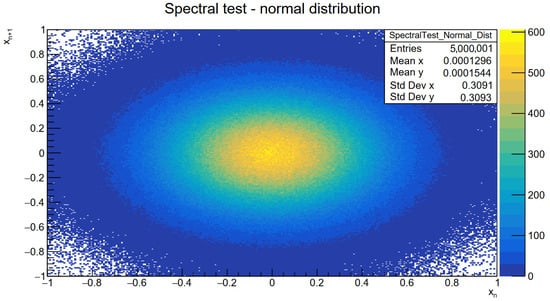
Figure 5.
Spectral test of SUNG-based CDBSGG.
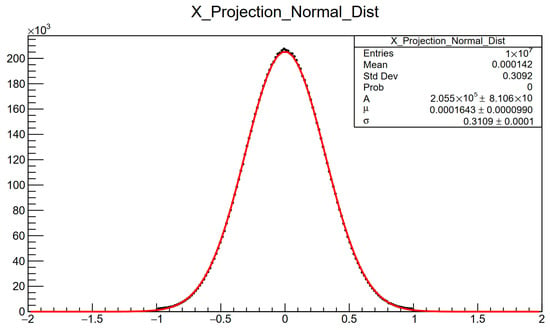
Figure 6.
Distribution of data generated using implemented CDBSGG with fitted theoretical function.
As mentioned before, the fit in Figure 6 unquestionably confirms the origin of the generated samples. It should also be noted that the result has an excellent approximation of the tails of the function. Some deviations in the vicinity of zero can be observed, but they are not significant (the mean value is still very close to zero). In addition, 100 data sets containing samples were generated. A theoretical function fit was performed for each of them to see how stable the values describing the normal distribution (mean value and standard deviation) behave.
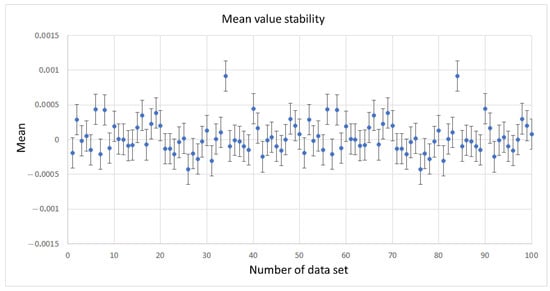
Figure 7.
Estimated mean values of 100 generated data sets. Error bars were obtained from the fitting function.
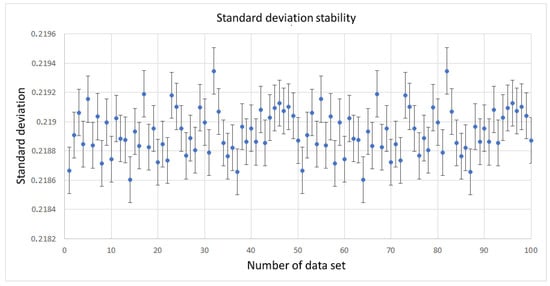
Figure 8.
Estimated standard deviation values of 100 generated data sets. Error bars were obtained from the fitting function.
Except for two outsiders, it can be seen that the mean values are equally spread around zero in both the positive and negative number directions. The standard deviation also has two points diverging from the trend. However, the other values oscillate evenly within the value of . The reason for the occurrence of two outlying points can be sought in the methodology of the algorithm. The normal distribution is a continuous function. In the implementation, this distribution should be limited on a given range of real numbers. Thus, there will always remain the question of how accurately the algorithm will reproduce the tails of the function. Greater precision within this region will result in greater blurring in the center (therefore impacting the accuracy of the determined mean values and standard deviations). CDBSGG faithfully reproduces the tails, thus preserving the good quality of the determined distribution parameters.
Resource utilization of the CDBSGG algorithm with comparison to examples of others is presented in Table 2:

Table 2.
Resource utilization of CDBSGG algorithm with comparison to examples of others.
In addition to the standard resources, the maximum throughput of the algorithm (M/s stands for Megasamples per second) is presented. Also, a metric is introduced to describe how efficient the algorithm is in relation to the allocated resources (Effective utilization). It was defined as follows:
The weights for the resources were selected in the following way. The most common resources in logic circuits are FFs and LUTs. FFs improve timings and are also required for various logic and arithmetic actions, therefore the weight is the lowest. LUTs are also a common resource in FPGAs, used for example for fast production of results (immediate). However, large use of them reduces significantly the timing performance, and therefore their weight is higher. The DSP and BRAM are the most limited in FPGAs, so the more of them are used the more they reduce the efficient utilization factor.
It can be seen that the proposed metric in Equation (7) allows for a simple comparison in the way of less = better. The algorithm is able to generate a sample every clock cycle. Analyzing Table 2, it can be noted that it is not the most efficient design but for sure the lightest one. A huge advantage of the HLS version is an independence from DSP and BRAM units, allowing the generator to be implemented on very tiny FPGAs. However, this comes with a concession. It can be noted that the constants defining the bins in Equation (6) are calculated only once and never change. In view of this, their magnitudes can be determined in preprocessing and stored in a register. This completely eliminates the need to use comparators. The true potential of the generator is emphasized by the effective utilization column—it has the highest performance per resource used. For the HDL version (based on a VHDL), the higher consumption of DSP units is due to the direct rewriting of the HLS algorithm. It should be noted that this implementation can be further optimized, but this requires a significant time investment—as an example, one can mention the use of complex multiplication functions to reduce the utilization of DSP units. However, this highlights the advantages of HLS, in particular, the simplicity and short engineering time.
It is worth mentioning that the proposed solution can also be implemented on a regular CPU. This is due to the use of C/C++ HLS coding, which can be compiled on CPUs platforms. In multithreaded computational algorithms based on the Monte Carlo approach, a decrease in computational performance can be experienced as the number of threads increases. This is due to the limited availability of the built-in pseudorandom number generator, which can handle a single thread at a time. The proposed CDBSGG solves this problem as it is purely software-based and, therefore, can be implemented separately for each thread, thus eliminating the bottleneck.
4.3. Distribution Tests of SUNG and CDBSGG
The final confirmation of the quality of the solutions presented is provided by the DIEHARD tests of randomness [20]—a battery of tests allowing for multilevel analysis of the quality of pseudorandom generators. It is widely considered to be one of the most stringent URNG tests. In addition, its application can be found in the testing methodology of other generators [16], which were compared earlier with the presented solutions (Table 1 and Table 2).
For both generators, the number of test samples was taken as . For the SUNG generator, 32-bit values were drawn and then scaled to a range of using ROOT. Then, the DIEHARD test was carried out. The analysis of the CDBSGG generator required more data processing which was performed using the ROOT framework. The most important limitation is that only uniform generators can be tested via the aforementioned test suite. It is therefore necessary to define a transformation that allows a uniform distribution to be obtained from a normal distribution. This can be achieved using the complementary error function (). In the first step, the drawn 32-bit values are scaled to the range. The mean value () and standard deviation () of the set of samples are then calculated. In the next step, the values (x) are rescaled using the relation (8), thus obtaining a variable from a normal distribution (y) with parameters :
The asymptotes of the function will be clipped due to the consideration of data within a certain range. At this stage, it is possible to obtain values from a uniform distribution (z) through the following equation:
Following these transformations, the DIEHARD test was run. In addition, an equal number of samples from the generators built into the ROOT environment were drawn as a reference (Gaussian samples were treated via the same conversion algorithm). The results are presented in Table 3:

Table 3.
DIEHARD test results for SUNG and CDBSGG alongside ROOT built-ins.
The version of DIEHARD tests available in [20] performs the individual test multiple times and checks the distribution of the returned p-values. Those p-values should be uniformly distributed in the range for truly random data. The Kolmogorov–Smirnov test is used to compare the obtained distribution with the expected uniform one. The values in Table 3 are the p-values returned by the Kolmogorov–Smirnov test. It is assumed that the generator passes the test if the value is above 0.005 and weakly passes the test if it is above 0.000001. All the tested generators passed all DIEHARD tests. However, the analysis and comparison of the p-values of the tests obtained cannot be a direct indication of the superior quality of one generator over another.
5. Summary
This paper considers the problem of pseudorandom number generation in FPGAs. Two algorithms have been proposed that are able to deliver numbers from a uniform and normal distribution with high efficiency—one sample per clock cycle. The proposed solution is distinguished from others primarily by its high flexibility—due to HLS tools, it can be implemented on both FPGAs and CPUs. In addition to this, those who do not have much experience with HDL languages and have existing algorithms written in C/C++ languages can significantly speed up the execution times of their calculations. The C/C++ codes can be implemented in existing applications, which is impossible to achieve using HDL designs. It is also important to underline that our algorithms provide high performance with low resource occupation compared to the others. The CDBSGG implementation does not consume valuable DSP or BRAM units, making it an ideal choice for small energy-efficient systems. The generator is an entirely software-based solution, making it an ideal choice for multithreaded applications, as it is not hardware-independent. It is also worth mentioning that using HLS tools and C/C++ languages in FPGAs makes it possible to receive better results than the classic HDL approach that the designer needs to optimize—the design time of the HLS approach is much faster.
In both cases of generators, a spectral test was applied, which confirmed the high randomness of the generated data. This was also confirmed via the strict DIEHARD tests suite. In addition, a fit of the theoretical Gaussian function to the drawn numbers was performed. On this basis, it was found that the resulting generator approximated the tails of the bell curve perfectly. In its central part, minor deviations from the theoretical curve can be observed, but these are minimal. The scatter of the distribution parameters was also examined. For this purpose, 100 distributions were generated, the theoretical curves were fitted to them, and the fitting parameters were extracted: mean value and standard deviation. Their values were plotted, thus confirming that they oscillate around constant values: , . The resulting numbers can be flexibly scaled to obtain the desired distribution ranges.
The proposed solutions were implemented using high-level synthesis tools on an Alveo U50 Data Centre Accelerator Card. Information on resource occupancy was collected and compared with solutions from other papers. The uniform distribution generator was confirmed to be one of the most efficient as well as the lightest solution. As far as the normal distribution number generator is concerned, it is extremely efficient; however, it was not possible to obtain an implementation with the lowest utilization of logical resources. Nevertheless, it provides the best performance ratio to implementation costs (effective utilization).
The algorithm is a part of a larger FPGA computation acceleration structure also based on HLS design [21]. Its main application is for high-energy physics algorithms for heavy ions collisions. Since the computations are based on Monte Carlo algorithms, fitting functions, and a large number of events to analyze, it is essential to work with an integrated, high-performance PRNG unit.
Author Contributions
Conceptualization: W.M.Z. and T.G. Methodology: W.M.Z. and T.G. Data curation: T.G., E.W., D.W. and M.K. Formal analysis: T.G., W.M.Z., P.S., H.Z., D.W. and D.P., Investigation: T.G., W.M.Z., A.W. and M.K. Resources: A.W. and H.Z. Software: T.G., E.W., D.W., M.K. and P.S. Supervision: A.W., H.Z. and W.M.Z. Validation: T.G., W.M.Z., E.W., H.Z., P.S., D.P. and M.K. Writing—original draft: T.G., A.W., P.S., H.Z., D.P. and D.W. All authors have read and agreed to the published version of the manuscript.
Funding
Research was funded by POB HEP of Warsaw University of Technology within the Excellence Initiative: Research University (IDUB) programme.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FPGA | field-programmable gate array |
| HLS | high-level synthesis |
| CPU | central processing unit |
| MC | Monte Carlo methods |
| CF | correlation function |
| (U/G)PRNG | (uniform/Gaussian) pseudorandom number generator |
| TRNG | true random number generator |
| LFSR | linear feedback shift register |
| CDF | cumulative distribution function |
| probability density function | |
| VHDL | very high-speed integrated circuit hardware description language |
| HDL | hardware description language |
| SUNG | stream uniform numbers generator |
| BBS | Blum Blum Shub |
| C-A | celluar automata |
| RO | ring oscillator |
| FF | flip-flop |
| LUT | lookup table |
| DSP | digital signal processor |
| BRAM | block random access memory |
| N/A | not available |
| CDBSGG | cumulative distribution-based stream Gaussian generator |
| B-M | Box–Muller |
| CLT | cumulative |
References
- Brown, R.H.; Twiss, R.Q. A Test of a New Type of Stellar Interferometer on Sirius. Nature 1956, 178, 1046–1048. [Google Scholar] [CrossRef]
- Brown, R.H.; Twiss, R.Q. Correlation between Photons in two Coherent Beams of Light. Nature 1956, 177, 27–29. [Google Scholar] [CrossRef]
- Koonin, S.E. Proton Pictures of High-Energy Nuclear Collisions. Phys. Lett. B 1977, 70, 43–47. [Google Scholar] [CrossRef]
- Pratt, S.; Csörgő, T.; Zimanyi, J. Detailed predictions for two-pion correlations in ultrarelativistic heavy-ion collisions. Phys. Rev. C 1990, 42, 2646. [Google Scholar] [CrossRef]
- Cochran, W.G. The χ2 Test of Goodness of Fit. Ann. Math. Statist. 1952, 23, 315–345. [Google Scholar] [CrossRef]
- Wieczorek, P.Z. An FPGA Implementation of the Resolve Time-Based True Random Number Generator with Quality Control. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 3450–3459. [Google Scholar] [CrossRef]
- Yu, F.; Li, L.; He, B.; Liu, L.; Qian, S.; Huang, Y.; Cai, S.; Song, Y.; Tang, Q.; Wan, Q.; et al. Design and FPGA Implementation of a Pseudorandom Number Generator Based on a Four-Wing Memristive Hyperchaotic System and Bernoulli Map. IEEE Access 2019, 7, 181884–181898. [Google Scholar] [CrossRef]
- Mohammed, B. Hardware Implementation of Pseudo Random Number Generator Based on Chaotic Iteration. Ph.D. Thesis, Université Bourgogne Franche-Comté, Besançon, France, 2018. [Google Scholar]
- Katti, R.; Srinivasan, S. Efficient hardware implementation of a new pseudo-random bit sequence generator. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009; pp. 1393–1396. [Google Scholar] [CrossRef]
- Moreno-Armendáriz, M.; Cruz-Cortés, N.; Duchanoy, C.; León-Javier, A.; Quintero, R. Hardware implementation of the elitist compact Genetic Algorithm using Cellular Automata pseudo-random number generator. Comput. Electr. Eng. 2013, 39, 1367–1379. [Google Scholar] [CrossRef]
- Gupta, M.D.; Chauhan, R.K. Efficient Hardware Implementation of Pseudo-Random Bit Generator Using Dual-CLCG Method. J. Circuits Syst. Comput. 2021, 30, 2150182. [Google Scholar] [CrossRef]
- Xilinx. Efficient Shift Registers, LFSR Counters, and Long Pseudo-Random Sequence Generators. 1996. Available online: https://docs.xilinx.com/v/u/en-US/xapp052 (accessed on 4 September 2023).
- Tsoi, K.; Leung, K.; Leong, P. Compact FPGA-based true and pseudo random number generators. In Proceedings of the 11th Annual IEEE Symposium on Field-Programmable Custom Computing Machines, Napa, CA, USA, 9–11 April 2003; pp. 51–61. [Google Scholar] [CrossRef]
- De Micco, L.; Antonelli, M.; Larrondo, H.A.; Boemo, E. RO-based PRNG: FPGA implementation and stochastic analysis. In Proceedings of the 2014 IX Southern Conference on Programmable Logic (SPL), Buenos Aires, Argentina, 5–7 November 2014; pp. 1–6. [Google Scholar] [CrossRef]
- CERN. ROOT Data Analysis Framework. Available online: https://root.cern/ (accessed on 4 September 2023).
- Su, J.; Han, J. An improved Ziggurat-based hardware Gaussian random number generator. In Proceedings of the 2016 13th IEEE International Conference on Solid-State and Integrated Circuit Technology (ICSICT), Hangzhou, China, 25–28 October 2016; pp. 1606–1608. [Google Scholar] [CrossRef]
- Malik, J.S.; Hemani, A.; Gohar, N.D. Unifying CORDIC and Box-Muller algorithms: An accurate and efficient Gaussian Random Number generator. In Proceedings of the 2013 IEEE 24th International Conference on Application-Specific Systems, Architectures and Processors, Washington, DC, USA, 5–7 June 2013; pp. 277–280, ISSN 2160-052X. [Google Scholar] [CrossRef]
- Malik, J.S.; Hemani, A.; Malik, J.N.; Silmane, B.; Gohar, N.D. Revisiting Central Limit Theorem: Accurate Gaussian Random Number Generation in VLSI. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 842–855. [Google Scholar] [CrossRef]
- Thomas, D.B. Parallel Generation of Gaussian Random Numbers Using the Table-Hadamard Transform. In Proceedings of the 2013 IEEE 21st Annual International Symposium on Field-Programmable Custom Computing Machines, Seattle, WA, USA, 28–30 April 2013; pp. 161–168. [Google Scholar] [CrossRef]
- Brown, R.G. Dieharder: A Random Number Test Suite. Available online: http://webhome.phy.duke.edu/~rgb/General/dieharder.php (accessed on 4 September 2023).
- Wojenski, A.; Zbroszczyk, H.; Kruszewski, M.; Szymanski, P.; Wawrzyn, E.; Wielanek, D.; Zabolotny, W.; Pawlowska, D.; Gniazdowski, T. Hardware acceleration of complex HEP algorithms with HLS and FPGAs: Methodology and preliminary implementation. Comput. Phys. Commun. 2024, 295, 108997. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).