Multicast Space-Conversion-Space Strict-Sense Nonblocking Switching Fabrics with Multicast Opportunity in the Last Stage for Continuous Multislot Connections
Abstract
:1. Introduction
1.1. The Background
1.2. Related Work
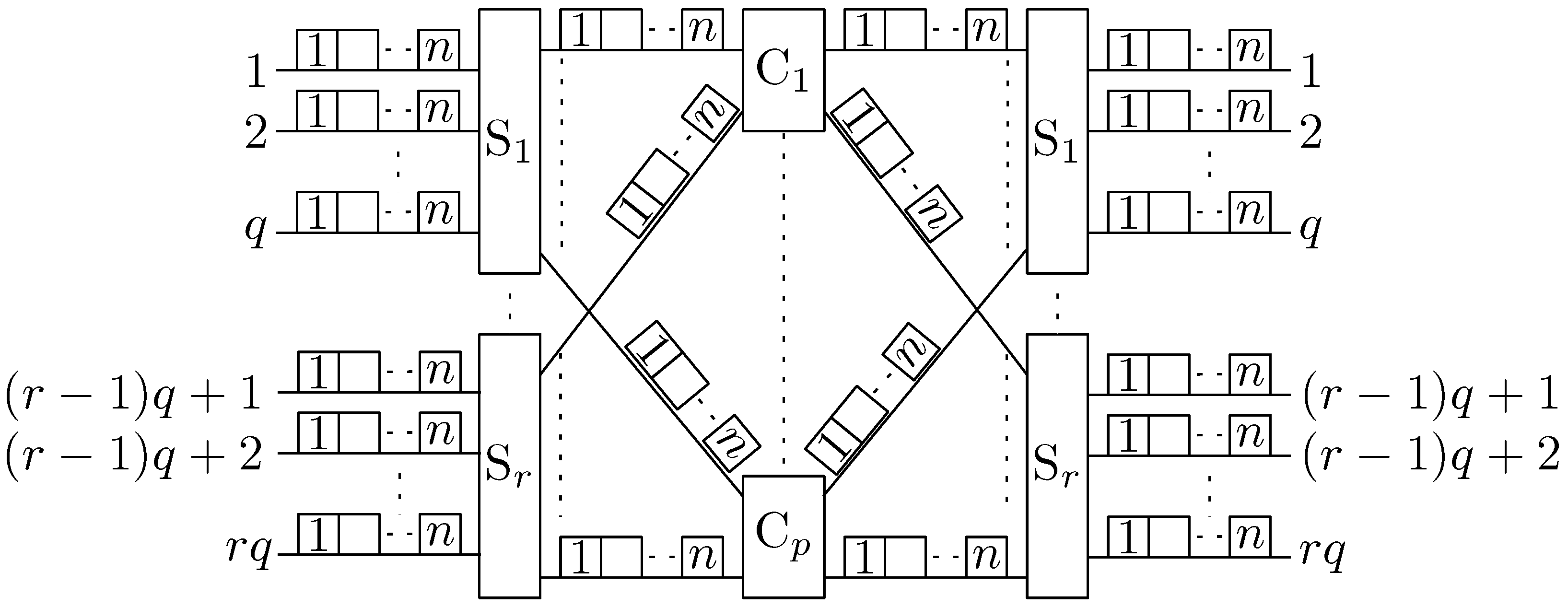
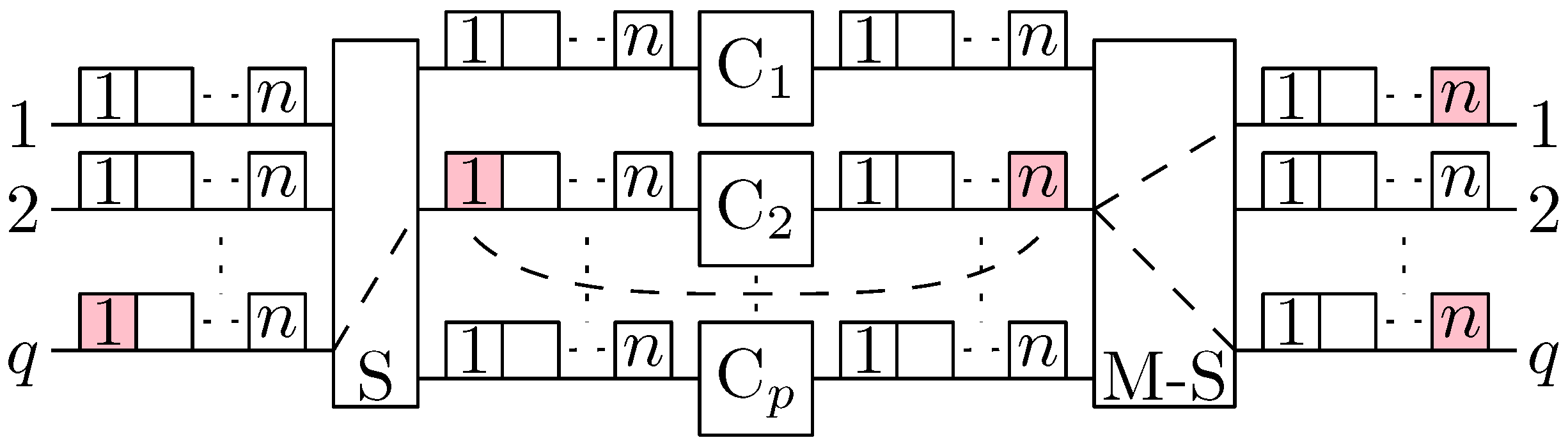
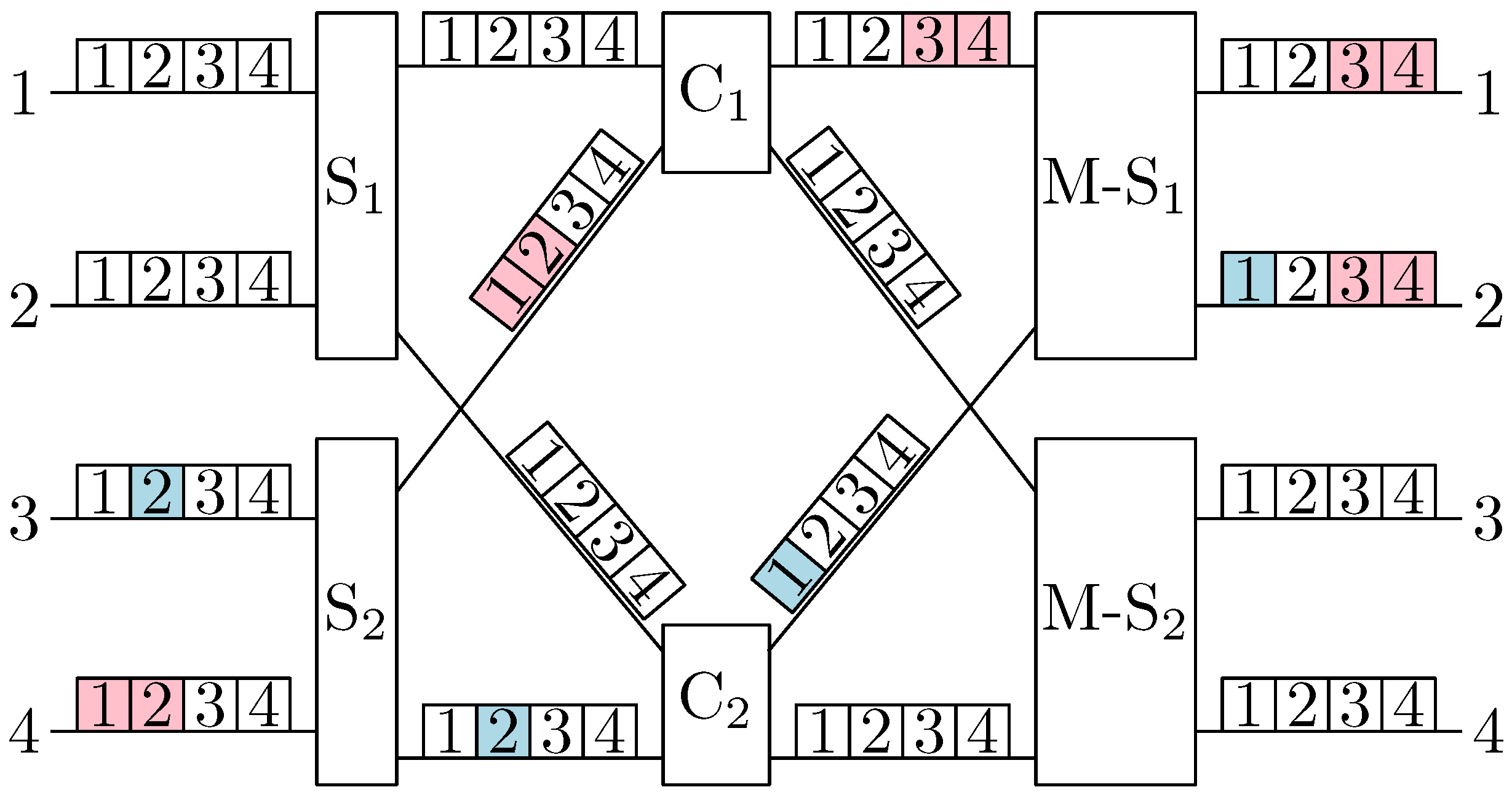
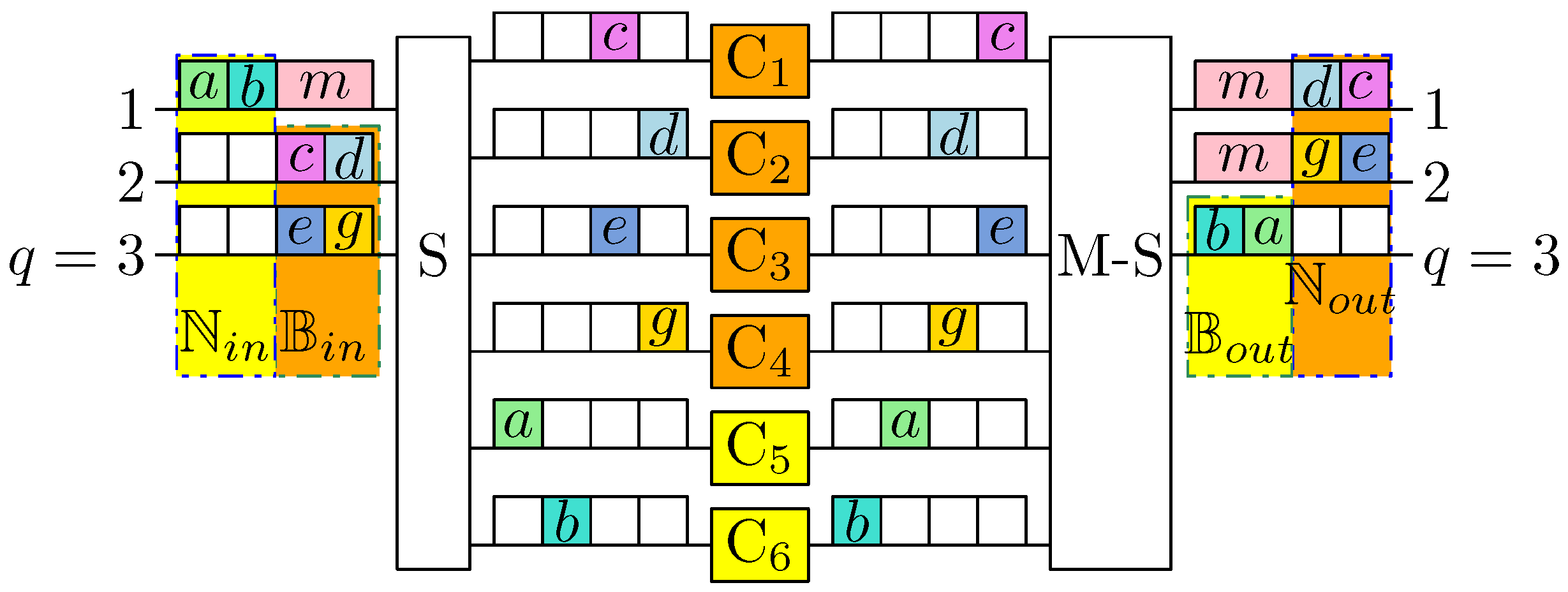
2. Multicast S-C-S Switching Fabrics
3. Problem Statement
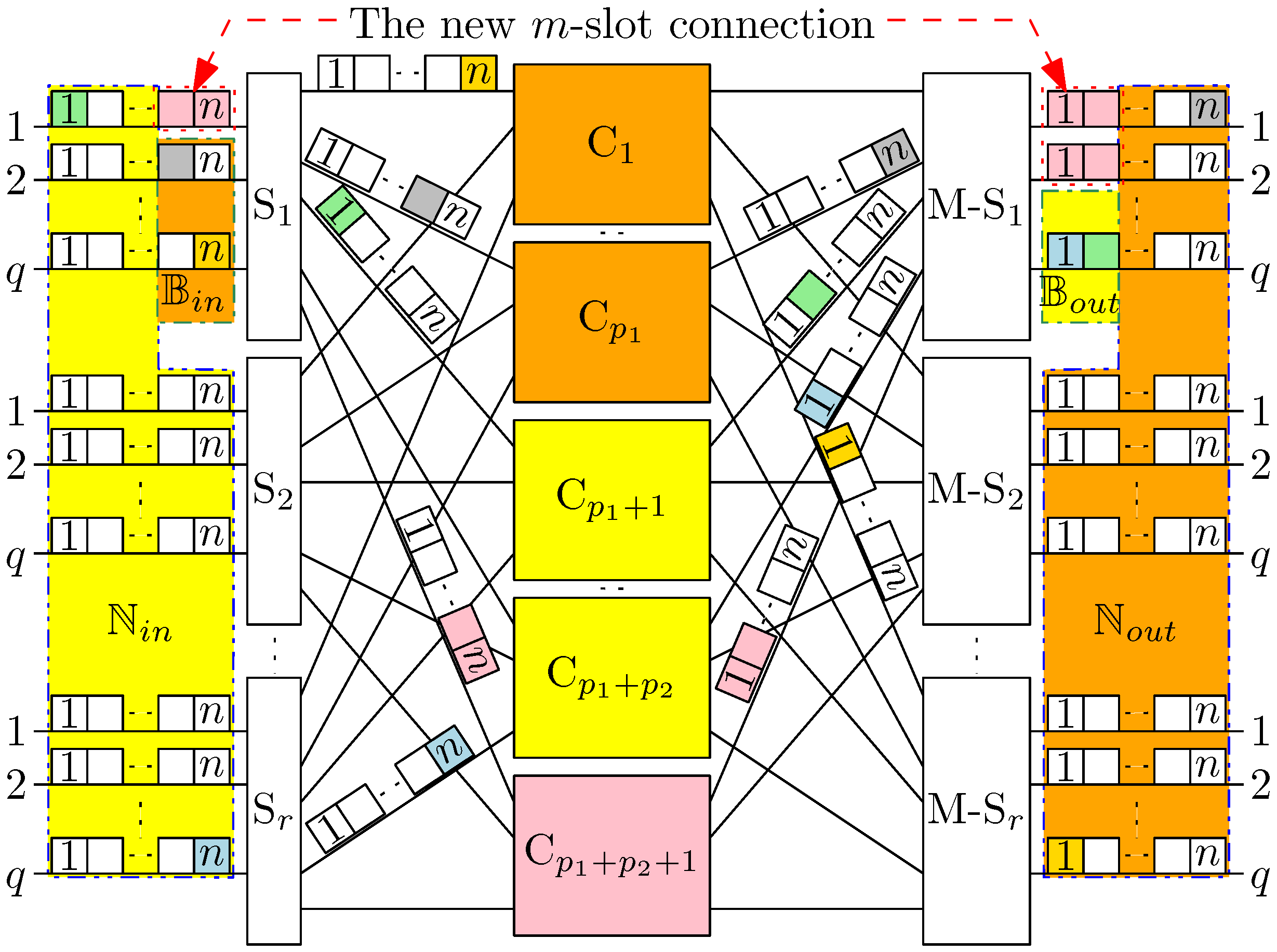
4. SSNB Conditions
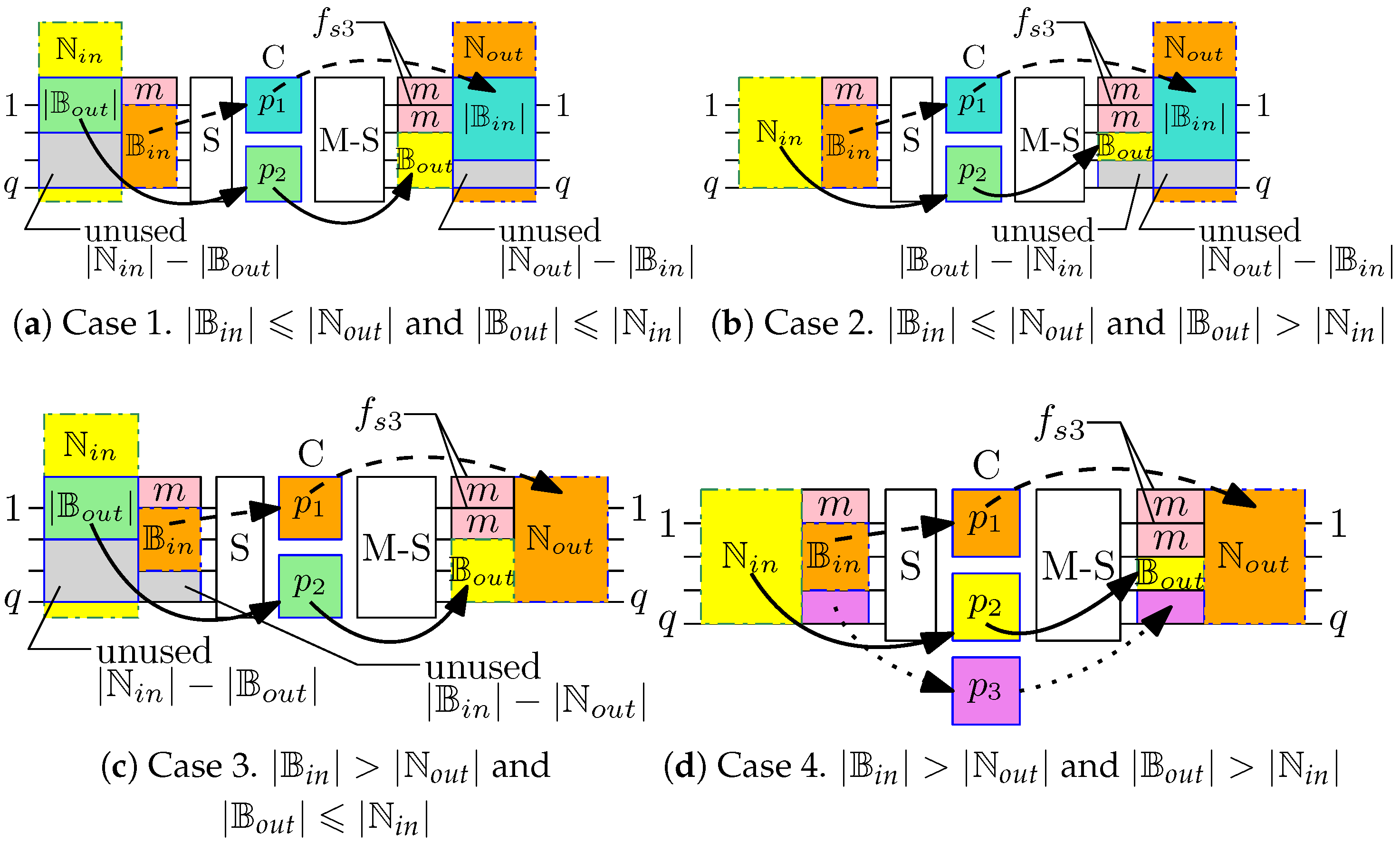
4.1. Potential Blocking and Nonblocking Connections
4.2. Number of Potential Blocking and Nonblocking Connections in M-SCS1
4.3. Number of Potential Blocking and Nonblocking Connections in M-SCS2
4.4. Number of Middle-Stage Switches Blocked in M-SCS1
4.5. Number of Middle-Stage Switches Blocked in M-SCS2
4.6. The Maximum Number of Blocked Middle-Stage Switches
4.7. Nonblocking Conditions
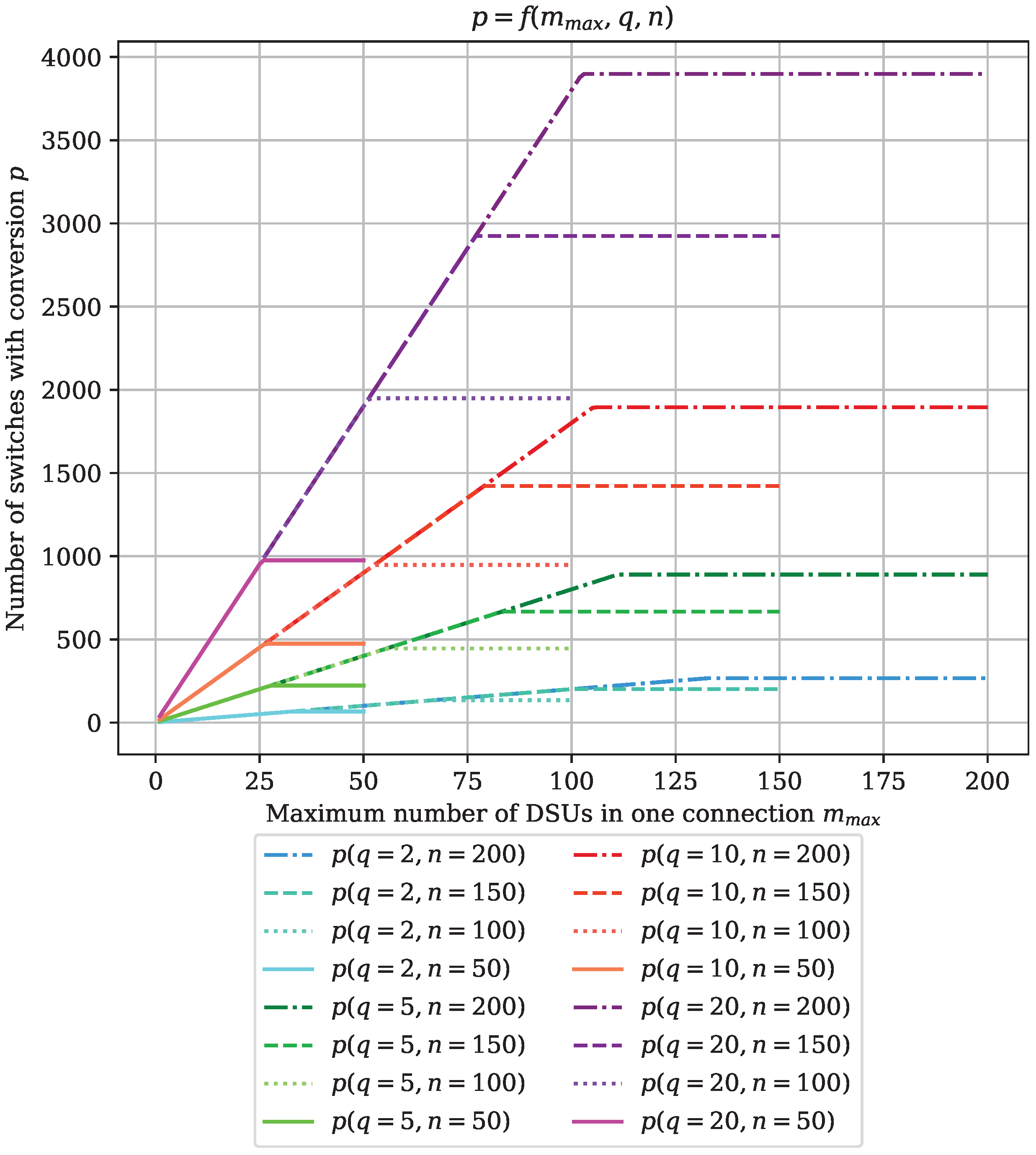
4.8. Numerical Results
4.8.1. M-SCS1 Switching Fabrics
4.8.2. M-SCS2 Switching Fabrics
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stare, E.; Munier, F.; Pham Van, D. 5G Multicast-Broadcast for Group Communication: Why It Matters and How It Works. Available online: https://www.ericsson.com/en/blog/2022/12/multicast-broadcast-group-communication (accessed on 12 September 2023).
- Stasiak, M.; Sobieraj, M.; Zwierzykowski, P. Modeling of Multi-Service Switching Networks with Multicast Connections. IEEE Access 2022, 10, 5359–5377. [Google Scholar] [CrossRef]
- Zhao, L.; Shi, P.; Zhang, H. Bi-Directional Benes With Large Port-Counts and Low Waveguide Crossings for Optical Network-on-Chip. IEEE Access 2021, 9, 115788–115800. [Google Scholar] [CrossRef]
- Khattak, M.K.; Tang, Y.; Fahim, H.; Rehman, E.; Majeed, M.F. Effective Routing Technique: Augmenting Data Center Switch Fabric Performance. IEEE Access 2020, 8, 37372–37382. [Google Scholar] [CrossRef]
- Wu, C.C.; Qiao, L.; Chen, Q. Design of a 640-Gbps Two-Stage Switch Fabric for Satellite On-Board Switches. IEEE Access 2020, 8, 68725–68735. [Google Scholar] [CrossRef]
- Lin, J.; Li, Y.; Shen, G. Clos-based All-optical Switching Architecture Supporting Mixed Unicast & Multicast Datacenter Services. In Proceedings of the 2023 Opto-Electronics and Communications Conference (OECC), Shanghai, China, 14 August 2023; pp. 1–3. [Google Scholar] [CrossRef]
- Listanti, M.; Roveri, A. Switching structures for ATM. Comput. Commun. 1989, 12, 349–358. [Google Scholar] [CrossRef]
- Lee, T.T. Non-blocking copy networks for multicast packet switching. In Proceedings of the 1988 International Zurich Seminar on Digital Communications—Mapping New Applications onto New Technologies, Zurich, Switzerland, 8–10 March 1988; pp. 221–229. [Google Scholar]
- Hui, J.Y. Switching and Traffic Theory for Integrated Broadband Networks; Springer: New York, NY, USA, 1990. [Google Scholar] [CrossRef]
- Clos, C. A study of non-blocking switching networks. Bell Syst. Tech. J. 1953, 32, 406–424. [Google Scholar] [CrossRef]
- Beneš, V.E. On rearrangeable three-stage connecting networks. Bell Syst. Tech. J. 1962, 41, 1481–1492. [Google Scholar] [CrossRef]
- Cantor, D.G. On non-blocking switching networks. Networks 1971, 1, 367–377. [Google Scholar] [CrossRef]
- Pattavina, A. Switching Theory: Architecture and Performance in Broadband ATM Networks; John Wiley & Sons, Ltd.: Chichester, UK, 1998. [Google Scholar] [CrossRef]
- Hwang, F.K. The Mathematical Theory of Nonblocking Switching Networks, 2nd ed.; World Scientific Publishing Company: Singapore, 2004. [Google Scholar]
- Kabaciński, W. Nonblocking Electronic and Photonic Switching Fabrics; Springer: Boston, MA, USA, 2005. [Google Scholar]
- Jajszczyk, A.; Jekel, G. A new concept-repackable networks. IEEE Trans. Commun. 1993, 41, 1232–1237. [Google Scholar] [CrossRef]
- Kabaciński, W.; Danilewicz, G. Wide-sense and strict-sense nonblocking operation of multicast multi-log2N switching networks. IEEE Trans. Commun. 2002, 50, 1025–1036. [Google Scholar] [CrossRef]
- Yu, C.; Jiang, X.; Horiguchi, S.; Guo, M. Overall Blocking Behavior Analysis of General Banyan-Based Optical Switching Networks. IEEE Trans. Parallel Distrib. Syst. 2006, 17, 1037–1047. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J. On blocking probability of multicast networks. IEEE Trans. Commun. 1998, 46, 957–968. [Google Scholar] [CrossRef]
- Stasiak, M.; Zwierzykowski, P.; Głąbowski, M. Blocking probability in the multi-service switching networks with multicast traffic. In Proceedings of the 2000 10th Mediterranean Electrotechnical Conference. Information Technology and Electrotechnology for the Mediterranean Countries, MeleCon 2000 (Cat. No.00CH37099), Lemesos, Cyprus, 29–31 May 2000; Volume 2, pp. 868–871. [Google Scholar] [CrossRef]
- Yang, Y.; Masson, G. Nonblocking broadcast switching networks. IEEE Trans. Comput. 1991, 40, 1005–1015. [Google Scholar] [CrossRef]
- Lea, C.T. Multi-log2N networks and their applications in high-speed electronic and photonic switching systems. IEEE Trans. Commun. 1990, 38, 1740–1749. [Google Scholar] [CrossRef]
- Shyy, D.J.; Lea, C.T. Log2(N,m,p) strictly nonblocking networks. IEEE Trans. Commun. 1991, 39, 1502–1510. [Google Scholar] [CrossRef]
- Danilewicz, G.; Kabaciński, W.; Rajewski, R. The New Banyan-Based Switching Fabric Architecture Composed of Asymmetrical Optical Switching Elements. In Proceedings of the GLOBECOM 2009—2009 IEEE Global Telecommunications Conference, Honolulu, HI, USA, 4 March 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Hwang, F. Choosing the best logk(N,m,P) strictly nonblocking networks. IEEE Trans. Commun. 1998, 46, 454–455. [Google Scholar] [CrossRef]
- Hwang, F.; Jajszczyk, A. On Nonblocking Multiconnection Networks. IEEE Trans. Commun. 1986, 34, 1038–1041. [Google Scholar] [CrossRef]
- Tscha, Y.; Lee, K.H. Nonblocking conditions for multi-log2N multiconnection networks. In Proceedings of the [Conference Record] GLOBECOM ’92-Communications for Global Users, Orlando, FL, USA, 6–9 December 1992; Volume 3, pp. 1600–1604. [Google Scholar] [CrossRef]
- Das, S.; Parulkar, G.; McKeown, N. Rethinking IP core networks. IEEE/OSA J. Opt. Commun. Netw. 2013, 5, 1431–1442. [Google Scholar] [CrossRef]
- Cisco Annual Internet Report (2018–2023) White Paper. Available online: https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.html (accessed on 20 May 2022).
- Jinno, M.; Takara, H.; Kozicki, B.; Tsukishima, Y.; Sone, Y.; Matsuoka, S. Spectrum-efficient and scalable elastic optical path network: Architecture, benefits, and enabling technologies. IEEE Commun. Mag. 2009, 47, 66–73. [Google Scholar] [CrossRef]
- Gerstel, O.; Jinno, M.; Lord, A.; Yoo, S.J.B. Elastic optical networking: A new dawn for the optical layer? IEEE Commun. Mag. 2012, 50, S12–S20. [Google Scholar] [CrossRef]
- Tomkos, I.; Azodolmolky, S.; Sole-Pareta, J.; Careglio, D.; Palkopoulou, E. A tutorial on the flexible optical networking paradigm: State of the art, trends, and research challenges. Proc. IEEE 2014, 102, 1317–1337. [Google Scholar] [CrossRef]
- Liew, S.C.; Lee, T.T. Principles of Broadband Switching and Networking; Wiley Series in Telecommunications and Signal Processing; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Iniewski, K.; Mccorsky, C.; Minoli, D. Network Infrastructure and Architecture: Designing High-Availability Networks; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Recommendation G.694.1. In Spectral Grids for WDM Applications: DWDM Frequency Grid; International Telecommunication Union (ITU-T): Geneva, Switzerland, 2020; Available online: https://www.itu.int/rec/T-REC-G.694.1/en (accessed on 11 October 2023).
- Niestegge, G. Nonblocking multirate switching networks. In Proceedings of the 5th ITC Seminar, Lake Como, Italy, 4–8 May 1987; pp. 449–458. [Google Scholar]
- Kabaciński, W. On nonblocking switching networks for multichannel connections. IEEE Trans. Commun. 1995, 43, 222–224. [Google Scholar] [CrossRef]
- Liew, S.C.; Ng, M.H.; Chan, C.W. Blocking and nonblocking multirate Clos switching networks. IEEE/ACM Trans. Netw. 1998, 6, 307–318. [Google Scholar] [CrossRef]
- Turner, J.S.; Melen, R. Multirate Clos networks. IEEE Commun. Mag. 2003, 41, 38–44. [Google Scholar] [CrossRef]
- Danilewicz, G.; Kabaciński, W.; Rajewski, R. Strict-sense nonblocking space-wavelength-space switching fabrics for elastic optical network nodes. IEEE J. Opt. Commun. Netw. 2016, 8, 745–756. [Google Scholar] [CrossRef]
- Danilewicz, G. Asymmetrical Space-Conversion-Space SCS1 Strict-Sense and Wide-Sense Nonblocking Switching Fabrics for Continuous Multislot Connections. IEEE Access 2019, 7, 107058–107072. [Google Scholar] [CrossRef]
- Danilewicz, G. Supplement to “Asymmetrical Space-Conversion Space SCS1 Strict-Sense and Wide-Sense Nonblocking Switching Fabrics for Continuous Multislot Connections”—The SCS2 Switching Fabrics Case. IEEE Access 2019, 7, 167577–167583. [Google Scholar] [CrossRef]
- Lin, B.C. Nonblocking conditions for a multicast WSW architecture based on subtree scheme for elastic optical networks. Opt. Switch. Netw. 2022, 44, 100660. [Google Scholar] [CrossRef]
- Lin, B.C. Rearrangeability and repackability of a multicast wavelength-space-wavelength elastic optical network. Opt. Switch. Netw. 2023, 50, 100741. [Google Scholar] [CrossRef]
- Zhang, P.; Li, J.; Guo, B.; He, Y.; Chen, Z.; Wu, H. Comparison of node architectures for elastic optical networks with waveband conversion. China Commun. 2013, 10, 77–87. [Google Scholar]
- Chen, Y.; Li, J.; Zhu, P.; Niu, L.; Xu, Y.; Xie, X.; He, Y.; Chen, Z. Demonstration of Petabit scalable optical switching with subband-accessibility for elastic optical networks. In Proceedings of the OptoElectronics and Communication Conference and Australian Conference on Optical Fibre Technology, Melbourne, VIC, Australia, 6–10 July 2014. [Google Scholar]
- Kabaciński, W.; Michalski, M.; Rajewski, R. Strict-sense nonblocking W-S-W node architectures for elastic optical networks. J. Light. Technol. 2016, 34, 3155–3162. [Google Scholar] [CrossRef]
- Kabaciński, W.; Michalski, M.; Rajewski, R.; Żal, M. Optical datacenter networks with elastic optical switches. In Proceedings of the IEEE ICC 2017, Paris, France, 21–25 May 2017. [Google Scholar]
- Wang, Q.; Chen, L.K. Performance analysis of multicast traffic over spectrum elastic optical networks. In Proceedings of the Optical Fiber Communication Conference, Los Angeles, CA, USA, 4–8 March 2012. [Google Scholar]
- Lin, R.; Zuckerman, M.; Shen, G.; Zhong, W.-D. Design of light-tree based optical inter-datacenter networks. J. Opt. Commun. Netw. 2013, 5, 1443–1455. [Google Scholar] [CrossRef]
- Gong, L.; Zhou, X.; Liu, X.; Zhao, W.; Lu, W.; Zhu, Z. Efficient resource allocation for all-optical multicasting over spectrum-sliced elastic optical networks. J. Opt. Commun. Netw. 2013, 5, 836–847. [Google Scholar] [CrossRef]
- Kmiecik, W.; Goścień, R.; Walkowiak, K.; Klinkowski, M. Two-layer optimization of survivable overlay multicasting in elastic optical networks. Opt. Switch. Netw. 2014, 14, 164–178. [Google Scholar] [CrossRef]
- Ruiz, M.; Velasco, L. Performance evaluation of light-tree schemes in flexgrid optical networks. IEEE Commun. Lett. 2014, 18, 1731–1734. [Google Scholar] [CrossRef]
- Yang, L.; Gong, L.; Zhou, F.; Cousin, B.; Molnár, M.; Zhu, Z. Leveraging light forest with rateless network coding to design efficient all-optical multicast schemes for elastic optical networks. J. Light. Technol. 2015, 33, 3945–3955. [Google Scholar] [CrossRef]
- Fan, Z.; Li, Y.; Shen, G.; Chan, C.C.-K. Dynamic resource allocation for all-optical multicast based on sub-tree scheme in elastic optical networks. In Proceedings of the Optical Fiber Communication Conference, Anaheim, CA, USA, 20–24 March 2016. [Google Scholar]
- Fan, Z.; Li, Y.; Shen, G.; Chan, C.C.-K. Distance-adaptive spectrum resource allocation using subtree scheme for all optical multicasting in elastic optical networks. J. Light. Technol. 2017, 35, 1460–1468. [Google Scholar] [CrossRef]
- Cai, A.; Xu, K.; Zukerman, M. Comparison of different multicast approaches in elastic optical networks. In Proceedings of the ICTON 2018, Bucharest, Romania, 1–5 July 2018. [Google Scholar]
- Kabaciński, W.; Michalski, M.; Abdulsahib, M. Wide-sense nonblocking elastic optical switch. Opt. Switch. Netw. 2017, 25, 71–79. [Google Scholar] [CrossRef]
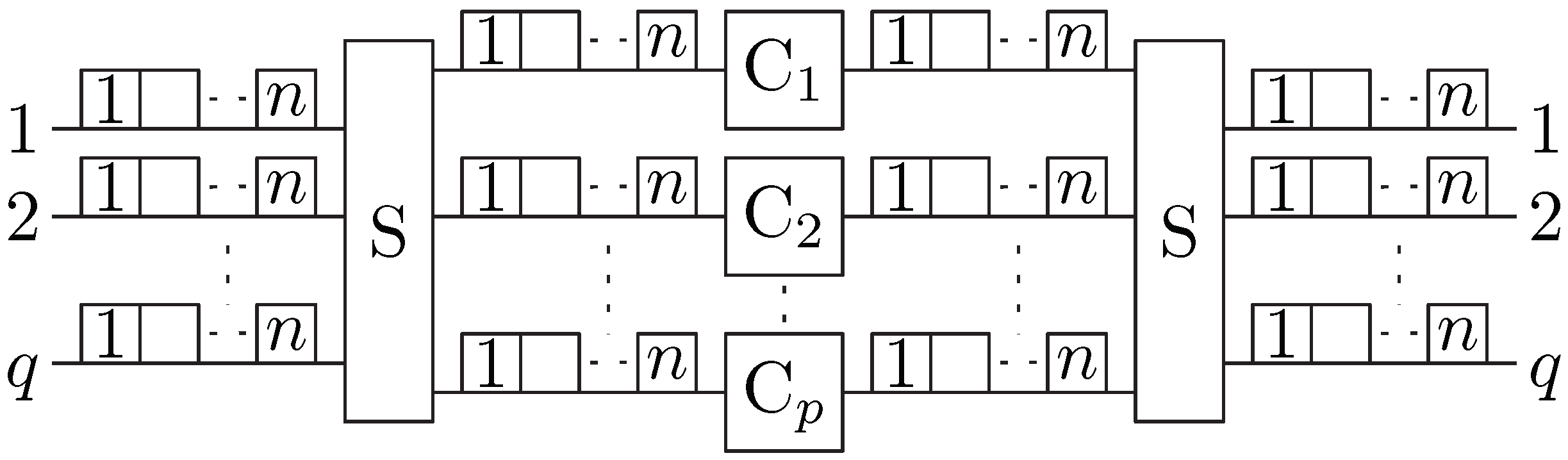
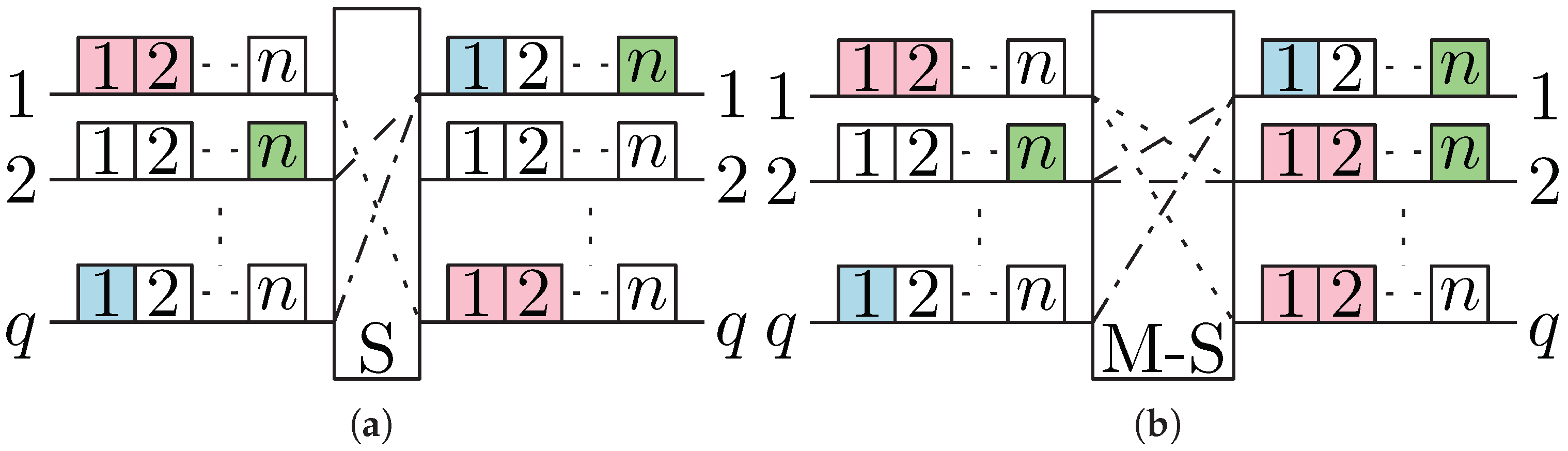
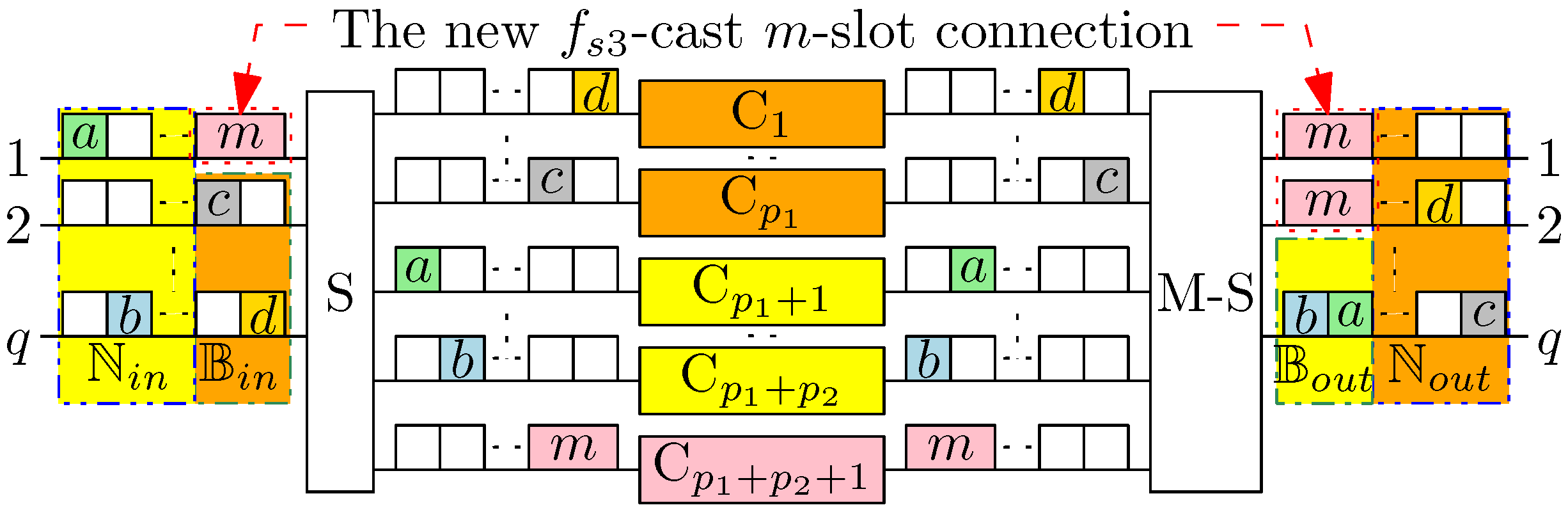
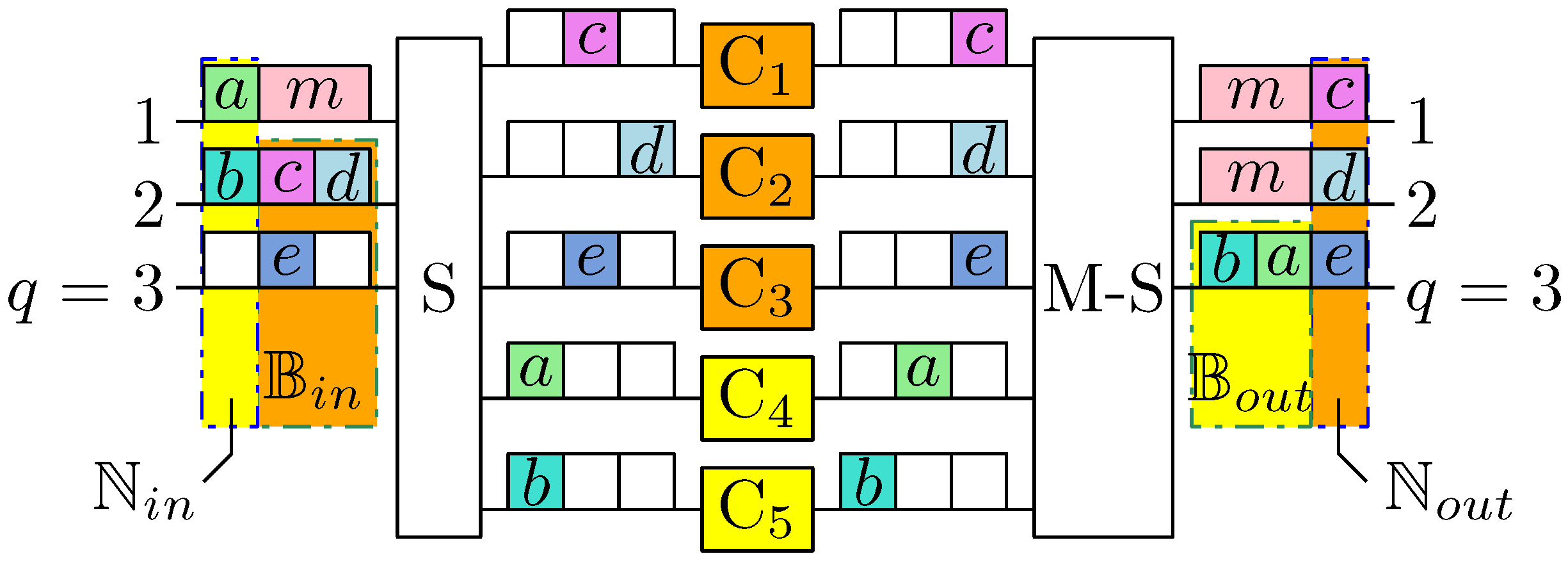
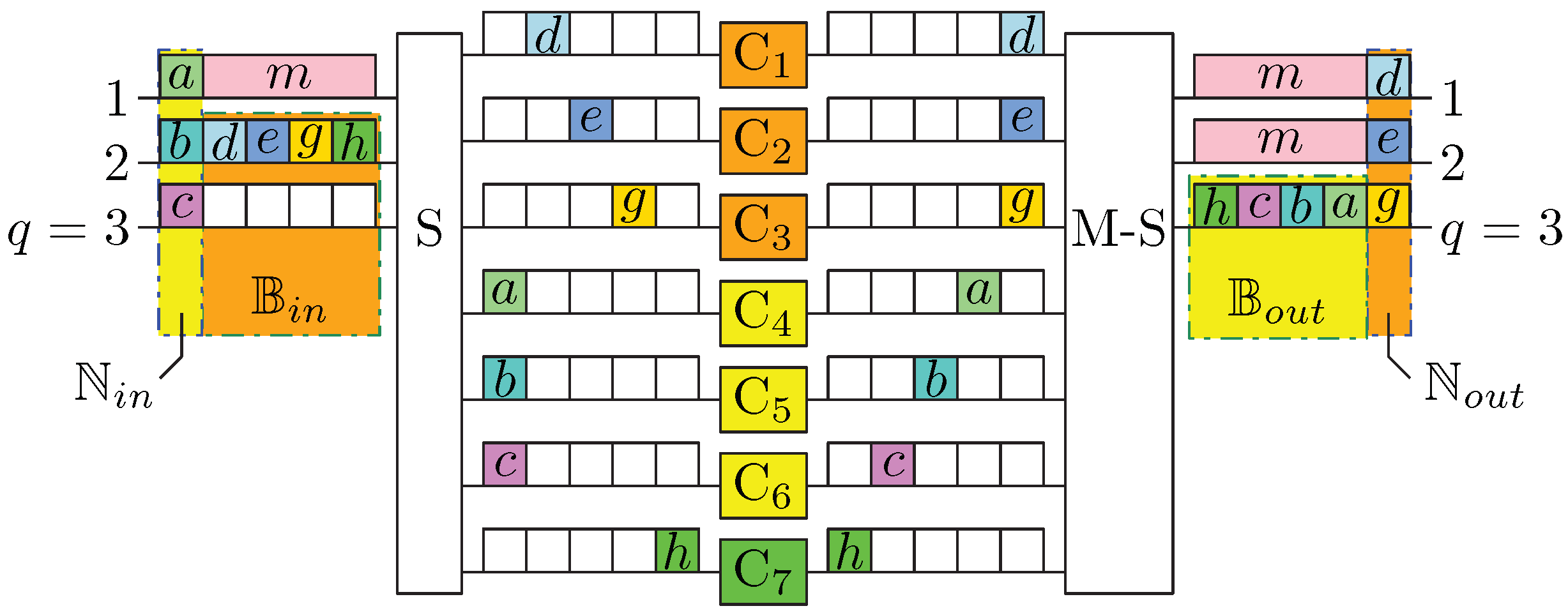
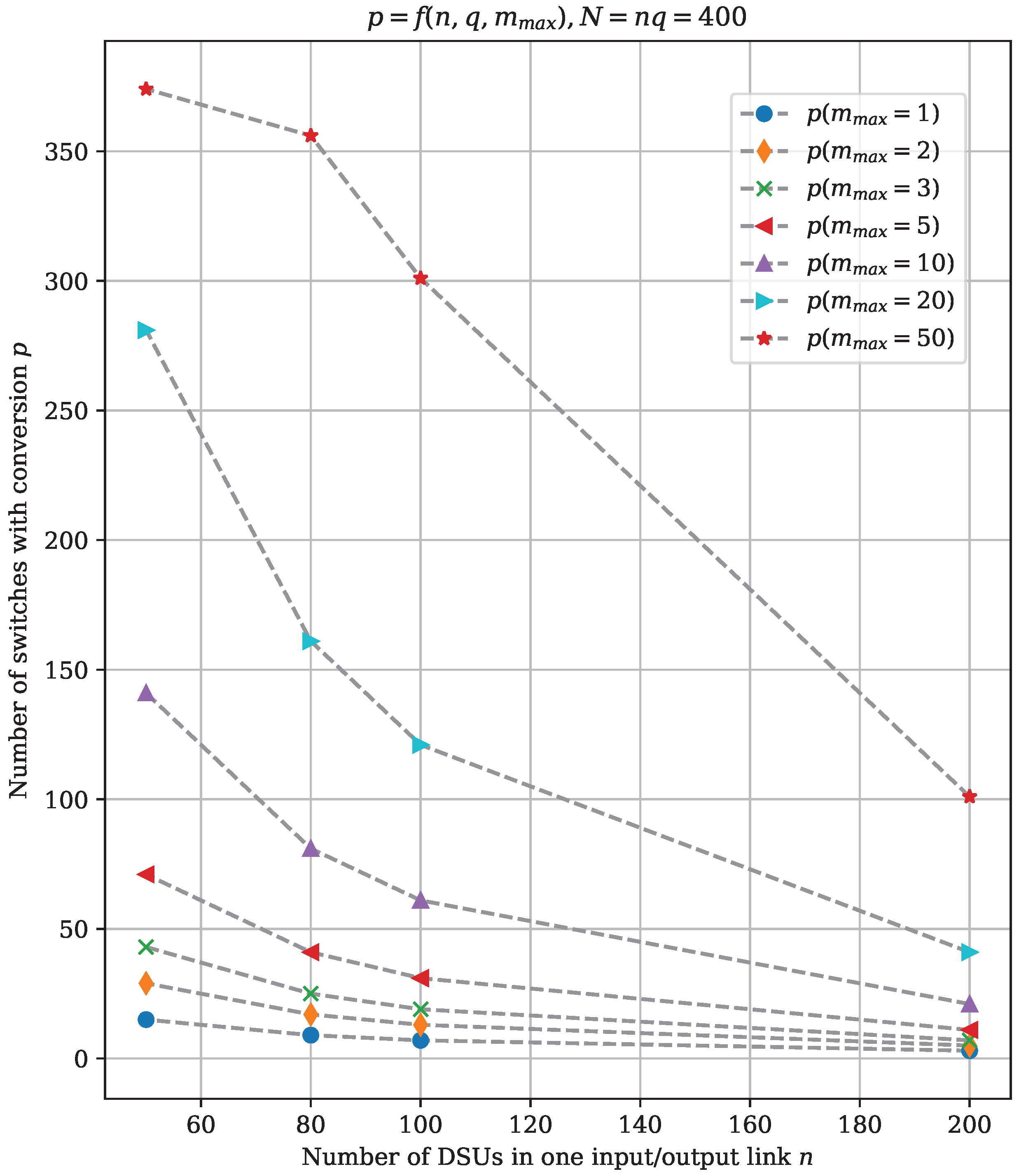
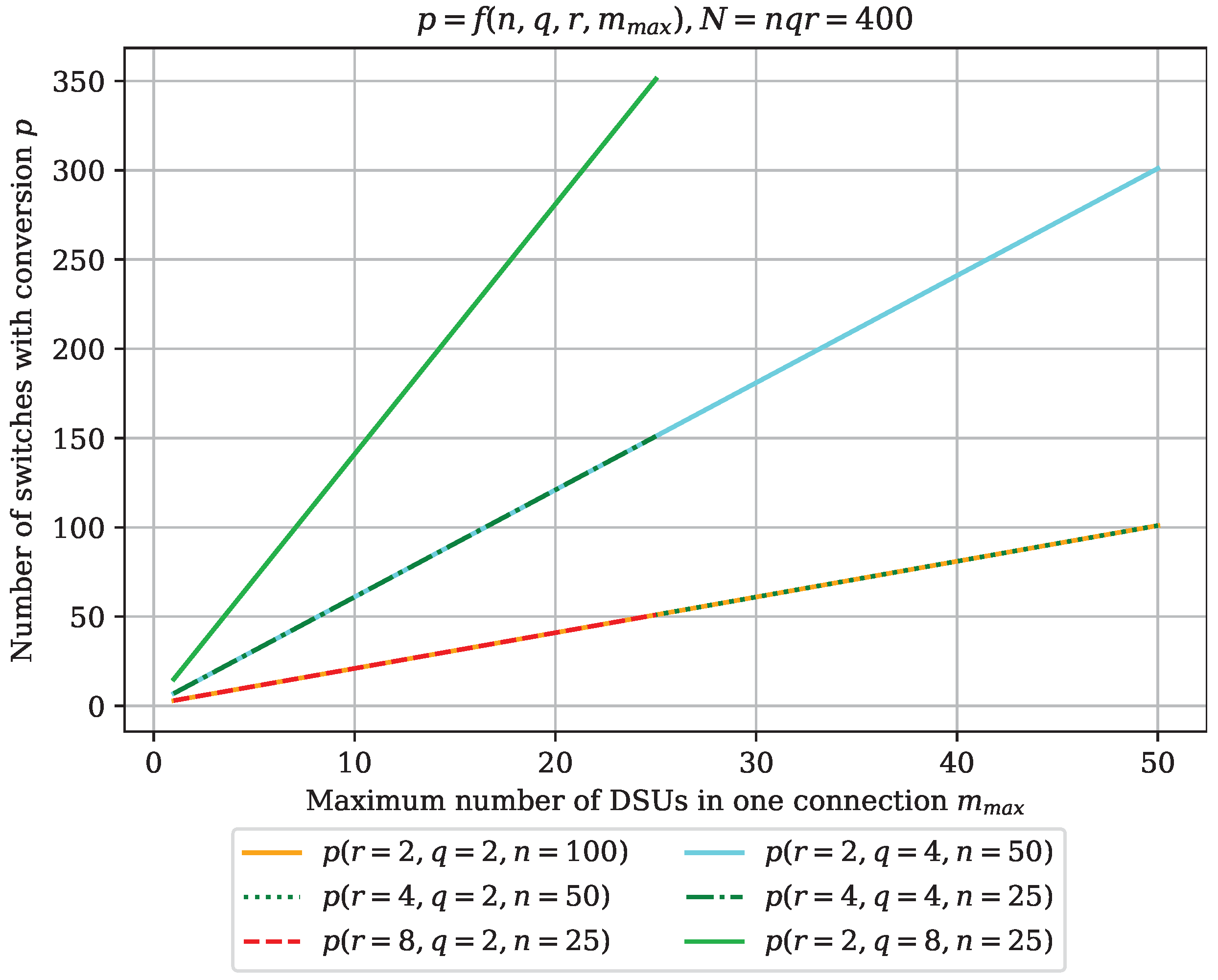
| M-SCS1, | M-SCS2 | ||||||
|---|---|---|---|---|---|---|---|
| 50 | 2 | 400 | 8 | 29 | 4 | 2 | 5 |
| 800 | 16 | 61 | 8 | 2 | 5 | ||
| 1000 | 20 | 77 | 10 | 2 | 5 | ||
| 5 | 400 | 8 | 71 | 4 | 2 | 11 | |
| 800 | 16 | 151 | 8 | 2 | 11 | ||
| 1000 | 20 | 191 | 10 | 2 | 11 | ||
| 10 | 400 | 8 | 141 | 4 | 2 | 21 | |
| 800 | 16 | 301 | 8 | 2 | 21 | ||
| 1000 | 20 | 381 | 10 | 2 | 21 | ||
| 100 | 2 | 400 | 4 | 13 | 2 | 2 | 5 |
| 800 | 8 | 29 | 4 | 2 | 5 | ||
| 1000 | 10 | 37 | 5 | 2 | 5 | ||
| 5 | 400 | 4 | 31 | 2 | 2 | 11 | |
| 800 | 8 | 71 | 4 | 2 | 11 | ||
| 1000 | 10 | 91 | 5 | 2 | 11 | ||
| 10 | 400 | 4 | 61 | 2 | 2 | 21 | |
| 800 | 8 | 141 | 4 | 2 | 21 | ||
| 1000 | 10 | 181 | 5 | 2 | 21 | ||
| 200 | 2 | 400 | 2 | 5 | 1 | 2 | 5 |
| 800 | 4 | 13 | 2 | 2 | 5 | ||
| 1000 | 5 | 17 | 3 | 2 | 5 | ||
| 5 | 400 | 2 | 11 | 1 | 2 | 11 | |
| 800 | 4 | 31 | 2 | 2 | 11 | ||
| 1000 | 5 | 41 | 3 | 2 | 11 | ||
| 10 | 400 | 2 | 21 | 1 | 2 | 21 | |
| 800 | 4 | 61 | 2 | 2 | 21 | ||
| 1000 | 5 | 81 | 3 | 2 | 21 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danilewicz, G. Multicast Space-Conversion-Space Strict-Sense Nonblocking Switching Fabrics with Multicast Opportunity in the Last Stage for Continuous Multislot Connections. Electronics 2023, 12, 4265. https://doi.org/10.3390/electronics12204265
Danilewicz G. Multicast Space-Conversion-Space Strict-Sense Nonblocking Switching Fabrics with Multicast Opportunity in the Last Stage for Continuous Multislot Connections. Electronics. 2023; 12(20):4265. https://doi.org/10.3390/electronics12204265
Chicago/Turabian StyleDanilewicz, Grzegorz. 2023. "Multicast Space-Conversion-Space Strict-Sense Nonblocking Switching Fabrics with Multicast Opportunity in the Last Stage for Continuous Multislot Connections" Electronics 12, no. 20: 4265. https://doi.org/10.3390/electronics12204265
APA StyleDanilewicz, G. (2023). Multicast Space-Conversion-Space Strict-Sense Nonblocking Switching Fabrics with Multicast Opportunity in the Last Stage for Continuous Multislot Connections. Electronics, 12(20), 4265. https://doi.org/10.3390/electronics12204265






