Similarity Distribution Density: An Optimized Approach to Outlier Detection

Abstract

When dealing with uncertain data, traditional model construction methods often ignore or filter out noise data to improve model performance. However, this simple approach can lead to insufficient data utilization, model bias, reduced detection ability, and decreased robustness of detection models. Outliers can be considered as data that are inconsistent with other patterns at certain specific moments and are not always negative data, so their emergence is not always bad. In the process of data analysis, outliers play a crucial role in sample vector recognition, missing value processing, and model stability verification. In addition, unsupervised models have very high computation costs when recognizing outliers, especially non-parameterized unsupervised models. To solve the above problems, we used semi-supervised learning processes and used similarity as a negative selection criterion to propose a local density verification detection model (Vd-LOD). This model establishes similarity pseudo-labels for multi-label and multi-type samples, verifies the accuracy of outlier values based on local outlier factors, and increases the detector’s sensitivity to outliers. The experimental results show that under different parameter settings with varying outlier quantities, Vd-LOD outperforms other detection models in terms of the significant increase in average time consumption caused by verifying the presence of relationships, while also achieving an approximate 6% improvement in average detection accuracy.

1. Introduction

With the development of information technology, uncertain data refers to data that carry a certain degree of uncertainty or fuzziness in the context of data generated by real-world models. This may be due to an anomaly or mutation that causes certain data points to differ from the regular data features. Such data are typically referred to as outliers or anomalies [1]. For example, in a set of parallel determinations, there may be individual measurement values that deviate significantly from the others. Furthermore, the definition of outliers in uncertain data differs from that of traditional discrete data. In uncertain data, outlier data may appear as isolated samples, but each sample is continuous in certain features and there are interrelationships between an independent sample vector and other vectors. These outliers often contain critical information, such as the network attack status and behavior in a network or the identification of mechanical failures in industrial equipment [2]. In these practical applications, there is no clear distinction between outliers and anomalies [3]. In such cases, the precise definition of these outliers often depends on hidden assumptions about the data structure and the detection methods employed [4]. An even more important issue is providing a formal definition for the concept of abnormal behavior or states, as different definitions of anomalies imply different detection methods [5]. Barnett [6] and Collett and Lewis [7] suggest that outliers generated during the observation process are values that deviate significantly from the other members of the sample. Hawkins [8] defines an anomaly as a value whose observed result differs significantly from the other results, leading to suspicion that it may have been influenced by other factors. This assumption is mainly based on the outlier property of the data sample.

Currently, most models for identifying such outliers are based on statistical methods, such as the Chanwennt criterion, as well as various linear regression methods based on histograms and boxplots constructed from sample vector values. However, these methods mostly employ unsupervised learning processes. The purpose of identifying outlier or abnormal values is only to remove the influence of these outliers on the fitting and training of conventional models. This makes it difficult for unsupervised learning models to propose a mathematical measurement method suitable for a wide range of datasets and scenarios to identify biases. Moreover, for computational systems, there is a gap between the way they determine normal and abnormal states among statistical sample vectors and human judgment. According to the key understanding of differentiating abnormal values from noise values by Salgado, C.M., et al. [9], for models that analyze data for anomaly detection, noise can be an example that is incorrectly labeled (class noise or false negative values) or an error in the data attributes (attribute noise or true negative values), as shown in Figure 1.

In conclusion, we propose a validation model for local outlier factors based on a semi-supervised learning process: the Local Outlier Density Verification Detection model (Vd-LOD). Instead of directly eliminating outlier data, this model analyzes the reasons behind data outliers by preserving them and improves the accuracy of the classification detection model by maximizing the retention of data features. It utilizes the similarity of individual classes as a prerequisite for negative selection and employs Lasso feature analysis to observe the mutual relationship between multi-type data vectors and targets. Additionally, it calculates the difference between independent vectors of different data types to determine their contribution to the overall data. Pseudo-labels are established based on the independent type of similarity among multi-class data, obtaining the density distribution of similarities. By validating the local outlier data based on the similarity distribution density of the global data, outlier factors are obtained by measuring the sensitivity of block vector similarity changes. This ultimately alters the overall detection results of the data. Finally, the effectiveness of this method is demonstrated by comparing the detection results with mainstream outlier detection models on public datasets.

2. Related Work

2.1. Outlier Data Analysis

One of the main limitations of data mining models in dealing with uncertain data samples is the computational issue. We tend to use a simple and fast method to alleviate the computational burden of the model. In this case, a dedicated outlier detection algorithm becomes highly valuable in processing time-series data if it can meet the system’s timeliness requirements. The generation of outliers in uncertain data mainly involves the following processes:

(1)

Sudden changes in data values, which are extreme manifestations of inherent variability in uncertain data in the overall numerical sense within the world model environment. Such outliers are essentially true and normal data, but their representation appears to be extreme. For example, a household may have minimal regular expenses but a large one-time purchase at a particular moment. Therefore, these outliers belong to the same population as the rest of the observations.

(2)

Due to the randomness inherent in specific experimental conditions, testing methods, or errors that arise during observation, recording, or calculation. These outliers are abnormal and erroneous data that do not belong to the same population as the rest of the observations.

Discrete samples of data are mainly classified into two types [10]: univariate and multivariate. Univariate discrete values often consist of data points composed of extreme values from the sample vector, while multivariate discrete values are obtained by combining at least two or more sample vectors that are mutually correlated and influencing each other. In unsupervised learning scenarios, the standard deviation of a set of sample vectors is often unknown, so analyzing the outlier status of the sample’s overall data based on another set of vectors to be tested often introduces bias.

The process of examining outlier data can be divided into two major categories [11,12]: one is the unsupervised detection process based on an unknown standard deviation environment. It utilizes the test data to establish features to analyze the outlier status in the data. The other is the supervised detection process based on a known standard deviation environment. It analyzes whether the outlier status in the data conforms to expectations by learning from known data. Under this premise, many current models attempt to use ensemble learning to solve the problem of inconsistent standards [13]. However, this approach ignores the independence of data sample vectors in outlier detection, i.e., the similarity between the sample vectors, and may mask outliers, thus overlooking the independent value of sample vectors [14]. Faced with high-dimensional data, outliers should be distinguished in terms of globality and independence. On one hand, the independence of vectors demonstrates fluctuations in sample vectors at a certain moment, but in terms of globality, they may tend to be normal and be ignored. On the other hand, global fluctuations can lead to the appearance of unknown labels. The ensemble learning model needs a standardization process for the results.

2.2. Outlier Detection Model

In recent years, many research results have appeared in the literature on anomaly detection, including exciting emerging research applications and discussions. This includes the development of universal, accurate, and efficient outlier detection models extending deep detection methods, which are being used in predicting [15,16], network security [17,18], sentiment analysis [19], clinical medicine [20], and other fields involving data mining [21,22]. Common outlier detection models include:

(1)

K-Means Clustering Algorithm: Divides the data into several clusters and determines if a sample is an outlier based on the distance between the sample and the cluster center.

(2)

DBSCAN Algorithm: Divides the data into clusters based on density and determines if a sample is an outlier by checking if its density is below a certain threshold.

(3)

Hierarchical Clustering Algorithm: Merges clusters hierarchically based on the distance between clusters and determines if a sample is an outlier based on this distance.

(4)

Isolation Forest Algorithm: Based on the random forest concept, it isolates normal samples into the leaf nodes of the trees and determines if a sample is an outlier based on the depth of the sample in the tree.

(5)

Outlier Detection Algorithms: Based on distance or density measures, such as Local Outlier Factor (LOF) and Local Correlation Integral (LOCI).

(6)

Semi-supervised Outlier Detection Algorithms: Combines labeled and unlabeled data, such as Support Vector Machines (SVM) and graph-based semi-supervised outlier detection.

(7)

Statistic-based Outlier Detection Algorithms: Uses statistical hypothesis testing, such as Z-test and T-test, to determine if a sample is an outlier.

(8)

Clustering-based Outlier Detection Algorithms: Uses the distance between samples and cluster centers to determine if a sample is an outlier.

These are just some common methods for outlier detection. There are many other outlier detection algorithms available, and the choice of method should consider the data characteristics and problem context.

Out of Distribution (OOD) [5,23,24] methods use machine learning processes to detect data instances far from the training distribution, typically assuming the distribution of normal class labels, to judge the differences in the fine-grained distribution of outliers. Curiosity-Guided methods [25] reward values in the data that satisfy definitions of novelty or rarity, driving the model to increase sensitivity to differential values, with the detection method being similar to reverse querying the data for novel/rare states or features. Li, Y., et al. [26] designed an AutoAD identification model: using a curiosity-guided search strategy to find the best deep neural network anomaly detection model, by introducing an experience replay mechanism based on self-imitation learning to improve sampling efficiency. Experimental results show that compared with existing manual models and traditional search methods, AutoAD recognition’s depth model has optimal performance.

Other interesting application studies include adversarial detection [27], fraud detection in recognition systems [28], and early detection of rare catastrophic events such as earthquake tsunami environmental alerts [29]. This presents a challenge for outlier detection, a significant reason being the identification of a rare and unlabeled instance in data with ultra-high dimensional data, no clear boundaries, massive data streams, and large-scale distributed or discrete state features. Raza, A. et al. [30] proposed A deepfake predictor (DFP) method based on a hybrid architecture of VGG16 and convolutional neural networks. We achieve high accuracy in deepfake detection, proving that the DFP method outperforms transfer learning techniques and other state-of-the-art research.

Most shallow and deep data instance anomaly detection models have probability-statistical assumptions [31,32]: independent and identically distributed (IID) of anomaly data, that is, at any time in a random process, the value is a random variable. If these random variables are from the same distribution and are independent of each other, then these random variables are independently identically distributed [33]. However, in practical application environments, anomalies may be influenced by some non-IID features. For example, in early disease detection, multiple synchronous disease symptom anomalies are mutually reinforcing. This requires considering the relationship between the global and local features of the sample data. This task is vital in complex situations, for instance, without considering these non-IID anomaly features’ connection, when anomaly values only exhibit slight deviations, they are likely to be overlooked by the model detector’s data space. For example, in medical diagnosis, suppose the real anomaly data represent a definite attribute of the disease, while noise can cause random changes in the detection information attribute. In Braei M. and others’ test [5] for anomaly detection in 20 univariate time series data among statistical, machine learning, and deep learning methods, the results showed that statistical methods performed best. As the deep learning model’s application spreads and research deepens in various fields, Peng G. and others [34] believe that deep learning-based anomaly detection methods outperform traditional models in complex data processing performance. This is because such methods have a high detection accuracy, and the interpretability and operability of the model structure facilitate understanding model decisions. However, they also suffer from uncertainty in the definition of anomaly features, making the interpretability and operability of deep model results unreliable [35]. Liao et al. [36] proposed a unified unsupervised Gaussian mixture variational autoencoder (VAE) for anomaly detection. This framework combines variational autoencoder, deep belief network, and Gaussian mixture model to jointly optimize the inference model. The simulation experiments on the dataset show that this framework outperforms the current state-of-the-art outlier detection methods. Li et al. [37] introduced an outlier detection method based on variational autoencoder (VAE), which combines low-dimensional representations with reconstruction errors to detect outliers. Experimental results demonstrate that the proposed method performs better than or at least comparable to existing methods.

2.3. Related Research

(1)

Data feature boundaries

The treatment of feature boundaries in sample vector features is of great importance in the outlier detection process. In the case of uncertain data generated by various high-precision sensors, especially when the boundary between redundant and unrelated data becomes blurry, the presence of redundant and unrelated data in the sample vector features can have a negative impact on the boundary. Additionally, an excessive iterative feature computing process can increase the cost of outlier detection, thus affecting the overall performance of the model. Therefore, it is necessary to consider selecting appropriate samples to establish sample boundaries. In the research process of data anonymization, some researchers have demonstrated the boundedness of data tuples [38] and conducted a series of exploratory work [39]. They have proposed a new algorithm for event boundary detection, which has achieved good results.

(2)

Detectors

In the current outlier detection methods based on immune theory, the research on detectors mainly focuses on intrusion detection or anomaly detection. The working mechanism of such models leads to a single target of the detector, and random sampling causes fluctuation in accuracy. Moreover, handling redundant data issues leads to wastage of computational resources, resulting in poor performance. In terms of the core mechanism of the model, it lacks flexibility and has poor dynamic adjustment ability for boundaries, making it unable to adapt to dynamically changing abnormal data environments. The researchers proposed a hybrid classification detector combining decision tree and rule-based concepts, which achieved some effectiveness [40].

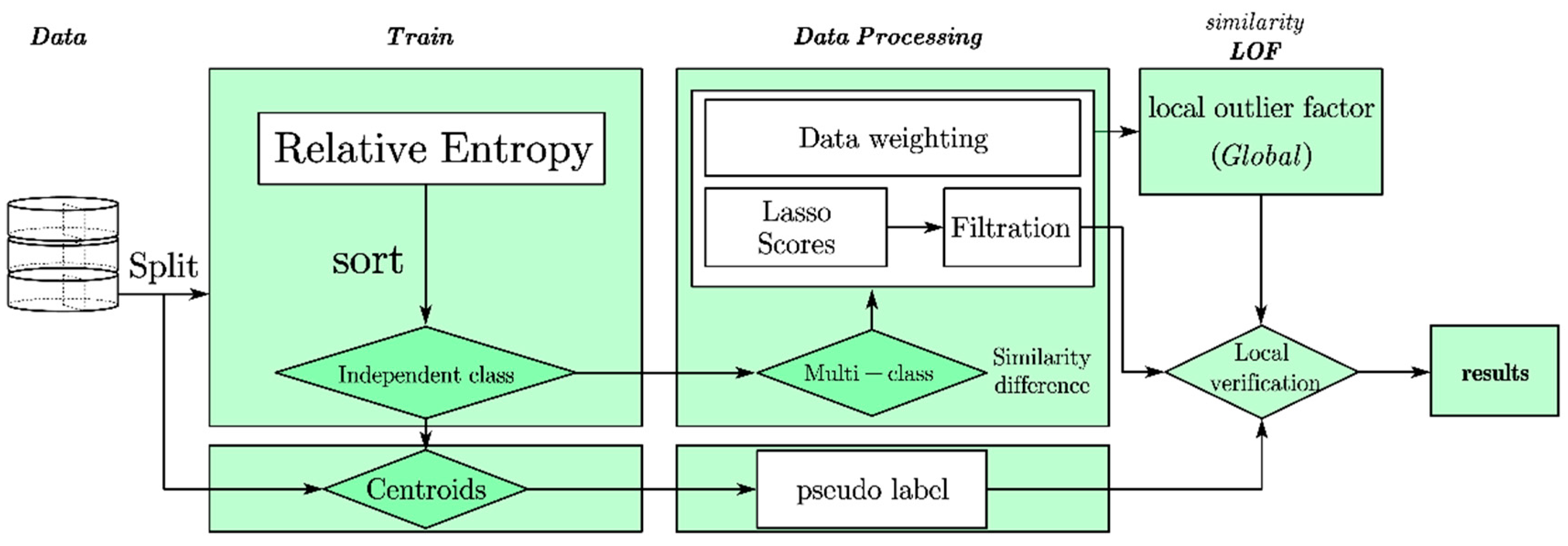
3. Detection Model Building

The goal of Vd-LOD is to improve training speed while ensuring acceptable predictive performance. It addresses the issues of data dimensionality and computational burden by employing the negative selection method. It is important to note that the purpose of Vd-LOD is to ensure training and prediction efficiency while utilizing pseudo-labeling to enable the model to learn. Vd-LOD primarily constructs the model in three aspects: feature selection for block vectors, local similarity density, and verification relationship establishment. The research architecture is illustrated in Figure 2 below.

3.1. Feature Selection for Block Vectors

Block vector is a data structure that facilitates the management and processing of large-scale data. It divides the data into blocks of a certain size and represents them in the form of vectors. Each block contains a certain number of data elements. The data block vector is a data structure that partitions large-scale data into a series of blocks and manages them through vector representation. It aims to improve data access efficiency and processing performance. Additionally, to enhance data reliability, importance, and model adaptability, in the face of imbalanced quantities of data samples in different categories and to avoid underestimating minority classes during model training, data can be weighted. We utilize the difference in Lasso feature scores to normalize the data, forming standard weighted data in block vector format. This is then combined with the information relative entropy method to obtain feature selection results.

Relative entropy, also known as Kullback–Leibler divergence or KL divergence, is a concept used to measure the difference between two probability distributions. In the study of entropy, scholars such as Clausius, Boltzmann, Gibbs, and Shannon have provided their own interpretations of entropy, and these definitions of entropy are essentially consistent [41]. At present, various studies on entropy describe it as a measure of disorder [42,43,44], where the entropy is minimal when a sample possesses a specific characteristic and increases as the deviation from that characteristic grows. According to the theory of entropy, for any independent vectors of similarly high similarity, they should always maintain an appropriate value. In this case, the entropy value of the data should be a small measure. Therefore, according to the theory of relative entropy, in time-sequential continuous data, the entropy of discrete data can be measured based on the entropy of continuous data. Relative entropy measures the relationship between two random distributions. When the distributions are the same, the relative entropy is zero, and it increases as the distributions differ. This relationship has also been confirmed in some studies [45,46,47,48].

Based on the research on relative entropy, the definition of model data weighting in relative entropy is as follows:

Definition 1.

The weighted relative entropy of information is defined as:

$$D\left(P\right|\left|Q\right)=\Sigma w_i\ast [P_i{\ast \mathit{log}(P}_i{/Q}_i)]$$

(1)

where $w_i$ represents the weight of the $i$ data point.

Definition 2.

First, the relative entropy of information for each data point’s probability distribution is defined as:

$$D\left(P_i\right|\left|Q_i\right)=P_i\ast log(P_i/Q_i)$$

(2)

By weighting and summing the relative entropy of information for each data point, we obtain the weighted relative entropy of information:

$$D\left(P\right|\left|Q\right)=\Sigma w_i\ast [P_i{\ast \mathit{log}(P}_i{/Q}_i)]$$

(3)

We can transform the division in the above equation to:

$$D\left(P\right|\left|Q\right)=\Sigma w_i\ast [P_i{\ast \left(\mathit{log}\right(P}_i{)-\mathit{log}(Q}_i))]$$

(4)

Based on the properties of logarithms, we can convert multiplication to addition:

$$D\left(P\right|\left|Q\right)=\Sigma w_i\ast [P_i{\ast \mathit{log}(P}_i)]-\Sigma w_i\ast [P_i{\ast \mathit{log}(Q}_i)]$$

(5)

Here, the first term $\Sigma w_i\ast [P_i{\ast \mathit{log}(P}_i)]$ can be seen as the weighted entropy of the probability distribution $P$, denoted as $H_w\left(P\right)$. The second term $\Sigma w_i\ast [P_i{\ast \mathit{log}(Q}_i)]$ can be seen as the weighted joint entropy of the probability distributions $P$ and $Q$, subtracted by the weighted entropy of the distribution Q, denoted as H_w(P,Q) − H_w(Q).

Therefore, the weighted relative entropy of information can be represented as:

$$D\left(P\right|\left|Q\right)=H_w(P,Q)-H_w\left(Q\right)$$

(6)

Here, H_w(P,Q) represents the weighted joint entropy of the probability distributions P and Q, and H_w(Q) represents the weighted entropy of the probability distribution Q.

The weighted relative entropy measures the differences between two probability distributions while considering the weights of the data. Similarly, when the two distributions are closer, the weighted relative entropy tends to zero, indicating a greater similarity between the distributions. When the distributions differ more, the weighted relative entropy is nonzero, indicating a larger difference between the distributions. By sorting the results of the relative entropy of mutual information and using the median as the initial boundary, we retain block vectors that contribute the most to the data samples. This yields independent preserved block vectors. Then, the entropy of the preserved vectors is normalized, and the preserved vectors are weighted with data for further differentiation.

3.2. Pseudo-Labeling

Pseudo-labeling is a semi-supervised learning paradigm that learns from both unlabeled and labeled data. It selects the class with the highest predicted probability as the pseudo-label. Formally, it is equivalent to entropy regularization or entropy minimization.

During the pseudo-labeling generation process, the relative entropy between the true distribution and the predicted distribution is minimized, which is equivalent to minimizing. By computing the similarity between the data vectors and the centroid vectors, an appropriate threshold is chosen to select the samples with predicted probabilities higher than the threshold as pseudo-labels, thus adjusting the predicted distribution to be closer to the true distribution. The main steps are as follows:

-

Step 1: Initial model training: Train an initial model using a small, labeled training dataset.

-

Step 2: Pseudo-label generation: Use the trained initial model to make predictions on unlabeled data and select samples with predicted probabilities higher than a threshold as pseudo-labels.

-

Step 3: Expand the training set: Combine the pseudo-labels with the existing labeled dataset to form an expanded training set.

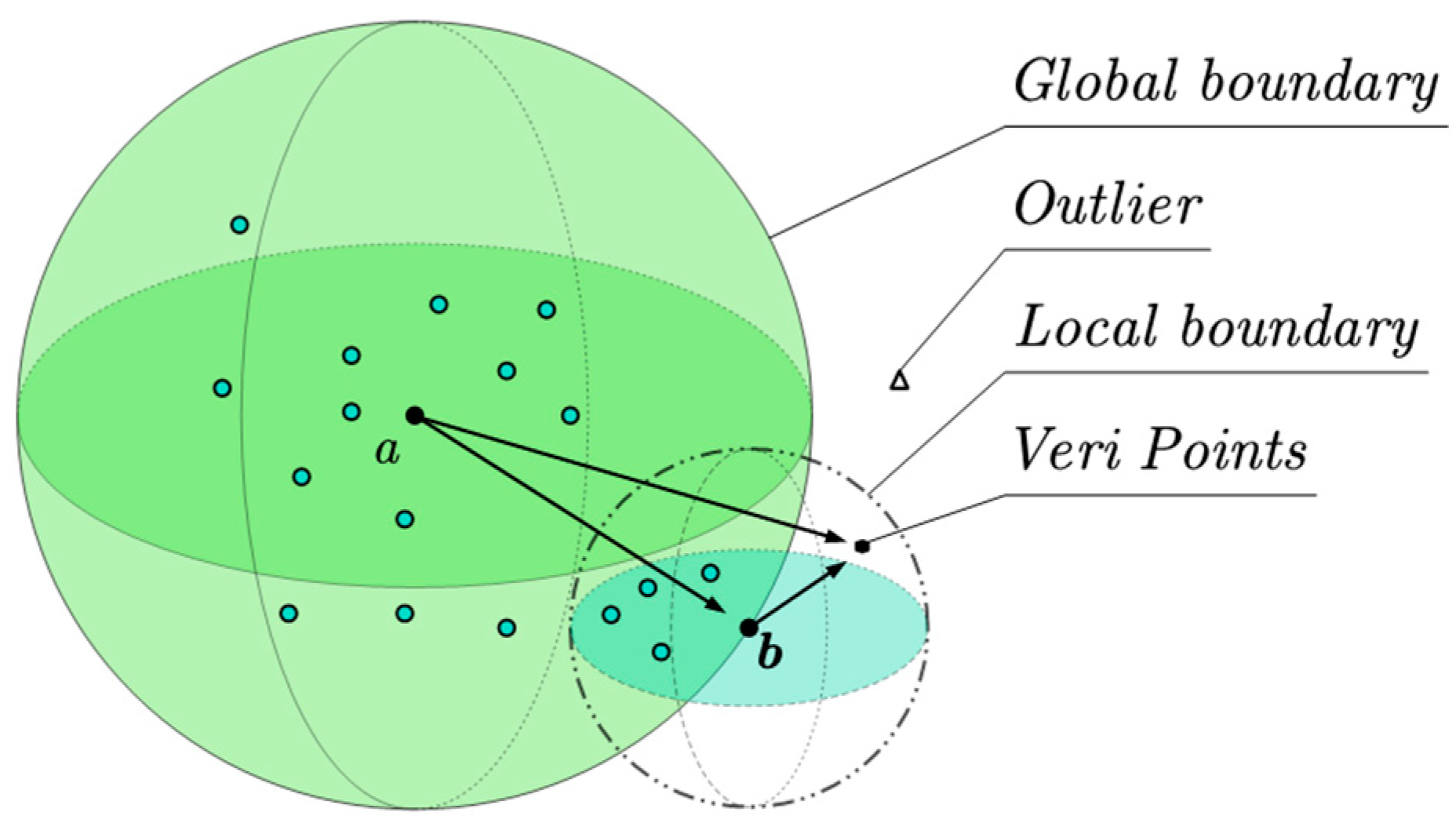
3.3. Local Similarity Density

In the process of identifying outliers in multi-sample and multi-type data samples, using density distribution is a faster way of outlier detection, and the Local Outlier Factor (LOF) method is a method based on the local density relationship between independent vectors of data samples. The traditional LOF algorithm measures the abnormality of a sample vector based on the relative density of the data sample vectors in its surrounding neighborhood. The basic assumption of density-based outlier detection methods is that the density around non-outlier objects is similar to the density around their neighborhood, while the density around outlier objects is significantly different from the density around their neighborhood. The definitions related to the local similarity density based on the LOF detection algorithm are as follows:

Definition 3.

If there exists a collection of time-ordered sample sets D, assuming there are n samples, and the data dimension is m, then for any sample $\forall X_i=(x_{i1},\cdots ,x_{im})\in D$, where $i\in n$.

The Bray–Curtis measure is expressed as follows.

$$d_{BrayCurtis}={\displaystyle \sum _i|}{X}_i-Y_i|/{\displaystyle \sum _i(}{X}_i+Y_i)$$

(7)

Definition 4.

For any sample vector x_i, the similarity measure between point x_med and centroid according to Formula (7) is called the similarity measure of point, denoted as, and we have:

$$s(x_i)={\displaystyle \sum _i|}{X}_i-Y_i|/{\displaystyle \sum _i(}{X}_i+Y_i)$$

(8)

Definition 5.

If there exists s(x_i), there will be a set S(x_i) of identical sample vectors s(x_i) in the sample, which satisfies s(x_i) ≤ n.

Definition 6.

If $x_i$ and the surrounding neighborhood points belong to the same cluster, then the reachable distance is more likely to be a smaller value of similarity $s\left(x_i\right)$. Additionally, the smaller ${\displaystyle {\sum }_{i=1}^{n}s\left(x_i\right)}$ is, the larger the local density becomes. Therefore, the definition of reachable density distance is related to the concept of $s\left(x_i\right)$. Consequently, when given parameter $k$, the reachable distance $d(x_j,x_i)$ from any data point $x_j$ to data point $x_i$ should be the maximum value between the similarity measure $s_k\left(x_i\right)$ of data point $x_i$ and the direct distance $s_k(x_j,x_i)$ between sample vectors $x_j$ and $x_i$. That is:

$$s_k(x_j,x_i)=max\left\{s_k\right(x_i),s(x_j,x_i)\}$$

(9)

Definition 7.

According to the aforementioned definition of the local reachable distance, the reachable similarity density of any $x_j$ is:

$${\rho }_k(x_j)=\frac{S_k\left(x_j\right)}{{\displaystyle {\sum }_{x_i\in S_k\left(x_j\right)}^{}{s}_k(x_j,x_i)}}$$

(10)

Calculate the local relative density of any data vector $x_j$ using formula (7), and obtain the local outlier factor of $Lo{F}_k\left(x_j\right)$:

$$Lo{F}_k(x_i)=\frac{{\displaystyle {\sum }_{x_i\in S_k\left(x_j\right)}^{}\frac{{\rho }_k\left(x_i\right)}{{\rho }_k\left(x_j\right)}}}{\left|S_k\left(x_j\right)\right|}$$

(11)

If the ratio of $Lo{F}_k\left(x_j\right)$ is closer to 1, it indicates that the neighborhood point density of $x_j$ is low, and it may belong to the same cluster as the neighborhood $S_k\left(x_i\right)$. If the ratio is less than 1, it means that the density at the location of $x_j$ is higher than the density of its neighborhood points, indicating that $x_j$ is a dense point. If the ratio is greater than 1, it suggests that $x_j$ may be an outlier.

In real-world datasets, outliers are often multiple rather than singular and have certain correlations. Under such conditions, if only considering the global sample correlation of the dataset from the traditional distance-based detection methods to find the properties of outliers, the found outliers are all global outliers. However, in reality, the data structure is more complex, and outlier objects may be considered as outliers with respect to their local neighborhoods rather than the entire data distribution. Therefore, it is necessary to analyze the local vectors through global data.

3.4. Negating the Matching Authentication Relationship

The model utilizes a negative selection process to reanalyze the consistency of overall density of discrete values in the samples. It performs mutation operations on the center lines that satisfy the similarity threshold and updates the prediction results after validating the inconsistent data. Following the negative selection method of the immune process, the method architecture is depicted in Figure 3, and the method demonstration is illustrated in Figure 4. The following definitions are established:

$m$: indicates the number of vectors contained in the independent sample, where $m\in N^{+}$;

$l$: indicates the length of the sample vector string, where $l\in N^{+}$;

$r$: indicates the number of consecutive matching digits, that is, the matching measure, where $r\in N^{+}$.

Definition 8.

Self $S$ is a collection of strings of length $m$, existing as $S=\{X_1,\cdots ,X_m\}$, with arbitrary strings $X_i=\{x_1,\cdots ,x_l\}$.

Definition 9.

If for $D$, successive bits of the string to be detected $Y=\{y_1,\cdots ,y_m\}$ and any $X$ existing in the detector $r$ are greater in similarity compared to the threshold, then it is inferred that $Y$ is a match to $X$.

Definition 10.

If two strings $Y$ and X match, then according to the matching rules L, starting from the leftmost end of the string of length $r$, there are consecutive matches that correspond to each other, that is,

$$Y\prime =\{y_i,\cdots ,y_r\}\iff X\prime =\{x_i,\cdots ,x_r\}$$

(12)

Then, the match probability is

$$\begin{array}{c}\underbrace{\frac{1}{m}\times \frac{1}{m}\cdots \frac{1}{m}}\\ r\end{array}=m^{-r}$$

(13)

Definition 11.

If the starting position of the match is from the $Y_i$ second bit to the first position on the left, there is an intermittent match, that is, there is always a mismatch at  $l-r+1$ before the starting position of each successful match. Then, there will be multiple independent matching values $\acute{r}$, and $r_i={\displaystyle \sum \acute{r}}$, and the probability of each successful match is

$$p\left(Y_i\right)=\frac{m-1}{m\times m^{-r_i}}$$

(14)

The match probability is approximate, and the total probability of two strings matching is.

$$p_m\approx m^{-r}[1+\frac{(l-r)(m-1)}{m}]$$

(15)

The value of $p_m$ is affected by $m$, $r$, and $l$. The $p_m$ value obtained based on $x_i$ is compared with the $s\left(x_i\right)$ value. If the matching similarity of the $p_m$ string is lower than $s\left(x_i\right)$, it indicates that the vector is closer to the density center and is regarded as a normal value; otherwise, a new density center is established.

According to the linear regression process and based on the results of the local density analysis of samples and local density outlier analysis of independent vectors, pseudo-labels can be used to establish a verification mechanism for the difference between global samples and sample vectors and relate global samples and sample vectors to each other, as shown in Figure 4.

4. Testing of Process

4.1. Experimental Environment

In this section, we compare the performance of our similarity outlier detection algorithm based on block vector entropy-weighted similarity in different datasets using the dissimilarity distance metric. The experiments were conducted on a cloud server environment with an Intel(R) Xeon(R) Platinum 8255C CPU @ 2.50 GHz processor and 8 GB RAM, running Ubuntu 22.04.1 LTS desktop version. The experiments were implemented in Python 3.11.

The ratio of the training set to the test set in the model is set to 0.3. Additionally, the preset parameter for the outlier detector, Outliers fraction, provides information about the proportion of anomalous values in the dataset. The values are set to 0.01, 0.1, and 0.15, respectively. The data prediction process of the model is conducted by sequentially inputting simulated time series data and calculating the results, followed by statistical analysis of the entire set of results.

(1)

Contrast algorithms

The main algorithms for outlier detection in the comparative testing are based on the Python Outlier Detection (PyOD) toolkit. The key algorithms and their corresponding parameters for comparison are listed in the following

Table 1. Correlation parameters of comparison models.

PyOD Algorithm	Outliers Fraction	Parameters
LOF	0.01/0.1/0.15	n_neighbors = 20, algorithm = ‘auto’, leaf_size = 30, metric = ‘minkowski’, p = 2, metric_params = None
SOS		perplexity = 4.5, metric = ‘euclidean’, eps = 1 × 10−5
KNN		n_neighbors = 5, method = ‘largest’, radius = 1.0, algorithm = ‘auto’, leaf_size = 30, metric = ‘minkowski’, p = 2,
HBOS		n_bins = 10, alpha = 0.1, tol = 0.5
IForest		n_estimators = 100, max_samples = “auto”, contamination = 0.1, max_features = 1., bootstrap = False,
MCD		store_precision = True, assume_centered = False, support_fraction = None,

.

• Local Outlier Factor (LOF): LOF is a density-based outlier detection method. It determines outlier points by calculating the difference in density between each sample point and its neighborhood points. If a sample point has a significantly lower density compared to its neighbors, it is likely to be an outlier.
• Local Correlation Integral (LOCI): LOCI is a method based on the principle of correlation. It determines outlier points by calculating the difference in density between a sample point and its neighboring points. Compared to global correlation integral methods, LOCI is more suitable for data with non-uniform density distribution.
• Stochastic Outlier Selection (SOS): SOS is a random selection-based outlier detection method. It determines outlier points by randomly selecting sample points and calculating their outlier scores. SOS method has good scalability and efficiency.
• k-Nearest Neighbors (KNN): KNN is a distance-based outlier detection method. It determines outlier points by calculating the distances between each sample point and its k-nearest neighbors. If a sample point has a large distance compared to its nearest neighbors, it is likely to be an outlier.
• Isolation Forest (IForest): IForest is a tree-based outlier detection method. It determines outlier points by randomly constructing binary search trees to partition the samples and calculating the path lengths of sample points in the trees. IForest method has high efficiency and scalability.
• Minimum Covariance Determinant (MCD): MCD is a method based on the distribution of high-dimensional data. It determines outlier points by selecting a subset with the minimum covariance determinant. MCD is suitable for high-dimensional data and multivariate anomaly detection.

(2)

Data set

The testing dataset primarily consists of publicly available data from the medical domain. This choice is made because in this domain, the feature differences in multi-class data are relatively small, requiring the model to be sensitive to data variations. The dataset is described as follows, and the distribution of testing samples is presented in

Table 2. Sample parameters of the test data.

	Data Set	Samples Number	Attributes Number	Classes Number
1	Breast_Cancer	569	30	2
2	HCV	598 1	13	4
3	ECG	1200	48 2	4

¹ For HCV dataset, number of original data samples was 616 cases, but only 598 cases were retained after null data items were removed during data preprocessing. ² The vector of the number of samples in the original data in the ECG dataset is 54 columns, and 48 columns are retained after eliminating null data items during data preprocessing.

:

• Wisconsin Breast Cancer (Diagnostics) Dataset (Breast Cancer) [49] (Kaggle). For this dataset, the data were extracted from digitized images of fine needle aspiration (FNA), by which breast lumps were diagnosed. Each feature in this dataset describes the characteristics of the nucleus found in the digitized image described earlier. There are three types of features in this dataset, where real-valued features are calculated from digitized images and contain information about regions, cell radii, textures, etc., which are used to predict whether a lump is benign or malignant (0 or 1).
• HCV Dataset: The HCV dataset contains laboratory values and demographic statistics such as age for blood donors and patients with Hepatitis C Virus (HCV). The target attribute for classification is the category, which includes blood donors and HCV (Hepatitis C, Fibrosis, Cirrhosis). All attributes, except for category and gender, are numeric real values. The laboratory data are represented in columns 5 to 14 of the sample vectors.
• ECG of Cardiac Ailments Dataset [50,51]: This dataset consists of 1200 cardiac electrocardiogram (ECG) records related to cardiovascular diseases. Each set of 300 records corresponds to a specific disease. A total of 54 features are extracted for each disease using the MODWPT technique, resulting in a file size of 1200 × 54 records.

(3)

Evaluation indicators

The Vd-LOD method is based on the local density factor for identifying uncertain data, and it also uses pseudo-labels to determine the outlying trend. This method is consistent with the evaluation conclusions of outlier detection models in the PyOD library. Therefore, model accuracy is compared by calculating the computation time and single identification detection results for outlying data. The difference is that the Vd-LOD model calculates the proportion of outlier detection based on the recognition of density outlier values of the global samples using the local vector verification method, whereas other models use default outlier value recognition proportions.

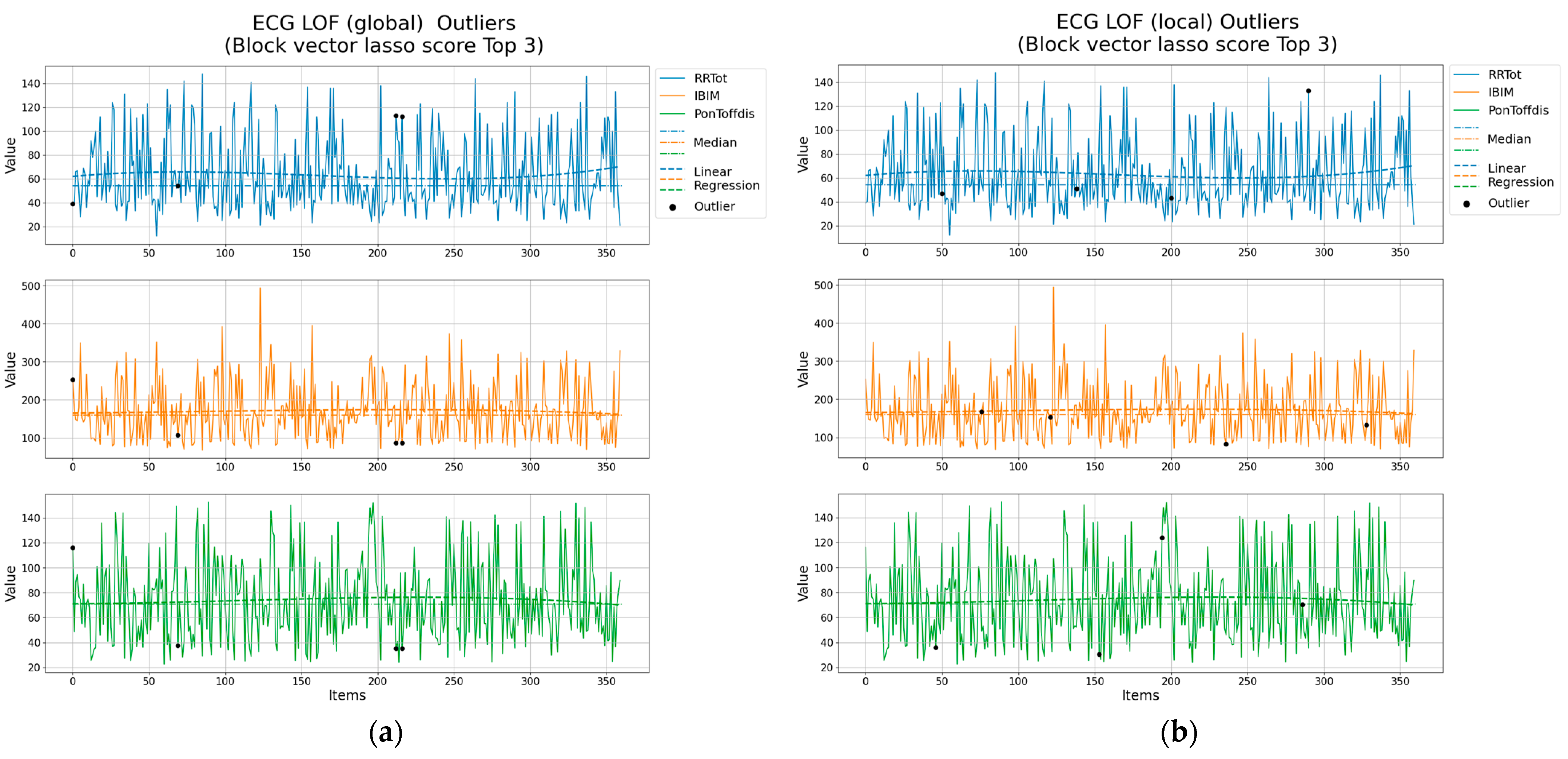
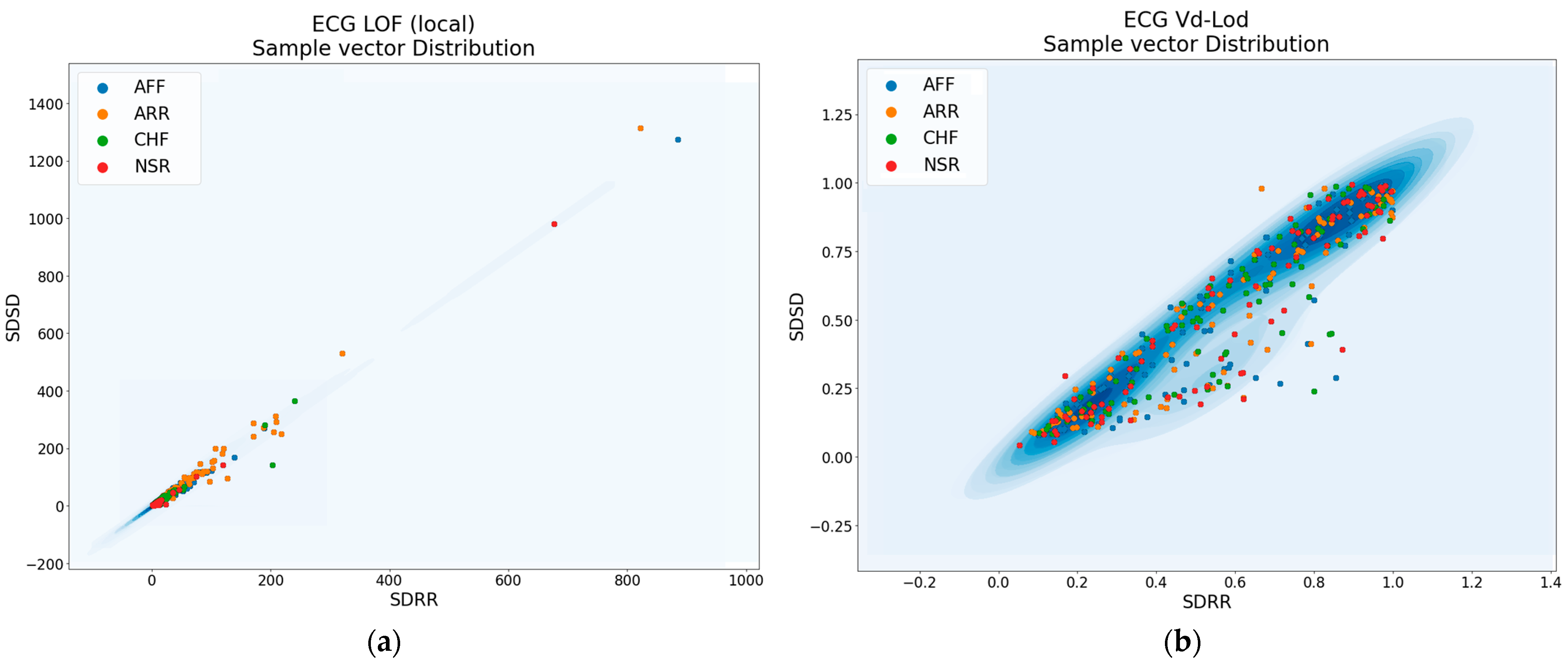
4.2. Result

To reduce the use of images, the ECG dataset combined with the LOF (Local Outlier Factor) model is used as the primary showcase for the model (taking the top three feature scores from Lasso). The parameter ‘Outliers fraction’ is set to 0.1 for the outlier data, while for other datasets, only the results are recorded.

By using the traditional LOF model, the calculation of outlier data for the global vector and block vector is performed, and data distribution Figure 5 are obtained. Comparing the Figure 5a,b, it can be observed that there is a clear difference in the distribution of outlier data obtained under the two conditions. By using similarity measurement methods, the calculation of outlier data for the reblocked vector is performed, resulting in Figure 6. It can be observed that the judgment of outlier data is more reasonable.

Combining the pseudo-labeling method with the judgement of outlier data distribution, as shown in Figure 7, it can be observed that the data with similarity-based pseudo-labels (Figure 7b) has clearer data boundaries compared to the original data (Figure 7a). This is because the similarity-based pseudo-labeling takes into account sample similarity when generating pseudo-labels, assigning similar unlabeled samples to the same class as labeled samples. Therefore, the additional samples generated by similarity-based pseudo-labeling can better integrate with the original data, making the overall data distribution more compact. Additionally, utilizing the data with similarity-based pseudo-labels can also help improve the performance of machine learning models. By introducing more data samples, we can better capture the characteristics and patterns of the data, thereby enhancing the model’s generalization ability and accuracy. The introduction of similarity-based pseudo-labeling enables the model to learn the details and boundaries of the data more effectively, assisting the model in better predicting the class of new samples.

The results obtained from tests under different parameter conditions are presented in

Table 3. Comparison of outlier recognition results between Vd-LOD and each model in different datasets.

Breast_Cancer Dataset					Digts: 2, Samples: 399, Features: 2
Split 0.3	0.01			0.1			0.15
Init	Time	Outliers	Acc	Time	Outliers	Acc	Time	Outliers	Acc
PRAISE	0.027 s	4	0.99	0.025 s	40	0.9	0.030 s	60	0.85
LOCI	81.994 s	30	0.925	84.140 s	26	0.935	82.732 s	32	0.92
SOS	0.677 s	4	0.99	0.688 s	40	0.9	0.687 s	60	0.85
KNN	0.006 s	4	0.99	0.005 s	40	0.9	0.016 s	60	0.85
CBLOF	1.793 s	4	0.99	1.937 s	40	0.9	1.832 s	60	0.85
HBOS	1.511 s	4	0.99	1.582 s	40	0.9	1.532 s	60	0.85
IForest	0.241 s	4	0.99	0.253 s	40	0.9	0.244 s	60	0.85
MCD	0.126 s	4	0.99	0.137 s	40	0.9	0.119 s	60	0.85
Vd-LOD	0.790 s	2	0.995	8.075 s	17	0.957	12.205 s	27	0.932
HCV Dataset					digts: 13, samples: 414, features: 4
Split 0.3	0.01			0.1			0.15
init	time	outliers	Acc	time	outliers	Acc	time	outliers	Acc
PRAISE	0.007 s	5	0.988	0.007 s	42	0.899	0.007 s	62	0.85
LOCI	98.691 s	44	0.894	98.906 s	46	0.889	100.202 s	42	0.899
SOS	0.684 s	5	0.988	0.679 s	42	0.899	0.682 s	62	0.85
KNN	0.005 s	5	0.988	0.005 s	42	0.899	0.005 s	62	0.85
CBLOF	1.573 s	5	0.988	1.554 s	42	0.899	1.549 s	62	0.85
HBOS	1.501 s	5	0.988	1.516 s	42	0.899	1.507 s	62	0.85
IForest	0.238 s	5	0.988	0.239 s	42	0.899	0.238 s	62	0.85
MCD	0.049 s	5	0.988	0.050 s	42	0.899	0.046 s	62	0.85
Vd-LOD	1.248 s	2	0.995	10.361 s	19	0.954	15.571 s	31	0.925
ECG Dataset					digts: 4, samples: 840, features: 4
Split 0.3	0.01			0.1			0.15
init	time	outliers	Acc	time	outliers	Acc	time	outliers	Acc
PRAISE	0.003 s	3	0.986	0.003 s	22	0.897	0.003 s	32	0.85
LOCI	13.157 s	9	0.958	12.998 s	11	0.948	13.017 s	10	0.953
SOS	0.560 s	3	0.986	0.558 s	22	0.897	0.552 s	32	0.85
KNN	0.002 s	3	0.986	0.002 s	22	0.897	0.002 s	31	0.854
CBLOF	1.536 s	3	0.986	1.949 s	22	0.897	1.559 s	32	0.85
HBOS	1.496 s	3	0.986	1.510 s	22	0.897	1.545 s	32	0.85
IForest	0.227 s	3	0.986	0.227 s	22	0.897	0.235 s	32	0.85
MCD	0.053 s	3	0.986	0.058 s	22	0.897	0.060 s	32	0.85
V-LOD	0.272 s	1	0.995	2.103 s	9	0.958	3.188 s	15	0.93

.

The Table 3 shows the processing time, number of outliers detected, and accuracy of outlier predictions for various outlier detection models during the testing process. As the preset parameter “Outliers fraction” changes, the number of outliers identified by each model also varies. The Vd-LOD model, however, incorporates adjustments based on the global outlier factor and uses independent block vectors to make predictions, resulting in consistently lower predicted outlier numbers compared to the other models.

For example, when testing the ECG dataset with a training set split ratio of 0.3 and an “Outliers fraction” parameter of 0.15, the standard number of outliers is calculated to be 126. The other models provide standard values based on the outlier ratio parameter, indicating that there are no significant outliers in the dataset. In contrast, the Vd-LOD model predicts 87 outliers, demonstrating its more reliable predictive ability.

However, it has also been observed that as the predetermined proportion of outliers increases, the computation time of the Vd-LOD model also increases. The main issue is that the time complexity of the local outlier verification process for independent block vectors is $O\left(k^n\right)$, where $k$ represents the verification process and $n$ represents the number of samples to be verified. Therefore, in the next step, it is necessary to improve and optimize the verification process to enhance efficiency. One approach is to use parallel computing to reduce the waiting time for verification. Another approach is to utilize deep learning models such as neural networks to obtain more accurate boundary features and minimize the number of samples requiring verification.

5. Summary

For the Outlier model, the quantity of outliers represents the model’s sensitivity towards outliers. From the perspective of outlier prediction models, a higher value indicates a better performance in boundary determination. However, this result is based on linear boundary judgments for data variations. When using nonlinear boundaries, the real relationship of outliers needs to be considered. Therefore, the Vd-LOD model employs a boundary verification method using local sample vectors to consider this relationship: by evaluating the nonlinear boundaries of local sample vectors and updating the recognition results of global samples, the final set of outlier data samples can be obtained. In other words, a sample is considered significantly outlier only when there is inconsistency between global and local analyses. When the model analysis is consistent, there may be partial outlier phenomena in the sample vectors, which do not require further processing. Test results show that the Vd-LOD model performs steadily in complex data environments with independent trend features but fuzzy boundaries. It can effectively extract outlier data. Therefore, this approach is feasible in precision medicine, biotechnology, industrial fault diagnosis, and other fields. Moreover, it offers the following advantages:

(1)

High accuracy: Density-based outlier detection models can identify samples with low density based on the distribution characteristics of the dataset, which are often the outliers. In this way, the Negative Selection Algorithm can further determine non-self-invading behaviors based on these samples, improving the accuracy of recognition.

(2)

High robustness: Density-based outlier detection models determine outlier samples based on the density distribution of samples. Compared to traditional distance-based or statistical methods, they exhibit stronger robustness. This robustness enables the Negative Selection Algorithm to be more reliable and stable when dealing with different types of outlier samples.

(3)

Scalability: Density-based outlier detection models typically do not require pre-specifying the number of outlier samples and can adaptively identify them based on the dataset’s characteristics. This scalability allows the Negative Selection Algorithm to handle datasets of different scales and complexities.

Density-based outlier detection models have achieved certain progress in the field of outlier detection. However, there are still research prospects and challenges, including:

(1)

Multi-level density models: Current density-based outlier detection models mainly rely on a single density threshold for judgment. However, real-world datasets often contain different density regions. Therefore, it is worth exploring multi-level density models to better adapt to outlier samples within different density ranges.

(2)

Dynamic density models: Existing density-based outlier detection methods typically assume static density models that do not change over time. However, in certain applications, the density of data may change over time. Therefore, research can be conducted on establishing dynamic density models that capture such changes.

(3)

Incremental learning and online outlier detection: Current density-based outlier detection models are mainly designed for offline datasets. For data streams or incremental updates, further research is needed on how to perform incremental learning and online outlier detection.

(4)

Integration with other techniques: Density-based outlier detection models can be combined with other machine learning and data mining techniques, such as clustering, classification, and anomaly detection, to enhance the performance and effectiveness of outlier detection models.

(5)

Real-world application and evaluation: Density-based outlier detection models face challenges in real-world applications, such as imbalanced datasets, noise, and missing labels. Therefore, more research is needed to evaluate and improve the performance of models in practical applications.

In conclusion, there are still many research directions and challenges for density-based outlier detection models. These research prospects will further drive the development and application of the field of outlier detection.