Cuckoo Matrix: A High Efficient and Accurate Graph Stream Summarization on Limited Memory

Abstract

The graph stream is defined as rapid edge streams on a huge domain of nodes. Nowadays, graph streams play important roles in network traffic, social networks, and cloud troubleshooting. Therefore, various summary structures for graph streams are proposed to obtain approximate evaluation results. However, these structures either sacrifice accuracy for guaranteed throughput or compromise memory consumption for high precision. In view of the limitations, we propose Cuckoo Matrix. It only uses one adjacency matrix to complete high accuracy queries while assuring large throughput. Meanwhile, Cuckoo Matrix is capable of preserving the connectivity of edges for the purpose of supporting both structural queries and weight-based estimations. The experimental results show that Cuckoo Matrix improves insertion throughput by 25% and reduces memory consumption by 25% compared to the state-of-the-art, which meets the current requirements of graph stream summarization.

1. Introduction

Along with the application of emerging technologies such as neural networks [1,2], the massive data streams bring huge challenges to data measurement, storage, and management [3]. However, with the development of the IoT and social networks, connectivity between information has become particularly important. As a result, more and more data are treated as a graph, and a lot of stream summarizations are increasingly adopted to process graph data. In the environment of streaming graphs (for ease of presentation, the terms “graph stream” and “streaming graph” are used interchangeably throughout this paper), the connectivity plays a crucial role in data processing applications, such as analyzing the log streams to perform real-time troubleshooting [4] and possible friend recommendations in social networks [5].

Graph streams are large and dynamic, for example, there are approximately 100 million user login data and 500 million tweets on Twitter each day. Similarly, in large ISP or data centers, there could be millions of packets every second in each link [6]. Consequently, it is not feasible to store all necessary data in memory for real-time queries. In order to process dynamic streaming data, fast and approximated answers are expected in the background of data streaming applications.

A specific example is given here to highlight the utility of streaming graph problems. In networks, communication is viewed as an edge, and users are seen as nodes of this edge. When the network is busy, a quick view of the communication status is expected. So we count the weights of traffic passed by node queries to determine whether the network nodes are normal or being maliciously attacked.

Thus, various graph stream summarization structures are proposed. Traditional approximate data structures such as CM sketch [7] and other sketches [8,9,10] are popular methods, which use a hash-based technique to compress data into a smaller space. Then, gsketch [11] was proposed. It can build the whole structure only when stream samples are available. However, these solutions ignore the connectivity of edges, so they cannot perform structural queries.

Subsequently, Three-Dimensional Count Main Sketch (TCM) [12] and its variants were introduced to support more structured queries, and they both include multiple matrices. As the graph stream is too large and rapid, a lot of nodes and edges will be aggregated. TCM only considers recording edges instead of distinguishing different edges that are mapped to the same location. Therefore, TCM sacrifices the accuracy of throughput. The variants of TCM either use a majority vote algorithm to reduce errors or are optimized for the labeled graph. However, their precision still needs to be improved.

To enhance the accuracy, Graph Stream Summarization (GSS) [13] is proposed. It consists of an adjacency matrix with an adjacency list buffer and uses square hashing to compact the data structure. Nevertheless, when all possible mapping buckets in the matrix are occupied, GSS stores the left-over edges in the buffer. When edges are recorded by the buffer, GSS must traverse the buffer to find the appropriate position of the current edge, which will increase memory consumption and slow down the update speed.

As far as we know, there is no previous work that supports both structural and weight-based queries with large throughput and high accuracy on limited memory. Therefore, we propose Cuckoo Matrix, which enables fast and accurate graph stream summarizations on limited memory. The key contributions of this paper are as follows:

• To support accurate estimations on both weight-based and structural queries, we propose a novel data structure named Cuckoo Matrix. The structure only consists of one adjacency matrix. The matrix is designed to have two kinds of buckets with numerous cells, which are called the original bucket and the alternative bucket. Each bucket records the fingerprint pairs of the edges as well as the weights. When edges keep coming, Cuckoo Matrix usually stores edges in the original bucket. When edges collide in the original bucket, one of the conflicting edges will be stored in the alternative bucket to improve the precision. Meanwhile, Cuckoo Matrix could be easily used to support various graph queries since the whole structure maintains information about the node-based structural relationships.
• Considering the conflicts caused by large-scale graph stream, we propose an exact and efficient insertion algorithm, which is designed to be $O\left(1\right)$. The algorithm helps Cuckoo Matrix to kick out the conflicting edge from the original bucket when a conflict occurs. Based on the fingerprint, the coordinates of the alternative bucket are calculated by the algorithm. Then Cuckoo Matrix reinserts the conflicting edge into the alternative bucket. Therefore, the accuracy of queries is improved. At the same time, Cuckoo Matrix places all conflicting edges in different cells in the same bucket as much as possible, which further enhances the insertion speed.
• We conduct theoretical analysis and experiments to evaluate the performance. Cuckoo Matrix and its comparison schemes have been experimented with datasets of up to $4.4\times {10}^9$ edges. We tested insertion throughput, edge query, node query, and so on. Extensive evaluations show that Cuckoo Matrix performs better compared to TCM and GSS. The average relative error of Cuckoo Matrix maintains around ${10}^{-5}$ in edge queries and stays at about ${10}^{-1}$ in node queries. Both its insertion throughput and edge query throughput are about $1.3\times {10}^6$ edges per second. Our solution also performs well in reachability queries and subgraph queries.

The rest of this paper is organized as follows: Related work is summarized briefly in Section 2. The preliminaries of the proposed sketch are introduced in Section 3. Section 4 describes Cuckoo Matrix in detail. Section 5 provides the query operations. Section 6 presents the theoretical analysis and Section 7 evaluates the experimental results on real-world datasets. Finally, Section 8 draws the conclusion and future works.

2. Related Work

The essence of graph stream summarization is to count the weights (frequencies) of edges or nodes in the graph stream in the network. As the basis of network statistics and planning, the booming development of networks in recent years has made graph stream summarization a hot research direction. At present, there have been some solutions for the graph stream summarization problem. In the beginning, the need for graph-based structure queries was not clear, so most of the solutions of network measurement were applied to summarize the graph stream. With the requirements becoming clear, structures for graph stream summarization were proposed one after another. In this section, these solutions are divided into two categories, which are solutions based on network measurements and solutions designed for graph stream summarizations.

2.1. Solutions Based on Network Measurements

Sketches, such as CM sketch [7], CU sketch [8], and so on [9,10] use d hash functions and a cell array. Each edge from the graph stream will be mapped by d pair-wise independent hash functions to d cells. Then, the algorithms utilize the information stored in the cells to offer a weight-based estimation. Based on the CM sketch, many solutions have been proposed to resolve conflicts among edges. gSketch [11] studies the synopsis construction of graph streams when a stream sample is available. Sketchlearn [14] is proposed to optimize the mapping strategy, and it contains multi-level sketches. By separating large and small streams, SketchLearn mitigates their conflicts and improves the accuracy of queries. Bloom Sketch [15] consists of a multi-layer sketch and a bloom filter. The low-level sketches are responsible for processing low frequency edges, and the high-level sketches handle the high frequency edges that cannot be counted in the low-level. Bloom filter is responsible for the streams that are not identified successfully, thus Bloom Sketch improves memory usage efficiency compared to CM sketch.

In recent years, in addition to optimization for data structures, machine learning based optimization methods are also becoming popular. MLsketch [16] continuously retrains machine learning models using a very small number of flows to reduce the dependence of sketch accuracy on network traffic features. To predict the frequent items in the data stream, SSS [17] is proposed. It assumes that the data streams are conforming to the Zipfian [18] distribution. Then it learns the distribution state of the streams from historical data and sets a threshold based on the distribution function to reduce false positives. iSTAMP [19] uses an intelligent sampling algorithm to select the most informative flows and adaptively measures the most valuable items, which reduces memory consumption and increases throughput.

However, with the development of the IoT and social networks, the data stream is no longer seen as an isolated sequence of elements, but as a series of connected edges. The above solutions only store each item independently, but ignore the connectivity among them. As a result, they are only able to perform weight-based queries, but cannot handle more complex structural queries.

2.2. Solutions Designed for Graph Stream Summarizations

Graph stream summarizations have been widely applied in various fields, most of which deal with generic cases such as TCM, while others such as SBG-Sketch [20] process the labeled graph streams. These solutions are described separately as follows.

Graphic sketches aim at preserving the graph structure while supporting a variety of query methods. TCM and its variants are designed as data structures that are made up of numerous adjacency matrices. These matrices maintained by different hashes store the compression of the streaming graph. For edge $E=(s,d)$ in graph stream $G=〈E_1,E_2,\cdots ,E_k〉$, TCM uses multiple hash functions $H(·)$ to compress graph stream G into a graph sketch $G_s$. When the memory is sufficient, multiple sketches are built with different hash functions to report the most accurate value in queries.

Based on TCM, the gMatrix [21] generates graph sketches using reversible hash functions, and it can also query heavy hitters and so on. Dmatrix [22] uses a majority vote algorithm to select keys with majority weight and reserves a field in each bucket for keys of interest. So it improves accuracy over TCM and reduces memory consumption over gMatrix.

GSS is the state-of-the-art summarization method, which consists of an adjacency matrix and an adjacency list buffer for left-over edges. GSS uses square hashing to map edges with the same source node s that are no longer mapped to one row, but r rows, sharing memory with other source nodes. This algorithm improves the accuracy. When edges E and $E^{\prime }$ are mapped to the same location in the matrix, GSS stores the subsequent edge $E^{\prime }$ in other available mapped buckets. Hence, GSS must record an additional index pair that indicates the position of this bucket in the mapped buckets sequence. When all mapped buckets are occupied, GSS has to store the current edge in the buffer, which increases memory consumption and reduces its speed.

The following works include SBG-sketch and LGS [23], which extend TCM to labeled graphs. SBG-Sketch proposes a ranking technique, which enables edges of high-frequency labels to automatically leverage unused memory previously assigned to low-frequency labels. It also guarantees that the edges of low-frequency labels can use that memory whenever needed in the future. It addresses the label-imbalance challenges in graph streams. For LGS, it utilizes the characteristics of prime numbers to encode the label information into a product of prime numbers, which handles query semantics that involve vertex or edge labels and edge expiration. LGS performs better than traditional sketches for analytics over labeled graph streams. Though the above schemes can summarize the labeled graph streams, the problem of poor accuracy still exists.

3. Preliminaries

Four definitions are presented in this section to help with the interpretation of the graph stream.

3.1. Graph Stream Definitions

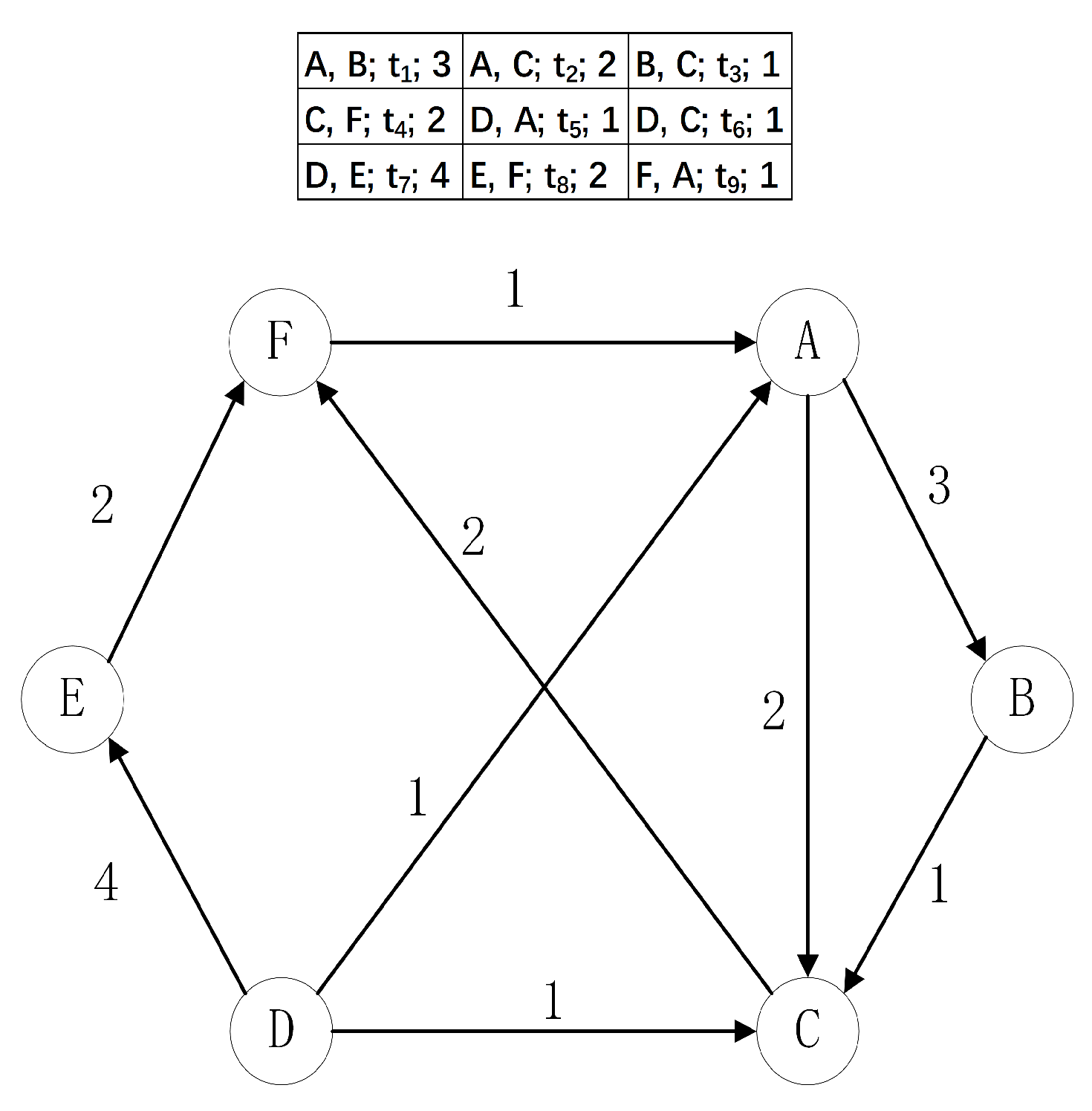
Graphs are drawn over a large number of nodes in various practical contexts, and edges arrive in the form of a graph stream. A directed edge from node s to node d with wight w is encountered at time-stamp t, according to the sequence of elements $E=(s,d;t;w)$. In Figure 1, a sample graph stream $G=〈E_1,E_2,\cdots ,E_k〉$ is shown. The edge streaming sequence forms a dynamic directed graph $G=(V,E)$ where V and E are the sets of nodes and edges.

Intuitively, s and d are viewed as identifiers that uniquely identify nodes, such as an IP address in the network or a user ID in the social network. It is important to note that the same edge may appear numerous times in the stream, e.g., user A may have multiple conversations with user B. The weight of such edge in the streaming graph G is the sum of all edge weights sharing the same endpoints.

3.2. Summarization and Query Definitions

Given a graph stream G, the problem of summarizing graph streams is to create a new data structure $G_s$ to represent $G=(V,E)$. The definitions are as follows:

(1)

$\left|Gs\right|<<\left|G\right|$: the size of $G_s$ is far less than G, preferably in linear space.

(2)

There is a function $H(·)$ that maps nodes in V to nodes in $V_h$.

(3)

The time to construct $G_s$ from G is in linear time, and $G_s$ supports various types of queries on graph stream G with small error tolerance.

(4)

$G_s$ is a graph.

Here, four types of queries on graph stream summarization are defined as follows:

(1)

Edge queries: Given two node identifiers s and d, return the weight w of the edge $(s,d)$.

(2)

Node queries: Given a node identifier s or d, return the out weight or the in weight w of the node.

(3)

Reachability queries: Given two node identifiers s and d, return a boolean result indicating whether there is a path from s to d.

(4)

Subgraph queries: Given a subgraph $G_{sub}=\left\{\left(s_1,d_1\right),\left(s_2,d_2\right)\cdots \left(s_k,d_k\right)\right\}$ belonging to graph stream G, return aggregated weights of $G_{sub}$.

With these queries, we can rebuild the whole graph. All edges in the graph could be found by the edge query and all nodes could be found by the node query. Likewise, the reachability query determines if there is a path connecting two places. All kinds of queries and algorithms can be supported as the graph is reconstructed.

3.3. Hash Collision Definitions

Hash functions are frequently adopted in the structures of graph stream summarizations to increase efficiency. The hash function used in this article is bob hash, and its information is described in detail in [24]. When edge E arrives, the hash function computes its mapping location $h\left(E\right)$ in the matrix. When the amount of data is large enough, the hash function has collisions, which means that n completely different edges will be mapped to the same location in the matrix. The original purpose of our design is to avoid hash collisions while using as less memory as possible. Therefore, we choose a better hash function (bob hash), which is an efficient and accurate hash function.

4. The Design of Cuckoo Matrix

Cuckoo Matrix is a novel graph sketch that supports various types of queries. The design goals are as follows:

(1)

High precision: Cuckoo Matrix supports accurate estimations on both weight-based queries and structural queries.

(2)

High efficiency: The time complexity of the insertion algorithm is designed to be $O\left(1\right)$, therefore it is efficient enough.

(3)

Various queries: Cuckoo Matrix supports all the queries mentioned in Section 3.2.

(4)

Smaller memory consumption: Cuckoo Matrix maintains compact data structures with small memory.

4.1. The Data Structure of Cuckoo Matrix

As shown in Figure 2, Cuckoo Matrix is designed to be an adjacency matrix with $m\times m$ buckets, each of which contains n cells (here, four cells are used as an example). In addition, all buckets in Cuckoo Matrix are divided into the original bucket and alternative bucket by the insertion algorithm. In Figure 2, the orange color represents the original bucket, respectively, the green color for the alternative bucket. Furthermor, the empty bucket means there is no edge in this bucket, so the empty bucket is blank. The original bucket records the edges from the graph stream, and the alternative bucket stores the conflicting edges. The smallest storage unit in Cuckoo Matrix is one cell, which occupies 6 bytes for the fingerprint pair $〈f\left(s\right),f\left(d\right)〉$ and the weight w of one edge. The fingerprint is a bit string derived using a hash function which is the unique identifier for edge E to distinguish from others. The weight means how many times this edge appears in the whole graph stream. Cuckoo Matrix stores the fingerprint pairs for each edge to ensure accurate query results.

When there is a conflict (i.e., as edges are inserted, the matrix will become increasingly occupied) between two edges, Cuckoo Matrix stores the conflicting edge in the next empty cell in this bucket. Only if there are no empty cells in this bucket, Cuckoo Matrix will kick out the conflicting one and reinsert it into the alternative bucket. Hence, Cuckoo Matrix further improves a large throughput by keeping all conflicting edges in the same bucket as much as possible to prevent cross-bucket kickouts.

4.2. The Insertion Process

The complete insertion process is shown in Algorithm 1. For edge $E=(s,d;w)$, Cuckoo Matrix calculates fingerprint pair $〈f\left(s\right),f\left(d\right)〉$ by the source node s and the destination node d. Edge E is mapped into the matrix by hash function $H(·)$, then $h\left(s\right)$ and $h\left(d\right)$ are obtained to form the coordinates of the original bucket. When there is an empty cell in the bucket corresponding to the coordinate, Cuckoo Matrix stores edge E and records it as $〈f\left(s\right),f\left(d\right),w〉$. When all cells are occupied, Cuckoo Matrix traverses through each cell and compares $〈f\left(s\right),f\left(d\right)〉$ with the fingerprint pair in the cell. If they are the same, add w to its weight, or else, then perform kicking out and reinsertion operation. We will discuss the process of proposing and reinserting in the following.

To mitigate conflicts among edges, Cuckoo Matrix creates an alternative bucket for each edge [25,26]. The coordinate of the alternative bucket is calculated by the following formula:

$$\begin{array}{cc}\hfill & h_b\left(s\right)=h\left(s\right)\oplus f\left(s\right)\hfill \\ \hfill & h_b\left(d\right)=h\left(d\right)\oplus f\left(d\right)\hfill \end{array}$$

(1)

In this way, $〈h_b\left(s\right),h_b\left(d\right)〉$ forms the alternative bucket in the matrix. Since the coordinates of the alternative bucket are computed from the hash value and the fingerprint, the original bucket and the alternative bucket are relatively random in Cuckoo Matrix. As shown in Figure 2, when all the cells in the original bucket, as well as the alternative bucket of edge E are occupied, E has to be mapped to one bucket randomly. As a consequence, E evicts any recorded edge (in the case of Figure 2, E kicks out $E^{\prime }$) and occupies the cell of $E^{\prime }$. For each kicking out operation, the maximum number of kicking out will be increased by 1. After that, $E^{\prime }$ will be mapped to the other bucket. If all cells in the other bucket of $E^{\prime }$ are also occupied, then $E^{\prime }$ will evict any edge and occupy its location. The evicted edge continues the process until every edge has been recorded in Cuckoo Matrix or the maximum number of kicking out is reached.

An error will be introduced when edges cannot be inserted after the maximum number of kicking out. If both the original bucket and the alternative bucket cannot be inserted, the insertion will be terminated. Assume that Cuckoo Matrix has a total of b buckets with n cells, and the probability that an edge cannot be inserted is $\frac{n^2}{b^2}$. In the experimental configuration, the number of cells is much smaller than the number of buckets, so this probability is small. Therefore, the error caused by several kicks is acceptable.

Algorithm 1 Insertion Progress.

Input: edge $E=(s,d;w)$   1: $h\left(s\right)\leftarrow hash\left(s\right),f\left(s\right)\leftarrow fingerprint\left(s\right)$   2: $h\left(d\right)\leftarrow hash\left(d\right),f\left(d\right)\leftarrow fingerprint\left(d\right)$   3: original bucket $\leftarrow 〈h\left(s\right),h\left(d\right)〉$   4: alternate bucket $\leftarrow 〈h\left(s\right)\oplus f\left(s\right),h\left(d\right)\oplus f\left(d\right)〉$   5: if the original bucket or the alternate bucket has an empty cell or edge E already exists    then   6:     insert edge E into the cell   7: else   8:     for the number of kicking out < MAXKICK do   9:           evict another recorded edge $E^{\prime }$ randomly 10:         insert edge E into that cell 11:         compute the other bucket coordinate of edge $E^{\prime }$ 12:         the number of kicking out +1 13:         if the other bucket has an empty cell or edge $E^{\prime }$ already exists in that bucket    then 14:            insert edge $E^{\prime }$ into the cell 15: return insertion failure

5. Query Operations

The query process of Cuckoo Matrix is explained in this section.

5.1. Edge Query

The edge query is to estimate the total weights from a source node s to its destination node d. The query results are denoted as ${\tilde{w}}_e(s,d)$, where s is the unique identifier of the source node and d is the unique identifier of the destination node.

In Algorithm 2, when edge $E=(s,d)$ is given, the hash values of s and d and the fingerprint pair $〈f\left(s\right),f\left(d\right)〉$ are calculated. Then, the coordinates of the original mapping bucket and alternative bucket are obtained. After that, Cuckoo Matrix matches $〈f\left(s\right),f\left(d\right)〉$ with the fingerprint pair recorded in each cell in the corresponding buckets. If matched, Cuckoo Matrix returns ${\tilde{w}}_e(s,d)$, otherwise, it means edge E does not exist in Cuckoo Matrix at all.

Cuckoo Matrix uses fingerprints to distinguish items. There is only a tiny probability that two different edges have the same fingerprint pairs, which will be analyzed in Section 6. Therefore, queries based on fingerprint pairs are quite accurate.

Algorithm 2 Edge Query.

Input: edge $E=(s,d)$ Output: estimate weight ${\tilde{w}}_e(s,d)$ 1: $h\left(s\right)\leftarrow hash\left(s\right),f\left(s\right)\leftarrow fingerprint\left(s\right)$ 2: $h\left(d\right)\leftarrow hash\left(d\right),f\left(d\right)\leftarrow fingerprint\left(d\right)$ 3: original bucket $\leftarrow 〈h\left(s\right),h\left(d\right)〉$ 4: alternate bucket $\leftarrow \langle h\left(\mathrm{s}\right)\oplus \mathrm{f}\left(\mathrm{s}\right),h\left(\mathrm{d}\right)\oplus \mathrm{f}\left(\mathrm{d}\right)\rangle$ 5: if the original bucket or the alternate bucket has edge E then 6:     return ${\tilde{w}}_e(s,d)$ 7: else 8:     return 0

5.2. Node Query

The definition of node query for directed graphs is, given unique identifier s of the source node or d of the destination node, estimate the out weight of source node ${\tilde{w}}_n(s,\to )$ or in weight of the destination node ${\tilde{w}}_n(d,\leftarrow )$. For undirected graphs, ${\tilde{w}}_n(n,-)$ denotes the results. In Algorithm 3, ${\tilde{w}}_n\left(s\right)$ is used for a simplified form of ${\tilde{w}}_n(s,\to )$. Cuckoo Matrix estimates the out weight as an example, in fact, it can also estimate all node queries mentioned above.

When given a node s, its hash value and fingerprint are calculated, and the coordinates of the original bucket and alternative bucket can be computed by first locating the row in the adjacency matrix corresponding to s. Then Cuckoo Matrix travels through all the buckets in these two rows and compares $f\left(s\right)$ with the fingerprints stored in cells. If the fingerprint of the source node is the same as $f\left(s\right)$, the weight of the cell is added to ${\tilde{w}}_n\left(s\right)$. At last, ${\tilde{w}}_n\left(s\right)$ is the aggregated weight of node s.

Algorithm 3 Node Query.

Input: Node s Output: estimate the out weight ${\tilde{w}}_n\left(s\right)$ 1: $h\left(s\right)\leftarrow hash\left(s\right),f\left(s\right)\leftarrow fingerprint\left(s\right)$ 2: original bucket $\leftarrow 〈h\left(s\right),width〉$ 3: alternate bucket $\leftarrow \langle hash\left(\mathrm{s}\right)\oplus \mathrm{f}\left(\mathrm{s}\right),width\rangle$ 4: for$width=0$ to $width=m-1$ do 5:     if the original bucket or the alternate bucket has node s then 6:         ${\tilde{w}}_n\left(s\right)\leftarrow {\tilde{w}}_n\left(s\right)+cell.weight$ 7: return ${\tilde{w}}_n\left(s\right)$

5.3. Reachability query

Given a pair of nodes s and d, the reachability query will tell whether a path from s to d exists between these two nodes. Here, Cuckoo Matrix uses the classical breadth-first search (BFS) for an illustration.

In Algorithm 4, if $(s,d)$ is directly connected in Cuckoo Matrix, which means there is a path from s to d. Otherwise, mark s as $visited$ and push s into queue q. Subsequently, Cuckoo Matrix will search the whole neighbor set of s and push the neighbor set into the queue, meanwhile marking them as visited. If the neighbor set contains d, return true, otherwise, Cuckoo Matrix examines its neighbor nodes till q is empty. When the traversal is complete, it means there is no path from s to d.

Algorithm 4 Reachability Query.

Input: Node s and d Output: whether there is a path from s to d   1: let q be a queue   2: if edge $(s,d)$ exists in Cuckoo Matrix then   3:     return true   4: $q.enqueue\left(s\right)$   5: mark s as $visited$   6: while q is not empty do   7:     $v\leftarrow q.dequeue\left(\right)$   8:     if $v==d$ then   9:         return true 10:     for all neighbors n of v in Cuckoo Matrix do 11:         if n is not visited then 12:            mark n is $visited$ 13:            $q.enqueue\left(n\right)$ 14: return false

5.4. Subgraph Weight Query

The subgraph query is to compute the aggregated weights of the subgraph $G_{\mathit{sub}}=\left\{\left(s_1,d_1\right),\left(s_2,d_2\right)\cdots \left(s_k,d_k\right)\right\}$ belonging to graph stream G. Cuckoo Matrix executes an edge query for each edge in the subgraph in Algorithm 5. The set of their weights denoted by ${\tilde{w}}_{sub}\left(G_{sub}\right)$ is returned once all edges in the subgraph have been queried.

Algorithm 5 Subgraph Weight Query.

Input: $G_{\mathrm{sub}}=\left\{\left(s_1,d_1\right),\left(s_2,d_2\right)\cdots \left(s_k,d_k\right)\right\}$ Output: estimate aggregated weight ${\tilde{w}}_{sub}\left(G_{\mathrm{sub}}\right)$ 1: for edge in $G_{\mathrm{sub}}$ do 2:     ${\tilde{w}}_e(s_i,d_i)\leftarrow EdgeQuery(s_i,d_i)$ 3:     ${\tilde{w}}_{sub}\left(G_{\mathrm{sub}}\right)\leftarrow {\tilde{w}}_{sub}\left(G_{\mathrm{sub}}\right)+{\tilde{w}}_e(s_i,d_i)$ 4: return ${\tilde{w}}_{sub}\left(G_{\mathrm{sub}}\right)$

6. Theoretical Analysis

In this section, both collision rate and error upper bound are presented.

6.1. Collision Rate

In Cuckoo Matrix, each edge is identified by the fingerprint pair and each fingerprint has f bits. Cuckoo Matrix consists of b buckets overall, each of which has n cells. The collision rate is defined as k edges colliding in the same two buckets.

When the edge E collides with the $k-1$ edge, they must:

(1)

have the same mapped original bucket or alternative bucket, which occurs with probability

$$P_b=\left(\frac{1}{b}+\frac{1}{b}\right)=\frac{2}{b}$$

(2)

(2)

have the same fingerprint pair, which occurs with probability

$$P_f=\left(\frac{1}{2^f}\right)\times \left(\frac{1}{2^f}\right)=\frac{1}{4^f}$$

(3)

Here, $\frac{1}{2^f}$ means how many fingerprints are possible for the source node s of an edge, and similarly $\frac{1}{2^f}$ fingerprints are possible for the destination node d. In Cuckoo Matrix, fingerprint length is 16 bits, hence the probability of two different edges with the same fingerprint pair is $\frac{1}{4^{16}}$, which is really small. Therefore, the collision rate of such k edges sharing the same two buckets is

$$P_c=P_b\times P_f={\left(\frac{2}{b}\times \frac{1}{4^f}\right)}^{k-1}$$

(4)

6.2. Error Upper Bound

For Cuckoo Matrix, collisions do not imply errors, because each bucket can maintain n different edges. Edges recorded in the Cuckoo Matrix are accurate because the Cuckoo Matrix distinguishes each edge with a fingerprint pair. As a result, a query error is introduced when a false fingerprint pair hits. In the least desirable case, the query will probe the original bucket and alternative bucket where each bucket has n cells, and for the edge to be queried, its two buckets are already known. Therefore, in each cell, the probability that a query is matched against the fingerprint pair of an edge and returns a false positive successful match is at most $\frac{1}{4^f}$. After making $2n$ such comparisons, the error upper bound of the probability of a false fingerprint hit is

$$P_e=1-{\left(1-\frac{1}{4^f}\right)}^{2n}\approx \frac{2n}{4^f}$$

(5)

7. Experimental Evaluation

Since TCM is considered as the classic solution, while GSS is state-of-the-art, these solutions are chosen as the comparisons of Cuckoo Matrix. Experimental studies of Cuckoo Matrix, TCM, and GSS are shown in this section. All these solutions were experimented on four datasets, the largest of which had at most $4\times {10}^9$ edges. In this section, first, we give a brief description of real-world datasets. Then the evaluation criteria and parameter configurations used are introduced. After that, we evaluated the performance of Cuckoo Matrix and other solutions in terms of throughput, accuracy, and memory consumption.

All experiments are performed on a Linux platform with an Intel Core i5-10500 CPU (3.10 GHz) and 16 GB memory, running Ubuntu. All algorithms including Cuckoo Matrix, TCM (https://github.com/Puppy95/Graph-Stream-Sketch, accessed on 15 May 2022), and GSS (https://github.com/Puppy95/Graph-Stream-Sketch, accessed on 15 May 2022) are implemented in C++.

7.1. Data Sets

To demonstrate the performance more visually of the three solutions while dealing with large data streams, the four datasets are incremented in order of the number of edges. Details of these four datasets are described as follows:

Autonomous systems by Skitter [27]: Skitter is generated from an internet topology graph collected from the real-world network. From several scattered sources to million destinations, source and destination nodes only represent two IPs that have communicated with each other. This dataset contains 1,696,415 nodes and 11,095,298 edges.

DBLP co-author stream [28]: We derived the author-pairs data from the latest DBLP archive. Regarding 3,058,581 authors as nodes and 37,860,428 author-pairs as edges with a weight of 1 for each edge, indicating a co-authorship. With the gradual increase of the cooperation between authors, the co-authorship between them shows time-evolving characteristics.

com-Orkut [29]: Orkut is a free online social network where users form friendships with each other. These files contain a list of all of the user-to-user links which are included in crawls. All links are treated as directed. This dataset contains 3,072,441 nodes and 117,185,083 edges.

Wikipedia links (en) [30]: This network consists of the wikilinks of Wikipedia in the English language (en). Nodes are Wikipedia articles, and directed edges are wikilinks, i.e., hyperlinks within one wiki. Only pages in the article namespace are included. This dataset contains 13,552,453 nodes and 437,217,425 edges.

7.2. Metrics

The performance is evaluated by accuracy and speed for a fixed memory. The accuracy is measured by ARE and True Negative Recall, and the speed is measured by throughput.

ARE: Let $w_q$ be the real answer of query q, and ${\tilde{w}}_q$ be the estimated answer, then the relative error (RE) of a query q is calculated as $\frac{|w_q-{\tilde{w}}_q|}{w_q}$. The average relative error (ARE) is calculated as $ARE=\frac{1}{\left|S\right|}{\sum }_{e\in S}\frac{|w_q-\widetilde{w_q}|}{w_q}$, where S is the number of query set.

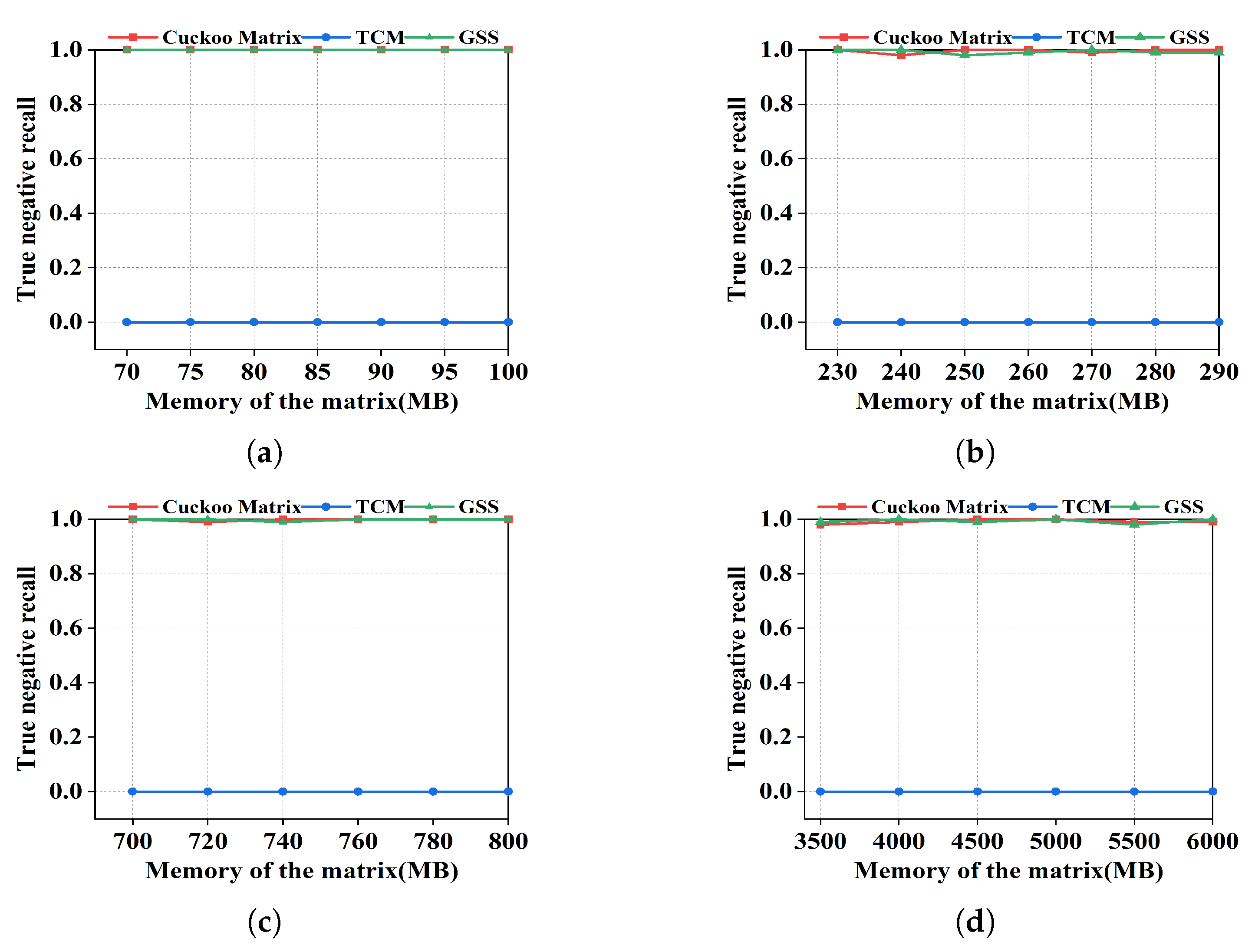
True Negative Recall: It measures the accuracy of the reachability query. Since TCM has a high false positive, the results of reachability queries are almost true. Thus, the unreachable point set $Q=\left\{q_1,q_2\cdots q_k\right\}$ is given to complete the reachability query, where source node s and destination node d in Q are unreachable. The true negative recall is defined as the number of queries reported as unreachable divided by the number of all queries in the query set Q.

Throughput: Let k be the number of edges or nodes of certain operations (insertion or query operations), and t be the total time the operation needs. For edge query, the throughput can be calculated as $Throughput=\frac{k}{t}\left(Eps\right)$, where Eps means edges per second. In node query, the throughput can be calculated as $Throughput=\frac{k}{t}\left(Nps\right)$, where Nps means nodes per second.

7.3. Experiments Settings

In experiments, Cuckoo Matrix and GSS use the same Bob hash function [24]. As for TCM, it applies 4 graph sketches to improve the accuracy. We set the maximum number of kicking out for Cuckoo Matrix to be 2000. Both Cuckoo Matrix and GSS use fingerprints which are computed in the same way. The remaining parameters of GSS are set by referring to the paper [13]. All experiments are repeated 100 times and the average results are reported. We vary the memory consumption to evaluate the accuracy and throughput of different solutions.

7.4. Insertion Throughput

In this section, the performance of these three solutions in insertion throughput is evaluated. Cuckoo Matrix consists of only one adjacency matrix, and TCM is made up of numerous adjacency matrices. For GSS, it includes an adjacency matrix and an adjacency list buffer. When all of the mapped buckets in the adjacency matrix are occupied, GSS must store the edges in the buffer. To ensure fairness, the memory of matrices of these three solutions is set to be the same. Except for the memory of the matrix, GSS takes up extra memory as a buffer, its memory consumption will be analyzed in Section 7.9.

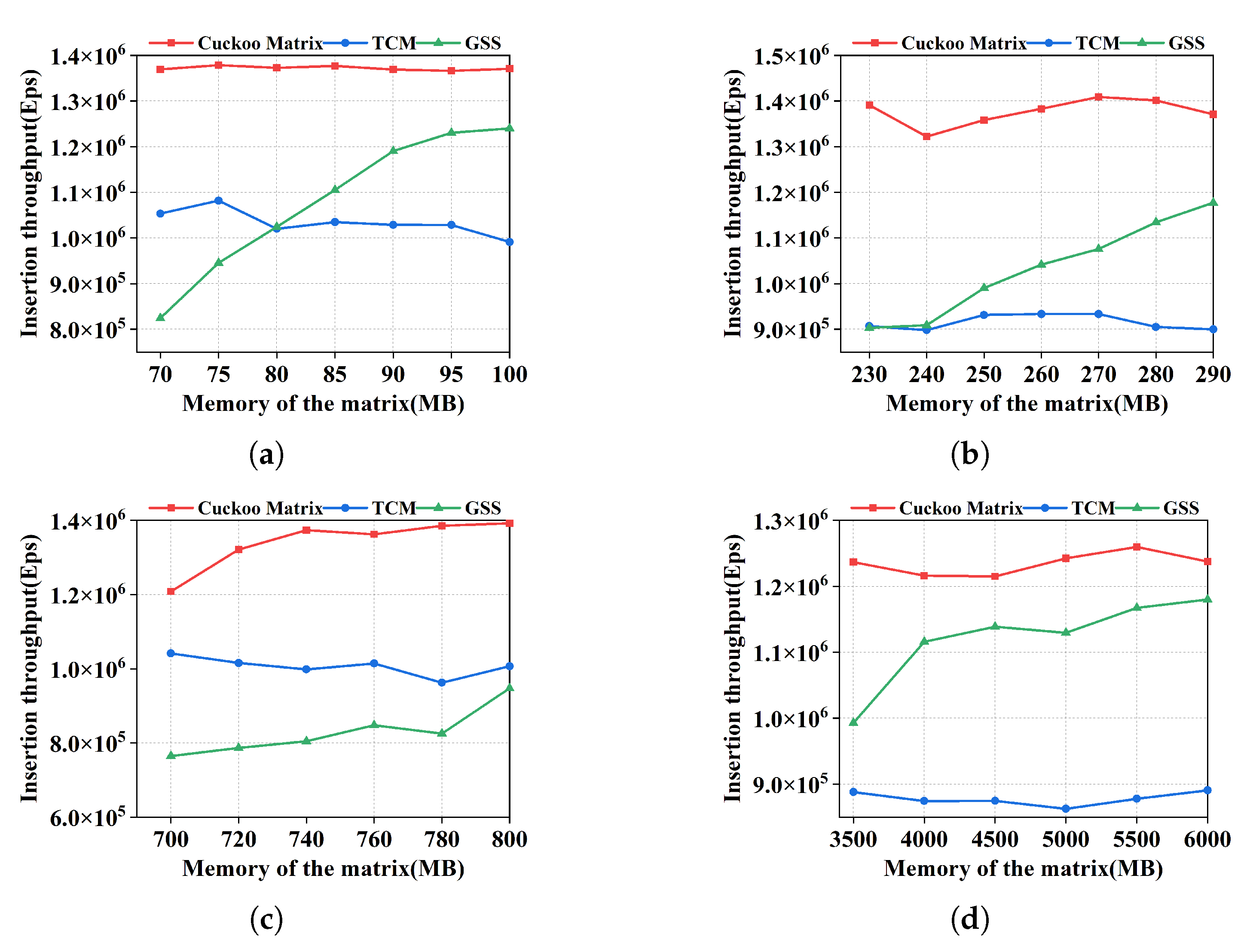
As shown in Figure 3, Cuckoo Matrix has the largest insertion throughput with a 25% improvement compared to GSS. Although Cuckoo Matrix has a kicking out and reinsertion operation, while n complete insertions are performed, each only requiring $O\left(1\right)$ time [26] on average. As the memory increases, Cuckoo Matrix needs to do kicking out and reinsertion operations less often, so its throughput keeps increasing. Since TCM only considers mapping and does not distinguish among different edges that are mapped to the same bucket, it also has $O\left(1\right)$ updating time cost. However, it uses four hash functions and generates four graphic sketches to improve its accuracy. Therefore, it is lower than Cuckoo Matrix. As for GSS, it has $O(1+B)$ time cost, where the matrix has $O\left(1\right)$ time and the buffer has $O\left(B\right)$ time. As shown in Figure 3a,b,d, the throughput of GSS varies rapidly because as the memory of the matrix increases, fewer edges are recorded in the buffer. When all the candidate buckets in the matrix are occupied, GSS stores the subsequent edges into the buffer. At this time, the buffer must be traversed to tell if the current edge already exists or not, which increases the insertion time. In Figure 3c, a significant portion of the edges is stored in the buffer, which causes GSS to have a relatively low throughput.

7.5. Edge Query

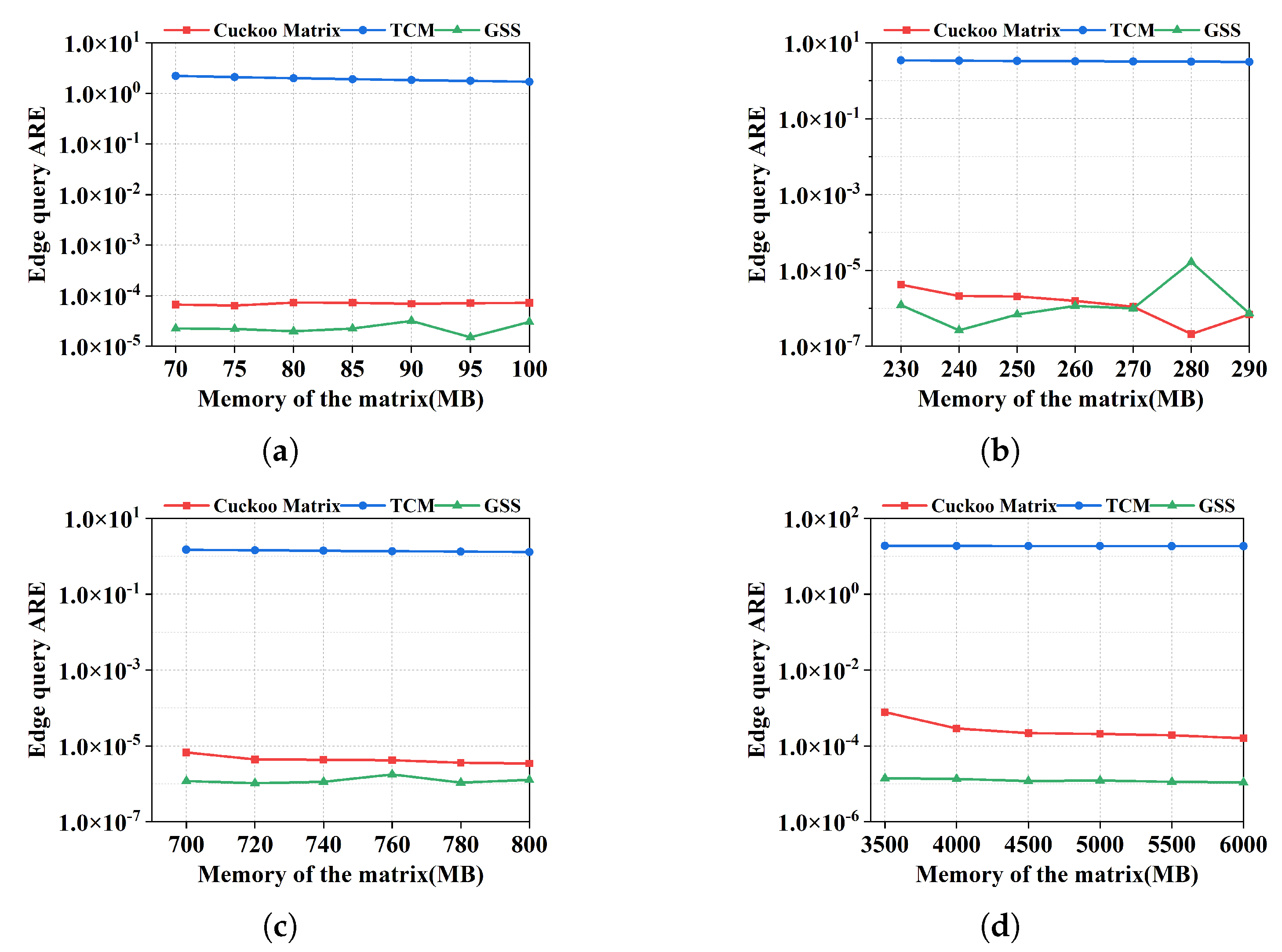
In this section, the performance of these three solutions in edge queries is evaluated. To reduce the random error introduced by the selection of the data sample, the edge query set contains all edges in the graph stream. Figure 4 shows ARE of edge queries on the four datasets with the same memory of the matrix. The results show that Cuckoo Matrix and GSS perform much better in supporting edge queries, their ARE will basically maintain between ${10}^{-6}$ and ${10}^{-4}$. When the memory of the matrix is the same, GSS uses an extra buffer to store left-over edges, so it is slightly more accurate than Cuckoo Matrix. TCM aggregates all different edges that are mapped to the same bucket, so it has poor accuracy.

Figure 5 shows the throughput of the edge queries on the four datasets with the same memory of the matrix. It can be clearly seen that the throughput of Cuckoo Matrix is the highest, and it is on average 20% higher than the throughput of GSS. Because Cuckoo Matrix only needs to check two buckets in edge query, it has $O\left(1\right)$ time complexity. However, the throughput of GSS increases as memory increases. Like the insertion throughput, the edge queries throughput of GSS is mainly limited by the buffer. As for TCM, its throughput is lower because it has to check four matrices to ensure accuracy.

7.6. Node Query

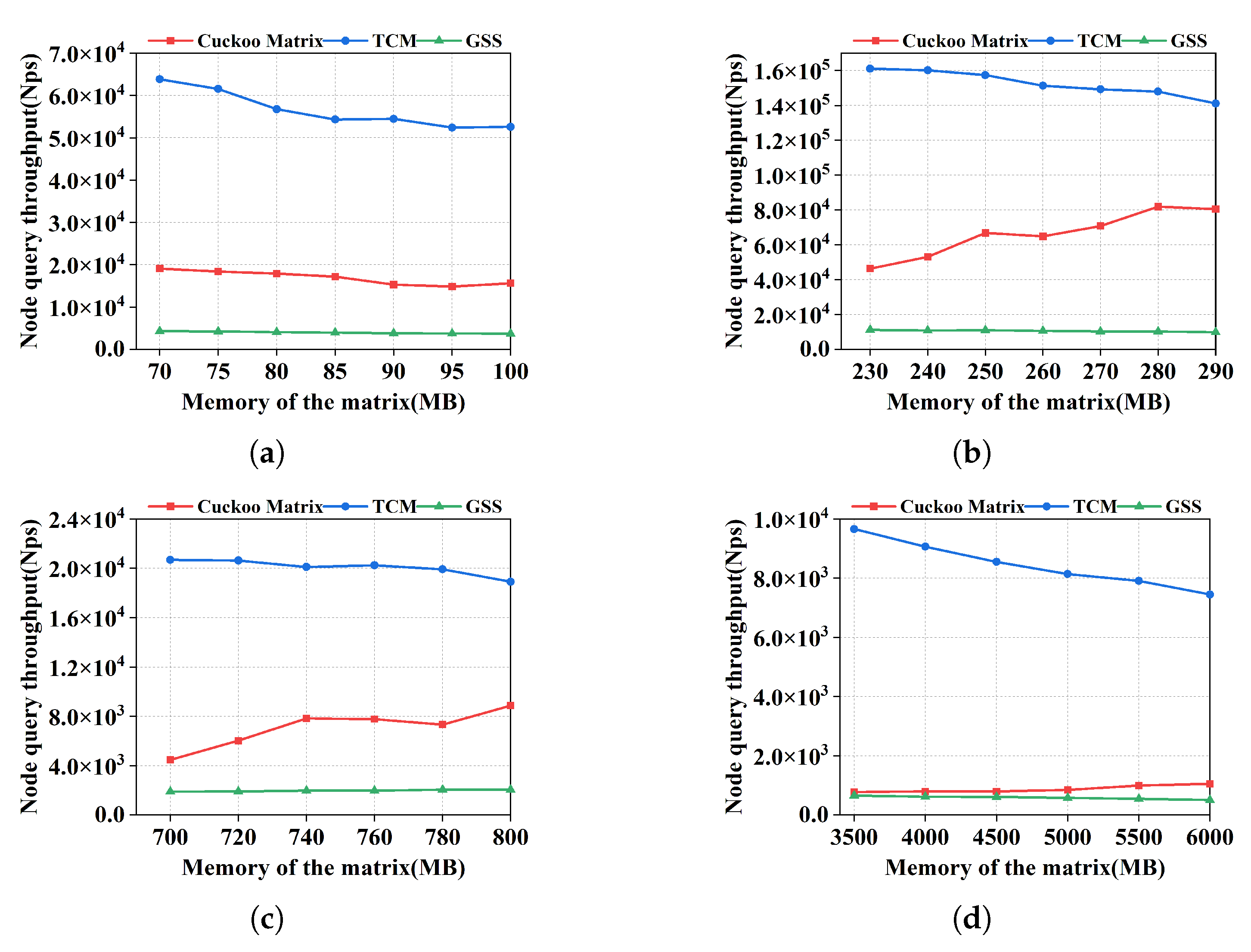
In this section, the performance of these three solutions in node queries is evaluated. For each dataset, the node query set contains all nodes in the graph stream. As shown in Figure 6, compared to Cuckoo Matrix and GSS, the ARE of TCM is too high. Because TCM does not distinguish among different edges that are mapped to the same location. Since Cuckoo Matrix keeps the fingerprint of each node, it can almost find every node accurately. Like edge query, GSS uses extra memory as a buffer to ensure accuracy, so it is a bit more accurate than Cuckoo Matrix.

Node query is different from edge query that it needs traversals. Given a node s, the query result can be computed by first locating the row in the adjacency matrix corresponding to s. Then Cuckoo Matrix will traverse through all the cells of all the buckets in this row. For Cuckoo Matrix, the number of buckets increases as the memory increases. While maintaining accuracy, the number of cells required is reduced more significantly. Overall, the time required to traverse is reduced or unchanged compared to when the memory is smaller. For GSS, the node query also needs to traverse the buffer, hence it has the lowest throughput. Thus, Cuckoo Matrix is on average 3.5 times faster than GSS, especially in Figure 7a–c. Since the memory of TCM is allocated to 4 matrices, each with a small width, the node query of TCM is really fast.

7.7. Reachability Query

In this section, the performance of these three solutions in reachability queries is evaluated. Referring to GSS [13], the reachability query set Q contains 100 unreachable node pairs that are randomly generated from the graph. From Figure 8, the queries of Cuckoo Matrix and GSS are accurate enough because each of the edges is recorded separately. In contrast, since the matrix of TCM aggregates a large number of edges, the results of reachability queries are almost true. Thus, the false positive of TCM is so high that the accuracy is poor.

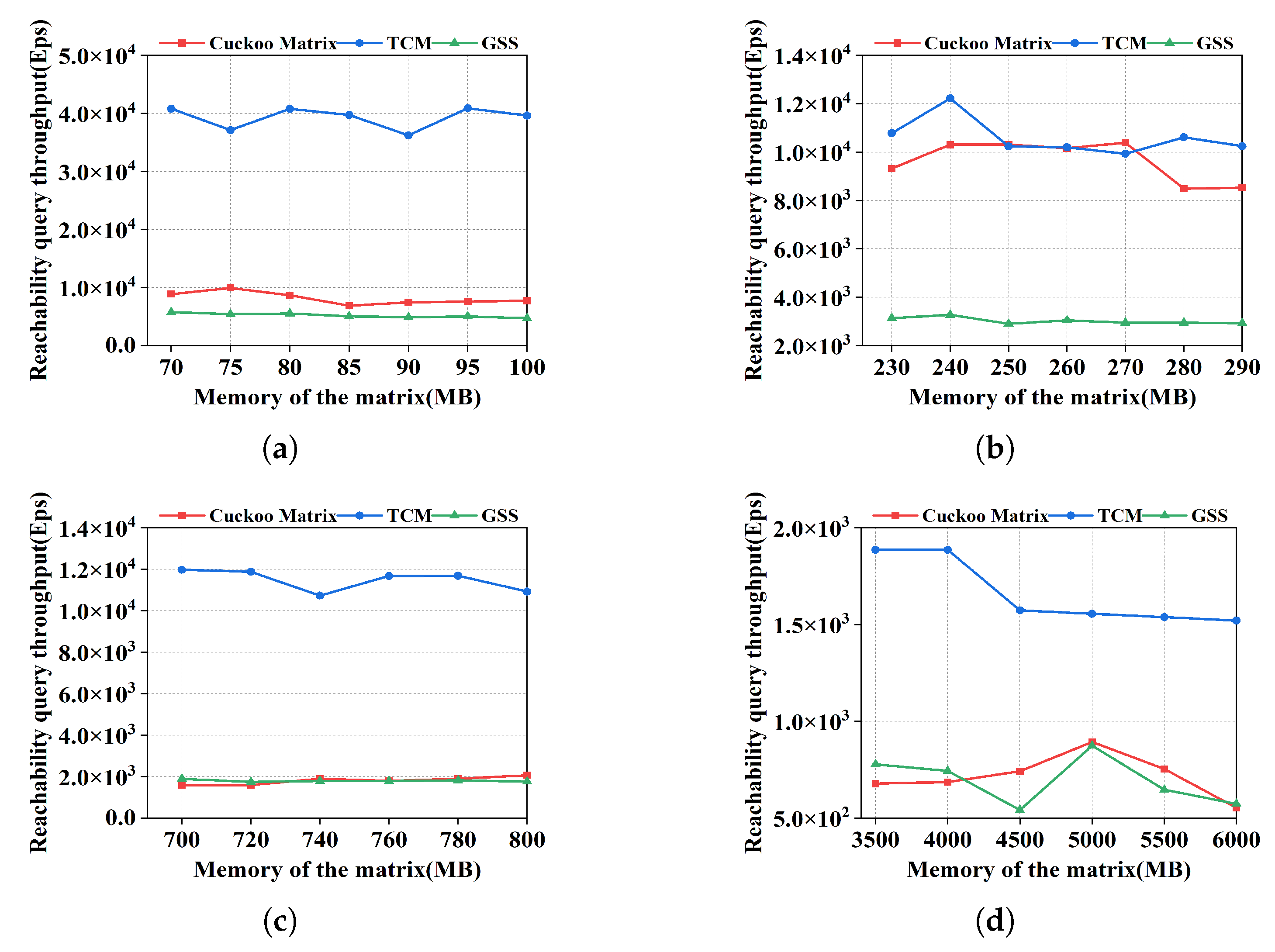
Reachability query is related to edge query and the number of neighbor nodes of each node. Consequently, the throughput is measured by Eps. TCM only identifies whether there is an edge at the corresponding position in the matrix, without caring whether this edge is the one to be queried. So it has the least accurate rate and the largest throughput as shown in Figure 9. For Cuckoo Matrix and GSS, they need to compare the fingerprint pairs of each edge to ensure the accuracy of the query, which needs some time. Thus their throughput is lower than that of TCM.

7.8. Subgraph Weight Query

In this section, the performance of these three solutions in subgraph weight queries is evaluated. For each dataset, 20 connected subgraphs with different shapes are generated from the original graph stream, and each of the subgraphs includes 10 edges. This is referenced to TCM [12]. The ARE is always 0 for Cuckoo Matrix and GSS, which means almost every query is ideal. As the memory of the matrix increases, the probability that different edges are aggregated together in TCM is smaller. Therefore, the ARE of TCM decreases as shown in Figure 10.

Since subgraph queries are considered as summing up the estimated edge queries of all graph edges, the trends in their throughputs are very similar. As shown in Figure 11, Cuckoo Matrix is the fastest because it only probes two locations at most. Meanwhile, GSS has to traverse the buffer so that it is slower than Cuckoo Matrix. As TCM needs to check multiple matrices, it has the lowest throughput in subgraph weight queries.

7.9. Memory Consumption

In this section, the performances in memory consumption are evaluated. The relationship between the memory of the matrix and the total memory is shown in Figure 12. Experiments are performed with the given ARE of edge queries.

Cuckoo Matrix has $O\left(E\right)$ memory cost, where E means the number of edges inserted into Cuckoo Matrix, and it only consists of one adjacency matrix, so the memory of the matrix is its total memory obviously.

For GSS, as mentioned before, when all the candidate buckets in the matrix are occupied, GSS stores the subsequent edges into the buffer. Therefore, the total memory of GSS consists of the matrix memory and the buffer memory. In Figure 12a–c, fewer and fewer edges are recorded in the buffer as the memory of the matrix increases. Therefore, GSS’s total memory is decreasing and is almost the same as the memory of the matrix. Unfortunately, the Wiki dataset is too large and dense, and a significant portion of the edges have conflicts in the matrix. In Figure 12d, the memory of the buffer is decreasing. Because as the matrix memory increases, there are fewer conflicts among edges. In conclusion, GSS has $O(E+B)$ memory cost.

It should be noted that when the memory of the matrix is 700 MB, the total memory of GSS exceeds 1600 MB, which is 2.34 times as much as the memory of the matrix. At the same time, Cuckoo Matrix is able to perform the insertion and query tasks with the same level of ARE and it only has a total memory of 700 MB.

TCM only uses matrices, and it has $O\left(E\right)$ memory cost. However, it cannot achieve such an ARE, so it does not perform in this comparison.

7.10. Discussion

Experimental results show that Cuckoo Matrix is able to maintain high accuracy and high throughput at low memory consumption. However, there are some problems with Cuckoo Matrix. An error will be introduced when edges cannot be inserted after the maximum number of kicking out. Moreover, when the amount of data is too large, Cuckoo Matrix takes some time to ensure that each edge has an exact position, which reduces the throughput.

Compared with Cuckoo Matrix, GSS and TCM have more disadvantages, which are quite obvious in the experiments. For GSS, it takes up too much memory and is extremely slow in some queries. For TCM, it is so imprecise that it cannot support certain queries at all. In summary, Cuckoo Matrix is a general-purpose, high-performance structure that is superior to existing solutions.

8. Conclusions and Future Works

Graph stream summarization is a research direction rising in many fields, whereas, as far as we know, there is no previous work that can support both structural and weight-based queries with large throughput and high accuracy on limited memory. In this paper, we propose Cuckoo Matrix, which has $O\left(E\right)$ memory cost and $O\left(1\right)$ update speed. It maintains the node-based structural relationships among distinct edges using only an adjacency matrix. In addition, Cuckoo Matrix is a general-purpose and high-performance structure that fits perfectly into the needs of graph stream summarization. The performance is evaluated and the experimental results show a significant improvement in Cuckoo Matrix in terms of memory consumption, accuracy, and throughput. In summary, Cuckoo Matrix meets the requirements of graph stream summarizations.

One promising future direction would be to optimize the current structure to reduce errors after the maximum number of kicking out, and another one is the experience we have learned from [1,2]. We will utilize efficient neural networks to predict the network state in order to plan and manage the network in advance [31]. Next, we will use the prediction results to control the congestion in the network in advance.