Optical Solitons in Magneto-Optic Waveguides Having Kudryashov’s Law of Nonlinear Refractive Index by Trial Equation Approach
Abstract
1. Introduction
Governing Model
2. Mathematical Analysis
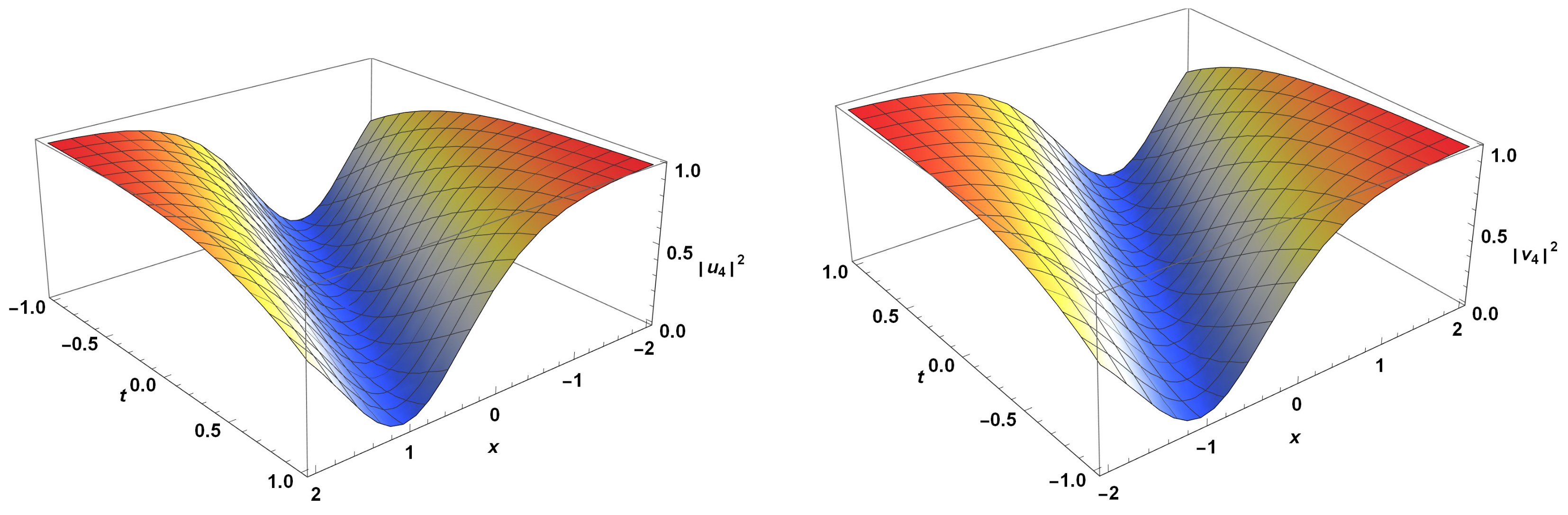
3. Exact Solutions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ozisik, M.; Secer, A.; Bayram, M. The bell-shaped perturbed dispersive optical solitons of Biswas–Arshed equation using the new Kudryashov’s approach. Optik 2022, 267, 169650. [Google Scholar] [CrossRef]
- Secer, A. Stochastic optical solitons with multiplicative white noise via Itô calculus. Optik 2022, 268, 169831. [Google Scholar] [CrossRef]
- Ozisik, M.; Secer, A.; Bayram, M. On the examination of optical soliton pulses of Manakov system with auxiliary equation technique. Optik 2022, 268, 169800. [Google Scholar] [CrossRef]
- Esen, H.; Secer, A.; Ozisik, M.; Bayram, M. Dark, bright and singular optical solutions of the Kaup–Newell model with two analytical integration schemes. Optik 2022, 261, 169110. [Google Scholar] [CrossRef]
- Esen, H.; Ozisik, M.; Secer, A.; Bayram, M. Optical soliton perturbation with Fokas–Lenells equation via enhanced modified extended tanh-expansion approach. Optik 2022, 267, 169615. [Google Scholar] [CrossRef]
- Ozdemir, N.; Esen, H.; Secer, A.; Bayram, M.; Sulaiman, T.A.; Yusuf, A.; Aydin, H. Optical solitons and other solutions to the Radhakrishnan-Kundu-Lakshmanan equation. Optik 2021, 242, 167363. [Google Scholar] [CrossRef]
- Ozisik, M.; Secer, A.; Bayram, M.; Aydin, H. An encyclopedia of Kudryashov’s integrability approaches applicable to optoelectronic devices. Optik 2022, 265, 169499. [Google Scholar] [CrossRef]
- Hutchings, D.C.; Holmes, B.M. Quasi-phase matching magneto-optical waveguides. MRS Online Proc. Libr. OPL 2011, 1291. [Google Scholar] [CrossRef]
- Choueikani, F.; Royer, F.; Jamon, D.; Siblini, A.; Rousseau, J.J.; Neveu, S.; Charara, J. Magneto-optical waveguides made of cobalt ferrite nanoparticles embedded in silica/zirconia organic-inorganic matrix. Appl. Phys. Lett. 2009, 94, 051113. [Google Scholar] [CrossRef]
- Wang, M.Y.; Biswas, A.; Yıldırım, Y.; Alshehri, H.M. Dispersive solitons in magneto-optic waveguides with Kudryashov’s form of self-phase modulation. Optik 2022, 269, 169860. [Google Scholar] [CrossRef]
- Sun, F. Propagation of solitons in optical fibers with generalized Kudryashov’s refractive index. Results Phys. 2021, 28, 104644. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alngar, M.E.; Biswas, A.; Asma, M.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Solitons in magneto–optic waveguides with Kudryashov’s law of refractive index. Chaos Solitons Fractals 2020, 140, 110129. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alngar, M.E.; Biswas, A.; Kara, A.H.; Asma, M.; Ekici, M.; Khan, S.; Alzahrani, A.K.; Belic, M.R. Solitons and conservation laws in magneto–optic waveguides with generalized Kudryashov’s equation. Chin. J. Phys. 2021, 69, 186–205. [Google Scholar] [CrossRef]
- Kudryashov, N.A. A generalized model for description of propagation pulses in optical fiber. Optik 2019, 189, 42–52. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Mathematical model of propagation pulse in optical fiber with power nonlinearities. Optik 2020, 212, 164750. [Google Scholar] [CrossRef]
- Liu, C.S. Applications of complete discrimination system for polynomial for classifications of traveling wave solutions to nonlinear differential equations. Comput. Phys. Commun. 2010, 181, 317–324. [Google Scholar] [CrossRef]
- Liu, C.S. Trial equation method based on symmetry and applications to nonlinear equations arising in mathematical physics. Found. Phys. 2011, 41, 793–804. [Google Scholar] [CrossRef]
- Liu, C. Trial equation method and its applications to nonlinear evolution equations. Acta Phys. Sin. 2005, 54, 2505–2509. [Google Scholar]
- Liu, C.S. Using trial equation method to solve the exact solutions for two kinds of KdV equations with variable coefficients. Acta Phys. Sin. 2005, 54, 4506–4510. [Google Scholar]
- Cheng-Shi, L. A new trial equation method and its applications. Commun. Theor. Phys. 2006, 45, 395. [Google Scholar] [CrossRef]
- Cheng-Shi, L. Exact travelling wave solutions for (1+1)-dimensional dispersive long wave equation. Chin. Phys. 2005, 14, 1710. [Google Scholar] [CrossRef]
- Tang, L. Bifurcation analysis and multiple solitons in birefringent fibers with coupled Schrödinger-Hirota equation. Chaos Solitons Fractals 2022, 161, 112383. [Google Scholar] [CrossRef]
- Tang, L. Bifurcations and dispersive optical solitons for the nonlinear Schrödinger–Hirota equation in DWDM networks. Optik 2022, 262, 169276. [Google Scholar] [CrossRef]
- Tang, L. Bifurcations and multiple optical solitons for the dual-mode nonlinear Schrödinger equation with Kerr law nonlinearity. Optik 2022, 265, 169555. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.-Y.; Biswas, A.; Yıldırım, Y.; Moraru, L.; Moldovanu, S.; Alghamdi, A.A. Optical Solitons in Magneto-Optic Waveguides Having Kudryashov’s Law of Nonlinear Refractive Index by Trial Equation Approach. Electronics 2023, 12, 331. https://doi.org/10.3390/electronics12020331
Wang M-Y, Biswas A, Yıldırım Y, Moraru L, Moldovanu S, Alghamdi AA. Optical Solitons in Magneto-Optic Waveguides Having Kudryashov’s Law of Nonlinear Refractive Index by Trial Equation Approach. Electronics. 2023; 12(2):331. https://doi.org/10.3390/electronics12020331
Chicago/Turabian StyleWang, Ming-Yue, Anjan Biswas, Yakup Yıldırım, Luminita Moraru, Simona Moldovanu, and Abdulah A. Alghamdi. 2023. "Optical Solitons in Magneto-Optic Waveguides Having Kudryashov’s Law of Nonlinear Refractive Index by Trial Equation Approach" Electronics 12, no. 2: 331. https://doi.org/10.3390/electronics12020331
APA StyleWang, M.-Y., Biswas, A., Yıldırım, Y., Moraru, L., Moldovanu, S., & Alghamdi, A. A. (2023). Optical Solitons in Magneto-Optic Waveguides Having Kudryashov’s Law of Nonlinear Refractive Index by Trial Equation Approach. Electronics, 12(2), 331. https://doi.org/10.3390/electronics12020331









