Abstract
The selection of the optimizer is critical for convergence in the field of on-chip training. As one second moment optimizer, adaptive moment estimation (ADAM) shows a significant advantage compared with non-moment optimizers such as stochastic gradient descent (SGD) and first-moment optimizers such as Momentum. However, ADAM is hard to implement on hardware due to the computationally intensive operations, including square, root extraction, and division. This work proposed Hardware-ADAM (HW-ADAM), an efficient fixed-point accelerator for ADAM highlighting hardware-oriented mathematical optimizations. HW-ADAM has two designs: Efficient-ADAM (E-ADAM) unit reduced the hardware resource consumption by around 90% compared with the related work. E-ADAM achieved a throughput of 2.89 MUOP/s (Million Updating Operation per Second), which is 2.8× of the original ADAM. Fast-ADAM (F-ADAM) unit reduced 91.5% flip-flops, 65.7% look-up tables, and 50% DSPs compared with the related work. The F-ADAM unit achieved a throughput of 16.7 MUOP/s, which is 16.4× of the original ADAM.
1. Introduction
Deep neural networks (DNNs) are excellent in discovering complex structures in high-dimensional data with high accuracy. Over the past decades, DNNs have played an important role in various domains, such as image classification [1], autonomous driving [2], and object detection [3]. For example, Krizhevsky et al. classified the 1.2 million high-resolution images in the ImageNet LSVRC-2010 competition into 1000 different classes by a large CNN [1]. Chenyi Chen et al. recognized image features for estimating affordance related to autonomous driving upon AlexNet framework [2]. Currently, the deep reinforcement learning (DRL) algorithm combining DNNs and RL has a great success in the field of robot control [4], speech recognition [5] and gaming [6].
However, the performance improvements typically come with the increased density of the DNNs and more time cost [7]. Therefore, there is a growing demand for accelerators with high training efficiency to accommodate the development of DNNs. Hardware accelerators such as graphic processing unit (GPU), application-specific integrated circuit (ASIC), and field programmable gate array (FPGA) have been implemented to improve the throughput of the DNNs [8]. FPGA and ASIC accelerators have lower power consumption compared with GPU-based accelerators [9,10], while FPGAs have higher flexibility and less cost compared with ASIC-based accelerators [11,12]. In the past practices, DNNs generally completed the backward propagation process off-line [13]. Then, the off-line trained DNNs are used in the forward propagation process to execute the inference tasks [14]. Therefore, most previous accelerators [15,16] focused only on the inference phase of DNNs.
With the development of edge computing, local DNN training with private data and domain-specific is required for personalization [17,18,19]. The training process of DNNs can be divided into three phases: forward propagation (FP), backward propagation (BP), and weight gradient update (WG). All the phases need to be accelerated in an on-chip learning system. Generally, DNN training introduces about 3× computational cost and consumes 10× to 100× memory compared with the single inference phase. On-chip learning also requires higher efficiency and lower power consumption [18].
On-chip learning has been widely studied by methods such as quantizing [20,21,22], and exploiting network sparsity [23]. Work [21] counts the maximum value of the layers and quantifies the synaptic weights as 8-bit floating point data, and work [22] computes the cosine similarity between the quantized weights and the original weights to obtain INT8 data. Work [24] combines algorithmic adaptation with dataflow and hardware optimization to improve energy efficiency and throughput. Work [17] proposes FGMP that divides features into FP8-group and FP16-group at the data-element level, considering the acceleration efficiency in both the inference and the training phases.
However, few researches have focused on weight gradient updating (WG) completed by the optimizer. The optimizer is one of the most important modules of the training process. The selection of the optimizer has a critical influence on the convergence and the performance of the trained model. Nowadays, sufficient researches have shown that second-moment optimizers have much better convergence and robustness than non-moment and first-moment optimizers [25]. However, most of the previous works of on-chip training focus on forward and backward propagation. Those works use simple non-moment optimizers such as gradient descent (GD) and stochastic gradient descent (SGD) [26] or complex optimizers without hardware optimization [27,28]. Work [29] implemented the second moment optimizers near the storage. However, the optimizer itself is not optimized. Some works have been proposed to accelerate the first-moment optimizers. Work [30] presented various highly scalable and parameterizable FPGA-based stochastic gradient descent implementations for performing linear model training. However, second-moment optimizers have not been designed and implemented with full hardware optimization. Adaptive moment estimation (ADAM) is one of the most widely adopted second-moment optimizers [31]. The ADAM calculates and stores the first and second moment for each weight of the neural network. The second-moment calculation comprises computationally intensive operations including square, root extraction, and division, resulting in high execution latency and hardware resource consumption. The storage of the first and second moment also consumes many hardware resources. Thus the ADAM is expensive to implement on hardware despite the high convergence and training efficiency. To solve these problems, this work proposed Hardware-ADAM (HW-ADAM), an efficient fixed-point accelerator for ADAM highlighting hardware-oriented mathematical optimizations. To our best knowledge, the proposed work is the first to make specific optimizations to accelerate the ADAM by mathematical methods. The main contributions of this work include:
1. Efficient-ADAM (E-ADAM) is proposed by simplifying the calculation of square and root extraction into the calculation of comparison, logic shifting, and addition. The hardware-oriented optimization for hyper-parameters and the approximation to the updating step are proposed to further simplify the circuit design. The proposed E-ADAM reduces the critical resource consumption by 85% while achieving a throughput of 2.89 MUOP/s (Million Updating Operation per Second), which is 2.8 times the original ADAM.
2. Fast-ADAM (F-ADAM) is proposed based on E-ADAM and accelerates the division in the calculation of updating step. We leverage the theory of Fast Inverse Square Root (Fast InvSqrt) [32] and propose a fast division calculation based on the storage format of single-precision floating-point number. The proposed F-ADAM achieves a throughput of 16.7 MUOP/s, which is 16.4 times the original ADAM.
2. Background Knowledge
2.1. Overview of Adaptive Moment Estimation
The training of the neural network is completed by the iteration of forward propagation, backward propagation, and weights updating. In one training iteration, the forward propagation is first executed to obtain the inference result, based on which the training loss is calculated. The gradient for each weight of the neural network is calculated by the backward propagation based on the training loss. Then the optimizer generates the updating step for each weight with a specific strategy. Then the weights are updated according to the updating steps. Different optimizers are thus defined by the different strategies of updating step calculation. There are three major types of optimizers: non-moment optimizers, first-moment optimizers, and second-moment optimizers. The updating methods of non-moment and first-moment optimizers are simple and hardware-friendly. In gradient descent (GD), the forward and backward propagation is executed on the whole training set and the updating steps are the resulting gradients. The weights are subtracted by the updating steps with the scale of the learning rate. The propagation and updating based on the whole data set may result in the over-fitting and local optimum. Stochastic gradient descent (SGD) reduces the probability of over-fitting and local optimum by training the model on a stochastic small batch of the data set in one iteration. The first-moment optimizers such as Momentum [33] and Nesterov [34] introduce the conception of the moment to improve convergence. The second-moment optimizers introduce the self-adaptive learning rate by calculating the second moment of the gradients. The second-moment optimizers have much better convergence and robustness compared with the previous types according to sufficient experiments. However, the calculation complexity on the hardware of the second moment optimizers increases significantly.
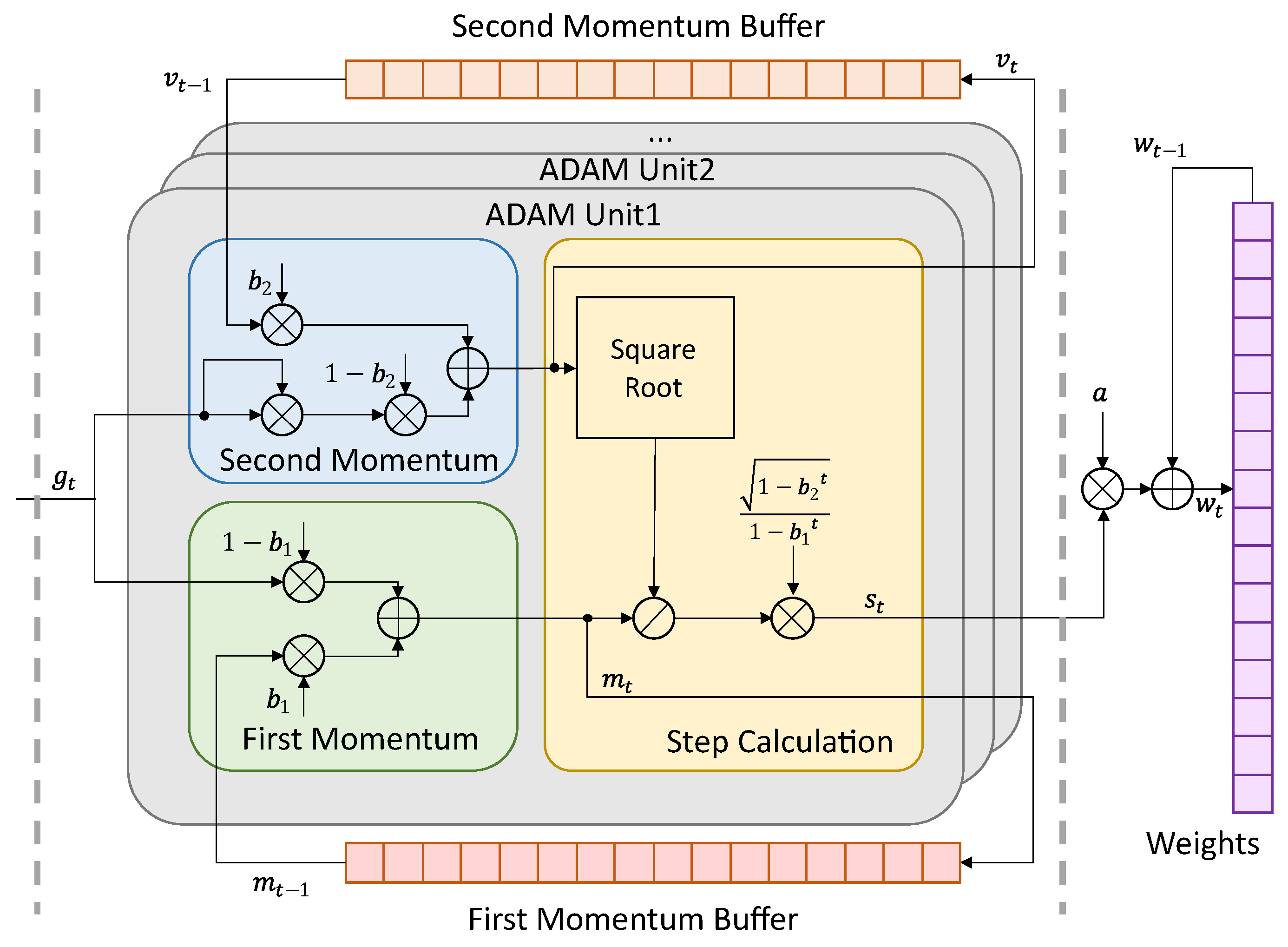
Adaptive moment estimation (ADAM) is the most widely used second-moment optimizer with high convergence and robustness. The overall structure of the original ADAM is shown in Figure 1. The ADAM calculates both the first and second moment. The first moment influences the updating direction. In ADAM, the resulting updating direction is the current moment, which is the weighted vector sum of the current gradient and the last moment. The direction shaping avoids the local optimal by providing inertia to the optimization process. The second moment influences the updating length (learning rate) for each weight. The updating is more efficient because each weight has an independent learning rate. In conclusion, the calculation of ADAM can be divided into three parts: first moment calculation, second moment calculation, and updating step calculation. The first and second moments are stored in the buffers and updated iteratively. A series of ADAM processing units can be implemented and run in parallel. One ADAM unit processes the updating of one weight at each time. The ADAM unit first receives the current gradient from the backward propagation. Then the ADAM unit reads the first moment and the second moment of the last updating step from buffers. The current first moment and the current second moment are calculated as Equations (1) and (2), where and are hyper-parameters recommended by [31] as and . The current updating step is calculated as Equation (3), where is a small value to avoid dividing by zero. Finally, the weights are updated as Equation (4) outside the ADAM unit with a learning rate a. The first moment and the second moment are stored back to the buffers at the end of the iteration. The overall algorithm is shown as Algorithm 1.
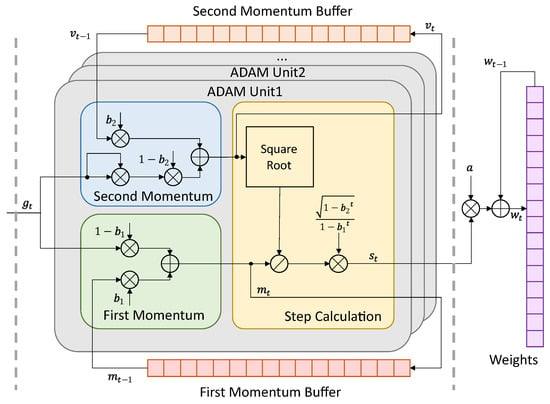
Figure 1.
Overall structure of original ADAM.
| Algorithm 1 The workflow of original ADAM. |
| Require:a: Stepsize |
| Require:, ∈ [0,1): Exponential decay rates for the moment estimates |
| Require:: Stochastic objective function with parameters |
| Require:: Initial parameter vector |
| 1: |
| 2: |
| 3: |
| 4: while not converged do |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: |
2.2. Overview of Fast Inverse Square Root
Fast inverse square root (Fast InvSqrt) provides a simple and efficient method to calculate the inverse square root without complex calculations including division and root extraction. The Fast InvSqrt leverages the storage format of single-precision floating point numbers shown in Figure 2. The actual value of the floating point number can be calculated as Equation (5), where is the exponent representing the shifting bits. The is the actual value of the significand part ranging from 0 to 1 when considered as a fixed-point number with no integer bit and 23 fraction bits. The value of exponent bias B is set as 127 in the IEEE 754 standard. When is relatively small, the logarithm of x can be estimated by Equation (6), where denotes the estimation error. Denoting the value of the significand part as when considered as an unsigned integer, we have , where . Regarding the 32-bit number as an unsigned integer , the relationship between and can be derived as Equation (7). Finally the estimation of is calculated as Equation (8). Given , Equation (9) is derived. According to Equations (8) and (9), the first estimation of can be calculated as Equation (10), where is actually in the format of floating point number. The estimation error is set as in the original work. Finally, the second estimation can be calculated by the Newton method. The Newton method is shown as Equation (11). To perform the Newton method on y, the calculation of is converted into the zero point of as shown in Equation (12). According to Equations (11) and (12), the second estimation is calculated as Equation (13).

Figure 2.
Storage format of floating point numbers.
3. Proposed Method
3.1. Design of Efficient-ADAM
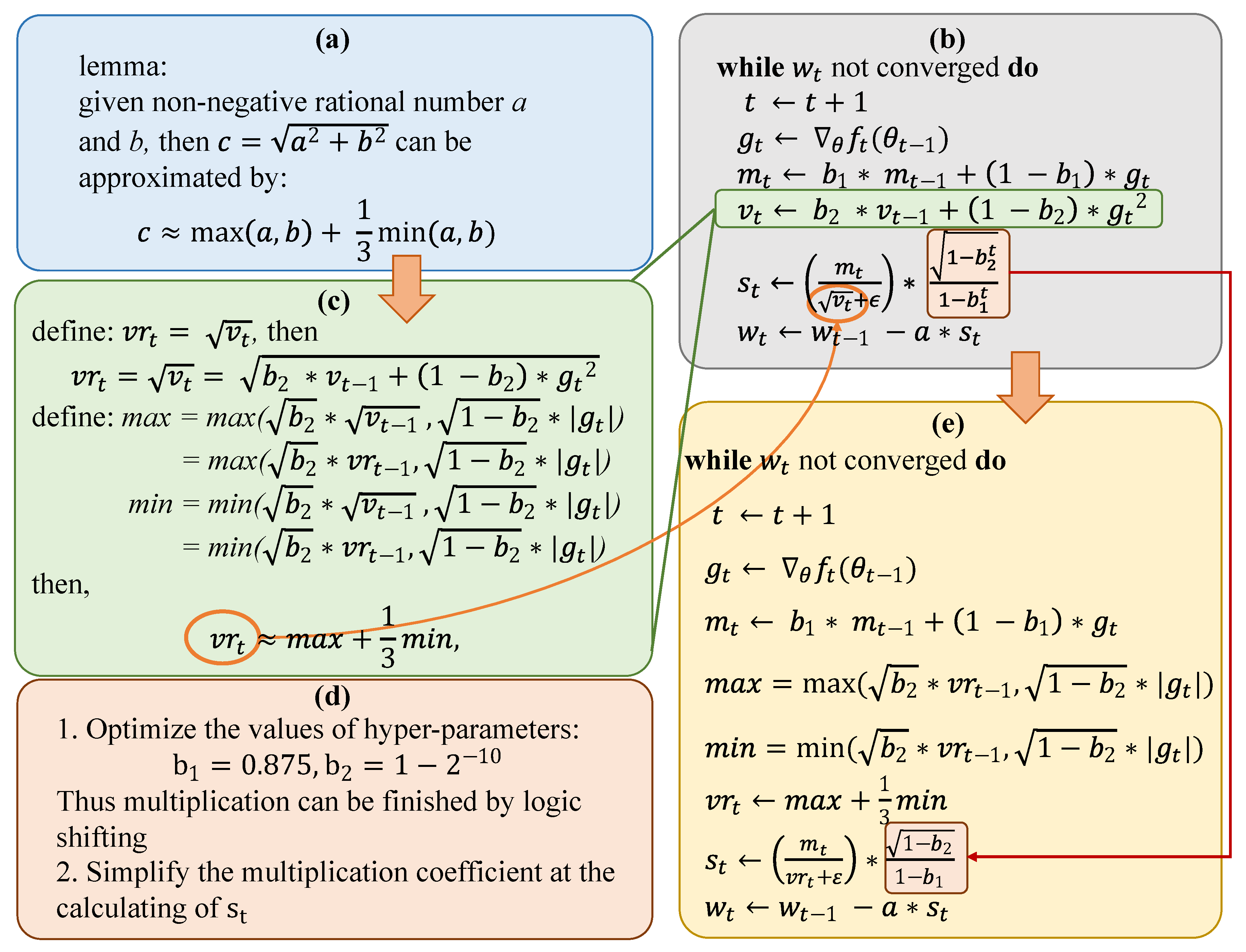
The proposed efficient-ADAM (E-ADAM) simplifies the calculation of the first and second moment. The calculation of the second moment requires the square operation, then the square root of the second moment is extracted when calculating the updating step. Both the squaring and extraction of the square root are time-and-resource-consuming for hardware implementation. To optimize the ADAM calculation, Lemma 1 is introduced with a brief proof. The overall optimization of the ADAM is shown in Figure 3, where Figure 3b is the original ADAM and Figure 3e is the E-ADAM. Firstly, we define a new variable which is the square root of . By introducing Lemma1, the calculation of can be derived as Figure 3c. The can be calculated iteratively by one comparison and two multiplications at each timestep. The original ADAM calculates by complex squaring and root extraction. Thus, the calculation is significantly simplified. Noting that the is the used in the calculation of updating step, the extraction of the square root is eliminated directly. The optimization of the hyper-parameters is designed to further simplify the circuit as shown in Figure 3d. The original hyper-parameters require multiplications during the calculation of updating step. However, when the hyper-parameters are designed as , the multiplication can be simplified as subtraction and bit shifting. In addition, the is simplified to , which further reduces the number of required multiplications. The overall workflow of E-ADAM is illustrated in Algorithm 2.
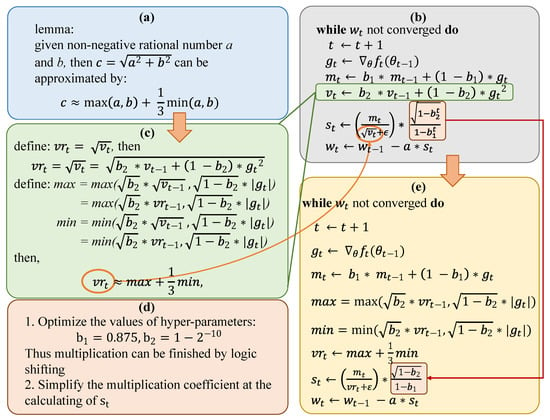
Figure 3.
Proposed optimization of Efficient-ADAM. Subgraph (a) is the introduced lemma. Subgraph (b) is the workflow of the original ADAM. Subgraph (c) is the proposed approximation. Subgraph (d) is the further optimization of the hyper-parameters and calculation. Subgraph (e) is the workflow of the proposed E-ADAM.
Lemma 1.
Given two non-negative rational numbers a and b, then can be approximated by:
Proof of Lemma 1.
Given , let , .
Let , ,
Then,
,
where is the approximation error. The equals 0 at the following two cases:
(1)
(2)
The has the max absolute value when and the .
Thus, . The relative error is within 5.72%, and equals to 0 at the following four cases:
(1)
(2)
(3)
(4) □
| Algorithm 2 The workflow of E-ADAM |
| Require:a: Stepsize |
| Require:, : Exponential decay rates for the moment estimates |
| Require:: Stochastic objective function with parameters |
| Require:: Initial parameter vector |
| 1: |
| 2: |
| 3: |
| 4: while not converged do |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: |
| 10: |
In addition to the efficiency improvement, the optimization also avoids the truncation error of fixed-point calculation. The original ADAM calculates the second moment . However, the gradients of the weights are usually quite small. Take an example of the calculation in the format of 16-bit fixed point number with 8 bits for the fraction part (denoted as fixed-point ⟨16,8⟩). When the is less than , the square equals to 0 due to the truncation error. The interval where thus becomes a blind area of the calculation. In the E-ADAM, the square operation is eliminated, thus the blind area is solved.
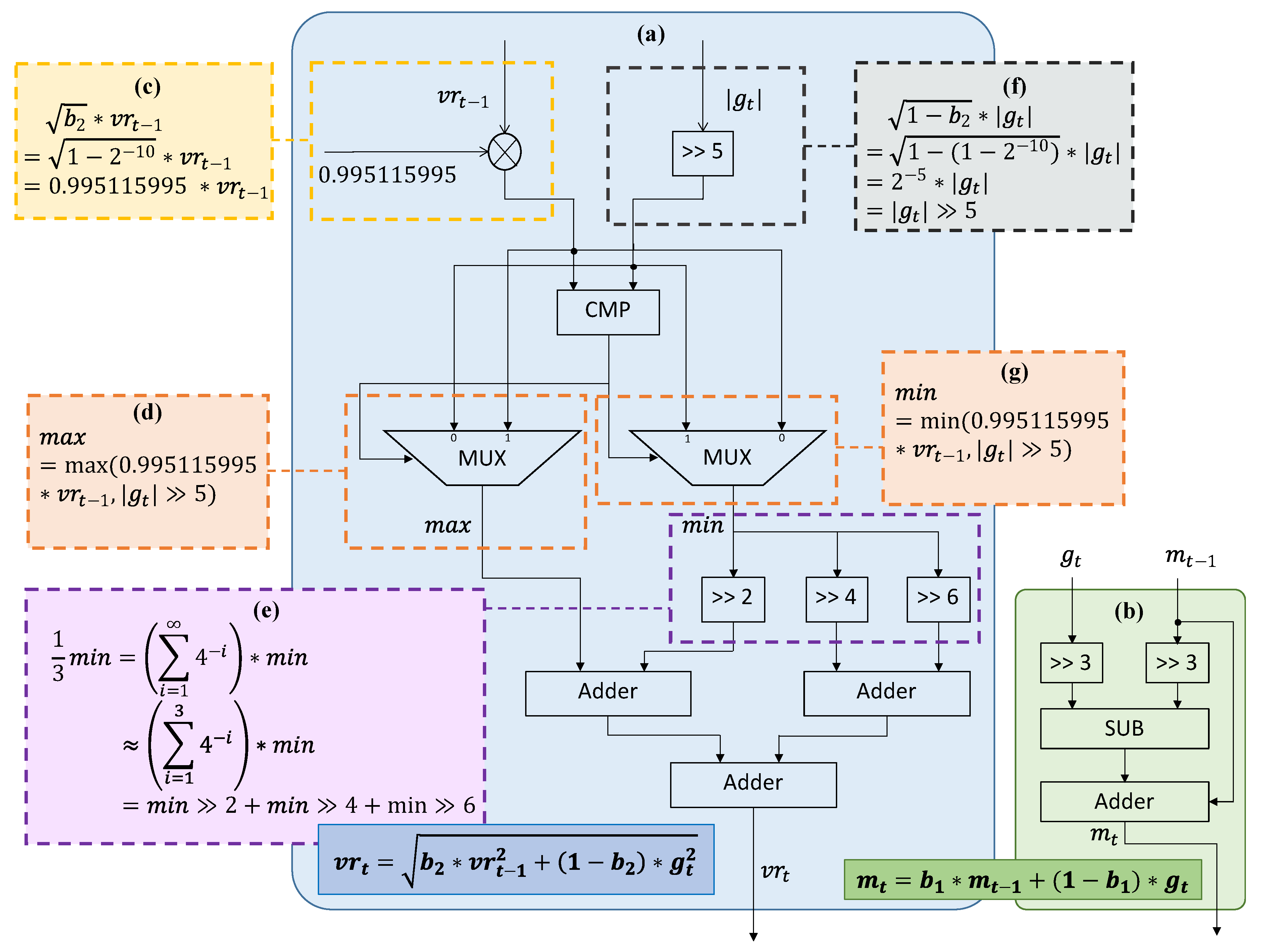
The hardware designs for the second and first moment estimation are respectively illustrated in Figure 4a,b. The hardware design can be used for different fixed point formats. To calculate the current second moment , the last second moment is first read from the buffer and then multiplied by the constant as shown in Figure 4c. The current gradient is input from the backward propagation and the absolute value is calculated directly. Then the should be multiplied by . Because of the optimized hyper-parameters, the value of is . Thus the multiplication can be simplified into logic right shifting as shown in Figure 4f. Then one comparer and two multiplexers are used to obtain the max and min value of and . The current second moment is calculated as the sum of max and min. To further reduce the hardware complexity, the series approximation is introduced as shown in Figure 4e. The operation of division by 3 can be decomposed as one series of logic shifting and addition. In the proposed design, the first three items of the series are reserved for the balance between accuracy and efficiency. The calculation of the first moment estimation is also optimized for hardware implementation. Both the multiplications for and are simplified as logic shifting because of the optimized hyper-parameter . To calculate the , the and are both shifted three bits to get and . Then the result is calculated by one subtractor and one adder. Thus, no multiplication is used during the calculation of the current first moment .
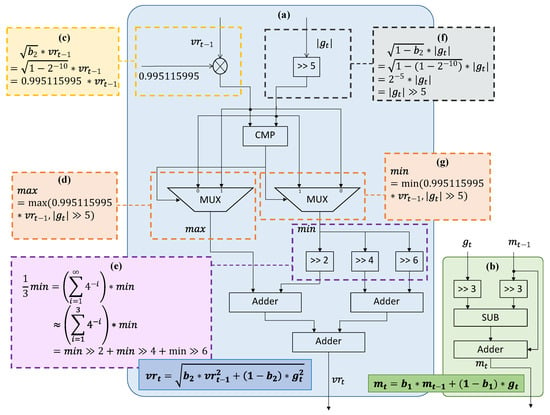
Figure 4.
Hardware design of Efficient-ADAM. Subgraph (a) is the overall structure of the second moment module. Subgraph (b) is the overall structure of the first moment module. Subgraph (c) is the optimized calculation of . Subgraph (f) is the optimized calculation of . Subgraph (d) and subgraph (g) are the selection of the max and min values. Subgraph (e) is the optimization of division by 3.
3.2. Design of Fast-ADAM
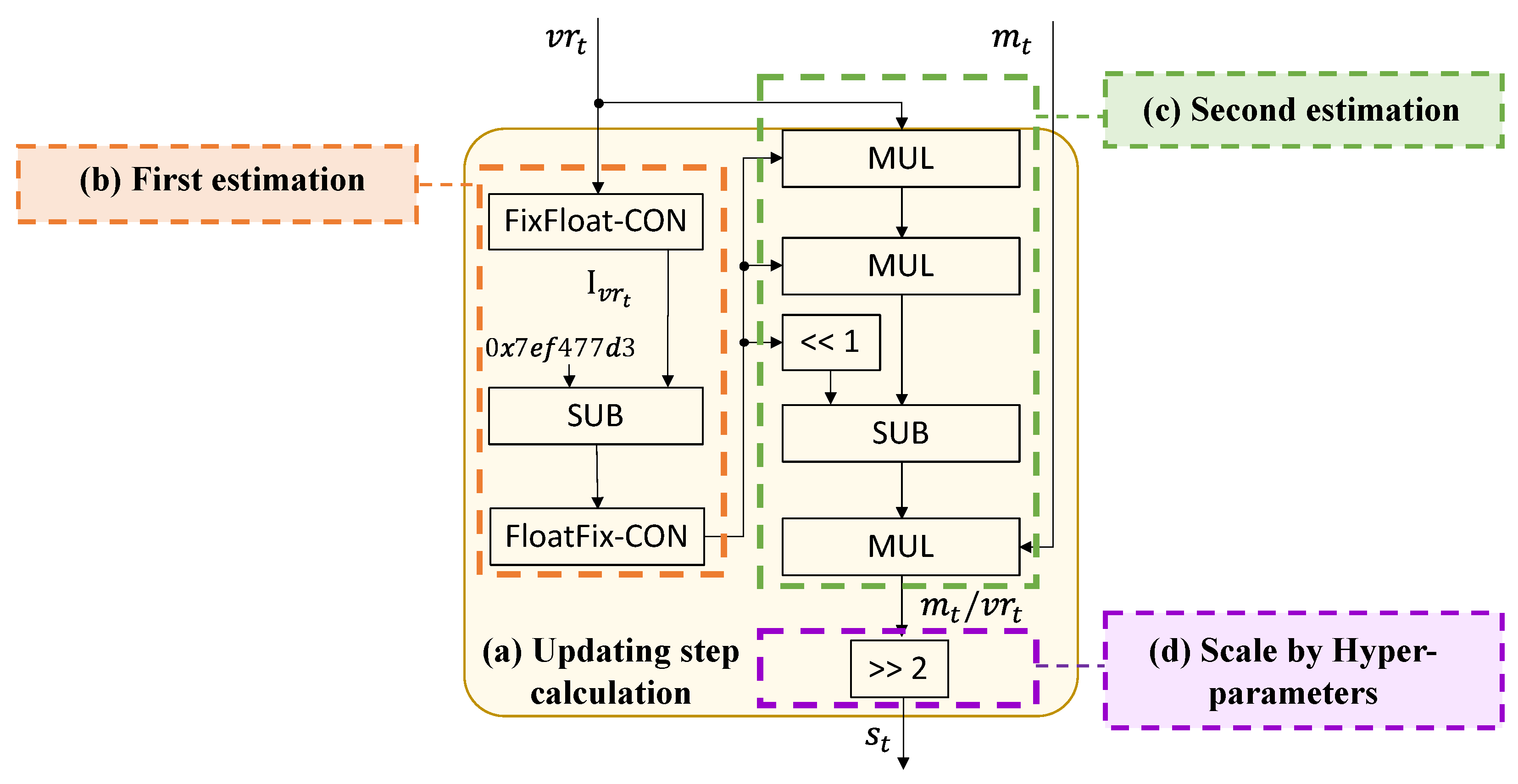
Fast-ADAM (F-ADAM) is proposed based on E-ADAM further optimizing the division during the calculation of updating step. The division is time-and-resource-consuming in the hardware design. To optimize the division, we propose the calculating workflow by introducing the theory of Fast InvSqrt. Firstly, we convert the division to the multiplication . Then the reciprocal is calculated leveraging the storage format of the single-precision floating point number. Given a single-precision floating point calculation , Equation (14) is derived by taking logarithm on both sides. According to Equation (8), both sides of Equation (14) can be approximated by simple logic shifting and subtraction, and Equation (15) is derived. Thus, the can be calculated as Equation (16) and the result is the first estimation in single-precision floating point format. To calculate the second estimation, the function shown as Equation (17) is introduced and the zero point of is the . Then the Newton method is used to calculate the second estimation of as Equation (18). The final updating step is calculated by the multiplication of the reciprocal of second moment , the first moment , and the scaling factor .
The hardware design for the updating step calculation is shown in Figure 5, where Figure 5a is the overall structure. The first estimation of is shown in Figure 5b. The Fast InvSqrt is designed based on the storage format of single-precision floating point, thus the is converted from fixed point number into the single-precision floating-point number first. Then the subtractor is used to calculate . Given , , and , the value of constant is 0x7ef477d3. Then the result is converted from floating-point number into the original fixed point number for the second estimation. The implementation for both directions of fixed-floating-point conversion is completed by Xilinx Vivado high-level synthesis (HLS) tools automatically. Then the second estimation is calculated as shown in Figure 5c which is in accordance with Equation (18). The multiplication of is simplified into the logic left shifting to reduce the calculation complexity. Finally the is multiplied by the scaling factor . The scaling factor equals to due to the optimized hyper-parameters. Thus the multiplication is also simplified into logic right shifting as shown in Figure 5d.
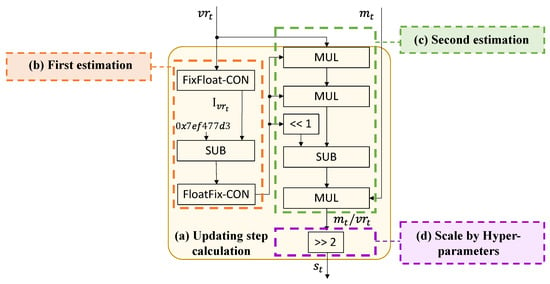
Figure 5.
Hardware design for the updating step calculation module of F-ADAM. Subgraph (a) is the overall structure of the updating step calculation module. Subgraph (b) is the first estimation of . Subgraph (c) is the second estimation of and the calculation of . Subgraph (d) is the optimized calculation of scaling by hyper-parameters.
4. Experimental Results
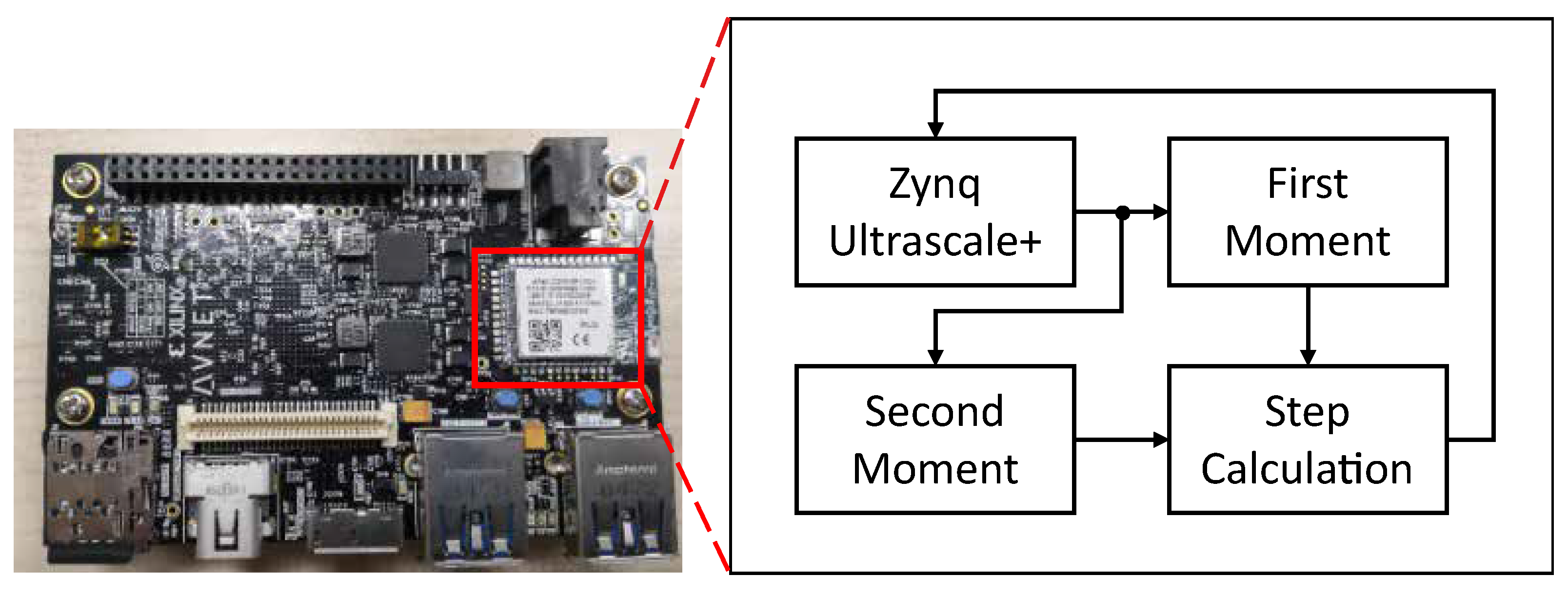
The proposed designs are validated on the Xilinx Ultra96-v2 FPGA board as shown in Figure 6. The proposed modules including first moment module, second moment module, and step calculation module, are implemented on the programable logic (PL) while the testbench environment is implemented on the processing system (PS). The fixed point format is set as , which has 32 bits in total and 16 bits for the fraction.
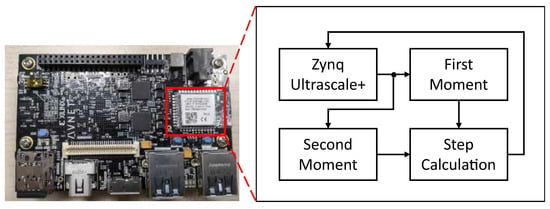
Figure 6.
Hardware implementation of the proposed method.
The reinforcement learning task HalfCheetah from PyBullet Gymperium [35] is used to validate the functionality of the proposed optimizers. The training of a reinforcement learning agent is unsupervised and consists of two stages: sampling and updating. At the sampling stage, the agent interacts with the environment for N times, where N is the number of samples collected in one training iteration. At each interaction, the environment first provides the states to the agent as the input of the neural network. Then the neural network executes forward propagation to get the action. The environment receives the action and entershe next state accordingly for the next iteration. The reward for the action chosen by the agent is output by the environment to calculate the objective function for updating. At the updating stage, the objective function is calculated from the rewards at each timestep. Then the neural network is updated based on the objective function to achieve higher rewards. The HalfCheetah is one classical environment where the neural network is trained to control the action of the HalfCheetah to walk forward. The HalfCheetah has 26 dimensions of state and 6 dimensions of action. Proximal policy optimization (PPO) [36] is used as the algorithm for neural network training. PPO maintains two neural networks including the agent actor and the assistant critic. The critic is used to calculate the objective function while the actor is the one controlling the HalfCheetah. Both neural networks are trained during the training process. When the training process is completed, only the actor is reserved as the training result. The actor neural network contains two fully connected layers with linear rectification function (ReLU) as an activation function. The shapes of the two layers are and . Taking bias into consideration, the total number of weights is 64 × 26 + 26 × 6 + 64 + 6 = 1890. The critic neural network has the same structure and size except for the last layer, which has only one output dimension. Thus, the number of weights is 64 × 26 + 26 × 1 + 64 + 1 = 1755. The updating of both the actor and the critic uses our proposed E-ADAM and F-ADAM to validate the functionality.
4.1. Accuracy Validation of the Proposed Approximation
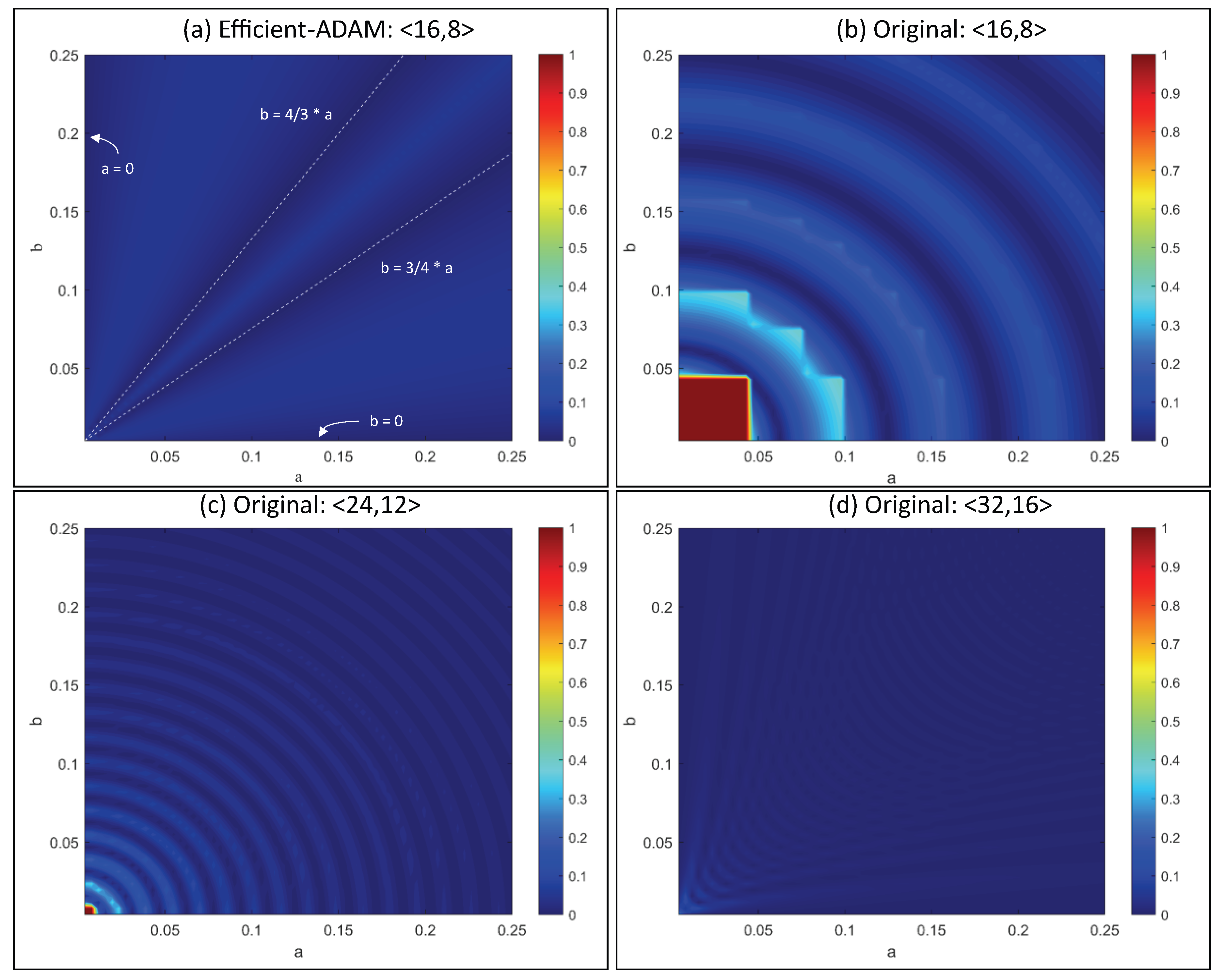
In this subsection, the accuracy of the approximation of Lemma 1 is validated. The heat maps in Figure 7 show the comparison of relative error for with different intermediate result bit widths, where the input a and b are small. The experiment is an abstraction of the calculation in the original ADAM. Small gradients are normal during the training of neural networks. In the original ADAM, intermediate results with more bits are required to avoid the truncation error and blind area caused by squaring operation. Given the input of total 16 bits, with 8 bits for the fraction , E-ADAM keeps a high accuracy when the intermediate results are in the same format as the input, as shown in Figure 7a. Four conditions where the relative error is zero are marked. The original algorithm with bit-width and has a high error and has a blind spot due to the square operation when the input is small, as shown in Figure 7b,c. Only when the intermediate width is doubled from the input width, the blind spot can be avoided, as shown in Figure 7d. Therefore, E-ADAM achieves better accuracy and reduces the bit width of intermediate results.
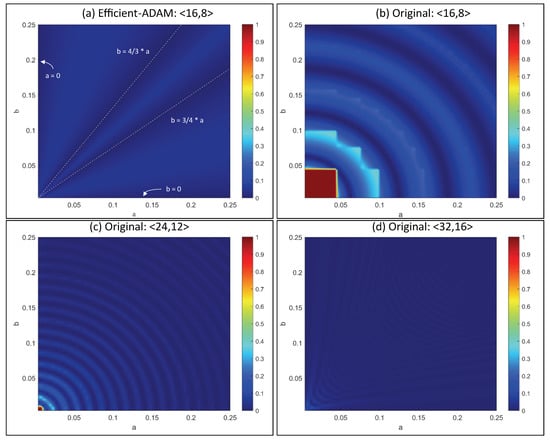
Figure 7.
The accuracy of the proposed approximation to the second moment estimation. The calculation is . Subgraph (a) is the relative error of E-ADAM with the fixed-point number. Four cases where the relative error is 0 are illustrated. Subgraph (b) is the relative error of the original ADAM with the fixed-point number. Subgraph (c) is the relative error of the original ADAM with the fixed-point number. Subgraph (d) is the relative error of the original ADAM with the fixed-point number.
4.2. Functionality Validation of the Proposed Design
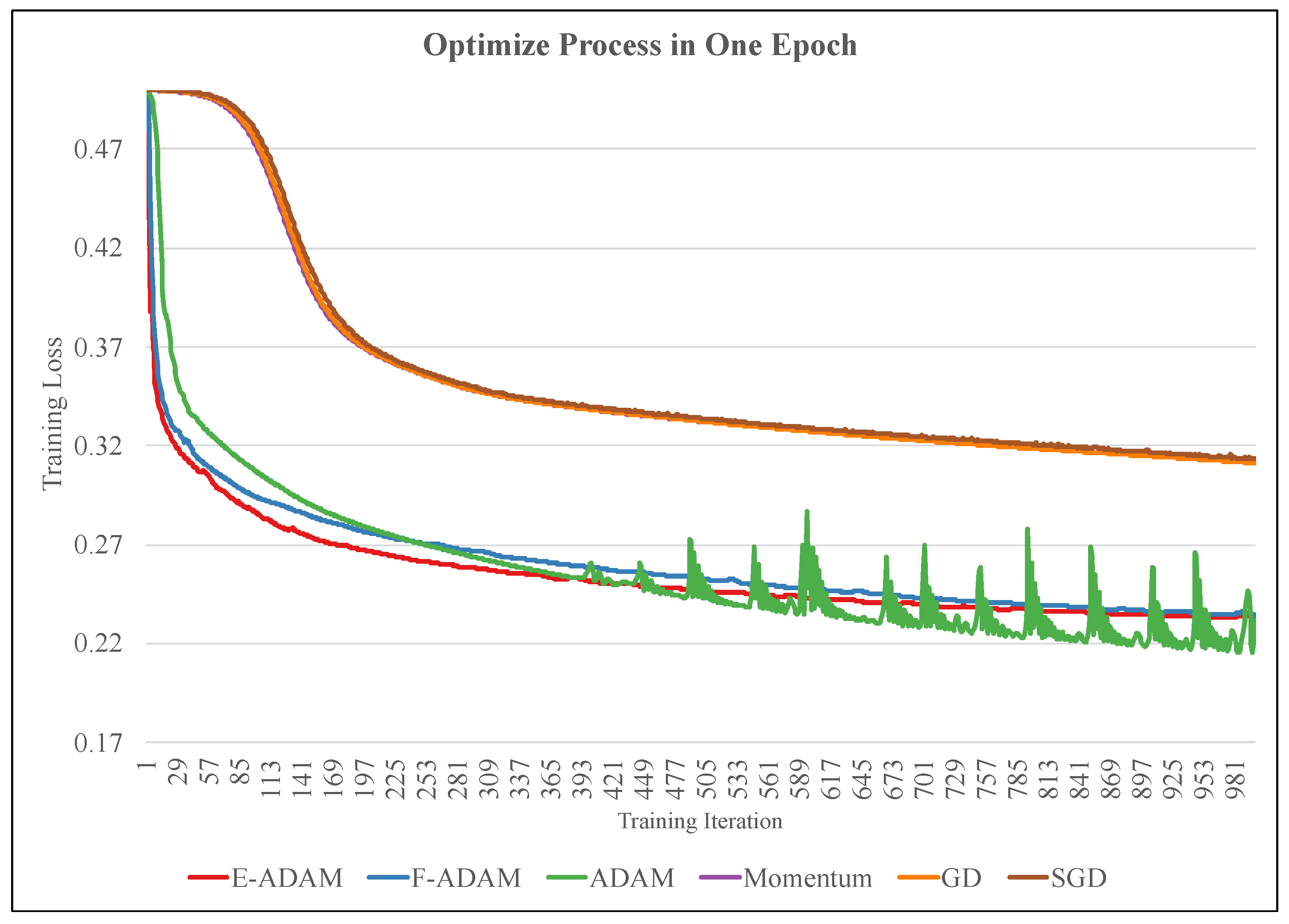
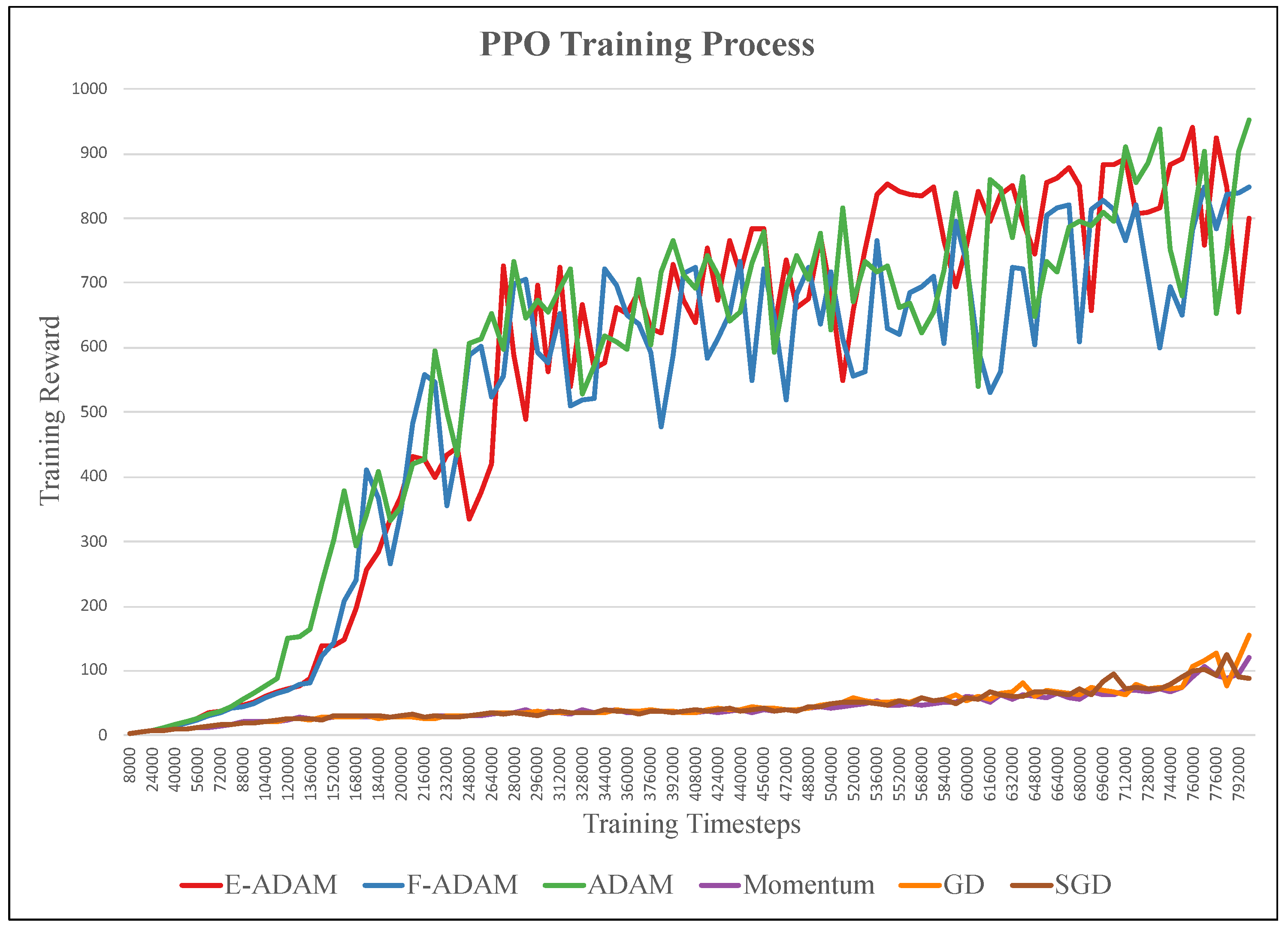
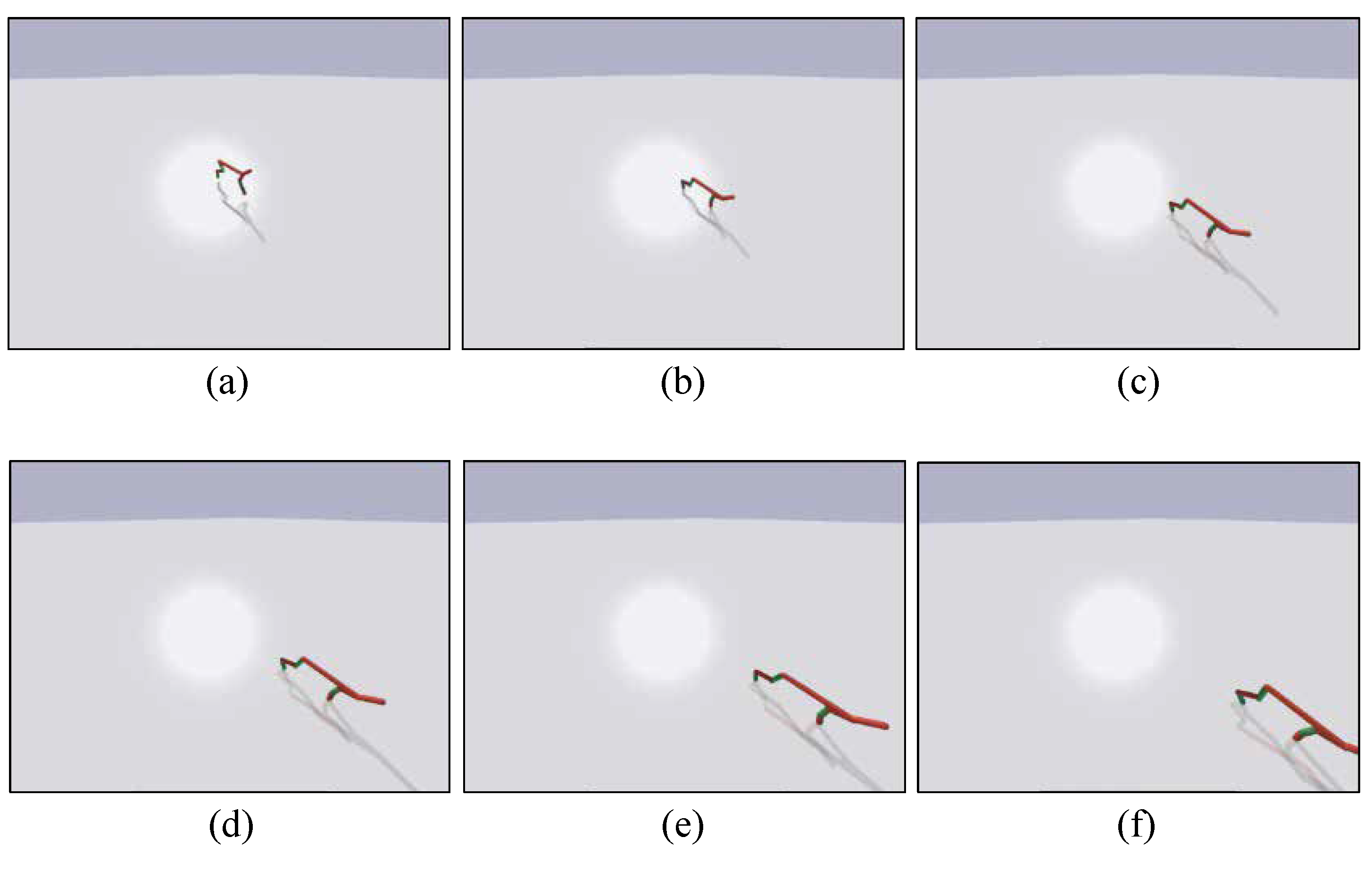
The functionality validation comprises two stages: performance in one epoch and performance in the overall training process of the task. The training processes of six different optimizers in one epoch are shown in Figure 8. The optimizers include the proposed E-ADAM, F-ADAM, the original ADAM, the Momentum, the GD, and the SGD. In one epoch, the loss is calculated based on the collected samples and the weights are updated according to the loss. The proposed E-ADAM and F-ADAM have similar convergence compared with the original ADAM while outperforming other algorithms significantly. In addition, the training curves of E-ADAM and F-ADAM are more stable compared with the original ADAM. This is because the approximation in the calculation of the second moment and updating step introduces a small noise into the training, which avoids over-fitting. The overall training process of the task is shown in Figure 9. The ADAM algorithms have much better convergence and efficiency compared with other tasks. The visualized training result is shown in Figure 10, where the HalfCheetah walks forward stably under the control of the trained agent.
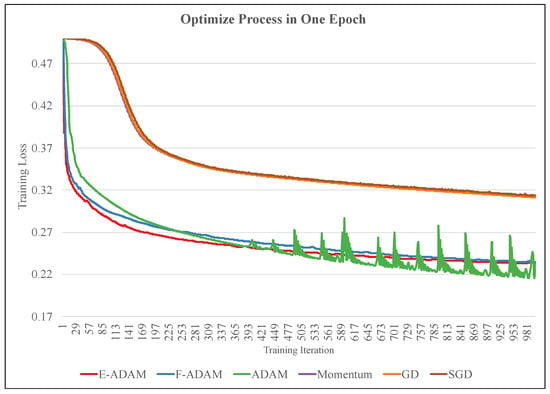
Figure 8.
The training process in one epoch.
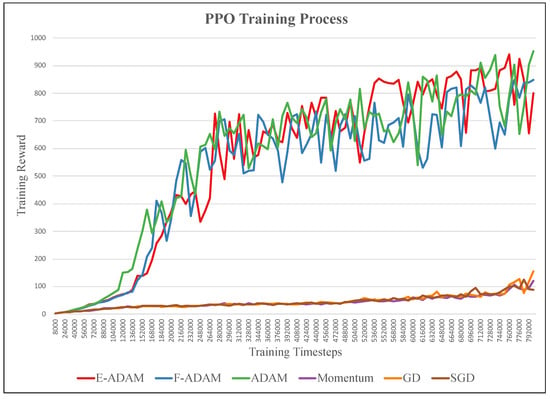
Figure 9.
The overall training process of the task.
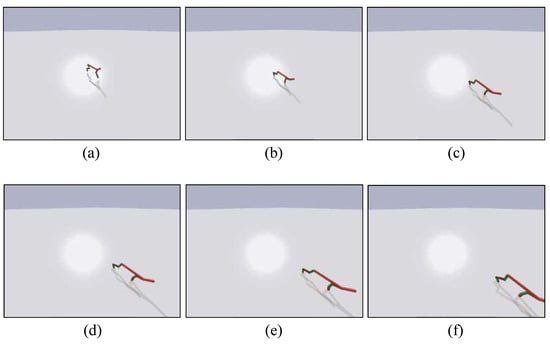
Figure 10.
The visualized training result.The subgraphs (a–f) are captured serially during the walking task of the trained HalfCheetah. The trained HalfCheetah is able to walk forward stably.
4.3. Efficiency Validation of the Proposed Design
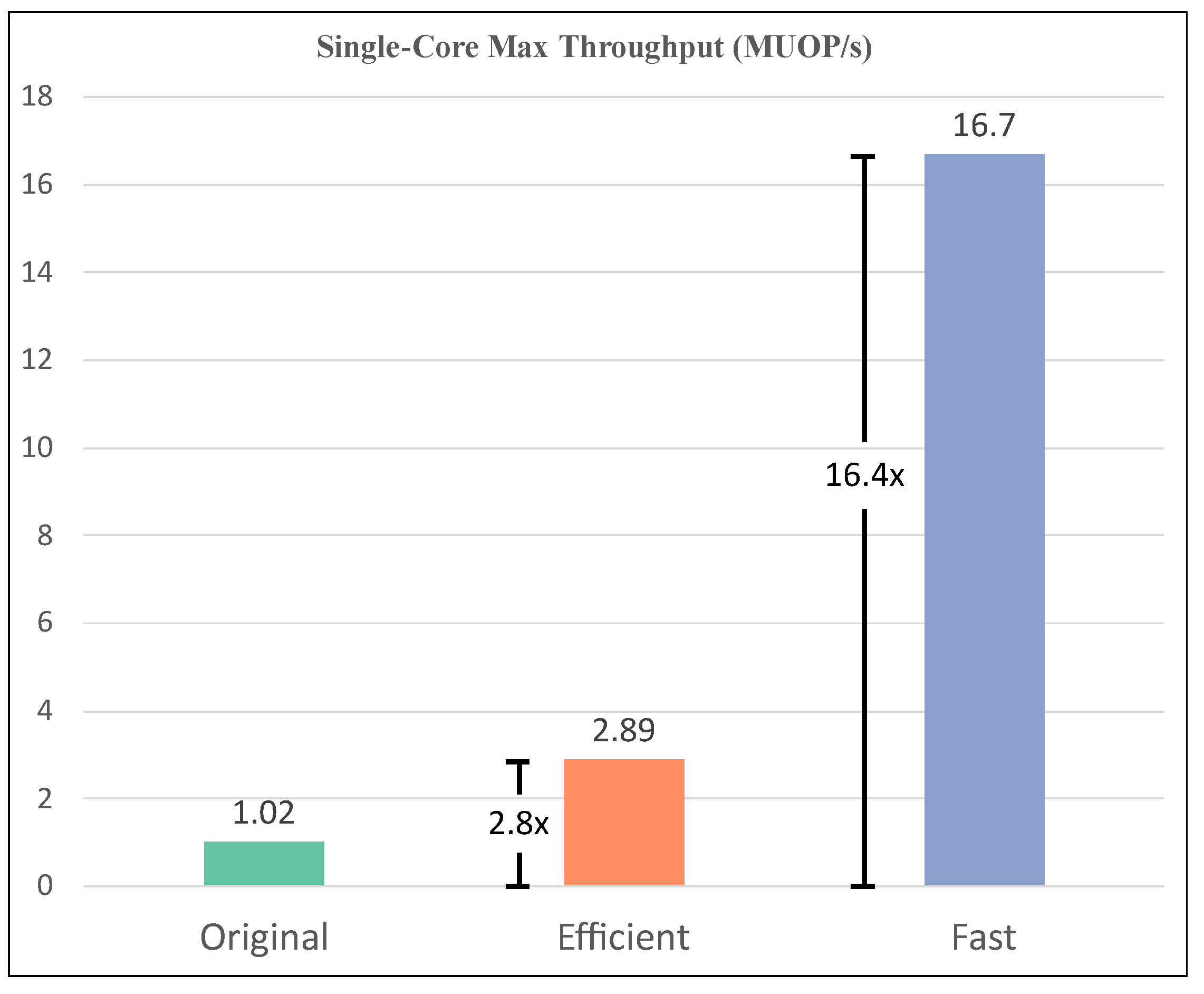
The throughput of the proposed design is shown in Figure 11. Though different second moment optimizers have been implemented in the previous works, the throughput is not provided explicitly. The original ADAM implemented on the same platform is set as the baseline. We measure the max throughput by the number of Million Updating Operations per Second (MUOP/s). The E-ADAM achieves 2.89 MUOP/s, which is 2.8 times compared with the original ADAM. The F-ADAM achieves 16.7 MUOP/s, which is 16.4 times compared with the original ADAM.
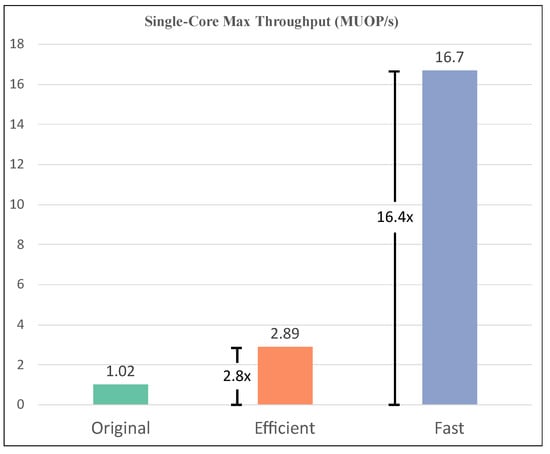
Figure 11.
The throughput of the proposed design.
The resource consumption of the proposed design is shown in Table 1. The E-ADAM reduces 72.3% flip-flops (FFs), 85.3% look-up-tables (LUTs), and 80% DSPs compared with the original ADAM. The F-ADAM reduces 73.9% FFs and 67.6% LUTs while consuming more DSPs. The proposed design also shows significant resource efficiency compared with reference work [27]. Work [27] implemented eight RMSProp [37] units in parallel, which has a similar calculation process to ADAM with division, squaring, and root extraction. Thus the presented consumption is divided by 8 to obtain the normalized consumption. The proposed E-ADAM reduces 91.0% FFs, 84.4% LUTs, and 92.9% DSPs compared with work [27]. The proposed F-ADAM reduces 91.5% FFs, 65.7% LUTs, and 50% DSPs compared with work [27]. When the resource is highly limited, the E-ADAM can be implemented with the least costs and the F-ADAM can be used if DSPs are sufficient. In the situation where all the resource is sufficient, the reduction of hardware resource consumption enables pipelining with more depth and more parallels, which can further improve the throughput significantly.

Table 1.
The resource consumption of the proposed design.
The proposed design achieves outstanding efficiency in both resource consumption and throughput. E-ADAM is suitable when the resource is highly limited, while F-ADAM is suitable for the high demand for performance. The implementation details are shown in Table 2.

Table 2.
The implementation details of the proposed design.
We provide the raw experimental data and the example HLS source code in the Supplementary Materials.
5. Conclusions
This work proposed Hardware-ADAM (HW-ADAM), an efficient fixed-point accelerator of adaptive moment estimation (ADAM). Three major optimizations are proposed to improve the throughput and reduce resource consumption. The approximation of the second moment is first proposed to avoid the squaring and extraction of the root, based on which the efficient-ADAM (E-ADAM) is designed. Then the fast algorithm for the division is proposed inspired by the theory of the Fast Inverse Square Root (Fast InvSqrt), based on which the fast-ADAM (F-ADAM) is proposed. The optimizations to the hyper-parameters and specific calculations such as multiplication and division by 3 are proposed to further improve the efficiency. Sufficient experiments are designed to validate the functionality, throughput, and resource consumption. Efficient-ADAM (E-ADAM) unit reduced the resource consumption by around 90% compared with the original ADAM while achieving the throughput of 2.89 MUOP/s (Million Updating Operation per Second), which is 2.8× of the original ADAM. Fast-ADAM (F-ADAM) unit achieved the throughput of 16.7 MUOP/s, 16.4× of the original ADAM. The hardware resource consumption of F-ADAM is also largely reduced compared with the related work. To our knowledge, we are the first to optimize the hardware implementation of the ADAM. The proposed design can be widely adopted in different on-chip training tasks to reduce resource consumption or improve the throughput. Moreover, while the mathematic-based designs for hardware and software show a great advantage in ADAM design, the optimization methods are also instructive and promising to be used for other applications.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/electronics12020263/s1.
Author Contributions
Conceptualization, W.Z. and L.N.; methodology, W.Z., L.N. and D.Z.; validation, G.W. and F.U.D.F.; writing—original draft preparation, W.Z. and L.N.; writing—review and editing, F.U.D.F. and C.Z.; supervision, C.Z.; project administration, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No.U20A20220).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ADAM | Adaptive moment estimation |
| GD | Gradient descent |
| SGD | Stochastic gradient descent |
| MUOP/s | Million updating operation per second |
| DNN | Deep neural network |
| CNN | Convolutional neural network |
| DRL | Deep reinforcement learning |
| RL | Reinforcement learning |
| GPU | Graphic processing unit |
| ASIC | Application specific integrated circuit |
| FPGA | Field programmable gate array |
| FP | Forward propagation |
| BP | Backward propagation |
| WG | Weight gradient update |
| Fast InvSqrt | Fast inverse square root |
| PPO | Proximal policy optimization |
| FF | Flip-flop |
| LUT | Look-up table |
| DSP | Data processing unit |
References
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. Deepdriving: Learning affordance for direct perception in autonomous driving. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2722–2730. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Sermanet, P.; Hadsell, R.; Scoffier, M.; Grimes, M.; Ben, J.; Erkan, A.; Crudele, C.; Miller, U.; LeCun, Y. A multirange architecture for collision-free off-road robot navigation. J. Field Robot. 2009, 26, 52–87. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Machupalli, R.; Hossain, M.; Mandal, M. Review of ASIC accelerators for deep neural network. Microprocess. Microsystems 2022, 89, 104441. [Google Scholar] [CrossRef]
- Shawahna, A.; Sait, S.M.; El-Maleh, A. FPGA-based accelerators of deep learning networks for learning and classification: A review. IEEE Access 2018, 7, 7823–7859. [Google Scholar] [CrossRef]
- Misra, J.; Saha, I. Artificial neural networks in hardware: A survey of two decades of progress. Neurocomputing 2010, 74, 239–255. [Google Scholar] [CrossRef]
- Esmaeilzadeh, H.; Sampson, A.; Ceze, L.; Burger, D. Neural acceleration for general-purpose approximate programs. In Proceedings of the 2012 45th Annual IEEE/ACM International Symposium on Microarchitecture, Vancouver, BC, Canada, 1–5 December 2012; pp. 449–460. [Google Scholar]
- Han, S.; Liu, X.; Mao, H.; Pu, J.; Pedram, A.; Horowitz, M.A.; Dally, W.J. EIE: Efficient inference engine on compressed deep neural network. ACM SIGARCH Comput. Archit. News 2016, 44, 243–254. [Google Scholar] [CrossRef]
- Du, L.; Du, Y.; Li, Y.; Su, J.; Kuan, Y.C.; Liu, C.C.; Chang, M.C.F. A reconfigurable streaming deep convolutional neural network accelerator for Internet of Things. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 65, 198–208. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritten zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing FPGA-based accelerator design for deep convolutional neural networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Monterey, CA, USA, 22–24 February 2015; pp. 161–170. [Google Scholar]
- Yuan, Z.; Yue, J.; Yang, H.; Wang, Z.; Li, J.; Yang, Y.; Guo, Q.; Li, X.; Chang, M.F.; Yang, H.; et al. Sticker: A 0.41-62.1 TOPS/W 8Bit neural network processor with multi-sparsity compatible convolution arrays and online tuning acceleration for fully connected layers. In Proceedings of the 2018 IEEE Symposium on VLSI Circuits, Honolulu, HI, USA, 18–22 June 2018; pp. 33–34. [Google Scholar]
- Ueyoshi, K.; Ando, K.; Hirose, K.; Takamaeda-Yamazaki, S.; Kadomoto, J.; Miyata, T.; Hamada, M.; Kuroda, T.; Motomura, M. QUEST: A 7.49 TOPS multi-purpose log-quantized DNN inference engine stacked on 96MB 3D SRAM using inductive-coupling technology in 40nm CMOS. In Proceedings of the 2018 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 5–9 February 2018; pp. 216–218. [Google Scholar]
- Lee, J.; Lee, J.; Han, D.; Lee, J.; Park, G.; Yoo, H.J. An energy-efficient sparse deep-neural-network learning accelerator with fine-grained mixed precision of FP8–FP16. IEEE Solid-State Circuits Lett. 2019, 2, 232–235. [Google Scholar] [CrossRef]
- Dai, P.; Yang, J.; Ye, X.; Cheng, X.; Luo, J.; Song, L.; Chen, Y.; Zhao, W. SparseTrain: Exploiting dataflow sparsity for efficient convolutional neural networks training. In Proceedings of the 2020 57th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 20–24 July 2020; pp. 1–6. [Google Scholar]
- Zhang, W.; Jiang, Y.; Farrukh, F.U.D.; Zhang, C.; Xie, X. A portable accelerator of proximal policy optimization for robots. In Proceedings of the 2021 IEEE International Conference on Integrated Circuits, Technologies and Applications (ICTA), Zhuhai, China, 24–26 November 2021; pp. 171–172. [Google Scholar]
- Imani, M.; Gupta, S.; Kim, Y.; Rosing, T. Floatpim: In-memory acceleration of deep neural network training with high precision. In Proceedings of the 2019 ACM/IEEE 46th Annual International Symposium on Computer Architecture (ISCA), Phoenix, AZ, USA, 22–26 June 2019; pp. 802–815. [Google Scholar]
- Yang, Y.; Deng, L.; Wu, S.; Yan, T.; Xie, Y.; Li, G. Training high-performance and large-scale deep neural networks with full 8-bit integers. Neural Netw. 2020, 125, 70–82. [Google Scholar] [CrossRef]
- Zhu, F.; Gong, R.; Yu, F.; Liu, X.; Wang, Y.; Li, Z.; Yang, X.; Yan, J. Towards unified int8 training for convolutional neural network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1969–1979. [Google Scholar]
- Han, S.; Pool, J.; Tran, J.; Dally, W. Learning both weights and connections for efficient neural network. Adv. Neural Inf. Process. Syst. 2015, 28, 1135–1143. [Google Scholar]
- Yang, D.; Ghasemazar, A.; Ren, X.; Golub, M.; Lemieux, G.; Lis, M. Procrustes: A dataflow and accelerator for sparse deep neural network training. In Proceedings of the 2020 53rd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Athens, Greece, 17–21 October 2020; pp. 711–724. [Google Scholar]
- Choi, D.; Shallue, C.J.; Nado, Z.; Lee, J.; Maddison, C.J.; Dahl, G.E. On empirical comparisons of optimizers for deep learning. arXiv 2019, arXiv:1910.05446. [Google Scholar]
- Robbins, H.; Monro, S. A stochastic approximation method. Ann. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Cho, H.; Oh, P.; Park, J.; Jung, W.; Lee, J. Fa3c: Fpga-accelerated deep reinforcement learning. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems, Providence, RI, USA, 13–17 April 2019; pp. 499–513. [Google Scholar]
- Yang, J.; Hong, S.; Kim, J.Y. FIXAR: A fixed-point deep reinforcement learning platform with quantization-aware training and adaptive parallelism. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 259–264. [Google Scholar]
- Zhao, Y.; Liu, C.; Du, Z.; Guo, Q.; Hu, X.; Zhuang, Y.; Zhang, Z.; Song, X.; Li, W.; Zhang, X.; et al. Cambricon-Q: A hybrid architecture for efficient training. In Proceedings of the 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture (ISCA), Valencia, Spain, 14–18 June 2021; pp. 706–719. [Google Scholar]
- Kara, K.; Alistarh, D.; Alonso, G.; Mutlu, O.; Zhang, C. FPGA-accelerated dense linear machine learning: A precision-convergence trade-off. In Proceedings of the 2017 IEEE 25th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), Napa, CA, USA, 30 April–2 May 2017; pp. 160–167. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lomont, C. Fast Inverse Square Root; Technical Report; Purdue University: Indianapolis, IN, USA, 2003. [Google Scholar]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. Ussr Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Nesterov, Y.E. A method for solving the convex programming problem with convergence rate O (1/k2). Dokl. Akad. Nauk. SSSR 1983, 269, 543–547. [Google Scholar]
- Ellenberger, B. PyBullet Gymperium. 2018–2019. Available online: https://github.com/benelot/pybullet-gym (accessed on 6 September 2021).
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-rmsprop: Divide the Gradient by a Running Average of Its Recent Magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).