Ship Diesel Engine Fault Diagnosis Using Data Science and Machine Learning
Abstract
:1. Introduction
- Poor-quality data (e.g., unbalanced data set);
- An insufficient amount of learning data;
- An incomplete learning data set—one or more types of inability states missing in the learning data set.
2. Materials and Methods
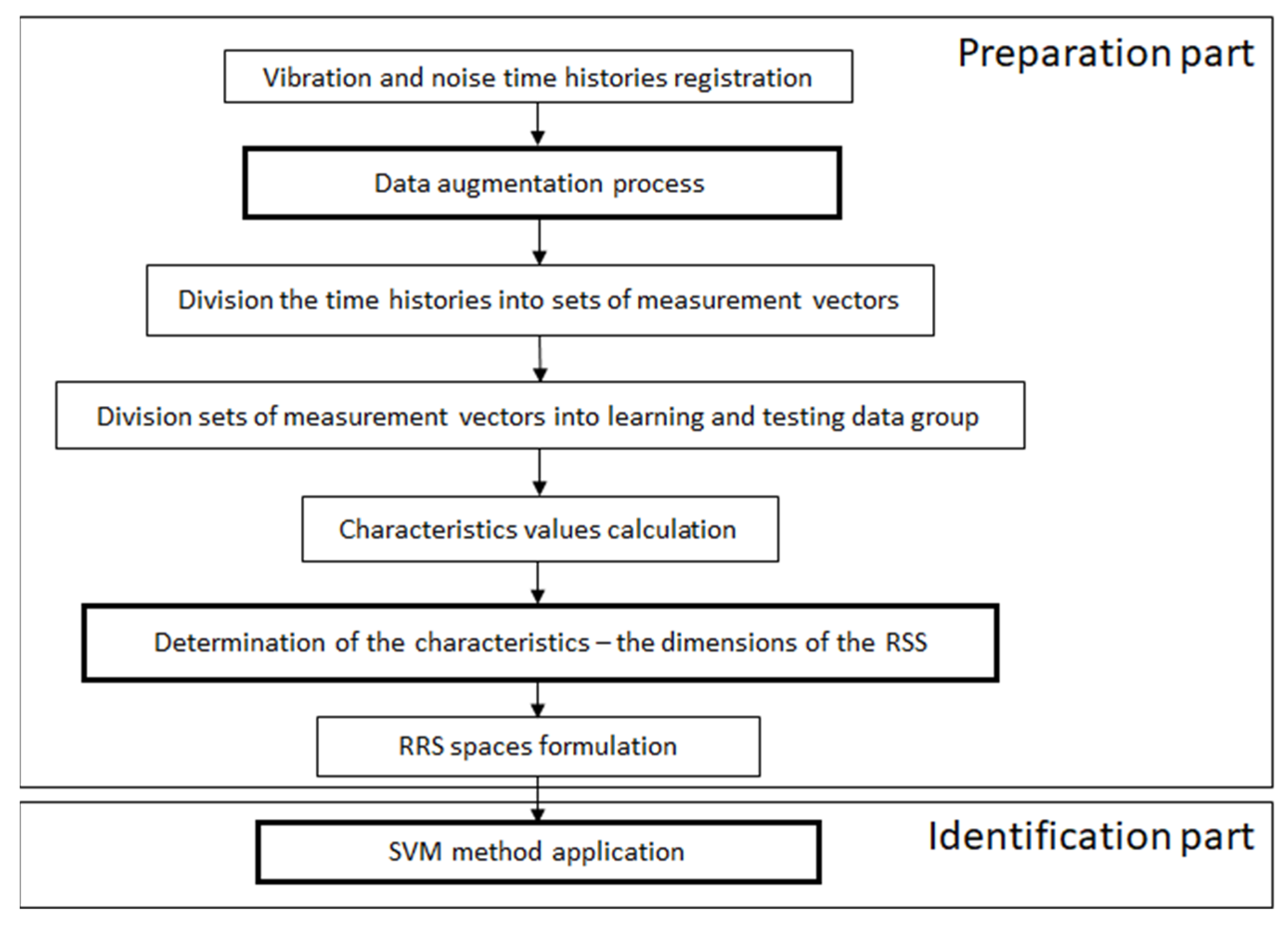
2.1. Reliability State Identification Procedure
- The characteristic can be used to uniquely identify the reliability state if it fulfills the condition described by Formula (18);
- The characteristic can be used to uniquely identify the type of the inability state if it fulfills the condition described by Formula (19) for all inability states.
2.2. Data Preprocessing
2.3. Identification Model—Support Vector Machine Method
3. Research Object and Performed Operational Tests
- VC02—operation of the engine with input and output valve clearances reduced to 0.2 mm for cylinder 4, and output valve clearances increased up to 1 mm for cylinder 1;
- VC08—operation of the engine with input and output valve clearances increased up to 0.8 mm for cylinder 4, and output valve clearances increased up to 1 mm for cylinder 1;
- CLE—operation of the engine with output valve clearances increased up to 1 mm for cylinder 1;
- PUMP—operation of the engine with simulated damage to the injection pump of cylinder 1—the maximal combustion pressure dropped by about 20, and the output valve clearances increased up to 1 mm for cylinder 1;
- INJ—operation of the engine with the opening pressure injector of cylinder 1 decreased to 23 MPa, and the output valve clearances increased up to 1 mm for cylinder 1.
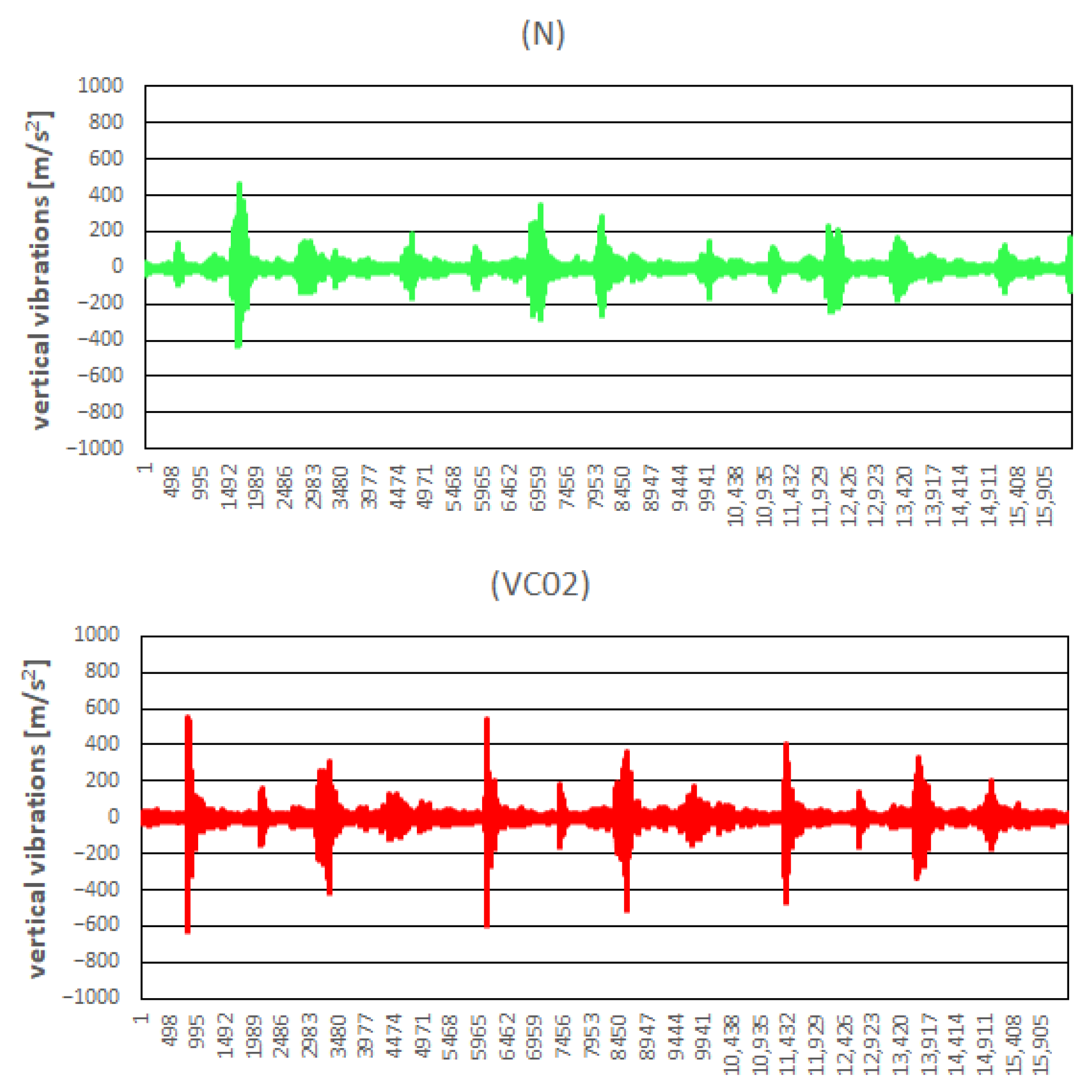
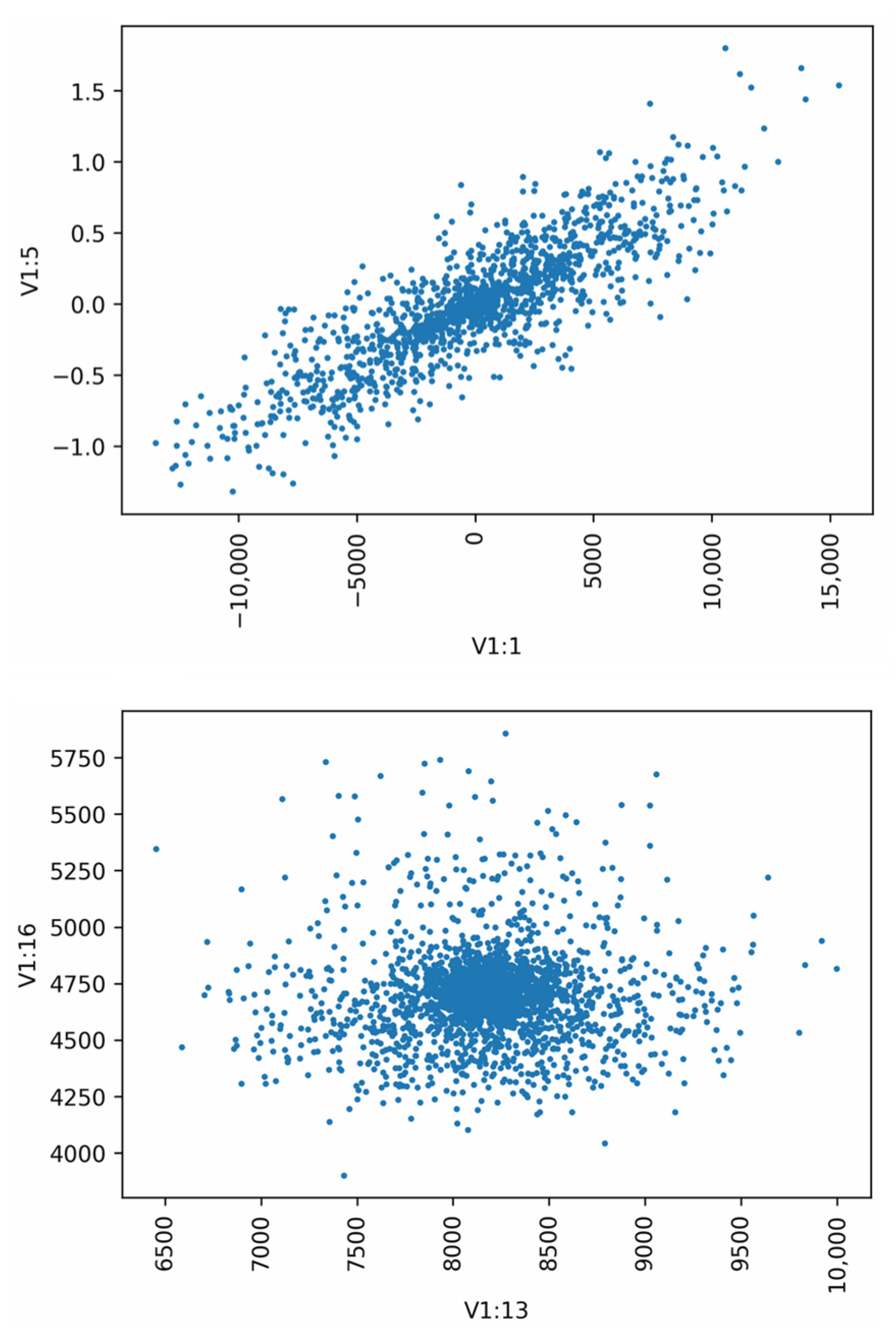
4. Recorded Data Preprocessing
- For vertical vibrations, characteristics number 1,3,7,8,9,11,12,13,14,15 for each cylinder;
- For horizontal vibrations, characteristics number 1,3,7,8,9,11,12,13,14,15 for each cylinder;
- For noise signal, characteristics number 9,11,12,13,14,15 for each cylinder and characteristic number 1 for cylinder 1.
5. Results
- The degree of kernel: 3,6,9;
- The constant term of the kernel: 1, 10, 100;
- The regularization parameter: 1, 3, 5.
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bayraktar, M.; Nuran, M. Reliability, availability, and maintainability analysis of the propulsion system of a fleet. Sci. J. Marit. Univ. Szczecin 2022, 70, 63–70. [Google Scholar]
- Liu, L.; Wu, Y.; Wang, Y.; Wu, J.; Fu, S. Exploration of environmentally friendly marine power technology -ammonia/diesel stratified injection. J. Clean. Prod. 2022, 380, 135014. [Google Scholar] [CrossRef]
- Mohd Ghazali, M.H.; Rahiman, W. Vibration Analysis for Machine Monitoring and Diagnosis: A Systematic Review. Shock Vib. 2021, 2021, 9469318. [Google Scholar] [CrossRef]
- Ren, G.; Jia, J.; Mei, J.; Jia, X.; Han, J.; Wang, Y. An improved variational mode decomposition method and its application in diesel engine fault diagnosis. J. Vibroeng. 2018, 20, 2363–2378. [Google Scholar] [CrossRef]
- Bianchi, D.; Mayrhofer, E.; Gröschl, M.; Betz, G.; Vernes, A. Wavelet packet transform for detection of single events in acoustic emission signals. Mech. Syst. Signal Process. 2015, 64–65, 441–451. [Google Scholar] [CrossRef]
- Adly, A.R.; Abdel Aleem, S.H.E.; Elsadd, M.A.; Ali, Z.M. Wavelet packet transform applied to a series-compensated line: A novel scheme for fault identification. Meas. J. Int. Meas. Confed. 2020, 151, 107156. [Google Scholar] [CrossRef]
- Yang, S.; Gu, X.; Liu, Y.; Hao, R.; Li, S. A general multi-objective optimized wavelet filter and its applications in fault diagnosis of wheelset bearings. Mech. Syst. Signal Process. 2020, 145, 106914. [Google Scholar] [CrossRef]
- Shi, Y.; Yi, C.; Lin, J.; Zhuang, Z.; Lai, S. Ensemble empirical mode decomposition-entropy and feature selection for pantograph fault diagnosis. J. Vib. Control 2020, 26, 2230–2242. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, Z.; Chen, B.; Zhang, W.; Huang, G. An improved complementary ensemble empirical mode decomposition with adaptive noise and its application to rolling element bearing fault diagnosis. ISA Trans. 2019, 91, 218–234. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, J.; Shi, J.; Shen, C.; Huang, W.; Zhu, Z. A coarse-to-fine decomposing strategy of VMD for extraction of weak repetitive transients in fault diagnosis of rotating machines. Mech. Syst. Signal Process. 2019, 116, 668–692. [Google Scholar] [CrossRef]
- Li, J.; Yao, X.; Wang, H.; Zhang, J. Periodic impulses extraction based on improved adaptive VMD and sparse code shrinkage denoising and its application in rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2019, 126, 568–589. [Google Scholar] [CrossRef]
- Saidi, L.; Ben Ali, J.; Bechhoefer, E.; Benbouzid, M. Wind turbine high-speed shaft bearings health prognosis through a spectral Kurtosis-derived indices and SVR. Appl. Acoust. 2017, 120, 1–8. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66–67, 679–698. [Google Scholar] [CrossRef]
- Dhal, A.; Panigrahi, I.; Mishra, C.; Samantaray, A.K. Order Tracking: Angular Domain Features Extraction Method for Condition Monitoring of Variable Speed. In Lecture Notes in Mechanical Engineering; Springer: Berlin, Germany, 2020; pp. 127–133. [Google Scholar]
- Wu, J.; Zi, Y.; Chen, J.; Zhou, Z. Fault diagnosis in speed variation conditions via improved tacholess order tracking technique. Meas. J. Int. Meas. Confed. 2019, 137, 604–616. [Google Scholar] [CrossRef]
- He, G.; Ding, K.; Li, W.; Jiao, X. A novel order tracking method for wind turbine planetary gearbox vibration analysis based on discrete spectrum correction technique. Renew. Energy 2016, 87, 364–375. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, R.; Jia, J.; Lü, L.; Zhang, G. Engine fault diagnosis based on work-cycle order tracking spectrum and fuzzy C-mean clustering. Qiche Gongcheng/Automotive Eng. 2014, 36, 1024–1028. [Google Scholar]
- Cai, B.; Wang, Z.; Zhu, H.; Liu, Y.; Hao, K.; Yang, Z.; Ren, Y.; Feng, Q.; Liu, Z. Artificial Intelligence Enhanced Two-Stage Hybrid Fault Prognosis Methodology of PMSM. IEEE Trans. Ind. Inform. 2022, 18, 7262–7273. [Google Scholar] [CrossRef]
- Kong, X.; Cai, B.; Liu, Y.; Zhu, H.; Yang, C.; Gao, C.; Liu, Y.; Liu, Z.; Ji, R. Fault Diagnosis Methodology of Redundant Closed-Loop Feedback Control Systems: Subsea Blowout Preventer System as a Case Study. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 1618–1629. [Google Scholar] [CrossRef]
- Han, Y.; Chen, S.; Gong, C.; Zhao, X.; Zhang, F.; Li, Y. Accurate SM Disturbance Observer-Based Demagnetization Fault Diagnosis With Parameter Mismatch Impacts Eliminated for IPM Motors. IEEE Trans. Power Electron. 2023, 38, 5706–5710. [Google Scholar] [CrossRef]
- Tseng, M.L.; Wu, K.J.; Ma, L.; Kuo, T.C.; Sai, F. A hierarchical framework for assessing corporate sustainability performance using a hybrid fuzzy synthetic method-DEMATEL. Technol. Forecast. Soc. Chang. 2019, 144, 524–533. [Google Scholar] [CrossRef]
- Xuan, Q.; Fang, B.; Liu, Y.; Wang, J.; Zhang, J.; Zheng, Y.; Bao, G. Automatic Pearl Classification Machine Based on a Multistream Convolutional Neural Network. IEEE Trans. Ind. Electron. 2018, 65, 6538–6547. [Google Scholar] [CrossRef]
- Mboo, C.P.; Hameyer, K. Fault diagnosis of bearing damage by means of the linear discriminant analysis of stator current features from the frequency selection. IEEE Trans. Ind. Appl. 2016, 52, 3861–3868. [Google Scholar] [CrossRef]
- Hu, N.; Chen, H.; Cheng, Z.; Zhang, L.; Zhang, Y. Fault Diagnosis for Planetary Gearbox Based on EMD and Deep Convolutional Neural Networks. Jixie Gongcheng Xuebao/J. Mech. Eng. 2019, 55, 9–18. [Google Scholar] [CrossRef]
- Li, J.; Deng, Y.; Sun, W.; Li, W.; Li, R.; Li, Q.; Liu, Z. Resource Orchestration of Cloud-Edge–Based Smart Grid Fault Detection. ACM Trans. Sen. Netw. 2022, 18, 1–26. [Google Scholar] [CrossRef]
- Kolar, D.; Lisjak, D.; Pająk, M.; Gudlin, M. Intelligent Fault Diagnosis of Rotary Machinery by Convolutional Neural Network with Automatic Hyper-Parameters Tuning Using Bayesian Optimization. Sensors 2021, 21, 2411. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, P.; Jayaswal, P. Diagnosis and Classifications of Bearing Faults Using Artificial Neural Network and Support Vector Machine. J. Inst. Eng. Ser. C 2020, 101, 61–72. [Google Scholar] [CrossRef]
- Wang, H.; Ren, B.; Song, L.; Cui, L. A Novel Weighted Sparse Representation Classification Strategy Based on Dictionary Learning for Rotating Machinery. IEEE Trans. Instrum. Meas. 2020, 69, 712–720. [Google Scholar] [CrossRef]
- Min, H.; Fang, Y.; Wu, X.; Lei, X.; Chen, S.; Teixeira, R.; Zhu, B.; Zhao, X.; Xu, Z. A fault diagnosis framework for autonomous vehicles with sensor self-diagnosis. Expert Syst. Appl. 2023, 224, 120002. [Google Scholar] [CrossRef]
- Grządziela, A.; Kluczyk, M. A Non-invasive Method of Marine Engines Fuel System Diagnostics. Pomor. Zb. 2020, 3, 381–388. [Google Scholar] [CrossRef]
- Pająk, M.; Muślewski, Ł.; Landowski, B.; Kałaczyński, T.; Kluczyk, M.; Kolar, D. Identification of Reliability States of a Ship Engine of the Type Sulzer 6AL20/24. SAE Int. J. Engines 2021, 15, 03-0015–04-0028. [Google Scholar] [CrossRef]
- Huang, N.; Chen, Q.; Cai, G.; Xu, D.; Zhang, L.; Zhao, W. Fault Diagnosis of Bearing in Wind Turbine Gearbox Under Actual Operating Conditions Driven by Limited Data with Noise Labels. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Jerzy, S. Fundamentals of the Signal Theory; WKŁ: Warszawa, Poland, 2007. [Google Scholar]
- Wen, Q.; Sun, L.; Yang, F.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time Series Data Augmentation for Deep Learning: A Survey. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 7–15 January 2020. [Google Scholar] [CrossRef]
- Iwana, B.K.; Uchida, S. An empirical survey of data augmentation for time series classification with neural networks. PLoS ONE 2021, 16, e0254841. [Google Scholar] [CrossRef]
- Fields, T.; Hsieh, G.; Chenou, J. Mitigating Drift in Time Series Data with Noise Augmentation. In Proceedings of the 2019 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 5–7 December 2019; pp. 227–230. [Google Scholar]
- Le Guennec, A.; Malinowski, S.; Tavenard, R. Data augmentation for time series classification using convolutional neural networks. In Proceedings of the ECML/PKDD Workshop on Advanced Analytics and Learning on Temporal Data, Riva del Garda, Italy, 19 September 2016. [Google Scholar]
- Um, T.T.; Pfister, F.M.J.; Pichler, D.; Endo, S.; Lang, M.; Hirche, S.; Fietzek, U.; Kulić, D. Data augmentation of wearable sensor data for parkinson’s disease monitoring using convolutional neural networks. In Proceedings of the 19th ACM International Conference on Multimodal Interaction, Glasgow, UK, 13–17 November 2017; ACM: New York, NY, USA, 2017; pp. 216–220. [Google Scholar]
- Ruan, D.; Zhang, F.; Yan, J. Transfer Learning Between Different Working Conditions on Bearing Fault Diagnosis Based on Data Augmentation. IFAC-PapersOnLine 2021, 54, 1193–1199. [Google Scholar] [CrossRef]
- Nguyen, T.-S.; Stuker, S.; Niehues, J.; Waibel, A. Improving Sequence-To-Sequence Speech Recognition Training with On-The-Fly Data Augmentation. In ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Proceedings of the ICASSP 2020 Table of Contents, Barselona, Spain, 4–8 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 7689–7693. [Google Scholar]
- Steven Eyobu, O.; Han, D.S. Feature Representation and Data Augmentation for Human Activity Classification Based on Wearable IMU Sensor Data Using a Deep LSTM Neural Network. Sensors 2018, 18, 2892. [Google Scholar] [CrossRef]
- Temizhan, E.; Mirtagioglu, H.; Mendes, M. Which Correlation Coefficient Should Be Used for Investigating Relations between Quantitative Variables? Am. Acad. Sci. Res. J. Eng. Technol. Sci. 2022, 85, 265–277. [Google Scholar]
- Dutta, A.; Mallick, P.K.; Mohanty, N.; Srichandan, S. Supervised Learning Algorithms for Mobile Price Classification. In Proceedings of the Cognitive Informatics and Soft Computing, Balasore, India, 21–22 August 2021; Mallick, P.K., Bhoi, A.K., Barsocchi, P., de Albuquerque, V.H.C., Eds.; Springer Nature Singapore: Singapore, 2022; pp. 653–666. [Google Scholar]
- De Oliveira Nogueira, T.; Palacio, G.B.A.; Braga, F.D.; Maia, P.P.N.; de Moura, E.P.; de Andrade, C.F.; Rocha, P.A.C. Imbalance classification in a scaled-down wind turbine using radial basis function kernel and support vector machines. Energy 2022, 238, 122064. [Google Scholar] [CrossRef]
- Da Cunha, G.L.; Fernandes, R.A.S.; Fernandes, T.C.C. Small-signal stability analysis in smart grids: An approach based on distributed decision trees. Electr. Power Syst. Res. 2022, 203, 107651. [Google Scholar] [CrossRef]
- Fonseca, G.A.; Ferreira, D.D.; Costa, F.B.; Almeida, A.R. Fault Classification in Transmission Lines Using Random Forest and Notch Filter. J. Control. Autom. Electr. Syst. 2022, 33, 598–609. [Google Scholar] [CrossRef]
- Lazakis, I.; Gkerekos, C.; Theotokatos, G. Investigating an SVM-driven, one-class approach to estimating ship systems condition. Ships Off. Struct. 2019, 14, 432–441. [Google Scholar] [CrossRef]
- Cai, C.; Zong, H.; Zhang, B. Ship diesel engine fault diagnosis based on the SVM and association rule mining. In Proceedings of the 2016 IEEE 20th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Bejing, China, 4–6 May 2016; pp. 400–405. [Google Scholar]
- AlShorman, O.; Irfan, M.; Saad, N.; Zhen, D.; Haider, N.; Glowacz, A.; AlShorman, A. A Review of Artificial Intelligence Methods for Condition Monitoring and Fault Diagnosis of Rolling Element Bearings for Induction Motor. Shock Vib. 2020, 2020, 8843759. [Google Scholar] [CrossRef]
- Poyhonen, S.; Negrea, M.; Arkkio, A.; Hyotyniemi, H.; Koivo, H. Support vector classification for fault diagnostics of an electrical machine. In Proceedings of the 6th International Conference on Signal Processing, Beijing, China, 26–30 August 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 2, pp. 1719–1722. [Google Scholar]
- Nafees, A.; Khan, S.; Javed, M.F.; Alrowais, R.; Mohamed, A.M.; Mohamed, A.; Vatin, N.I. Forecasting the Mechanical Properties of Plastic Concrete Employing Experimental Data Using Machine Learning Algorithms: DT, MLPNN, SVM, and RF. Polymers 2022, 14, 1583. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S. Damage degree evaluation of masonry using optimized SVM-based acoustic emission monitoring and rate process theory. Measurement 2022, 190, 110729. [Google Scholar] [CrossRef]
- Wang, Z.; He, X.; Shen, H.; Fan, S.; Zeng, Y. Multi-source information fusion to identify water supply pipe leakage based on SVM and VMD. Inf. Process. Manag. 2022, 59, 102819. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2019; ISBN 1492032646. [Google Scholar]
- Merkisz, J.; Waligórski, M. Influence of operating parameters of maritime engine on its acoustic and toxic emission characteristics. Combust. Engines 2015, 162, 399–406. [Google Scholar]
- Vasegh, M.; Sharifi Miavaghi, A. A Novel Method for Flexible Solar Energy Generation System Fault Detection Using Optimally Structured Convolution Neural Networks. SSRN Electron. J. 2021. [Google Scholar] [CrossRef]
- Pan, J.; Qu, L.; Peng, K. Sensor and Actuator Fault Diagnosis for Robot Joint Based on Deep CNN. Entropy 2021, 23, 751. [Google Scholar] [CrossRef]
- Nam, J.; Kang, J. Classification of Chaotic Squeak and Rattle Vibrations by CNN Using Recurrence Pattern. Sensors 2021, 21, 8054. [Google Scholar] [CrossRef]
- Yasir, M.; Zhan, L.; Liu, S.; Wan, J.; Hossain, M.S.; Isiacik Colak, A.T.; Liu, M.; Islam, Q.U.; Raza Mehdi, S.; Yang, Q. Instance segmentation ship detection based on improved Yolov7 using complex background SAR images. Front. Mar. Sci. 2023, 10, 1113669. [Google Scholar] [CrossRef]
- Pająk, M.; Lisjak, D.; Kolar, D. Identification of Inability States of Rotating Subsystems of Vehicles and Machines. J. KONES 2019, 26, 111–118. [Google Scholar] [CrossRef]
- Pająk, M.; Muślewski, Ł.; Landowski, B.; Grządziela, A. Fuzzy Identification of The Reliability State of The Mine Detecting Ship Propulsion System. Polish Marit. Res. 2019, 26, 55–64. [Google Scholar] [CrossRef]
- Zhu, K.H.; Song, X.G.; Xue, D.X. Roller bearing fault diagnosis based on IMF kurtosis and SVM. In Proceedings of the Advanced Materials Research. Trans. Tech. Publ. 2013, 694, 1160–1166. [Google Scholar]
- Heydarzadeh, M.; Madani, N.; Nourani, M. Gearbox fault diagnosis using power spectral analysis. In Proceedings of the 2016 IEEE International Workshop on Signal Processing Systems (SiPS), Dallas, TX, USA, 26–28 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 242–247. [Google Scholar]
- Zhu, Y.; Yan, Q.; Lu, J. Fault diagnosis method for disc slitting machine based on wavelet packet transform and support vector machine. Int. J. Comput. Integr. Manuf. 2020, 33, 1118–1128. [Google Scholar] [CrossRef]
- Bi, F.; Liu, Y. Fault diagnosis of valve clearance in diesel engine based on BP neural network and support vector machine. Trans. Tianjin Univ. 2016, 22, 536–543. [Google Scholar]



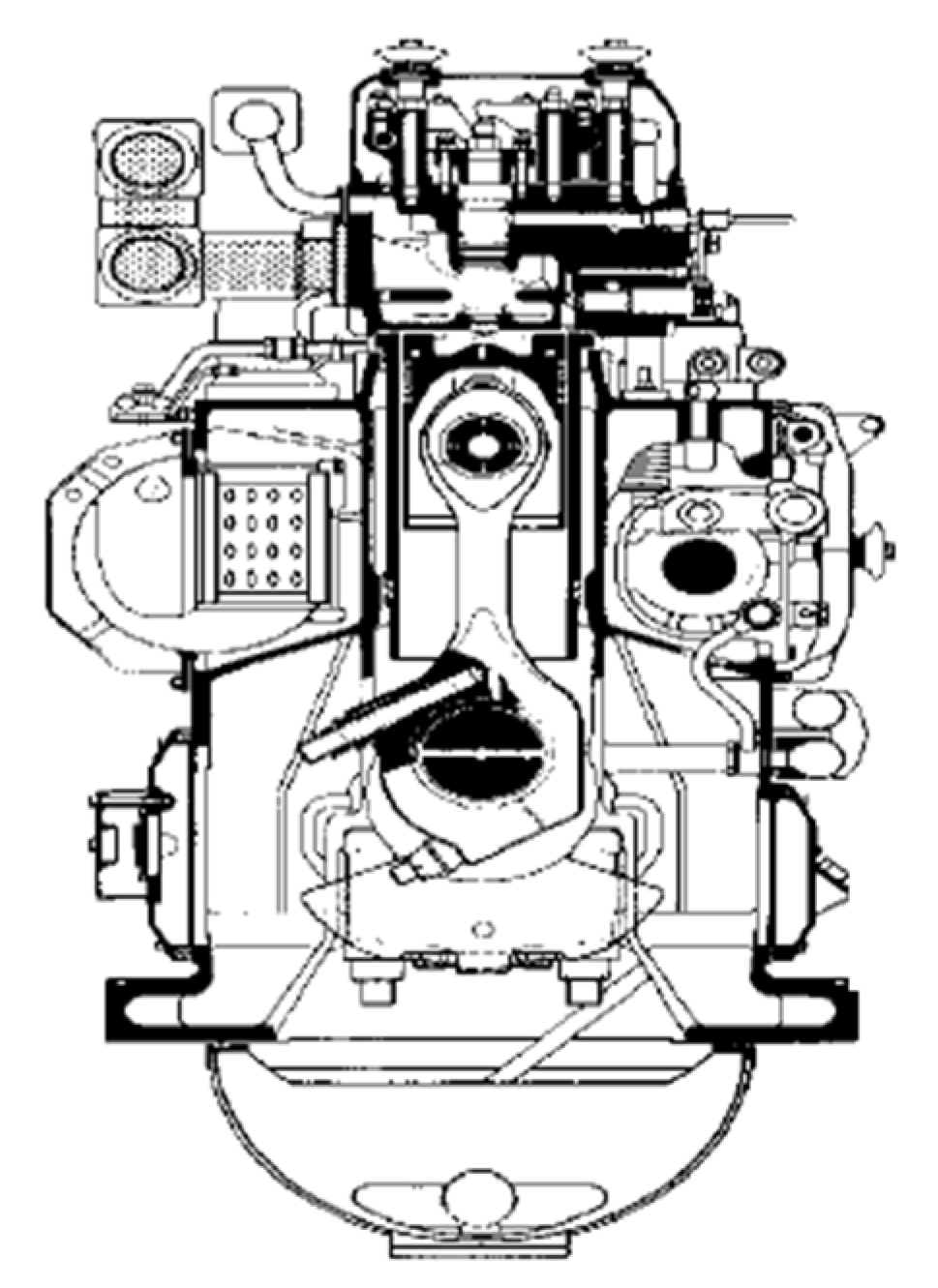

| Parameter | Value | Unit |
|---|---|---|
| Cylinder diameter | 200 | mm |
| Cylinder stroke | 240 | mm |
| Displacement volume of one cylinder | 7450 | cm3 |
| Compression ratio | 1:12.7 | - |
| Nominal rotational speed | 750 | rpm |
| Mean piston velocity | 6 | m/s |
| Nominal load | 420 | kW |
| Mean effective pressure | 1.693 | MPa |
| Pressure of injection | 24.5 | MPa |
| Maximum combustion pressure | 12.95 | MPa |
| Reliability State | p(RSi)test | p(RSi)total | serr[%] |
|---|---|---|---|
| N | 0.183306 | 0.184142 | 0.453722 |
| VC02 | 0.184943 | 0.184142 | 0.435084 |
| VC08 | 0.184943 | 0.184142 | 0.435084 |
| CLE | 0.191489 | 0.190695 | 0.416758 |
| INJ | 0.170213 | 0.171035 | 0.480965 |
| PUMP | 0.085106 | 0.085845 | 0.416758 |
| Reliability State | Original Samples * | Transformed Samples * | Original and Transformed Samples * |
|---|---|---|---|
| N | V:30|H:27|N:9 | V:30|H:29|N:8 | V:30|H:29|N:8 |
| VC02 | V:28|H:21|N:10 | V:29|H:30|N:10 | V:29|H:30|N:10 |
| VC08 | V:30|H:24|N:71 | V:30|H:30|N:68 | V:30|H:30|N:70 |
| CLE | V:24|H:21|N:11 | V:30|H:29|N:10 | V:30|H:29|N:11 |
| INJ | V:28|H:24|N:9 | V:29|H:29|N:9 | V:30|H:29|N:10 |
| PUMP | V:29|H:24|N:11 | V:29|H:30|N:10 | V:29|H:29|N:11 |
| Actual Values | Predicted Values | |||||
|---|---|---|---|---|---|---|
| Reliability State | N | VC02 | VC08 | CLE | INJ | PUMP |
| N | 112 | 0 | 0 | 0 | 0 | 0 |
| VC02 | 0 | 112 | 0 | 0 | 0 | 0 |
| VC08 | 0 | 0 | 112 | 0 | 0 | 0 |
| CLE | 0 | 0 | 0 | 116 | 0 | 0 |
| INJ | 0 | 0 | 0 | 0 | 104 | 0 |
| PUMP | 0 | 0 | 0 | 0 | 0 | 52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pająk, M.; Kluczyk, M.; Muślewski, Ł.; Lisjak, D.; Kolar, D. Ship Diesel Engine Fault Diagnosis Using Data Science and Machine Learning. Electronics 2023, 12, 3860. https://doi.org/10.3390/electronics12183860
Pająk M, Kluczyk M, Muślewski Ł, Lisjak D, Kolar D. Ship Diesel Engine Fault Diagnosis Using Data Science and Machine Learning. Electronics. 2023; 12(18):3860. https://doi.org/10.3390/electronics12183860
Chicago/Turabian StylePająk, Michał, Marcin Kluczyk, Łukasz Muślewski, Dragutin Lisjak, and Davor Kolar. 2023. "Ship Diesel Engine Fault Diagnosis Using Data Science and Machine Learning" Electronics 12, no. 18: 3860. https://doi.org/10.3390/electronics12183860
APA StylePająk, M., Kluczyk, M., Muślewski, Ł., Lisjak, D., & Kolar, D. (2023). Ship Diesel Engine Fault Diagnosis Using Data Science and Machine Learning. Electronics, 12(18), 3860. https://doi.org/10.3390/electronics12183860







