Investigation of the Feasibility of the Dynamic Equivalent Model of Large Photovoltaic Power Plants in a Harmonic Resonance Study
Abstract
:1. Introduction
| References | Spot | Resonant Frequency/Hz | Possible Cause of Resonance |
|---|---|---|---|
| [7] | Offshore wind farms in Denmark (Horns Rev) | 300–350, 750–800 | Filters, Submarine Cables |
| [8] | A 49 MW photovoltaic power station in Yueyang City | 1050–1200 | Filter |
| [9] | A photovoltaic power station in Huyanghe City | 2500 | Static Synchronous Compensator |
| [10] | Offshore wind farms in Germany (BorWin1) | 250–300 | Voltage Source Converter |
| [11] | A 50 MW photovoltaic power station in Qinghai Province | 1050–1350 | Voltage Source Converter |
| [12] | A wind farm in Guangdong province | 650 | Filter |
| [13] | A wind farm in Guangdong province | 3–12 | weak grid |
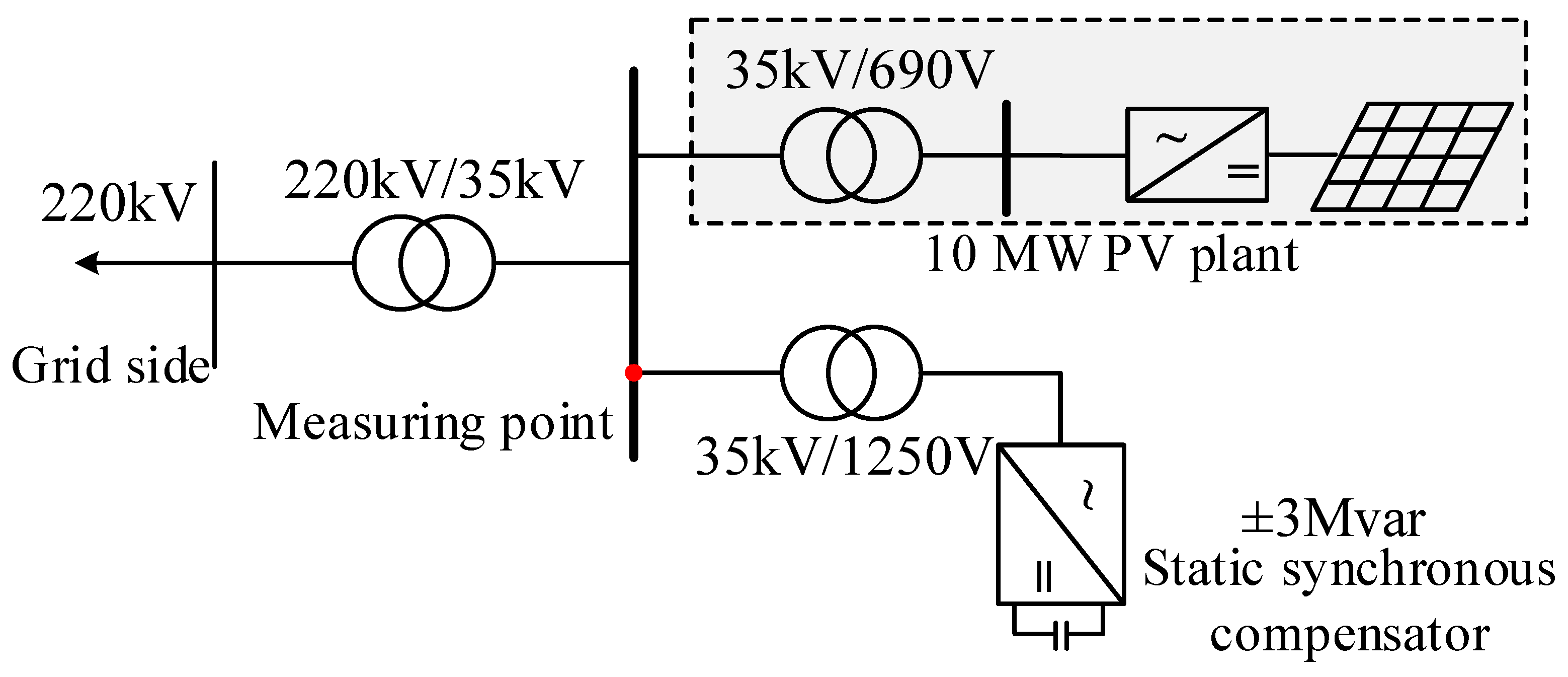
2. System Structure and Parameters of the PV Plant
3. Accurate Impedance Model of the PV Plant
3.1. Grid-Connected PV Inverters
3.2. Collector Lines
3.3. Double-Split Transformer
3.4. Complete Impedance Model
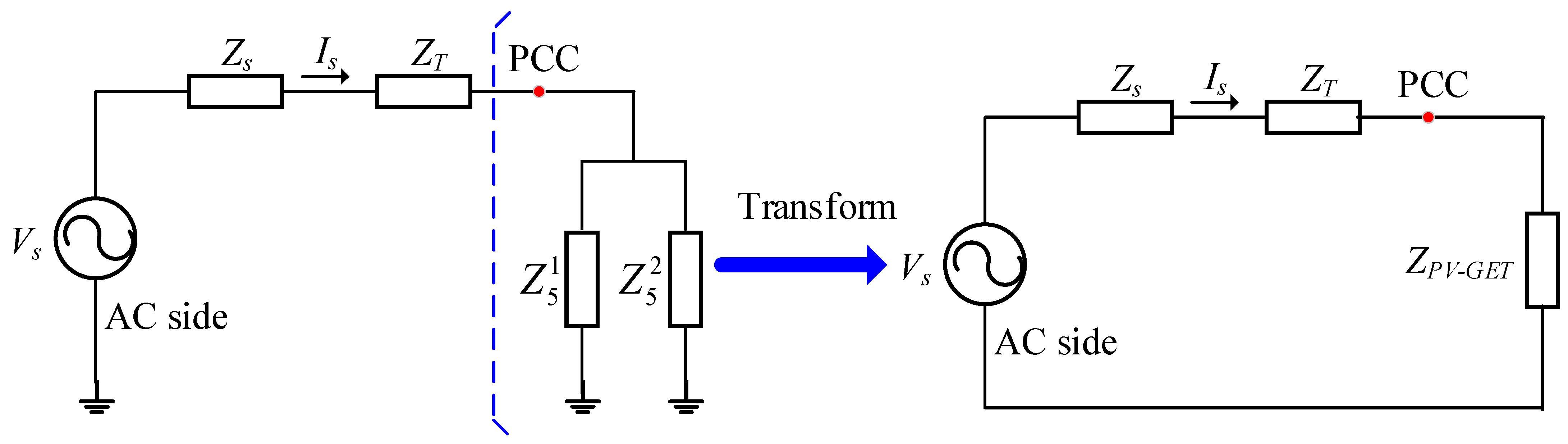
4. Dynamic Equivalent Model of the PV Plant
4.1. Equivalent Parameters of the PV Inverters
4.2. Equivalent Parameters of the Transformers
4.3. Equivalent Parameters of the Collector Lines
5. Comparative Study
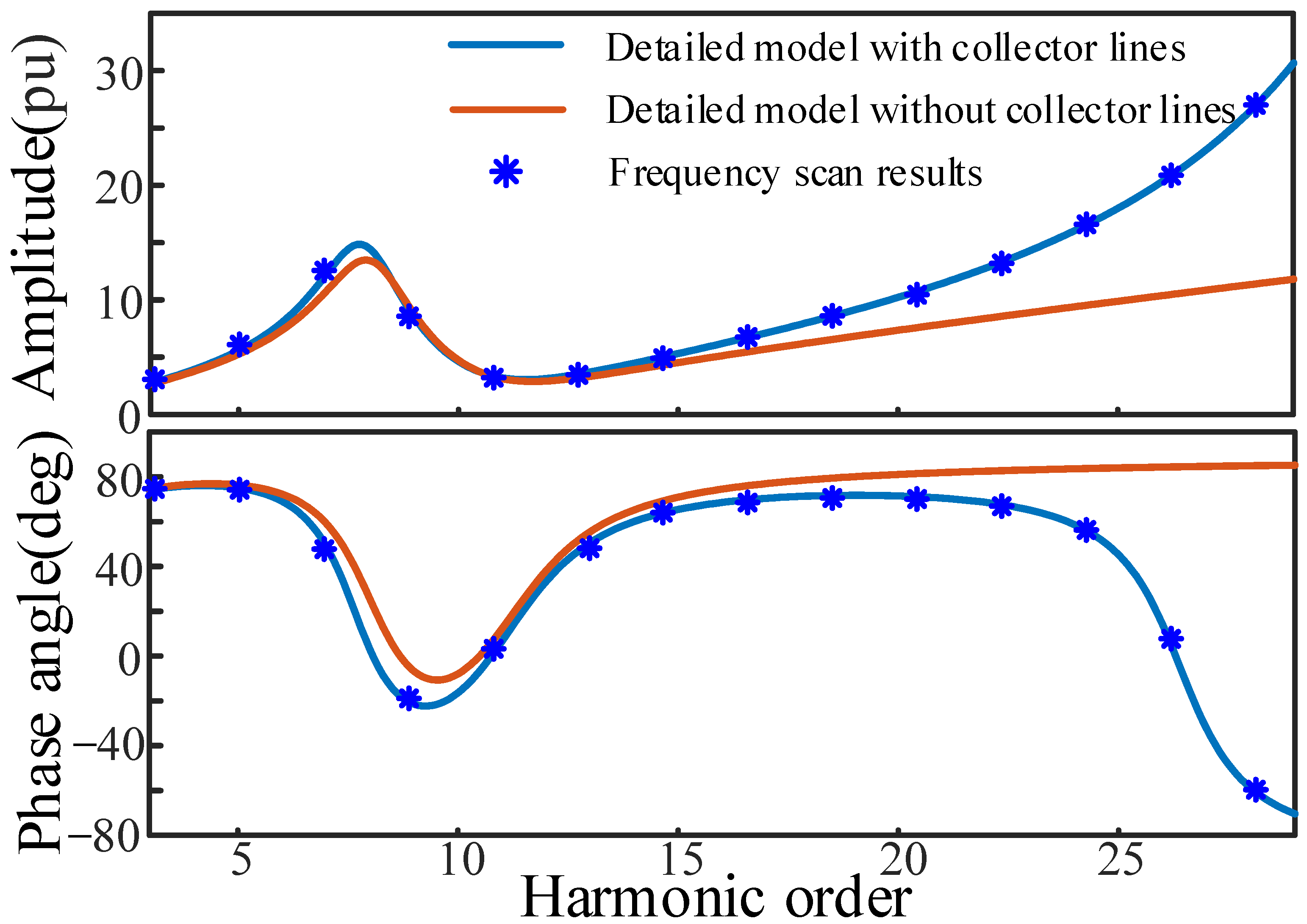
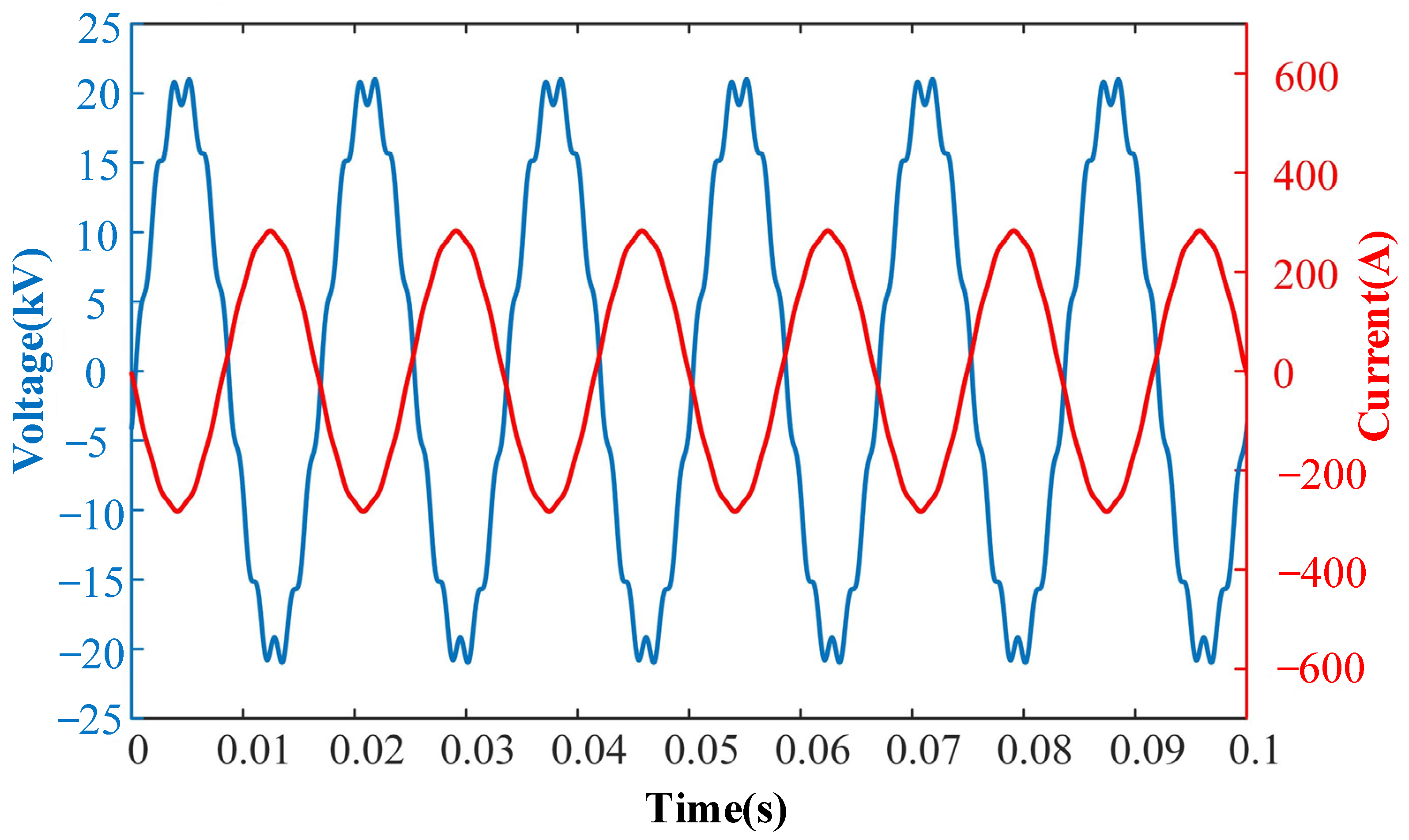
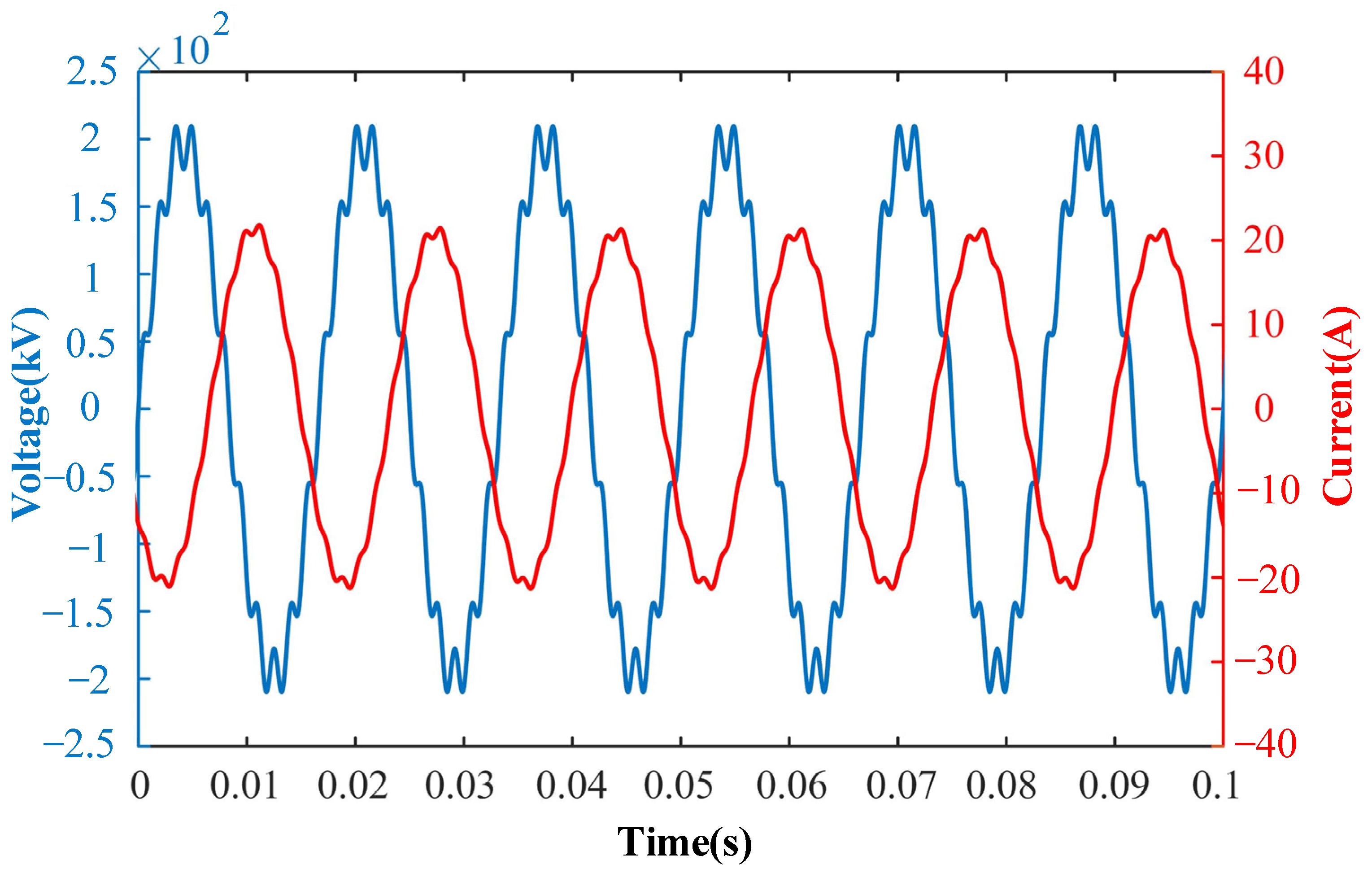
5.1. Validation of Detailed Model
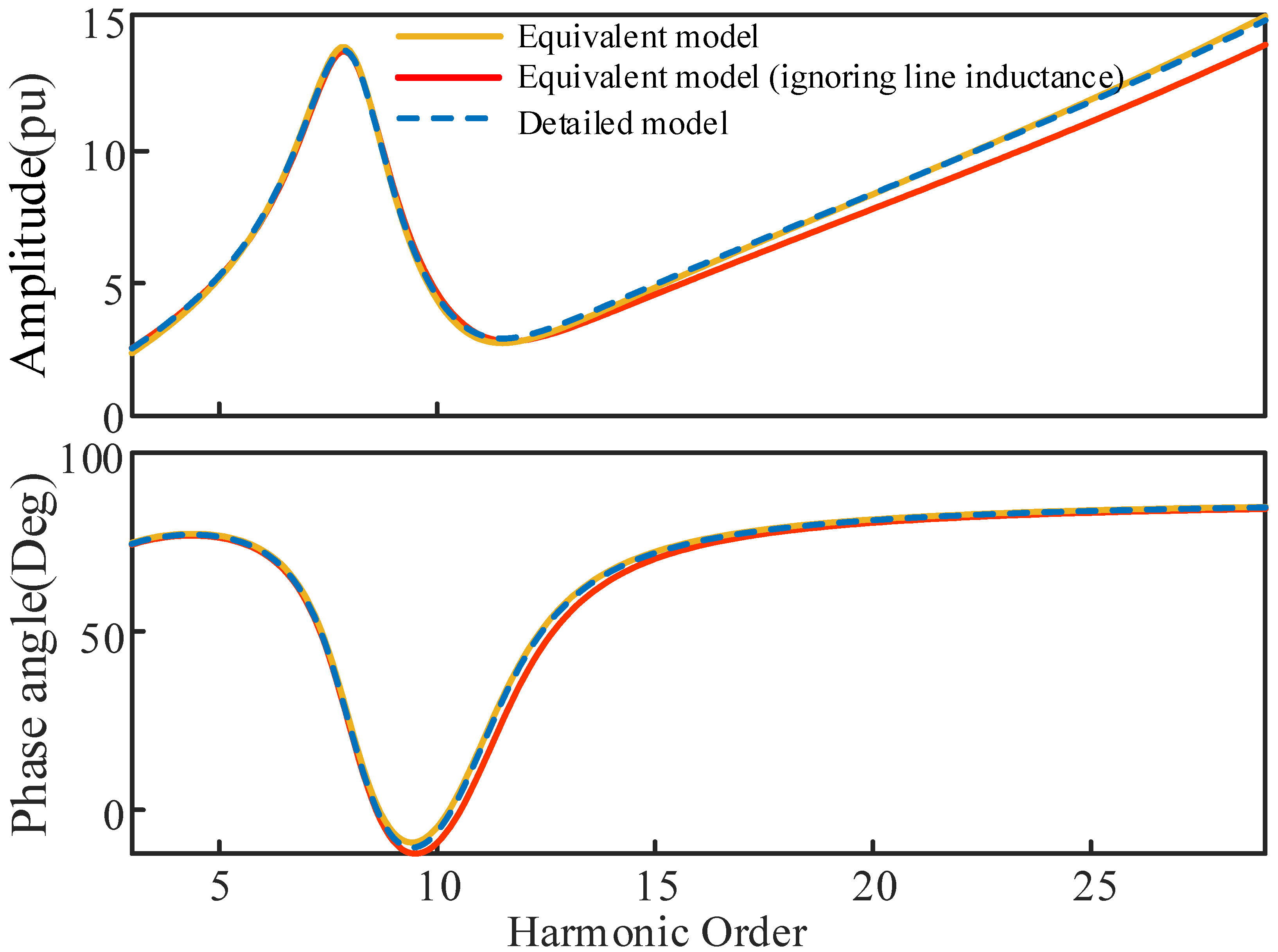
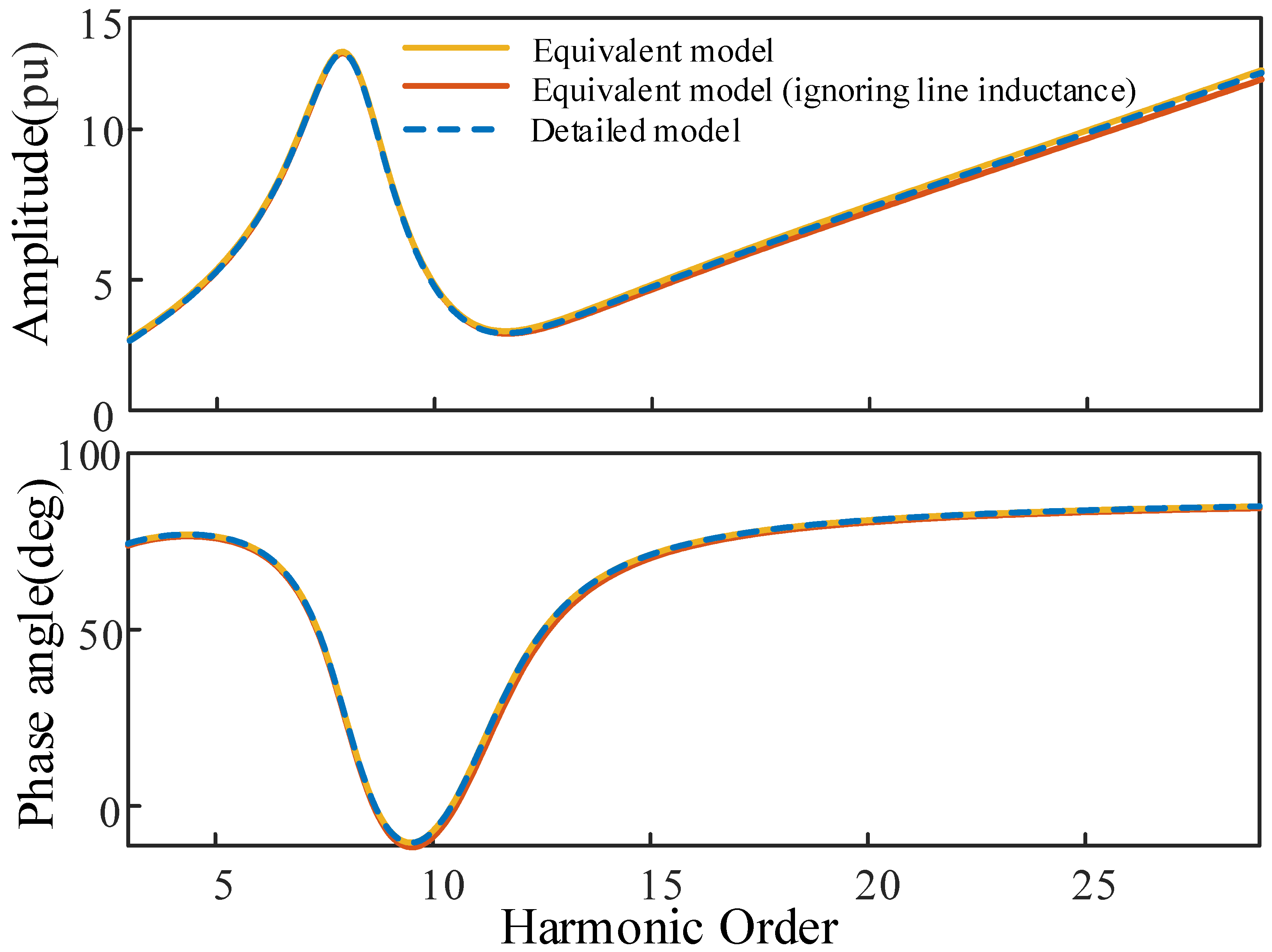
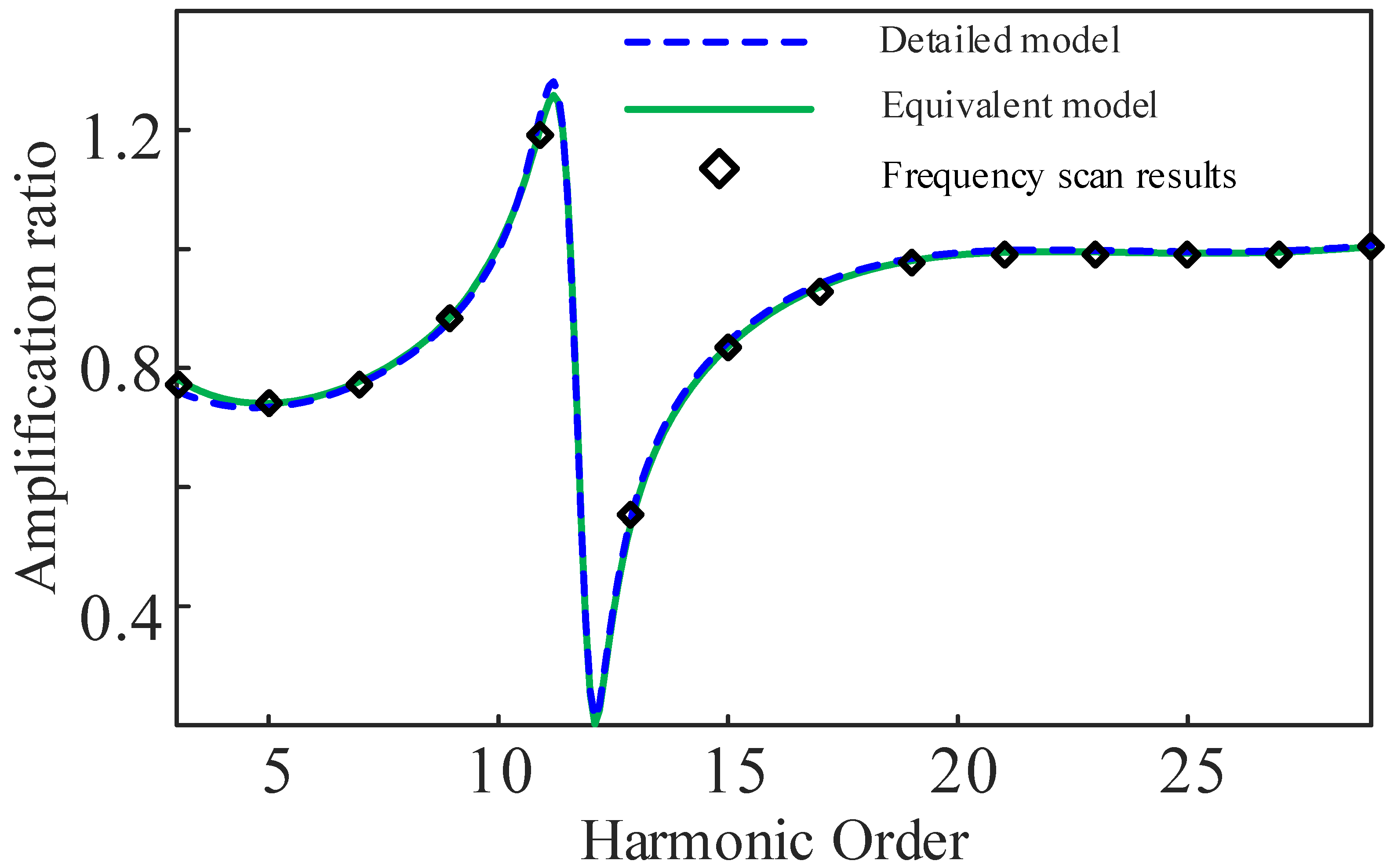
5.2. Validation of the Dynamic Equivalent Model
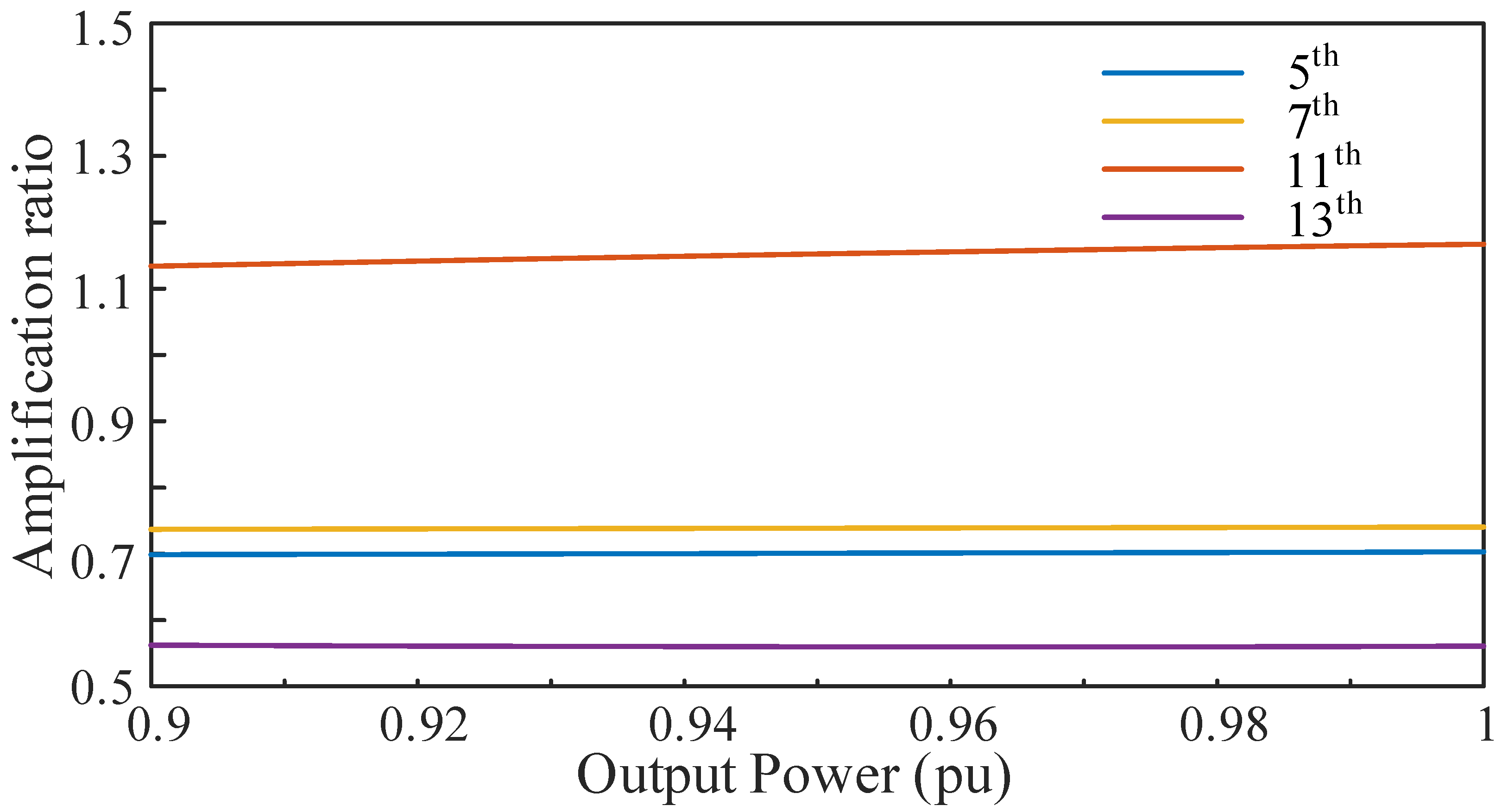
5.3. Harmonic Resonance Analysis
6. Conclusions
- The equivalent model exhibits good consistency with the detailed model across the entire frequency range. Therefore, the frequency scan result of the dynamic equivalent model can be used for harmonic resonance analysis with confidence.
- The collector lines between the PV units have a significant impact on the impedance models of the plant at the harmonic frequency. Therefore, the assumption of ignoring collector lines that has been used in many papers is not acceptable.
- The capacitance of the collector line has a dominant impact on the harmonic impedance of the PV plant, while the impact of the series impedance is much smaller. If a precise quantitative analysis is not needed, the equivalent model of the collector line can be further simplified as a capacitor. The error is expected to be below 10%, if the harmonic order of interest is not higher than the 30th harmonic.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, F.; Mu, Y.; Chen, Z. Control Strategy for Improving the Voltage Regulation Ability of Low-Carbon Energy Systems with High Proportion of Renewable Energy Integration. Electronics 2023, 12, 2513. [Google Scholar] [CrossRef]
- Tong, D.; Farnham, D.J.; Duan, L.; Zhang, Q.; Lewis, N.S.; Caldeira, K.; Davis, S.J. Geophysical constraints on the reliability of solar and wind power worldwide. Nat. Commun. 2021, 12, 6146. [Google Scholar] [CrossRef]
- Gao, B.; Wang, Y.; Xu, W. Modeling Voltage Source Converters for Harmonic Power Flow Studies. IEEE Trans. Power Deliv. 2021, 36, 3426–3437. [Google Scholar] [CrossRef]
- Dai, L.; Wang, H.; Qin, Y.; Shi, G.; Zhang, J.; Cai, X. Analysis and Suppression of High-Frequency Resonance for Offshore Wind Power Grid-Connected Converter Considering Cable Capacitance Effect. Electronics 2023, 12, 2638. [Google Scholar] [CrossRef]
- Gao, B.; Wang, Y.; Xu, W. An Improved Model of Voltage Source Converters for Power System Harmonic Studies. IEEE Trans. Power Deliv. 2022, 37, 3051–3061. [Google Scholar] [CrossRef]
- Zheng, T.; Kong, F.; Li, G.; Wang, Z.; Chen, Y. A Gray-Box Stability Analysis Method of Grid-Connected Inverter Considering Synchronization Dynamics. Electronics 2023, 12, 2509. [Google Scholar] [CrossRef]
- Ackermann, T. Transmission systems for offshore wind farms. IEEE Power Eng. Rev. 2003, 22, 23–27. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, F.; Zou, R.; Li, Y. Harmonic Resonance Characteristic of Large-scale PV Plant: Modelling, Analysis and Engineering Case. IEEE Trans. Power Deliv. 2022, 37, 2359–2368. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, X.; Yang, S. Analysis of High-Frequency Resonance and Suppression Strategy of Photovoltaic Power Plant with Static Reactive Power Compensation Device. Proc. CSEE 2022, 1–15. [Google Scholar]
- Buchhagen, C.; Rauscher, C.; Menze, A.; Jung, J. BorWin1—First Experiences with harmonic interactions in converter dominated grids. In Proceedings of the International ETG Congress 2015; Die Energiewende—Blueprints for the Renewable Energy Age, Bonn, Germany, 17–18 November 2015; pp. 1–7. [Google Scholar]
- Ning, X.; An, L.; Ma, F. Harmonic interaction between large-scale photovoltaic power stations and grid. Proc. CSEE 2013, 33, 9–16. [Google Scholar]
- Qin, S.; Li, S.; Wang, R. Resonance and suppression strategy of large-capacity permanent magnet synchronous generator wind turbine system. Autom. Electr. Power Syst. 2014, 38, 11–16. [Google Scholar]
- Wang, L.; Xie, X.; Jiang, Q.; Liu, H.; Li, Y.; Liu, H. Investigation of SSR in Practical DFIG-Based Wind Farms Connected to a Series-Compensated Power System. IEEE Trans. Power Syst. 2015, 30, 2772–2779. [Google Scholar] [CrossRef]
- Erlich, I.; Feltes, C.; Shewarega, F. Enhanced Voltage Drop Control by VSC–HVDC Systems for Improving Wind Farm Fault Ridethrough Capability. IEEE Trans. Power Deliv. 2014, 29, 378–385. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, X.; Chen, L.; Min, Y.; Li, G.; Wang, L.; Zhang, Y. A Strictly Sufficient Stability Criterion for Grid-Connected Converters Based on Impedance Models and Gershgorin’s Theorem. IEEE Trans. Power Deliv. 2020, 35, 1606–1609. [Google Scholar] [CrossRef]
- Messo, T.; Luhtala, R.; Aapro, A.; Roinila, T. Accurate Impedance Model of Grid-Connected Inverter for Small-Signal Stability Assessment in High-Impedance Grids. In Proceedings of the 2018 International Power Electronics Conference, Niigata, Japan, 20–24 May 2018; pp. 3156–3163. [Google Scholar] [CrossRef]
- Ren, W.; Larsen, E. A Refined Frequency Scan Approach to Sub-Synchronous Control Interaction (SSCI) Study of Wind Farms. IEEE Trans. Power Syst. 2016, 31, 3904–3912. [Google Scholar] [CrossRef]
- Wang, Y. Vector-fitting-based quantitative ssci analysis for Seriescompensated wind power systems. IET Renew. Power Gener. 2020, 14, 3023–3034. [Google Scholar] [CrossRef]
- Zhu, L.; Hu, X.; Li, S. High-Frequency Resonance of DFIG-Based Wind Generation under Weak Power Network. In Proceedings of the 2018 International Conference on Power System Technology, Guangzhou, China, 10–12 September 2018; pp. 2719–2724. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, X.; Xie, X.; Yang, X.; Xiao, X. Identifying Sources of Subsynchronous Resonance Using Wide-Area Phasor Measurements. IEEE Trans. Power Deliv. 2021, 36, 3242–3254. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; He, J.; Xu, T.; Yu, Z.; Wang, C.; Zhang, C. Subsynchronous Interaction Between Direct-Drive PMSG Based Wind Farms and Weak AC Networks. IEEE Trans. Power Syst. 2017, 32, 4708–4720. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Zhang, C.; Li, Y.; Liu, H.; Hu, Y. Quantitative SSR Analysis of Series-Compensated DFIG-Based Wind Farms Using Aggregated RLC Circuit Model. IEEE Trans. Power Syst. 2017, 32, 474–483. [Google Scholar] [CrossRef]
- Remon, D.; Cantarellas, A.M.; Rodriguez, P. Equivalent Model of Large-Scale Synchronous Photovoltaic Power Plants. IEEE Trans. Ind. Appl. 2016, 52, 5029–5040. [Google Scholar] [CrossRef]
- Li, W.; Chao, P.; Liang, X.; Ma, J.; Xu, D.; Jin, X. A Practical Equivalent Method for DFIG Wind Farms. IEEE Trans. Sustain. Energy 2018, 9, 610–620. [Google Scholar] [CrossRef]
- Hussein, D.N.; Matar, M.; Iravani, R. A Type-4 Wind Power Plant Equivalent Model for the Analysis of Electromagnetic Transients in Power Systems. IEEE Trans. Power Syst. 2013, 28, 3096–3104. [Google Scholar] [CrossRef]
- Shao, H.; Yan, H.; Cai, X.; Qin, Y.; Zhang, Z. Aggregation Modeling Algorithm of PMSM Wind Farm Considering Submarine Cable Power Loss. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 1169–1174. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Zhang, M.; Peng, Y.; Tian, Y.; Lin, G.; Chang, F. Harmonic Resonance Suppression with Inductive Power Filtering Method: Case Study of Large- Scale Photovoltaic Plant in China. IEEE Trans. Power Electron. 2023, 38, 6444–6454. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, H.; Gao, B.; Xiao, X.; Torquato, R.; Trindade, F.C. Harmonic resonance analysis in high-renewable-energy-penetrated power systems considering frequency coupling. Energy Convers. Econ. 2022, 3, 333–344. [Google Scholar] [CrossRef]

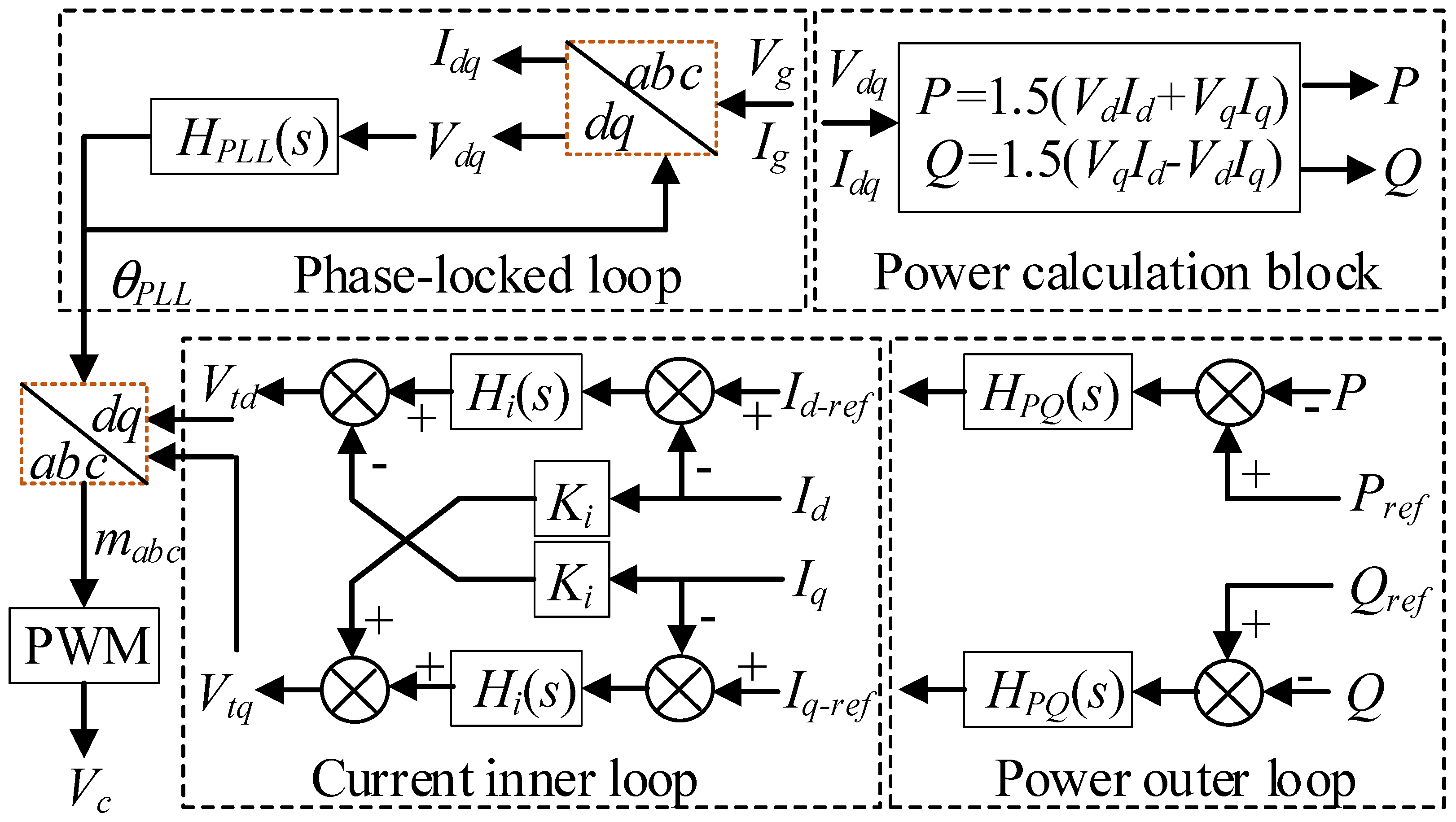

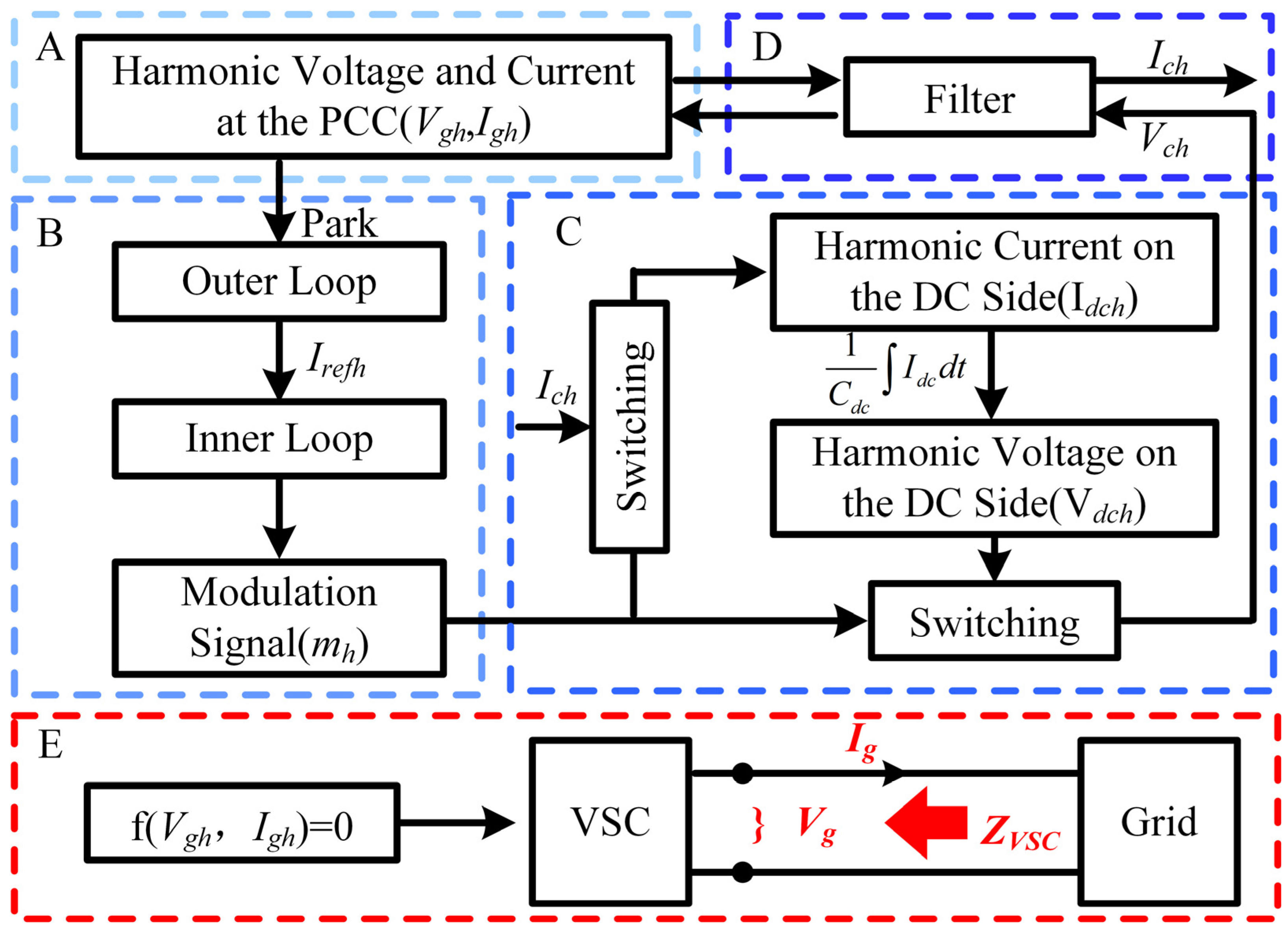

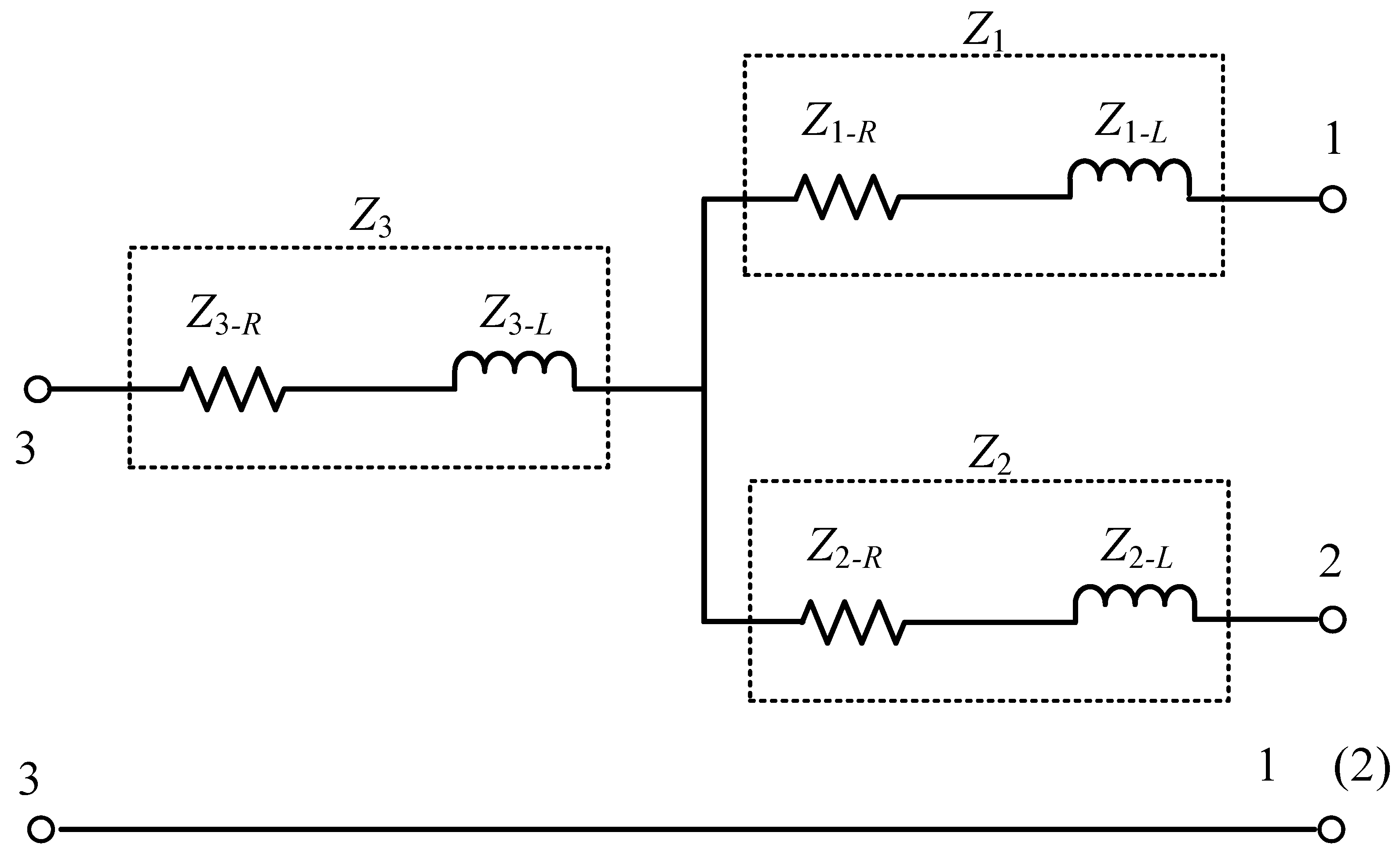
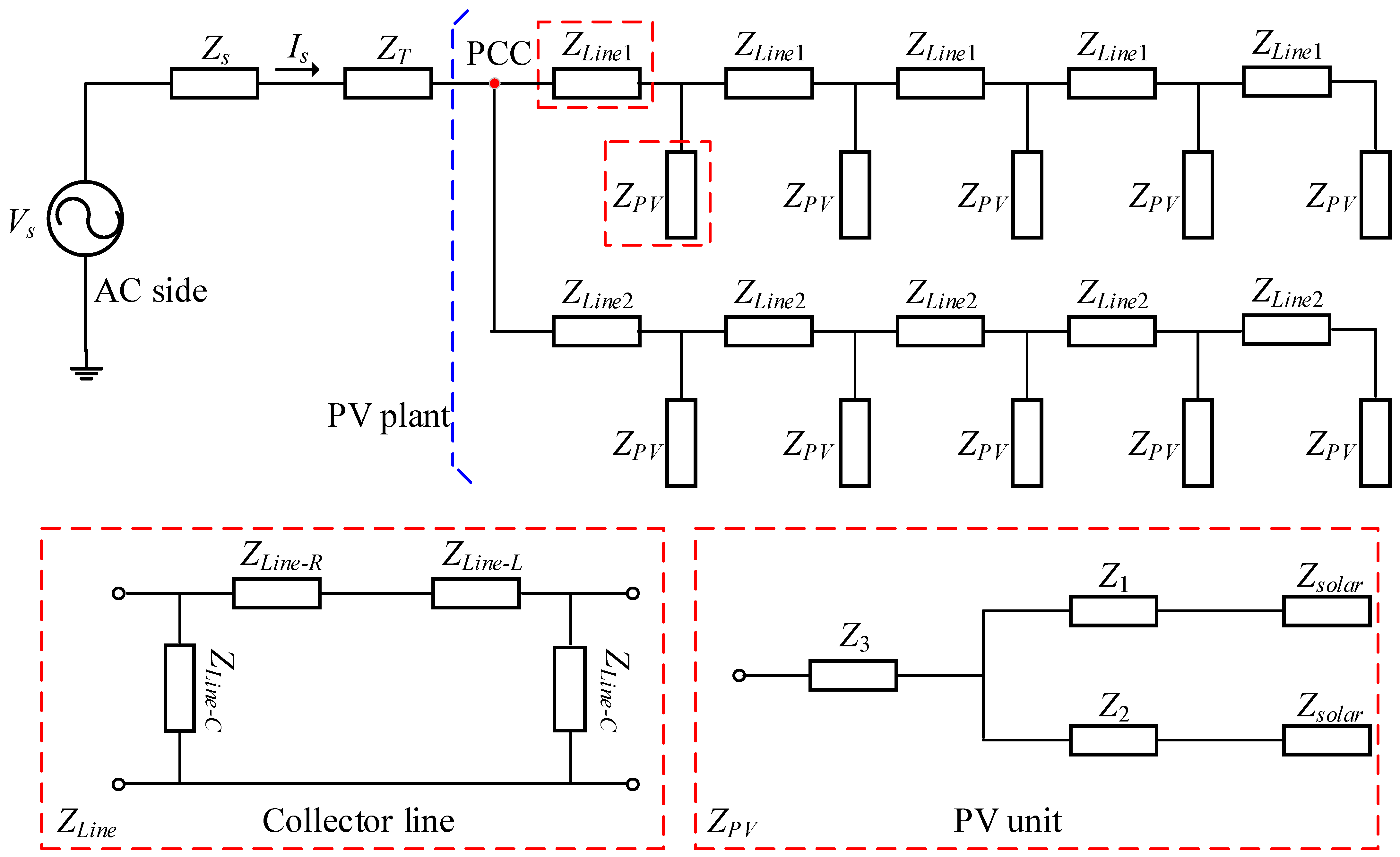

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated line voltage | 690 | Direct current Capacitor/μF | 1300 |
| Filter inductance/mH | 1 | Filter capacitance/μF | 100 |
| Outer loop power control PI KiPQ | 4 | Outer loop power control PI KpPQ | 0.04 |
| Current inner loop PI Kii | 200 | Current inner loop PI Kpi | 0.6 |
| Cross-Section of the Cable/(mm2) | Resistance/(Ω/km) | Inductance/(mH/km) | Capacitance/(μF/km) |
|---|---|---|---|
| 50 | 0.3448 | 2.51681 | 0.163398 |
| 95 | 0.1815 | 2.45092 | 0.205812 |
| 120 | 0.1437 | 2.42775 | 0.224132 |
| 185 | 0.0932 | 2.38438 | 0.264385 |
| 240 | 0.0718 | 2.35517 | 0.296633 |
| 300 | 0.0575 | 2.33258 | 0.324904 |
| Parameter | Value |
|---|---|
| Transformer ratio/kV | 35/0.69 |
| Short-circuit impedance/% | 8 |
| Fission coefficient | 3.5 |
| Rated capacity/kVA | 1250 |
| Connected group | D,yn11-yn11 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated line voltage | 2165 V | DC voltage | 5000 V |
| Filter inductance | 0.8 mH | Filter capacitance | 45 µF |
| AC voltage PI Kiac | 2500 | AC voltage PI Kpac | 0.55 |
| DC voltage PI Kidc | 0.15 | DC voltage PI Kpdc | 0.001 |
| current PI Kii | 200 | current PI Kpi | 0.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; He, Y.; Zhou, X.; Zhang, Z. Investigation of the Feasibility of the Dynamic Equivalent Model of Large Photovoltaic Power Plants in a Harmonic Resonance Study. Electronics 2023, 12, 3746. https://doi.org/10.3390/electronics12183746
Xie Y, He Y, Zhou X, Zhang Z. Investigation of the Feasibility of the Dynamic Equivalent Model of Large Photovoltaic Power Plants in a Harmonic Resonance Study. Electronics. 2023; 12(18):3746. https://doi.org/10.3390/electronics12183746
Chicago/Turabian StyleXie, Yuzhe, Yanhua He, Xuntian Zhou, and Zhigang Zhang. 2023. "Investigation of the Feasibility of the Dynamic Equivalent Model of Large Photovoltaic Power Plants in a Harmonic Resonance Study" Electronics 12, no. 18: 3746. https://doi.org/10.3390/electronics12183746
APA StyleXie, Y., He, Y., Zhou, X., & Zhang, Z. (2023). Investigation of the Feasibility of the Dynamic Equivalent Model of Large Photovoltaic Power Plants in a Harmonic Resonance Study. Electronics, 12(18), 3746. https://doi.org/10.3390/electronics12183746





