System Model
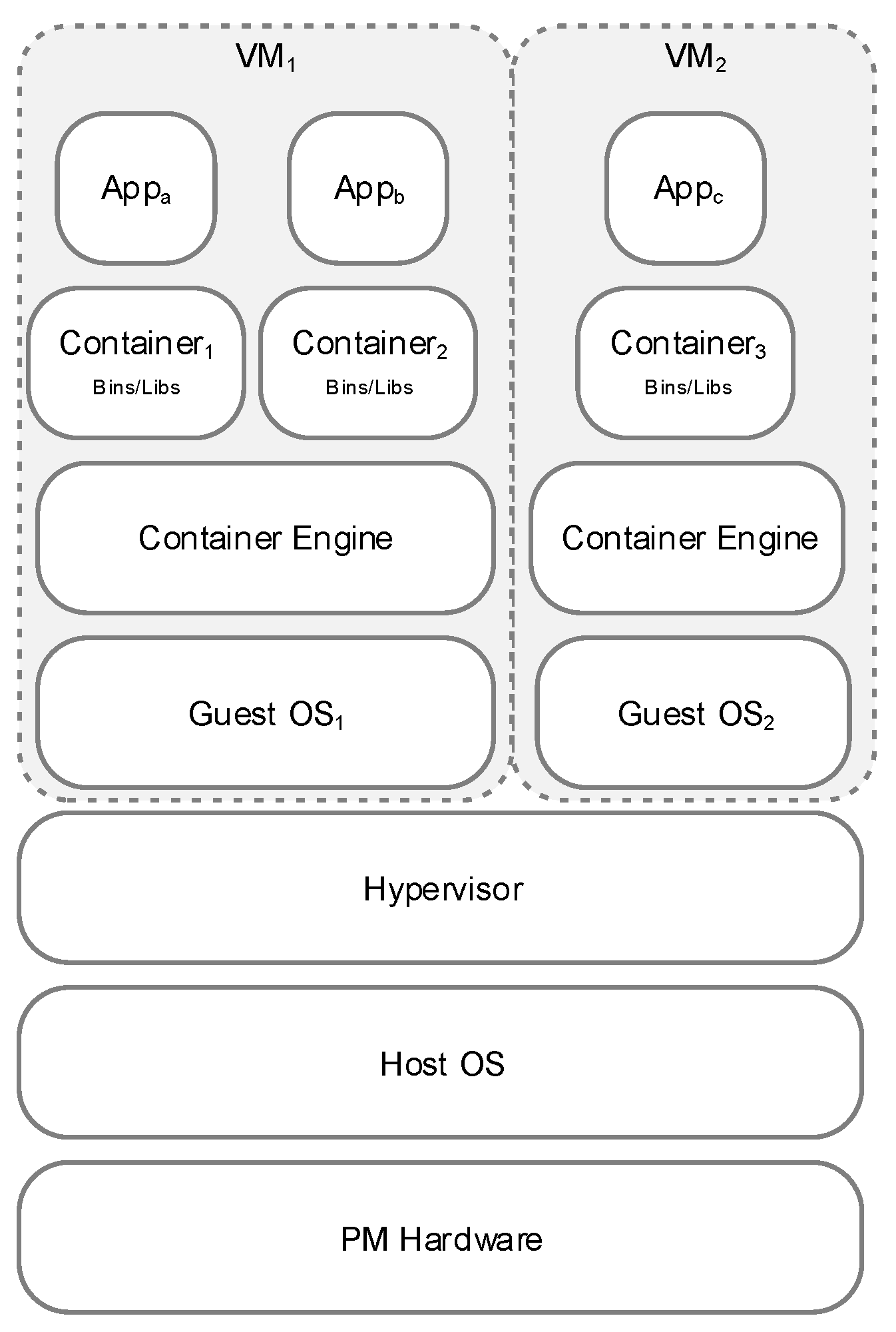
Figure 2 illustrates two mechanisms, namely, A and B, that can be adopted in CaaS cloud systems. Mechanism A does not focus on power consumption; therefore, it distributes the VMs around two different PMs, whereas Mechanism B places the three VMs on one PM if the PM can host all the VMs. Mechanism B can help reduce the overall power consumption provided that the second PM is in a power-saving mode. However, CP mechanisms can affect the overall performance of CaaS clouds because the overhead of finding an appropriate solution for CP can delay the processing of jobs in CaaS systems [
35]. Therefore, the optimal mechanism should involve a trade-off between reducing the energy consumption and improving the system performance.
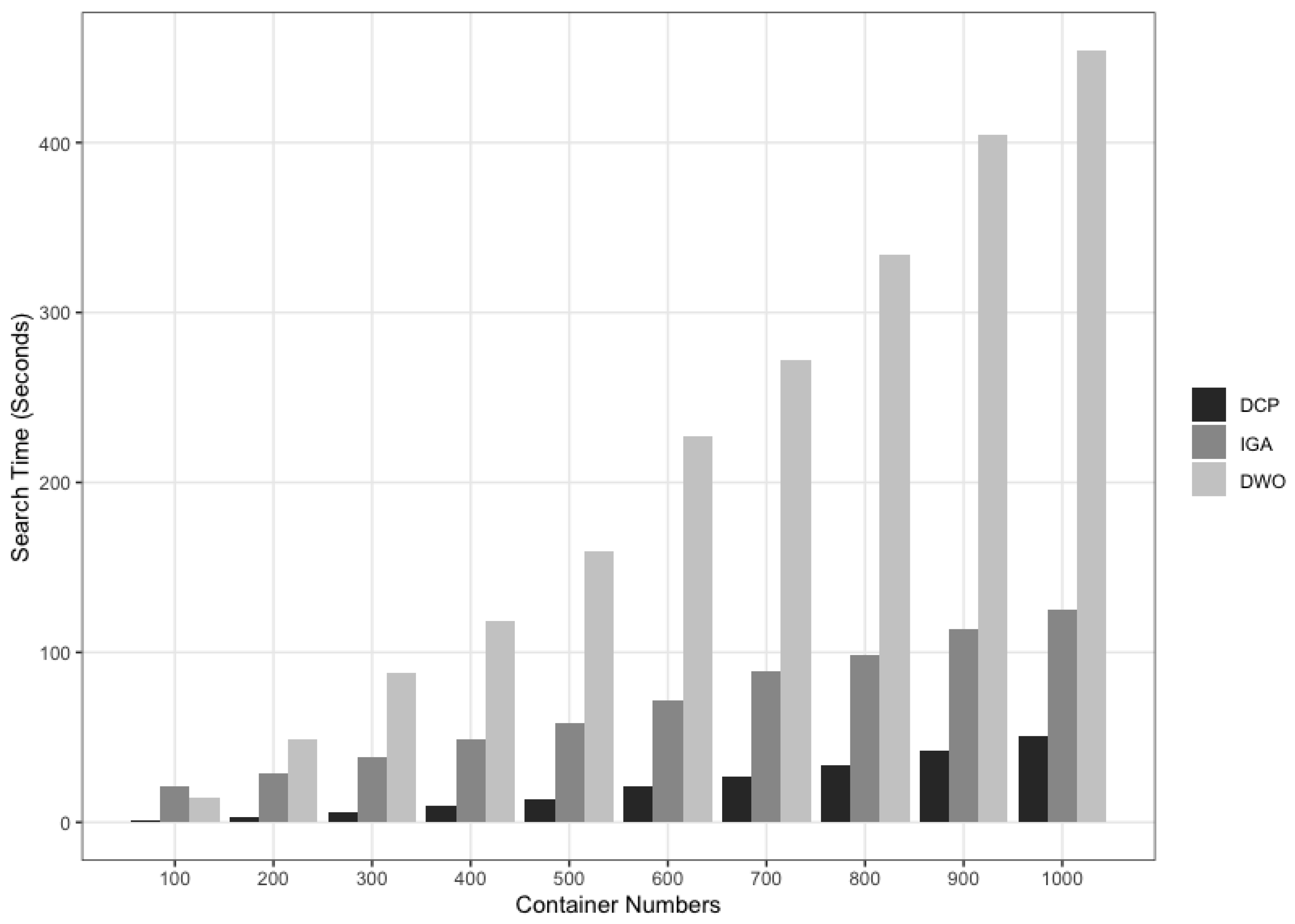
This section presents the proposed DCP mechanism that extends the DWO mechanism [
16], which is a container placement mechanism designed to improve resource utilization and reduce power consumption in CaaS-based cloud systems. DWO adopts the WOA [
31], which is a meta-heuristic optimization algorithm that imitates the social behavior of humpback whales. A group of Humpback whales (i.e., search agents) make a spiral shape around the prey and then swim up to hunt the prey (i.e., a solution) inside the circles. Three phases are used by the humpback whale: (i) encircling, (ii) spiral bubble-net feeding, and (iii) searching for prey. The position of the prey is unknown; therefore, the current best search agent can be any position near the prey in the search space. Other search agents then update their positions according to the current search agent [
16].
The algorithm employs a search process that commences with a randomly generated population of solutions (a matrix of solutions), which then evolves over successive generations. The solutions are always combined to form the next generation of solutions, allowing the matrix to be enhanced over the course of generations. However, the main difference between the current work and recently published papers in the literature (particularly the DWO mechanism [
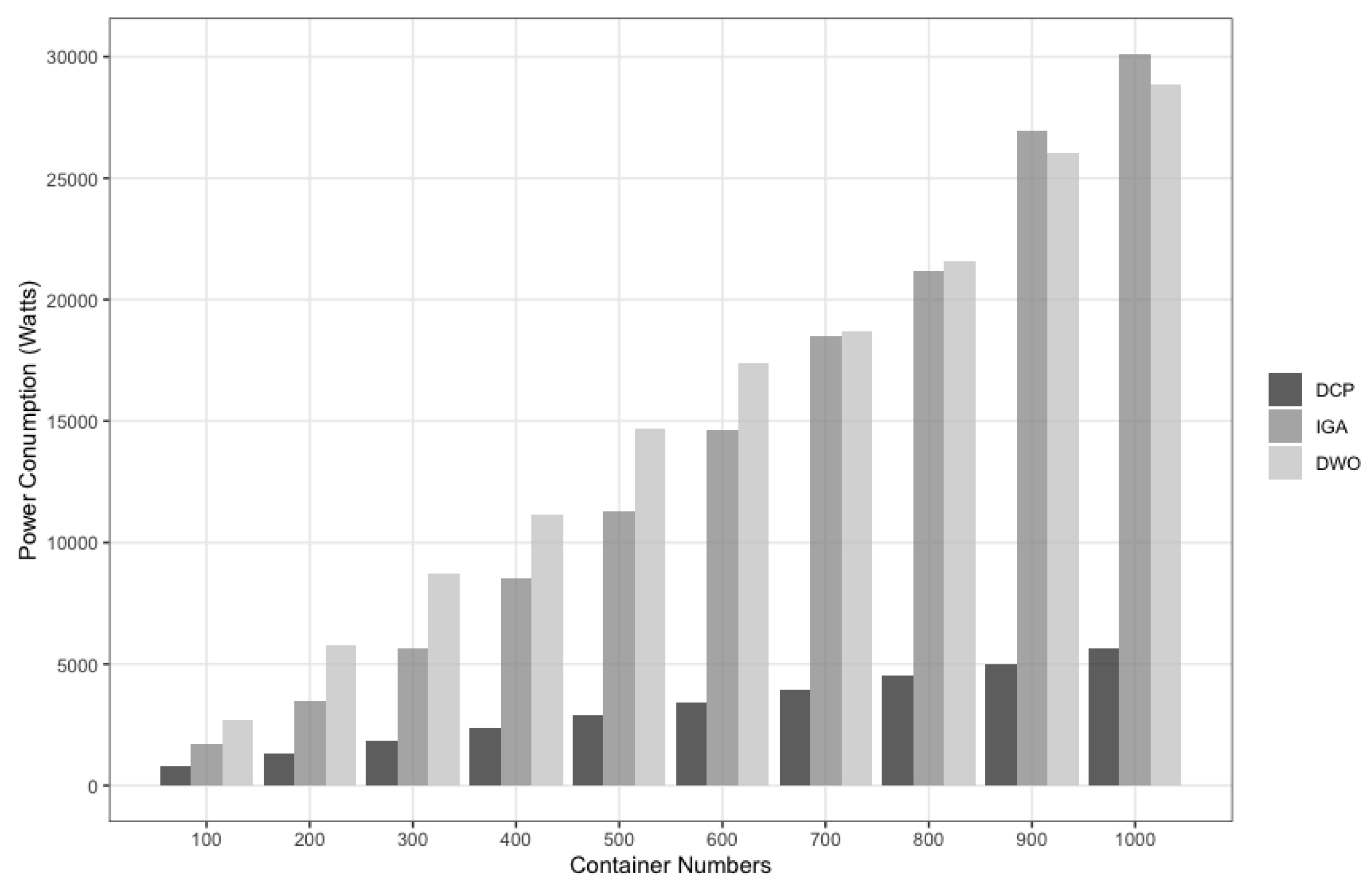
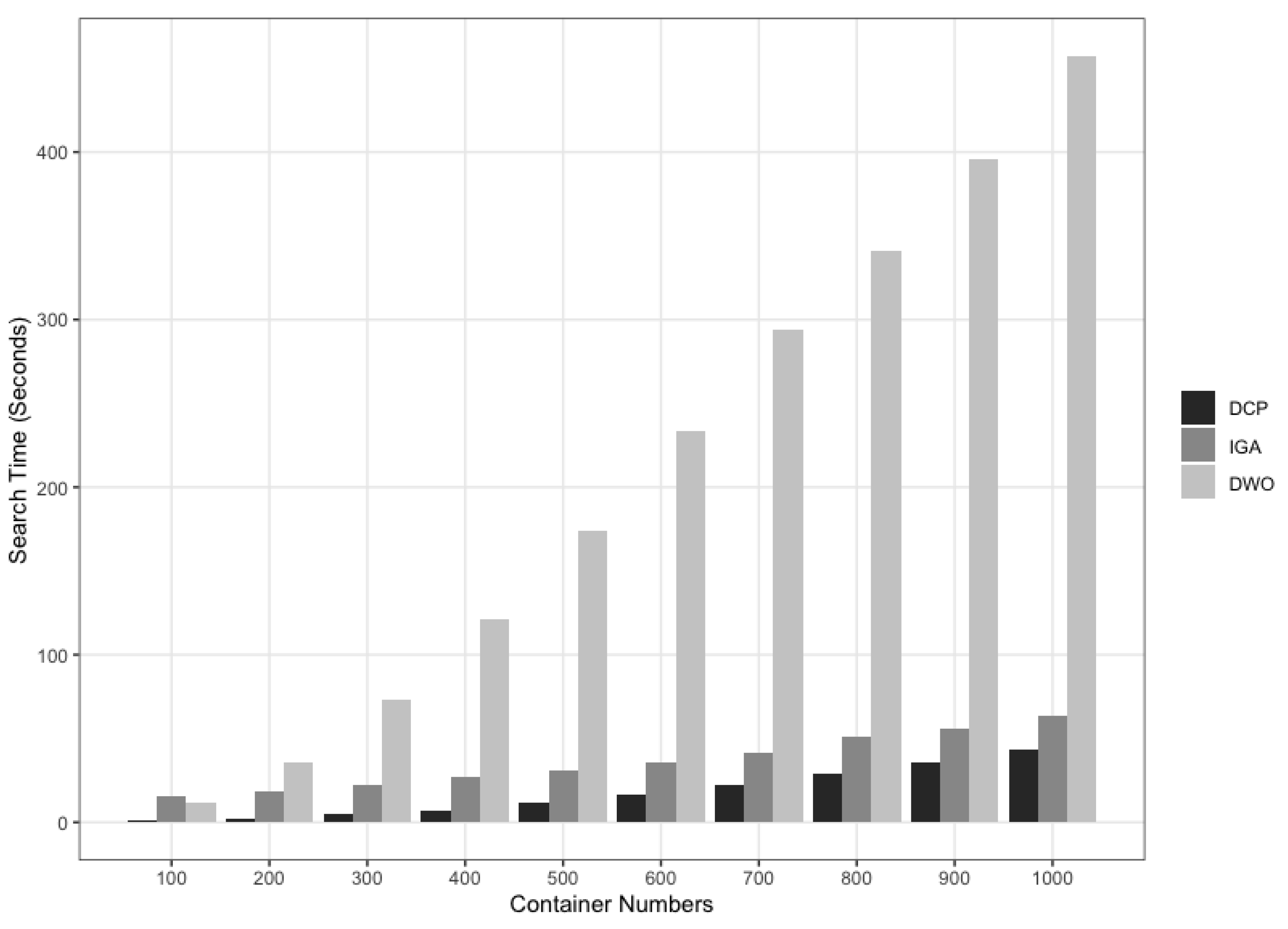
16]) is that the proposed DCP mechanism utilizes a heuristic approach to direct (hence, the name of the mechanism) the search process in the mechanism. This approach plays a vital role in reducing the overall power consumption of CaaS cloud systems with an acceptable overhead time.
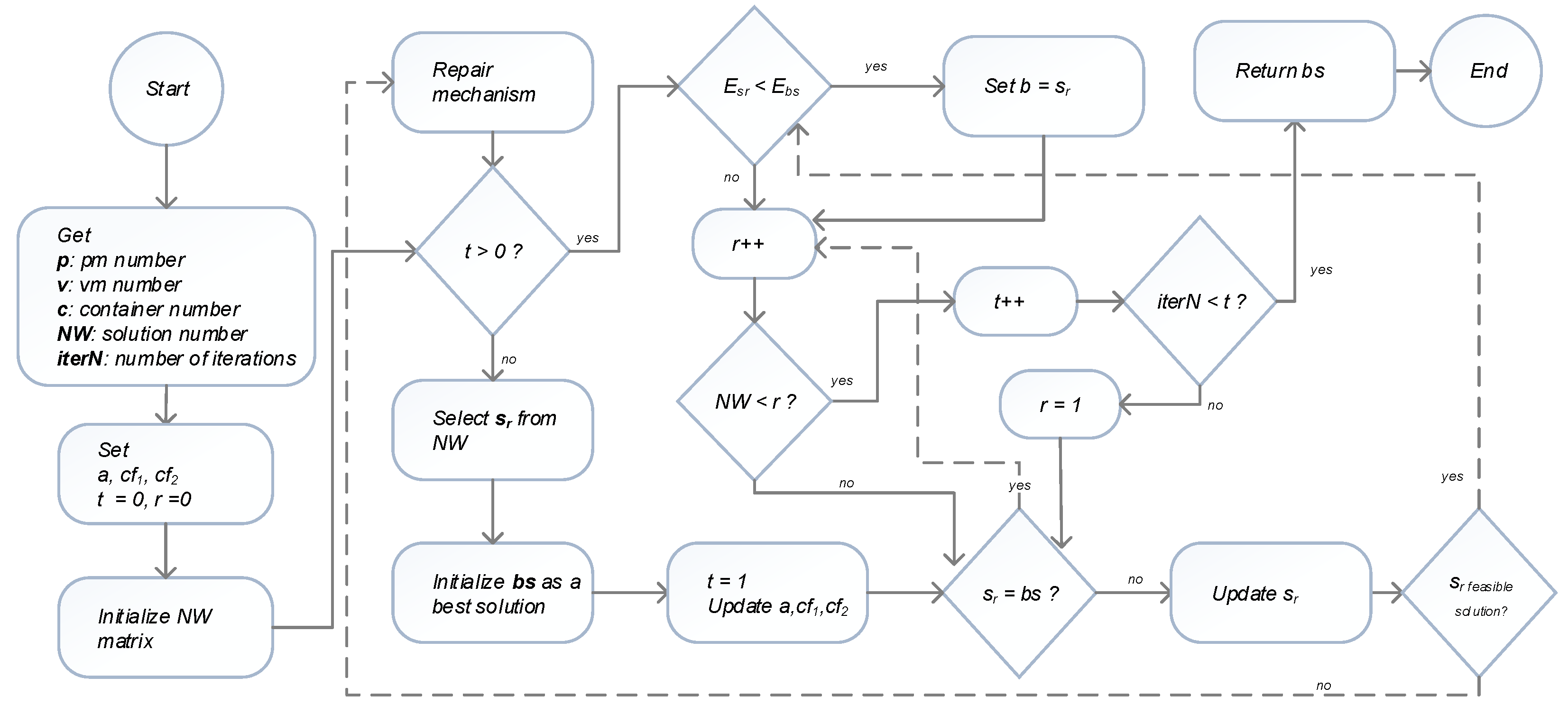
The workflow of the DCP policy is depicted in
Figure 3, which contains two phases: initialization and search. The initialization phase uses the number of PMs (
p), VMs (
v), and containers (
c) as the input parameters. The mechanism also obtains the number of possible solutions (
) and total number of iterations (
) to search for the best solution. The mechanism sets
a as a double random number
that is linearly decreased from 2 to 0 [
31]. The number of iterations
t is set as zero.
t is an iteration counter from one to
. Moreover,
and
are the coefficient vectors that are employed to determine how to update current solutions [
31]. Those vectors are calculated as follows:
Next, the policy initializes the solution matrix (), which is a matrix of NW possible solutions, and each solution can be implemented using the CP mechanism in a cloud system. It randomly assigns containers to the VMs and allocates VMs to the PMs. Furthermore, the policy in the next step employs a repair mechanism that repairs the solutions in the because the random allocation of containers to VMs can overload some VMs with containers, i.e., the CPU or RAM requirements of the containers are greater than those of a VM that hosts those containers. Similarly, some PMs can be overloaded with VMs. Overloaded VMs or PMs must be repaired by migrating containers and VMs from overloaded VMs and PMs, respectively.
The repair mechanism employs a two-factor approach to identify the most suitable containers (or VMs) for migration. Next, an appropriate candidate VM (or PM) is selected as the new host for these containers (or VMs) [
16]. This approach aims to decrease the total power consumption by improving resource utilization. The first factor is the overloaded factor
, which is a function employed to select a guest element
. The guest element can be a container or VM to be migrated from an overloaded hosting element
, which can be a VM or PM. The overloaded factor can be calculated as follows:
is a generic term that refers to either containers or VMs, and
is a generic term that refers to either VMs or PMs. The second factor is the selection factor
, which is a function employed to select the VM (or PM) that is the most suitable candidate among all available choices. It can be calculated as follows:
Both Equations (
12) and (
13) are utilized to minimize the idle fragmentation of resources and help to efficiently harness the available resources to the maximum extent possible with an aim to improve resource utilization.
The repair mechanism fixes one solution at a time as shown in Algorithm 1. The mechanism input is a list of
. If
is overloaded, the mechanism retrieves all
elements to select the elements to be migrated. The mechanism selects the
element with the minimum
. Subsequently, it removes it from the current
and adds it to the migration list as illustrated in lines 3–14 in the algorithm. Furthermore, the mechanism selects an appropriate destined host (
) for each
in the migration list,
. The
with the least
is selected to host
provided that
can host it as given in Equation (
3) or Equation (
6) if it is a VM or PM, respectively.
In the next step, DCP initializes the best solution (
) by creating a solution that allocates VMs to the PMs based on the first-fit (FF) heuristic. The best solution initialization mechanism is presented in Algorithm 2. DCP employs the FF approach with the aim of reducing power consumption by stacking more VMs, which improves resource utilization. In contrast to other mechanisms based on the WOA, such as [
36] and [
16], DCP does not choose the best solution among the NW solutions in the solution matrix. Rather, it constructs a solution that can direct the search process, resulting in a reduced search time. The next step is to select the first solution
in the
and compare it with
in terms of energy consumption, according to Equation (
9). If
consumes less energy, it is selected as the new
.
The search phase begins by updating the parameters a, , and as mentioned in the initialization phase. Subsequently, if the current solution is not the same as the best solution, is updated using the aforementioned parameters and , as explained in the WOA. Otherwise, DCP chooses the next solution in the matrix and continues the search process. The feasibility of the updated solution of is checked to determine if it needs repair by sending it to the repair mechanism. Next, is evaluated if it consumes less energy than ; subsequently, becomes as explained in the previous stage. The search phase then selects the next solution in the solution matrix to repeat the same steps in this stage until the last solution in the matrix.
The entire search phase undergoes
iterations, and each iteration is supposed to generate better solutions with
being updated. Finally, DCP generates the optimal solution
, which preserves the optimal energy in the CaaS cloud system under consideration.
| Algorithm 1 Repair mechanism. |
- 1:
input: - 2:
foreach in do - 3:
while do - 4:
- 5:
- 6:
- 7:
foreach in do - 8:
//Equation ( 12) - 9:
if then - 10:
- 11:
- 12:
end if - 13:
- 14:
- 15:
end for - 16:
end while - 17:
end for - 18:
foreach in do - 19:
- 20:
- 21:
foreach in do - 22:
if then - 23:
//Equation ( 13) - 24:
if then - 25:
- 26:
- 27:
end if - 28:
end if - 29:
end for - 30:
- 31:
- 32:
- 33:
end for
|
| Algorithm 2 Best solution initialization. |
- 1:
input:, , - 2:
output: - 3:
foreach in do - 4:
foreach in do - 5:
if then - 6:
- 7:
end if - 8:
end for - 9:
end for - 10:
foreach in do - 11:
foreach in do - 12:
if then - 13:
- 14:
end if - 15:
end for - 16:
end for - 17:
- 18:
return
|