Tuning of PID/PIDD2 Controllers for Second-Order Oscillatory Systems with Time Delays
Abstract
:1. Introduction
1.1. Background
1.2. Analysis of the Existing Literature
- (1)
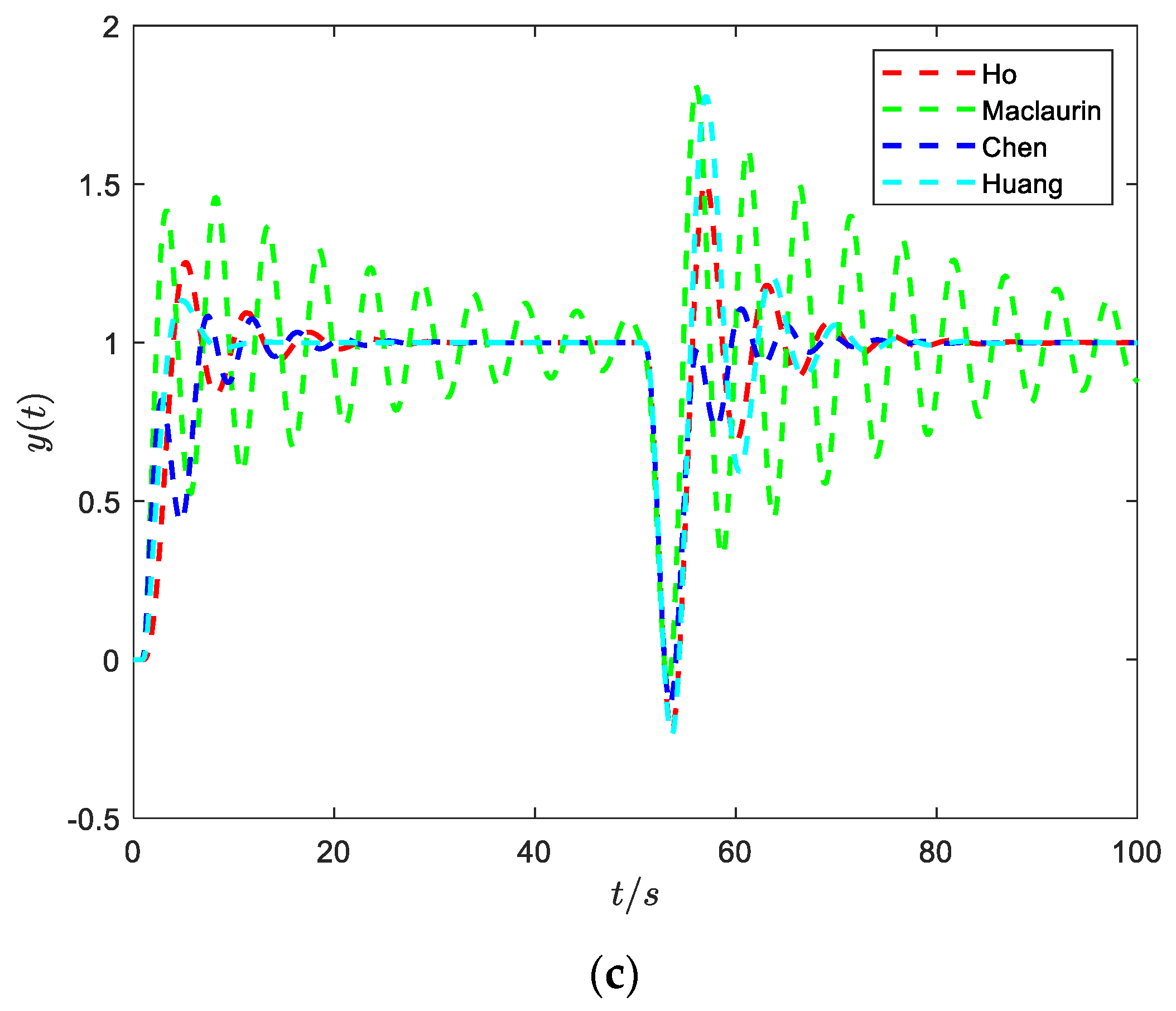
- The robustness value and ITAE of Maclaurin’s method [30] are apparently larger than the other three methods; thus, it is very sensitive to unmodeled dynamics. The step response of Maclaurin’s method is also seriously oscillatory.
- (2)
- (3)
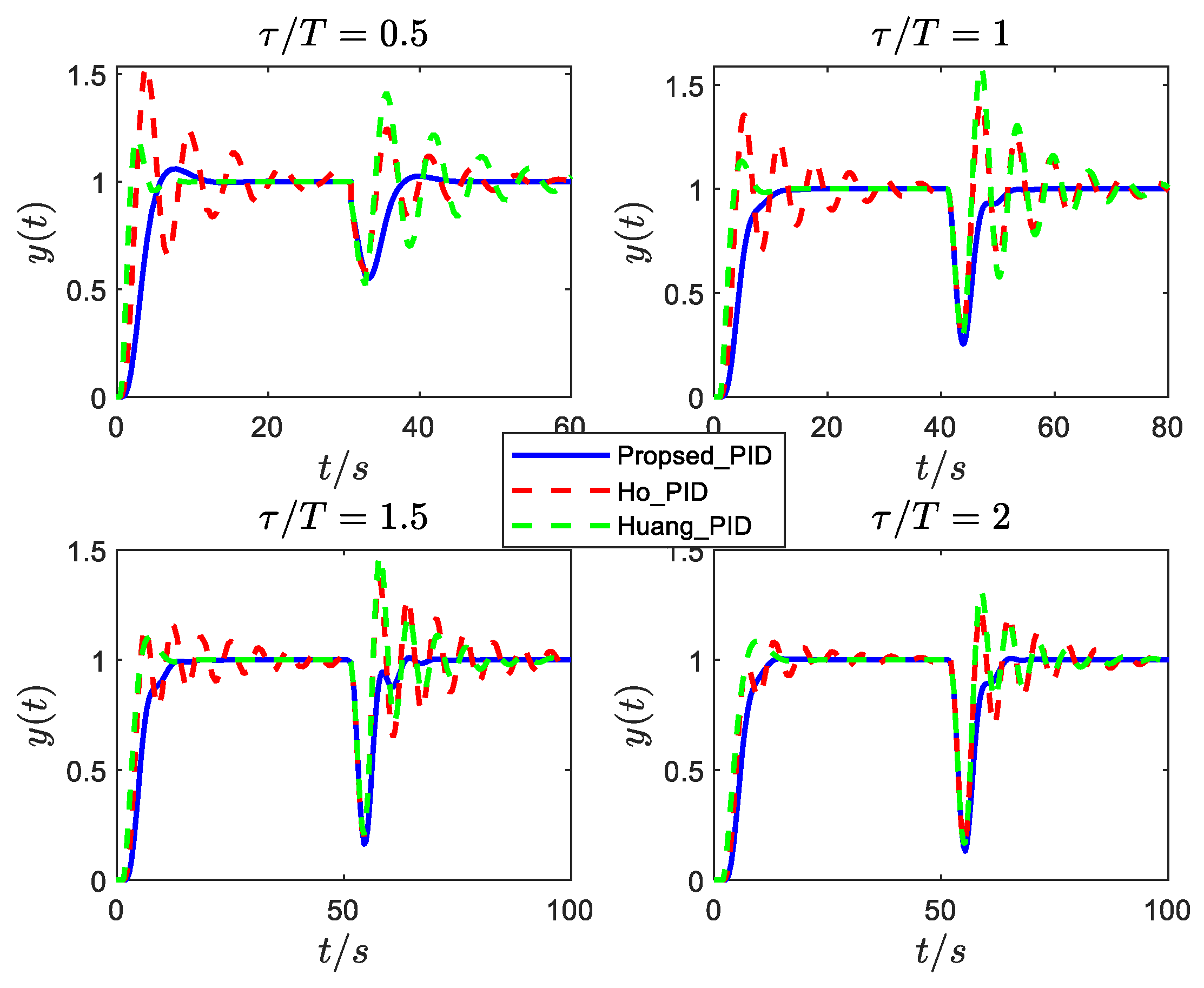
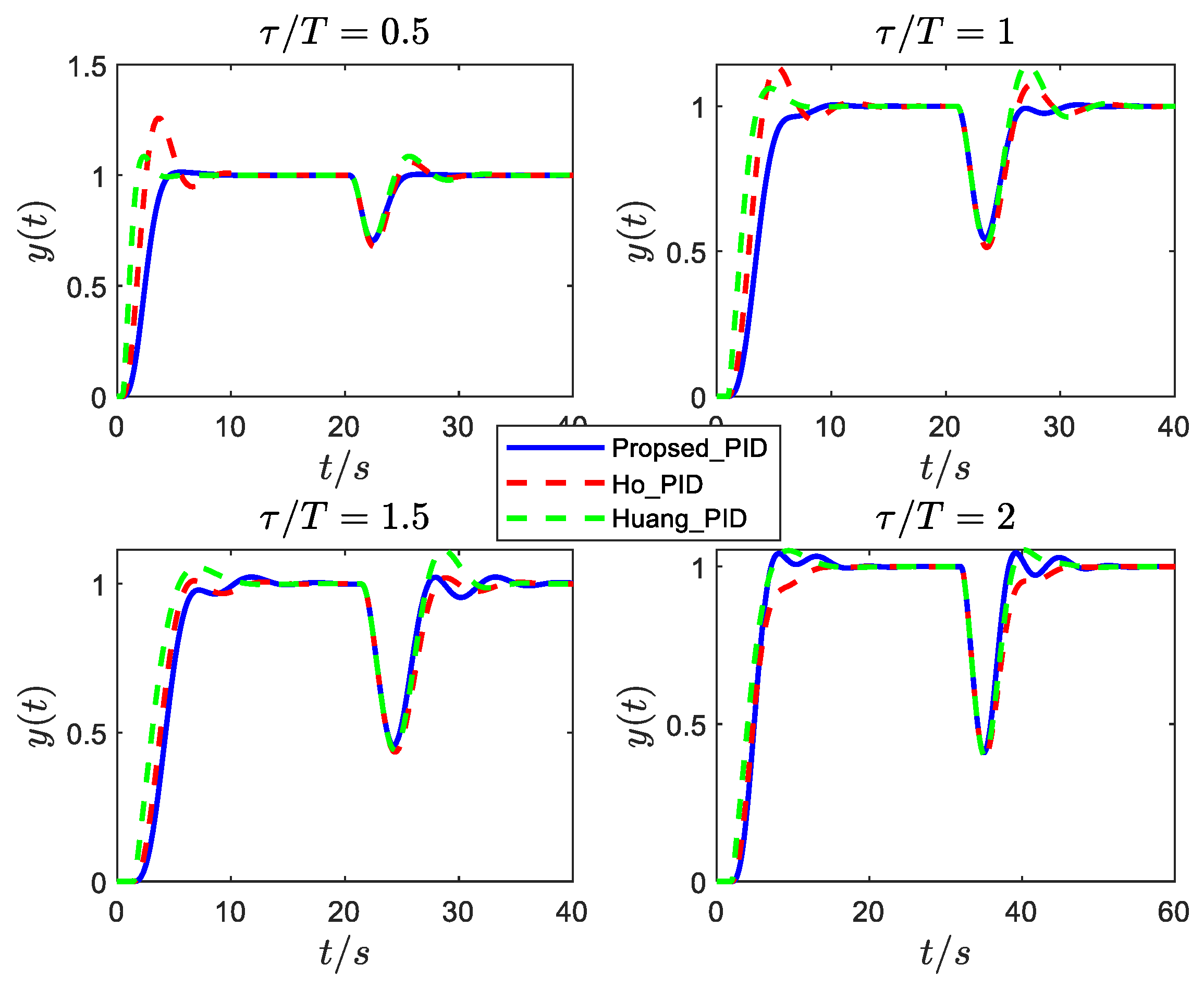
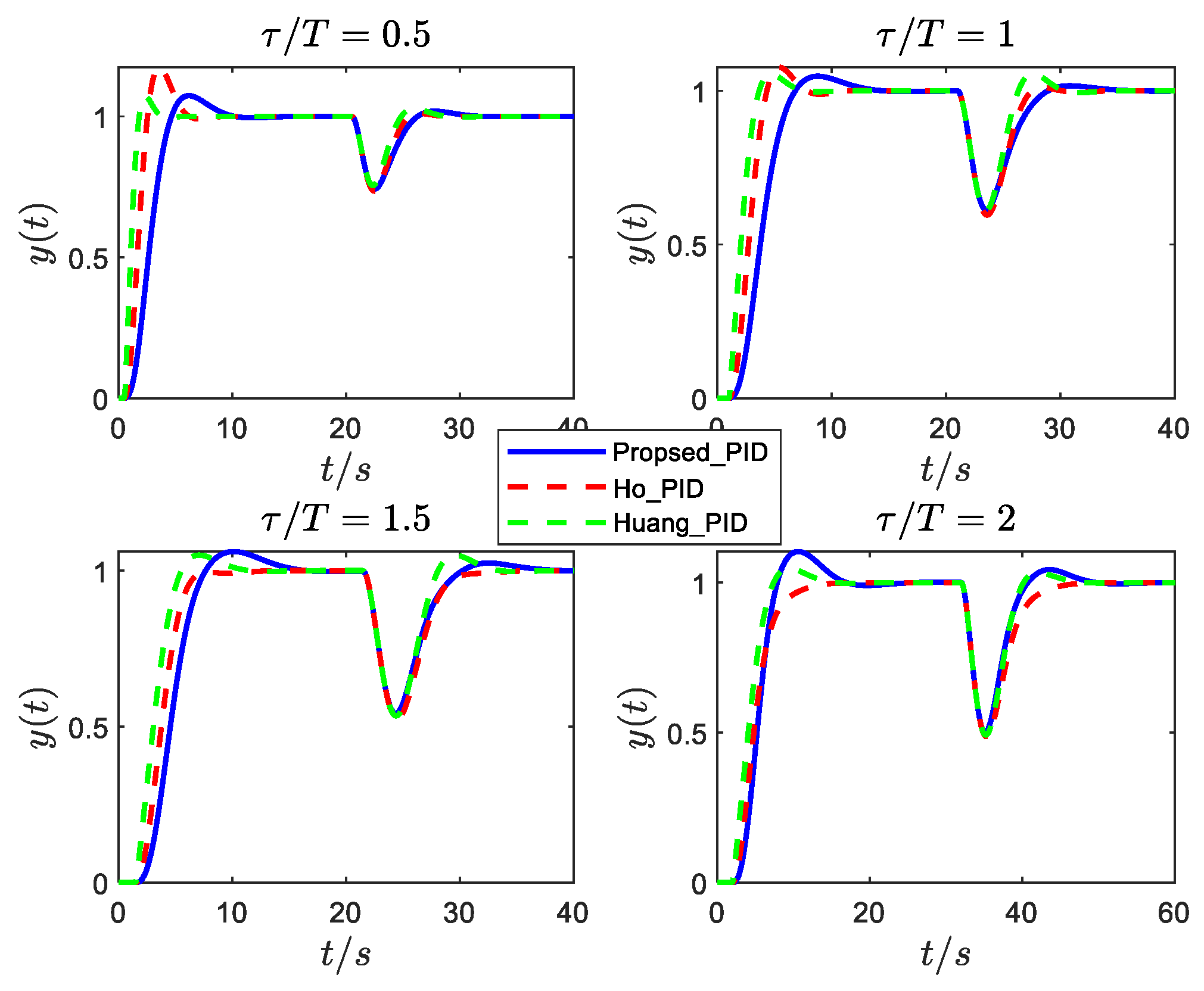
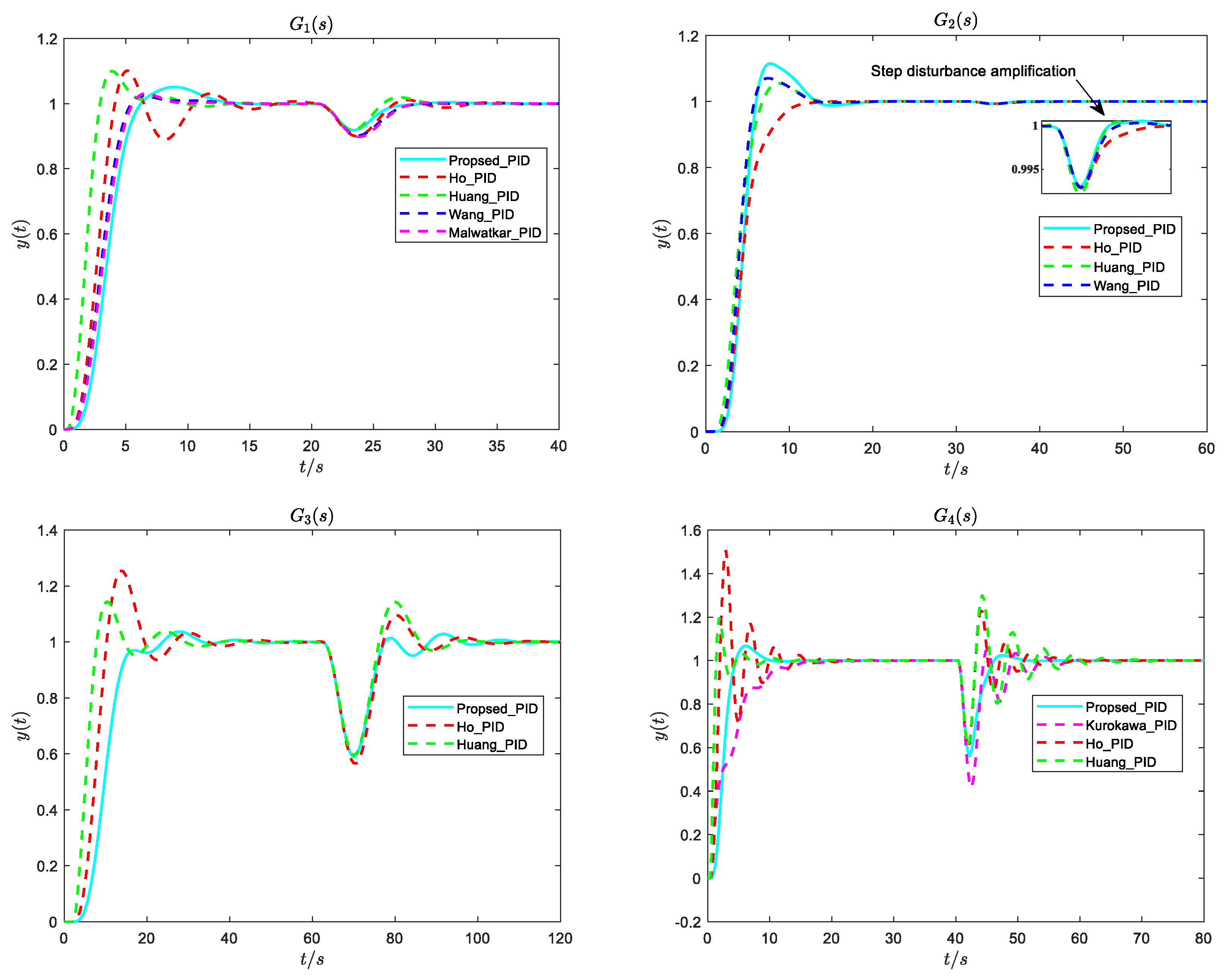
- Maclaurin’s and Huang’s methods are based on the model inverse; for the moderate oscillatory system (Figure 1c), the disturbance response is still oscillating and not eliminated. At the same time, Ho et al.’s approach can be included in addition to the above problems and also needs to select a suitable gain and phase for different underdamped systems, which is not conducive to practical engineering practice. The step response of Chen et al. eliminates the oscillation; however, from the point of view of both disturbance resistance and robustness, it is not optimal.
1.3. Motivation and Contribution of the Paper
- (1)
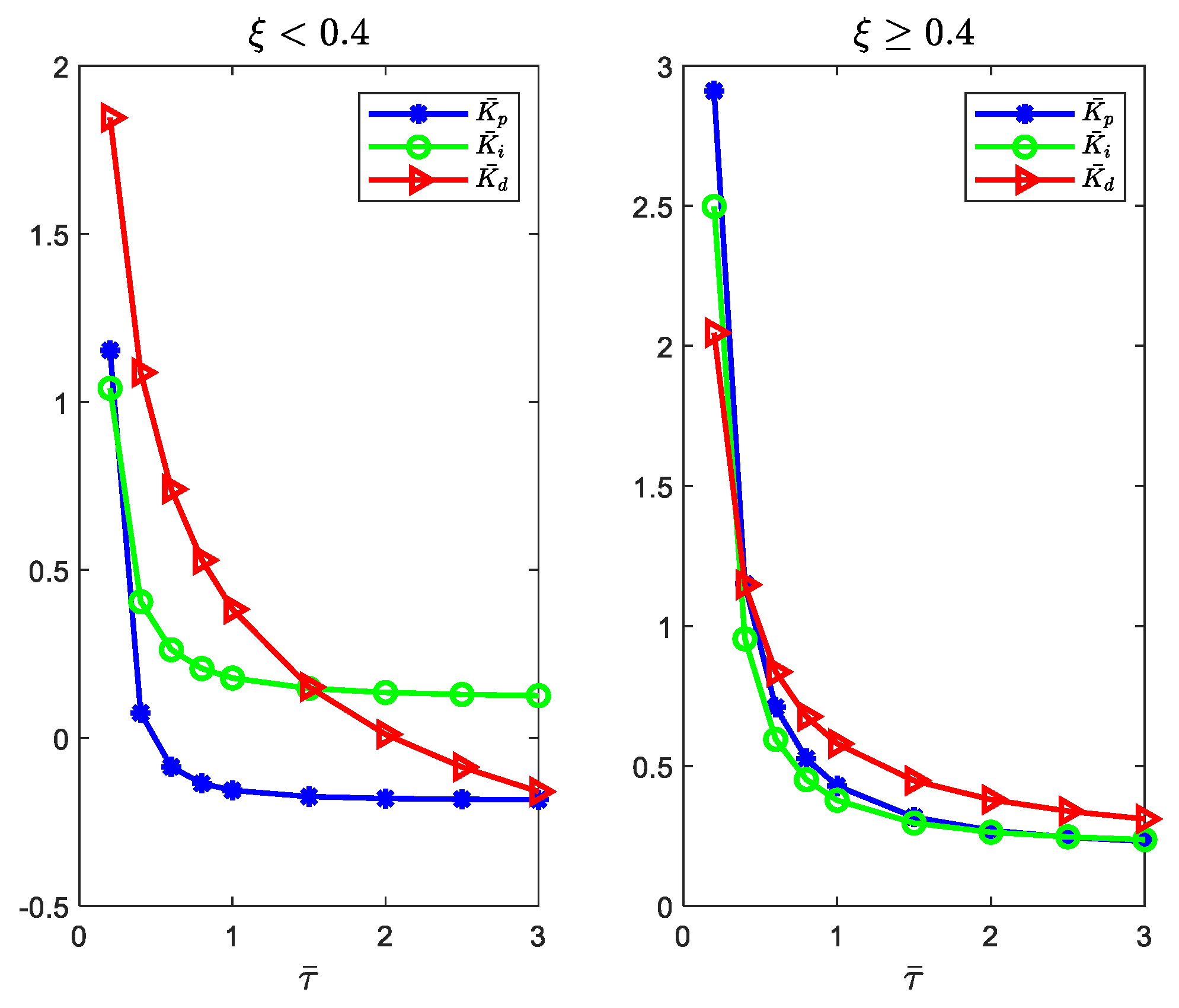
- The two methods are different, and the tuning formulas in [39] need to be fitted twice, and the derivation process is complicated. In this paper, a simplified method is adopted to divide the oscillating system according to the damping ratio , which greatly reduces the fitting process and is more convenient for practical engineering applications. In addition, both use different controllers and have different control structures: [39] uses state space PIDD2, and this paper uses PID and PIDD2.
- (2)
- The disturbance rejection performance and robustness of [39] are not as good as PIDD2.
- The tuning formulas of PID/PIDD2 for the underdamped oscillatory plant are proposed.
- The parameters of the tuning formula are obtained by minimizing the integral of time and absolute error (ITAE) under a prescribed robustness through the optimization algorithm. The simulation results verify the applicability of the proposed formulas.
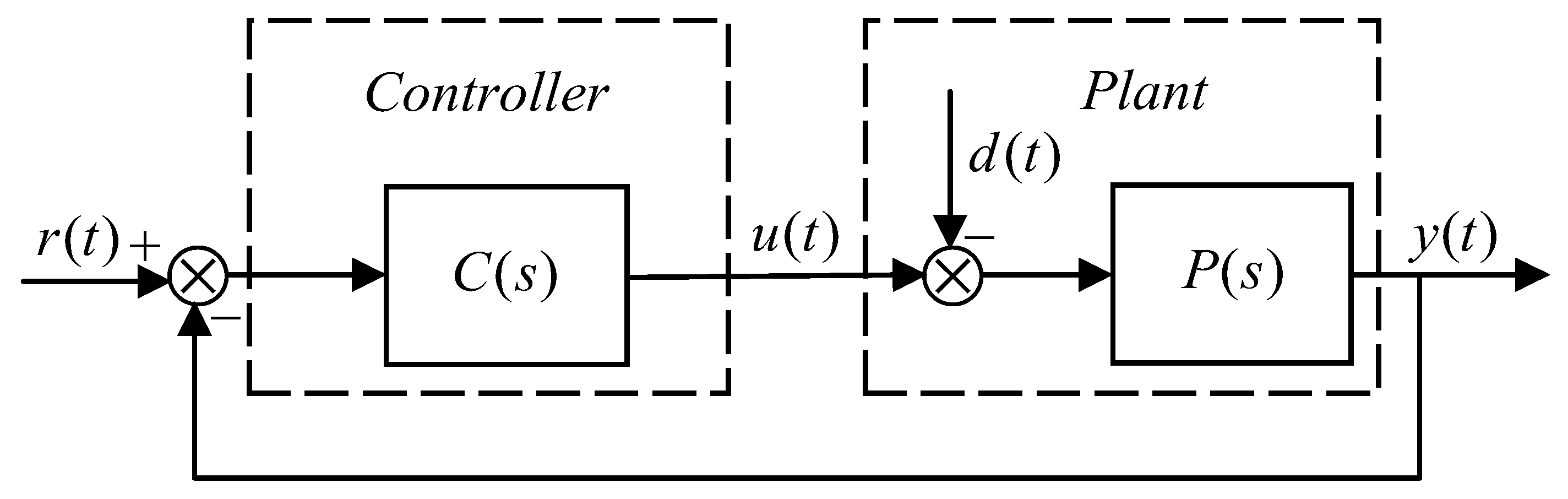
2. System Models and Robustness Design
2.1. System Models
2.2. Robustness Design of Controller
3. Parameter Tuning of PID Controllers
4. Parameter Tuning of PIDD2 Controllers
- (1)
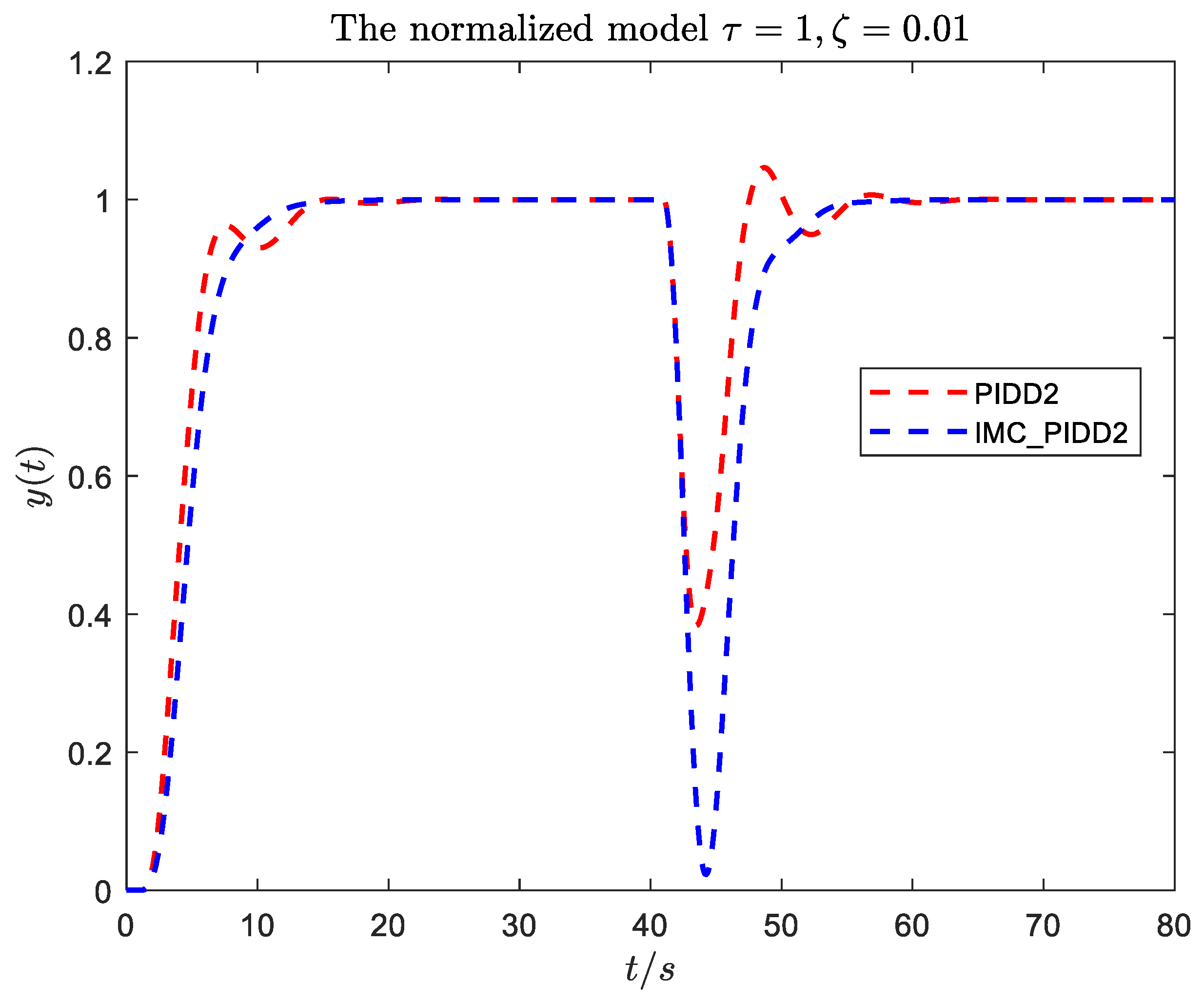
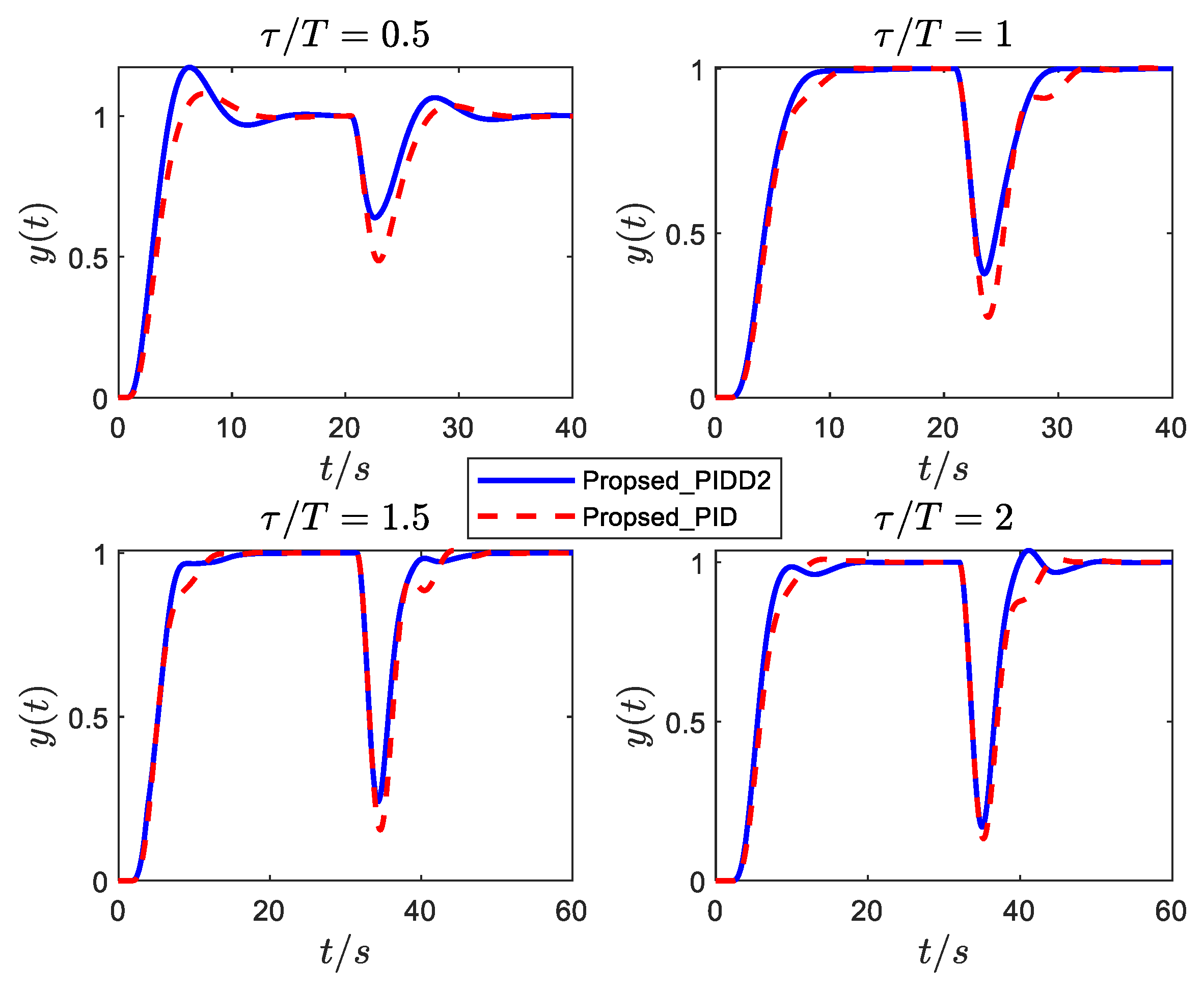
- The control performance (especially disturbance rejection performance) of the proposed PIDD2 is improved compared with that of PID.
- (2)
- The control performance of PIDD2 has no significant advantage over the proposed PID as the increases. Therefore, PIDD2 can improve the performance of PID for SOPDT systems with small delay; however, for large delay, the control improvement of PIDD2 is not noticeable.
5. Application in Power System Control
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albatran, S.; Smadi, I.A.; Bataineh, H.A. Generalized Optimal and Explicit PI/PID Tuning Formulas for Underdamped Second-order Systems. Int. J. Control Autom. Syst. 2020, 18, 1023–1032. [Google Scholar] [CrossRef]
- Kim, M.; Lee, S.-U. PID with a Switching Action Controller for Nonlinear Systems of Second-order Controller Canonical Form. Int. J. Control Autom. Syst. 2021, 19, 2343–2356. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Zhang, Y.-J.; He, X.-L.; Gao, Z.-J. Adaptive PID Control and Its Application Based on a Double-Layer BP Neural Network. Processes 2021, 9, 1475. [Google Scholar] [CrossRef]
- Chao, C.-T.; Sutarna, N.; Chiou, J.-S.; Wang, C.-J. An optimal fuzzy PID controller design based on conventional PID control and nonlinear factors. Appl. Sci. 2019, 9, 1224. [Google Scholar] [CrossRef] [Green Version]
- Halikias, G.D.; Zolotas, A.C. Optimal design of PID controllers using the QFT method. IEE Proc. Control Theory Appl. 1999, 146, 585–589. [Google Scholar]
- Chevalier, A.; Francis, C.; Copot, C.; Ionescu, C.M.; De Keyser, R. Fractional-order PID design: Towards transition from state-of-art to state-of-use. ISA Trans. 2019, 84, 178–186. [Google Scholar] [CrossRef]
- Gundes, A.N.; Ozguler, A.B. PID Stabilization of MIMO Plants. IEEE Trans. Autom. Control 2007, 52, 1502–1508. [Google Scholar] [CrossRef]
- Huey, J.R.; Sorensen, K.L.; Singhose, W.E. Useful applications of closed-loop signal shaping controllers. Control Eng. Pract. 2008, 16, 836–846. [Google Scholar] [CrossRef]
- Ghorai, P.; Majhi, S.; Kasi, V.R.; Pandey, S. Parameter Identification of Delayed Under-Damped Systems Using On-Line Relay Autotuning. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1197–1201. [Google Scholar] [CrossRef]
- Ghorai, P.; Majhi, S.; Pandey, S. Closed-loop Relay Experiment for Modeling of Underdamped Plant Dynamics. In Proceedings of the 2019 Fifth Indian Control Conference (ICC), New Delhi, India, 9–11 January 2019; pp. 424–429. [Google Scholar]
- Singhose, W.; Seering, W. Control of flexible manipulators with input shaping techniques. In Flexible Robot Manipulators: Modelling, Simulation and Control; The Institution of Engineering and Technology: Stevenage, UK, 2008. [Google Scholar]
- Tan, W. Tuning of PID load frequency controller for power systems. Energy Convers. Manag. 2009, 50, 1465–1472. [Google Scholar] [CrossRef]
- Fu, C.; Tan, W. Decentralised load frequency control for power systems with communication delays via active disturbance rejection. IET Gener. Transm. Distrib. 2018, 12, 1397–1403. [Google Scholar] [CrossRef]
- Singer, N.C.; Seering, W.P. Preshaping command inputs to reduce system vibration. J. Dyn. Syst. Meas. Control 1990, 112, 76–82. [Google Scholar] [CrossRef]
- Singhose, W. Command shaping for flexible systems: A review of the first 50 years. Int. J. Precis. Eng. Manuf. 2009, 10, 153–168. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, W.; Cui, W. Tuning of linear active disturbance rejection controllers for second-order underdamped systems with time delay. ISA Trans. 2021, 118, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Tan, W.; Cui, W.; Han, W.; Guo, Q. Linear active disturbance rejection control for oscillatory systems with large time-delays. J. Frankl. Inst. 2021, 358, 6240–6260. [Google Scholar] [CrossRef]
- Vrančić, D.; Oliveira, P.M. Design of feedback control for underdamped systems. IFAC Proc. Vol. 2012, 45, 98–103. [Google Scholar] [CrossRef]
- Ho, W.K.; Hang, C.C.; Zhou, J. Self-tuning PID control of a plant with under-damped response with specifications on gain and phase margins. IEEE Trans. Control Syst. Technol. 1997, 5, 446–452. [Google Scholar]
- Wang, Q.-G.; Lee, T.-H.; Fung, H.-W.; Bi, Q.; Zhang, Y. PID tuning for improved performance. IEEE Trans. Control Syst. Technol. 1999, 7, 457–465. [Google Scholar] [CrossRef]
- Shen, J.-C. Fuzzy neural networks for tuning PID controller for plants with underdamped responses. IEEE Trans. Fuzzy Syst. 2001, 9, 333–342. [Google Scholar] [CrossRef]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.-P.; Lee, M.-W.; Chen, C.-L. Inverse-based design for a modified PID controller. J. Chin. Inst. Chem. Eng. 2000, 31, 225–236. [Google Scholar]
- Lee, Y.; Park, S.; Lee, M.; Brosilow, C. PID controller tuning for desired closed-loop responses for SI/SO systems. AIChE J. 1998, 44, 106–115. [Google Scholar] [CrossRef]
- Chen, D.; Seborg, D.E. PI/PID Controller Design Based on Direct Synthesis and Disturbance Rejection. Ind. Eng. Chem. Res. 2002, 41, 4807–4822. [Google Scholar] [CrossRef]
- Ho, S.-J.; Shu, L.-S.; Ho, S.-Y. Optimizing fuzzy neural networks for tuning PID controllers using an orthogonal simulated annealing algorithm OSA. IEEE Trans. Fuzzy Syst. 2006, 14, 421–434. [Google Scholar] [CrossRef]
- Malwatkar, G.M.; Sonawane, S.H.; Waghmare, L.M. Tuning PID controllers for higher-order oscillatory systems with improved performance. ISA Trans. 2009, 48, 347–353. [Google Scholar] [CrossRef]
- Eris, O.; Kurtulan, S. A direct digital PID tuning rule for SOPDT systems. In Proceedings of the 2012 2nd Australian Control Conference, Sydney, NSW, Australia, 15–16 November 2012; pp. 66–69. [Google Scholar]
- Kurokawa, R.; Sato, T.; Vilanova, R.; Konishi, Y. Design of optimal PID control with a sensitivity function for resonance phenomenon-involved second-order plus dead-time system. J. Frankl. Inst. 2020, 357, 4187–4211. [Google Scholar] [CrossRef]
- Panda, R.C.; Yu, C.-C.; Huang, H.-P. PID tuning rules for SOPDT systems: Review and some new results. ISA Trans. 2004, 43, 283–295. [Google Scholar] [CrossRef]
- McFarlane, D.C.; Glover, K. Robust Controller Design Using Normalized Coprime Factor Plant Descriptions; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Koley, I.; Sarkar, B.; Datta, A.; Panda, G.K. Load Frequency Control of a Wind Energy Integrated Multiarea Power System With CSA Tuned PIDD Controller. In Proceedings of the 2020 IEEE First International Conference on Smart Technologies for Power, Energy and Control (STPEC), Nagpur, India, 25–26 September 2020; pp. 1–6. [Google Scholar]
- Izvoreanu, B.; Cojuhari, I. The Tuning of the PID and PIDD2 Algorithms to the Model Objects with Inertia and Identical Elements and Time Delay. 2013. Available online: http://repository.utm.md/handle/5014/17375 (accessed on 12 June 2023).
- Sonkar, P.; Rahi, O.P. Unified tuning of PID-derivative filter load frequency controller for two area interconnected system including wind power plant. In Proceedings of the 2016 IEEE Uttar Pradesh Section International Conference on Electrical, Computer and Electronics Engineering (UPCON), Varanasi, India, 9–11 December 2016; pp. 388–393. [Google Scholar]
- Chatterjee, S.; Dalel, M.A.; Palavalasa, M. Design of PID plus second order derivative controller for automatic voltage regulator using whale optimizatio algorithm. In Proceedings of the 2019 3rd International Conference on Recent Developments in Control, Automation & Power Engineering (RDCAPE), Noida, India, 10–11 October 2019; pp. 574–579. [Google Scholar]
- Mohanty, B. Performance analysis of moth flame optimization algorithm for AGC system. Int. J. Model. Simul. 2019, 39, 73–87. [Google Scholar] [CrossRef]
- Mohanty, B. Hybrid flower pollination and pattern search algorithm optimized sliding mode controller for deregulated AGC system. J. Ambient Intell. Humaniz. Comput. 2020, 11, 763–776. [Google Scholar] [CrossRef]
- Kalyan, C.N.s. UPFC and SMES based Coordinated Control Strategy for Simultaneous Frequency and Voltage Stability of an Interconnected Power System. In Proceedings of the 2021 1st International Conference on Power Electronics and Energy (ICPEE), Bhubaneswar, India, 2–3 January 2021; pp. 1–6. [Google Scholar]
- Hu, X.; Hou, G.; Tan, W. Tuning of PIDD2 controllers for oscillatory systems with time delays. Front. Control Eng. 2023, 3, 32. [Google Scholar]
- Segovia, V.R.; Hagglund, T.; Astrom, K.J. Noise filtering in PI and PID Control. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 1763–1770. [Google Scholar]
- Zhang, B.; Tan, W.; Li, J. Tuning of linear active disturbance rejection controller with robustness specification. ISA Trans. 2019, 85, 237–246. [Google Scholar] [CrossRef]
- Veinović, S.; Stojić, D.; Ivanović, L. Optimized PIDD2 controller for AVR systems regarding robustness. Int. J. Electr. Power Energy Syst. 2023, 145, 108646. [Google Scholar] [CrossRef]
- Kumar, M.; Hote, Y.V. PIDD2 Controller Design Based on Internal Model Control Approach for a Non-Ideal DC-DC Boost Converter. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021; pp. 1–6. [Google Scholar]
- Jayasinghe, S.G.; Vilathgamuwa, D.M.; Madawala, U.K. Direct integration of battery energy storage systems in distributed power generation. IEEE Trans. Energy Convers. 2011, 26, 677–685. [Google Scholar] [CrossRef]
- de Souza Ribeiro, L.A.; Saavedra, O.R.; De Lima, S.L.; de Matos, J. Isolated micro-grids with renewable hybrid generation: The case of Lençóis island. IEEE Trans. Sustain. Energy 2010, 2, 1–11. [Google Scholar] [CrossRef]
- Pham, T.N.; Trinh, H.; Van Hien, L. Load frequency control of power systems with electric vehicles and diverse transmission links using distributed functional observers. IEEE Trans. Smart Grid 2015, 7, 238–252. [Google Scholar] [CrossRef]






| 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | |||
|---|---|---|---|---|---|---|---|
| 0.8 | Ho [19] | = 2.6742 | 2.2971 | 2.1900 | 2.1387 | 2.1099 | 2.0913 |
| ITAE = 167.8861 | 147.0132 | 134.4632 | 126.8786 | 122.2789 | 119.6878 | ||
| Maclaurin [30] | = 10.2749 | 20.4934 | 8.2138 | 6.4983 | 5.4516 | 4.9848 | |
| ITAE = 181.0100 | 152.0334 | 134.7830 | 123.8297 | 116.3050 | 111.0823 | ||
| Chen [25] | = 15.2057 | 21.0351 | 7.8210 | 5.2678 | 4.2224 | 3.6717 | |
| ITAE = 163.0601 | 142.4455 | 128.8943 | 120.5432 | 115.5798 | 112.6540 | ||
| Huang [23] | = 3.2782 | 2.8444 | 2.6859 | 2.6020 | 2.5550 | 2.5224 | |
| ITAE = 176.2622 | 153.3725 | 139.1954 | 130.1162 | 123.8912 | 119.4415 | ||
| 1.2 | Ho [19] | = 2.1639 | 2.0346 | 2.0047 | 2.0090 | 2.0156 | 2.0187 |
| ITAE = 170.7906 | 151.0417 | 140.0866 | 134.2907 | 131.5404 | 130.7761 | ||
| Maclaurin [30] | = 4.3237 | 33.6121 | 11.5089 | 6.5598 | 5.4500 | 4.7244 | |
| ITAE = 219.7949 | 189.0479 | 165.3703 | 148.7675 | 137.2231 | 129.2231 | ||
| Chen [25] | = 1.9443 | 3.6429 | 3.0389 | 2.3784 | 2.0517 | 1.9003 | |
| ITAE = 152.5156 | 143.8841 | 140.3592 | 138.5792 | 137.1669 | 135.8013 | ||
| Huang [23] | = 2.9966 | 2.6885 | 2.5766 | 2.5183 | 2.4856 | 2.4641 | |
| ITAE = 171.4444 | 154.4553 | 144.0193 | 137.7687 | 133.8287 | 131.1532 | ||
| 1.6 | Ho [19] | = 1.9820 | 1.9861 | 1.9913 | 1.9962 | 2.0005 | 2.0042 |
| ITAE = 169.3500 | 151.5267 | 142.8030 | 139.5709 | 139.8092 | 140.5478 | ||
| Maclaurin [30] | = 3.4187 | 13.9663 | 10.0828 | 6.1866 | 4.8760 | 4.2371 | |
| ITAE = 220.5395 | 193.8723 | 172.8015 | 157.2165 | 146.3086 | 138.7042 | ||
| Chen [25] | = 2.5808 | 2.2093 | 2.1180 | 2.0634 | 1.9639 | 1.9684 | |
| ITAE = 160.6442 | 158.0982 | 156.4578 | 154.9632 | 153.5713 | 152.2662 | ||
| Huang [23] | = 2.8441 | 2.6061 | 2.5199 | 2.4760 | 2.4519 | 2.4356 | |
| ITAE = 167.8376 | 152.6414 | 144.7046 | 141.1966 | 139.7917 | 138.8289 | ||
| 2.0 | Ho [19] | = 1.9948 | 1.9964 | 1.9982 | 2.0001 | 2.0019 | 2.0036 |
| ITAE = 167.7916 | 152.2218 | 147.2653 | 147.2348 | 147.8758 | 148.5063 | ||
| Maclaurin [30] | = 5.6069 | 17.3869 | 6.7806 | 4.8391 | 4.0691 | 3.6961 | |
| ITAE = 210.8966 | 188.2239 | 170.9862 | 158.5524 | 149.8659 | 143.8656 | ||
| Chen [25] | = 2.7157 | 2.5561 | 2.4301 | 2.3322 | 2.2574 | 2.2047 | |
| ITAE = 171.0477 | 169.3779 | 167.9577 | 166.6392 | 165.3989 | 164.2274 | ||
| Huang [23] | = 2.7512 | 2.5563 | 2.4891 | 2.4548 | 2.4340 | 2.4202 | |
| ITAE = 165.9403 | 151.9473 | 146.8995 | 145.7931 | 145.4290 | 145.2653 |
| Methods | Controller Parameters | Disturbance Rejection | Robustness Index | ITAE Index | ||||
|---|---|---|---|---|---|---|---|---|
| % | ||||||||
| PIDD2 | 0.0028 | 0.2218 | 0.5467 | 0.2217 | 10.5 | 60 | 2.5106 | 1.063 × 10³ |
| IMC_PIDD2 | −0.3954 | 0.1238 | 0.2618 | −0.0187 | 14.7 | 97 | 3.1120 | 2.103 × 10³ |
| System Parameters | Methods | Controller Parameters | Disturbance Rejection | Robustness Index | ITAE Index | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| % | |||||||||||
| G1 | 0.4911 | 0.8370 | 1.1207 | Proposed_PID | 2.5314 | 1.9243 | 3.5821 | 8.5894 | 7.1 | 2.1349 | 121.0161 |
| Malwatkar_PID [27] | 1.3039 | 1.3104 | 1.3351 | 8.328 | 10.18 | 1.8672 | 164.6253 | ||||
| Wang_PID [20] | 1.503 | 1.366 | 1.715 | 10.287 | 8.96 | 1.7707 | 155.7447 | ||||
| Huang_PID [23] | 2.9570 | 2.6864 | 3.3740 | 8.724 | 8.07 | 2.4594 | 116.8912 | ||||
| Ho_PID [19] | 2.147 | 1.484 | 0.777 | 14.756 | 9.96 | 2.7118 | 193.5172 | ||||
| G2 | 0.4927 | 1.8540 | 0.7927 | Proposed_PID | 20.7364 | 26.0712 | 22.8381 | 4.7 | 0 | 2.4471 | 13.1827 |
| Wang_PID [20] | 17.562 | 22.485 | 14.13 | 4.86 | 0 | 2.3796 | 13.1787 | ||||
| Huang_PID [23] | 17.342 | 22.203 | 13.953 | 4.88 | 0 | 2.3956 | 13.5873 | ||||
| Ho_PID [19] | 13.712 | 17.051 | 10.715 | 4.82 | 0 | 2.0124 | 16.3049 | ||||
| G3 | 0.4154 | 2.3 | 3.2024 | Proposed_PID | 0.5858 | 0.1553 | 2.3418 | 43.7 | 40 | 3.0569 | 3.86 × 103 |
| Huang_PID [23] | 0.5784 | 0.2174 | 2.2294 | 47.1925 | 36 | 3.0657 | 5.32 × 103 | ||||
| Ho_PID [19] | 0.4950 | 0.1669 | 1.7121 | 44.82 | 43.5 | 2.4928 | 5.14 × 103 | ||||
| G4 | 0.13 | 0.37 | 0.7692 | Proposed_PID | −0.0196 | 0.4743 | 0.7879 | 10.0878 | 44.8 | 2.1503 | 393.2047 |
| Kurokawa_PID [29] | 0.0932 | 0.2903 | 0.2311 | 17.6833 | 58.2 | 2.1007 | 939.5594 | ||||
| Huang_PID [23] | 0.3003 | 1.5015 | 0.8885 | 24.6275 | 39.1 | 2.9645 | 1.326 × 103 | ||||
| Ho_PID [19] | 0.3565 | 1.1531 | 0.6823 | 19.0112 | 39.2 | 2.5466 | 844.5659 | ||||
| System Parameters | Methods | Controller Parameters | Disturbance Rejection | Robustness Index | ITAE Index | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % | ||||||||||||
| G5 | 0.1999 | 0.2 | 0.4468 | PIDD2 PID | 0.4533 0.0136 | 1.4191 0.7958 | 0.6539 0.44 | 0.0558 | 3.11 6.72 | 23.8 40 | 1.7173 1.7548 | 102.1007 181.4656 |
| G6 | 0.3650 | 0.48 | 0.8111 | PIDD2 PID | 0.1835 −0.083 | 0.4920 0.3380 | 0.8813 0.6093 | 0.1726 | 12.482 15.721 | 33.4 42.9 | 1.6918 1.9740 | 575.9491 888.3398 |
| G7 | 0.2289 | 0.4 | 0.1207 | PIDD2 PID | −0.232 −0.812 | 5.7124 4.5834 | −0.081 −0.106 | 0.0045 | 3.5782 4.0958 | 16 16 | 3.5385 3.5748 | 16.3339 21.6371 |
| G8 | 0.6 | 2.2 | 0.4775 | PIDD2 PID | 0.5191 0.2080 | 0.5211 0.4661 | 0.2224 0.1247 | 0.0746 | 32.006 36.163 | 53.9 53.9 | 5.5247 5.9557 | 2.36 × 103 3.96 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Tan, W.; Hou, G. Tuning of PID/PIDD2 Controllers for Second-Order Oscillatory Systems with Time Delays. Electronics 2023, 12, 3168. https://doi.org/10.3390/electronics12143168
Hu X, Tan W, Hou G. Tuning of PID/PIDD2 Controllers for Second-Order Oscillatory Systems with Time Delays. Electronics. 2023; 12(14):3168. https://doi.org/10.3390/electronics12143168
Chicago/Turabian StyleHu, Xingqi, Wen Tan, and Guolian Hou. 2023. "Tuning of PID/PIDD2 Controllers for Second-Order Oscillatory Systems with Time Delays" Electronics 12, no. 14: 3168. https://doi.org/10.3390/electronics12143168
APA StyleHu, X., Tan, W., & Hou, G. (2023). Tuning of PID/PIDD2 Controllers for Second-Order Oscillatory Systems with Time Delays. Electronics, 12(14), 3168. https://doi.org/10.3390/electronics12143168





