A Block-Based Concatenated LDPC-RS Code for UAV-to-Ground SC-FDE Communication Systems

Abstract

To enhance the reliability of UAV-to-Ground data transmission in SC-FDE, this study proposes a combined MMSE equalization and LDPC-RS concatenated code approach, utilizing source redundancy to mitigate errors in low-elevation G2A communication. The proposed coding scheme combines a binary LDPC code as the outer code and an improved RS code as the inner code, resulting in improved resistance to burst and random errors. To address the coding aspect, this paper designs a coding table using RS coding as the underlying logic, enabling efficient coding. For decoding, a decoding scheme based on the minimum Euclidean distance criterion is devised, enabling high-performance decoding. Simulation results demonstrate that the proposed LDPC-RS concatenated coding scheme significantly enhances the performance of the communication system, thereby offering considerable potential for application in UAV video transmission systems.

1. Introduction

In recent years, unmanned aerial vehicle (UAV) communication has undergone significant development in various applications [1] and is widely used in traffic monitoring, emergency rescue, navigation, tracking, and military reconnaissance as a new aeronautical communication system [2,3,4,5]. Due to the high flexibility and strong mobility of drones, they can assist in completing tasks that are challenging for humans and accessing areas that are difficult to reach due to the lack of physical infrastructure [6]. Therefore, establishing a reliable UAV communication link is crucial. The UAV data transmission system is a typical wireless communication system. During transmission, factors such as long communication distance, complex topography, a mobile station’s moving speed, and a complex propagation path can result in severe multipath fading and Doppler frequency shift, which significantly impact the performance of the wireless communication system and reduce the reliability of UAV communication. Consequently, extensive research is currently focused on improving drone data transmission. Additionally, the security aspects of drone communications and the optimal deployment of the drone-BS (base station) are also important areas of study. However, this paper primarily focuses on the reliability of drone communications, and readers can refer to the references [7,8,9,10] for research on the security of drone communications.

Inter-symbol interference (ISI) channels are common in communication systems and can significantly degrade performance [11]. To combat ISI, orthogonal frequency division multiplexing (OFDM) modulation [12,13] is often used. However, OFDM systems have high peak-to-average power ratios, which can result in low power amplifier efficiency. Additionally, OFDM systems are highly sensitive to phase noise and carrier frequency offset [14]. Recently, there has been increased interest in single-carrier frequency-domain equalization (SC-FDE) as an alternative to OFDM. SC-FDE offers similar performance, efficiency, and low signal processing complexity advantages as OFDM, while being less sensitive to radio frequency impairments such as power amplifier nonlinearities. By performing operations in the frequency domain through the discrete Fourier transform (DFT), the complexity of processing can be reduced. High data rates and error-rate performance approaching theoretical limits are important trends in digital wireless communication, particularly in aeronautical communication. However, when aircraft encounter complex terrain such as mountains, forests, or artificial buildings, or when they are in a state of rapid maneuver, the communication performance of certain types of airborne data links deteriorates sharply, leading to a sharp increase in bit error rate and equipment disconnection from the network. Therefore, it is urgent to take measures to improve the reliability of the system and ensure continuous equipment connectivity. Furthermore, the use of SC-FDE systems in UAV-to-Ground communication processes is advantageous because single-carrier modulation can achieve better communication performance with less power [15,16].

In a ground-to-air data transmission system, an equalizer is commonly used to reduce ISI between codes, while channel coding is employed to combat interference and noise. The equalizer can be seen as the inverse filter of the channel, with transmission characteristics that are opposite to those of the channel. By compensating for channel-induced distortion and combining with channel coding, the equalizer enhances the reliability and performance of information transmission. Forney proposed concatenated coding in 1966 to address the issue of increasing complexity and hardware cost with longer codes [17]. Concatenated codes can leverage the advantages of various coding techniques, learn from each other, and meet the requirements of error-resistant communication in complex channels. They combine two short component codes with low decoding complexity to construct longer codes, resulting in low computational complexity and strong error-correcting capabilities [18]. The existing literature has proposed several application cases of concatenated codes. For instance, a coding method called RS-CC, which concatenates RS outer code with convolutional code as the inner code, has been proposed [19,20]. The RS code can correct error bits that may remain after decoding the convolutional code, thereby improving the demodulation performance of received signal data in complex multipath environments. Additionally, a rate-compatible LDPC-RS product code structure has been proposed for terrestrial digital broadcasting transmission systems [21]. This decoding scheme adjusts the sequence of different decoding technologies and performs error estimation and soft value modification at appropriate stages, significantly improving error performance in low signal-to-noise ratio regions compared to simple LDPC and RS splicing decoding. It also reduces computational complexity in medium and high signal-to-noise ratio regions.

Considering the fast and low-delay transmission requirements of the current UAV video transmission system, it is necessary to further reduce the system latency, decoding complexity, and hardware utilization rate of each module. At this point, the construction of anti-interference and error-correcting ability of LDPC-RS cascade coding technology is a potential solution to achieve this goal. RS-LDPC code was first introduced in [22], which has a large girth and good performance. A low-density parity-check (LDPC) is a kind of linear block code with a sparse check matrix proposed by Gallager in 1963 [23]. It was further studied in 1996 by D MacKay, M Neal, and others, who found that LDPC codes can provide remarkable performance close to the Shannon limit and are among the best candidates for error control in systems requiring high reliability and efficiency. Because of this, several scholars have conducted extensive research on LDPC code [24,25,26]. RS code is a multi-base code that can correct multiple consecutive binary error codes. For wireless communication transmission, the RS code has a strong ability to correct errors and performs well in combating burst errors. On the other hand, the LDPC code takes full advantage of the channel’s soft information and performs well in combating random errors. They can play a key role in combating interference.

To ensure robust anti-interference transmission capability for real-time UAV video streaming, the adoption of several key technologies is necessary, with error correction codes playing a crucial role. Traditionally, in receivers, equalization and decoding are treated as independent functional modules that jointly perform signal detection. However, from an information processing perspective, processing equalization and decoding independently may result in information loss. Therefore, an optimal detection approach combines equalization and decoding to achieve higher performance gains. Presently, most of the literature simulates RS decoding using traditional hard decision decoding, where the demodulator solely decodes binary code words as either 0 or 1. This hard decision mode can cause loss of statistical information regarding channel interference contained in the signal when the decision threshold is greater than 1 or less than 0. To improve the accuracy of code word determination, it is necessary to consider the balanced signal information before inputting it into the demodulator. The soft decision concept involves sending the balanced signal information first into the demodulator, creating a simple 0 or 1 bit stream, and subsequently passing it to the decoder for algebraic decoding. The approach of joint equalization and channel decoding has been explored in the prior literature. The authors of [27] propose a joint equalization and channel decoding (JECD) method to overcome inter-code crosstalk caused by the multipath effect in underwater acoustic channels. This method achieves joint optimization of channel equalization and channel decoding with linear complexity, yielding improved equalization and decoding performance under measured conditions. The proposed JECD method also provides a low-complexity solution for source-channel joint decoding.

In order to enable the UAV image transmission or data transmission system to obtain better and more stable performance and user experience, based on the statistical characteristics of unmanned aerial vehicle (UAV) ground-to-air multipath channel fading, the reliable coding technology of UAV ground-to-air communication channel was studied in view of the unreliable transmission of low-altitude and multipath effects and the movement of UAV. Based on the dual coding model theory of the channel, a coding framework with LDPC code outside and RS code inside is constructed, which breaks through the error-resistant capability of complex multi-path channels with low elevation, improves system redundancy, and provides effective support for reliable data transmission of UAV-to-Ground.

The main contributions of the block-based concatenated LDPC-RS Code for UAV-to-Ground SC-FDE communication systems proposed in this paper are summarized as follows:

• The information loss caused by equalization and decoding is reduced, and the performance gain is higher by combining equalization and decoding.
• A LDPC-RS concatenated coding and decoding scheme based on minimum Euclidean-distance criterion is proposed.
• The proposed block-based LDPC-RS concatenated encoding and decoding scheme based on minimum Euclidian distance decoding greatly improves the performance of the UAV ground-to-air communication system.

The remainder of this paper is organized as follows. In Section 2, the UAV communication scenario and SC-FDE system is briefly described. In Section 3, we introduce the coding method and implementation process of LDPC-RS. In Section 4, reports the simulation results and analysis. Finally, we draw the conclusion in Section 5.

2. UAV Communication Scenario and SC-FDE System

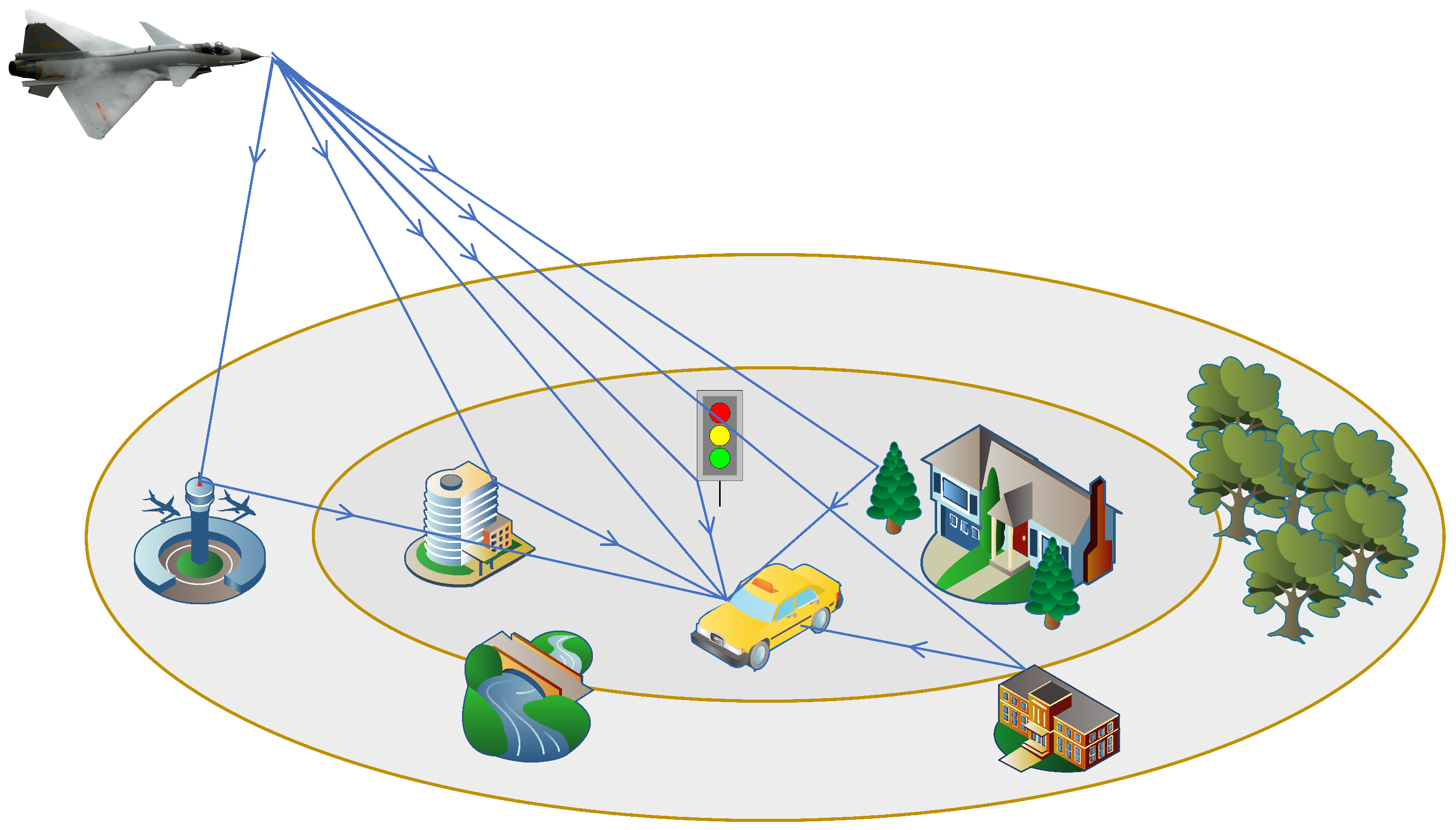
UAVs (unmanned aerial vehicles) or drones as they are popularly known are paving their ways into different fields of applications, which has led to their increased presence in the consumer market. Drones help us in reaching areas difficult to access often because of the lack of physical infrastructure. As a consequence, drones are often used for critical operations such as rescue, surveillance, transportation in various types of fields, including agriculture, forestry, environmental protection, and security. Other than that, in the military sector, its development followed the rhythm of the great conflicts of the twentieth century. Drones are more economical while avoiding jeopardizing the lives of pilots and deploying ground troops, in particular for reconnaissance, surveillance and targeted attacks. Their use within armies and police forces has become predominant. In the civil sector, many fields have seen drones give rise to new applications thanks to their ability to embed cameras, infrared cameras or environmental sensors. Typical application scenarios of UAV systems are shown in Figure 1.

The UAV communication scenario shown in Figure 1 is a typical urban environment, and it can be seen that the environment encountered by UAV communication is relatively complex. At present, some channel models that have been proposed are more in line with the characteristics of UAV channels, such as HT channel in COST207 standard. In addition, the UAV channel is a time-varying channel, and the transmission loss and transmission delay constantly change with the change of the surrounding environment during operation, and a typical multi-path transmission phenomenon appears. Of course, the focus of this paper is to propose the encoding and decoding algorithm that can eliminate these multipath effects as much as possible. In the following experimental part, we mainly conduct it based on the simulation model.

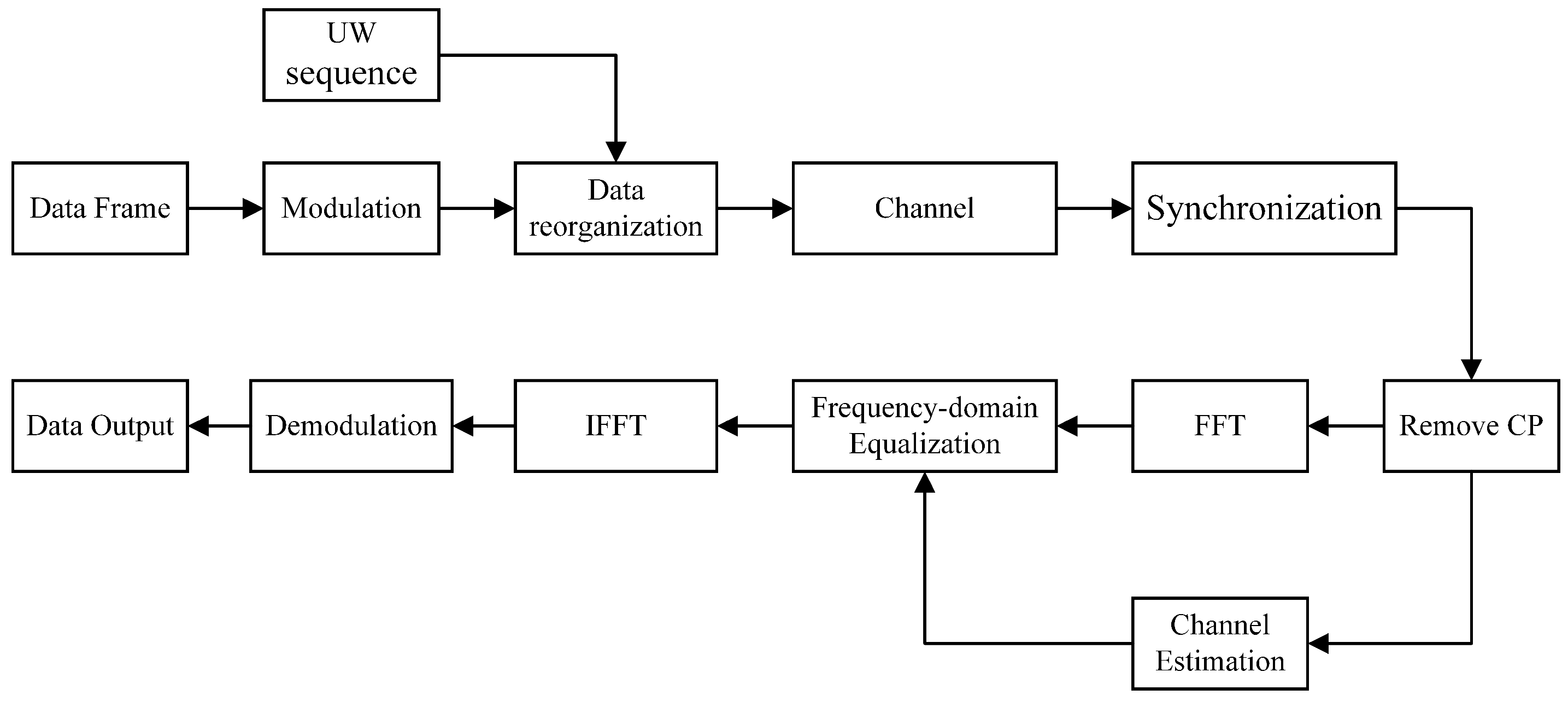
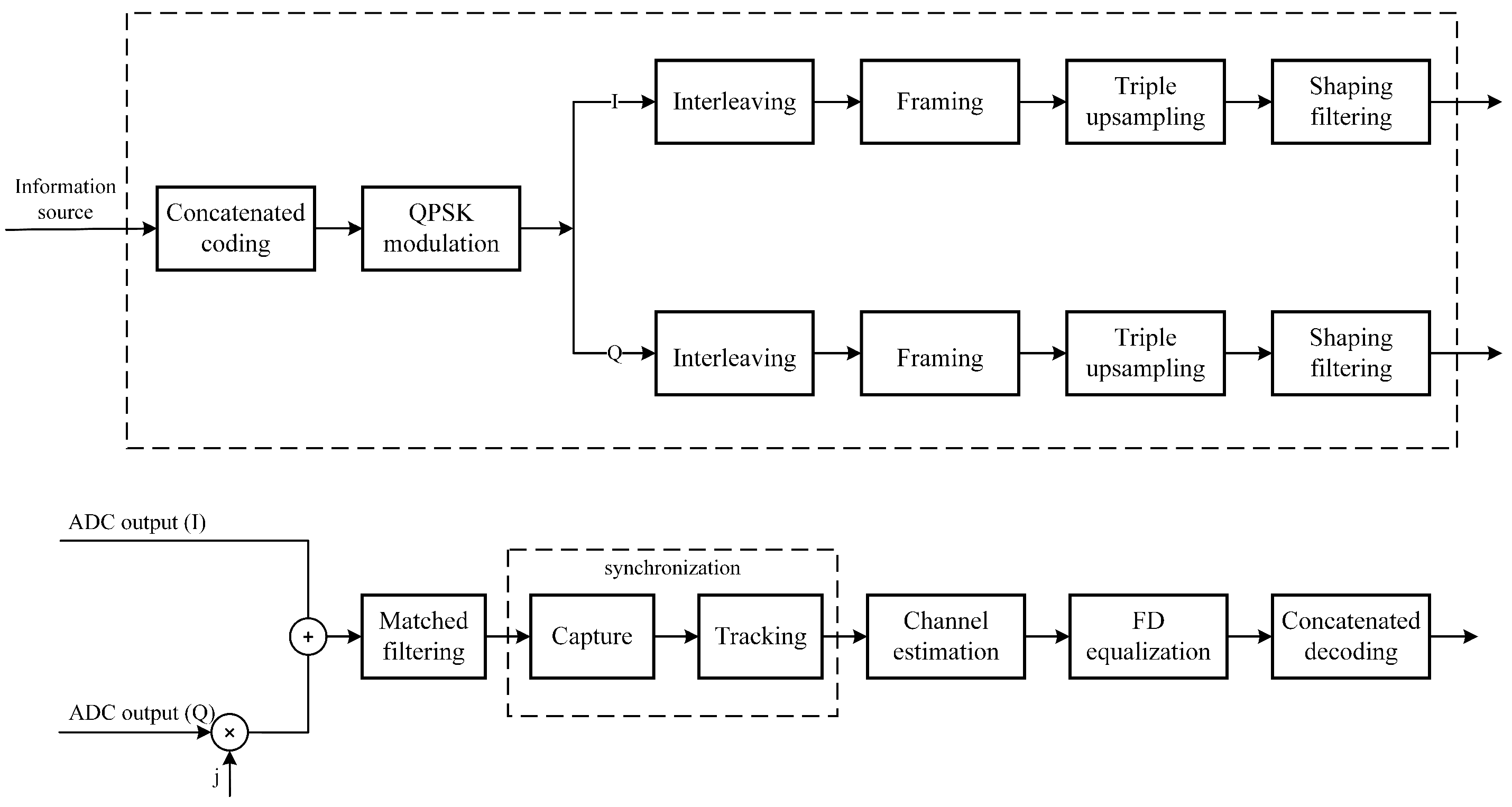
A typical SC-FDE communication system mainly includes synchronization, channel estimation, and frequency equalization. The steps of modulating and combining frames are completed at the transmitter of the system, and synchronization and channel estimation are completed at the receiver of the system. After obtaining relatively accurate channel estimation results in the time domain, the channel response is transformed into the frequency domain by FFT. Then, equalization is completed in the frequency domain and the equalization results are converted back to the time domain through IFFT. Finally, the demodulation is completed and the decision is made to obtain the restored sent data bit stream information. The basic block diagram of the SC-FDE system is illustrated in Figure 2.

At the transmitter, the time-domain samples of one SC-FDE signal can be written as $x\left(n\right)$, ($0\le n\le N-1$). After modulation and CP addition, the signal goes through the mobile radio channel. At the receiver, the signal is received along with noise. After synchronization, down sampling, and CP removal, the baseband model of the received samples can be formulated as

$$y\left(n\right)=\sum _{l=0}^{L-1}x(n-l)h\left(l\right)+w\left(n\right),0\le n\le N-1$$

(1)

where L is the number of sample-spaced channel taps, $x\left(n\right)$ is the transmitted data, $w\left(n\right)$ is the additive white Gaussian noise (AWGN) sample with zero mean and variance of ${\sigma }_w^2$, and $h\left(l\right)$ is the CIR in time domain. After removing the CP, the received signal is transformed into the frequency domain by fast Fourier transform (FFT), the frequency domain signal is written as

$$Y\left(k\right)=X\left(k\right)H\left(k\right)+W\left(k\right),0\le k\le N-1$$

(2)

where $X\left(k\right)$, $Y\left(k\right)$, $H\left(k\right)$ and $V\left(k\right)$ denotes the input signal, output signal, channel frequency response (CFR) and AWGN of the k-th sub-channel, respectively.

The baseband CIR can be described as

$$h\left(t\right)=\sum _{l=0}^{L-1}{\alpha }_l\left(t\right)\delta (\tau -{\tau }_l)$$

(3)

where ${\tau }_l$ is the delay of l-th path and ${\alpha }_l\left(t\right)$ is the complex amplitude of l-th path, which is assumed to be wide-sense-stationary (WSS) complex Gaussian processes and independent between different paths.

3. Construction of LDPC-RS Concatenation Code

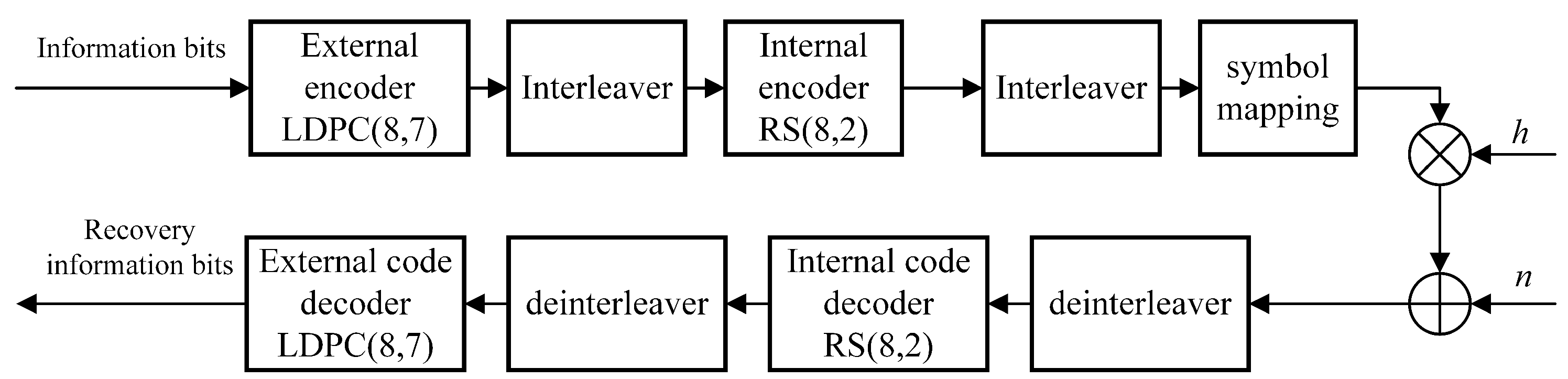
The generation and receiving model of LDPC-RS concatenated code designed in this paper is shown in the Figure 3. The following parts of this section will briefly introduce the encoding and decoding principles of LDPC code and RS code respectively, and focus on the generation and decoding process of LDPC-RS concatenated code proposed in this paper.

3.1. LDPC Coding Technology

As a linear block error correction code, Low-density parity check (LDPC) codes can provide remarkable performance, which is very close to the Shannon limit. Its most basic feature is that the test matrix has sparsity, which means that the number of non-0 in the matrix is far less than the number of 0. The number of non-0 elements in a row in the check matrix is called the row weight, represented by $\rho$, and the number of non-0 elements in each column is called the column weight, represented by $\gamma$. Because of the sparsity of LDPC verification matrix, it has low complexity and high performance of encoding and decoding. Assuming that LDPC code is a linear block code with code length n and information bit length k, and its parity bit length $m=n-k$, the LDPC code can be uniquely defined by its parity matrix H. H is a two-dimensional matrix $m\times n$, whose rows and columns correspond to the check equation and code word of LDPC code respectively, and H and C satisfy the relation $H*C^T=0$. Equation (4) is a check matrix and its check equations.

$$\begin{array}{c}H=\left[\begin{array}{cccccccccc}1& 1& 1& 1& 0& 0& 0& 0& 0& 0\\ 1& 0& 0& 0& 1& 1& 1& 0& 0& 0\\ 0& 1& 0& 0& 1& 0& 0& 1& 1& 0\\ 0& 0& 0& 1& 0& 1& 1& 0& 0& 1\\ 0& 0& 1& 0& 0& 0& 0& 1& 1& 1\end{array}\right]\hfill \\ \to \left\{\begin{array}{c}{c}_1+c_2+c_3+c_4=0\\ c_1+c_5+c_6+c_7=0\\ c_2+c_5+c_8+c_9=0\\ c_4+c_6+c_7+c_{10}=0\\ c_3+c_8+c_9+c_{10}=0\end{array}\right.\hfill \end{array}$$

(4)

LDPC codes are divided into regular LDPC codes and irregular LDPC codes based on whether the row recolumns are the same. If the row recolumns are the same, the LDPC codes are regular LDPC codes; otherwise, the LDPC codes are irregular LDPC codes. Regular LDPC codes can be represented by $\left(N,\gamma ,\rho \right)$, and irregular LDPC codes can be described by degree distribution functions.

The process of Gaussian elimination method in LDPC code is as follows: after a suitable generation matrix G is constructed, the check matrix H is converted into a lower triangular matrix by Gaussian elimination method. Let the dimension of the check matrix G be $M\times N$, and the code word generated after encoding be. The code word can be divided into two parts: system bit and check bit, namely $x=\left(s,p\right)$, where s is the system bit and p is the check bit. The specific encoding steps are as follows:

(1)

The information bit of length k is directly assigned to the system bit s;

(2)

The $i\left(i=1,2,\cdots ,M\right)$-th check bit $p_i$ is obtained by backward recursion.

$$p_i=\sum _{j=1}^{N-M}{H}_{i,j}{s}_j+\sum _{j=1}^{i-1}{H}_{i,j+N-M}{p}_j$$

(5)

3.2. RS Coding Technology

In Galois field GF($2^m$), the symbol RS(n, k) represents: the length of RS code is n, the length of information bit is k, the length of supervision bit is $n-k$, and error correction ability is $(n-k)/2$. If the error-correcting ability is t, then the generated polynomial is constructed as follows:

$$g\left(x\right)=(x-\alpha )(x-{\alpha }^2)\cdots (x-{\alpha }^{2t})$$

(6)

where $\alpha$ is the primitive element in GF(q), we know that the element in GF(q) can be expressed in the form of ${\alpha }^i$.

• RS coding: write the input information code element into a polynomial form $M\left(x\right)$, and generate a polynomial $g\left(x\right)$ composed of minimum polynomials. Then, the output element polynomial of the encoder is:

  $$C\left(x\right)=M\left(x\right)·x^{n-k}+\left(M\left(x\right)·x^{n-k}\right)modg\left(x\right)$$

  (7)

  where $\left(M\left(x\right)·x^{n-k}\right)modg\left(x\right)$ is the supervision element polynomial.
• RS decoding: Iterative decoding algorithm process based on BM (Berlekamp-Massey) is shown in Figure 4:

Figure 4. Iterative decoding algorithm process based on BM (Berlekamp-Massey).

Figure 4. Iterative decoding algorithm process based on BM (Berlekamp-Massey).

Step 1: according to the receiving code R and the check matrix H, the adjoint is calculated as $S^T=H·R^T$;

Step 2: calculate the error position polynomial $\sigma \left(x\right)$ according to the adjoint expression $S\left(s_1,s_2,\cdots ,s_{2t}\right)$, and determine the error position by money search;

Step 3: determine the error value $e_{\gamma 1},e_{\gamma 2},\cdots ,e_{\gamma t}$ and complete error correction.

3.3. Design and Construction of LDPC-RS Concatenation Code

For LDPC coding, considering the needs of transceiver power consumption, cost, and easy implementation, we use binary LDPC code, and the receiver uses the mature minimum sum algorithm for LDPC decoding. The innovation point of this paper is mainly around the design of RS code, so this section focuses on the design and construction of RS code. The parameters of RS code used in this paper are shown in

Table 1. The parameters of RS code used in this paper.

Parameters	Parameter Values
Code length/$f_d$	$n=8$
Information segment	$k=2$
Supervisory section	$2t=6$
Minimum code distance	$D=7$

. The encoding process is consistent with the conventional encoding process. The only difference is that the interleaving operation is added in the encoding process, which makes the anti-interference of the RS code stronger.

The design process of the RS code in this paper is as follows:

Step 1: Select the k symbol sequence $u=\left(u_1,u_2\right)$ of GF($2^m$) domain successively, where $u_1,u_2\in \mathrm{GF}\left(2^m\right)$. Then, there are 256 combinations, that is, there are 256 kinds of information symbol data available to us. The $\left(u_1,u_2\right)$ in the symbol sequence was converted to m bit binary sequence respectively and combined into a set of $2m$ bit binary data.

Step 2: Interweave the bit data obtained in step 1, and then convert it into k decimal data, and encode the obtained decimal data as a message in the RS code structure of $(n,k)$;

Step 3: After the above steps, encoded symbols with length n will be obtained, and all of them belong to GF($2^m$). After the binary conversion and combination of each symbol, a number of binary bits with length $n\times m$ will be obtained. The above operation is performed on all 256 groups of information symbol data, and finally, we get a $256\times (n·m)$ dimension bit matrix, then we get the original table for RS encoding and decoding in the subsequent simulation of this paper.

Step 4: This step illustrates the role of the above original table in the simulation. In the simulation process, we will generate one or more frames of binary bit data, and every eight bits is defined as a small encoding frame. After decimal conversion calculation of the small frame, any value from 0 to 255 will be obtained. At this time, we select the 32-bit data with the number of rows in the original coding table as the encoded bit number, so as to complete the RS coding proposed in this paper.

Step 5: For decoding, the criterion we adopt is the minimum Euclidean distance criterion. Take the receiver using the MMSE equalizer as an example. In the past, the receiver would input the data after the equalizer into the demodulation signal obtained by judging the constellation diagram, and then convert it into binary graduation data, and then send it into the decoder module for decoding. In the decoding scheme proposed in this paper, the traditional demodulation process is abandoned, and the received data is computed line by line with the original table in the way of a coded frame. The final decoding result is determined by the behavior corresponding to the minimum Euclidean distance, and then the row number corresponding to the minimum Euclidean distance is converted into binary bits to obtain the transmitted bit data.

After the above steps, we can get the coding framework of LDPC-RS concatenated code, as shown in Figure 5.

4. Simulation Results

In this section, the simulation assumes that ideal synchronization has been achieved. The evaluation indexes is bit error rate (BER), which is used to verify the influence of the algorithm proposed in this paper on communication quality and reflects the performance of communication system. It should be pointed out that the theoretical curve in the simulation represents the error performance curve of QPSK modulation in the Gaussian white noise channel.

$$BER=\frac{1}{N_r}\sum _{k=1}^{N_r}\left|S_{dk}-S_k\right|$$

(8)

where $S_{dk}$ is the demodulated bit data stream, $S_k$ is the original information bit data stream of transmitter, $S_{dk}$ and $S_k$ are both bit data streams as $010011101\dots$, and $N_r$ is the bit stream data length.

4.1. Error Experiment and Analysis

In this section, we mainly adopt RS (8, 2) encoding mode to compare the performance of table lookup method and algebraic method. We randomly generated one million bits and random error ratio from 0 to 20% in each simulation by using the Monte Carlo simulation idea to repeat the experiment 100 times. Through simulation, error performance curves of the both encoding and decoding methods can be obtained as shown in the Figure 6, so as to observe their error correction performance. As can be seen from the figure, when 10% error is set, it can be improved by four percentage points compared with algebraic method, using the table-lookup method based on the minimum Euclidean distance criterion proposed in this paper, which proves that the table-lookup method proposed in this paper has better error correction performance.

4.2. Decoding Performance Analysis in the Gaussian Channel

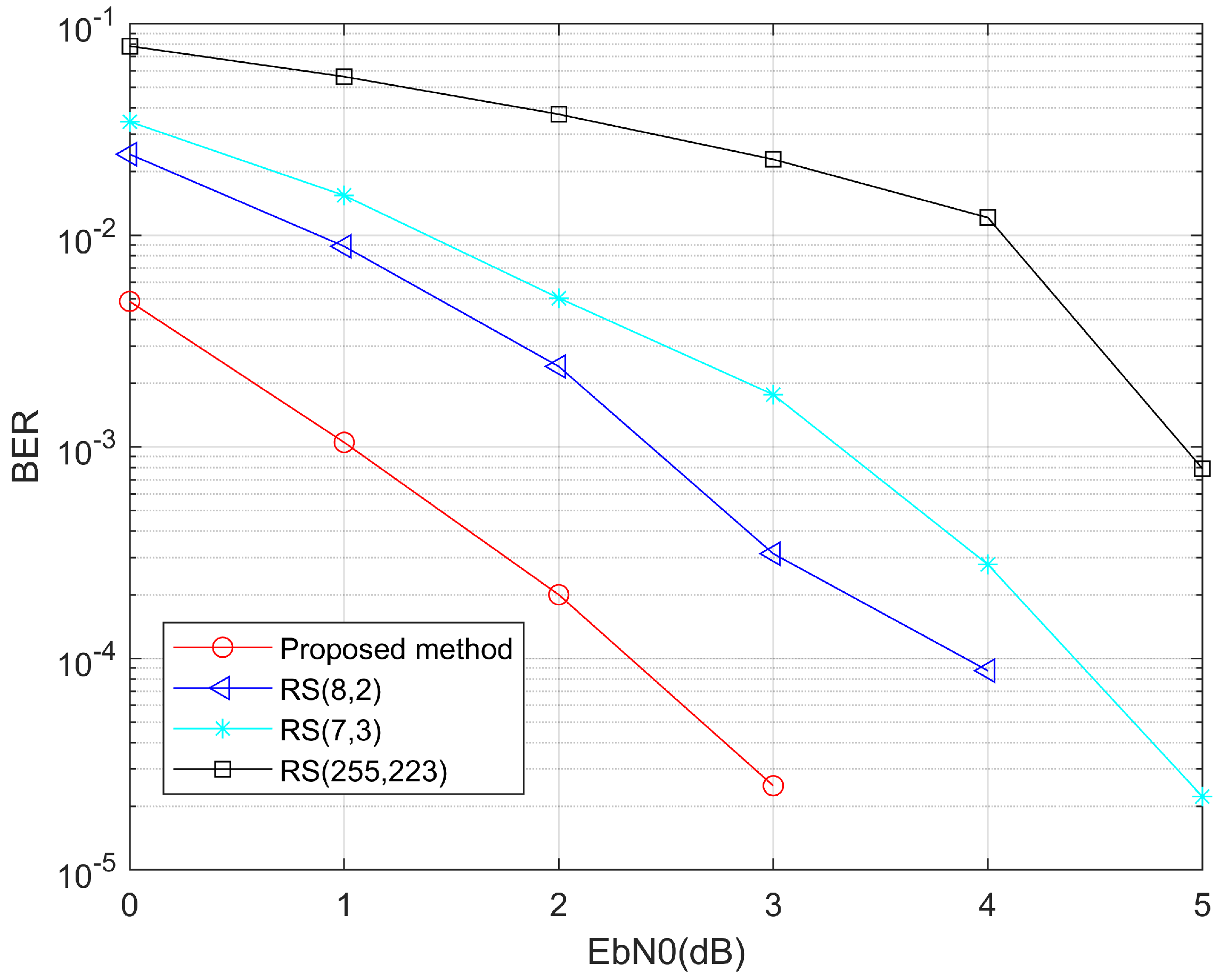
In the simulation, we first observe and analyze the performance of the improved RS encoding and decoding. Three different encoding modes with RS (8, 2), RS (7, 3) and RS (255, 223) are taken as the comparison group, and the decoding method based on the minimum Euclidean distance criterion proposed in this paper is taken as the experimental group. Their error correction performance in the Gaussian white noise channel is observed, and the bit error rate curve is shown in Figure 7. From the bit error rate curve, we find that RS (8, 2) encoding method can obtain better error code performance than the other two encoding methods. In addition, we can also see that the table lookup method based on the minimum Euclidean distance proposed in this paper can further improve the performance of error correction code, and the improved performance is relatively high.

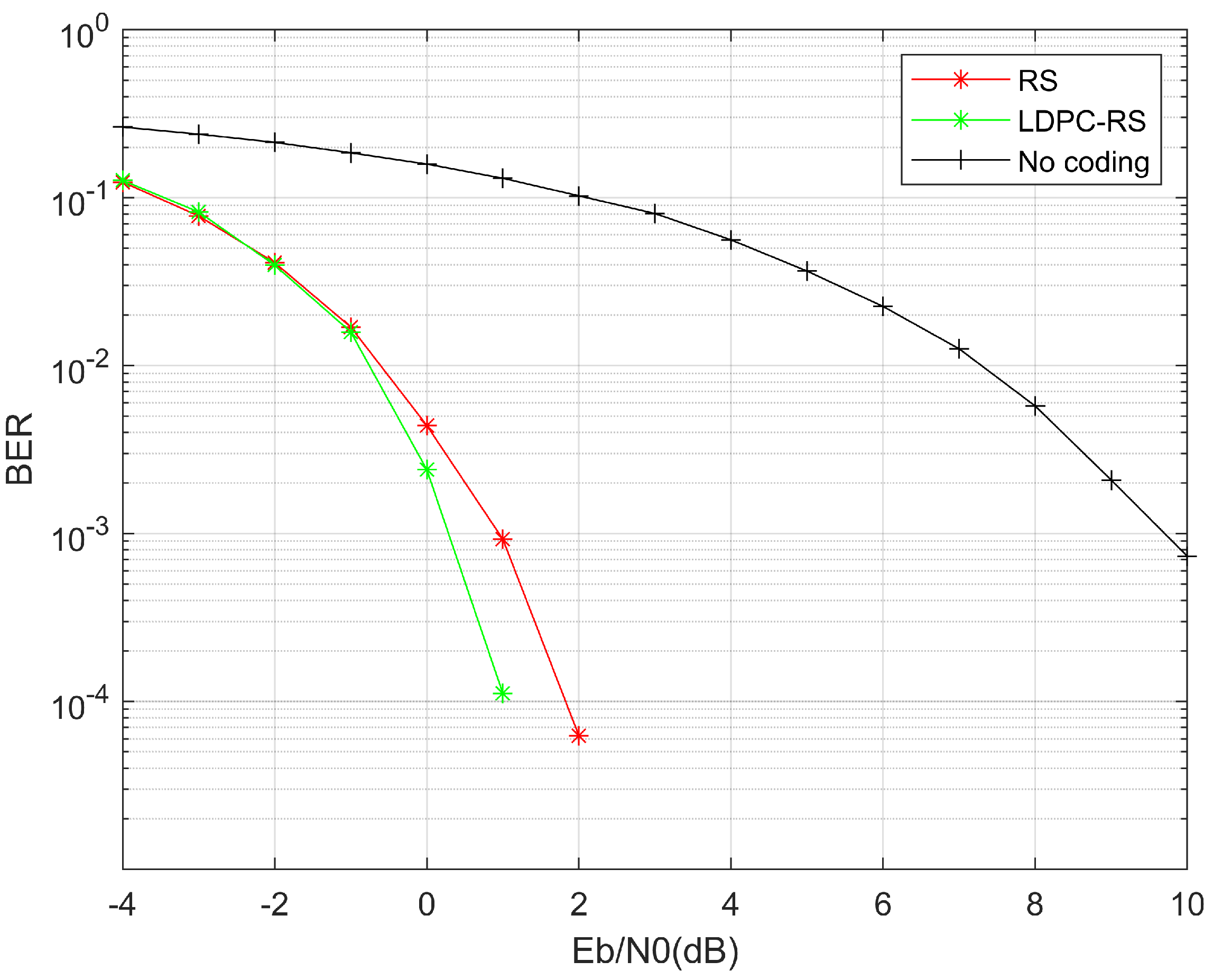
After that, we compare the error correction performance of the concatenated code proposed in this paper and the improved RS code alone in the Gaussian white noise channel, and the error curve is shown in Figure 8. In Gaussian channel, it can be seen that the performance of LDPC-RS concatenation code and the improved RS code are excellent. Generally speaking, the concatenated code has better error correction performance when the signal-to-noise ratio is greater than −1 dB.

4.3. System Performance Analysis

The transceiver system structure adopted in this section is shown in the block diagram as Figure 9.

After receiving the source, the transmitter first performs LDPC-RS cascade coding in the coding module. Then, after QPSK modulation, interleaving frame and other operations, the modulated signal is sent out. After a series of operations such as synchronization, channel estimation, channel equalization, and concatenation decoding are carried out by the receiver to the received signal, the message sequence is obtained. Then, the performance gain brought by the concatenated code processing to the system is analyzed.

In order to verify the performance of the algorithm, it is necessary to design the multipath channel first to obtain channels with different Ricean factors. Secondly, according to the prior information of the channel, it is necessary to design the frame structure of the SC-FDE system to obtain the optimal system performance. The parameters of the SC-FDE communication system designed in this paper are shown in

Table 2. The parameters of SC-FDE.

Parameters	Parameter Values
Maximum Doppler shift/$f_d$	10 Hz
The length of FFT	512
The length of UW	64
The type of UW	Chu sequence
Modulation mode	QPSK
Constellation point mapping	Gray code
The type of noise	AWGN

.

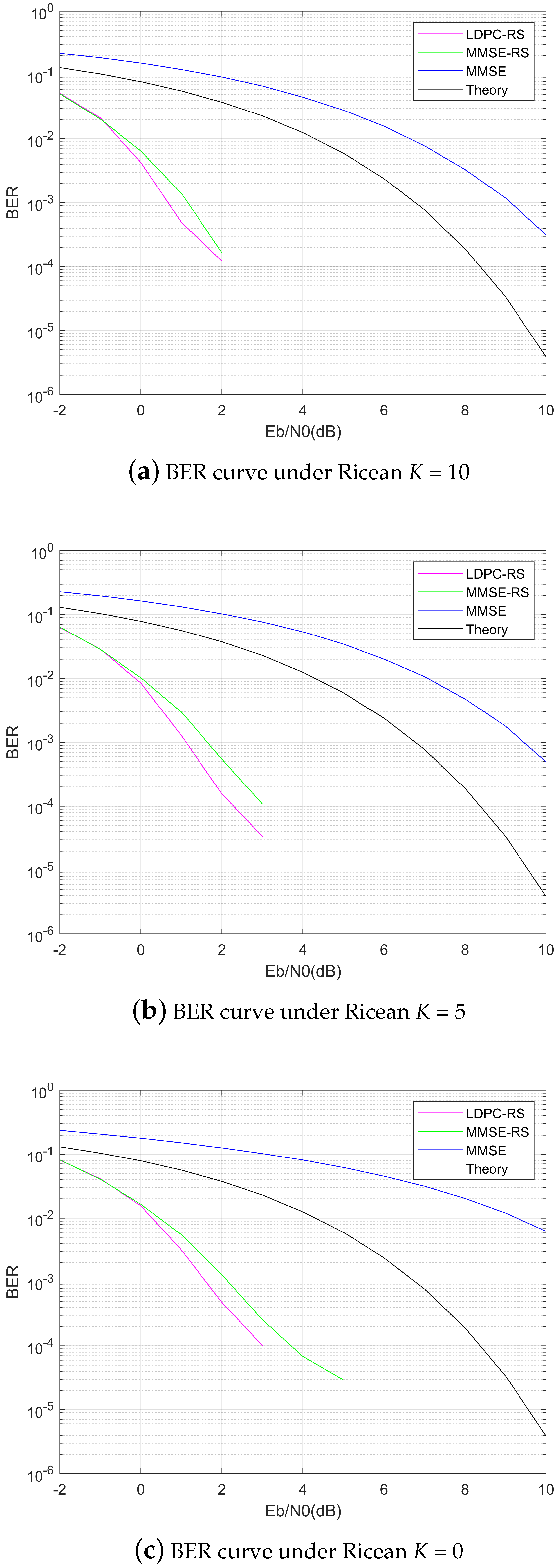
The simulation in this section is divided into two parts. The first part verifies, through simulation, that the concatenated code proposed in this paper exhibits robust error correction performance in multi-path fading channels with low Rice factor. In the simulation, three multi-path channels with Rice factors of 0, 5, and 10 are selected. The simulation results are shown in Figure 10, which demonstrate that the system utilizing the concatenated code outperforms simple equalization in terms of error correction performance. The concatenated code effectively mitigates the non-line-of-sight (NLOS) characteristics of the channel. Specifically, even when the Rice factor approaches very low values close to a Rayleigh fading channel, the proposed concatenated code still achieves excellent error correction performance. This ensures that the communication system maintains reliable performance.

The second part mainly compares the performance of several algorithms, including MMSE equalization, decision feedback equalization (DFE), iterative decision feedback equalization (IBDFE), convolutional code after MMSE equalization, RS code after MMSE equalization, and LDPC-RS concatenated code proposed in this paper. In addition, there are two algorithms proposed in the recent literatures [28,29]. The simulation results are shown in Figure 11. We can see that the performance of the system will be improved qualitatively when the encoding and decoding module is added to the system. In addition, compared with RS coding, algorithm in the literature [28] and algorithm in literature [29], the proposed LDPC-RS concatenated code has better error correction performance.

The simulation results in this section demonstrate the significant improvement in communication system performance achievable through the LDPC-RS concatenated coding scheme proposed in this paper. It is important to note that while we present a coding and decoding scheme specifically designed to enhance the anti-multipath capability of UAV communication systems, this does not limit the applicability of our proposed scheme solely to aviation communication. Its main advantage lies in the potential for scholars to extend its strong anti-multipath capability to other systems such as satellite communications, digital television broadcast communications, and even 5G and 6G mobile communications. However, it should be emphasized that the innovation of the LDPC-RS code presented in this paper primarily focuses on the improvement of RS encoding and decoding. If further improvements can be made to the error correction performance of the LDPC code, it would lead to further enhancement of the performance of our proposed concatenated code.

5. Conclusions

This paper discusses the LDPC-RS concatenated code, which offers robustness and superior error correction performance for UAV-to-Ground video data transmission systems. The LDPC-RS concatenation code designed in this study employs binary LDPC code as the outer code and RS code as the inner code. Furthermore, to strike a balance between complexity and performance of encoding and decoding algorithms in the UAV communication environment, this paper effectively improves RS encoding and decoding. For coding purposes, a coding code table is designed based on RS coding as the underlying logic, enabling fast coding. As for decoding, a decoding scheme is devised using the minimum Euclidean distance criterion to achieve high-performance decoding. Simulation results on Gaussian and multipath channels demonstrate that the tabular algorithm based on the minimum Euclidean distance criterion significantly enhances error correction performance compared to traditional algebraic algorithms. Moreover, the proposed concatenated coding scheme exhibits a gain of nearly 1dB and 2dB in comparison to RS coding and convolutional coding, respectively. These results are obtained through simulations. Future work will focus on further improving the performance of the concatenated code and its optimal application in actual UAV communication systems.