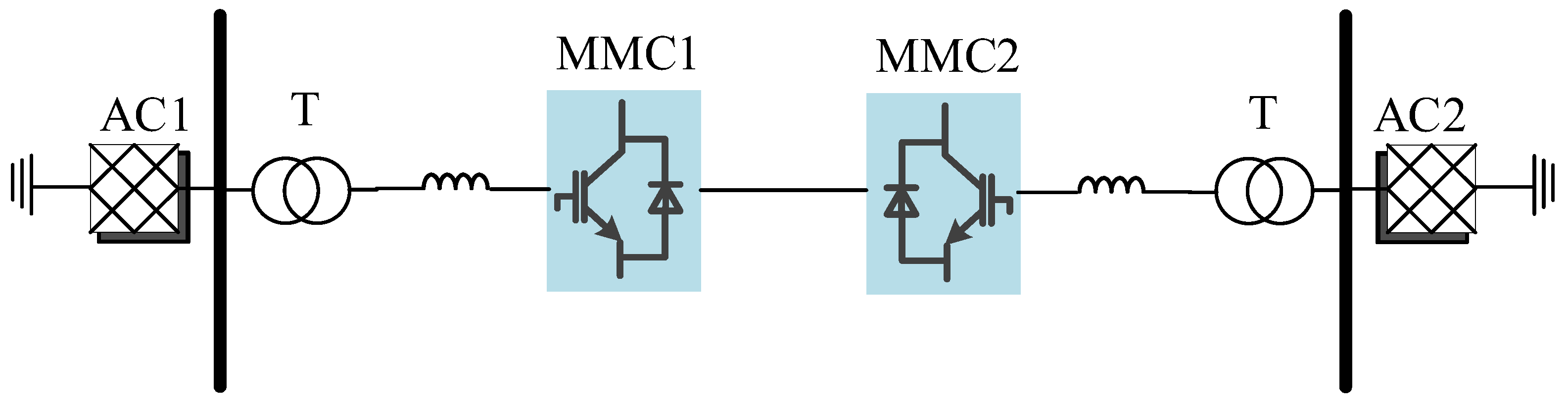
1. Introduction
The modular multilevel converter-based high voltage direct current (MMC-HVDC) is an innovative transmission technology that offers several advantages, including independent control over active and reactive power, power support for weak current networks and passive loads, low harmonic levels, and avoidance of commutation failures. As a result, it has found extensive application in areas such as high-voltage DC transmission and new energy grid integration [
1,
2]. However, MMCs encounter several challenges, with a significant one being high-frequency oscillations (HFOs). The presence of resonance points at specific frequencies between the MMC and the equivalent impedance of the AC system can result in resonance within the AC/DC system. Furthermore, the multi-timescale dynamic characteristics of MMCs amplify the risk of resonance in AC/DC systems. HFO adversely impacts the stability and safety of the system [
3,
4,
5], and in severe cases, it can even result in system runaway.
In resonance analysis, the primary methods used for theoretical analysis are modal analysis and impedance analysis. References [
6,
7,
8] investigated the oscillation mechanism of MMCs using the modal analysis method. However, this approach necessitates the re-derivation of the state matrix to accommodate modifications in system structure, parameters, or control strategies. In practical engineering, communication systems exhibit complex characteristics, posing challenges in obtaining feature matrices. Therefore, the impedance analysis method has garnered significant attention in recent years. In [
9], they developed a hybrid interconnected system impedance model between MMCs and a weak AC power grid, analyzing the coupling relationship between MMC impedance and AC power grid impedance. Reference [
10] employed the multi-harmonic linearization method to establish a calculation approach for the AC- and DC-side impedances of series-type MMCs, while also presenting a detailed derivation process. To address the issue of neglecting internal dynamics in modeling the high-frequency range of flexible DC transmission stations, the author in [
11] developed an MMC DC impedance model that takes into account various control conditions and analyzed the output characteristics of DC ports. Reference [
12] introduced a precise impedance model that accounts for the impact of phase-locked loops, power outer loops, and voltage–current inner loops on the impedance characteristics of MMC. This model serves as a crucial theoretical foundation for resolving system stability and HFO issues.
To address the HFO phenomenon in flexible DC transmission technology, reference [
13] developed a mathematical model for the high-frequency impedance of MMCs, taking into account link delay. They also proposed a strategy for suppressing HFOs by incorporating a band-stop filter in the voltage feedforward link. The authors in [
14,
15] uncovered that the negative damping characteristics of MMC impedance in the mid to high frequency range serve as the fundamental cause of HFOs in flexible DC grid-connected systems. Consequently, they proposed an additional damping control strategy to suppress resonance. References [
16,
17] summarized four strategies for suppressing HFOs using additional damping control. They also analyzed the impact of these four additional damping controls on improving the negative damping characteristics of MMCs and suppressing HFOs. However, the additional damping suppression strategy in [
16,
17] only focuses on adjusting the reference voltage through voltage or current feedback, resulting in limited effectiveness in suppressing oscillations. Hence, this paper proposes a joint additional damping control strategy that combines voltage feedback and current feedback to address the shortcomings of single additional damping control in suppressing HFOs and enhancing system stability.
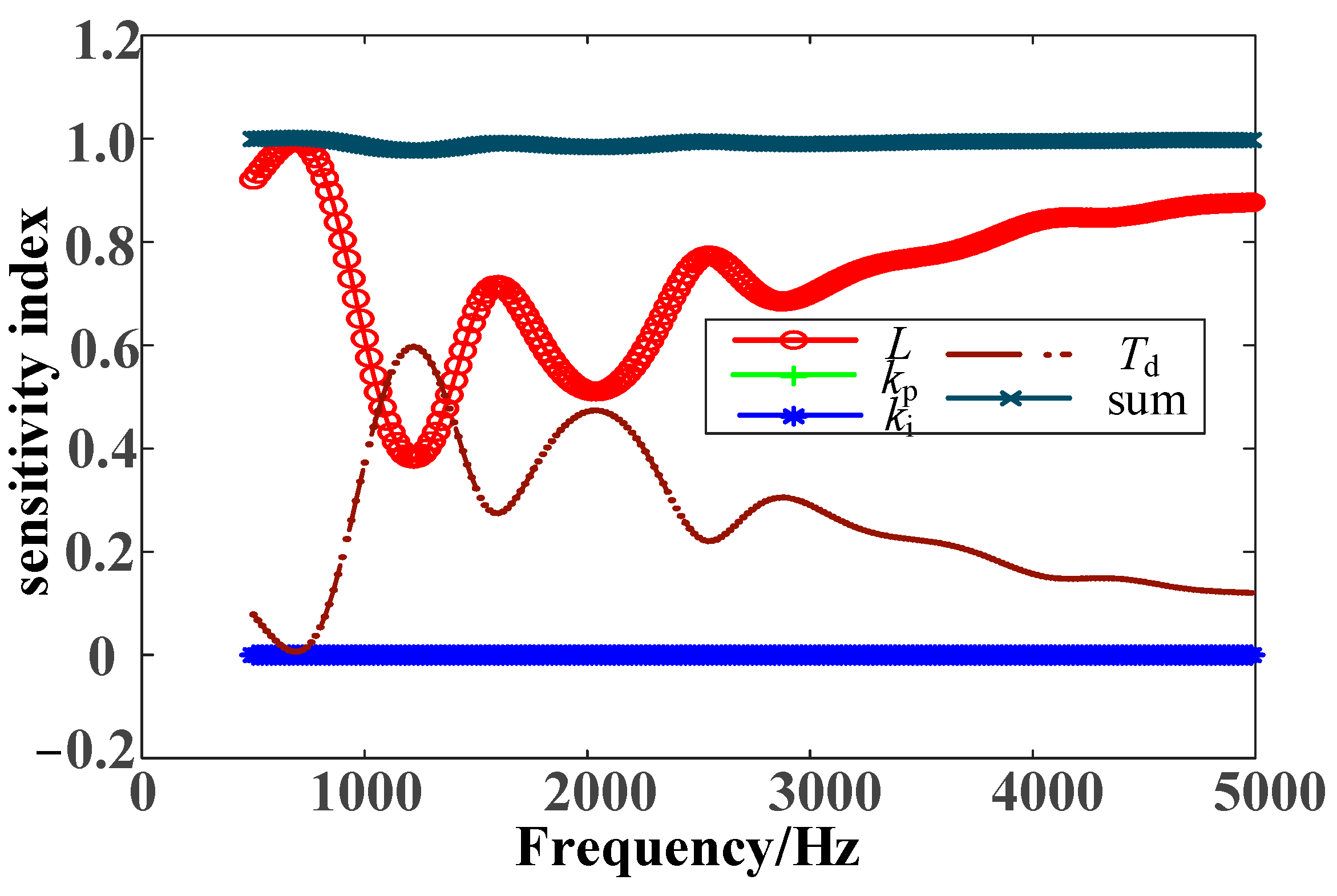
This article initially examines the current inner loop control to develop a simplified control model for MMCs. It employs Sobol’s method to analyze the factors influencing the AC side impedance of MMCs. Subsequently, this article introduces a combined approach for additional damping suppression that integrates virtual passive filtering and equivalent current sampling. The proposed method mitigates HFOs by incorporating filters into the voltage feedforward. Lastly, this article employs PSCAD for time-domain simulations to validate the accuracy of the analysis findings regarding the influencing factors and the resonance suppression strategy.
This article introduces an additional damping controller based on impedance analysis method to suppress HFOs in MMC-HVDC systems. In comparison to traditional additional damping controllers, this controller incorporates current feedback during the design process, resulting in a more potent suppression effect. Using the dual-ended flexible DC transmission system as an example, this article presents the following main contributions:
(1) Utilizing the MMC impedance model that accounts for current inner loop control, the Sobol algorithm was employed to analyze the impact of different factors on HFOs, and the significant factors influencing MMC impedance in distinct frequency ranges were identified.
(2) A novel additional damping controller is proposed, which combines the virtual passive filtering method and the equivalent current sampling method. The controller employs output voltage and current as its state variables, resulting in a more potent damping suppression effect.
The remainder of the article is structured as follows:
Section 2 presents the impedance model based on a dual-ended flexible DC transmission system. Subsequently,
Section 3 employs sensitivity calculations using the Sobol algorithm to analyze the primary factors influencing HFOs in each frequency band.
Section 4 introduces an additional damping controller and compares the suppression effects of various damping controllers. The effectiveness of the proposed method for suppressing HFOs is verified through simulation analysis in
Section 5. The article concludes with
Section 6.
4. Effect of Additional Damping Control on Impedance Characteristics
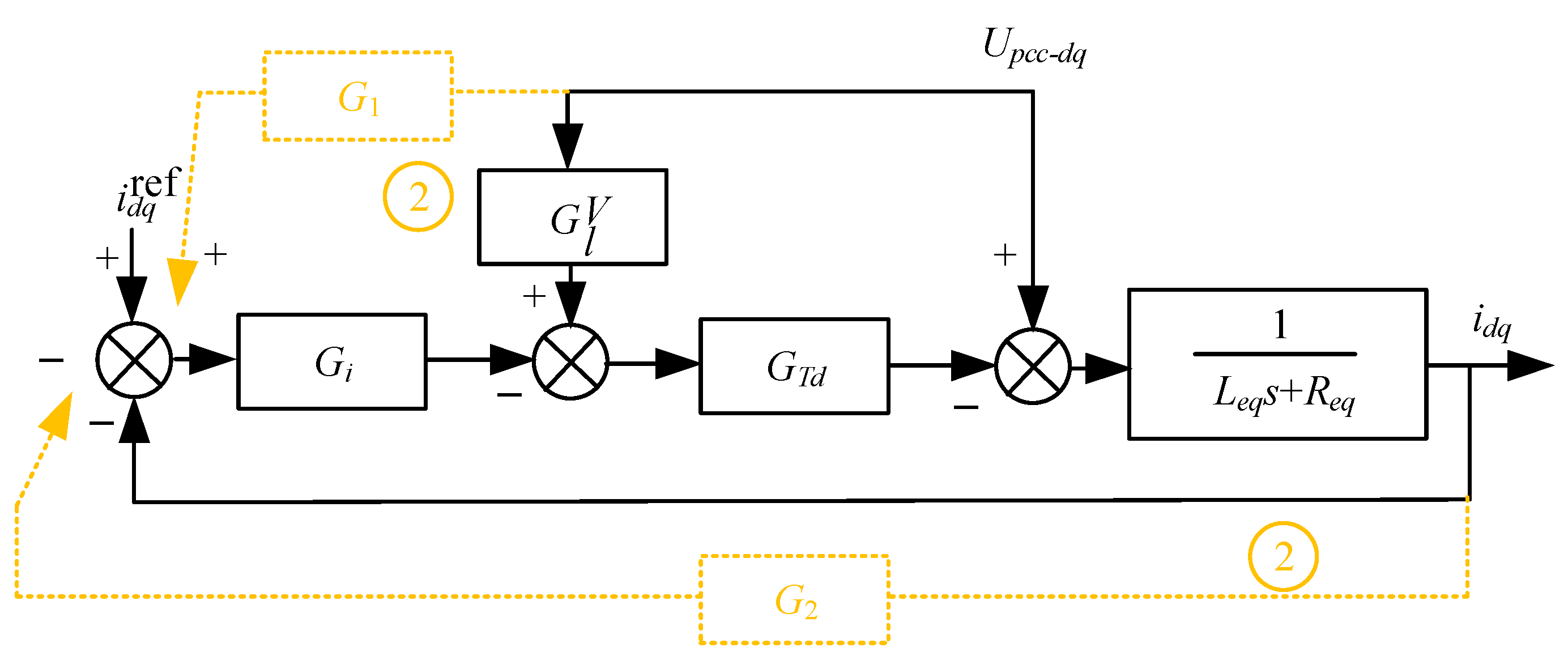
As mentioned previously, the primary factors influencing MMC impedance in the high-frequency range are equivalent inductance and system delay. Adjusting these parameters in existing practical engineering to suppress system oscillation proves challenging. Hence, this study investigated the impact of additional damping control on MMC impedance. The existing additional damping control primarily entails overlaying the instantaneous value of the feedforward voltage onto the reference current via the HFO damping controller
G1. It is then added to the reference voltage after undergoing adjustment by the current inner loop [
13,
15], as depicted in
Figure 10. In this article, a novel joint additional damping control method is proposed. This approach combines the instantaneous values of the feedforward voltage and output current with the reference current through HFO damping controllers
G1 and
G2. Subsequently, they were added to the reference voltage via current inner loop adjustment. The control principle of this method is presented in
Figure 11.
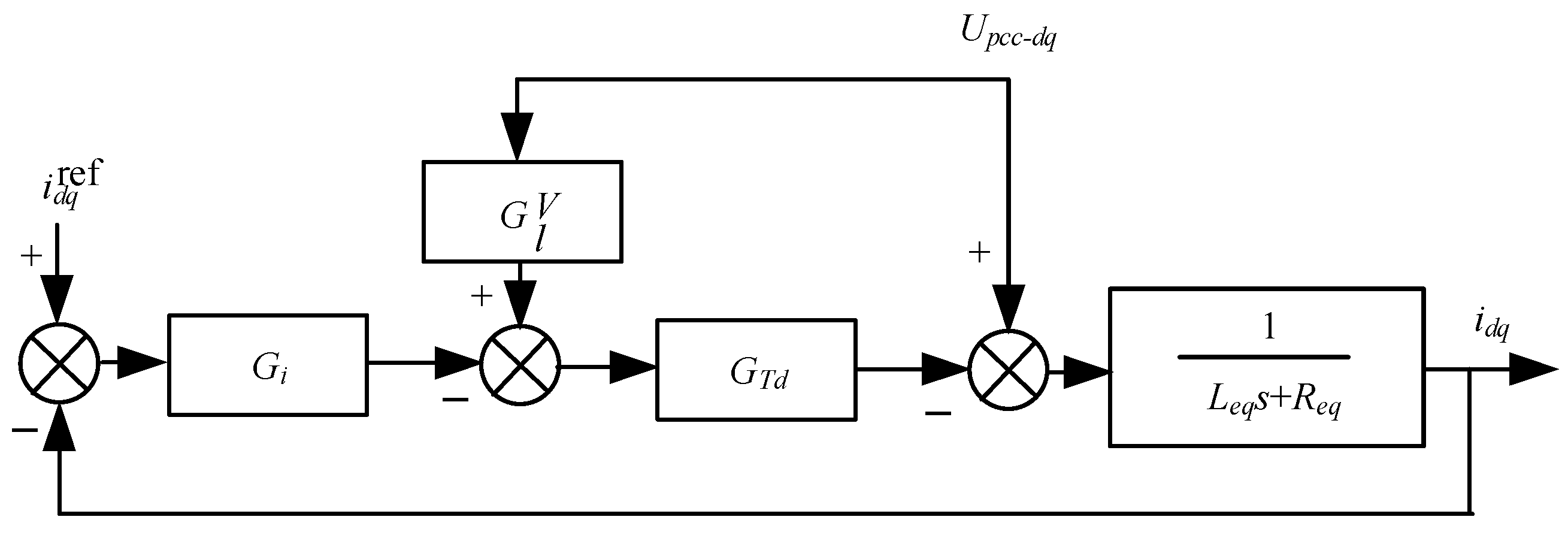
In
Figure 10 and
Figure 11,
Req is the equivalent resistance on the line;
Leq is the equivalent inductance of the converter and MMC, which is equal to the sum of 1/2 of the MMC bridge arm reactor
Larm and the leakage inductance
Lt of the connecting transformer;
GTd is the transfer function of the system control delay link;
Gi is the current inner loop transfer function;
GVl is the voltage feedforward transfer function;
iref dq is the inner loop current reference value;
Upcc-dq is the dq axis component of the grid point voltage; and
idq is the output current dq axis component.
Figure 10 presents a simplified control model for the MMC utilizing the pre-existing additional damping control. For the sake of simplicity, this control is denoted as Scheme 1.
Figure 11 displays a simplified control model for the MMC featuring combined additional damping control, as depicted in the block diagram. This control variant will be designated as Scheme 2 for the sake of simplicity.
4.1. The Effect of Virtual Passive Filtering Method on the Impedance Characteristics of MMC
According to
Figure 10, combining Equation (1), it can be inferred that the high-frequency impedance
ZMMC at this time is:
Common filters can be divided into low-pass filters, band-stop filters, and nonlinear filters. This article mainly analyzes second-order damping controllers [
15] and band-stop filters [
13]. The second-order damping controller mainly consists of a low-pass filter, a high-pass filter, and a gain
ks. When using a second-order damping controller, the expression of
G1 is:
In the formula, fHPF and fLPF are the bandwidth frequencies of the high-pass and low-pass filters, respectively. This article takes ks = −0.8, fLPF = 800 Hz, and fHPF = 100 Hz as the initial research objects.
Next, the gain
ks of the second-order damping controller is adjusted. The amplitude and phase angle characteristics of the MMC converter station impedance and the AC system impedance when the gains
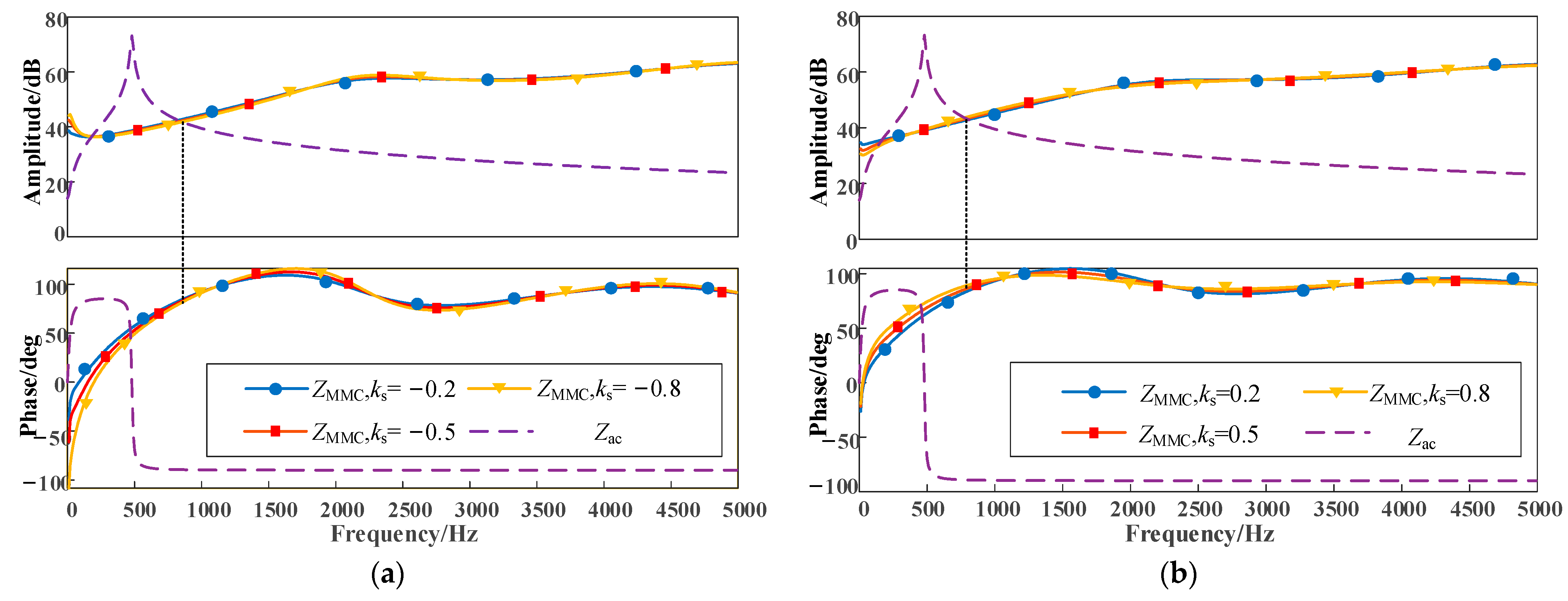
ks are −0.8, −0.5, −0.2, 0.2, 0.5, and 0.8, are shown in
Figure 12a,b. Due to the effect of an additional filter, when
ks = −0.2, the frequency at the amplitude intersection point was 820 Hz, and the phase difference was 171.6963°. When
ks = −0.5, the phase difference was 169.8732°, and when
ks = −0.8, the phase difference was 168.25°. When
ks = 0.8, the phase difference was 179.5452°, when
ks = 0.5, the phase difference was 176.8408°, and when
ks = 0.2, the phase difference was 174.4537°, which is lower than when no additional filter was added. Consequently, the inclusion of an additional filter aids in mitigating the negative damping characteristics of the MMC and enhances system stability.
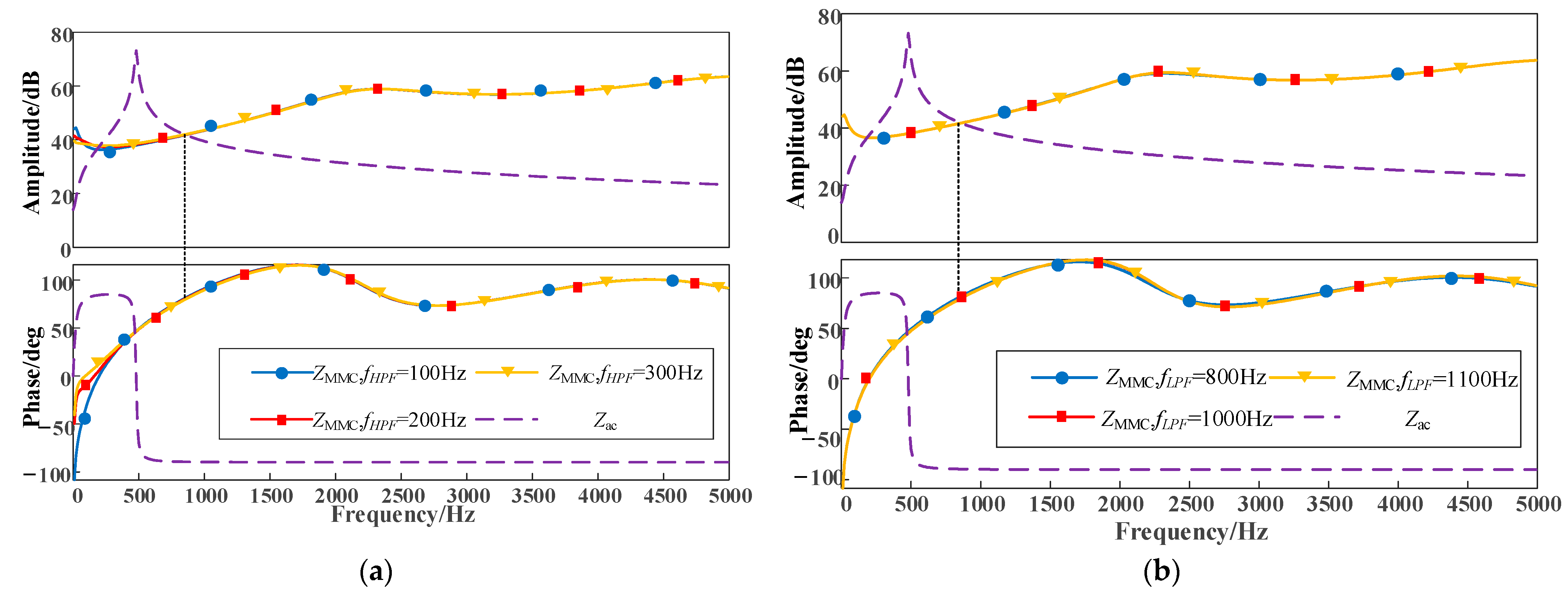
After adjusting the bandwidth frequency of the high-pass and low-pass filters, the amplitude and phase characteristics of the MMC impedance and the AC system impedance are shown in
Figure 13a, where the bandwidth frequency of the high-pass filter was 100 Hz, 200 Hz, and 300 Hz. The amplitude and phase characteristics of the MMC impedance and the AC system impedance when the bandwidth frequencies of the low-pass filter were 800 Hz, 1000 Hz, and 1100 Hz are shown in
Figure 13b. From
Figure 13a, it can be seen that a slight change in the bandwidth frequency of the high-pass filter had little effect on the phase. The frequency at the intersection of the amplitudes was 820 Hz, and the phase difference was 169.7867°. From
Figure 13b, it can be seen that a slight change in the bandwidth frequency of the low-pass filter had little effect on the phase, and the frequency at the intersection of the amplitudes was 870 Hz. The phase difference was 170.0786°.
When using a band-stop filter, the expression for
G1 is:
In the formula, ξ represents the damping coefficient of the band-stop filter, while the center frequency
f0 is calculated as half the sum of the upper and lower cutoff frequencies of the band-stop filter, denoted as
f0 = (
f1 +
f2)/2. Here,
f1 represents the upper cutoff frequency,
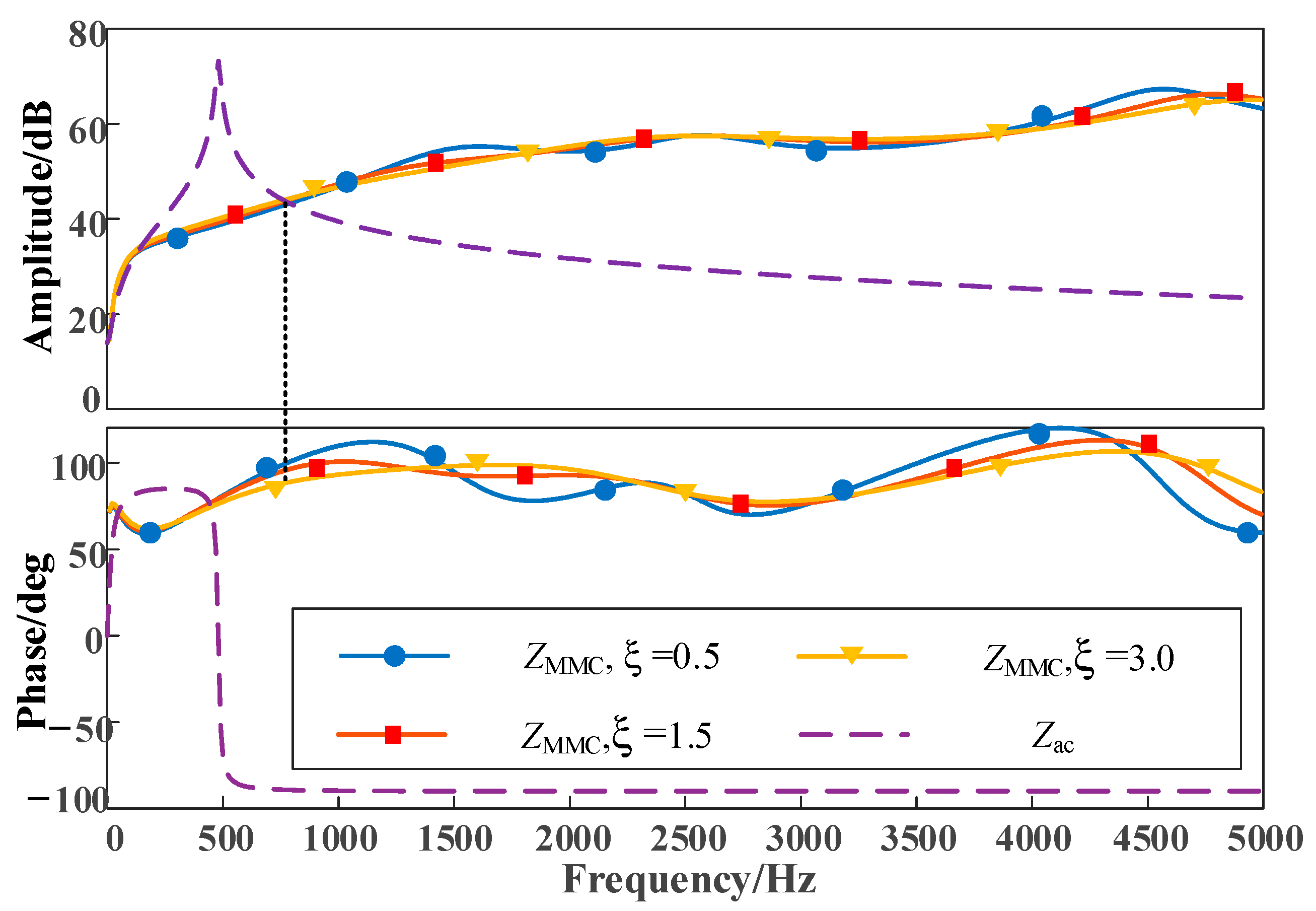
f2 denotes the lower cutoff frequency, and for this study, the center frequency is fixed at 2500 Hz. The damping coefficient of the band-stop filter was adjusted, and the resulting amplitude and phase characteristics of both the MMC impedance and the AC system impedance are illustrated in
Figure 14.
The results depicted in
Figure 14 demonstrate that the presence of an additional filter reduced the phase difference between the amplitude intersection at a frequency of 790 Hz. At this point, the maximum phase difference measured 189.9985°, while the minimum phase difference was 178.3057°. Comparing these values to the phase difference observed without an additional filter, it is evident that the inclusion of the filter led to a reduction in phase difference. Consequently, the addition of the filter aided in eliminating the negative damping characteristics of the MMC, thereby enhancing system stability. Moreover, when comparing the two types of filters, it was observed that the second-order damping controller exhibits a smaller phase difference at the amplitude intersection, thereby providing better prospects for eliminating negative damping characteristics, enhancing system stability and suppressing HFOs.
4.2. The Effect of Joint Damping Control on the Impedance Characteristics of MMC
Based on
Figure 11 and Equation (1), it can be inferred that the high-frequency impedance
ZMMC at this point is:
Based on the previous analysis, it is evident that the use of a second-order damping controller yields superior results. Hence, this section employs a second-order damping controller in the voltage feedback loop and two types of filters in the current feedback loop to compare and analyze the efficacy of joint damping control in suppressing HFOs.
Figure 15 illustrates the amplitude and phase characteristics of the MMC converter station impedance and the AC system impedance when employing a second-order damping controller with specific parameters:
ks = −0.55,
fLPF = 1050 Hz, and
fHPF = 80 Hz.
Figure 15 reveals that the frequency at the amplitude intersection was 820 Hz. Using only Method 1 resulted in a phase difference of 168.25° at the amplitude intersection. However, when employing Method 2, which incorporates both the output current and feedforward voltage to adjust the reference current, the phase difference at the amplitude intersection decreased to 167.4411°, remaining below 180°. Consequently, Method 2 demonstrated superior capability in mitigating the negative damping frequency band of MMC impedance and effectively suppressing HFOs, surpassing the effectiveness of Method 1.
Figure 16 illustrates the amplitude and phase characteristics of MMC impedance and AC system impedance when a band-stop filter with a center frequency of 2000 Hz is employed.
The amplitude intersection frequency in
Figure 16 was observed to be 810 Hz. For Method 1 alone, the phase difference at the amplitude intersection was 168.25°. However, when employing Method 2, the output current and feedforward voltage are simultaneously introduced to modify the reference current. In this case, the phase difference at the amplitude intersection was measured to be 167.5309°, which is below 180°.
Figure 15 and
Figure 16 represent the MMC impedance characteristics when utilizing low-pass filters and bandpass filters, respectively. Under the simulation conditions described in this article, the two types of filters exhibited similar filtering effects, resulting in the relatively similar impedance characteristic curves in
Figure 15 and
Figure 16. But no matter which filter is used, Method 2 proved to be more efficient in eliminating the negative damping frequency range of MMC impedance and effectively suppressing HFOs when compared to Method 1.
6. Conclusions
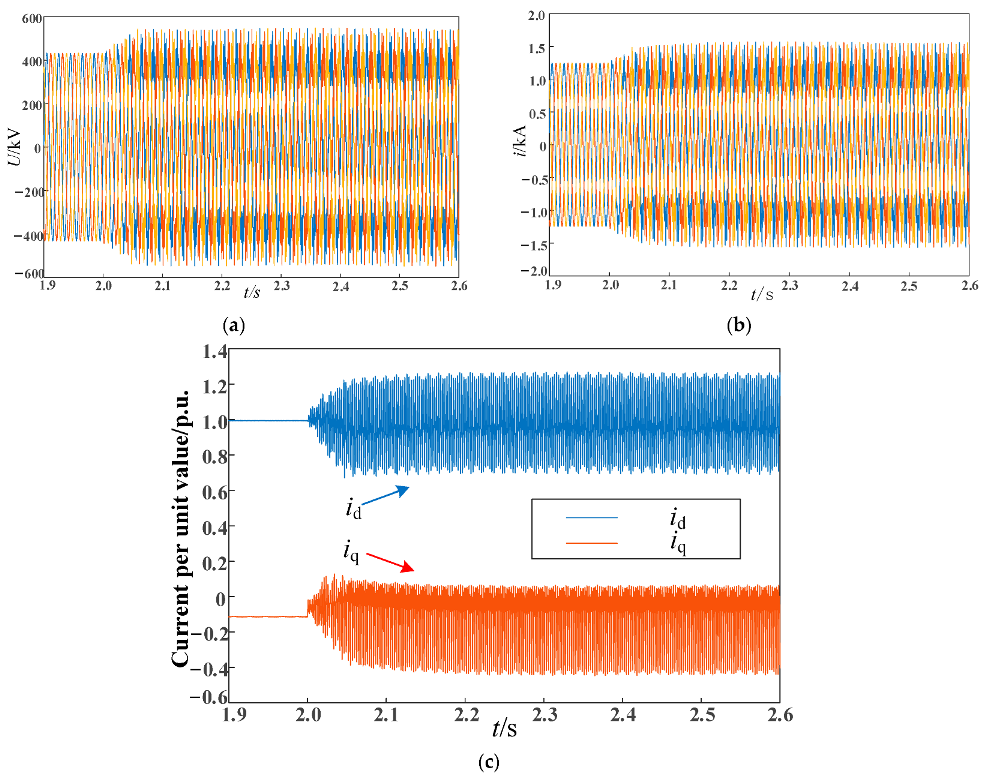
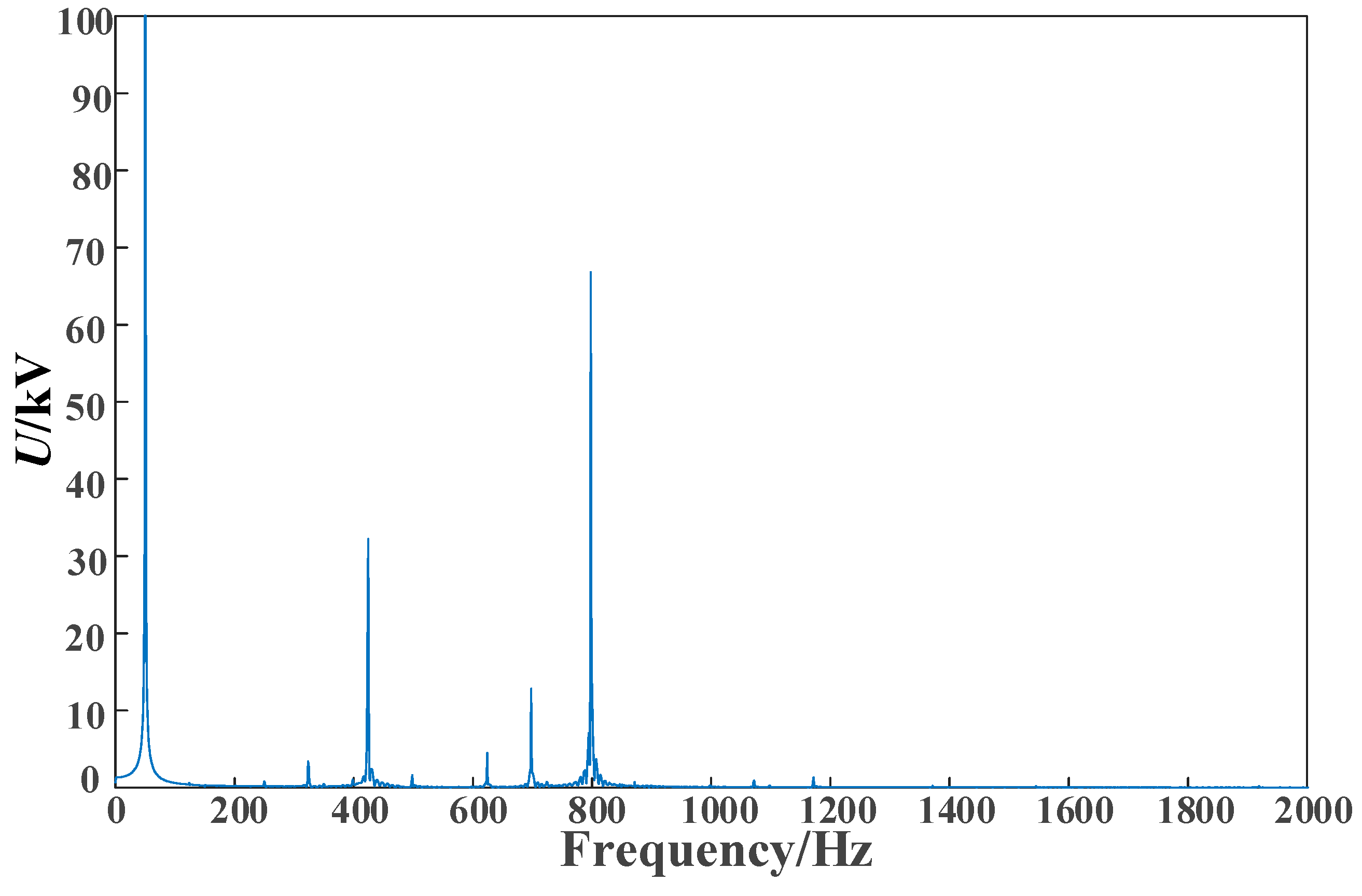
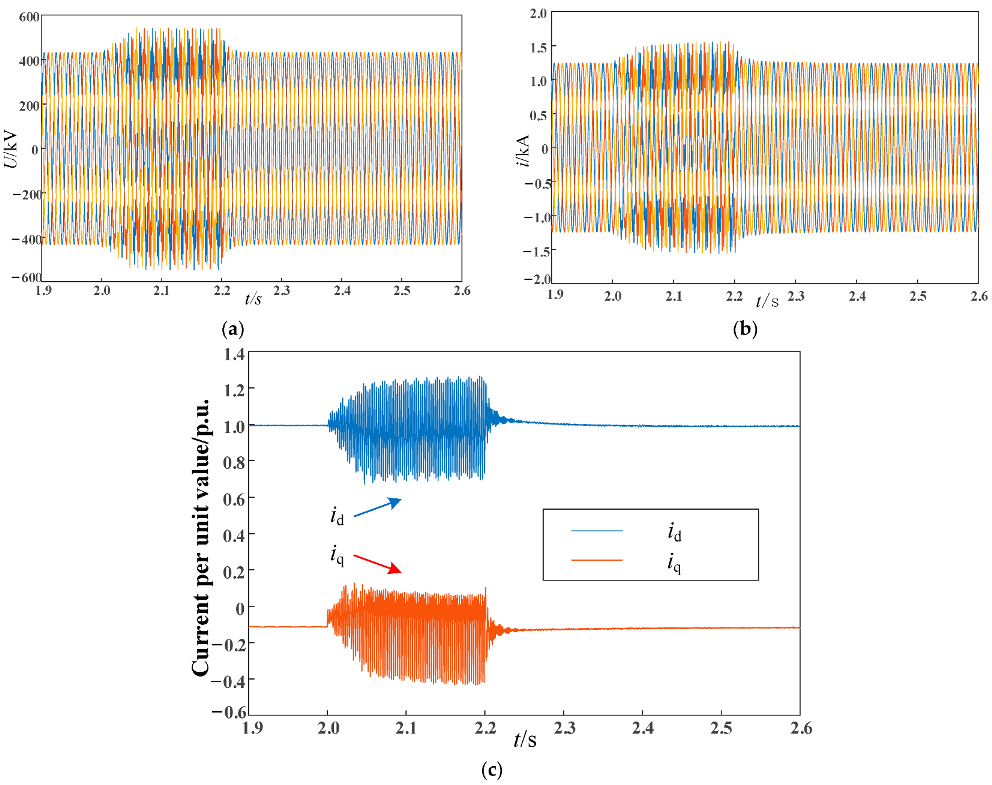
This article addressed the issue of HFOs resulting from delay in flexible DC grid-connected systems. It established a simplified control model for MMCs and a high-frequency impedance model for the AC system. The key factors that contribute to HFOs in flexible DC grid-connected systems were analyzed using the Sobol algorithm. To mitigate HFOs, a suppression strategy was proposed, which combines virtual passive filtering and equivalent current sampling filtering. The effectiveness of this suppression strategy was verified through simulations conducted in the PSCAD electromagnetic transient model. The following conclusions can be drawn:
(1) The stability of the system is affected by system delay, equivalent inductance, and filter cutoff frequency. Therefore, fluctuations in the operating mode of the AC power grid and filter parameters may lead to changes in the resonance frequency of the system.
(2) The HFO suppression strategy based on joint additional damping control proposed in this article is effective. Compared to the virtual passive filtering method, it can suppress the occurrence of HFOs within a certain delay range and improve the stability margin of the system to a certain extent.