Spatial-Temporal Self-Attention Transformer Networks for Battery State of Charge Estimation

Abstract

Over the past ten years, breakthroughs in battery technology have dramatically propelled the evolution of electric vehicle (EV) technologies. For EV applications, accurately estimating the state-of-charge (SOC) is critical for ensuring safe operation and prolonging the lifespan of batteries, particularly under complex loading scenarios. Despite progress in this area, modeling and forecasting the evaluation of multiphysics and multiscale electrochemical systems under realistic conditions using first-principles and atomistic calculations remains challenging. This study proposes a solution by designing a specialized Transformer-based network architecture, called Bidirectional Encoder Representations from Transformers for Batteries (BERTtery), which only uses time-resolved battery data (i.e., current, voltage, and temperature) as an input to estimate SOC. To enhance the Transformer model’s generalization, it was trained and tested under a wide range of working conditions, including diverse aging conditions (ranging from 100% to 80% of the nominal capacity) and varying temperature windows (from 35 °C to −5 °C). To ensure the model’s effectiveness, a rigorous test of its performance was conducted at the pack level, which allows for the translation of cell-level predictions into real-life problems with hundreds of cells in-series conditions possible. The best models achieve a root mean square error (RMSE) of less than 0.5 test error and approximately 0.1% average percentage error (APE), with maximum absolute errors (MAE) of 2% on the test dataset, accurately estimating SOC under dynamic operating and aging conditions with widely varying operational profiles. These results demonstrate the power of the self-attention Transformer-based model to predict the behavior of complex multiphysics and multiscale battery systems.

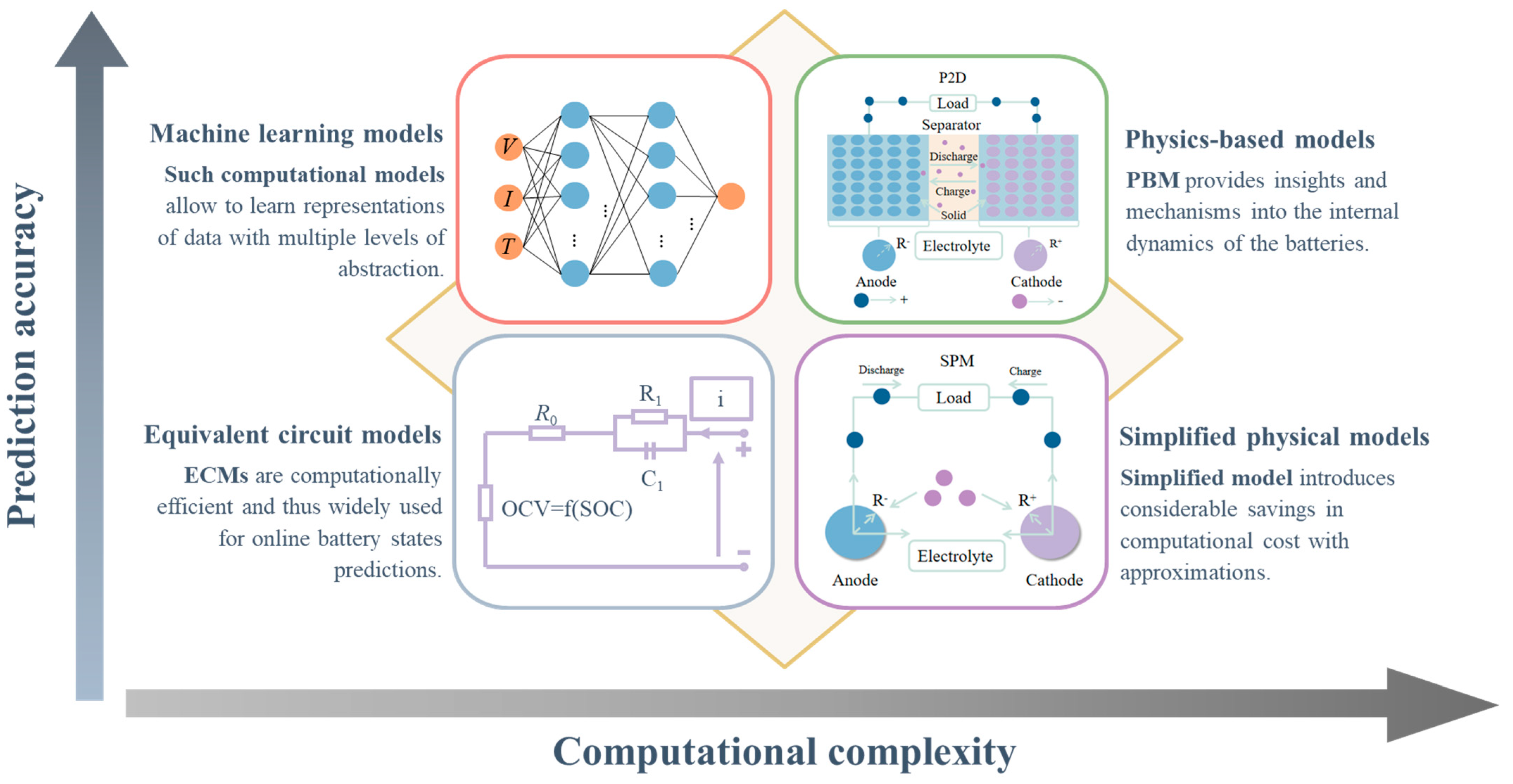
1. Introduction

Vehicle electrification is considered as an important decarbonization pathway for climate change mitigation [1]. Global electric vehicles (EVs) sales are stepping into steadily escalating phases, from less than 10,000 in 2010 to more than 10 million units in 2022, surpassing 20 million cumulative sales [2]. In total, billions of lithium-ion batteries are used as energy storage devices in today’s EVs. In EV applications, cell performance is highly dependent on operating conditions. Under abuse conditions, such as over-charging [3] or over-discharging [4], battery voltage can move beyond their safe operating windows, which can accelerate degradation and increase the risk of battery failure after long-term incubation. Accurate estimation of battery state-of-charge (SOC) under various operating conditions is critical for effective battery management in both large-scale EVs [5] and photovoltaic-assisted applications [6]. However, accurate SOC estimation faces multiple sources of uncertainty, including complex physio-chemical mechanisms, significant cell-to-cell variation, and dynamic operating conditions. These challenges are exacerbated when cases involve uncertain aging conditions, noisy data, and missing initial/boundary conditions, such as those found in EV field applications.

1.1. Current Methods for SOC Estimation

The traditional methods for battery SOC estimation can be classified by the form of mechanisms into a variety of categories, including Coulomb counting methods [7,8], open circuit voltage (OCV)-based estimation [9,10], filter-based algorithms [11,12,13], and model-based estimation [14,15]. Despite relentless progress, there is always a trade-off between the computational cost and the accuracy of model-based predictions for online SOC estimation. Coulomb (ampere hour) counting methods provide a simple, straightforward estimation method based on the definition of SOC. Due to the low computational complexity, Coulomb counting methods have been widely used for online SOC estimation in the EV industry. However, this method generally achieves a limited accuracy and poor robustness resulted from unknown initial SOC and capacity degradation, as well as current sensor drift [16]. In addition, the energy loss during charging and discharging process and self-discharge would also cause further accumulating errors. OCV-based methods are also commonly used for SOC estimation due to their stable and monotonical relationship. There is very little variation among the cells that have the same chemistries and cell design in terms of the SOC–OCV relationship, which provides tools for practical applications by mapping the look-up table under different test conditions. However, it can be a time-consuming process, especially considering capacity degradation [17] and working temperature [18]. In addition, OCV-based methods can only be used to describe the electrode potential difference in the open circuit condition. In order to obtain a stable electrode potential, it requires a long rest time for the lithium-ion battery to reach a stable potential due to the slow diffusion, which generally takes a few hours for most operating conditions. Such a requirement greatly limits its utility and prediction accuracy for EV applications. A recent study introduced an efficient methodology for determining the OCV–SOC curve for lithium-ion batteries under dynamic temperature conditions to improve model generalizability [19]. Considering the variability of the OCV–SOC curve with temperature and battery age, the research proposed a multi-output Gaussian process (MOGP) model utilizing current–voltage data, thereby bypassing the need for direct OCV measurement or estimation. This model efficiently captures correlations across various temperatures and constructs an accurate OCV–SOC curve for a specific temperature, significantly diminishing prediction errors. This pioneering technique provides enhanced SOC estimation precision, paving the way for a more pragmatic and accurate SOC determination approach under diverse operating conditions.

Closed-loop-based filter algorithms have been widely developed to tackle uncertainties and disturbances based on feedback correction over the past decade. Filter-based SOC estimation has two components: a battery voltage model and a filter algorithm, such as Kalman Filter family [20], particle filter [21], and H-infinity [22]. When a filter model is available, a first- or second-order equivalent circuit model (ECM) is widely used for online EV applications. High-order ECM models [23] and physics-based models (PBM) [24] achieve a higher voltage accuracy at the cost of computational complexity. One comment, PBM, is the pseudo-two-dimensional (P2D) model. This model provides deeper insights into the internal dynamics of batteries. However, the complexity of the governing equations and the high computational cost makes P2D less practical for online applications. Additionally, traditional PBMs do not consider detailed material information, which is vital for understanding battery degradation behavior. To manage the computational demand, a primary strategy involves simplifying the PBMs. However, such approximations must still retain sufficient physical information to accurately predict battery behavior. A widely studied model that adopts this simplified approach is the single-particle model (SPM). This model operates under the key assumptions that each electrode is represented by a spherical particle and that the potential and concentration effects in the solution phase are disregarded. These approximations contribute to a significant reduction in computational time. Nonetheless, the SPM model falls short in accuracy when applied to high-rate simulations.

Due to the availability of high-throughput computing and open-source software, data-driven and machine learning-based approaches have been successful in helping scientists and engineers in the energy storage realm [25,26,27,28,29,30]. Machine learning techniques play crucial roles in modeling and forecasting the dynamics of multiphysics and multiscale battery systems within the framework of Industry 4.0 [31]. Particularly, deep learning enables the creation of computational models that consist of multiple processing layers, which can learn data representations with various levels of abstraction. Through the backpropagation algorithm, deep learning uncovers complex structures in large datasets and guides a machine to adjust its internal parameters that compute representations in each layer from the previous layer’s representations. In prediction tasks, the top layers of deep learning models heighten critical features while filtering out unnecessary variations. This layered approach of enhancing and reducing data helps to extract vital patterns, resulting in accurate prediction. This technique has emerged as a promising alternative, with particular advantages in determining cell states [32,33]. Figure 1 illustrates the balance between prediction accuracy and anticipated computational cost for the aforementioned methods.

In the recent technological era, a multitude of innovative machine learning methods and deep neural networks have been advanced for the estimation of the SOC for EV applications. These novel proposals are meticulously designed to substantially augment model accuracy, thus contributing to more precise and efficient energy management within the burgeoning field of electric vehicles. One such example is the use of convolutional neural network (CNN). Innovative research has centered on crafting a universal SOC estimator capable of addressing variations in battery type and sensor noise [34]. A unique closed-loop paradigm, employing a deep convolutional neural network (DCNN), was put forward in this study, employing transfer learning and pruning techniques for swift adaptability in distinct scenarios. The proposed model showcased its effectiveness across diverse battery types and stages of aging, achieving root mean square errors (RMSE) below 2.47% by adjusting the final layers. Recurrent neural networks (RNNs) offer significant benefits for tasks that demand sequential inputs and time-series data over convolutional neural networks (CNNs). Processing each data sequence element individually, RNNs preserve a state vector with crucial historical sequence data in their hidden units. The concept becomes apparent when the outputs of hidden units across discrete time steps are viewed as outputs of neurons in a deep, multilayered network, illuminating how backpropagation can train RNNs. Specialized RNNs, known as long short-term memory (LSTM) networks, bring a novel structure called a memory cell into play, which includes three gate types (input, forget, and output) that control the memory cell’s information flow. A recent study introduced a fusion network marrying a multi-dimensional residual shrinkage network (MRSN) with an LSTM, enhancing SOC estimation in lithium-ion batteries [35]. The combined network efficiently manages multi-dimensional interaction, noise interference, and precludes data leakage using a sequence-to-point processing strategy. Further advancements in SOC estimation techniques for lithium-ion batteries involve a LSTM-RNN augmented with extended input and constrained output (EI-LSTM-CO) [36]. This model includes an additional input, the sliding window average voltage, and an Ampere-hour integration-based state flow approach for output constraint. These enhancements significantly improved SOC estimation performance by curbing output volatility. The encouraging results underscore the potential of the EI-LSTM-CO for real-world SOC estimation. In addition, a multi-forward-step SOC prediction method based on LSTM demonstrates its effectiveness for battery systems in real-world EV applications. The developed Weather-Vehicle-Driver analysis method considers how drivers’ actions and the weather affect a battery system’s performance in real-world operating circumstances. In addition to preventing LSTM from overfitting, the proposed dropout technology and correlation analysis efficiently choose the best parameters prior to training. Additionally, by using LSTM and multiple linear regression algorithms, a joint-prediction strategy was applied to achieve dual control of prediction accuracy and prediction horizon. It offers an opportunity to control the prediction steps of LSTM while ensuring acceptable prediction accuracy by using the one-forward-step prediction accuracy of linear regression as the accuracy benchmark [37]. To capture temporal dependencies in both forward and backward directions, a bidirectional LSTM neural network was used for the SOC estimation [38]. Moreover, the bidirectional LSTM layers are stacked to improve the predictive ability of the non-linear and dynamic relationship between the input parameters and cell SOC on a layer-by-layer basis. Compared to LSTM, the gated recurrent unit (GRU) employs a simpler structure with low-dimensional non-linear manifold and was given a great deal of attention in relation to the prediction of battery conditions. For example, a RNN with GRU was applied to estimate the cell SOC from measured time-series signals, including current, voltage, and temperature [39]. The proposed method improves estimation accuracy over traditional feed-forward neural networks by making use of data from previous SOCs and measurements. To determine the SOC of lithium batteries, a single hidden layer GRU-RNN-based momentum-optimized algorithm was investigated [40]. To prevent oscillation of the weight change and to increase the training speed of the estimation, the current weight change direction compromises the gradient direction at the current instant and historical time. The GRU-RNN-based momentum algorithm offers tools to obtain the battery SOC estimates and the related estimation errors by tweaking noise variances, epochs, and hidden layer neuron counts. In a recent study, the GRU-RNN was applied to pre-estimate battery SOC, and the adaptive Kalman filter (AKF) was used to smooth the output of the GRU model to obtain the final results [41]. In the proposed framework, it is not necessary to construct the intricate battery model because GRU-RNN model is well-suited to establish the non-linear mapping between the measured battery variables (voltage, current, and temperature) and SOC over the entire temperature range. Moreover, since the AKF process the outputs of the GRU-RNN, there would be more flexible to design the network’s hyperparameters, which introduces savings in computational cost. The enhanced noise adaptive algorithm not only makes it easier to choose the initial noise covariance but also makes the proposed GRU-AKF more adaptable to the more complex loading scenarios. In line with recent advancements, a unique SOC estimation approach for lithium-ion batteries was introduced that utilizes a deep feed-forward neural network (DFFNN), optimized through an attention mechanism relevant to stochastic weight algorithms (RAS) [42]. This strategy efficiently extracts pertinent features from input data and updates the weights and biases, addressing gradient issues and augmenting the DFFNN’s applicability across a range of operational conditions. Additionally, it implements a shifting-step unscented Kalman filter (SUKF) for the adaptive adjustment of error covariance, thus providing robustness against spontaneous error noise. This strategy has been verified to deliver precise SOC estimates, showcasing impressive error metrics in trials, indicating its potential applicability in managing batteries for electric vehicles.

Collectively, these research findings demonstrate that RNNs are effective in modelling sequential and time-series data. However, training them has proven difficult. The backpropagated gradients either increase or decrease at each time step, so they usually explode or vanish for the prediction tasks which require learning of the sequences with the limited use of parallelization across multiple timescales.

The attention-based Transformer model [43], which is primarily employed in natural language processing, recently made ground-breaking advancements in time-series prediction. Over the past few years, some researchers estimated SOC with good potential using the encoder-decoder structure, self-attention mechanism, and sequence-to-sequence method. The Transformer model can be calculated in parallel, which permits faster training and better use of GPU resources, unlike conventional RNNs. For example, the encoder-based Transformer neural networks have been demonstrated to be a powerful tool to estimate battery SOC in a self-supervised data-driven manner without considerable domain expertise to design features or adaptive filtering [44]. To explore the current and voltage data separately, a two-encoder architecture was developed, which is composed of one linear layer and two identical encoder layers for each encoder [45]. The outputs of the encoders were then concatenated into a single sequence and used as the inputs for the decoder. Moreover, an immersion and invariance adaptive observer was proposed to reduce the oscillations of the Transformer prediction. Moreover, self-attention Transformer model has demonstrated remarkable power in achieving accurate co-estimation of battery states [46]. Self-supervised Transformer neural networks unveil new avenues for assimilating representations derived from observational data. These intricate networks offer a gradation of abstractions, thereby simplifying the incorporation of attention mechanisms, an essential feature in the data processing pipeline. Their integration with a synergistic cloud-edge computing framework, when combined with the versatility of deep learning, substantially augments the predictive prowess of these networks. Such an approach ultimately aids in effectively capturing and decoding long-range spatio-temporal dependencies that span across diverse scales, thus enhancing the accuracy of analyses and predictions.

Table 1. Advantages and disadvantages of the common methods used for battery SOC estimation.

Methods	Advantages	Disadvantages
Ampere-hour Counting	Low computational complexity, straightforward method	Susceptible to errors, depends heavily on initial SOC
Open Circuit Voltage	Simple, easy to implement	Not suitable for real-time SOC, requires resting state
Model-Based Estimation	Can be used for online applications, low computational demand	Limited accuracy, requires careful parameterization
Physics-Informed Methods	Provides insights into the internal battery dynamics	Complex equations, high computational cost
Filter-based Methods	Capable of handling noise and estimation uncertainty	Requires accurate system model, might be computationally heavy
Machine Learning	Can handle complex relationships, potential for high accuracy	Needs a large amount of data, requires training phase

presents a comprehensive comparison of the merits and demerits associated with these aforementioned techniques, particularly in the context of battery SOC estimation. This balanced evaluation provides a clear understanding of the applicability and potential challenges of each method in real-world settings.

1.2. Contributions and Structure of the Work

In this study, we have meticulously designed a custom Transformer network architecture. This specific construct is aimed at accurately predicting the state of charge (SOC) of a battery under real-world operating conditions, thereby eliminating the need for prior knowledge of the underlying physical principles. Time-series data, in this case, are understood as a sequential aggregation of samples, observations, and unique features mapped over a temporal dimension. When compiled at a predetermined sampling interval, these data points aggregate into time-series datasets, serving as a valuable source of analytical information. The contributions of this study, embodying innovation, rigor, and the knowledge gained, can be summarized as follows:

(1)

The specialized Transformer model, termed as Bidirectional Encoder Representations from Transformers for Batteries (BERTtery), offers an effective tool to learn the non-linear relationship between SOC and input time-series data (e.g., current, voltage, and temperature), and to uncover intricate structures.

(2)

For efficient implementation of the Transformer, it is beneficial to create models and algorithms considering different operating conditions, such as charging and discharging processes. Consequently, the encoder network converts observational data into token-level representation, where each feature in the sequence is replaced with fixed-length positional and operational encoding.

(3)

A variable-length sliding window has been designed to produce predictions adhering to the underlying physico-chemical (thermodynamic and kinetic) principles. The sliding window aids in enriching the network with temporal memory, enabling BERTtery to generalize well beyond the training samples and to better exploit temporal structures in long-term time-series data.

(4)

For real-world applications, the accuracy of model performance is essential. Therefore, we have collected a diverse range of operating conditions and aging states from field applications to test the generalization capabilities of the machine learning model.

(5)

We devised a dual-encoder-based architecture to preserve the symplectic structure of the underlying multiphysics battery system. The channel-wise and temporal-wise encoders pave the way for broader exploration and capture epistemic uncertainty across multiple timescales, facilitating the assimilation of long-term time-series data while considering the influence of past states or forcing variables.

In the subsequent sections, we initially outline the machine learning pipeline, which includes data generation and the implementation of the self-attention Transformer model. Our specialized Transformer neural networks consist of three key components: embedding, a two-tower structure, and a gating mechanism. The selection of hyperparameters is also briefly discussed. Following this, we used field data to train and evaluate the Transformer model across a broad range of operating and aging conditions at both the cell and pack levels. We then discuss potential applications for real-world electric vehicle (EV) usage. Considering the fast-paced advancements in this field, we conclude by providing an outlook that includes reflections on the model’s current limitations.

2. Materials and Methods

2.1. Data Generation

Transferring academic advancements to commercial applications can be a challenging task, even with open data sharing. This is mainly due to reproducibility issues resulting from the gap between laboratory settings and end-use scenarios. The high-dimensional parameter space that parameterizes the state of charge (SOC) of lithium-ion batteries presents a significant challenge to probe, given the diverse aging mechanisms, numerous capacity fade processes, and manufacturing uncertainties involved.

To address this challenge, we collected two comprehensive datasets from real-world electric vehicle (EV) applications. As shown in

Table 2. Datasets used for machine learning modelling.

Datasets	Entity	Cell Specification	SOH	Operating Temperature Window
Group A (Cell level)	5 large-scale NMC cells	105 Ah, 115 Ah and 135 Ah	100%, 90% and 80%.	−5 °C to 40 °C
Group B (Pack level)	1 battery pack	92 NMC cells in-series	8 consecutive months of service time in an EV	10 °C to 35 °C

, Group #A comprises three lithium-ion cells with widely varying state-of-health (SOH), ranging from 100% to 80%, while Group #B comprises one large-scale battery pack after eight consecutive months of service under realistic conditions. All charging–discharging data were cycled under varied random charging and discharging conditions, with commercial cell balancing and thermal management. By deliberately varying the aging conditions, we generated a dataset that captures a wide range of SOH, from approximately 100% to 80% of nominal capacity. Although the cell temperature is controlled for security reasons in real-world applications, it can still vary by up to 45 °C due to the large amount of heat generated during charge and discharge. In this study, we probed discharging rates ranging from 0.1 C to 5 C pulse power for acceleration and multi-step charging rates ranging from 0.5 to 1.5 C.

Despite significant advancements in battery states estimation research, a prevalent gap remains between the simulated models and their real-world applicability. This disconnect arises due to the complex nature of lithium-ion batteries and the diverse range of operating conditions they encounter in real-world scenarios, which are often oversimplified or overlooked in simulation-based studies.

The authors of this study address this gap by amassing comprehensive datasets that depict the true behavior of lithium-ion batteries under a wide variety of real-world operating conditions. These datasets are not limited to idealized or laboratory conditions but encompass a broad spectrum of real-world scenarios, thus presenting a more realistic representation of battery performance. The introduction of these detailed and representative datasets paves the way for the development and validation of more accurate, robust, and reliable predictive models for battery diagnosis and prognosis. By employing these datasets, researchers can better understand the multifaceted dynamics of lithium-ion batteries in real-world scenarios and, consequently, enhance the transferability of academic advancements to commercial applications. This, in turn, facilitates the creation of effective battery management strategies, ultimately extending the lifespan and improving the safety of lithium-ion batteries in practical applications. For a comprehensive exploration of the disparity between laboratory testing and real-world applications, please refer to the detailed discussion presented in [47].

2.2. Transformer-Based Neural Network

Recently, Transformer models have been increasingly utilized across diverse facets of time-series analysis. Transformers address these complexities using self-attention mechanisms and positional encodings. These strategies permit them to concurrently concentrate on the immediate data samples and capture their sequence details. The Transformer′s structure is designed to identify relationships between various input segments. This is achieved by integrating positional data into these segments and employing the dot product operation. For a comprehensive understanding of the algorithm and mathematics, please refer to the resource provided in [48]. The proposed Transformer model (Figure 2) consists of four main modules: a dual-embedding module, a two-tower encoder module, sequence predictions, and a gating module. Below are the relationships between our Transformer model and BERT (bidirectional encoder representations from transformers): (i) Our BERTtery adopts the BERT methodology for self-supervised pretraining and employs Transformer as the model backbone. (ii) Although our embedding and encoder structure differs from BERT in several ways, it has special capabilities for exploring specific knowledge in the battery domain. (iii) We used two embeddings: positional embedding and operational embedding. (iv) Two duel-wise encoders—channel-wise encoder and temporal-wise encoder—were designed to capture the long-range spatio-temporal features automatically.

2.2.1. Normalization

The self-attention mechanism can be conceptualized as a procedure consisting of two stages. Initially, a normalized dot product is computed among all pairs of input vectors present in a specific input sequence. This normalization is accomplished through the application of the softmax operator, which can be expressed as:

$${\omega }_{\mathrm{ij}}=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}({\mathrm{x}}_i{}^{\mathrm{T}}{\mathrm{x}}_j)=\frac{e^{x_i{}^T{x}_j}}{\sum k^{e^{x_i{}^T{x}_k}}}$$

(1)

where ${\mathrm{x}}_i$ represent the input segments, ${\displaystyle {\sum }_{j=1}^n{\omega }_{ij}=1}$ and $1\le i,j\le n$.

In the subsequent phase, we identify a fresh representation, denoted as ${\mathrm{z}}_i$, for a specific input segment ${\mathrm{x}}_i$. This representation is a weighted aggregate of all segments ${\left\{{\mathrm{x}}_{\mathrm{i}}\right\}}_{j=\mathrm{i}}^n$ within the input:

$$z_{\mathrm{i}}={\displaystyle \sum _{j=1}^n{w}_{ij}{x}_j,\forall \stackrel{}{}1\le i\le n}$$

(2)

2.2.2. Embedding

To encode the position of the battery operational profiles in the sequence, we used both positional and operational (charging and discharging) embedding to encoder the position of the time-series data in the sequence. The operational embedding is designed to produce a sequence-level representation for battery data under different energy storage mechanisms. A sine-cosine encoding method was used in this study for both absolute and relative positional embeddings.

$$\mathrm{P}\mathrm{E}{(\mathrm{p}\mathrm{o}\mathrm{s})}_{2i}=\mathrm{s}\mathrm{i}\mathrm{n}(\mathrm{p}/10000^{2i/d_x})$$

(3)

$$\mathrm{P}\mathrm{E}{(\mathrm{p}\mathrm{o}\mathrm{s})}_{2i+1}=\mathrm{c}\mathrm{o}\mathrm{s}(\mathrm{p}/10000^{2i/d_x})$$

(4)

where 2i stands for the even dimensions and 2i + 1 stands for the odd ones. The position embedding technique can reflect both absolute and relative position information of the cell states.

(i)

Positional Encoding

BERTtery uses positional encoding to stamp the position of the tokens in the sequence. In applications to the electrochemical system, positional encoding plays an important role, as the underlying mechanism is related to the detection of the subtle variations in the parameters (current, voltage, and temperature) over long length and time scales. As time passes, the cell charge storage behaviors would significantly change under irregular cycling patterns and varying operating conditions for evaluating the electrochemical performance of energy storage devices. The introduction of embedding time into the input embedding improves the performance of the learning algorithm by forecasting long range dependencies and interactions in sequential data.

(ii)

Operational Encoding

In addition to positional encoding, battery operational (working condition) encoding was established to improve the performance of the learning algorithm, and then it applies a dropout technology to enhance the generalization and robustness [49]. Considering the unique operating conditions these batteries undergo in daily use, such as discharging, charging, and resting/idle periods, operational encoding plays a crucial role in improving the learning algorithm’s ability to accurately predict battery behavior. These distinct operating conditions significantly alter the cells’ behavior and underlying physical (thermodynamic and kinetic) properties, thus necessitating distinct model interpretations for each state. By integrating operational encoding, we acknowledge the differential behaviors and influences during these states and provide an enriched representation of the input data.

2.2.3. Two-Tower Structure

A two-tower architecture with channel-temporal encoders was developed for multivariate time-series regression. Each encoder block is composed of multi-head self-attention and feed forward network connected back-to-back with residual connections and normalization layers around each of the sub-layers. Residual connections offer an effective and simple technique for improving the model accuracy towards stable and efficient training of robust neural networks. The layer normalization substantially reduces the training time with a faster training convergence. Compared to the traditional single-tower architecture, the two-tower model can capture deeper electrochemical parameter changes or hidden representations, which may reflect an early stage of aging and open-circuit relaxation process. Capturing both the step-wise (temporal) and channel-wise (spatial) information provides powerful tools for learning the evolution of non-linear multiscale and multiphysics systems with inhomogeneous degradation behavior, considerably advancing the capabilities of SOC estimation under different aging and operating conditions.

The core of the Transformer neural network is the multi-head self-attention mechanism, which is made up of various scaled dot-product attention functions and enables the model to capture significant information in a sequence.

Vectors corresponding to input x_i, such as query q_i, key k_i, and value v_i, can be derived by employing the following method:

$$q_i=W_q{x}_i, k_i=W_k{x}_i, \mathrm{a}\mathrm{n}\mathrm{d} v_i=W_v{x}_i$$

(5)

The matrices W_q and W_k of dimension R^d*d_k, as well as W_v of dimension R^d*d_v, embody adjustable weight matrices. Consequently, the resultant output vectors, indicated by {z_i} from i = 1 to n, can be determined as follows:

$$z_i={\displaystyle \sum _j\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(q_i{}^{\mathrm{T}}{k}_j)v_j}$$

(6)

It is important to highlight that the weighting attributed to the value vector v_i is reliant on the evaluated correlation between the query vector q_i at the i-th position and the key vector k_j at the j-th position. The dot product’s magnitude tends to augment with the growth in the size of query and key vectors. Due to the softmax function’s susceptibility to large magnitudes, the attention weights undergo scaling proportional to the square-root of the size of the query and key vectors, denoted by dq, as follows:

$$z_i={\displaystyle \sum _j\mathrm{softmax}(\frac{q_i{}^{\mathrm{T}}{k}_j}{\sqrt{d_q}})v_j}$$

(7)

In the matrix form, the self-attention mechanism can be succinctly expressed as:

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q,K,V)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\frac{Q{K}^T}{\sqrt{d_K}})V$$

(8)

where Q, K, and V represent query, key, and value matrix, respectively, and d_k is the dimension of the key matrix.

Multi-head attention empowers the model to concurrently focus on data from varied representational spaces at diverse positions. This capacity is stifled by averaging in a model utilizing a singular attention head.

$$M\mathrm{ul}tiHead(Q,K,V)=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}(\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_1,\dots ,\mathrm{h}\mathrm{e}\mathrm{a}{\mathrm{d}}_{\mathrm{n}}){\mathrm{W}}^O$$

(9)

$$where hea{d}_{\mathrm{i}}=\mathrm{Attention}(Q{W}_{\mathrm{i}}{}^Q,K{W}_{\mathrm{i}}{}^K,V{W}_{\mathrm{i}}{}^V)$$

(10)

(i)

Temporal-Wise Encoder

The two-tower architecture, featuring a temporal self-attention decoder, is employed in this study for its exceptional ability to learn long-term dependencies in time-series data. This design proves particularly advantageous in extracting implicit features across a broad spectrum of charging and discharging activities. Incorporation of the self-attention mechanism and positional encoding techniques not only curtails computational cost but also enhances the analysis of current data samples within the sequence. Furthermore, the use of a dual encoder opens exciting avenues for modeling temporal evolutionary patterns, thereby allowing for precise estimation of the multiphysics battery system and prediction of future developments. A notable strength of the Transformer model is its combination of stacked self-attention and point-wise, feed-forward layers. This architectural decision ensures that the model effectively recognizes fine-scale features, thereby increasing the model’s prediction accuracy and operational efficiency.

(ii)

Channel-Wise Encoder

In the two-tower architecture, channel-wise attention plays a crucial role in capturing channel features extracted along the temporal dimension. By calculating attention weights or scores, this mechanism amplifies the contribution of informative channels while diminishing the impact of less significant ones, ensuring a more nuanced and accurate representation of the data. The channel-wise encoder, armed with masked multi-head attention, adeptly captures spatial correlations among both proximate and remote charging/discharging dynamics, adding another layer of depth to the analysis. The potential to broaden diagnostic techniques also emerges from this setup, particularly through modeling spatial dependencies. This process, which takes into account the continuity and periodicity of time-series data, can provide deeper insights into the temporal patterns and variations inherent in the battery’s performance. This approach offers a more comprehensive and dynamic understanding of battery operations.

2.2.4. Gating Mechanism

The gating mechanism serves as a practical and straightforward method for amalgamating the outputs of the two encoder towers. Its role in efficiently integrating the learned representations ensures an optimal synthesis of insights gathered from both towers. In conjunction, a linear layer and softmax operation, acting as a normalized exponential function, were implemented. This arrangement functions like a multinomial logistic regression, effectively generating the final prediction results. The utilization of these techniques not only streamlines the prediction process but also enhances the accuracy and reliability of the results. By harnessing the power of these methods, we ensure that the model benefits from the full range of information captured by both encoders, leading to more robust and precise estimations.

2.2.5. Hyperparameter Determination

In the present research, we conducted a thorough exploration on how various hyperparameters can impact SOC estimation for large-scale, real-world EV batteries (Figure 3). The variables we studied include the quantity of attention heads, the size of embeddings, and the layer count in the self-attention Transformer model. Each of these elements affects the model’s capacity to learn an array of attention patterns and complex representations. Key hyperparameters, such as the learning rate that affects the velocity of learning, and the method of positional encoding that impacts the comprehension of temporal relationships, were also considered. Other variables, such as the dropout rate, batch size, and weight initialization techniques, were evaluated for their influence on the learning performance and efficiency of the model. These hyperparameters were fine-tuned with careful consideration to factors such as model performance, computational expenditure, and the specific requirements of our task. Below are the details of our chosen configurations:

(i)

The model dimension in both the channel-wise and temporal-wise encoders was set at 64, enabling it to capture rich feature information.

(ii)

We used four layers in both the channel-wise and temporal-wise encoder, with a batch size of 384, balancing between learning capability and computational cost.

(iii)

Each multi-head attention for each layer was set to eight heads, allowing the model to focus on multiple input features simultaneously.

(iv)

We conducted 1300 training epochs to ensure thorough learning.

(v)

A dropout rate of 0.1 was applied as a regularization technique to prevent the model from overfitting.

(vi)

We employed the Adam optimizer for loss minimization, setting the initial learning rate at 2 for faster convergence.

(vii)

Gradient clipping with a value set at 1 was used to prevent the gradient values from becoming too large, known as the exploding gradients problem.

(viii)

A weight decay rate of 0.0001 was chosen to provide additional regularization.

(ix)

Batch normalization was implemented to accelerate learning and stabilize the neural network.

3. Results

3.1. Model Performance

We leveraged battery time-series charging–discharging data by pre-training a two-tower transformer encoder to extract dense vector representations of multivariate time-series. In this study, we initially pre-trained the Transformer model using observational data from tens of cells that were randomly collected throughout their operational lifetime. These data, with a sampling frequency of 10 s using onboard sensor measurements, were input into the Transformer model. The model’s output, in turn, is the corresponding SOC estimations for each of these sampling points. The proposed method can be immediately applied to transient data while preserving prediction accuracy, obviating the necessity for a steady-state detector and allowing for very large time-steps with high accuracy. The Transformer architecture is characterized by large data volumes, dynamic loading operations, and high correlations between the dots for each sliding window when taking into account the high-dimensional stochastic dynamics and probability distributions for industry-scale time-series data in physical problems. It was discovered that the Transformer model provides efficient, easy-to-implement, meshless implementations for the kind of pattern identification associated with persistently positive connectivity between these regions across the sliding window (Figure 4).

The attention mechanism is a fundamental component of the Transformer model that lends it the power to handle sequences of data. The attention mapping is typically performed through what is known as multi-head attention. This mechanism allows the model to focus on different parts of the input sequence for each element in the output sequence. It provides a weighted combination of all input positions for each output position, wherein the weights denote the relevance or attention the model pays to each input element when generating a specific output element. Multi-head attention calculates the compatibility or similarity score between different positions in the sequence through a dot product, which is then scaled and passed through a softmax function to yield the attention weights. These weights are then used to create a weighted sum of the input values, allowing the model to focus on certain inputs while generating specific outputs.

Current rates, temperature, and aging conditions are three important factors to validate the generalization performance of SOC estimation model. Therefore, a wide range of cell aging conditions and operating voltage/current/temperature windows are adopted to train and test the data-driven model for improving accuracy and enhancing generalization. In this context, our investigation extends across a total of 5 Li-ion cells and 1 large-scale battery pack, as presented in Table 2. We have divided the model development dataset randomly into two distinct sections, namely the training and testing sets. These sets feature random real-world application scenarios, adding a layer of practical complexity to the investigation. The estimation results are summarized in

Table 3. The test errors over the cell and pack dataset.

Datasets	RMSE	APE	MAE	Operating Conditions
Cell_1	0.4857	0.59%	1.6507%	dynamic temperatures −4 °C to 4 °C
Cell_2	0.4356	0.71%	1.3208%	dynamic temperatures 0 °C to 35 °C
Cell_3	0.4047	0.67%	1.1275%	aging conditions, 100% SOH
Cell_4	0.4046	0.60%	0.9461%	aging conditions, 90% SOH
Cell_5	0.4218	0.41%	1.0836%	aging conditions, 80% SOH
Battery pack, Cell_V_max	0.4033	0.95%	1.4876%	Pack level, 20 °C to 25 °C, ~97.5% SOH
Battery pack, Cell_V_min	0.4497	0.88%	1.7525%	Pack level, 20 °C to 25 °C, ~97.5% SOH

.

3.1.1. Cell Level SOC Estimation at Dynamic Temperatures

A prime objective behind the development of new algorithms is their ability to withstand and function robustly in the face of field data. Factors such as missing or noisy data, outliers, and other inconsistencies can drastically influence the model performance. When considering model performance, predictive accuracy, and estimation robustness against temperature uncertainty, scattered sensor measurements and sensor drift emerge as significant considerations during the design of appropriate model architectures and novel training algorithms. This holds particularly true for real-world applications, where practical constraints and dynamic environmental factors come into play.

We trained and tested the proposed Transformer algorithm at two dynamic operating temperature windows, ensuring that we scrutinized its performance under varying conditions. Figure 5 and Figure 6 detail these temperature windows. This process not only tests the robustness of the algorithm against temperature fluctuations but also gauges its adaptability and consistency of performance under dynamic conditions. It showcases the robustness of the BERTtery model and its ability to handle imperfect data and temperature uncertainties efficiently. The validation process thus serves as a testament to the BERTtery model’s resilience and adaptability, affirming its applicability and potential in practical, real-world scenarios.

3.1.2. Cell Level SOC Estimation at Different Aging Conditions

Aging is an intrinsic property of lithium-ion batteries that significantly influences their performance and lifespan. Degradation phenomena, such as the loss of lithium inventory (LLI) and the loss of active material (LAM), pose considerable challenges to assess SOC estimation for batteries under varying aging conditions.

The Transformer model leverages additional information gleaned from the relationship between SOC and input data across different aging conditions. This ability to adapt to changes brought on by aging increases the model’s accuracy and its effectiveness in real-world scenarios. A battery is typically considered to have reached its end-of-life when its full charge capacity diminishes to 80% of the nominal value—a key threshold in battery manufacturing. Our training and testing cover this entire spectrum, allowing us to understand the performance of the BERTtery model in a range of scenarios reflecting the service life of batteries. This process is divided into three groups, each representing different stages in the battery life, as illustrated in Figure 7, Figure 8 and Figure 9. In essence, by evaluating the model’s performance under dynamic aging conditions, we delve into an often overlooked but crucial aspect of battery SOC estimation. This helps ensure that our model remains robust, adaptable, and accurate across the full lifespan of a battery, thereby enhancing its practical applicability and usability in real-world applications.

3.1.3. SOC Estimation at Pack Level

The intricate operation of a lithium-ion battery rests upon a multitude of factors such as diffusion pathways, electron/ion transport, various phase transformations, electrochemical redox reactions, both reversible and irreversible, charge–transfer reactions, and several material-dependent elements. However, these operations become exponentially complex in practical applications, where hundreds or even thousands of lithium-ion batteries are interconnected in a series-parallel architecture to provide sufficient power and energy. Pack design modifications, environmental conditions, and loading scenarios are a few among many factors that can significantly impact the overall performance of the battery system. Ambient temperature variations, cell packaging alterations, batch-to-batch and cell-to-cell inconsistencies originating from differing synthesis conditions, electrolyte wetting procedures, and mechanical properties can lead to substantial deviations in the predicted outcomes. These complexities emphasize the importance of the practical application performance of predictive models. After all, it is the real-world efficacy of these models that determines their value. Accordingly, we further scrutinize the Transformer model’s performance by employing it on one large-scale battery pack operating under dynamic conditions. Figure 10 represents these tests. To concisely present the estimation, only the cells with the maximum and minimum voltage are depicted in the plots.

In this respect, the validation process transcends beyond a mere algorithmic scrutiny and extends into a comprehensive examination of the model’s adaptability to intricate, multifactorial, and dynamic conditions. As the reliance on lithium-ion batteries in practical applications continues to increase, the necessity for sophisticated, robust, and reliable predictive models escalates correspondingly. It is this critical juncture of theoretical models and practical applications in which the true value of a predictive model is ascertained, ultimately contributing to the continuous evolution and optimization of battery technology.

3.2. Model Training and Evaluation

Numerous stochastic processes are involved in the instantiation of deep learning models. All experiments were run with a predetermined seed value to guarantee the uniformity and repeatability of the results. Unlabeled vectors of input sequence were utilized in the pre-training stage to train the model. The metrics that are used in the loss function and model evaluation are described as follows.

3.2.1. Loss Function

The Transformer model was trained using an end-to-end approach, and the choice of loss function is crucial in guiding this process. The loss function quantifies how far the model’s predictions deviate from the actual values and serves as the criteria that the learning algorithm seeks to minimize. The mean squared error (MSE) in regression problems can be expressed as:

$$\mathcal{L}\mathrm{M}\mathrm{S}\mathrm{E}(\mathrm{y},\widehat{\mathrm{y}})=\frac{1}{\mathrm{N}}{{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}({\mathrm{y}}_{\mathrm{i}}-{\widehat{\mathrm{y}}}_{\mathrm{i}})}}^{{}_{{}_{{}_2}}}$$

(11)

where $y_i^{}$ and ${\widehat{y}}_i^{}$ are the observed and estimated value, respectively, of the i-th samples, and n is the total number of samples in the dataset.

Mean Squared Error (MSE) is frequently chosen for regression tasks, mainly due to its simplicity, computational efficiency, and focus on amplifying larger discrepancies. It is differentiable, which is advantageous for optimization methods such as gradient descent, and is a common yardstick for gauging the performance of regression models. MSE quantifies the deviation between the predicted SOC and the actual values. To minimize this loss, the Adam optimizer [50] was deployed with a user-defined learning rate, which dynamically adjusts the model parameters during the training process, thereby ensuring a smoother and more efficient convergence.

3.2.2. Evaluation Metrics

In this study, three metrics were adopted to evaluate the performance of SOC estimation model, including root mean square error (RMSE), the maximum absolute error (MAE), and average percentage error (APE). (a). RMSE is a widely used metric for evaluating the accuracy of predictions. It measures the square root of the average of the squared differences between the predicted SOC values and the corresponding ground truth values. (b). MAE measures the maximum absolute difference between the predicted SOC values and the true values. It provides an insight into the worst-case scenario of prediction error. (c). APE quantifies the average percentage difference between the predicted SOC values and the true values. It provides a measure of the relative error in the predictions.

These evaluation metrics were chosen to capture different aspects of the model’s performance. RMSE and MAE focus on the absolute error, while APE provides insights into the relative error. By considering all three metrics, researchers can assess the accuracy, worst-case scenario, and relative performance of the SOC estimation model, facilitating a comprehensive evaluation of its effectiveness in capturing battery SOC.

${\mathrm{y}}_{\mathrm{i}}^{\ast }$ is the observed SOC, ${\widehat{\mathrm{y}}}_{\mathrm{i}}^{\ast }$ is the predicted SOC, and n is the total number of observational data. Therefore, RMSE can be calculated as:

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}{\left(\frac{{\widehat{\mathrm{y}}}_{\mathrm{i}}^{\ast }-{\mathrm{y}}_{\mathrm{i}}^{\ast }}{{\mathrm{y}}_{\mathrm{i}}^{\ast }}\right)}^2}}$$

(12)

Maximum absolute error (MAE) can be given by:

$$\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}{\mathrm{r}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\underset{1\pounds \mathrm{i}<<\mathrm{n}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|{\widehat{\mathrm{y}}}_{\mathrm{i}}^{\ast }-{\mathrm{y}}_{\mathrm{i}}^{\ast }\right|\times 100$$

(13)

The average percentage error (APE) is defined as:

$$\mathrm{E}\mathrm{r}\mathrm{r}\mathrm{o}{\mathrm{r}}_{\mathrm{A}\mathrm{P}\mathrm{E}}=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}\left|\frac{{\widehat{\mathrm{y}}}_{\mathrm{i}}^{\ast }-{\mathrm{y}}_{\mathrm{i}}^{\ast }}{{\mathrm{y}}_{\mathrm{i}}^{\ast }}\right|}\times 100$$

(14)

3.3. Model Development and Applications

In this research, we utilized MATLAB for handling and manipulating the EV battery field data, whereas Python, in tandem with open-source deep learning libraries such as TensorFlow and PyTorch, was employed for constructing the Transformer model. Our computing infrastructure is comprised of an Intel Core i7-4790K CPU clocked at 4.00 GHz, coupled with 32 GB of RAM, and a robust Nvidia GeForce RTX3090 GPU. Machine learning models considerably enhance predictive capacity, especially for long-range spatial connections spanning various time scales, all while reducing computational costs. However, the computational and storage limitations of current on-board Microcontroller unit (MCU) necessitate model pretraining for optimal performance.

The model’s deployment comprises two phases: offline pretraining (training and testing) and online application. We utilized a private cloud for offline training, which had been previously used for developing multiple machine learning techniques for assessing battery state of health (SOH) and state of safety (SOS). References for the data generation, methodology, and cloud framework can be found in the cited literature [26,27,51]. The BMS’s embedded software is updated or calibrated using over-the-air (OTA) technology, enabling Software as a Service (SAAS) for connected EVs, as shown in Figure 11.

4. Discussion and Outlook

Machine learning methods, particularly deep learning [52], offer promising avenues for advancing our understanding and management of multiphysics and multiscale battery systems, pushing the boundaries of efficiency and accuracy. Amidst our relentless pursuit of sustainable and digitalized energy systems, these models play a pivotal role, demonstrating superior capabilities in extracting meaningful insights from high-dimensional and complex data, and thus facilitating accurate predictions and expedited training times. However, certain challenges necessitate careful consideration. Real-life observational data, which often includes time-series, lab data, and field data, are frequently scarce, noisy, and not directly accessible for certain variables of interest. Therefore, it is crucial to leverage specialized network architectures or kernel-based regression networks that excel in generalization beyond limited data and adapt to dynamic operating conditions and different aging levels.

As battery technologies rapidly evolve with new cell chemistries and architectures, predictive models must adapt swiftly. Variabilities within the same battery chemistry, caused by factors such as the manufacturing processes, cell packaging, and equipment differences, compound this challenge. The models that can efficiently accommodate these variables and maintain high accuracy will undoubtedly garner greater attention. Moreover, domain adaptation techniques that learn from diverse data sources and hybrid modeling approaches combining physics-based and data-driven models can improve model generalization and accuracy. The innovative learning paradigm has found a contemporary manifestation in the development of Physics-Informed Neural Networks (PINNs) [53]. This nascent category of deep learning algorithms proficiently integrates data with advanced mathematical constructs, including partial differential equations (PDEs), even in instances where specific physics principles are omitted or not factored in. The future of cloud battery management system [54,55] heavily relies on tackling these challenges, leading to the creation of more precise and trustworthy predictive models across various applications. An in-depth investigation into the extent of generalization of these transformations is crucial, identifying the range of observations for which one model can reliably map to another. Equally critical is defining the boundaries of this generalization—the point beyond which these models fail to transform or calibrate in relation to each other.

Addressing these challenges is paramount in advancing towards a more sustainable and digitalized energy landscape, where the role of machine learning in battery management becomes increasingly crucial. This continual evolution also paves the way for the convergence of digital technologies with sustainable energy systems, shaping the future of the energy sector.

5. Conclusions

Deep learning has revolutionized the field of machine learning by allowing computational models composed of multiple processing layers to learn data representations with multiple levels of abstraction. By leveraging the backpropagation algorithm, deep learning uncovers intricate structures in large datasets, indicating how a machine should adjust its internal parameters to compute the representation in each layer from the representation in the previous layer. Transformer models employ a multi-headed attention system, making them proficient in handling time series data. They concurrently seize the context—both prior and succeeding—of each sequence element. The use of multiple attention heads facilitates the analysis of different representational subspaces, enhancing the probing of diverse relevance aspects among input elements within time series data. This capability allows machines to be fed with raw time-series data and to automatically discover the representations and extract temporal features required for classification or regression. In this study, we showcase a bespoke two-tower Transformer neural network technique for predicting the SOC of lithium-ion batteries, using field data from practical electric vehicle (EV) applications. This model leverages the multi-head self-attention mechanism, which is instrumental in achieving precise predictions. This mechanism excels at discerning and emphasizing critical data points while simultaneously mitigating the influence of less relevant information. This model’s unique advantage is its ability to be trained solely on battery time-series data, effectively eliminating the need for laborious feature engineering. The strength of this approach lies in its adaptability to the dynamic nature of battery data, aided by a 10 s sampling frequency, enabling the capture of battery states amidst fluctuating operating conditions. The self-attention mechanism also allows the model to focus on varying sequence lengths and dependencies, making it particularly effective in dealing with the temporal nature of battery data. Furthermore, the two-tower architecture ensures that the model can learn intricate correlations, maximizing the extraction of relevant information. This study underscores the potential of integrating machine learning tools with sparse sensor measurements, pushing the frontiers of battery state estimation in complex, real-world scenarios.