Performance Analysis of a Reconfigurable-Intelligent-Surfaces-Assisted V2V Communication System

Abstract

Novel reconfigurable Intelligent Surfaces (RISs) area technology can improve the communication performance by changing the wireless transmission environment. Introducing RIS technology into Vehicle-to-Vehicle (V2V) communication environments can enhance the communication reliability by creating Line-of-Sight (LoS) communication links, thereby effectively improving the communication performance. However, in RIS-assisted V2V large-scale communication networks, the stochasticity of network nodes and random interference can impact performance. In this article, we examine the outage communication transmission performance of an RIS-assisted V2V communication network. We select the signal transmission mode based on the obstacle presence between vehicles and use the stochastic geometry theory to calculate the probabilities of the two modes: direct mode and RIS-assisted mode. By deriving the communication distance distribution and the aggregate interference distribution, we evaluate V2V communication in the direct mode to assess its transmission performance in two scenarios and obtain the overall outage probability. The numerical results demonstrate a better performance in RIS-assisted V2V networks, with an improved optimal phase shift scheme over that of the original V2V network. Monte Carlo simulation validated our analytical findings.

1. Introduction

As one of the key components of Intelligent Transportation Systems (ITS), the Internet of Vehicles (IoV) can meet ITS’ needs in traffic safety and information services [1]. With the explosive growth in the number of private vehicles, future IoV will have higher throughput, lower latency, and higher reliability [2]. However, the currently used wireless radio interface technologies in the IoV are deployed in sub-6G frequency bands. Most sub-6G frequency bands have already been allocated, which cannot meet future communication requirements for the IoV. The millimeter-wave (mmWave) frequency band has many unallocated bandwidths [3]; so, it should be considered for use in IoV. The communication network based on mmWave can reduce latency and increase the data transmission rates. Therefore, introducing mmWave technology into V2X communication can provide higher data rates for vehicle connectivity. mmWave-based V2X communication technology has great research value and application prospects [4]. However, there are still some unresolved issues with the mmWave-based vehicular network, such as: (1) High path loss [5]. Compared to existing Ultra-High Frequency (UHF) low-level microwave communications, the mmWave band experiences greater propagation loss. (2) Vulnerability to blockage [4,6]. Compared to microwave systems, mmWave systems (with wavelengths less than 1 cm) are more susceptible to obstacles. This includes large obstacles, such as buildings, as well as smaller ones, such as vehicles and pedestrians, which can significantly impact the performance of the mmWave system.

Various technologies are being developed to achieve future reliable and high-capacity vehicular networks. These techniques include effective modulation and coding schemes, time–space–frequency diversity techniques to compensate for channel shadowing and fading, dynamic power and rate control based on channel conditions, and beamforming. However, these technologies cannot alter the wireless channel itself. Recently, a new concept emerged based on the progress of programmable metamaterials: controllable/reconfigurable RIS. RIS solves this limitation with an innovative approach that can change the wireless propagation environment [7]. RIS is a cost-effective and innovative technology that can improve mmWave-based communication systems [8,9]. It enhances transmission coverage and signal quality by controlling the direction of electromagnetic wave propagation [10,11]. Composed of numerous low-cost passive components, RIS can be programmed with software to adjust the phase and amplitude of the incident signal to enhance the signal quality [12]. When RIS reflects an incident signal, it generates an additional phase shift. The controller assists RIS in guiding the incident signal in the receiver’s direction [13]. By exploiting the characteristics of RIS, we improve the vulnerability of mmWave-based communication systems to obstacles. Therefore, investigating the performance of RIS-assisted communication networks is crucial. Unlike existing technologies, such as MIMO, relay or beamforming techniques, RIS technology improves wireless communication systems by reflecting low-impact electromagnetic waves, which makes it similar to multi-antenna relays. Deploying RIS in wireless communication networks assists signal propagation between transmitters and receivers, while effectively improving fading loss and interference problems associated with wireless channels [14,15].

As an emerging technology, RIS can effectively improve wireless communication signal losses and multipath fading effects. Therefore, it has received widespread attention for enhancing wireless transmissions. Numerous studies have been conducted on the performance analysis of RIS-assisted communication network systems. For instance, the authors of [16] analyzed path loss and the bit error rate by studying the general communication theory model of RIS in wireless networks and focused on the open research issues it brought about. The authors of reference [17] proposed two different transmission schemes for RIS and derived closed-form expressions for indicators, such as outage probability, average bit error rate, and average channel capacity. In [18], a new closed-form expression was derived to explore the impact of spatial channel correlation on the outage probability in RIS-assisted SISO communication systems, considering an arbitrary phase shift and indirect channel correlation matrix. Based on statistical channel state information and traversal spectrum efficiency upper limits, the authors of [19] analyzed the performance of large-scale antenna systems based on RIS and proposed an optimal phase shift design to achieve maximum ergodic spectral efficiency. In [20], the author provided an analysis framework for evaluating the Ergodic Capacity (EC) of RIS-assisted systems under a high signal-to-noise ratio and a high reflection unit conditions, giving approximate values of the EC. Furthermore, a novel ground-to-air communication scenario based on RIS was pro-posed in [21]. An alternating optimization method was developed to study the maximum sum rate of UAV trajectory and RIS phase movement.

Some have already introduced RIS into vehicular communication and studied the performance of RIS-based vehicular communication. For example, RIS can assist in resource allocation and spectrum sharing for vehicular communication. The authors of reference [22] considered the resource allocation problem of RIS-assisted vehicle communication, where V2V and V2I links with different QoS requirements share a spectrum to maximize V2I’s the total capacity. A joint optimization framework for power allocation, reflection coefficient, and spectrum allocation was proposed to verify the effectiveness of RIS-assisted vehicle communication. Meanwhile, the authors of [23] studied the physical security issues of RIS-based vehicular networks, focusing on two modes of vehicular network systems: RIS-based access points for V2V communication at the source, and RIS-based relays on buildings (in the form of Vehicle Ad hoc Networks (VANETs)).

Additionally, RIS enhances the transmission signals from the infrastructure to the vehicle. In [24], the authors proposed a signal transmission model for RSU–RIS–vehicle, which constructs a Line-of-Sight communication link between RSU and the vehicle through RIS, jointly optimizing the resource scheduling at RSU and passive beamforming at RIS to enhance the signal transmission performance. Furthermore, the authors of ref. [25] designed an intelligent and efficient hybrid vehicle communication framework combining Dedicated Short Range Communications (DSRC) based on RIS and cellular communication to maximize the energy efficiency and achieve efficient and low-latency communication. The authors of reference [26] investigated the downlinks in RIS-assisted vehicular communication networks where vehicle distribution is modeled using a Poisson Point Process (PPP). The article derived an expression for outage probability with central limit theorems and series expansions. The authors of reference [27] analyzed the use of Large Intelligent Reflective Surfaces (LIS) in vehicular networks, focusing on system performance under Weibull fading conditions and assumed that interference from a single cellular user affects vehicular communication. The paper derived a closed expression for the outage probability, and also, discussed approximate values for three cases: a high signal-to-noise ratio, a low signal-to-noise ratio, and weak interference. Therefore, the authors of most existing research on RIS-assisted communication have applied RIS to traditional wireless communication scenarios. Some have studied RIS-assisted vehicular communication and adopted corresponding optimization strategies to improve the communication performance. Furthermore, the authors of a few studies have analyzed the performance of RIS-assisted vehicular communication. However, unlike traditional wireless networks, the impact of node randomness on network performance needs to be considered in vehicular network analysis. At the same time, the impact of random interference on RIS-assisted vehicular networks also deserves attention.

In this paper, we present a novel RIS-assisted V2V communication model that considers the stochasticity of the vehicle and RIS location distribution. Unlike previous works, we use the Homogeneous Poisson Point Process (HPPP) and Matérn Hard Core Process (MHCP) to model the location distribution of vehicles and RISs. Additionally, we analyze the random interference caused by other vehicles. Our proposed framework can effectively capture the impact of stochasticity in RIS and vehicle locations, as well as aggregate interference from interfering vehicles. The main contributions are summarized below:

• We establish an RIS-assisted V2V communication model to analyze the performance improvement from introducing RIS technology into V2V networks. This article uses PPP and MHCP to describe the stochasticity of vehicle and RIS location distribution.
• We study the distance distribution between communication nodes based on the stochasticity of vehicle and RIS positions in the proposed RIS-assisted V2V communication model. Finally, we obtain the outage probability of the RIS-assisted V2V communication network.
• Simulation results are presented to validate the analysis results and to identify the behavior of OP for several important parameters, namely, the number of RIS reflective elements, hard core distance of RIS distribution, signal-to-interference and noise ratio (SINR) threshold, and vehicle density. Numerical results provide valuable insights into the impact of RIS-assisted V2V communication networks.

The remainder of this paper is organized as follows. Section 2 introduces the RIS-assisted V2V communication model. In Section 3, we derive the interference distribution, distance distribution, and final outage probability. Section 4 presents a set of simulation results to corroborate our analytical results. Section 5 provides the concluding remarks of this paper.

2. System Model

This paper focuses on a V2V communication system assisted by RIS, which involves multiple vehicles and RISs. Figure 1 illustrates the RIS-assisted V2V communication system in RIS-assisted transmission and direct transmission modes. The vehicle locations follow a 1D HPPP, whereas the locations of the RISs follow a 1D MHCP to avoid the deployment distance between RIS being too small. We considered a communication scenario involving one RIS in service and one V2V pair, which are represented as a user transmitter (UT) and user receiver (UR), respectively. The distance between the UT and UR was fixed at $L$.

When a vehicle obstacle is present on the communication path between UT and UR, it blocks the direct communication link. This results in a Non-Line-of-Sight (NLoS) channel between UT and UR, which means minimal direct communication will occur during propagation. Instead, strong emissions or diffractions are mainly used for transmission [28]. In these cases, UT selects the nearest RIS to assist with communication. Conversely, when no other vehicles are on the path, UT and UR establish an LoS channel for communication.

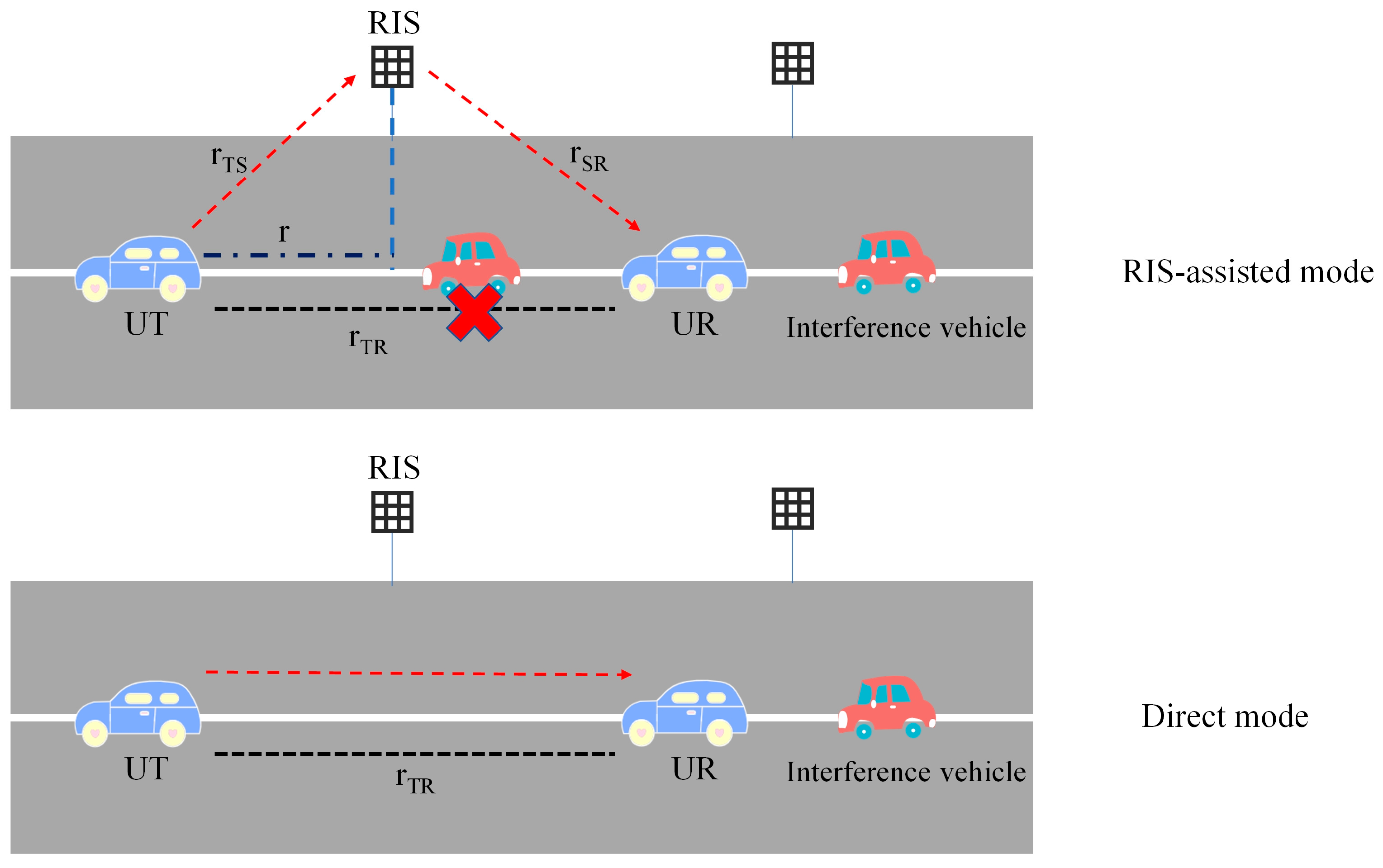
2.1. Network Deployment

In this paper, the distribution of vehicle locations on the road was modeled using a 1D HPPP ${\mathsf{\Phi }}_V$ with an intensity of ${\lambda }_V$. The RIS’ location distribution was also modelled using the 1D MHCP ${\mathsf{\Phi }}_R$ with an intensity of ${\lambda }_R$. The MHCP is a two-step point process generated from PPP ${\mathsf{\Phi }}_P$, with density ${\lambda }_P$. The first step is to associate each point in ${\mathsf{\Phi }}_P$ with a uniformly distributed mark, $m(m\sim Unif[0,1])$. Secondly, points are deleted if their marks exceed any other points within the hard-core distance $d_h$. Additionally, points are removed if there are other points within a specific range (hard-core distance) around them, and they have smaller markers for each point in [29]. Consequently, the probability that an arbitrary point in ${\mathsf{\Phi }}_P$ is retained as follows:

$$P_{re}(d_h)={\displaystyle {\int }_0^1\exp (-2m{\lambda }_p{d}_h)d}m=\frac{1-\exp (-2{\lambda }_p{d}_h)}{2{\lambda }_p{d}_h}$$

(1)

2.2. Channel Model

Assuming that the RIS is equipped with $N$ reflecting elements, we use $h_{TS}=[h_{TS,1},\cdots ,h_{TS,n},\cdots ,h_{TS,N}]$ and $h_{SR}=[h_{SR,1},\cdots ,h_{SR,n},\cdots ,h_{SR,N}]$ to characterize the channels of both UT-RIS and RIS-UR links, respectively. Path loss can be defined as $l(r)=r^{-\alpha }$, where $\alpha$ denotes the pathloss exponent, and $r$ is the communication distance. Subsequently, $h_{TS,n}$ and $h_{SR,n}$ can be expressed by:

$$h_{TS,n}=\sqrt{l(r_{TS})}{\tilde{h}}_{TS,n}=\sqrt{l(r_{TS})}\left|{\tilde{h}}_{TS,n}\right|e^{j{\varphi }_n}$$

(2)

$$h_{SR,n}=\sqrt{l(r_{SR})}{\tilde{h}}_{SR,n}=\sqrt{l(r_{SR})}\left|{\tilde{h}}_{SR,n}\right|e^{j{\omega }_n}$$

(3)

where ${\tilde{h}}_{TS,n}$ and ${\tilde{h}}_{SR,n}$ denote small-scale fading; $r_{TS}$ and $r_{SR}$ denote the distance between UT-RIS and RIS-UR, respectively; ${\varphi }_n$ and ${\omega }_n$ are the corresponding channel phase, which are uniformly distributed within $(-\pi ,\pi ]$.

2.3. Signal and Interference Model

For the RIS-assisted mode, we can write the received signal at UR from the nearest RIS as:

$$y_1=\sqrt{P_T}{h}_{SR}^T\mathsf{\Theta }{h}_{TS}{x}_T+I+n_R$$

(4)

where $\mathsf{\Theta }=diag\left(\left[{\eta }_1{e}^{j{\theta }_1},\cdots ,{\eta }_n{e}^{j{\theta }_n},\cdots ,{\eta }_N{e}^{j{\theta }_N}\right]\right)$ is a diagonal matrix, ${\eta }_n\in [0,1]$ refers to the fixed reflecting amplitude coefficient, ${\theta }_n\in [0,\pi ]$ stands for the phase shift of the n-th reflecting element of RIS, and $x_T$ is the desired signal, satisfying $\mathbb{E}\left\{{\left|x_T\right|}^2\right\}=1$. In addition, we let $n_R$ indicate the zero-mean complex Gaussian noise, with variance $N_0$.

Hence, the signal power received by the typical user from the nearest RIS is given as:

$$S_R=P_T{\left|h_{SR}^T\mathsf{\Theta }{h}_{TS}\right|}^2=P_T{\left|{\displaystyle \sum _{n=1}^N{\eta }_n\left|h_{TS,n}\right|\left|h_{SR,n}\right|e^{-j\left({\varphi }_n+{\omega }_n+{\theta }_n\right)}}\right|}^2$$

(5)

where $P_T$ indicates the transmission power of the signal at UT in RIS-assisted mode.

Each reflecting element can be intelligently and continuously controlled using smart software, allowing ${\theta }_n{}^{\ast }$ to be the optimal setting, such as ${\theta }_n{}^{\ast }=-\left({\varphi }_n+{\omega }_n\right)$ stated in [30]. Assuming that the reflection amplitude of each reflecting element is approximately equal (i.e., ${\eta }_n=\eta$ for all n), and in combination with Equations (2) and (3), the optimal received signal power at UR can be expressed as:

$$\begin{array}{l}{S}_R{}^{\ast }={\eta }^2{P}_T{\left|{\displaystyle \sum _{n=1}^N\left|h_{TS,n}\right|\left|h_{SR,n}\right|}\right|}^2\\ ={\eta }^2{P}_T{\left|{\displaystyle \sum _{n=1}^N\left|\sqrt{l(r_{TS})}{\tilde{h}}_{TS,n}\right|\left|\sqrt{l(r_{SR})}{\tilde{h}}_{SR,n}\right|}\right|}^2\\ ={\eta }^2{P}_T{r}_{TS}{}^{-\alpha }{r}_{SR}{}^{-\alpha }{\left|{\displaystyle \sum _{n=1}^N\left|{\tilde{h}}_{TS,n}\right|\left|{\tilde{h}}_{SR,n}\right|}\right|}^2\end{array}$$

(6)

The amplitudes, $\left|{\tilde{h}}_{TS,n}\right|\left|{\tilde{h}}_{SR,n}\right|$, for the UT-RIS and RIS-UR links follow the double-Nakagami-$m$ distribution with parameters, $m_1$, $m_2$, ${\mathsf{\Omega }}_1$, and ${\mathsf{\Omega }}_2$. The probability density function (PDF) of the double-Nakagami-$m$ distribution is given by [31]:

$$f_{\left|{\tilde{h}}_{TS,n}\right|\left|{\tilde{h}}_{SR,n}\right|}(u)=\frac{4u^{m_1+m_2-1}}{\mathsf{\Gamma }\left(m_1\right)\mathsf{\Gamma }\left(m_2\right)}{\left(\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}\right)}^{\frac{m_1+m_2}{2}}\times K_{m_1-m_2}\left(2u\sqrt{\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}}\right)$$

(7)

where $m$ denotes the fading parameter of the channel, $\mathsf{\Omega }=\mathbb{E}\left[{\left|\tilde{h}\right|}^2\right]$ represents the mean power of $\tilde{h}$, $\mathsf{\Gamma }\left(\bullet \right)$ is the gamma function, and $K_v\left(\bullet \right)$ is the ν-th order modified Bessel function of the second kind [32].

The interference at UR in the RIS-assisted mode comes from the interfering vehicles. The aggregate interference can be expressed as follows:

$$I={\displaystyle \sum _{j\in {\mathsf{\Phi }}_V}{P}_I{\left|h_j\right|}^2{d}_j{}^{-\alpha }}$$

(8)

where $h_j$ and $d_j$ are the small-scale fading channel and the distance between UR and the interfering vehicle, respectively. The Rayleigh fading channel is used for modeling the interfering channel, $h_j$, and the probability density function (PDF) of the Rayleigh distribution is given by:

$$f_{h_j}(x)=\frac{x}{{\sigma }_0^2}{e}^{-\frac{x^2}{2{\sigma }_0^2}},(x>0)$$

(9)

where ${\sigma }_0{}^2$ denotes the variance of the components in a Rayleigh variable.

Therefore, the received SINR at UR in the RIS-assisted mode can be expressed as:

$$SIN{R}_1=\frac{S_R{}^{\ast }}{I+N_0}=\frac{{\eta }^2{P}_T{\left|{\displaystyle \sum _{n=1}^N\left|h_{TS,n}\right|\left|h_{SR,n}\right|}\right|}^2}{I+N_0}$$

(10)

For the direct mode, we can write the received signal at UR as:

$$y_2=\sqrt{{\widehat{P}}_T}{H}_{TR}{x}_T+I+n_R$$

(11)

where $H_{TR}=\sqrt{l\left(r_{TR}\right)}{h}_{TR}$ indicates the UT-UR link channel, $h_{TR}$ denote small-scale fading, $r_{TR}$ the distance between UT and UR, and ${\widehat{P}}_T$ the transmission power of the signal at UT in direct mode.

Therefore, the power of the signal transmitted from UT to UR is:

$$S_D={\widehat{P}}_T{\left|H_{TR}\right|}^2$$

(12)

where ${\widehat{P}}_T$ is the transmission power of the signal at UT in direct mode.

Since the interference at UR in direct communication mode is equivalent to (8), the received SINR at UR in the direct mode can be expressed as:

$$SIN{R}_2=\frac{S_D}{I+N_0}=\frac{{\widehat{P}}_T{r}_{TR}{}^{-\alpha }{\left|h_{TR}\right|}^2}{I+N_0}$$

(13)

3. Performance Analysis

Since the reliability of the communication system is generally evaluated using the outage probability, we examine the outage probability of RIS-assisted V2V communication networks in this section. There are two modes of communication between UT and UR, depending on the presence of obstacles: RIS-assisted V2V transmission mode and direct V2V transmission mode. We had to separately calculate the outage probability for each mode.

The outage event occurs when the received SINR falls below a predetermined threshold, $\tau$. Hence, the outage probability can be expressed by:

$$P_O=P\left[SINR<\tau \right]$$

(14)

For a PPP with density $\lambda$, let us denote $N([a,b))$ as the number of points (events) within the interval $[a,b)$, the distribution of which is derived as:

$$P[N([a,b))=k]=e^{-\lambda (b-a)}\frac{{[\lambda (b-a)]}^k}{k!}$$

(15)

When $k=0$ and $b-a=L$ occur, it indicates that no other vehicles are present between UT and UR. This implies the existence of an LOS channel between UT and UR. The probability of the UT-UR channel being unblocked (LOS) is denoted by $P_{TR,L}$, while the probability of it being blocked (NLOS) is denoted by $P_{TR,N}=1-P_{TR,L}$. After performing some mathematical manipulations, we obtained:

$$P_{TR,L}=e^{-{\lambda }_{V}L}$$

(16)

$$P_{TR,N}=1-e^{-{\lambda }_{V}L}$$

(17)

3.1. Outage Probability in RIS-Assisted Mode

The outage probability of UR in the RIS-assisted mode can be expressed as:

$$P_{O_R}=P_r(SIN{R}_1<\tau )=P_r(\frac{S_R{}^{\ast }}{I+N_0}<\tau )=P_r(\frac{{\eta }^2{P}_T{r}_{TS}{}^{-\alpha }{r}_{SR}{}^{-\alpha }{\left|{\displaystyle \sum _{n=1}^N\left|{\tilde{h}}_{TS,n}\right|\left|{\tilde{h}}_{SR,n}\right|}\right|}^2}{I+N_0}<\tau )$$

(18)

Let $X={\displaystyle \sum _{n=1}^N\left|{\tilde{h}}_{TS,n}\right|\left|{\tilde{h}}_{SR,n}\right|}$, $C_2=\eta P_T{r}_{TS}{}^{-\alpha }{r}_{SR}{}^{-\alpha }$, $Z=S_R=C_2{X}^2$, and $Y=I$. Meanwhile, the outage probability can be expressed as:

$$F_{SIN{R}_1}(x)={\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{F}_Z\left(x\left(y+N_0\right)|r\right)f_{\rho }\left(r\right)dr}{f}_I\left(y\right)dy}$$

(19)

where $F_Z\left(z\right)$ is the CDF of $Z$; $f_{\rho }\left(r\right)$ is the PDF of $r$, which indicates the distance from the closest point to the typical point in the process of 1D MHCP; $f_I\left(y\right)$ is the PDF of the interference variable. Next, we had to derive the distribution of $Z$, $r$, and $I$.

According to [33], the CDF of X can be expressed by:

$$\begin{array}{cc}\hfill F_X(x)=& {\displaystyle \sum _{k_1=0}^{m_1-1}\cdots {\displaystyle \sum _{k_N=0}^{m_1-1}{\displaystyle \prod _{n=1}^N\frac{{(m_2)}_{m_1-1-k_n}{(1-m_2)}_{k_n}}{\left(m_1-1-k_n\right)!k_n!}}}}\hfill \\ & \times \left[1-\frac{2}{\left(u-1\right)!}{\left(\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}x\right)}^{{}^u}{K}_u\left(2\sqrt{\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}x}\right)\right]\hfill \end{array}$$

(20)

The CDF of Z under condition $r$ can be further expressed as:

$$\begin{array}{cc}\hfill F_{Z|R}(z|r)& =F_X(\sqrt{\frac{z}{C_2}})={\displaystyle \sum _{k_1=0}^{m_1-1}\cdots {\displaystyle \sum _{k_N=0}^{m_1-1}{\displaystyle \prod _{n=1}^N\frac{{(m_2)}_{m_1-1-k_n}{(1-m_2)}_{k_n}}{\left(m_1-1-k_n\right)!k_n!}}}}\hfill \\ & \times \left[1-\frac{2}{\left(u-1\right)!}{\left(\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}\times \sqrt{\frac{z}{C_2}}\right)}^{{}^u}{K}_u\left(2\sqrt{\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}\times \frac{z}{C_2}}\right)\right]\hfill \end{array}$$

(21)

where $u=N(m_1+m_2-1)-{\displaystyle \sum _{n=1}^N{k}_n}$, and $r$ indicates the distance from the closest point to the typical point in the process of 1D MHCP; ${\left(n\right)}_k$ represents the Pochhammer symbol.

3.1.1. Distance Distribution

Figure 2 shows the location of the selected RIS in relation to UT and UR in the three cases. Based on the geometric relationship of the distance between $r$ and $r_{TS}$, we can separately represent $r_{TS}$ and $r_{SR}$ in different situations ($W$ represents the road’s width).

When the selected RIS is located between UT and UR, $r_{TS}=\sqrt{r^2+W^2}$ and $r_{SR}=\sqrt{{\left(L-r\right)}^2+W^2}$. The corresponding probability of case (a) is $P=1-e^{-{\lambda }_{R}L}$. When the selected RIS is located to the left of UT, $r_{TS}=\sqrt{r^2+W^2}$ and $r_{SR}=\sqrt{{(L+r)}^2+W^2}$. The probability of case (b) is $P=\frac{e^{-{\lambda }_{R}L}}{2}$. When the selected RIS is located to the right of UR, $r_{TS}=\sqrt{{\left(L+r\right)}^2+W^2}$ and $r_{SR}=\sqrt{r^2+W^2}$. The probability of case (c) is $P=\frac{e^{-{\lambda }_{R}L}}{2}$.

To proceed, we had to examine the distribution of $r$. MHCP ${\mathsf{\Phi }}_R$ can be seen as a thinning process of generating PPP ${\mathsf{\Phi }}_P$.

Theorem 1.

In the MHCP ${\mathsf{\Phi }}_R$, the thinning probability $\rho \left(r\right)$ for the nearest point is conditional on the nearest distance $r$, which is given by:

$$\rho (r)\approx \left\{\begin{array}{l}\frac{1-e^{-{\lambda }_P(2d_h-r)}}{{\lambda }_P(2d_h-r)},r\le \frac{d_h}{2}\\ \frac{1-e^{-{\lambda }_P{d}_h}}{{\lambda }_P{d}_h},r>\frac{d_h}{2}\end{array}\right.$$

(22)

The PDF of $r$ can be expressed as:

$$f_{\rho }(r)={\lambda }_p\rho (r)\exp (-{\lambda }_p{\displaystyle \underset{0}{\overset{r}{\int }}\rho (t)}dt)$$

(23)

Proof of Theorem 1.

We assume a typical point at $(X_0,Y_0)$, and the nearest point to this typical point at $(X_S,Y_S)$ in MHCP ${\mathsf{\Phi }}_R$. We denote the void range from $X_0$ to $X_S$ by $l$. The corresponding thinning probability $\rho (r)$ is defined such as in [34]:

$$\rho (r)=\mathbb{P}\left[X_S\in {\mathsf{\Phi }}_R|{\mathsf{\Phi }}_R\cap l=\varnothing \right]$$

(24)

In a limited region, $l$, MHCP ${\mathsf{\Phi }}_R$ can be approximated by its generating PPP ${\mathsf{\Phi }}_P$. The corresponding thinning probability can be analyzed under two cases shown in Figure 3: Case 1, where $r<\frac{d_h}{2}$, and Case 2, where $r\ge \frac{d_h}{2}$. □

For Case 1, if the mark for $X_S$ is $m_{X_S}$, its safety region, Lx, is from $(X_S-d_h,Y_S)$ to $(X_S+d_h,Y_S)$. The probability for retaining this point in a region, $l\in L_{X_S}$, is $\exp (-m_{X_S}{\lambda }_{p}l)$. Then, the corresponding thinning probability can be expressed as:

$$\begin{array}{l}\rho (r)=\mathbb{P}\left[X_S\in {\mathsf{\Phi }}_R|{\mathsf{\Phi }}_R\cap l=\varnothing \right]\\ =\mathbb{P}\left[(L_{X_S}-l)\cap l=X_S\right]=\mathbb{P}\left[(2d_h-l)\cap l=X_S\right]\\ ={\displaystyle \underset{0}{\overset{1}{\int }}{e}^{-m{\lambda }_p(2d_h-l)}dm=\frac{1-e^{-{\lambda }_P(2d_h-r)}}{{\lambda }_P(2d_h-r)}}\end{array}$$

(25)

For Case 2, the corresponding thinning probability is:

$$\begin{array}{l}\rho (r)=\mathbb{P}\left[X_S\in {\mathsf{\Phi }}_R|{\mathsf{\Phi }}_R\cap l=\varnothing \right]\\ =\mathbb{P}\left[d_h\cap l=X_S\right]={\displaystyle \underset{0}{\overset{1}{\int }}{e}^{-m{\lambda }_p{d}_h}dm=\frac{1-e^{-{\lambda }_P{d}_h}}{{\lambda }_P{d}_h}}\end{array}$$

(26)

3.1.2. Interference Analysis

The interference, $I$, can be approximated by a Gamma distributed variable, $\tilde{I}$, with parameters $k$ and $\theta$. We can use Campbell’s theorem to calculate the mean and variance of $I$, given that the channel gain follows an exponential distribution with a mean of 1:

$$\begin{array}{l}\mathbb{E}\left[I\right]=\mathbb{E}\left\{{\displaystyle \sum _{j\in {\mathsf{\Phi }}_V}{P}_I{\left|h_j\right|}^2{d}_j{}^{-\alpha }}\right\}\\ ={\displaystyle \underset{R_c}{\overset{\infty }{\int }}{P}_I{\left|h_j\right|}^2{d}_j{}^{-\alpha }{\lambda }_{V}d{d}_j}={\lambda }_V{P}_I{R}_c{}^{1-\alpha }/(\alpha -1)\end{array}$$

(27)

$$\begin{array}{l}Var\left[I\right]=Var\left\{{\displaystyle \sum _{j\in {\mathsf{\Phi }}_V}{P}_I{\left|h_j\right|}^2{d}_j{}^{-\alpha }}\right\}\\ ={\displaystyle \underset{R_c}{\overset{\infty }{\int }}{\left(P_I{\left|h_j\right|}^2{d}_j{}^{-\alpha }\right)}^2{\lambda }_{V}d{d}_j}={\lambda }_V{P}_I{}^2{R}_c{}^{1-2\alpha }/(2\alpha -1)\end{array}$$

(28)

Via second-moment matching, the parameters of the Gamma distribution, $k$ and $\theta$, can be obtained by using the relations $\mathbb{E}\left[\tilde{I}\right]=k\theta$ and $Var\left[\tilde{I}\right]=k{\theta }^2$, respectively. Then, we can compute $k$ and $\theta$ by exploiting the mean value and the variance, $k={\lambda }_V{R}_c(2\alpha -1)/{(\alpha -1)}^2$ and $\theta =P_I{R}_c{}^{-\alpha }(\alpha -1)/(2\alpha -1)$, respectively. The PDF of the interference can be expressed as:

$$f_I\left(y\right)=f_{\tilde{I}}\left(y\right)=\frac{y^{k-1}{e}^{-\frac{y}{\theta }}}{\mathsf{\Gamma }\left(k\right){\theta }^k}$$

(29)

By substituting the distance distribution (23) and the interference distribution (29) into (19), we can express the outage probability in RIS-assisted communication mode as follows:

$$\begin{array}{cc}\hfill P_{O_R}=F_{SIN{R}_1}(\tau )=& {\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \sum _{k_1=0}^{m_1-1}\cdots {\displaystyle \sum _{k_N=0}^{m_1-1}{\displaystyle \prod _{n=1}^N\frac{{(m_2)}_{m_1-1-k_n}{(1-m_2)}_{k_n}}{\left(m_1-1-k_n\right)!k_n!}}}}}}\hfill \\ & \hspace{1em}\times \left[1-\frac{2}{\left(u-1\right)!}{\left(\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}\times \sqrt{\frac{\tau (y+N_0)}{C_2}}\right)}^{{}^u}{K}_u\left(2\sqrt{\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}\times \frac{\tau (y+N_0)}{C_2}}\right)\right]\hfill \\ & \hspace{1em}\times f_{\rho }(r)dr\frac{y^{k-1}{e}^{-\frac{y}{\theta }}}{\mathsf{\Gamma }\left(k\right){\theta }^k}dy\hfill \end{array}$$

(30)

3.2. Outage Probability in Direct Mode

The outage probability of UR with the direct mode of communication can be expressed as:

$$\begin{array}{cc}\hfill P_{O_D}& =P_r\left(SIN{R}_2<\tau \right)=P_r\left(\frac{S_D}{I+N_0}<\tau \right)\hfill \\ & =1-P_r\left(\frac{S_D}{I+N_0}\ge \tau \right)=1-P_r\left(\frac{{\widehat{P}}_T{r}_{TR}{}^{-\alpha }{\left|h_{TR}\right|}^2}{I+N_0}\ge \tau \right)\hfill \end{array}$$

(31)

where $h_{TR}$ and $r_{TR}$ are the small-scale fading channel and the distance between UT and UR, respectively.

Since $h_{TR}$ follows the Nakagami-m distribution, according to [35], the partial derivation in Equation (31) can be expressed as:

$$\begin{array}{l}{P}_r\left(\frac{{\widehat{P}}_T{r}_{TR}{}^{-\alpha }{\left|h_{TR}\right|}^2}{I+N_0}\ge \tau \right)==P_r\left({\left|h_{TR}\right|}^2\ge \frac{\tau \left(I+N_0\right)}{{\widehat{P}}_T{r}_{TR}{}^{-\alpha }}\right)\stackrel{(a)}{=}{\mathbb{E}}_I\left[\frac{\mathsf{\Gamma }(m,C_1\left(I+N_0\right))}{\mathsf{\Gamma }(m)}\right]\\ \stackrel{(b)}{=}{\displaystyle \sum _{k=0}^{m-1}\frac{1}{k!}{\left[C_1\left(I+N_0\right)\right]}^k}\exp \left[-C_1\left(I+N_0\right)\right]={\displaystyle \sum _{k=0}^{m-1}\frac{1}{k!}{C}_1{}^k}{\mathbb{E}}_I\left[{\left(I+N_0\right)}^k\exp \left[-C_1\left(I+N_0\right)\right]\right]\\ \stackrel{(c)}{=}{\displaystyle \sum _{k=0}^{m-1}\frac{1}{k!}{C}_1{}^k}{\mathbb{E}}_I\left[\exp \left[-C_1\left(I+N_0\right)\right]{\displaystyle \sum _{n=0}^k\left(\begin{array}{c}k\\ n\end{array}\right)}{I}^{k-n}{N}_0{}^n\right]\\ \stackrel{(d)}{=}{\displaystyle \sum _{k=0}^{m-1}\frac{1}{k!}{C}_1{}^k}{\displaystyle \sum _{n=0}^k\left(\begin{array}{c}k\\ n\end{array}\right)}{\left(-1\right)}^{k-n}\frac{d^{k-n}{L}_I(C_1)}{d^{k-n}{C}_1}\times \exp \left(-C_1{N}_0\right)N_0{}^n\end{array}$$

(32)

where $C_1=\frac{m\tau }{\mu {\widehat{P}}_T{r}_{TR}{}^{-\alpha }}$, (a) is obtained using ${\left|h_{TR}\right|}^2$ following a gamma distribution, (b) is derived from the definition of the exponential sum function when $m$ is an integer, (c) is obtained by exploiting the binomial expansion, and (d) is derived by using the following property:

$${\mathbb{E}}_I\left[e^{-gI}{I}^n\right]={(-1)}^n\frac{d^n{\mathbb{E}}_I\left[e^{-gI}{I}^n\right]}{d^{n}g}={(-1)}^n\frac{d^n{L}_I\left(g\right)}{d^{n}g}$$

(33)

The expression of $L_I\left(s\right)$ can be obtained by the following derivation:

$$\begin{array}{l}{L}_{I|r_{TS}}\left(s\right)=\mathbb{E}\left[e^{-s{\displaystyle \sum _{j\in {\mathsf{\Phi }}_v}{\widehat{P}}_T{\left|h_j\right|}^2{d}_j^{-\alpha }}}\right]=\mathbb{E}\left[{\displaystyle \prod _{j\in {\mathsf{\Phi }}_v}{e}^{-s{\widehat{P}}_T{\left|h_j\right|}^2{d}_j^{-\alpha }}}\right]\\ \stackrel{(a)}{=}\mathbb{E}\left[{\displaystyle \prod _{j\in {\mathsf{\Phi }}_v}\frac{1}{1+s{\widehat{P}}_T{\left|h_j\right|}^2{d}_j^{-\alpha }}}\right]\\ \stackrel{(b)}{=}\exp (-\lambda {\displaystyle \underset{0}{\overset{\infty }{\int }}(1-\frac{1}{1+s{\widehat{P}}_T{\left|h_j\right|}^2{d}_j^{-\alpha }})d{d}_j})\\ \stackrel{(c)}{=}\exp \left[-\lambda \frac{1}{\alpha }{(s{\widehat{P}}_T)}^{\frac{1}{\alpha }}\beta (\frac{1}{\alpha },1-\frac{1}{\alpha })\right]\end{array}$$

(34)

where $\beta \left(\bullet ,\bullet \right)$ represents the beta function, (a) is obtained by applying the LT of ${\left|h_j\right|}^2$ and ${\left|h_j\right|}^2~\exp (1)$, (b) directly follows from the PGFL of 1D PPP, and (c) is obtained by approximating the integral as a beta function.

The outage probability in the RIS-assisted communication mode can be expressed as:

$$\begin{array}{cc}\hfill P_{O_D}& =1-{\displaystyle \sum _{k=0}^{m-1}\frac{1}{k!}{\left(\frac{m\tau }{\mu {\widehat{P}}_T{r}_{TR}{}^{-\alpha }}\right)}^k}{\displaystyle \sum _{n=0}^k\left(\begin{array}{c}k\\ n\end{array}\right)}{\left(-1\right)}^{k-n}\hfill \\ & \times \frac{d^{k-n}{L}_I(\frac{m\tau }{\mu {\widehat{P}}_T{r}_{TR}{}^{-\alpha }})}{d^{k-n}\left(\frac{m\tau }{\mu {\widehat{P}}_T{r}_{TR}{}^{-\alpha }}\right)}\exp \left(-\frac{m\tau }{\mu {\widehat{P}}_T{r}_{TR}{}^{-\alpha }}\times N_0\right)N_0{}^n\end{array}$$

(35)

3.3. Overall Outage Probability

According to the overall outage probability given by (30), the probability of the direct mode and RIS-assisted mode, given by (16) and (17), the outage probability of direct mode (35), the outage probability of RIS-assisted mode (30), and the overall outage probability can be expressed as:

$$\begin{array}{cc}\hfill P_O& =e^{-{\lambda }_{V}L}\times \left(1-{\displaystyle \sum _{k=0}^{m-1}\frac{1}{k!}{C}_1{}^k}{\displaystyle \sum _{n=0}^k\left(\begin{array}{c}k\\ n\end{array}\right)}{\left(-1\right)}^{k-n}\frac{d^{k-n}{L}_I(C_1)}{d^{k-n}{C}_1}\exp \left(-C_1{N}_0\right)N_0{}^n\right)\hfill \\ & +\left(1-e^{-{\lambda }_{V}L}\right)\times \left(\begin{array}{cc}\hfill {\displaystyle \underset{0}{\overset{\infty }{\int }}\underset{0}{\overset{\infty }{\int }}\sum _{k_1=0}^{m_1-1}}& \cdots {\displaystyle \sum _{k_N=0}^{m_1-1}{\displaystyle \prod _{n=1}^N\frac{{(m_2)}_{m_1-1-k_n}{(1-m_2)}_{k_n}}{\left(m_1-1-k_n\right)!k_n!}}}\hfill \\ & \hspace{1em}\times \left[1-\frac{2}{\left(u-1\right)!}{\left(\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}\times \sqrt{\frac{{\tau }_1(y+N_0)}{C_2(r)}}\right)}^{{}^u}{K}_u\left(2\sqrt{\frac{m_1{m}_2}{{\mathsf{\Omega }}_1{\mathsf{\Omega }}_2}\times \frac{{\tau }_1(y+N_0)}{C_2(r)}}\right)\right]\hfill \\ & \hspace{1em}\times f_{\rho }(r)dr\frac{y^{k-1}{e}^{-\frac{y}{\theta }}}{\mathsf{\Gamma }\left(k\right){\theta }^k}dy\hfill \end{array}\right)\hfill \end{array}$$

(36)

4. Simulation Results

In this section, we evaluate the analytical results obtained in the previous section. Monte Carlo simulations are provided to verify the analytical results. Unless they are specified otherwise, default network parameters were used for both simulation experiments and theoretical analyses. Based on [26,30,36,37], the transmission power for the RIS-assisted mode and direct mode is $P_T=20$ W and ${\widehat{P}}_T=20$ W, respectively. The transmission power for interference is $P_I=5$ W, and the noise power spectral density is $N_0={10}^{-10}$ W/HZ. Without the loss of generality, the communication distance between UT and UR is $r_{TR}=100$ m.

Assuming that ${\mathsf{\Phi }}_R$ generates PPP ${\mathsf{\Phi }}_P$ with ${\lambda }_P=0.02$ nodes/m, we obtained a comparison of the analytical results and Monte Carlo simulations for the approximated cumulative distribution function of the distance between UT to the closest RIS in MHCP, as shown in Figure 4. We plotted three sets of curves with different hard-core distances, $d_h$ (200, 300, and 400 m). The figure clearly shows that an increase in hard-core distance, $d_h$, leads to an increase in the distance, $r$, between UT and its closest RIS.

Figure 5 depicts the comparison of analytical results and Monte Carlo simulations for the outage probability versus the vehicle density in direct mode. We assume $\alpha =3$, and the vehicle intensity takes values distributed in $(0\sim 0.02)$. Different thresholds are plotted in the figure ($\tau =$ 0.5, 1, 4 dB). We observed that the analytical results of the outage probability basically matched the Monte Carlo simulations. The vehicle density increased, and the outage probability became larger. This was because the increase in vehicle density aggravated the aggregate interference from vehicles. When the vehicle density increased to around 0.03, the outage probability tended to 1.

Figure 6 demonstrates the influence of threshold on the outage probability in the RIS-assisted mode and the corresponding Monte Carlo simulations. The relative parameters were set as $N=32$, $d_h=200$ m, $\alpha =3$, and ${\lambda }_p=0.02$ nodes/m. Different thresholds are plotted in Figure 6 ($\tau =$ 0.5, 1, 4 dB). We observed that with a larger vehicle density, the outage probability increased at the same SINR threshold. We observed that as the vehicle density increased, the outage probability also increased at the same SINR threshold. This is also because an increase in the vehicle density intensifies the interference.

To compare the outage probabilities of the original V2V communication and the proposed RIS-based V2V communication, Figure 7 shows the Monte Carlo simulation results and analysis results for both communication networks. The relevant parameters were set to $N=32$, $d_h=200$ m, $\alpha =3$, and ${\lambda }_p=0.02$ nodes/m. As expected, introducing RIS to a congested V2V communication network can effectively reduce the occurrence of communication interruptions. When the vehicle density increases, the performance improvement caused by introducing RIS becomes more significant.

Figure 8 plots the Monte Carlo simulation results and analytical results of the overall outage probability versus vehicle density for the RIS-based V2V communication network. Different numbers of RIS reflective elements are provided in Figure 8 ($N$ = 32, 64, 128). In addition, we assume that the relevant parameters were set to $d_h=200$ m, $\alpha =3$, and ${\lambda }_p=0.02$ nodes/m. The overall outage probability became smaller when the number of RIS reflective elements increased. Furthermore, the effect of improving the communication quality by increasing the number of RIS reflective elements was more pronounced at higher vehicle densities.

Figure 9 presents the Monte Carlo simulation results and analysis of the overall outage probability versus vehicle density for the RIS-assisted V2V communication network with different hard-core distances. Here, the system parameters were set to $N=32$, $\alpha =3$, and ${\lambda }_p=0.02$ nodes/m. As expected, when $d_h$ increased, the distribution of RIS in the communication network became sparser. This increases the likelihood that the RIS serving V2V communication systems are too far away from communicating vehicles, resulting in an increase in the outage probability.

5. Conclusions

In this work, we evaluated the RIS-assisted V2V network communication performance using outage probability as a key indicator. Firstly, we determined the communication mode based on whether there were obstacles between communicating vehicles: direct transmission and RIS-assisted transmission. Then, we derived the aggregate interference distribution and analyzed the distance distribution using the stochastic geometry theory. Based on these results, an approximate expression for the outage probability in the proposed network model was obtained. The analysis results, which were further validated via Monte Carlo simulation, show that the transmission performance of V2V networks is further enhanced by the introduction of RIS compared to that of the original V2V network.