Ethereum Smart Contract Vulnerability Detection Model Based on Triplet Loss and BiLSTM
Abstract
1. Introduction
- (1)
- A novel vulnerability detection scheme is proposed from the perspective of feature representation space optimization. In contrast to existing methods that improve the feature learning ability by combining multiple models, we optimize and evaluate the features extracted by the model based on metric learning, making smart contracts of the same category more cohesive and smart contracts of different categories more discrete, improving the accuracy of vulnerability detection.
- (2)
- The proposed model enhances the interpretability of contract vulnerability detection. Our approach involves using the source code of Ethereum smart contracts as input data, which is then subjected to word vectorization and an attention mechanism. This process allows us to identify the critical features associated with vulnerabilities, aiding in pinpointing the root cause of the issue.
- (3)
- We construct a large-scale dataset of smart contracts. We collected 165,000 verified source codes of smart contracts and used a variety of vulnerability detection tools to assign vulnerability labels to provide more comprehensive data support for detection.
- (4)
- The proposed model improves detection accuracy. Experiments prove that compared with traditional methods and other deep learning models, the proposed scheme can better extract vectorized features of smart contracts and effectively improve the accuracy of vulnerability detection.
2. Background
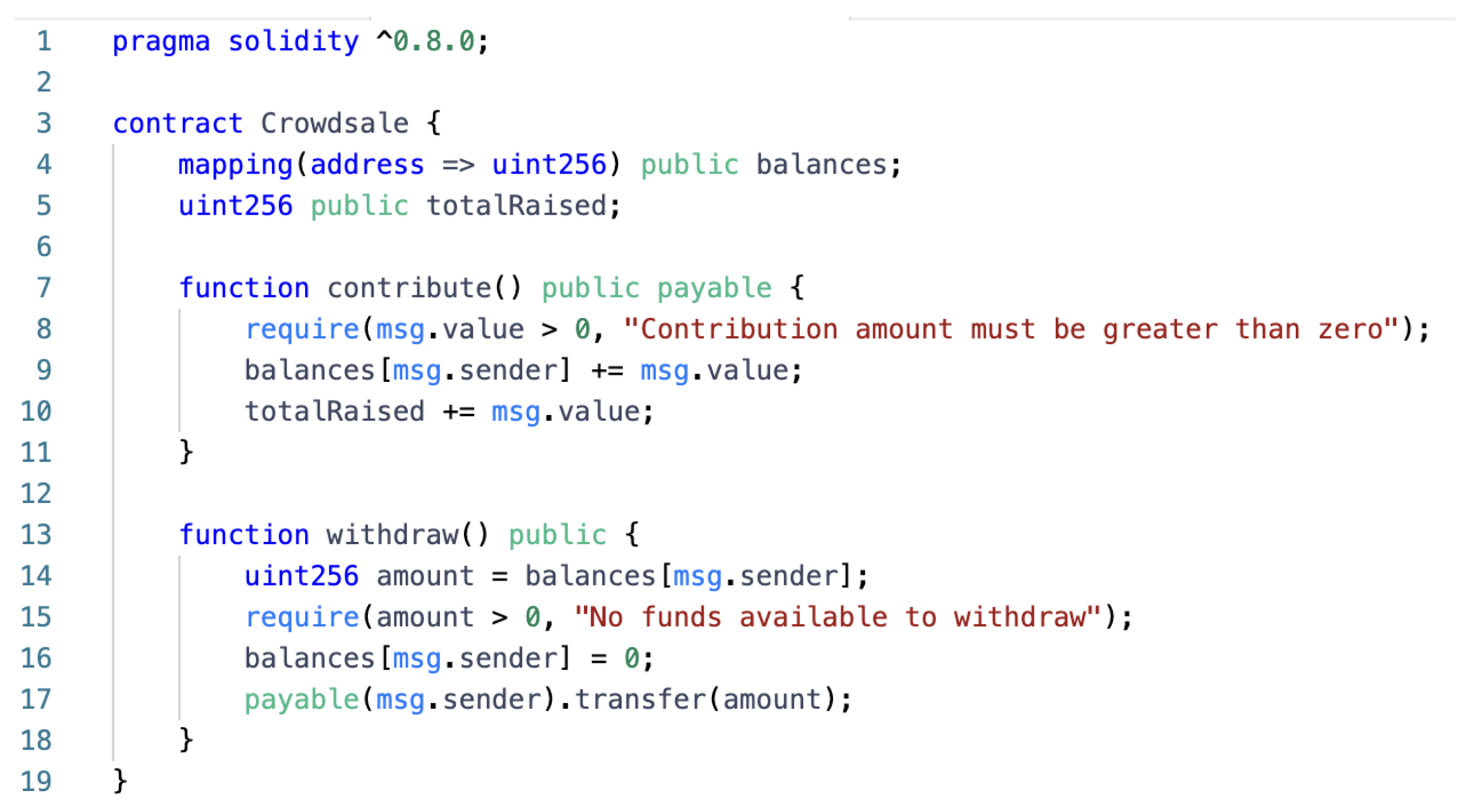
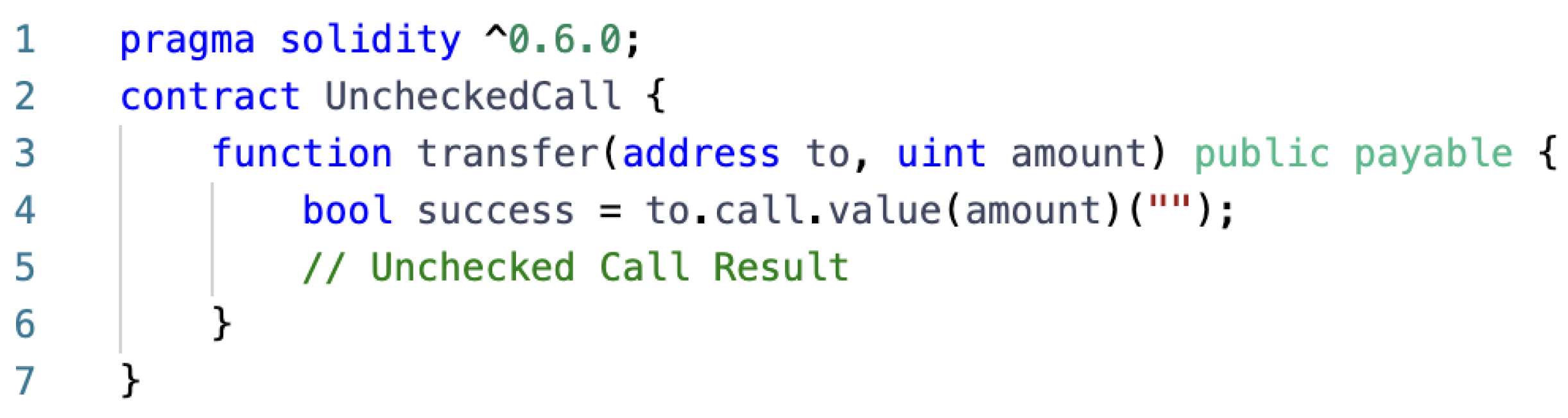
2.1. Smart Contract Vulnerabilities
2.2. Current Smart Contract Vulnerability Detection Methods
- (1)
- The degree of automation is low. Traditional methods must rely on expert experience to perform complex modeling of existing vulnerabilities and match them during vulnerability detection. For unmodeled vulnerabilities, the detection accuracy of traditional methods is unreliable. After a traditional method is tested, it is generally necessary to perform a manual audit.
- (2)
- The accuracy rate is not high. When performing vulnerability detection through the superposition of hard rules, complex contracts may generate high false-positive rates, resulting in a decrease in accuracy.
- (3)
- The detection time is extended. Most traditional methods are based on symbolic execution. When the code length is long, the number of execution paths increases exponentially, and the corresponding detection time is also lengthened, making it even more difficult to solve.
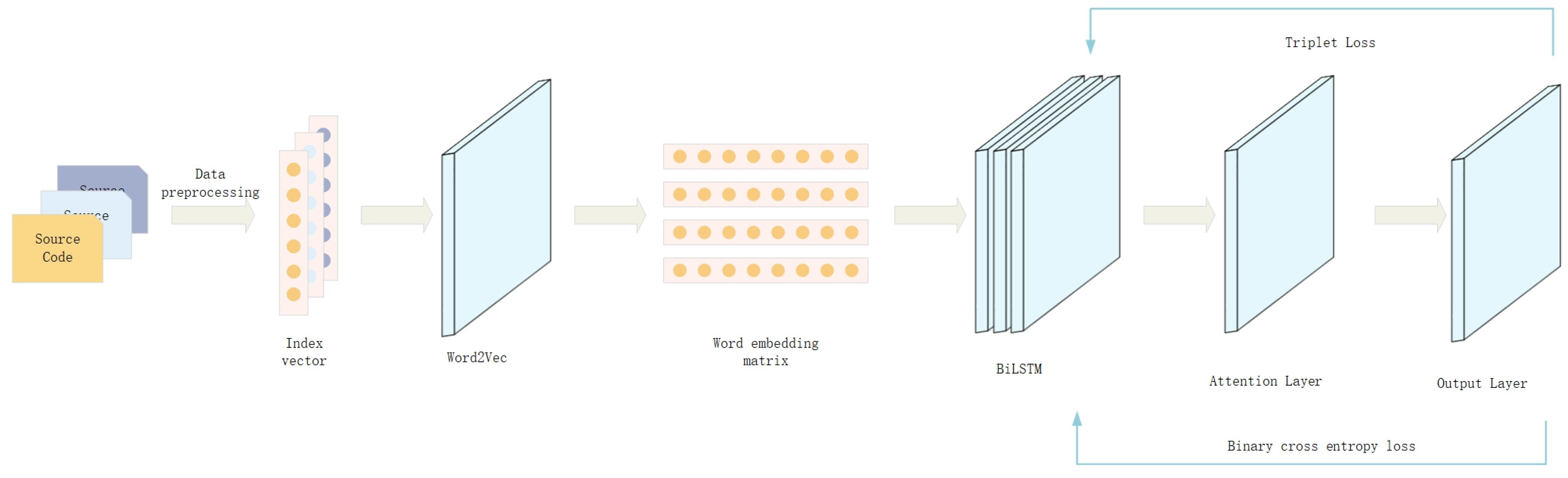
3. Method
- Data preprocessing: Perform data cleaning on the contract code, including removing irrelevant information, such as comments, versions, and variable names, to retain the core part of the code and perform word segmentation on it.
- Word-embedding layer: The token list obtained after word segmentation is converted into a word vector through the word-embedding model to represent the semantic information of the contract.
- BiLSTM layer: The feature representation of the contract code is extracted through the BiLSTM layer.
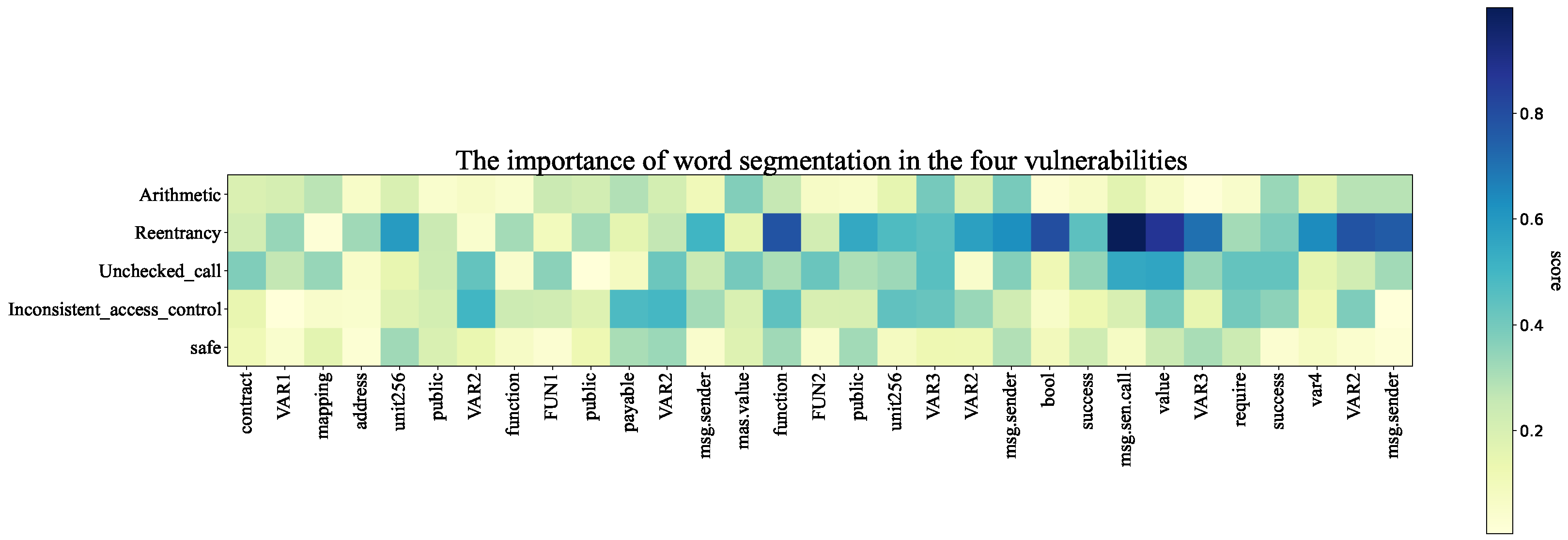
- Attention layer: To highlight the critical features in the contract code, we introduce an attention mechanism, using different weights to allocate the degree of attention to different features to improve the contract code classification performance.
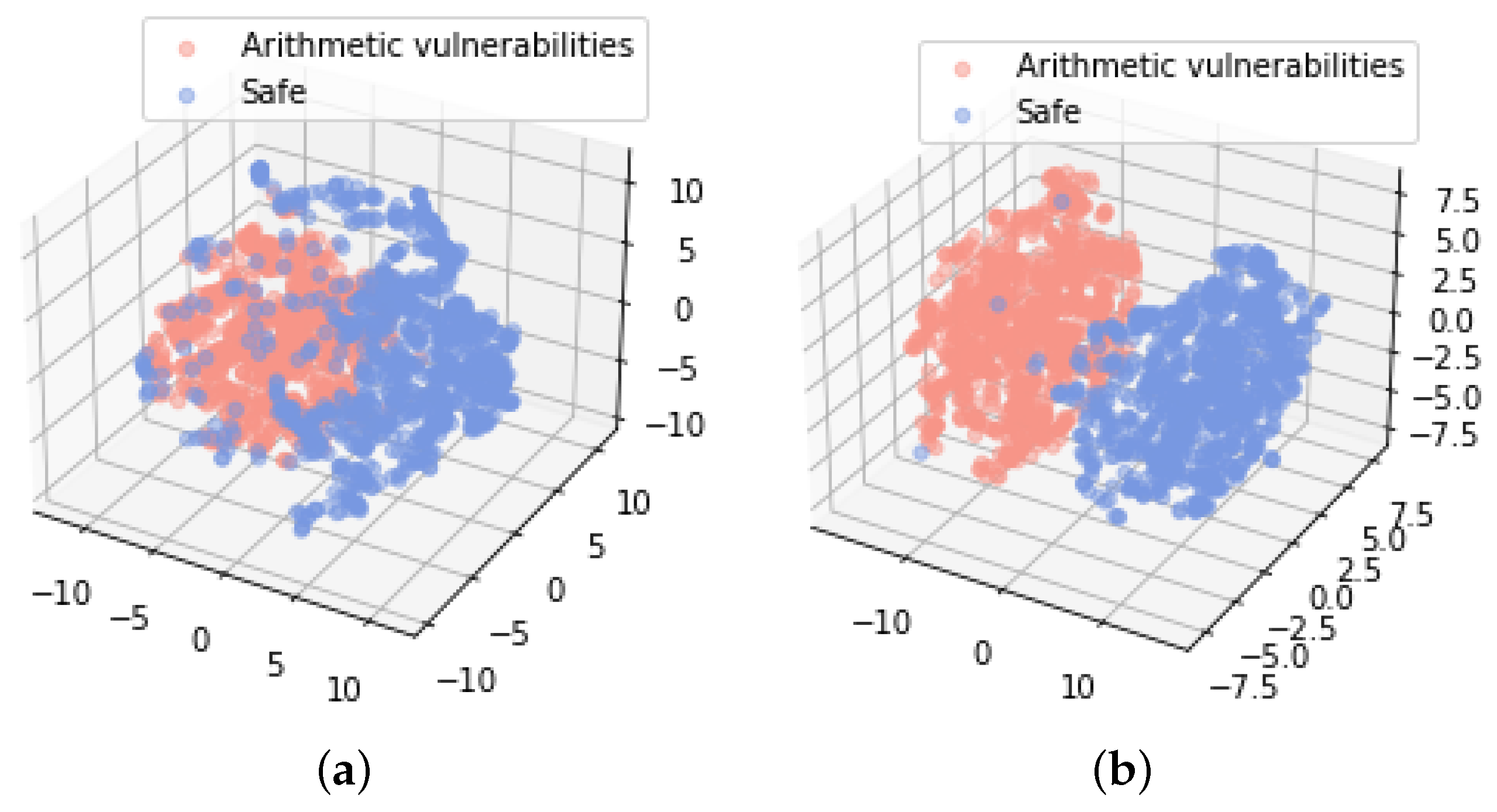
- Vulnerability detection layer: Based on the binary classification loss function, a triplet loss function is introduced to optimize the feature representation ability through backpropagation. During the training process, by continuously updating the parameters, the normal contract code and the contract code with vulnerabilities can be better distinguished in the feature vector space, thereby improving the model’s classification performance.
3.1. Data Preprocessing
- Remove comments: Comments have nothing to do with code functions, so they can be removed from the code through regular expressions.
- Remove useless characters such as spaces, tabs, and new lines: spaces, tabs, and new lines have no substantial impact on the semantics of the code, but they increase the dimensionality of the vectorized representation.
- Remove the code compiler version information. Contracts usually specify the compiler version on the first line, which is not associated with a vulnerability.
- Standardized code style: There may be different code styles in the smart contract source code, such as indentation, naming conventions, etc. To ensure the consistency of vectorized representation, we uniformly standardize the variable names or function names customized by developers as VAR plus numbers or FUN plus numbers.
3.2. Word-Embedding Layer
- Split code: We use regular expressions and spaces as separators to split the contract source code (C) into a word list: ;
- Construct vocabulary: Construct a vocabulary based on the obtained word list, including all unique words that appear in the training data;
- Word embedding: The word-embedding model can capture the semantic relationship between words and convert each word (t) into a fixed-length vector representation: . The Word2Vec model is currently one of the most widely used word-embedding models, including two algorithms: Skip-Gram and Continuous Bag of Words (CBOW). Skip-Gram takes a word as input and predicts the context within a certain window. CBOW accepts the context within a certain window to predict the central word. Since CBOW uses the average value of the context, it converges faster than Skip-Gram. Considering that when the function of the contract is complex, the size of the code text increases, making the features more complex, the model proposed in this paper adopts the Word2Vec word-embedding model based on the CBOW algorithm;
- Combined input: The word vector (D) is combined to form a feature representation of the contract code, usually using a convolutional or recurrent neural network structure to capture local or global features.
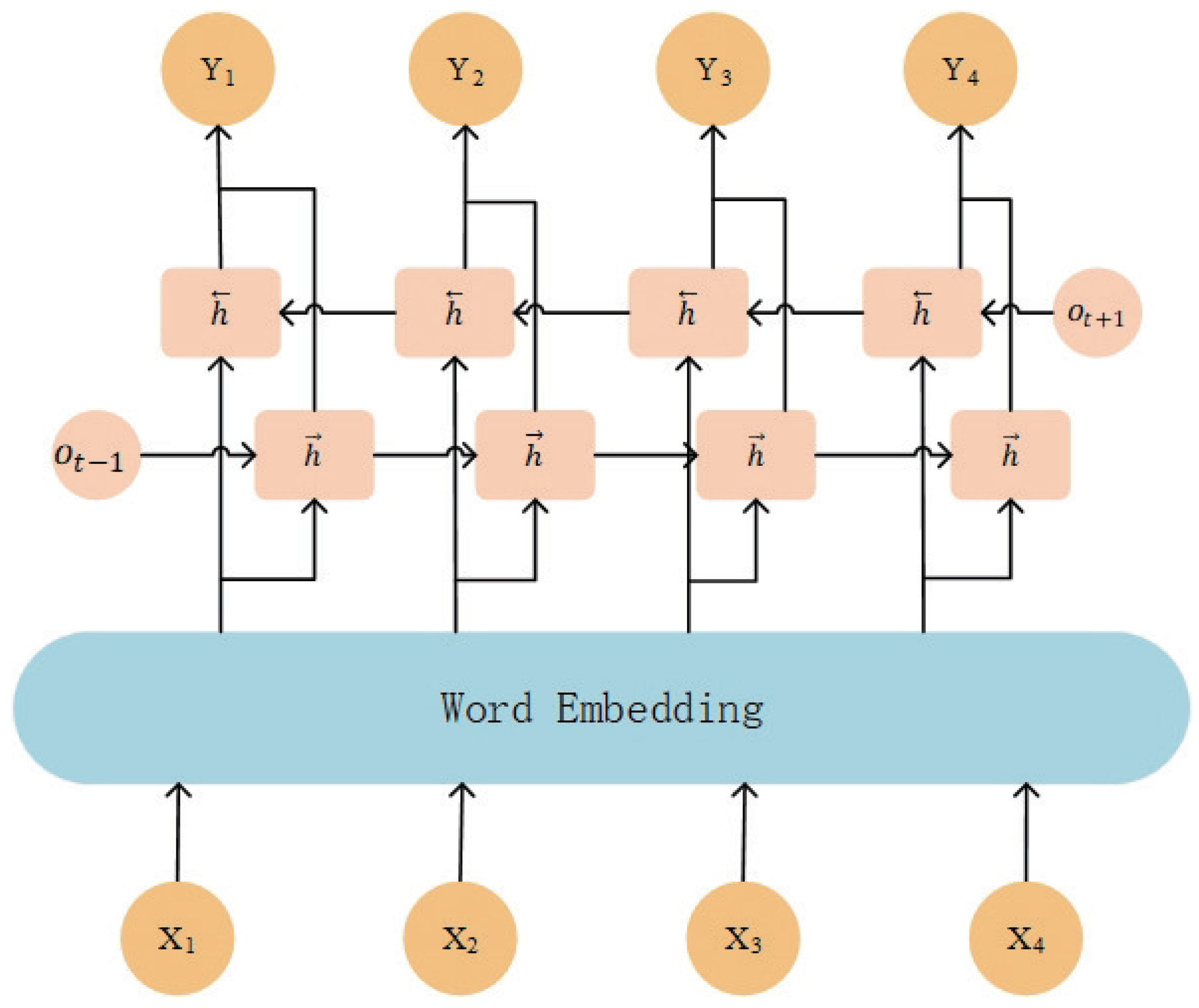
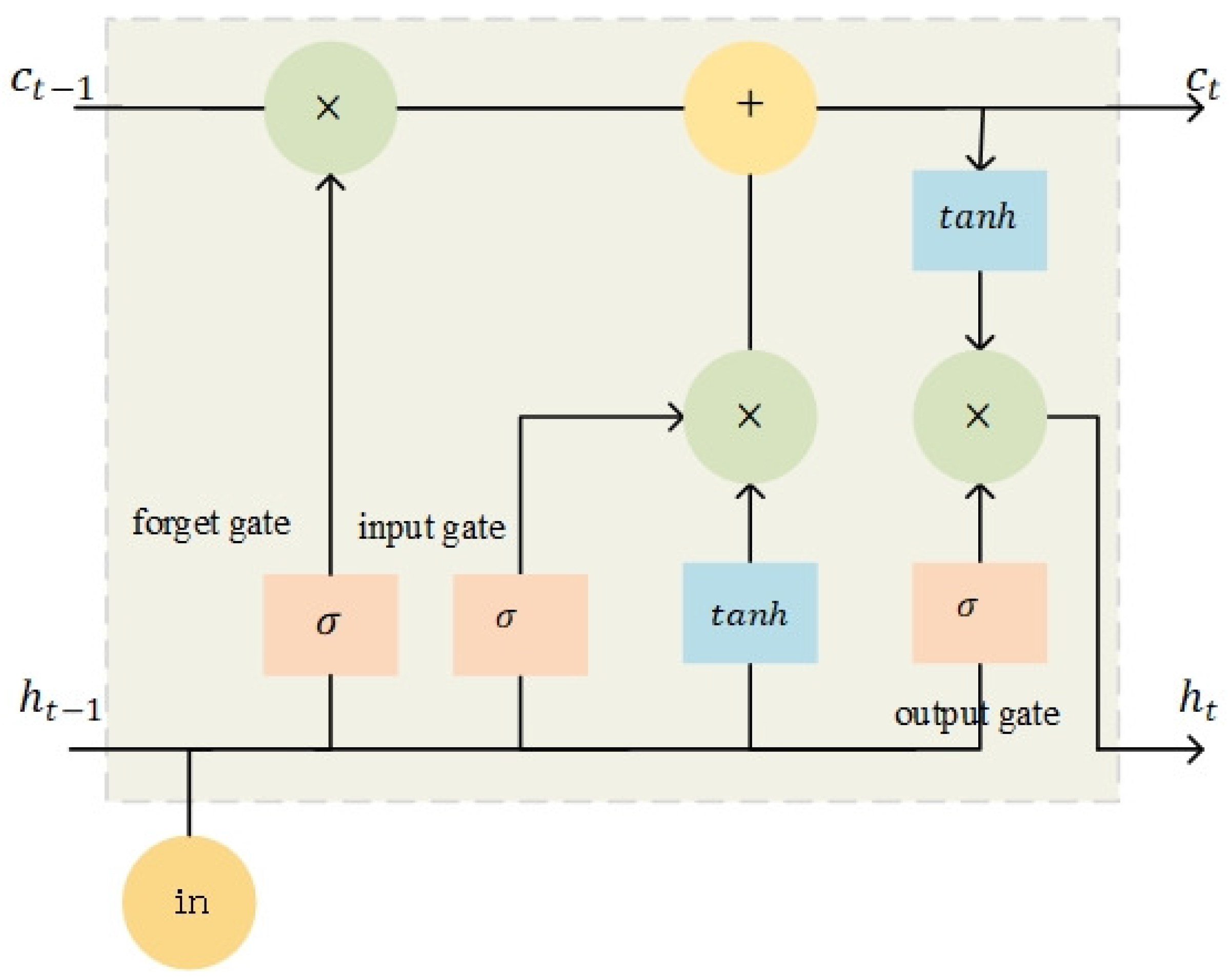
3.3. BiLSTM Layer
3.4. Attention Layer
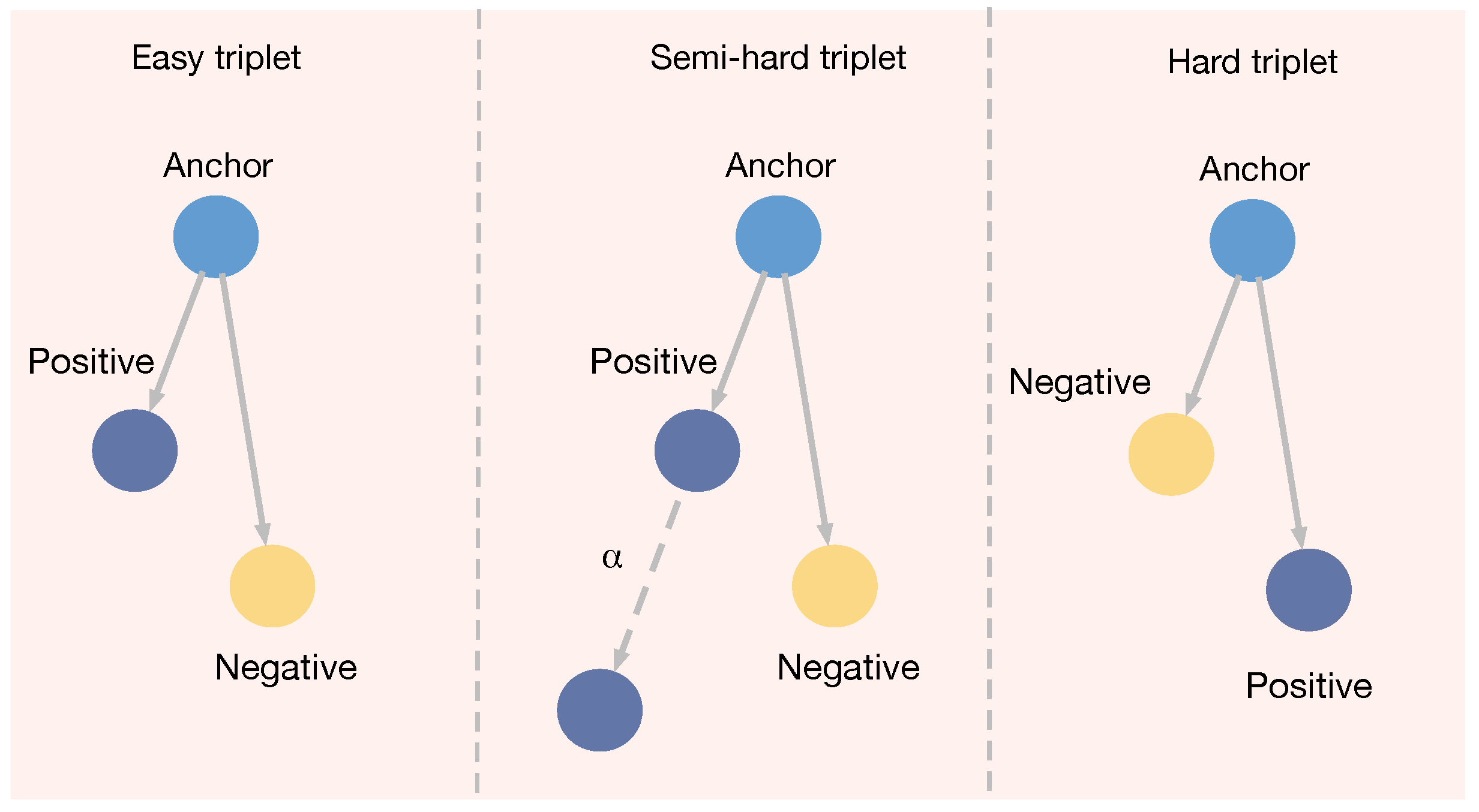
3.5. Vulnerability Detection Layer Optimized by Triplet Loss
4. Experiments
4.1. Dataset
4.2. Evaluation Indicators
4.3. Experimental Results
4.3.1. Ablation Experiment
4.3.2. Comparative Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, S.; Ouyang, L.; Yuan, Y.; Ni, X.; Han, X.; Wang, F.Y. Blockchain-enabled smart contracts: Architecture, applications, and future trends. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 49–77. [Google Scholar] [CrossRef]
- Capocasale, V.; Perboli, G. Standardizing smart contracts. IEEE Access 2022, 10, 91203–91212. [Google Scholar] [CrossRef]
- Ivashchenko, N.P.; Shastitko, A.Y.; Shpakova, A.A. Smart contracts throught lens of the new institutional economics. J. Institutional Stud. 2019, 11, 64–83. [Google Scholar] [CrossRef]
- Sharma, A.; Tomar, R.; Chilamkurti, N.; Kim, B.G. Blockchain based smart contracts for internet of medical things in e-healthcare. Electronics 2020, 9, 1609. [Google Scholar] [CrossRef]
- Lu, J.; Wu, S.; Cheng, H.; Song, B.; Xiang, Z. Smart contract for electricity transactions and charge settlements using blockchain. Appl. Stoch. Model. Bus. Ind. 2021, 37, 37–53. [Google Scholar] [CrossRef]
- Goudarzi, A.; Ghayoor, F.; Waseem, M.; Fahad, S.; Traore, I. A Survey on IoT-Enabled Smart Grids: Emerging, Applications, Challenges, and Outlook. Energies 2022, 15, 6984. [Google Scholar] [CrossRef]
- Waseem, M.; Adnan Khan, M.; Goudarzi, A.; Fahad, S.; Sajjad, I.A.; Siano, P. Incorporation of Blockchain Technology for Different Smart Grid Applications: Architecture, Prospects, and Challenges. Energies 2023, 16, 820. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R.; Gupta, G.P.; Tripathi, R. A Distributed framework for detecting DDoS attacks in smart contract-based Blockchain-IoT Systems by leveraging Fog computing. Trans. Emerg. Telecommun. Technol. 2021, 32, e4112. [Google Scholar] [CrossRef]
- Zhou, Q.; Zheng, K.; Zhang, K.; Hou, L.; Wang, X. Vulnerability Analysis of Smart Contract for Blockchain-Based IoT Applications: A Machine Learning Approach. IEEE Internet Things J. 2022, 9, 24695–24707. [Google Scholar] [CrossRef]
- Gupta, R.; Patel, M.M.; Shukla, A.; Tanwar, S. Deep learning-based malicious smart contract detection scheme for internet of things environment. Comput. Electr. Eng. 2022, 97, 107583. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, S.; Dai, H.N.; Chen, W.; Chen, X.; Weng, J.; Imran, M. An overview on smart contracts: Challenges, advances and platforms. Future Gener. Comput. Syst. 2020, 105, 475–491. [Google Scholar] [CrossRef]
- Ullah, F.; Al-Turjman, F. A conceptual framework for blockchain smart contract adoption to manage real estate deals in smart cities. Neural Comput. Appl. 2021, 35, 1–22. [Google Scholar] [CrossRef]
- Wang, W.; Song, J.; Xu, G.; Li, Y.; Wang, H.; Su, C. Contractward: Automated vulnerability detection models for ethereum smart contracts. IEEE Trans. Netw. Sci. Eng. 2020, 8, 1133–1144. [Google Scholar] [CrossRef]
- Wang, X.; Sun, J.; Hu, C.; Yu, P.; Zhang, B.; Hou, D. EtherFuzz: Mutation Fuzzing Smart Contracts for TOD Vulnerability Detection. Wirel. Commun. Mob. Comput. 2022, 2022, 1565007. [Google Scholar] [CrossRef]
- Sun, T.; Yu, W. A formal verification framework for security issues of blockchain smart contracts. Electronics 2020, 9, 255. [Google Scholar] [CrossRef]
- Shafay, M.; Ahmad, R.W.; Salah, K.; Yaqoob, I.; Jayaraman, R.; Omar, M. Blockchain for deep learning: Review and open challenges. Clust. Comput. 2022, 14, 1–25. [Google Scholar]
- Cai, J.; Li, B.; Zhang, J.; Sun, X.; Chen, B. Combine sliced joint graph with graph neural networks for smart contract vulnerability detection. J. Syst. Softw. 2023, 195, 111550. [Google Scholar] [CrossRef]
- Dai, M.; Yang, Z.; Guo, J. SuperDetector: A Framework for Performance Detection on Vulnerabilities of Smart Contracts. J. Phys. Conf. Ser. 2022, 2289, 012010. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.; Wang, W.; Jin, Z.; Zhao, C.; Cai, Z.; Chen, H. A novel smart contract vulnerability detection method based on information graph and ensemble learning. Sensors 2022, 22, 3581. [Google Scholar] [CrossRef]
- Liu, Z.; Qian, P.; Wang, X.; Zhuang, Y.; Qiu, L.; Wang, X. Combining graph neural networks with expert knowledge for smart contract vulnerability detection. IEEE Trans. Knowl. Data Eng. 2021, 35, 1296–1310. [Google Scholar] [CrossRef]
- Ye, J.; Ma, M.; Lin, Y.; Ma, L.; Xue, Y.; Zhao, J. Vulpedia: Detecting vulnerable ethereum smart contracts via abstracted vulnerability signatures. J. Syst. Softw. 2022, 192, 111410. [Google Scholar] [CrossRef]
- Mossberg, M.; Manzano, F.; Hennenfent, E.; Groce, A.; Grieco, G.; Feist, J.; Brunson, T.; Dinaburg, A. Manticore: A user-friendly symbolic execution framework for binaries and smart contracts. In Proceedings of the 2019 34th IEEE/ACM International Conference on Automated Software Engineering (ASE), San Diego, CA, USA, 11–15 November 2019; pp. 1186–1189. [Google Scholar]
- Perez, D.; Livshits, B. Smart contract vulnerabilities: Does anyone care? arXiv 2019, arXiv:1902.06710. [Google Scholar]
- Mueller, B. Smashing ethereum smart contracts for fun and real profit. HITB SECCONF Amst. 2018, 9, 54. [Google Scholar]
- Jiang, B.; Liu, Y.; Chan, W.K. Contractfuzzer: Fuzzing smart contracts for vulnerability detection. In Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, Leipzig, Germany, 3–7 September 2018; pp. 259–269. [Google Scholar]
- Abdellatif, T.; Brousmiche, K.L. Formal verification of smart contracts based on users and blockchain behaviors models. In Proceedings of the 2018 9th IFIP International Conference on New Technologies, Mobility and Security (NTMS), Lisbon, Portugal, 26–28 February 2018; pp. 1–5. [Google Scholar]
- Sun, Y.; Gu, L. Attention-based machine learning model for smart contract vulnerability detection. J. Phys. Conf. Ser. 2021, 1820, 012004. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Wang, X. Smart Contract Vulnerability Detection Method based on Bi-LSTM Neural Network. In Proceedings of the 2022 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 20 August 2022; pp. 38–41. [Google Scholar]
- Wang, B.; Chu, H.; Zhang, P.; Dong, H. Smart Contract Vulnerability Detection Using Code Representation Fusion. In Proceedings of the 2021 28th Asia-Pacific Software Engineering Conference (APSEC), Taiwan, China, 6 December 2021; pp. 564–565. [Google Scholar]
- Zhang, L.; Li, Y.; Jin, T.; Wang, W.; Jin, Z.; Zhao, C.; Cai, Z.; Chen, H. SPCBIG-EC: A robust serial hybrid model for smart contract vulnerability detection. Sensors 2022, 22, 4621. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Chen, W.; Wang, W.; Jin, Z.; Zhao, C.; Cai, Z.; Chen, H. Cbgru: A detection method of smart contract vulnerability based on a hybrid model. Sensors 2022, 22, 3577. [Google Scholar] [CrossRef]
- Qian, S.; Ning, H.; He, Y.; Chen, M. Multi-Label Vulnerability Detection of Smart Contracts Based on Bi-LSTM and Attention Mechanism. Electronics 2022, 11, 3260. [Google Scholar] [CrossRef]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Hoffer, E.; Ailon, N. Deep metric learning using triplet network. In Similarity-Based Pattern Recognition, Proceedings of the Third International Workshop, SIMBAD 2015, Copenhagen, Denmark, 12–14 October 2015; Proceedings 3; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 84–92. [Google Scholar]




| Arithmetic | Re-Entrancy | Unchecked Calls | Inconsistent Access Control | Security Contract | |
|---|---|---|---|---|---|
| Amount | 20,044 | 39,098 | 42,573 | 28,171 | 35,130 |
| Model | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| ANN | 55.43% | 51.84% | 49.02% | 50.39% |
| ANFIS | 58.73% | 53.06% | 51.93% | 52.49% |
| LSTM | 70.46% | 65.31% | 69.42% | 67.30% |
| BiLSTM | 79.94% | 78.50% | 77.03% | 77.47% |
| BiLSTM-ATT | 81.40% | 81.53% | 78.64% | 80.93% |
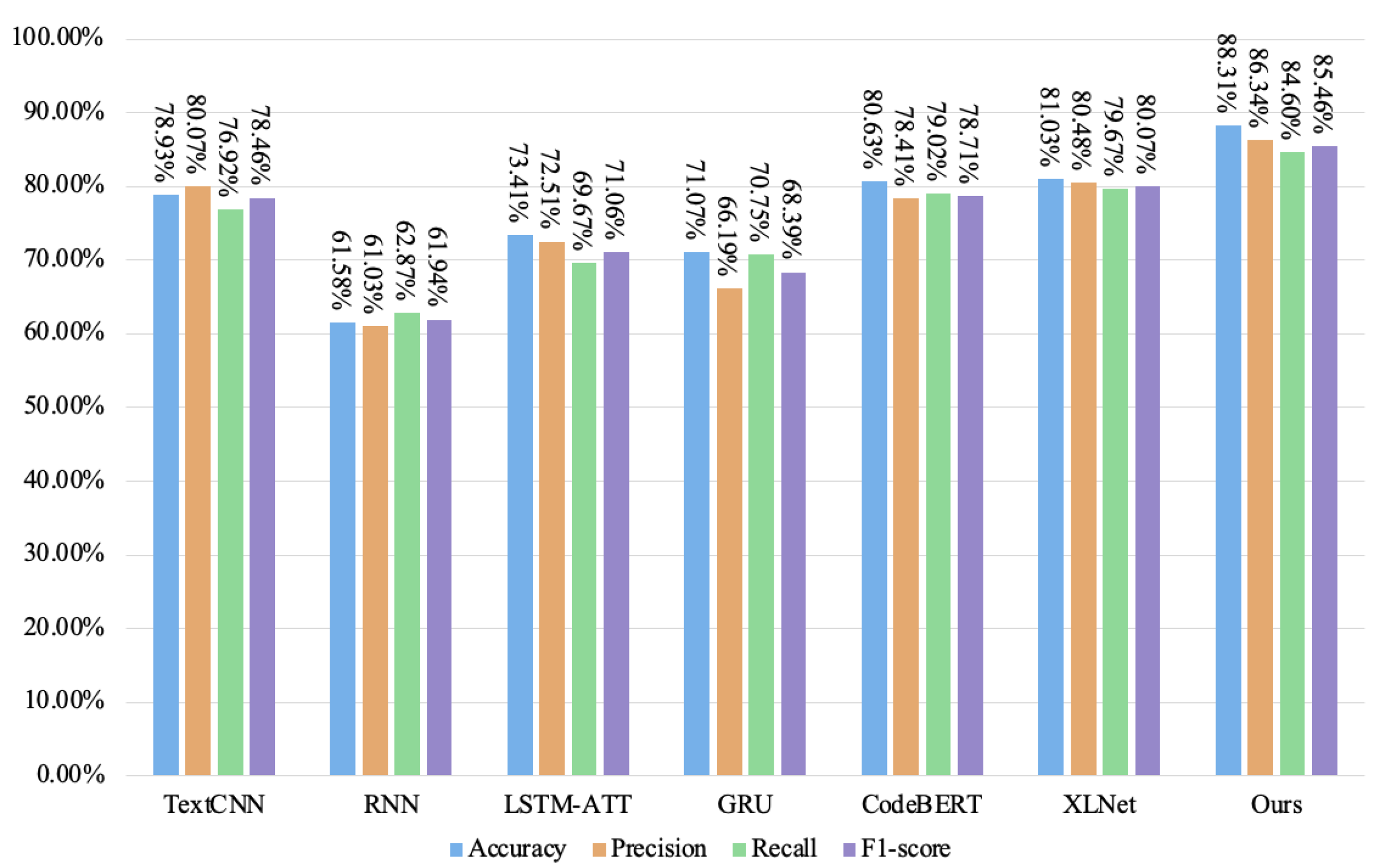
| Ours | 88.31% | 86.34% | 84.60% | 85.46% |
| Model | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| ANN | 54.82% | 51.61% | 51.93% | 51.77% |
| ANFIS | 61.91% | 57.37% | 51.94% | 54.52% |
| LSTM | 72.31% | 71.58% | 69.93% | 70.75% |
| BiLSTM | 81.07% | 78.93% | 80.06% | 79.71% |
| BiLSTM-ATT | 88.21% | 86.49% | 84.21% | 86.20% |
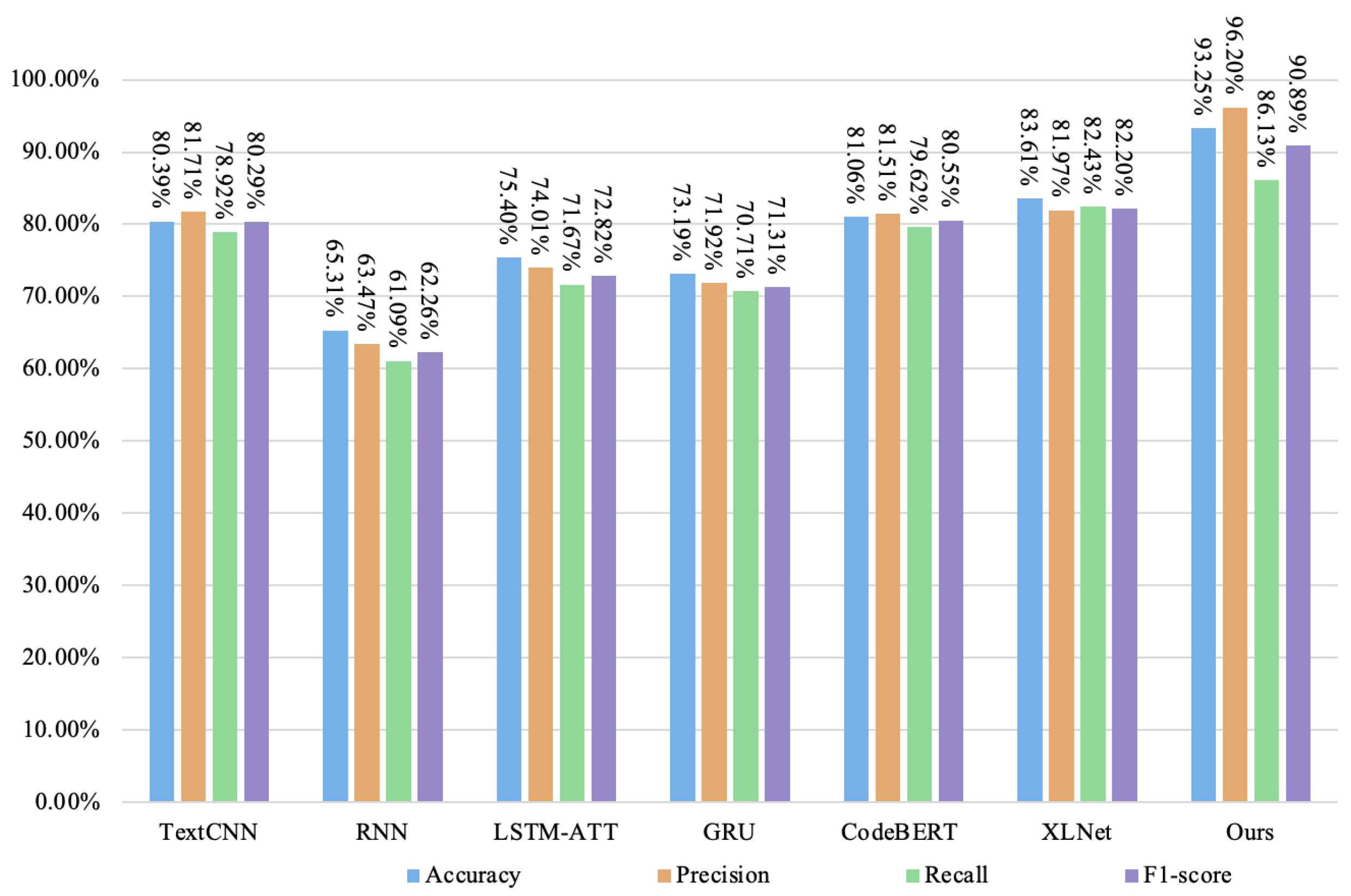
| Ours | 93.25% | 96.20% | 86.13% | 90.89% |
| Arithmetic | Re-Entrancy | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | Accuracy | Precision | Recall | F1-Score | Accuracy | Precision | Recall | F1-Score |
| Mythril | 61.53% | 59.65% | 52.63% | 55.92% | 60.01% | 49.58% | 51.69% | 50.61% |
| Oyente | 64.02% | 61.35% | 54.07% | 57.48% | 67.01% | 53.52% | 57.43% | 55.41% |
| Ours | 88.31% | 86.34% | 84.60% | 85.46% | 93.25% | 96.20% | 86.13% | 90.89% |
| Unchecked Calls | Inconsistent Access Control | |||||||
|---|---|---|---|---|---|---|---|---|
| Model | Accuracy | Precision | Recall | F1-Score | Accuracy | Precision | Recall | F1-Score |
| Mythril | 59.85% | 52.04% | 56.93% | 54.38% | 60.31% | 54.91% | 56.74% | 55.81% |
| Oyente | 68.01% | 54.83% | 61.04% | 57.77% | 63.92% | 57.47% | 57.06% | 57.26% |
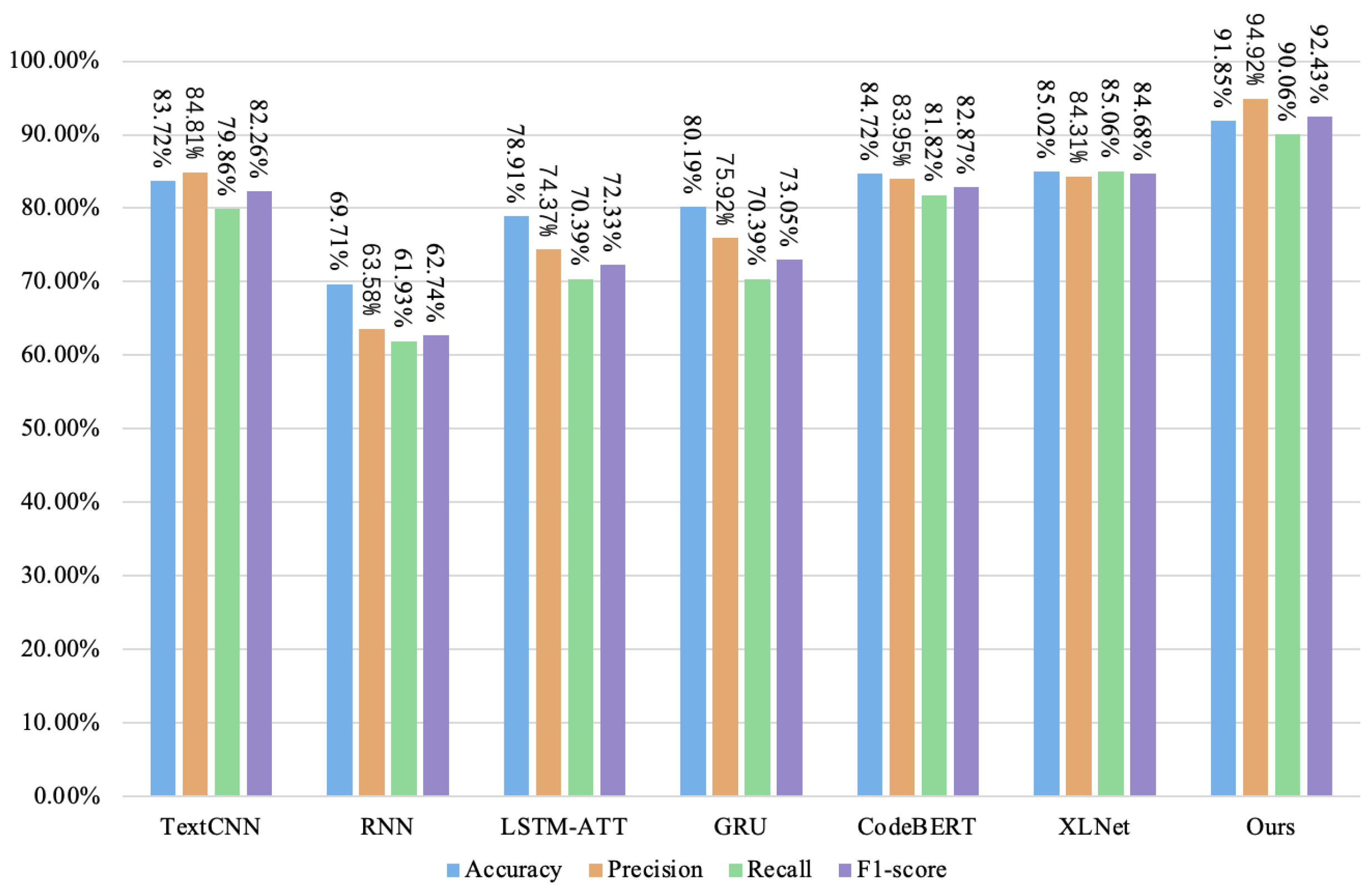
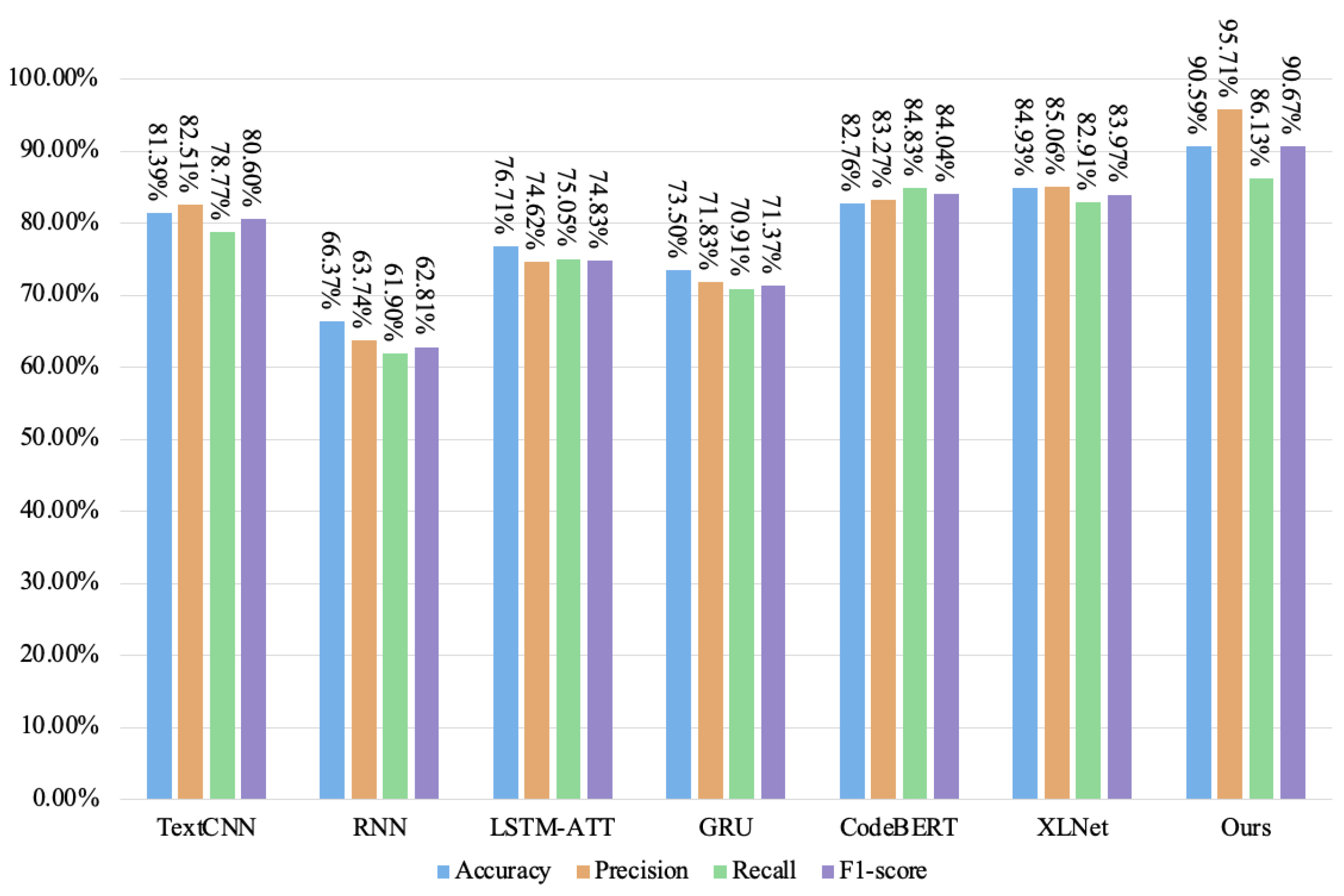
| Ours | 91.85% | 94.92% | 90.06% | 92.43% | 90.59% | 95.71% | 86.13% | 90.67% |
| Average Time | Mythril | Oyente | Ours |
|---|---|---|---|
| Arithmetic | 4.13 s | 5.01 s | 0.34 s |
| Re-entrancy | 4.53 s | 4.41 s | 0.09 s |
| Unchecked calls | 4.69 s | 4.68 s | 0.13 s |
| Inconsistent access control | 4.57 s | 5.01 s | 0.12 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Xie, Z.; Wen, X.; Li, J.; Zhou, K. Ethereum Smart Contract Vulnerability Detection Model Based on Triplet Loss and BiLSTM. Electronics 2023, 12, 2327. https://doi.org/10.3390/electronics12102327
Wang M, Xie Z, Wen X, Li J, Zhou K. Ethereum Smart Contract Vulnerability Detection Model Based on Triplet Loss and BiLSTM. Electronics. 2023; 12(10):2327. https://doi.org/10.3390/electronics12102327
Chicago/Turabian StyleWang, Meiying, Zheyu Xie, Xuefan Wen, Jianmin Li, and Kuanjiu Zhou. 2023. "Ethereum Smart Contract Vulnerability Detection Model Based on Triplet Loss and BiLSTM" Electronics 12, no. 10: 2327. https://doi.org/10.3390/electronics12102327
APA StyleWang, M., Xie, Z., Wen, X., Li, J., & Zhou, K. (2023). Ethereum Smart Contract Vulnerability Detection Model Based on Triplet Loss and BiLSTM. Electronics, 12(10), 2327. https://doi.org/10.3390/electronics12102327




