Abstract
Transformer models have emerged as the state-of-the-art in many natural language processing and computer vision applications due to their capability of attending to longer sequences of tokens and supporting parallel processing more efficiently. Nevertheless, the training and inference of transformer models are computationally expensive and memory intensive. Meanwhile, utilizing the sparsity in deep learning models has proven to be an effective approach to alleviate the computation challenge as well as help to fit large models in edge devices. As high-performance CPUs and GPUs are generally not flexible enough to explore low-level sparsity, a number of specialized hardware accelerators have been proposed for transformer models. This paper provides a comprehensive review of hardware transformer accelerators that have been proposed to explore sparsity for computation and memory optimizations. We classify existing works based on the strategies of utilizing sparsity and identify their pros and cons in those strategies. Based on our analysis, we point out promising directions and recommendations for future works on improving the effective sparse execution of transformer hardware accelerators.
1. Introduction
Natural language processing (NLP) has become an integral part of modern daily life due to various applications such as search engines, personal assistants, language translation, customer services, and numerous others. Advancements in deep learning models have made NLP possible for practical use cases. From the implementation perspective, most NLP applications deal with sequences of audio or text data for which recurrent neural networks (RNNs), long short-term memory (LSTM) networks, and gated recurrent unit (GRU) networks have been popular solutions in the early 2000s. However, accurate prediction of NLP systems relies on extracting relations and knowledge from past sequences. RNNs, LSTMs, and GRUs have a comparatively shorter attention span. As a result, these models may struggle to find contexts in long text or audio sequences. Moreover, these networks are dominantly sequential in nature, making it challenging to speed up in hardware implementation. Transformer [1] models, proposed in the late 2010s, preserve long dependencies in longer sequences and support parallel hardware computation. Transformer-based models have reached unparalleled performance in various difficult tasks in natural language processing and computer vision. The core component in a transformer model is the attention mechanism, which identifies relevant information in an input sequence for a target output [1,2,3]. Based on this attention mechanism, several breakthrough models have been proposed such as BERT( Google) [4], RoBERTa (Facebook) [5], GPT (OpenAI) [6], MegatronLM (NVIDIA) [7], and Turing-NLG (Microsoft) [8].
Transformer-based models employ two types of attention mechanisms: self-attention and cross-attention. While both mechanisms are similar in computation, self-attention operates only on the tokens in the input sequence, whereas cross-attention relates the output token to the input sequence tokens. The attention mechanism considers all the possible past tokens to compute the dependencies, thus resulting in more accurate and higher-quality output. However, the performance of attention comes at an immense computational expense. It is usually computed as dense matrix operations in conventional hardware. General-purpose computational devices such as CPUs and even GPUs compute attention with a relatively low throughput due to complex data movement [9]. The attention computes the similarity across all search tokens and the computational complexity is quadratic to the number of search tokens in the initial transformer models [10]. This means that the retrieval of relevant knowledge over a larger external knowledge base will require more computation. Consequently, it becomes a bottleneck when implemented in smaller devices as it takes a substantial amount of time and energy to compute. Meanwhile, transformer model implementation also has an immense memory footprint, as a large amount of memory is required to store the parameters during inference. This poses a significant constraint for low-resource edge devices, which have limited computing power and capacity. Training transformer models, while typically not performed in edge devices, have a significant carbon footprint [11,12] and a considerable negative environmental impact.
Recently, sparse computation has received increased attention as an alternative to address computational and memory challenges for transformer model implementation. Deep neural networks are usually sparse or can be processed as sparse. The sparsity in neural networks refers to the repetition of the value “0” in weights or activations, which allows the elimination of unnecessary computations [13]. Although GPUs are highly optimized in non-sparse dense matrix multiplication, they may not be efficient in reaping the full benefits of sparse matrix multiplication [10,14]. Different layers of a neural network exhibit sparsity in unique ways, which necessitates specialized hardware due to variations in the computation nature. As a result, new domain-specific and task-specific hardware are needed to explore the sparsity in transformer models due to the dissimilarities in computation and sparsity patterns with other neural networks [9].
In this paper, we focus on hardware accelerators that are designed to explore the sparsity in transformer models and handle the computation and memory challenges. We first provide an elaborate discussion on the transformer model architecture and sparsity. Then, hardware accelerators based on different strategies of utilizing sparsity are explained and compared. To cope with the memory constraints, some accelerators deploy compression techniques to fit the sparse parameters into memory. Compression techniques require additional encoding and decoding units in hardware that incur extra computational complexity [15]. Some accelerators instead explore the inherent sparsity present in activation and parameters, although the resultant holistic hardware efficiency is often not adequate. In addition to the inherent static sparsity, it is also possible to utilize dynamic sparsity that is generated with respect to different inputs during attention computation. Accelerators based on dynamic sparsity can further reduce computational complexity and have started to demonstrate the prospect of achieving practical hardware constraints [2,3,9,14]. We classify different accelerators based on these and other sparsity exploration strategies and identify their pros and cons. This is followed by a discussion of promising future directions in designing hardware accelerators for transformer models.
2. Background
In this section, the architecture of transformer models and their sparsity are discussed. More focus is placed on the attention mechanism as it is the heart of the computation in accelerators.
2.1. Transformer Architecture
Similar to previous state-of-the-art transduction models, the transformer model consists of encoder–decoder blocks. However, the core is the attention mechanism that captures the knowledge. This attention allows the encoder and decoder to attend to all the input sequences and make decisions based on importance. Unlike other sequential models, these attention mechanisms have a parallelization opportunity to improve speed while maintaining long-range relations.
The encoder in transformers takes an input sequence of symbol representations x = () and converts it to a sequence of continuous representations of z = (). The decoder then computes on z and generates an output sequence y = () of symbols one element at a time. The transformer consists of stacked encoder and decoder layers, as shown in Figure 1. Each encoder layer includes self-attention and a fully connected layer. Additionally, the decoder also has a masked attention layer. The model is auto-regressive as it uses previously generated outputs as input when it generates the next output [1,16].
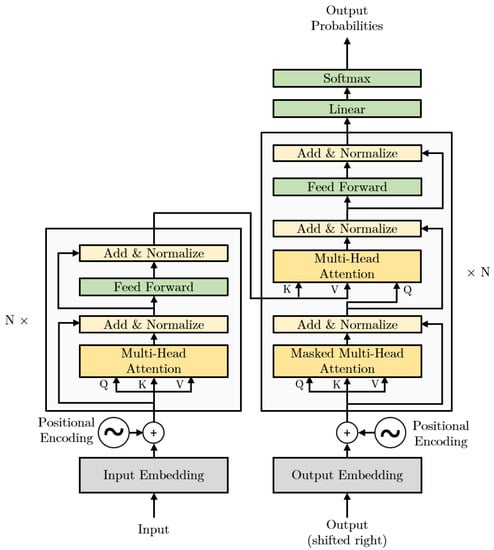
Figure 1.
A typical transformer architecture with N numbers of encoder and decoder layers [1].
2.1.1. Encoder
The encoder stack of the transformer model consists of several identical encoder layers (e.g., six layers in the original paper [1]). Each encoder layer has two sub-layers: a multi-head self-attention mechanism and a simple, position-wise fully connected feed-forward network. These two sub-layers have a residual connection [17] and are followed by a layer normalization [18]. The residual connections in all the sub-layers are of the same length (e.g., 512 in [1]).
2.1.2. Decoder
Similar to the encoder, the decoder stack is also composed of several identical layers (again, six in the original implementation [1]). The structure of the decoders is very similar to the encoders. In addition to the two sub-layers of the encoder, the decoder layer also has an additional multi-head attention that computes the attention over the output of the encoder. At each step, the decoder takes all the previously generated outputs as the input and generates the next output. To make sure that the generation of current output does not depend on itself, the masking along with the output embedding is offset by one.
2.1.3. Transformer Attention Mechanism
The main computational focus in the transformer is the attention function that maps a query and a set of key–value pairs to an output. The model uses multi-head attention where each head is a single attention block, referred to as the scaled dot-product attention. This mechanism searches over the input sequence and calculates the relevance of the input and determines where to attend [1,10].
Scaled Dot-Product Attention: The scaled dot-product attention block takes in three vectors: queries () and keys (), both of the dimensions of , and a corresponding value () of dimension as inputs. Here, i denotes the ith token of an input sequence. At first, a score is calculated for a query with all the keys. In the example presented in Figure 2, all the words in the sentence are scored with respect to the word “Natural”. The scores are calculated by taking the dot product of query () and key vectors ( and ). Based on the scores, the attention mechanism puts importance on other words in the sentence while encoding a word at a specific position. The second step scales the scores by for stable gradients. The intuition behind this is to avoid a large dot-product result pushing the softmax function of the next step into regions where the gradient is insignificant. After softmax, all the scores are normalized, made positive, and summed to one. In the last step of scaled dot-product attention, all the values () are multiplied with the corresponding softmax normalized scores.
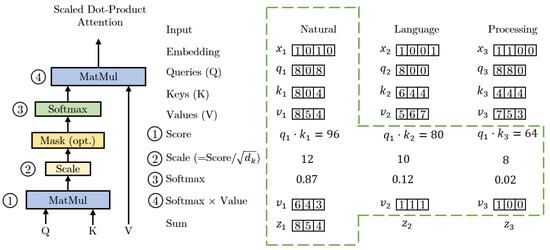
Figure 2.
Calculation steps in scaled dot-product attention. The dotted section shows the output of the attention layer for the query . The ’Score’ step involves calculating a score for each key () related to a specific query by means of dot-product. After obtaining the scores for the keys, they are scaled and subjected to the softmax operation to determine their relevance with respect to the query compared to the other keys. Each value () is multiplied by the corresponding softmax score of its key () after the softmax operation. Finally, the softmax weighted values are summed up to generate the attention output for a key with respect to the query .
In practice, the attention is calculated in matrices to perform multiple calculations simultaneously. Thus, the output is calculated as
where Q, K, and V are matrices of queries, keys, and values. Between two popular attention mechanisms, namely additive attention and dot-product attention, the transformer model uses the scaled dot-product attention due to faster and space-efficient matrix multiplication.
Multi-Head Self Attention: The complexity of directly computing attention with -dimensional keys, values, and queries in a single attention block is very high. Instead, it is beneficial to linearly project the queries, keys, and values h times with different, learned linear projections to , , and dimensions, respectively. This makes it possible to perform the attention function in parallel, yielding -dimensional output values in each of these projected versions of queries, keys, and values. The final outputs of these heads are concatenated and once again projected, resulting in the final values. The linear projection-based, multi-head attention allows the model to jointly attend to information from different representation sub-spaces at different positions, which is not possible with a single attention head.
2.1.4. Position-Wise Feed-Forward Network
The encoder and decoder blocks have fully connected feed-forward networks (FFNs) in addition to attention units. An FFN consists of two linear transformations with ReLU and is applied to each position separately and identically. In each layer, the same transformation is applied, but they learn different parameters. The weight and bias parameters of the feed-forward network are denoted by W and b, respectively, in the equation below.
2.1.5. Embedding and Positional Encoding
Like other sequence transduction models, learned embeddings are used to convert the input tokens and output tokens to vectors. At the output, the usual learned linear transformation and the softmax function are used to convert the decoder output to the predicted next-token probabilities. The transformer does not contain recurrence and convolution. Instead, to reflect the order of tokens in the sequence, the model injects positional information in the form of “positional encodings” to the input embeddings at the start of the encoder and decoder stacks.
2.2. Sparsity in Deep Learning Models
Deep networks achieve state-of-the-art performance in solving many real-life problems, but in many cases, these models are over-parameterized. Many studies show that there is significant redundancy exists in the data of large models [19]. Execution of these models can be improved significantly by reducing computation, communication, and memory requirements through efficient compression of redundant data tensors. Highly compact models can be achieved by compressing tensors through the exploitation of (a) sparsity, (b) tensor size reduction, and (c) value quantization. In this paper, our primary focus is the exploration of the sparsification approaches.
Interestingly, deep neural networks (DNNs) are typically sparse in nature or can be made sparse through efficient processing techniques. The sparsity of data is usually expressed as a percentage of zeros. Sparsity due to zeros offers multiple architectural benefits. Firstly, sparsity eliminates ineffectual computations. Since multiplication by zero reduces multiply–accumulate (MAC) operation, sparsity reduces execution time and energy by computing only the non-zeros. Secondly, sparsity encodes only non-zeros which reduces the footprint of the data, allows more data to fit in on-chip memory, and decreases off-chip memory accesses. As a result, device throughput improves and energy consumption decreases. Lastly, sparsity increases speedup due to less communication required as the data movement is reduced.
Sparsity can be generated, for example, by an activation unit. ReLU turns all negative activation values to zero and introduces sparsity. Pruning is a special method that can introduce more sparsity by converting certain values to zero via thresholding. Pruning can be applied to both activation and weights of a model. Apart from these, transformer attention computation can harness dynamical sparsity based on input features.
3. Overview of the Transformer-Based Accelerators Exploring Sparsity
In this section, we give a concise overview of transformer-based accelerators that leverage sparsity for improved performance in practical applications. We categorize and compile a list of these accelerators based on their commonalities, which will be described further in more detail in the next section. Table 1 compares the hardware accelerators used for NLP applications that employ transformer-based models.

Table 1.
Comparison of transformer-based hardware accelerators.
The computation of attention is heavily influenced by the length of the input sequence, with computational complexity increasing as the square of the sequence length. Some have attempted to mitigate this complexity by segmenting the sequence, but this often results in degraded accuracy due to the inability of establishing connections between distant input tokens. Additionally, the attention mechanism often accounts for the majority of execution time in transformer-based models, while the model parameters are typically large and challenging to fit into embedded system memory. Furthermore, computing these models incurs high energy consumption and latency due to the substantial DRAM accesses required. Sparse computation can remedy these problems but are difficult to utilize in mainstream processors. GPUs, for example, when compared with purposely-built accelerators, are much less efficient when performing attention inference due to complex data movement and low computing intensity.
In transformer models, static sparsity can be introduced in the weights of linear layers, such as Q, K, and V, as well as in the feed-forward neural network modules. By leveraging these opportunities for static sparsity, unnecessary computations in the transformer model can be greatly reduced, leading to improved computational efficiency. Along this line of research, OPTIMUS [20] explores the intrinsic static sparsity in the weights of transformer decoders to skip redundant computations. In decoders, all the previous queries (K) and values (V) are retained to remove redundant re-computations for later stages. In addition, the proposed set-associated rearranged compressed sparse column (SA-RCSC) ensures efficient processing of sparse matrix-dense vector multiplication by mitigating load imbalance and load miss. EdgeBERT [15] applies movement pruning [27] and magnitude pruning [28] to explore static sparsity in embedding and encoder layers, based on hardware optimization techniques to reduce latency and energy consumption in BERT-based model inference. Meanwhile, FPGA-based transformer accelerator, FTRANS [21], utilizes enhanced block-circulant matrix (BCM) weight representation to compress large-scale language model weights to fit into an FPGA but it does not explore sparsity.
The hardware design for static sparsity can leverage knowledge from other domains, whereas a distinct design approach is required for dynamic sparsity. Utilizing dynamic sparsity has the potential to eliminate unnecessary computation to a greater extent than static sparsity, and, as a result, most research endeavors to employ different approaches to implement dynamic sparsity. The main idea behind dynamic sparsity is to calculate attention only for the important query–key pairs. The important query–key pairs are approximated prior to attention computation. The first transformer-based accelerator under this category, [10], accelerates the attention mechanism through an approximation method based on a top-k engine to reduce search targets. The accelerator can process long sequences and achieves significant speed up and energy efficiency over conventional hardware. The SpAtten [9] dynamically sparsifies based on each input by performing cascade pruning on redundant attention heads and tokens. Compared to prior memory-bounded accelerators, SpAtten can optimize both memory and computation-bounded models. Both [10] and SpAtten [9] utilize a top-k engine for the selection of important query–key pairs which incurs high computational overhead, resulting in less computational efficiency. To mitigate the issue of quadratic complexity that arises from processing long sequence data, ELSA [3] employs an approximate approach that involves computing hashes and norms of the input during runtime. It identifies the keys that have the highest similarity to a given query by utilizing their hash distance, and then calculates only those query–key pairs to minimize computational complexity. All the prior accelerators mostly explore coarse grain sparsity and cannot optimize maximum hardware optimization. DOTA [22,23] proposes a fine-grained Dynamic Sparse Attention (DSA) approach that deploys an approximate attention detector to predict dynamic sparse patterns in attention weights. Rather than relying on a top-k engine, the method is trained using a random sparse projection pattern to generate low-precision attention computations that identify the most important query–key pairs, albeit with a slight reduction in accuracy.
Different from the aforementioned methods that are based on full-precision, Sanger [2] and Energon [14] deploy low-precision compute attention to explore dynamic sparsity. Sanger [2] proposes a method that can process dynamic fine-grain sparsity and achieves higher hardware efficiency compared to existing accelerators. It employs pack and split encoding, as well as a score-stationary dataflow, to handle all dynamic computations. Similarly, Energon [14] proposes an approximation method that uses mixed-precision filtering to dynamically detect output-varying query–key pairs and reduce computational complexity. It employs a data fetcher to compute sparse attention efficiently based on the selected query–key pairs from the mixed-precision filtering. Both methods apply full-precision attention computation only on the selected query–key pairs to maintain output accuracy.
The combination of structured and unstructured sparsity in hybrid sparsity presents additional opportunities for efficient processing in sparse attention computation. This approach allows for the fine-tuning of models and the generation of compact models, which can help to improve computational efficiency. SALO [24] explores hybrid sparse attention mechanisms and processes the hybrid patterns with a systolic array-based spatial accelerator. Ampere graphics processing units have shown significant inference performance improvement with 2:4 sparse tensor (two zeros within four continuous parameters) capabilities [29]. To design a more flexible accelerator that can compute different sparsity proportions, authors of [25,26] propose an accelerator, Sparse Transformer (STA), that can handle N:M sparse tensors and achieves comparable speedup compared to GPUs. STA’s ability to process N:M sparse tensors enables it to efficiently handle arbitrary sparse patterns.
Various optimization techniques can be utilized by accelerators to further minimize redundant computations in transformer-based models. The proposed FPGA-based accelerator in [30] accelerates the multi-head attention (MHA) and the position-wise feed-forward network (FFN) blocks. The proposed matrix partition method allows the MHA and FFN blocks to share hardware resources, thus increasing hardware utilization in the systolic array-based accelerator. The paper also demonstrates that quantization is useful to fit the final model in an FPGA with a negligible accuracy loss. TranCIM [31] computes sparse transformer models using a fully digital computing-in-memory (CIM) module. To reduce redundant memory access and computation, it supports both pipeline/parallel reconfigurable models. AccelTran, another accelerator proposed in [32,33], uses DynaTran, a granular and hardware-aware dynamic inference framework that applies pruning to all the activations in order to reduce ineffective MAC operations, to sparsify transformer models. The proposed accelerator utilizes tiled-matrix operations to compute weight-pruned transformer models. A novel mapping scheme is employed to optimize these operations, maximizing hardware utilization and parallelization. Furthermore, the framework investigates various dataflows to identify the optimal one that maximizes data reuse, thereby enhancing energy efficiency.
4. In-Depth Analysis of Key Approaches
In this section, we delve into the architectural designs in existing accelerators. A brief explanation is provided for each main approach, followed by an analysis of the respective advantages and disadvantages.
4.1. Accelerators Exploring Static Sparsity
EdgeBERT: The EdgeBERT [15] accelerator takes an algorithm-hardware co-design approach to design a latency-aware energy-efficient accelerator for multi-task NLP applications on resource-constrained embedded systems. Adhering to target latency constraints, it employs entropy-based early exit to execute dynamic voltage-frequency (DVFS) to reduce energy consumption. Moreover, EdgeBERT reduces computational and memory footprint by exploring the combination of adaptive attention span, selective network pruning, and floating-point quantization.
EdgeBERT investigates sparsity by employing movement pruning [27] and magnitude pruning [28] in the embedding and encoder layers of BERT. Movement pruning eliminates the weights that are dynamically moving toward zero during model fine-tuning. In transfer learning, movement pruning is more efficient compared to magnitude pruning as it keeps near-zero values based on their behavior during fine-tuning. On the other hand, magnitude pruning is more beneficial in high-sparsity regimes due to its specific characteristic. To encode and decode sparse matrices in hardware, bit-mask encoding and decoding methods are utilized. Moreover, the hardware datapath includes a skip logic that disregards zero elements.
4.2. Accelerators Exploring Sparsity with Approximate Candidate Selection
: The [10] accelerator is a pioneering work that utilizes specialized hardware algorithmic approximation to accelerate attention mechanism computation. The similarity between all search targets is computed by the attention matrix, allowing for a content-based search that takes into account semantic significance. When the attention mechanism needs to retrieve knowledge over a longer period of past states, i.e., a longer sequence of input data, the computational complexity of this attention matrix increases quadratically [10]. To alleviate the computational cost and limit the number of search targets, developed an approximate candidate selection mechanism that considers the fact that only a small subset of the targets are pertinent to a given task. Employing algorithm-hardware co-design, implements an energy-efficient accelerator that can handle long input data sequences and achieve multiple orders of magnitude speedup over conventional hardware while maintaining model accuracy.
The softmax operation in the attention mechanism results in most of the score values being converted to near zero, indicating that the matrix–vector multiplication between the key matrix and query matrix has minimal influence on the final score. Preprocessing the key matrix enables the accelerator to identify important rows and reduce unnecessary computations. The proposed approximation algorithm preprocesses the key matrix and eliminates the need to compute the score for rows of the key value matrix that will result in near-zero values after softmax computation. Interestingly, the key matrix preprocessing can be performed when acquiring the query, resulting in no significant overhead for the key matrix preprocessing. To preprocess the key matrix, employs a candidate selection module (presented in Figure 3a) that stores sorted keys and their corresponding indices in SRAM buffers. Two circular queues buffer query and key multiplication component results to find the max and min values in the component products using a comparator tree. The maximum and minimum values are stored in registers and , and the greedy score module is updated to select a set of keys.
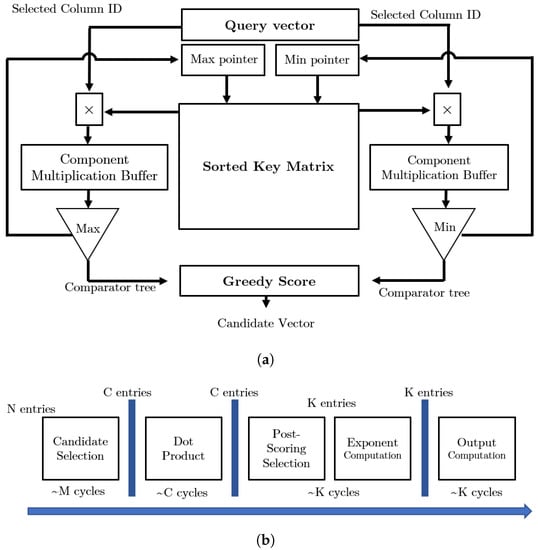
Figure 3.
Overview of the accelerator [10]. utilizes a greedy algorithm to choose candidates by first finding the maximum and minimum values of query and key products. The candidate selection module takes around M cycles to identify C candidates. The approximated attention computation for the chosen candidates takes a total of cycles, where is a constant and K represents the top entries chosen by the post-scoring selection module. (a) candidate selection module [10]. (b) High level implementation steps of accelerator [10].
Using a candidate selection module, the accelerator preprocesses the key matrix and extracts a list of rows for computation in the dot-product module. The dot-product module generates results for the provided list of candidates, which are then passed on to the post-scoring selector module. The post-scoring selector module chooses a small subset of important rows for calculation in the exponent unit, and the final weighted sum is then computed in the output computation module. Figure 3b displays the clock cycles necessary for computing attention. The modular design of allows it to function as a co-processor alongside CPUs and GPUs.
SpAtten: Transformer models are known for their high performance but come at a significant computational cost. Due to their unique computational and memory-bound characteristics, they can be challenging to accelerate. As a result, different transformer models require specific computational optimizations to achieve optimal performance. SpAtten [9] implements cascade token, head pruning, and progressive quantization to leverage token sparsity, head sparsity, and quantization opportunities to optimize both computation-bounded and memory-bounded models. Figure 4 depicts an illustration of the SpAtten architecture overview.
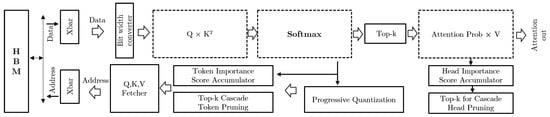
Figure 4.
Overview of SpAtten architecture [9].
When performing cascade pruning, the removal of an element (such as a token or a head) in one layer results in its removal from all subsequent layers. To minimize memory (e.g., DRAM) access, cascade token pruning eliminates structural and non-essential tokens such as articles, prepositions, and adverbs. Cascade head pruning eliminates unnecessary heads from the attention mechanism by considering their impact on the output, thereby reducing redundancy. Consequently, token pruning decreases sentence length, whereas head pruning decreases features. As a result, SpAtten is more amenable to retrieving knowledge from longer input sequences while minimizing computation and memory access redundancy. In addition, progressive quantization modifies bit-widths in different attention heads and layers based on attention probability distribution, leading to additional reduction in DRAM access [9].
To dynamically process each input for efficient hardware execution, a specialized high parallelism top-k engine is designed for SpAtten to rank token and head importance scores for pruning. By utilizing a quick-select module that selects the kth largest element as a threshold to filter the input, this top-k engine achieves linear time complexity , i.e., the runtime scales linearly with the size of the input. The top-k engine retrieves the k most relevant keys (K) for a given query (Q) by evaluating the importance score of each token and ranking them accordingly. After identifying the relevant query–key pairs, a matrix–vector module is used to compute their corresponding attention scores. These scores are then passed through a softmax unit to calculate the attention probabilities. The resulting probabilities are subsequently sent to an on-chip bit-width converter, which performs progressive quantization. Following that, based on the top-k selected k-most important values, the final attention output is computed. Once all the necessary computations are completed within a single head, the head’s importance score is calculated. After computing all the heads in a layer, the top-k engine prunes the ones that are deemed unimportant. This cascade pruning technique ensures that the pruned heads are not computed in the subsequent layers. This helps to reduce DRAM access, thereby improving the overall efficiency of the system.
ELSA: In order to overcome the quadratic challenges that arise with lengthy input sequences, numerous techniques divide the sequence into smaller segments. Nevertheless, when using such methods in conjunction with an attention mechanism, there is a limitation in that it is incapable of establishing connections between two tokens that belong to separate segments. By employing an approximation scheme on the input sequence, ELSA [3], an efficient and lightweight self-attention accelerator, considerably reduces energy consumption and run-time. With the proposed approximation scheme, computational inefficiency is significantly reduced by eliminating irrelevant relations in the input sequence, which does not affect the final output. This enables the processing of long sequences without dividing them into segments.
When the dimensions of query and key are in self-attention, the intermediate score matrix (referred to as the attention matrix) S (=) involves multiplications. Despite this, most of the values in the score matrix become nearly zero after the softmax operation, leading to a sparse output. To mitigate this problem, ELSA identifies a specific subset of keys that are expected to have significant attention scores for each query, thus reducing the number of multiplications necessary for the score matrix (). ELSA determines the relevance of a key to a query by calculating the similarity between their vectors based on their angle and comparing the approximate similarity with a threshold. This method is employed to achieve the goal of reducing the number of multiplications needed for the score matrix. Figure 5 presents a block diagram that depicts the high-level data flow of the ELSA accelerator pipeline.
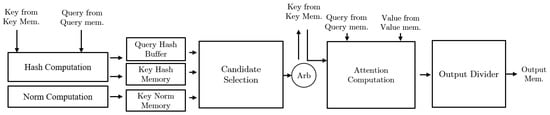
Figure 5.
Overview of ELSA architecture [3].
The ELSA accelerator comprises hash and norm computation units that calculate hash and norm values for each row of the key matrix. Once these values are stored in their respective memories, candidate selection modules determine the selected candidate key IDs for each module’s output queue. An arbitrator processes these selected key IDs, which are then computed in the attention computation module. This module calculates and aggregates the selected key’s contribution to the current query. The output division module performs division once all the selected keys for a specific query have been computed. The accelerator repeats all computations until all queries are processed. This accelerator can be viewed as a specialized functional unit for self-attention computation and can be integrated with CPUs, GPUs, and other accelerators.
DOTA: In order to address the challenges posed by quadratic time and space complexity, DOTA [22,23] introduces the Dynamic Sparse Attention (DSA) technique. This method leverages an approximate attention predictor to anticipate the dynamic sparse patterns present in attention weights. DSA investigates dynamic sparsity in attention without static constraints while maintaining low computational cost and full attention effectiveness. Figure 6 presents an illustration of the DSA overview. The standard attention mechanism calculates the attention score and the final attention output using a general matrix–matrix multiplication (GEMM) operation. The DSA algorithm computes the approximate attention score using the expression , where P represents a sparse random projection, and and denote the approximation weights for the keys K and queries Q, respectively. The sparse attention mask M is obtained by thresholding the approximate score, which can be fine-tuned using the validation set or calculated using a top-k engine. The sparse attention masks M are employed to generate the final sparse outputs.
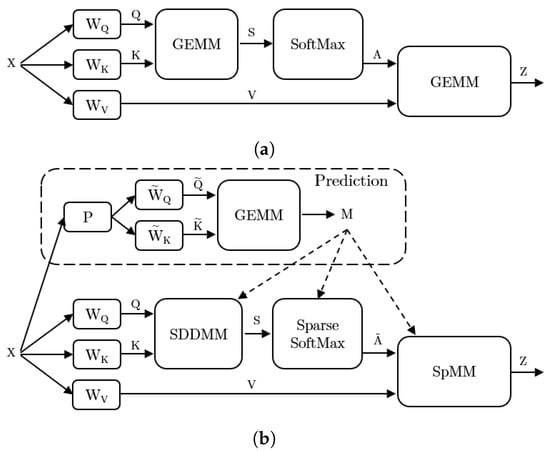
Figure 6.
Sparse computation with approximation-based prediction in dynamic sparse attention (DSA). The predictor is trained using a sparse random projection matrix P to calculate low-precision query and key. The sparse attention mask M is produced by applying thresholding to the low-precision query–key product. (a) Dense computation steps in non-sparse attention computation. (b) Sparse computation steps in DSA.
Figure 7 depicts the abstraction of the DOTA accelerator, which implements DSA. While the model is limited to processing a single sequence at a time, it can be scaled out to multiple instances, enabling sequence-level parallelism. The encoder conducts three data-dependent sequential GEMM computations: linear transformation, multi-head attention, and FFN. These sequential operations are partitioned into four chunks (four lanes in Figure 7) to enhance performance. Each lane operates on a portion of , , and , with the final outcomes from these lanes aggregated by the accumulator. If more chunk-level parallelism is required by the application, the number of lanes can be increased. Each lane comprises a Re-configurable Matrix Multiplication Unit (RMMU), an Attention Selection Detector, and a Multi-Function Unit. The RMMU is capable of performing different-precision GEMM operations. The detector computes attention selection based on RMMU’s low-precision computations, with the Scheduler in the detector organizing computations to balance the computational load and memory access.
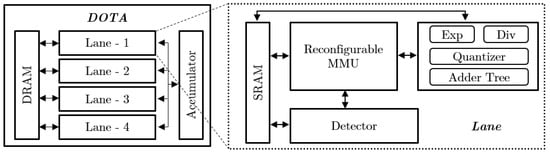
Figure 7.
Overview of DOTA Accelerator [22,23]. The input is divided among multiple parallel lanes, with each lane handling a section of the input before the results are merged once all lanes have finished processing.
4.3. Accelerators Exploring Dynamic Sparsity with Mixed-Precision Selection
Sanger: The approaches that explore irregular or regular coarse-grained sparsity patterns in attention mechanisms are less effective in utilizing the higher computational benefits of fine-grained sparsity. Furthermore, irregular sparse patterns pose challenges for parallelization due to irregular data movement and can lead to data imbalance across processing elements (PEs) when not distributed evenly. Sanger [2] employs a ’pack and split’ based encoding scheme to transform a dynamic unstructured sparse pattern into load-balanced multiple fine-grained structured blocks. Sanger [2], with a score-stationary dataflow and reconfigurable systolic array-based hardware architecture, overcomes additional overheads due to decoding and memory transfer. The ability to handle dynamic fine-grained and structured patterns allows Sanger to exploit higher sparsity and speed up compared to [10] and SpAtten [9].
Sanger takes a software-hardware co-design approach to optimize the model inference. The overview of the proposed Sanger framework is depicted in Figure 8. An attention-pruning algorithm is applied to the attention matrix during software-level optimization, generating an unstructured sparse pattern. By computing a low-bit attention matrix () on quantized (e.g., 4-bit) matrices of query (Q) and keys (K), a sparse attention mask is then pruned from the low-bit attention matrix using binary thresholding. The resultant sparse attention mask is unstructured and exhibits higher sparsity due to the dynamic sparse pattern captured from each input query and keys. To overcome the challenges in accelerating unstructured fine-grained sparsity, Sanger proposes an encoding method to pack and split the attention mask and transforms it into multiple structured blocks while maintaining balanced workloads.
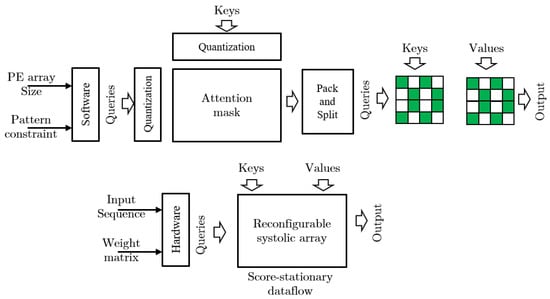
Figure 8.
Overview of Sanger framework [2].
Sanger hardware accelerator is designed with a re-configurable systolic array (RSA) that unifies and performs both SDDMM and SpMM operations in a score-stationary dataflow. In the RSA, the processing elements can dynamically handle queries, keys, and values with different indices, enabling a flexible distribution of non-zero values within a block. This feature is useful in improving the compression ratio during pruning. During inference, the accelerator takes the input and generates sparse masks that implement the pruning algorithm, including quantization, thresholding, and encoding. Finally, the sparse computations are computed on the RSA.
Energon: Performing real-time inference on resource-constrained edge-computing devices poses a significant challenge. To reduce latency and improve throughput, Energon [14] proposes a Mix-Precision Multi-Round Filtering (MP-MRF) algorithm to dynamically identify result-dependent query–key pairs at runtime to tackle the quadratic computational complexity. During the filtering stage, the accelerator utilizes low-precision computation to determine the crucial query–key pairs. Nevertheless, for these significant pairs, high-precision tensors are utilized in the attention computation to preserve the model’s accuracy. Energon achieves significant speed up and energy reduction compared to CPU and GPU implementations on many CV and NLP benchmarks at a negligible accuracy loss [14].
The MP-MRF strategy searches for important keys for each query by performing mix-precision filtering for multiple rounds (as depicted in Figure 9). The computation of the query–key () is first performed using an extremely low bit-width (e.g., 2 bit) in the initial round. Subsequently, the bit-width is gradually increased in each successive round to filter out additional keys. The MP-MRF approach utilizes mean filtering to identify query–key pairs in each round, which is a hardware-efficient alternative to top-k selection. Despite the use of specialized hardware, the top-k engine remains computationally demanding due to the need for full precision attention score computation and a sorting engine to determine the top candidates. Typically, mean filtering is responsible for pruning around 50% of the elements in each round. However, in the case of Energon, an adjustable parameter has been incorporated to regulate the degree of pruning. Once the low-bit-width filtering round has identified the query–key pairs, the final sparse attention computation is performed using high-precision tensors. This approach enables the MP-MRF strategy to minimize computational complexity by leveraging mix-precision tensor computations.
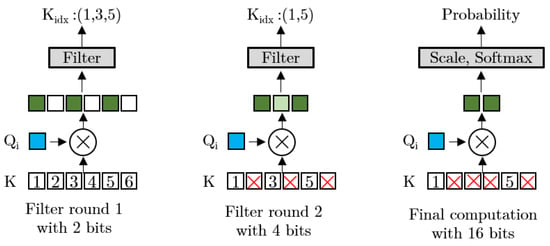
Figure 9.
Filtering steps of MP-MRF [14]. Starting from the left side of the diagram, the bit-width is progressively increased in order to eliminate less significant keys for a given query. Final computation uses full 16-bit precision.
The overview of Energon accelerator architecture is illustrated in Figure 10. The filtering unit (FU) fetches query–key pairs from memory and performs MP-MRF to find the indices of important keys. The attention unit (AU) takes the key indices and computes sparse attention and stores it back to DRAM. In the filtering unit, the result-reusable mix-precision Inner-Product Unit (IPU) and key data layout are employed for better efficient processing and on-chip resource savings. During pipeline execution of attention computation in the attention unit, Energon implements an On-Demand Fetching (ODF) to reduce DRAM access.

Figure 10.
Overview of Energon Accelerator [14]. The process of selecting essential keys for each query is carried out by the Filtering Unit (FU) through multi-round mix-precision filtering. Once the filtering is complete, the attention unit (AU) computes high-precision sparse attention on the selected keys.
4.4. Accelerators Exploring Hybrid Sparse Pattern
SALO: The SALO [24] work presents an innovative solution to address the computational and memory challenges that arise when processing lengthy input sequences. By employing a hybrid sparse attention mechanism that incorporates both local window and global attention patterns, the authors are able to reduce the computational complexity to a linear scale, thereby enhancing the efficiency of sequence processing. By transforming a sparse pattern into a hybrid pattern and utilizing a spatial accelerator, SALO achieves a considerable increase in processing speed when compared to CPU and GPU implementations. Figure 11 provides an overview of the SALO framework.
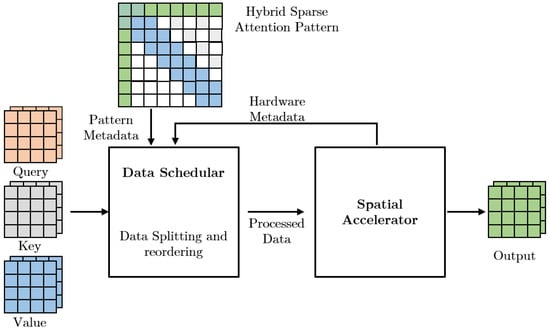
Figure 11.
Overview of SALO framework [24]. Data scheduler performs data reordering and splitting on the hybrid pattern. On the processed data from the data scheduler, the spatial accelerator performs sparse computation.
The SALO comprises a data scheduler and a systolic array-based spatial accelerator. The hybrid sparse attention patterns in SALO are transformed by the data scheduler to meet the constraints required for executing them in the spatial accelerators. This process involves data reordering and splitting, which enable the dataflow and size constraints to be satisfied. SALO’s dataflow design focuses on maximizing data reuse during hybrid sparse attention computation to reduce memory accesses and shorten the data path. Sliding window patterns and global attention are divided into tiles for multiple passes while dilated patterns are reordered into sliding window patterns to be processed by the accelerator. The data scheduler thus facilitates the processing of long input sequences using hybrid sparse attention and ensures that they fit into the spatial accelerator. The spatial accelerator consists of processing element (PE) arrays, including global PE units that accumulate row and column-wise from the arrays. To maximize data reuse, the PE arrays feature diagonal connections. SALO evaluation mostly compares CPU and GPU implementations which is promising; however, comparison with existing accelerators is limited. SALO, similar to Sanger [2], computes using systolic arrays and achieves speedup compared to Sanger [2].
STA: Aggressive weight pruning can cause transformer models to become heavily sparsed, resulting in the generation of N:M sparse patterns (such as 1:8 or 2:8). As a result, STA [25,26] has proposed an accelerator that focuses on accelerating fine-grained N:M sparse tensors in transformers, following this concept. These sparse tensors have N zeros within M continuous parameters, and recent research [34] indicates that utilizing them can lead to significant performance improvements compared to unstructured sparsity.
In N:M sparse pattern generation, existing methods such as SR-STE [34] and NVIDIA ASP [35] suffers from performance degradation at a higher sparse ratio. To alleviate this, the proposed approach uses an inherited dynamic pruning (IDP)-based sparsity inheritance mechanism to achieve an N:M sparse pattern. During the conversion process using IDP, prior knowledge of N:M sparse models is utilized to facilitate faster and more effective convergence of the current model. In order to fully leverage the advantages of the sparse model, the N:M sparse transformer is compressed through bitmap-based compression, resulting in a significant reduction in memory requirements (). Upon completion of all algorithmic optimizations, the automatic hardware generator utilizes the optimized model and a hardware template library of FPGAs to generate a custom STA architecture. The overview of the STA architecture is illustrated in Figure 12.
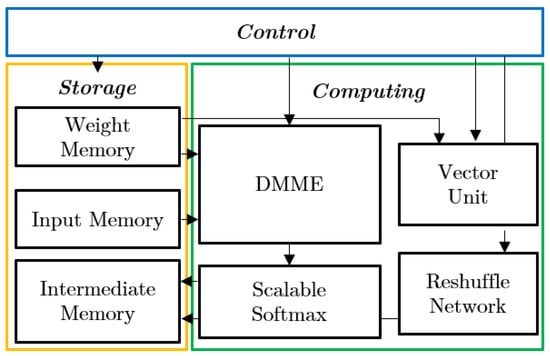
Figure 12.
Overview of STA architecture [25].
The three primary components of the STA architecture are the storage block, the computing block, and the control block. Within the computing blocks, there are several elements including a Diverse MatMul computing engine called DMME, a scalable softmax module, a vector unit, and a data reshuffle network. DMME performs N:M sparse operations: sparse–dense and dense–dense matrix multiplication during run time with dynamic configuration while maintaining high efficiency. The computational efficiency of sparse–dense matrix multiplications is significantly improved by selecting only the non-zero weight parameters and their corresponding activation values for computation, thereby reducing the number of unnecessary computations. Meanwhile, multi-headed attention residual computations can be executed without off-chip memory transfer in the scalable softmax, thus eliminating off-chip memory access. Intermediate memory block stores all the intermediate results to reduce additional communication to off-chip memory.
5. Discussions and Future Directions
Analyzing the sparse accelerators for transformers, it is evident that dynamic sparsity can provide higher sparsity but is challenging to accelerate in hardware due to the inherent unstructured sparse patterns. [10] can harvest dynamic sparsity and improve computational complexity. It can accelerate computationally bounded models such as BERT. However, to achieve that, needs to load the full uncompressed QKV vectors to on-chip memory from DRAM. As it cannot reduce DRAM accesses, it is memory bounded and cannot handle memory-bound models like GPT. On the contrary, cascade pruning allows SpAtten [9] to handle long sequences and process memory-bound models efficiently. The top-k engine in SpAtten, which is used to select items for pruning, is computationally expensive and inefficient in dynamic sparsity acceleration due to the low pruning ratio. Similar to [10], ELSA [3] uses an approximation method and dot-product module to calculate attention. It speeds up by utilizing more parallel computing units. However, the approximation method and candidate selection suffer from high computational overhead. EdgeBERT [15] mostly depends on hardware design optimization techniques to reduce computation. Explored sparsity ratio is not adequate and has limited savings in computation. Sanger [2] and SALO [24] both show similar performance by using a systolic array as the computing unit. However, Sanger’s attention pruning suffers from latency due to long sequence quadratic complexity. While the spatial accelerator in SALO [24] is efficient, there is a limitation in its ability to fully utilize the efficiency of the hybrid sparse pattern, as it does not have knowledge of the input data during inference. OPTIMUS [20] requires computation in the Fourier domain which requires complex value computation and limits achievable speedup. FTRANS [21] uses a compression technique to optimize memory consumption; however, it does not utilize sparsity for computational optimization. Most of the recent research has focused on optimizing the attention calculation based on dynamic prediction or approximation of the important query–key pairs. Dynamic sparsity has the highest pruning ratio and can reduce computation by a significant amount. This can be utilized by using mixed-precision computation to determine the importance of the query–key pairs before the full computation of the attention matrix. Mixed-precision-based computations typically suffer from a certain degree of error. Based on these observations and analysis, we have synthesized several main future opportunities in exploring sparsity for transformer accelerators.
Sparsification Methods: Hardware acceleration has significant potential for further development and application of sparsification methods. During inference, current dynamic sparsity is utilized almost exclusively in the attention computation, but its effect on sparsity in other computational units is minimal. Magnitude pruning and movement pruning can be applied for exploring sparsity in other computational layers, such as fully connected layers, as these methods are comparatively easier to train. Regularization methods can also achieve a high level of sparsity, but they are challenging to train [36]. One example of a sparsification method is L1 regularization, which encourages many weights in a model to be zero, resulting in a high degree of sparsity. In contrast, the Lasso method can induce structured sparsity by promoting groups of related weights to be zero. Therefore, additional investigation on addressing the difficulties associated with training using regularization techniques could satisfy the additional design needs. Moreover, hardware architecture along with model architecture can be co-explored in optimizing sparsification methods for achieving optimal performance and energy efficiency on a given hardware platform.
Hardware Architecture for Unstructured sparsity: Existing accelerators are efficient in processing structured sparse patterns. Currently, additional layers of computation are required to preprocess the unstructured pattern for efficient hardware execution. A significant amount of computation can be reduced if this step is removed. An optimized hardware architecture for unstructured fine-grained sparsity is still an open research direction that can further accelerate the inference of transformer-based models.
Linearized Transformers: To alleviate quadratic computation complexity, low-rank approximation [37] and kernelization [38,39,40,41] of attention computation have been popular recently [42]. In the attention matrix, a low-rank approximation-based Linformer [37] projects keys and values in lower dimensions to reduce memory complexity. The attention matrix decomposes to where . Meanwhile, kernelization does not require explicit computation of the () attention matrix. Both such approximation methods reduce computational complexity to an approximated . Hardware accelerators can utilize these linearization techniques to handle quadratic computation and memory challenges.
Flexible Accelerators for Training: For many applications in various domains, deep learning models are trained on high-performance computing clusters with a large number of CPUs and GPUs, incurring a large amount of cost and carbon footprint [11,12]. In the ever-changing deep learning paradigm, accelerators can be less preferred for training due to financial considerations and the flexibility of GPUs. While some works have started to explore flexible accelerators for training, substantially more research is needed to improve the performance, energy efficiency, and flexibility of accelerators. Accelerators for computer vision tasks such as ScaleDeep [43] and HyPar [44] report significant performance gains even without exploring sparsity opportunities in CNNs. Ampere architecture-based GPUs from NVidia support 1:2 structured sparsity which reports significant performance improvement over its predecessors [29]. Accelerators for training can utilize data reuse and mixed precision with high sparsity. It may be worth exploring the combined use of GPUs and sparsity-exploring accelerators to further alleviate training challenges.
Unified Evaluation Framework: It is difficult to evaluate and compare accelerators as there is no unified framework to conduct comparative measures effectively. Hardware accelerators use different hardware technologies. It is challenging to compare an FPGA implementation with an ASIC implementation. Usually, ASIC implementations can be optimized over FPGAs. Furthermore, different ASIC technologies used in accelerator implementation have a significant impact on accelerator performance. A better implementation choice for an average design choice may achieve a better performance than a better design approach with an older implementation process. A standard implementation process may assist in identifying a better hardware architecture. Although there are several frameworks [45,46,47] available for developing accelerators, they are not designed for sparse computation [19]. At the software level, harnessing sparsity using different approaches vastly depends on the target objective, experimental setup, and hyperparameter settings. Several benchmarks such as MLPerf [48], Deep500 [49], and [50] have been popular in evaluating algorithms by applying standard setup for specific tasks. A unified evaluation framework combining hardware and software optimizations can help achieve target constraints [36].
6. Conclusions
Transformer-based models have become the driving force for sequence modeling tasks, but their computational requirement is the bottleneck for low-resource devices. Hardware accelerators can alleviate the challenges, but in-depth optimizations of software and hardware are crucial for their effectiveness. Sparsity has emerged as a promising approach for hardware accelerators, as it reduces redundancy and enhances hardware efficiency. This paper discusses and analyzes accelerators for transformers that utilize sparsity to address the challenges of computation and memory. Prior research has investigated various aspects of sparsity and hardware architecture, but the majority of studies focus on optimizing computational efficiency using static and dynamic sparsity. Analysis shows that dynamic and fine-grained sparsity significantly reduces redundancy and improves hardware efficiency. Nevertheless, the problem of reducing overhead caused by encoding and decoding the sparse computation pattern through architectural exploration remains a challenge. Furthermore, investigating sparsity in linearized transformers can mitigate the existing limitations in hardware implementation.
Author Contributions
Conceptualization, K.A.A.F. and L.C.; formal analysis, K.A.A.F. and L.C.; methodology, K.A.A.F.; software, K.A.A.F.; supervision, L.C.; validation, L.C.; writing—original draft, K.A.A.F., and L.C.; writing—review & editing, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded, in part, by the National Science Foundation grants 2223483 and 2223484.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Lu, L.; Jin, Y.; Bi, H.; Luo, Z.; Li, P.; Wang, T.; Liang, Y. Sanger: A Co-Design Framework for Enabling Sparse Attention Using Reconfigurable Architecture. In Proceedings of the MICRO ’21, MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture, Virtual, 18–22 October 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 977–991. [Google Scholar] [CrossRef]
- Ham, T.J.; Lee, Y.; Seo, S.H.; Kim, S.; Choi, H.; Jung, S.J.; Lee, J.W. ELSA: Hardware-Software Co-design for Efficient, Lightweight Self-Attention Mechanism in Neural Networks. In Proceedings of the 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture (ISCA), Valencia, Spain, 14–18 June 2021; pp. 692–705. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. Roberta: A robustly optimized bert pretraining approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Shoeybi, M.; Patwary, M.; Puri, R.; LeGresley, P.; Casper, J.; Catanzaro, B. Megatron-lm: Training multi-billion parameter language models using model parallelism. arXiv 2019, arXiv:1909.08053. [Google Scholar]
- Rosset, C. Turing-NLG: A 17-Billion-Parameter Language Model by Microsoft. 2020. Available online: https://www.microsoft.com/en-us/research/blog/turing-nlg-a-17-billion-parameter-language-model-by-microsoft/ (accessed on 19 December 2022).
- Wang, H.; Zhang, Z.; Han, S. SpAtten: Efficient Sparse Attention Architecture with Cascade Token and Head Pruning. arXiv, 2012. [Google Scholar]
- Ham, T.; Jung, S.; Kim, S.; Oh, Y.H.; Park, Y.; Song, Y.; Park, J.; Lee, S.; Park, K.; Lee, J.W.; et al. A3: Accelerating Attention Mechanisms in Neural Networks with Approximation. In Proceedings of the 2020 IEEE International Symposium on High Performance Computer Architecture (HPCA), San Diego, CA, USA, 22–26 February 2020; IEEE Computer Society: Los Alamitos, CA, USA, 2020; pp. 328–341. [Google Scholar] [CrossRef]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and policy considerations for deep learning in NLP. arXiv 2019, arXiv:1906.02243. [Google Scholar]
- So, D.; Le, Q.; Liang, C. The evolved transformer. In Proceedings of the International Conference on Machine Learning. PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 5877–5886. [Google Scholar]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, J.; Gu, Z.; Sun, G. Energon: Towards Efficient Acceleration of Transformers Using Dynamic Sparse Attention. arXiv, 2010. [Google Scholar]
- Tambe, T.; Hooper, C.; Pentecost, L.; Jia, T.; Yang, E.Y.; Donato, M.; Sanh, V.; Whatmough, P.; Rush, A.M.; Brooks, D.; et al. EdgeBERT: Sentence-Level Energy Optimizations for Latency-Aware Multi-Task NLP Inference. In Proceedings of the MICRO ’21, MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture, Virtual, 18–22 October 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 830–844. [Google Scholar] [CrossRef]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2013, arXiv:1308.0850. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]
- Dave, S.; Baghdadi, R.; Nowatzki, T.; Avancha, S.; Shrivastava, A.; Li, B. Hardware acceleration of sparse and irregular tensor computations of ml models: A survey and insights. Proc. IEEE 2021, 109, 1706–1752. [Google Scholar] [CrossRef]
- Park, J.; Yoon, H.; Ahn, D.; Choi, J.; Kim, J.J. OPTIMUS: OPTImized matrix MUltiplication Structure for Transformer neural network accelerator. Proc. Mach. Learn. Syst. 2020, 2, 363–378. [Google Scholar]
- Li, B.; Pandey, S.; Fang, H.; Lyv, Y.; Li, J.; Chen, J.; Xie, M.; Wan, L.; Liu, H.; Ding, C. Ftrans: Energy-efficient acceleration of transformers using fpga. In Proceedings of the ACM/IEEE International Symposium on Low Power Electronics and Design, Boston, MA, USA, 10–12 August 2020; pp. 175–180. [Google Scholar]
- Liu, L.; Qu, Z.; Chen, Z.; Tu, F.; Ding, Y.; Xie, Y. Dynamic Sparse Attention for Scalable Transformer Acceleration. IEEE Trans. Comput. 2022, 71, 3165–3178. [Google Scholar] [CrossRef]
- Qu, Z.; Liu, L.; Tu, F.; Chen, Z.; Ding, Y.; Xie, Y. DOTA: Detect and Omit Weak Attentions for Scalable Transformer Acceleration. In Proceedings of the ASPLOS ’22, 27th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Lausanne, Switzerland, 28 February–4 March 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 14–26. [Google Scholar] [CrossRef]
- Shen, G.; Zhao, J.; Chen, Q.; Leng, J.; Li, C.; Guo, M. SALO: An Efficient Spatial Accelerator Enabling Hybrid Sparse Attention Mechanisms for Long Sequences. In Proceedings of the DAC ’22, 59th ACM/IEEE Design Automation Conference, San Francisco, CA, USA, 10–14 July 2022; Association for Computing Machinery: New York, NY, USA, 2022; pp. 571–576. [Google Scholar] [CrossRef]
- Fang, C.; Zhou, A.; Wang, Z. An Algorithm–Hardware Co-Optimized Framework for Accelerating N:M Sparse Transformers. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2022, 30, 1573–1586. [Google Scholar] [CrossRef]
- Fang, C.; Guo, S.; Wu, W.; Lin, J.; Wang, Z.; Hsu, M.K.; Liu, L. An Efficient Hardware Accelerator for Sparse Transformer Neural Networks. In Proceedings of the 2022 IEEE International Symposium on Circuits and Systems (ISCAS), Austin, TX, USA, 27 May–1 June 2022; pp. 2670–2674. [Google Scholar] [CrossRef]
- Sanh, V.; Wolf, T.; Rush, A. Movement Pruning: Adaptive Sparsity by Fine-Tuning. In Proceedings of the Advances in Neural Information Processing Systems, Online, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 20378–20389. [Google Scholar]
- Han, S.; Mao, H.; Dally, W.J. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv 2015, arXiv:1510.00149. [Google Scholar]
- NVIDIA. NVIDIA AMPERE GA102 GPU Architecture; Technical Report; NVIDIA: Santa Clara, CA, USA, 2021. [Google Scholar]
- Lu, S.; Wang, M.; Liang, S.; Lin, J.; Wang, Z. Hardware accelerator for multi-head attention and position-wise feed-forward in the transformer. In Proceedings of the 2020 IEEE 33rd International System-on-Chip Conference (SOCC), Virtual, 8–11 September 2020; pp. 84–89. [Google Scholar]
- Tu, F.; Wu, Z.; Wang, Y.; Liang, L.; Liu, L.; Ding, Y.; Liu, L.; Wei, S.; Xie, Y.; Yin, S. TranCIM: Full-Digital Bitline-Transpose CIM-based Sparse Transformer Accelerator With Pipeline/Parallel Reconfigurable Modes. IEEE J. Solid-State Circuits 2022, 1–12. [Google Scholar] [CrossRef]
- Tuli, S.; Jha, N.K. EdgeTran: Co-designing Transformers for Efficient Inference on Mobile Edge Platforms. arXiv 2023, arXiv:2303.13745. [Google Scholar]
- Tuli, S.; Jha, N.K. AccelTran: A sparsity-aware accelerator for dynamic inference with transformers. arXiv 2023, arXiv:2302.14705. [Google Scholar] [CrossRef]
- Zhou, A.; Ma, Y.; Zhu, J.; Liu, J.; Zhang, Z.; Yuan, K.; Sun, W.; Li, H. Learning N: M fine-grained structured sparse neural networks from scratch. arXiv 2021, arXiv:2102.04010. [Google Scholar]
- Mishra, A.; Latorre, J.A.; Pool, J.; Stosic, D.; Stosic, D.; Venkatesh, G.; Yu, C.; Micikevicius, P. Accelerating sparse deep neural networks. arXiv 2021, arXiv:2104.08378. [Google Scholar]
- Hoefler, T.; Alistarh, D.; Ben-Nun, T.; Dryden, N.; Peste, A. Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks. J. Mach. Learn. Res. 2021, 22, 10882–11005. [Google Scholar]
- Wang, S.; Li, B.Z.; Khabsa, M.; Fang, H.; Ma, H. Linformer: Self-attention with linear complexity. arXiv 2020, arXiv:2006.04768. [Google Scholar]
- Qin, Z.; Sun, W.; Deng, H.; Li, D.; Wei, Y.; Lv, B.; Yan, J.; Kong, L.; Zhong, Y. cosFormer: Rethinking Softmax in Attention. arXiv 2022, arXiv:2202.08791. [Google Scholar]
- Choromanski, K.; Likhosherstov, V.; Dohan, D.; Song, X.; Gane, A.; Sarlos, T.; Hawkins, P.; Davis, J.; Mohiuddin, A.; Kaiser, L.; et al. Rethinking attention with performers. arXiv 2020, arXiv:2009.14794. [Google Scholar]
- Katharopoulos, A.; Vyas, A.; Pappas, N.; Fleuret, F. Transformers are rnns: Fast autoregressive transformers with linear attention. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 5156–5165. [Google Scholar]
- Peng, H.; Pappas, N.; Yogatama, D.; Schwartz, R.; Smith, N.A.; Kong, L. Random feature attention. arXiv 2021, arXiv:2103.02143. [Google Scholar]
- Tay, Y.; Dehghani, M.; Bahri, D.; Metzler, D. Efficient transformers: A survey. ACM Comput. Surv. 2022, 55, 1–28. [Google Scholar] [CrossRef]
- Venkataramani, S.; Ranjan, A.; Banerjee, S.; Das, D.; Avancha, S.; Jagannathan, A.; Durg, A.; Nagaraj, D.; Kaul, B.; Dubey, P.; et al. ScaleDeep: A Scalable Compute Architecture for Learning and Evaluating Deep Networks. In Proceedings of the ISCA ’17, 44th Annual International Symposium on Computer Architecture, Toronto, ON, Canada, 24–28 June 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 13–26. [Google Scholar] [CrossRef]
- Song, L.; Mao, J.; Zhuo, Y.; Qian, X.; Li, H.; Chen, Y. Hypar: Towards hybrid parallelism for deep learning accelerator array. In Proceedings of the 2019 IEEE International Symposium on High Performance Computer Architecture (HPCA), Washington, DC, USA, 16–20 February 2019; pp. 56–68. [Google Scholar]
- Zhang, X.; Wang, J.; Zhu, C.; Lin, Y.; Xiong, J.; Hwu, W.; Chen, D. DNNBuilder: An automated tool for building high-performance DNN hardware accelerators for FPGAs. In Proceedings of the 2018 IEEE/ACM International Conference on Computer-Aided Design, ICCAD 2018—Digest of Technical Papers, San Diego, CA, USA, 5–8 November 2018. [Google Scholar] [CrossRef]
- Sharma, H.; Park, J.; Mahajan, D.; Amaro, E.; Kim, J.K.; Shao, C.; Mishra, A.; Esmaeilzadeh, H. From high-level deep neural models to FPGAs. In Proceedings of the 2016 49th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), Taipei, Taiwan, 15–19 October 2016; pp. 1–12. [Google Scholar] [CrossRef]
- Kwon, H.; Samajdar, A.; Krishna, T. MAERI: Enabling Flexible Dataflow Mapping over DNN Accelerators via Reconfigurable Interconnects. SIGPLAN Not. 2018, 53, 461–475. [Google Scholar] [CrossRef]
- Mattson, P.; Cheng, C.; Diamos, G.; Coleman, C.; Micikevicius, P.; Patterson, D.; Tang, H.; Wei, G.Y.; Bailis, P.; Bittorf, V.; et al. Mlperf training benchmark. Proc. Mach. Learn. Syst. 2020, 2, 336–349. [Google Scholar]
- Ben-Nun, T.; Besta, M.; Huber, S.; Ziogas, A.N.; Peter, D.; Hoefler, T. A modular benchmarking infrastructure for high-performance and reproducible deep learning. In Proceedings of the 2019 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Rio de Janeiro, Brazil, 20–24 May 2019; pp. 66–77. [Google Scholar]
- Blalock, D.; Gonzalez Ortiz, J.J.; Frankle, J.; Guttag, J. What is the state of neural network pruning? Proc. Mach. Learn. Syst. 2020, 2, 129–146. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).