Efficient Multiclass Classification Using Feature Selection in High-Dimensional Datasets
Abstract
1. Introduction
2. Background
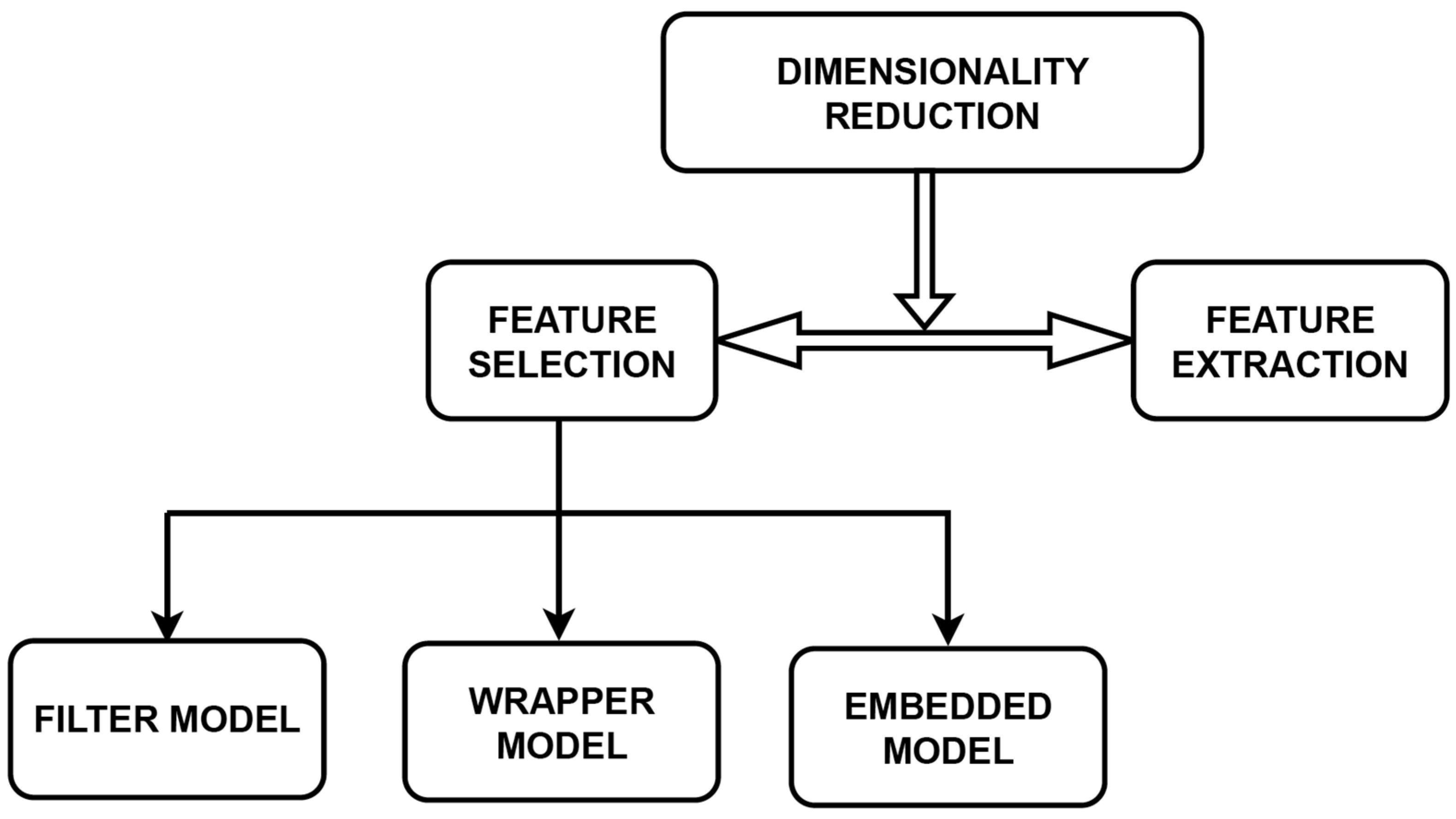
2.1. Dimensionality Reduction
- Is there any methodology to find the optimal features?
- Is there any evaluation process that could determine that the selected features are optimal?
- Is there a methodology used for independent feature-selection applications?
- In the first step, generate the feature subset by applying some methodology.
- After that, evaluate the feature subset.
- Then the termination conditions are applied.
- Finally, the result is validated.
2.2. Model for Feature Selection
3. Related Work
4. Methodology
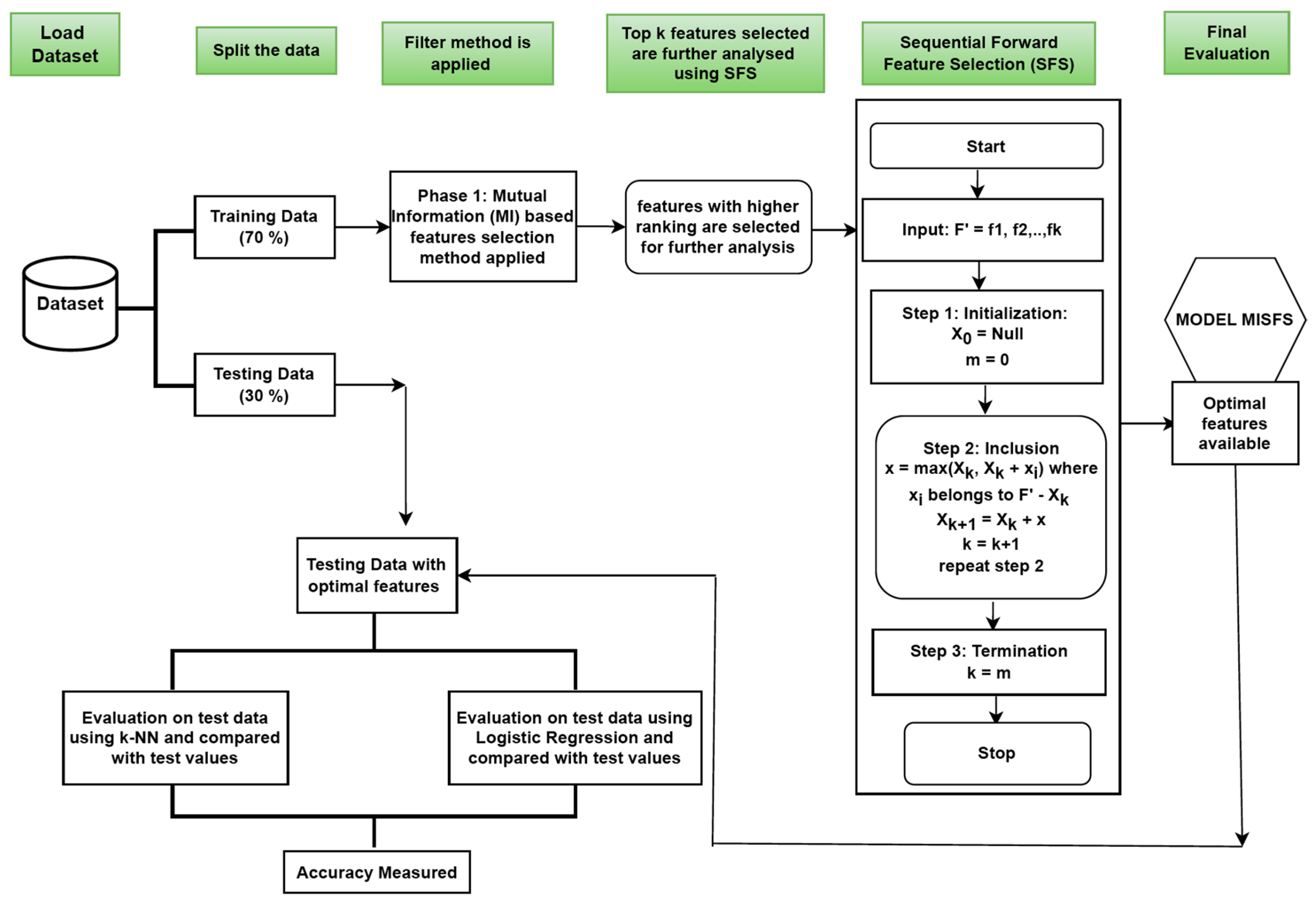
4.1. Overview of MISFS Approach
4.2. Abstract View of MISFS and Comparison Methods
- First, after calculating the accuracy of MISFS, we implemented different classifiers on the original dataset, calculated the classification rate, and compared the result with MISFS.
- Then, again, we implemented the Pearson Correlation method for feature selection, calculated the accuracy of the different threshold values, and compared the result with MISFS.
- Again, we compared the MISFS results with the prevailing work results.
4.3. Implementation of MISFS
- (i.)
- First phase: We implemented the filter approach, and in the second phase, we implemented the wrapper approach. The main task of the algorithm is to calculate the improved classification rate of the datasets after feature selection. So, in the first phase, we implemented Mutual Information, which is a filter method, for feature selection. Through this method, we selected features highly correlated with the output class. After that, by selecting these features, we implemented our second phase.
- (ii.)
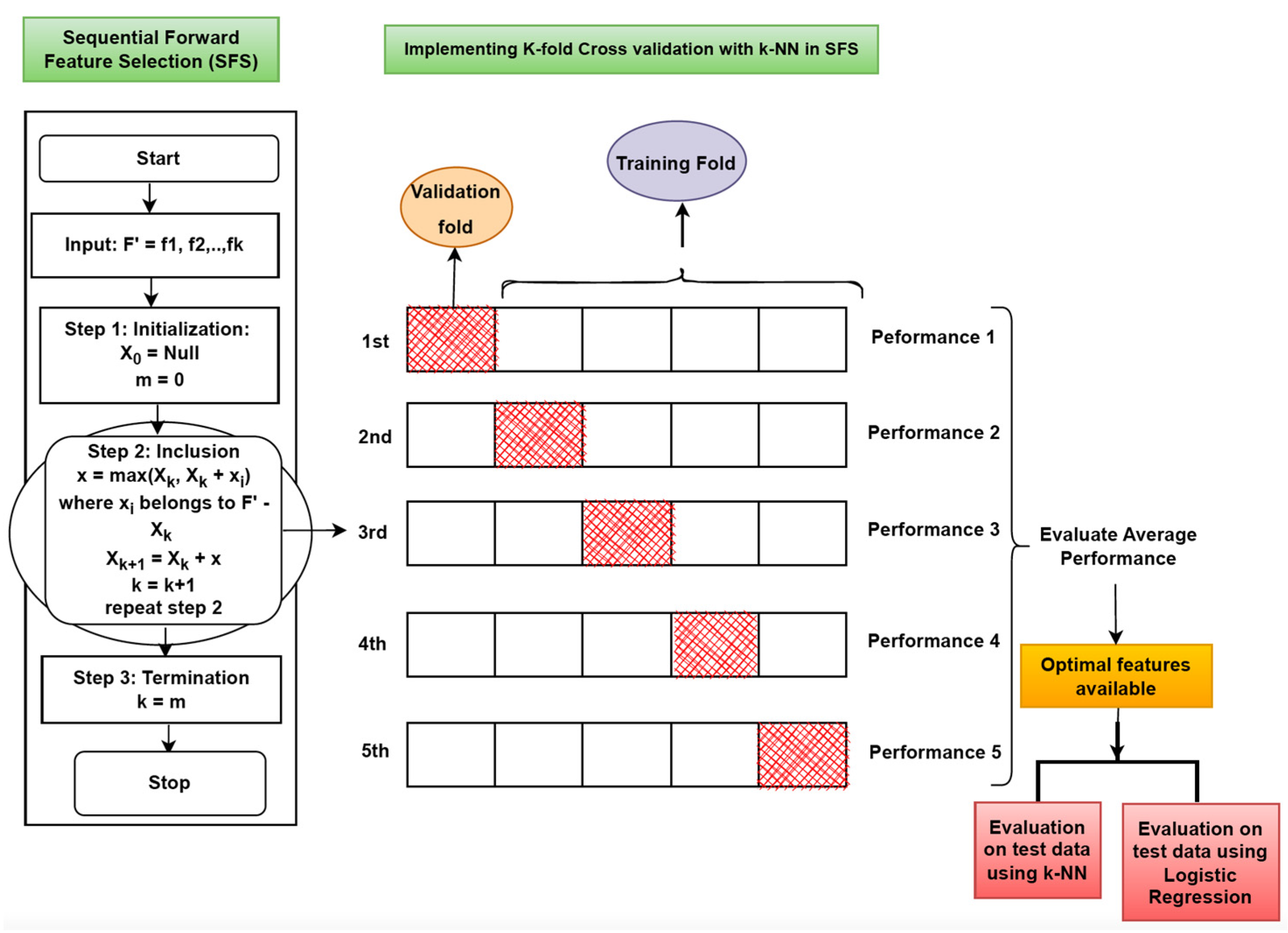
- Second phase: We implemented the Sequential Forward Feature-Selection (SFS) method, a wrapper model, for feature selection. This methodology is based on the greedy approach. Here, the classifier first calculates the performance of each feature individually. After that, in the next step, it selects the feature with the best performance, pairs it with the remaining features, and evaluates the classifier’s performance. For clarification, let us say there are four features f1, f2, f3, and f4. In the first step, the individual performance of each feature is evaluated. Let f2 be the feature with the best performance. In the next step, we start from f2 and pair it with the remaining features (pair will be {f2 f1}, {f2 f3}, {f2 f4}) and evaluate their performance. Then we again start with the best-performing pair and repeat the same process by adding the remaining features. Finally, we obtain the optimal feature set with maximum performance. KNN classifier is used with SFS while evaluating the performance and selecting the optimal features.
4.4. Method and Algorithm
- (i.)
- We used the concept of probability density function to calculate Mutual Information between A and B, defined aswhere
- H(.) denotes entropy;
- H(A|B) and H(B|A) are conditional entropies;
- H (A; B) is the joint entropy of A and B
- (ii.)
- The joint entropy H (A; B) is calculated aswhere
- is the joint probability density function;
- are the marginal density functions of A and B, respectively.
- (iii.)
- The marginal density functions are
- (iv.)
- By substituting Equations (2)–(4) into Equation (1), the Mutual Information equation will be
| Algorithm 1: MISFS model | ||
| Input: d, total features available in repository P | ||
| selected after applying MISFS. | ||
| Phase 1: Mutual Information (MI) | ||
| 1. | d, total features available in dataset P | |
| 2. | apply Mutual Information (MI) for ranking the features as in step | |
| 3. | for each d do | |
| 4. | compute MI (, C) | |
| 5. | & arrange them in descending order | |
| 6. | end for | |
| 7. | Select top k features based on ranking for phase II | |
| Phase 2: Sequential Forward Feature Selection (SFS) | ||
| Input: k features selected after MI (from step 7) | ||
| Output: Through SFS we selected the best m features where m < k, and it is a subset of features in . | ||
| 8. | Initialization At the initial stage of SFS, we consider an empty set , so the m = 0 (where m is the subset of features from k features). | |
| Inclusion: | ||
| 9. | ||
| 10. | ||
| 11. | ||
| goes again to step 9 | ||
| 12. | Termination: m = p | |
| 13. | Cross-validation and k-NN used with SFS Cross-validation is used while working in Phase 2. | |
4.5. Workflow of the MISFS
5. Experimental Evaluation
5.1. Experimental Setup
5.1.1. Datasets
- i.
- PIMA Indian Diabetes: This dataset is available on the UCI machine learning repository. It has 768 samples from female patients of PIMA Indian tradition, with 8 numeric valued features and output as a binary class. The dataset is used to diagnose type 2 diabetes. It contains information on women 21 years or older and is of non-linear type. It includes two classes: Class 1 is normal with 500 samples, and Class 2 is patients with PIMA Indian Diabetes with 268 samples. The eight features are pregnancies, glucose, BP, BMI, skin thickness, age, insulin, and diabetes pedigree function.
- ii.
- Spectfheart: This dataset is made available from the UCI machine learning repository. It contains 267 samples diagnosing Cardiac Single Proton Emission Computed Tomography (SPECT) images. It consists of 44 features, and the classes for classifying patients are normal and abnormal. The details of 44 features can be examined from the UCI repository.
- iii.
- Breast Cancer: This dataset is available on the UCI machine learning repository. It comprises 569 samples of heart disease patients, having 33 features and output as a binary class. The output is a challenge to classify whether each person’s tumor lies malignant or benign. The 33 feature details are given in the UCI repository.
- iv.
- Parkinson dataset: The UCI machine learning repository makes the dataset available. It comprises 195 samples of heart disease patients, having 24 features and output as a binary class. Output is the “status” feature, representing 0 for healthy and 1 for Parkinson’s disease. The details of features are given in the UCI repository.
- v.
- COS dataset: This dataset is made available from the UCI machine learning repository. It contains information from 10 different hospitals. It contains 541 samples of PCOS patients, with 45 features and output as a binary class. The output is whether the male person is infected with PCOS or not. The details of the 45 features are given in the UCI repository.
- vi.
- Cleveland dataset: The UCI machine learning repository makes the dataset available. It comprises 297 samples of heart disease patients, with 13 integer-valued features and output as 5 classes from 0 to 4. The output is to see that the patient has heart disease, and 0 to 4 signifies the absence and distinguished occurrence of disease. The 13 features are age, sex, cp, tpb, sc, fbs, resting electrocardiographic results, mhr received, exercise-induced angina, op, the peak exercise slope, major vessel amount, and thal.
5.1.2. Performance Metrics
- Confusion Matrix: This matrix is used to measure how many samples are perfectly classified and how many samples are misclassified. Four terms are considered in the confusion matrix.
- True positive (TPOS): Samples that are labeled positive are predicted to be positive.
- True Negative (TNEG): Samples that are labeled negative are predicted to be negative.
- False Positive (FPOS): Samples that are labeled negative are misclassified as positive.
- False Negative (FNEG): Samples that are labeled positive are misclassified as negative.
- Accuracy or Classification Rate: This calculates the total ratio of classes predicted properly by the classifier.
- Sensitivity (or Recall): This calculates what ratio of class labels that are predicted as positive belongs to positive.
- Specificity: This calculates what ratio of class labels that are predicted as negative belongs to negative labels.
- Precision: This demonstrates the number of predicted classes on all positively classified labels.
- F-measure: Precision and recall are inversely proportional to each other; increasing one usually decreases the other. This inverse relationship between precision and recall is called F-measure. It is calculated using HM of precision and recall and considering both measures. It is computed as follows:
5.1.3. Comparison Techniques
- At the first level, we calculated the accuracy of the datasets considered in this work with different classifiers, taking into account all the features, and compared them with the proposed algorithm.
- At the second level, we implemented the Pearson Correlation method to select the optimal features and then applied dissimilar classifiers considered in point (a) to calculate the accuracy and compare it with the proposed algorithm.
- At the last level, we compared the performance of MISFS with the existing methods.
5.2. Results and Discussion
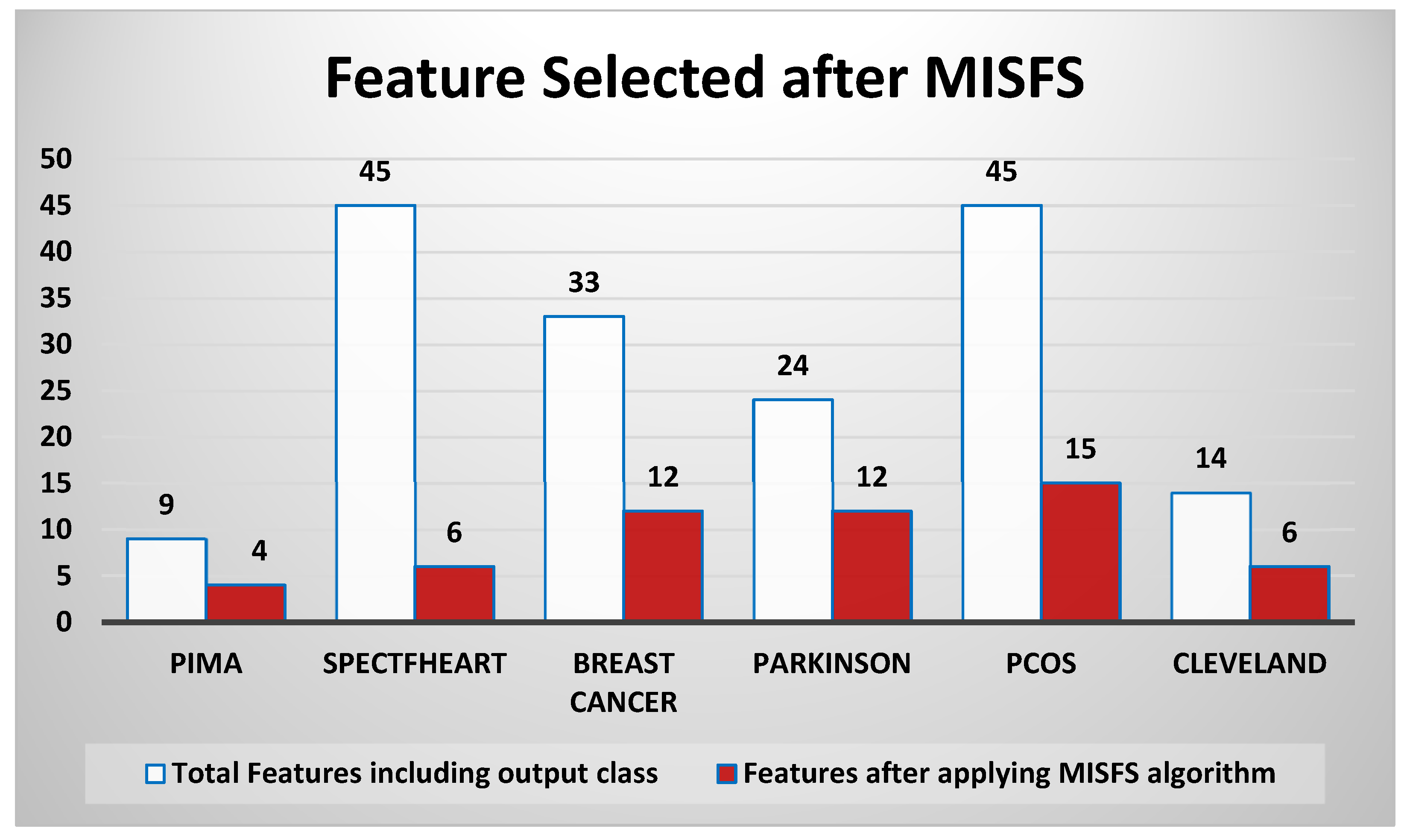
5.2.1. Features Selected
5.2.2. Performance on Different Datasets
5.2.3. Comparison of the Proposed Algorithm with LR, KNN, and PCC
5.2.4. Comparison of the Proposed Algorithm with the Existing Algorithm
5.2.5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Kianat, J.; Khan, M.A.; Sharif, M.; Akram, T.; Rehman, A.; Saba, T. A joint framework of feature reduction and robust feature selection for cucumber leaf diseases recognition. Optik 2021, 240, 166566. [Google Scholar] [CrossRef]
- Shekhawat, S.S.; Sharma, H.; Kumar, S.; Nayyar, A.; Qureshi, B. bSSA: Binary salp swarm algorithm with hybrid data transformation for feature selection. IEEE Access 2021, 9, 14867–14882. [Google Scholar] [CrossRef]
- Agarwal, R.; Shekhawat, N.S.; Kumar, S.; Nayyar, A.; Qureshi, B. Improved Feature Selection Method for the Identification of Soil Images Using Oscillating Spider Monkey Optimization. IEEE Access 2021, 9, 167128–167139. [Google Scholar] [CrossRef]
- Driss, K.; Boulila, W.; Batool, A.; Ahmad, J. A Novel Approach for Classifying Diabetes’ Patients Based on Imputation and Machine Learning. In Proceedings of the 2020 International Conference on UK-China Emerging Technologies (UCET), Glasgow, UK, 20–21 August 2020; pp. 1–4. [Google Scholar]
- Batra, S.; Khurana, R.; Khan, M.Z.; Boulila, W.; Koubaa, A.; Srivastava, P. A Pragmatic Ensemble Strategy for Missing Values Imputation in Health Records. Entropy 2022, 24, 533. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R.; Lima, A.A.; Das, S.C.; Mridha, M.F.; Prodeep, A.R.; Watanobe, Y. A Comprehensive Survey on the Process, Methods, Evaluation, and Challenges of Feature Selection. IEEE Access 2022, 10, 99595–99632. [Google Scholar] [CrossRef]
- Peterson, L.E. K-Nearest Neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient Boosting Machines, a Tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support Vector Machine. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Desicion-Theoretic Generalization of on-Line Learning and an Application to Boosting. In Proceedings of the Computational Learning Theory: Second European Conference, EuroCOLT’95, Barcelona, Spain, 13–15 March 1995; Springer: Berlin/Heidelberg, Germany, 1995; pp. 23–37. [Google Scholar]
- Hashemi, A.; Dowlatshahi, M.B.; Nezamabadi-pour, H. Ensemble of Feature Selection Algorithms: A Multi-Criteria Decision-Making Approach. Int. J. Mach. Learn. Cybern. 2022, 13, 49–69. [Google Scholar] [CrossRef]
- Al-Sarem, M.; Saeed, F.; Boulila, W.; Emara, A.H.; Al-Mohaimeed, M.; Errais, M. Feature Selection and Classification Using CatBoost Method for Improving the Performance of Predicting Parkinson’s Disease. In Advances on Smart and Soft Computing; Springer: Singapore, 2020; pp. 189–199. [Google Scholar]
- Liu, H.; Li, J.; Wong, L. A Comparative Study on Feature Selection and Classification Methods Using Gene Expression Profiles and Proteomic Patterns. Genome Inform. 2002, 13, 51–60. [Google Scholar] [PubMed]
- Bolón-Canedo, V.; Sánchez-Maroño, N.; Alonso-Betanzos, A. A Review of Feature Selection Methods on Synthetic Data. Knowl. Inf. Syst. 2013, 34, 483–519. [Google Scholar] [CrossRef]
- Inza, I.; Larranaga, P.; Blanco, R.; Cerrolaza, A.J. Filter versus Wrapper Gene Selection Approaches in DNA Microarray Domains. Artif. Intell. Med. 2004, 31, 91–103. [Google Scholar] [CrossRef]
- Al-Sarem, M.; Saeed, F.; Alsaeedi, A.; Boulila, W.; Al-Hadhrami, T. Ensemble Methods for Instance-Based Arabic Language Authorship Attribution. IEEE Access 2020, 8, 17331–17345. [Google Scholar] [CrossRef]
- Ansari, G.; Ahmad, T.; Doja, M.N. Ensemble of Feature Ranking Methods Using Hesitant Fuzzy Sets for Sentiment Classification. Int. J. Mach. Learn. Comput. 2019, 9, 599–608. [Google Scholar] [CrossRef]
- Sambyal, N.; Saini, P.; Syal, R. A Review of Statistical and Machine Learning Techniques for Microvascular Complications in Type 2 Diabetes. Curr. Diabetes Rev. 2021, 17, 143–155. [Google Scholar] [CrossRef]
- Mirza, S.; Mittal, S.; Zaman, M. Decision Support Predictive Model for Prognosis of Diabetes Using SMOTE and Decision Tree. Int. J. Appl. Eng. Res. 2018, 13, 9277–9282. [Google Scholar]
- Choubey, D.K.; Kumar, P.; Tripathi, S.; Kumar, S. Performance Evaluation of Classification Methods with PCA and PSO for Diabetes. Netw. Model. Anal. Health Inform. Bioinform. 2020, 9, 5. [Google Scholar] [CrossRef]
- Fatima, M.; Pasha, M. Survey of Machine Learning Algorithms for Disease Diagnostic. J. Intell. Learn. Syst. Appl. 2017, 9, 1. [Google Scholar] [CrossRef]
- Hasan, S.; Shamsuddin, S.M. Multi-Strategy Learning and Deep Harmony Memory Improvisation for Self-Organizing Neurons. Soft Comput. 2019, 23, 285–303. [Google Scholar] [CrossRef]
- Lewis, D.D. Feature Selection and Feature Extraction for Text Categorization. In Proceedings of the Speech and Natural Language: Proceedings of a Workshop Held at Harriman, New York, NY, USA, 23–26 February 1992. [Google Scholar]
- Battiti, R. Using Mutual Information for Selecting Features in Supervised Neural Net Learning. IEEE Trans. Neural Netw. 1994, 5, 537–550. [Google Scholar] [CrossRef] [PubMed]
- Salem, H.; Attiya, G.; El-Fishawy, N. Classification of Human Cancer Diseases by Gene Expression Profiles. Appl. Soft Comput. 2017, 50, 124–134. [Google Scholar] [CrossRef]
- Sahu, B. A Combo Feature Selection Method (Filter+ Wrapper) for Microarray Gene Classification. Int. J. Pure Appl. Math. 2018, 118, 389–401. [Google Scholar]
- Subanya, B.; Rajalaxmi, R.R. Feature Selection Using Artificial Bee Colony for Cardiovascular Disease Classification. In Proceedings of the 2014 International Conference on Electronics and Communication Systems (ICECS), Coimbatore, India, 13–14 February 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6. [Google Scholar]
- Subanya, B.; Rajalaxmi, R. A Novel Feature Selection Algorithm for Heart Disease Classification. Int. J. Comput. Intell. Inform. 2014, 4, 117–124. [Google Scholar]
- Ojagh, S.; Cauteruccio, F.; Terracina, G.; Liang, S.H. Enhanced Air Quality Prediction by Edge-Based Spatiotemporal Data Preprocessing. Comput. Electr. Eng. 2021, 96, 107572. [Google Scholar] [CrossRef]
- Theerthagiri, P.; Ruby, A.U.; Vidya, J. Diagnosis and Classification of the Diabetes Using Machine Learning Algorithms. SN Comput. Sci. 2022, 4, 72. [Google Scholar] [CrossRef]
- Chatrati, S.P.; Hossain, G.; Goyal, A.; Bhan, A.; Bhattacharya, S.; Gaurav, D.; Tiwari, S.M. Smart Home Health Monitoring System for Predicting Type 2 Diabetes and Hypertension. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 862–870. [Google Scholar] [CrossRef]
- Apoorva, S.; Aditya, S.K.; Snigdha, P.; Darshini, P.; Sanjay, H.A. Prediction of Diabetes Mellitus Type-2 Using Machine Learning. In Computational Vision and Bio-Inspired Computing: ICCVBIC 2019; Springer: Cham, Switzerland, 2020; pp. 364–370. [Google Scholar]
- Ding, Y.; Zhu, H.; Chen, R.; Li, R. An Efficient AdaBoost Algorithm with the Multiple Thresholds Classification. Appl. Sci. 2022, 12, 5872. [Google Scholar] [CrossRef]
- Cui, X.; Li, Y.; Fan, J.; Wang, T. A Novel Filter Feature Selection Algorithm Based on Relief. Appl. Intell. 2022, 52, 5063–5081. [Google Scholar] [CrossRef]
- Qu, Y.; Fang, Y.; Yan, F. Feature Selection Algorithm Based on Association Rules. J. Phys. Conf. Ser. Shanghai 2019, 1168, 052012. [Google Scholar] [CrossRef]
- Deep, K. A Random Walk Grey Wolf Optimizer Based on Dispersion Factor for Feature Selection on Chronic Disease Prediction. Expert Syst. Appl. 2022, 206, 117864. [Google Scholar]
- Elsadig, M.A.; Altigani, A.; Elshoush, H.T. Breast Cancer Detection Using Machine Learning Approaches: A Comparative Study. Int. J. Electr. Comput. Eng. 2023, 13, 736–745. [Google Scholar] [CrossRef]
- Kadhim, R.R.; Kamil, M.Y. Comparison of Machine Learning Models for Breast Cancer Diagnosis. IAES Int. J. Artif. Intell. 2023, 12, 415. [Google Scholar] [CrossRef]
- Al-Azzam, N.; Shatnawi, I. Comparing Supervised and Semi-Supervised Machine Learning Models on Diagnosing Breast Cancer. Ann. Med. Surg. 2021, 62, 53–64. [Google Scholar] [CrossRef]
- Khan, F.; Khan, M.A.; Abbas, S.; Athar, A.; Siddiqui, S.Y.; Khan, A.H.; Saeed, M.A.; Hussain, M. Cloud-Based Breast Cancer Prediction Empowered with Soft Computing Approaches. J. Healthc. Eng. 2020, 2020, 8017496. [Google Scholar] [CrossRef]
- Nguyen, T.-N.-Q.; Vo, H.-T.-T.; Nguyen, H.A.; Van Huynh, T. Machine Learning in Classification of Parkinson’s Disease Using Electroencephalogram with Simon’s Conflict. In Computational Intelligence Methods for Green Technology and Sustainable Development: Proceedings of the International Conference GTSD2022; Springer: Cham, Switzerland, 2022; pp. 110–122. [Google Scholar]
- Devi, B.; Srivastava, S.; Verma, V.K. Multiclass-Based Support Vector Machine for Parkinson’s Disease Detection on Speech Data. In Information Systems and Management Science: Conference Proceedings of 4th International Conference on Information Systems and Management Science (ISMS) 2021; Springer: Cham, Switzerland, 2022; pp. 540–557. [Google Scholar]
- Lamba, R.; Gulati, T.; Alharbi, H.F.; Jain, A. A Hybrid System for Parkinson’s Disease Diagnosis Using Machine Learning Techniques. Int. J. Speech Technol. 2022, 25, 583–593. [Google Scholar] [CrossRef]
- Senturk, Z.K. Early Diagnosis of Parkinson’s Disease Using Machine Learning Algorithms. Med. Hypotheses 2020, 138, 109603. [Google Scholar] [CrossRef]
- Sreejith, S.; Nehemiah, H.K.; Kannan, A. A Clinical Decision Support System for Polycystic Ovarian Syndrome Using Red Deer Algorithm and Random Forest Classifier. Healthc. Anal. 2022, 2, 100102. [Google Scholar] [CrossRef]
- Bharati, S.; Podder, P.; Mondal, M.R.H.; Surya Prasath, V.B.; Gandhi, N. Ensemble Learning for Data-Driven Diagnosis of Polycystic Ovary Syndrome. In Intelligent Systems Design and Applications: 21st International Conference on Intelligent Systems Design and Applications (ISDA 2021) Held During 13–15 December 2021; Springer: Cham, Switzerland, 2022; pp. 1250–1259. [Google Scholar]
- Nandipati, S.C.; Chew, X.; Khaw, K.W. Polycystic Ovarian Syndrome (PCOS) Classification and Feature Selection by Machine Learning Techniques. Appl. Math. Comput. Intell. 2020, 9, 65–74. [Google Scholar]
- Bharati, S.; Podder, P.; Mondal, M.R.H. Diagnosis of Polycystic Ovary Syndrome Using Machine Learning Algorithms. In Proceedings of the 2020 IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, 5–7 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1486–1489. [Google Scholar]
- Cintra, M.E.; Camargo, H.A.; Monard, M.C. Genetic Generation of Fuzzy Systems with Rule Extraction Using Formal Concept Analysis. Inf. Sci. 2016, 349, 199–215. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Tavana, M.; Alikar, N.; Zandieh, M.A. Tuned Hybrid Intelligent Fruit Fly Optimization Algorithm for Fuzzy Rule Generation and Classification. Neural Comput. Appl. 2019, 31, 873–885. [Google Scholar] [CrossRef]
- Sanz, J.A.; Fernandez, A.; Bustince, H.; Herrera, F. IVTURS: A Linguistic Fuzzy Rule-Based Classification System Based on a New Interval-Valued Fuzzy Reasoning Method with Tuning and Rule Selection. IEEE Trans. Fuzzy Syst. 2013, 21, 399–411. [Google Scholar] [CrossRef]
- Rehman, M.U.; Shafique, A.; Ghadi, Y.Y.; Boulila, W.; Jan, S.U.; Gadekallu, T.R.; Driss, M.; Ahmad, J. A Novel Chaos-Based Privacy-Preserving Deep Learning Model for Cancer Diagnosis. IEEE Trans. Netw. Sci. Eng. 2022, 9, 4322–4337. [Google Scholar] [CrossRef]
- Ullah, Z.; Mohmand, M.I.; Zubair, M.; Driss, M.; Boulila, W.; Sheikh, R.; Alwawi, I. Emotion recognition from occluded facial images using deep ensemble model. Comput. Mater. Contin. 2022, 73, 4465–4487. [Google Scholar]
- Rehman, M.U.; Driss, M.; Khakimov, A.; Khalid, S. Non-Invasive Early Diagnosis of Obstructive Lung Diseases Leveraging Machine Learning Algorithms. Comput. Mater. Contin. 2022, 72, 5681–5697. [Google Scholar] [CrossRef]
- Ben Atitallah, S.; Driss, M.; Boulila, W.; Koubaa, A.; Ben Ghezala, H. Fusion of convolutional neural networks based on Dempster–Shafer theory for automatic pneumonia detection from chest X-ray images. Int. J. Imaging Syst. Technol. 2022, 32, 658–672. [Google Scholar] [CrossRef]


| Dataset | #Samples | #Attributes | #Classes | Variable Description |
|---|---|---|---|---|
| PIMA [a] | 768 | 9 | 2 | 768 × 9 |
| Spectfheart [b] | 267 | 45 | 2 | 267 × 45 |
| Breast Cancer [c] | 569 | 33 | 2 | 569 × 33 |
| Parkinson [d] | 195 | 24 | 2 | 195 × 24 |
| PCOS [e] | 541 | 45 | 2 | 541 × 45 |
| Cleveland [f] | 297 | 13 | 5 | 297 × 13 |
| Dataset | Total Features Including Output Class | Features after Applying the MISFS Algorithm |
|---|---|---|
| PIMA | 9 | 4 |
| Spectfheart | 45 | 6 |
| Breast Cancer | 33 | 12 |
| Parkinson | 24 | 12 |
| PCOS | 45 | 15 |
| Cleveland | 14 | 6 |
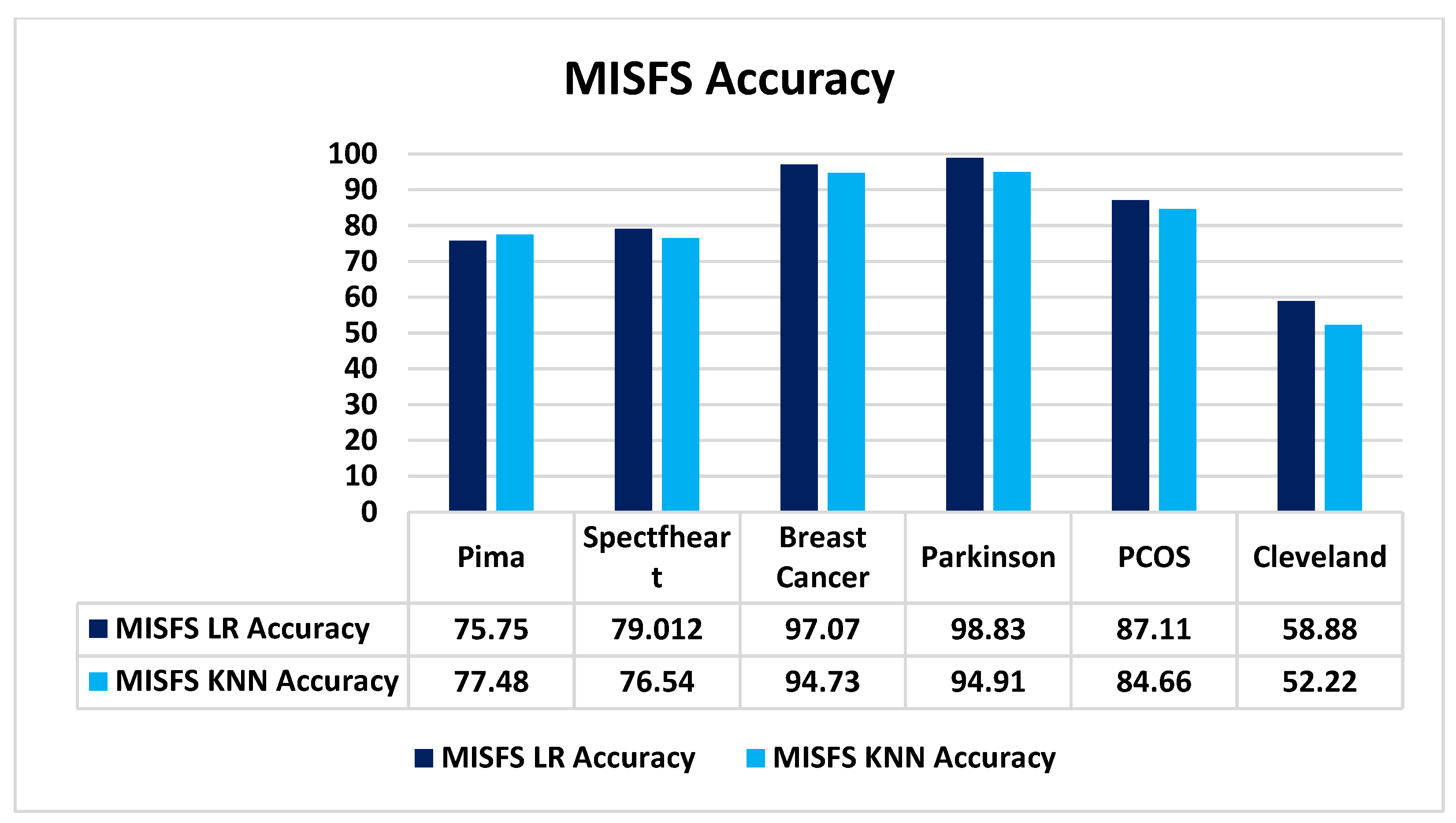
| Dataset | Proposed Method | Accuracy | Precision | Recall | F1-Score | Support |
|---|---|---|---|---|---|---|
| PIMA | MISFS+KNN | 77.48 | 0.8098 | 0.8400 | 0.8250 | 231 |
| MISFS+LR | 75.75 | 0.7853 | 0.8854 | 0.8323 | ||
| Spectfheart | MISFS+KNN | 76.540 | 0.5 | 0.6316 | 0.5581 | 81 |
| MISFS+LR | 79.012 | 0.6 | 0.3158 | 0.4138 | ||
| Breast Cancer | MISFS+KNN | 94.73 | 0.9626 | 0.9537 | 0.9581 | 171 |
| MISFS+LR | 97.07 | 0.97 | 0.97 | 0.97 | ||
| Parkinson | MISFS+KNN | 94.91 | 0.95 | 0.95 | 0.95 | 59 |
| MISFS+LR | 89.83 | 0.89 | 0.90 | 0.90 | ||
| PCOS | MISFS+KNN | 84.66 | 0.85 | 0.85 | 0.84 | 163 |
| MISFS+LR | 87.11 | 0.87 | 0.87 | 0.87 | ||
| Cleveland | MISFS+KNN | 52.22 | 0.54 | 0.59 | 0.59 | 90 |
| MISFS+LR | 58.88 | 0.54 | 0.59 | 0.59 | 90 |
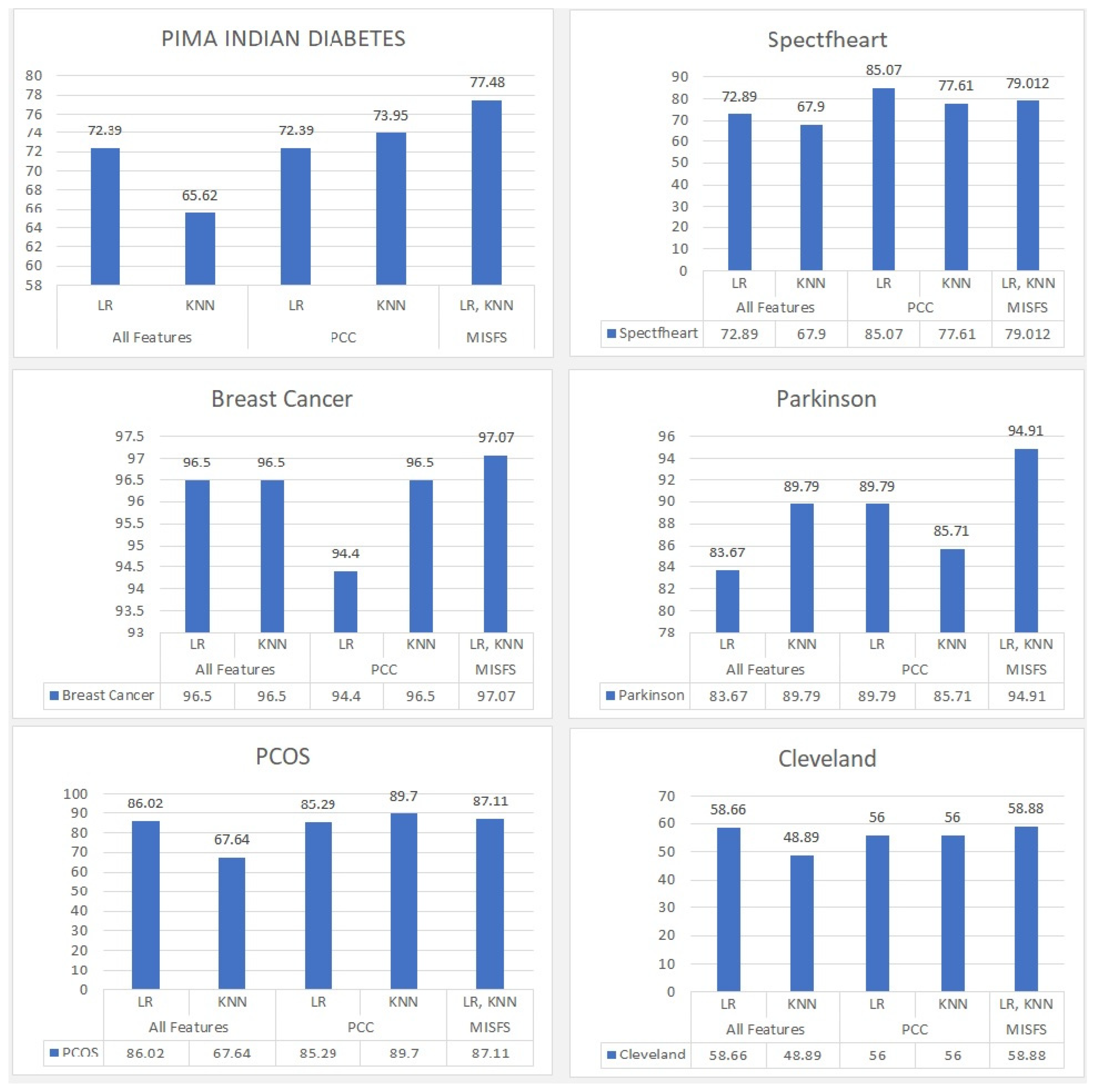
| Dataset | Result | Methodology | ||||
|---|---|---|---|---|---|---|
| MISFS (Proposed) | LR | KNN | PCC+KNN | PCC+LR | ||
| PIMA | FS | 4 | 9 | 9 | 9 | 9 |
| Accuracy | 77.48 | 72.39 | 65.62 | 73.95 | 72.39 | |
| Spectfheart | FS | 6 | 45 | 45 | 45 | All |
| Accuracy | 79.012 | 72.89 | 67.90 | 77.61 | 85.07 | |
| Breast Cancer | FS | 12 | 33 | 33 | 28 | 28 |
| Accuracy | 97.07 | 96.50 | 96.50 | 96.50 | 94.40 | |
| Parkinson | FS | 12 | 24 | 24 | 13 | 13 |
| Accuracy | 94.91 | 83.67 | 89.79 | 85.71 | 89.79 | |
| PCOS | FS | 15 | 45 | 45 | 38 | 38 |
| Accuracy | 87.11 | 86.02 | 67.64 | 89.70 | 85.29 | |
| Cleveland | FS | 7 | 14 | 14 | All | All |
| Accuracy | 58.88 | 58.66 | 48.89 | 56 | 56 | |
| PIMA Indian Diabetes Dataset | |||
|---|---|---|---|
| Authors | Techniques | Accuracy | Feature Selected |
| Choubey et al. [23] | PCA_C4.5 DT, PCA_KNN | 74.78% | 4 |
| Theerthagiri et al. [32] | Naïve Bayes, KNN, DT, Extra Trees | 72.4137 | - |
| Chatrati et al. [33] | KNN, SVM | 75 | 3 |
| Apoorva et al. [34] | SVM, DT | 75.06 | |
| MISFS (Proposed) | LR, KNN | 77.48 | 4 |
| Spectfheart Dataset | |||
|---|---|---|---|
| Authors | Techniques | Accuracy | Feature Selected |
| Ding et al. [35] | Adaboost with Threshold Classification (TC) Multi (TC) | 70.59 75.40 | - |
| Cui et al. [36] | Relief with new relief-feature weighting objective function | 76.86 | - |
| Qu et al. [37] | RFE with SVM | 77.1368 | 14 |
| Deep [38] | Grey Wolf Optimizer with KNN | 79.40 | 23 |
| MISFS | LR, KNN | 79.012 | 6 |
| Breast Cancer Dataset | |||
|---|---|---|---|
| Authors | Techniques | Accuracy | Feature Selected |
| Elsadig et al. [39] | Chi-square, SVM, Random Forest, Naïve Bayes, Logistic Regression | 97.0 | 17 |
| Kadhim and Kamil [40] | Gradient Boosting | 96.77 | - |
| Al-Azzam and Shatnawi [41] | LR with area under the curve | 96 | - |
| Khan et al. [42] | SVM | 97.06 | - |
| Deep [38] | Grey Wolf Optimizer with KNN | 94.60 | 3 |
| MISFS | LR, KNN | 97.07 | 12 |
| Authors | Techniques | Accuracy | Feature Selected |
|---|---|---|---|
| Nguyen et al. [43] | ICA + DWT + LSVM | 84.5 | - |
| Devi et al. [44] | PCM with SVM | 89 | - |
| Lamba et al. [45] | Extra Tree, MI Gain, GA with Naïve Bayes, K-Nearest Neighbor, RF | 95.58 | 11 |
| Senturk [46] | Recursive Feature Elimination, Feature Importance, SVM, ANN, CART | 93.84 | - |
| MISFS | LR, KNN | 97.07 | 12 |
| Authors | Techniques | Accuracy | Feature Selected |
|---|---|---|---|
| Sreejith et al. [47] | Red Deer Algorithm with RF | 89.81 | 20 |
| Bharati et al. [48] | LR with 5-fold cross-validation | 85.022 | 13 |
| Nandipati et al. [49] | KNN, SVM | 90.83 | 10 |
| Bharati et al. [50] | LR | 83 | 14 |
| MISFS | LR, KNN | 87.11 | 15 |
| Cleveland Dataset | |||
|---|---|---|---|
| Authors | Techniques | Accuracy | Feature Selected |
| Cintra et al. [51] | FS + R | 54.54 | - |
| Mousavi et al. [52] | FURIA | 56.57 | - |
| Sanz et al. [53] | FARC | 57.92 | - |
| MISFS | LR, KNN | 58.88 | 6 |
| MISFS | PCC | ALL FEATURES | ||||
|---|---|---|---|---|---|---|
| Classifier | LR | KNN | LR | KNN | LR | KNN |
| PIMA | 75.75 | 77.48 | 72.39 | 73.95 | 72.39 | 65.62 |
| Spectfheart | 79.012 | 76.540 | 85.07 | 77.61 | 72.89 | 67.90 |
| Breast cancer | 97.07 | 94.73 | 94.40 | 96.50 | 96.50 | 96.50 |
| Parkinson | 89.83 | 94.91 | 89.79 | 85.71 | 83.67 | 89.79 |
| PCOS | 87.11 | 84.66 | 85.29 | 89.70 | 86.02 | 67.64 |
| Cleveland | 58.88 | 52.22 | 56 | 56 | 58.66 | 48.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Kaur, A.; Singh, P.; Driss, M.; Boulila, W. Efficient Multiclass Classification Using Feature Selection in High-Dimensional Datasets. Electronics 2023, 12, 2290. https://doi.org/10.3390/electronics12102290
Kumar A, Kaur A, Singh P, Driss M, Boulila W. Efficient Multiclass Classification Using Feature Selection in High-Dimensional Datasets. Electronics. 2023; 12(10):2290. https://doi.org/10.3390/electronics12102290
Chicago/Turabian StyleKumar, Ankur, Avinash Kaur, Parminder Singh, Maha Driss, and Wadii Boulila. 2023. "Efficient Multiclass Classification Using Feature Selection in High-Dimensional Datasets" Electronics 12, no. 10: 2290. https://doi.org/10.3390/electronics12102290
APA StyleKumar, A., Kaur, A., Singh, P., Driss, M., & Boulila, W. (2023). Efficient Multiclass Classification Using Feature Selection in High-Dimensional Datasets. Electronics, 12(10), 2290. https://doi.org/10.3390/electronics12102290








