Stochastic Fixed-Time Tracking Control for the Chaotic Multi-Agent-Based Supply Chain Networks with Nonlinear Communication
Abstract
1. Introduction
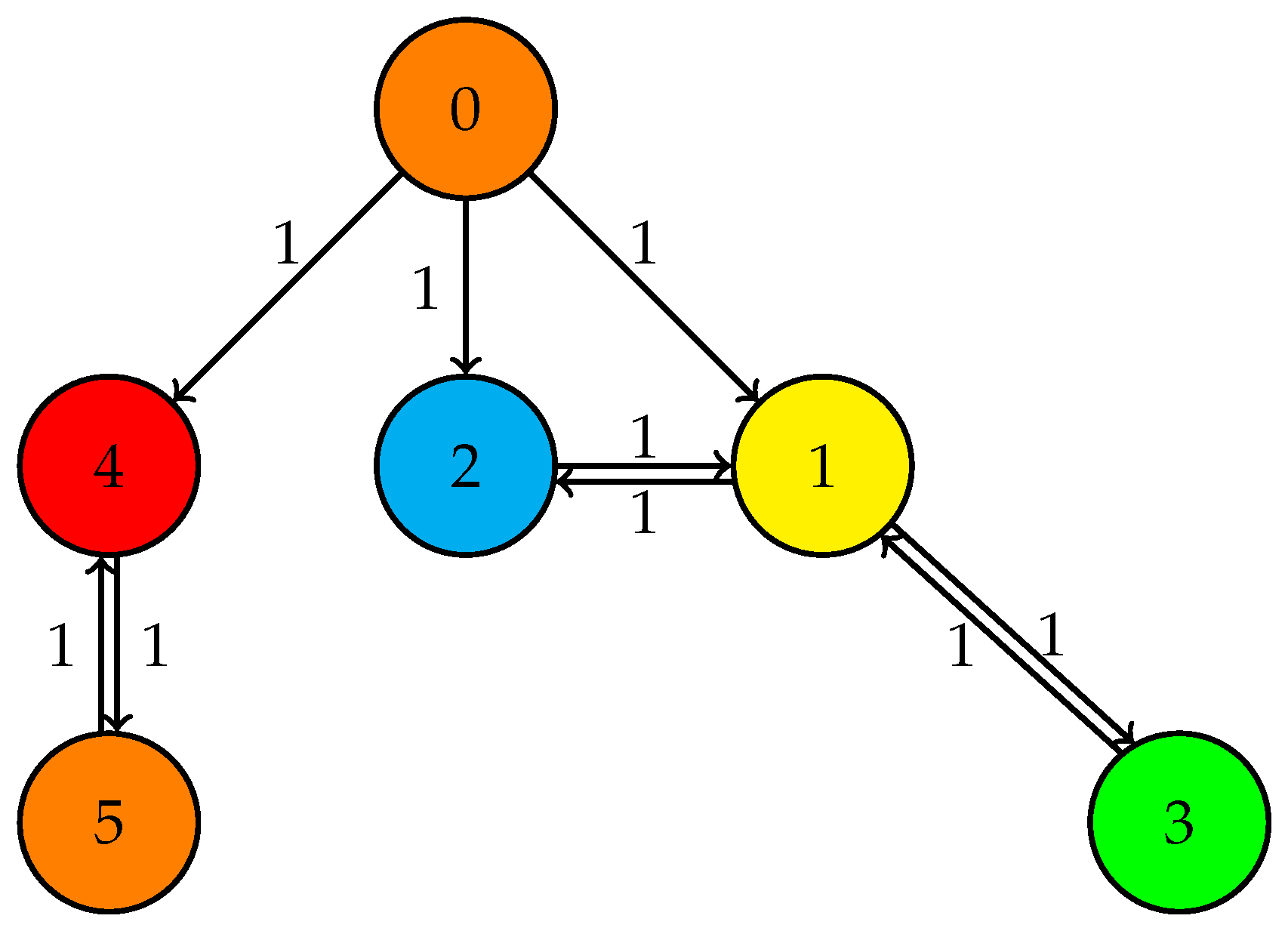
2. Multi-Agent Three-Echelon Supply Chain Networks
3. Preliminaries
- (1)
- The Laplacian matrix has a zero eigenvalue with multiplicity 1, and all eigenvalues of satisfy ;
- (2)
- , for all satisfing = 0.
- (1)
- when
- (2)
- when
4. Main Results
4.1. Problem Formulation
4.2. Control Design and Stability Analysis
5. Illustrative Example
5.1. Model Description
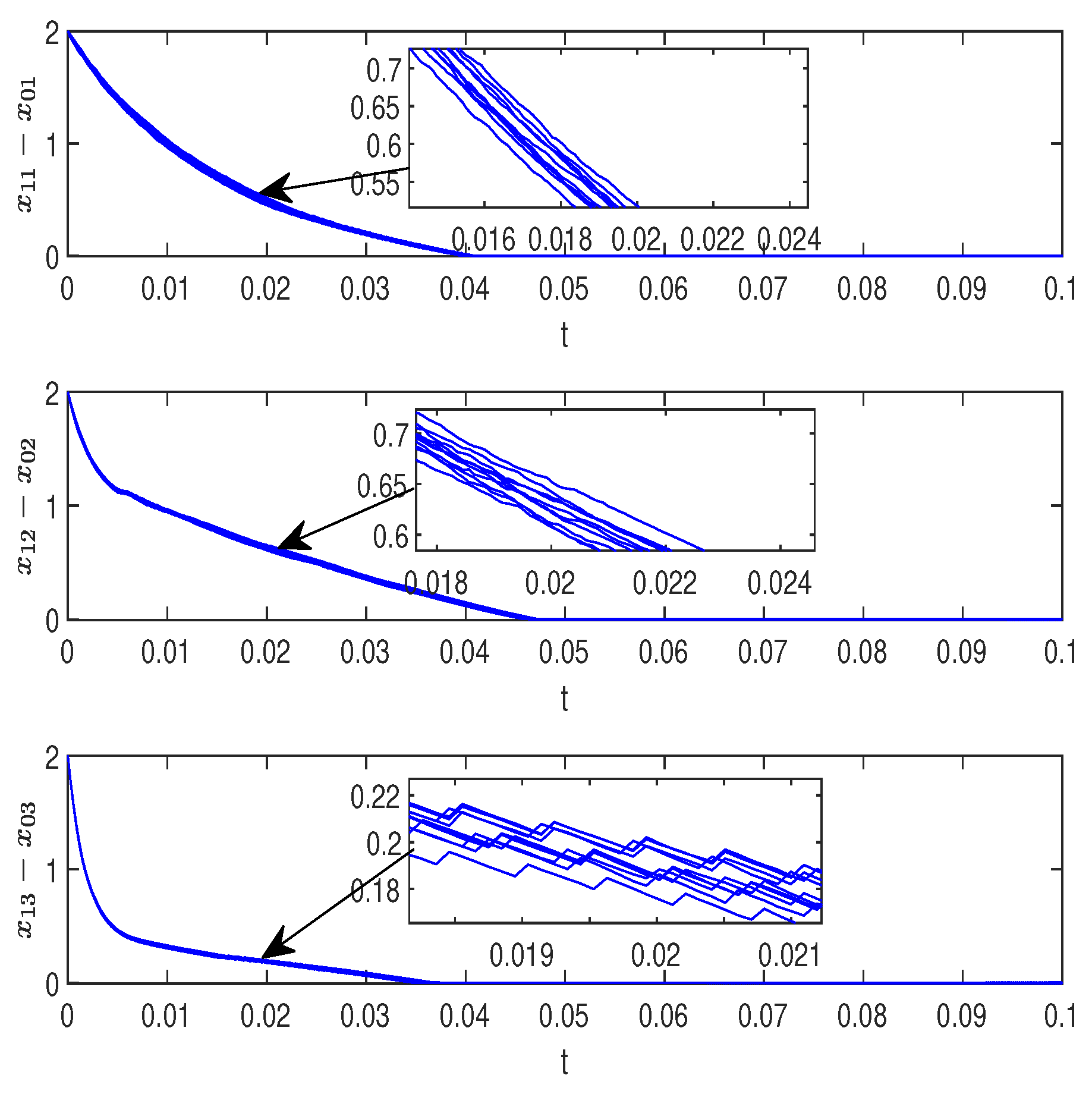
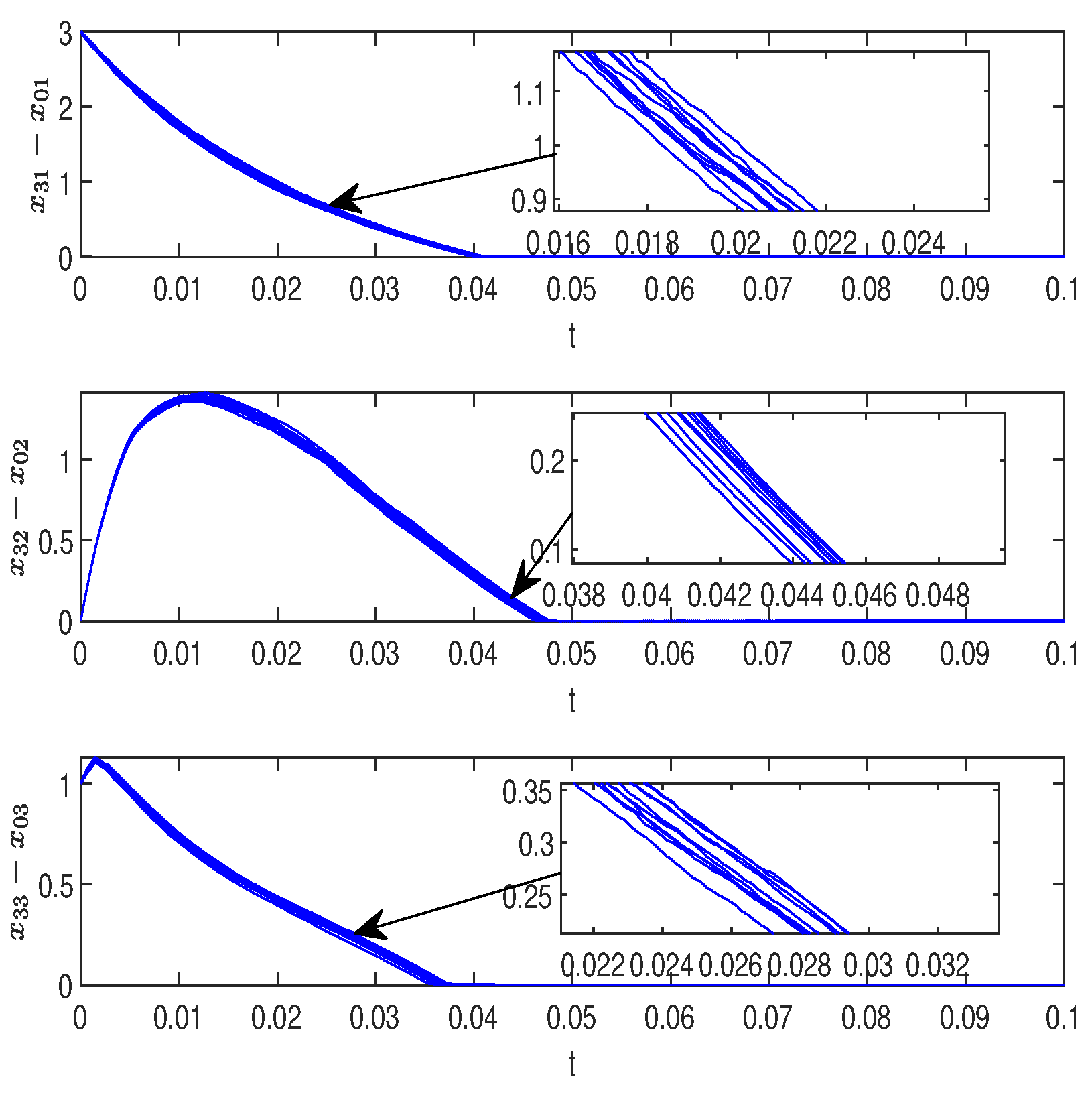
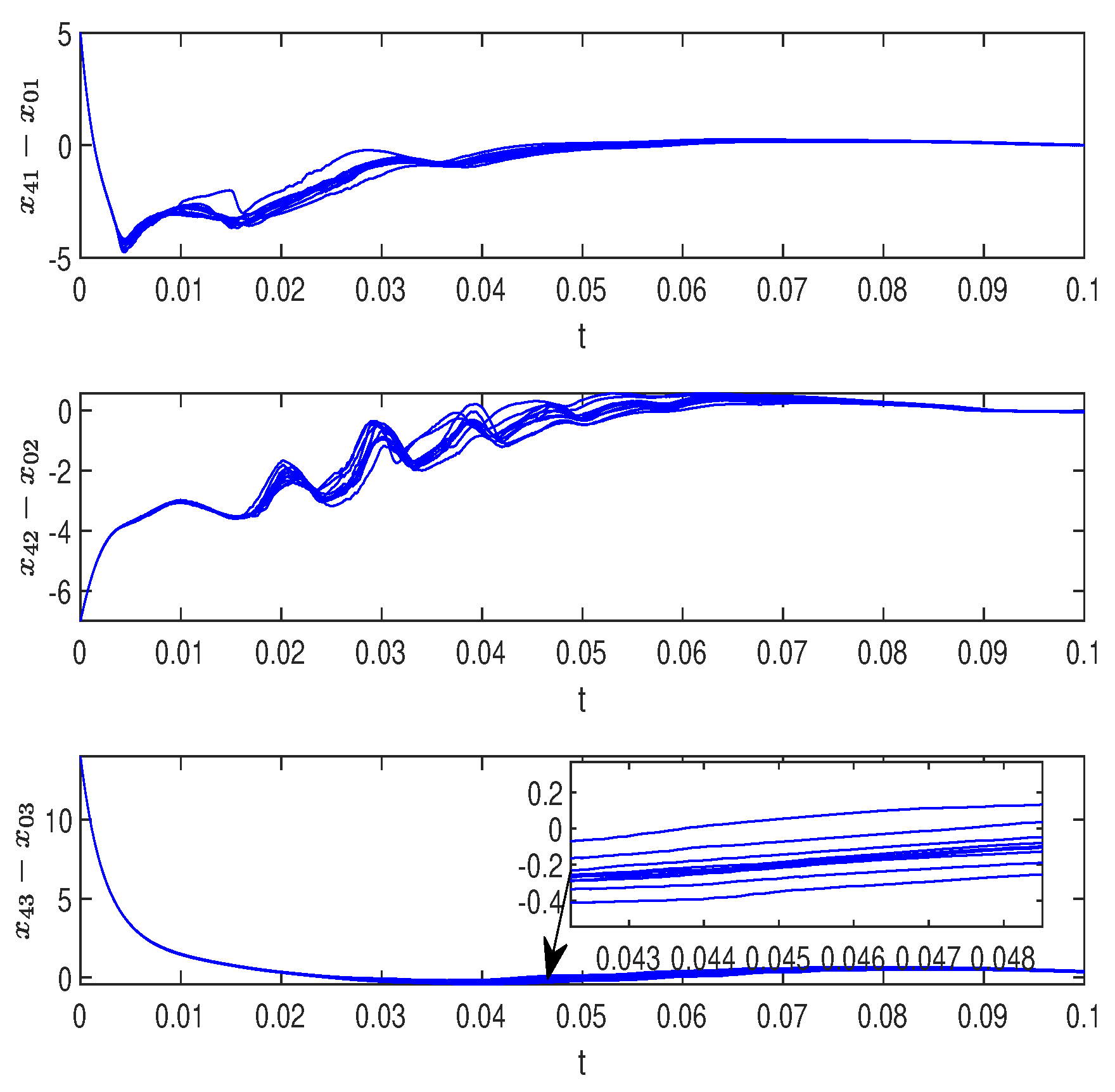
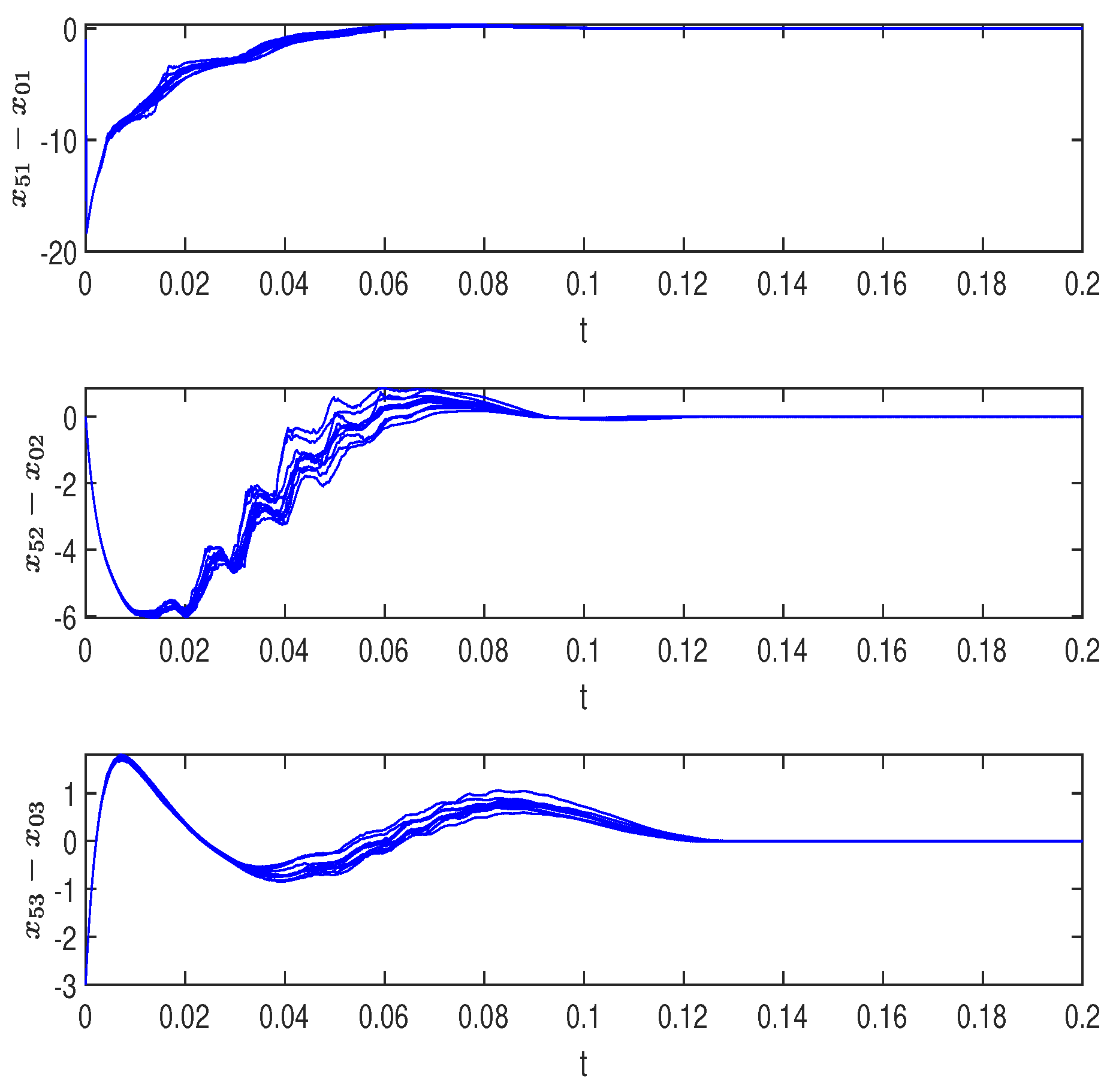
5.2. Simulation Analysis
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hove-Sibanda, P.; Pooe, R. Enhancing supply chain performance through supply chain practices. J. Transp. Supply Chain. Manag. 2018, 12, a400. [Google Scholar] [CrossRef]
- Green, K.; Inman, R.; Sower, V.; Zelbst, P. Comprehensive supply chain management model. Supply Chain.-Manag.-Int. J. 2019, 24, 590–603. [Google Scholar] [CrossRef]
- Schulz, K.; Freund, D. A multichain architecture for distributed supply chain design in industry 4.0. Bus. Inf. Syst. Work. 2018, 339, 277–288. [Google Scholar]
- Yang, A.; Li, Y.; Liu, C.; Li, J.; Zhang, Y.; Wang, J. Research on logistics supply chain of iron and steel enterprises based on block chain technology. Future Gener. Comput. Syst. 2019, 101, 635–645. [Google Scholar] [CrossRef]
- Mangla, S.; Kazançoğlu, Y.; Yıldızbaşı, A.; Öztürk, C.; Çalık, A. A conceptual framework for blockchain-based sustainable supply chain and evaluating implementation barriers: A case of the tea supply chain. Bus. Strategy Environ. 2022, 31, 3693–3716. [Google Scholar] [CrossRef]
- Gai, T.; Cao, M.; Chiclana, F.; Zhang, Z.; Dong, Y.; Herrera-Viedma, E.; Wu, J. Consensus-trust driven bidirectional feedback mechanism for improving consensus in social network large-group decision making. Group Decis. Negot. 2022, 1–30. [Google Scholar] [CrossRef]
- Song, Q.; Chen, Y.; Zhong, Y.; Lan, K.; Fong, S.; Tang, R. A supply-chain system framework based on internet of things using Blockchain technology. ACM Trans. Internet Technol. 2021, 21, 1–24. [Google Scholar] [CrossRef]
- Li, D.; Han, D.; Crespi, N.; Minerva, R.; Li, K. A blockchain-based secure storage and access control scheme for supply chain finance. J. Supercomput. 2022, 1–30. [Google Scholar] [CrossRef]
- Lee, J.; Kim, C. Multi-agent systems applications in manufacturing systems and supply chain management: A review paper. Int. J. Prod. Res. 2008, 46, 233–265. [Google Scholar] [CrossRef]
- Frayret, J.; Damours, S.; Rousseau, A.; Harvey, S.; Gaudreault, J. Agent-based supply-chain planning in the forest products industry. Int. J. Flex. Manuf. Syst. 2007, 19, 358–391. [Google Scholar] [CrossRef]
- Long, Q. Distributed supply chain network modelling and simulation: Integration of agent-based distributed simulation and improved SCOR model. Int. J. Prod. Res. 2014, 52, 6899–6917. [Google Scholar] [CrossRef]
- Caridi, M.; Cavalieri, S. Multi-agent systems in production planning and control: An overview. Prod. Plan. Control 2004, 15, 106–118. [Google Scholar] [CrossRef]
- Swaminathan, J.; Smith, S.; Sadeh, N. Modeling supply chain dynamics: A multiagent approach. Decis. Sci. 1998, 29, 607–632. [Google Scholar] [CrossRef]
- Sun, T.; Yousefpour, A.; Karaca, E.; Alassafi, M.; Ahmad, A.; Li, Y. Dynamical investigation and distributed consensus tracking control of a variable-order fractional supply chain network using a multi-agent neural network-based control method. Fractals 2022, 30, 2240168. [Google Scholar] [CrossRef]
- Li, Q.; Lin, H.; Tan, X.; Du, S. H∞ consensus for multiagent-based supply chain systems under switching topology and uncertain demands. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4905–4918. [Google Scholar] [CrossRef]
- Liu, Z.; Jahanshahi, H.; Volos, C.; Bekiros, S.; He, S.; Alassafi, M.; Ahmad, A. Distributed consensus tracking control of chaotic multi-agent supply chain network: A new fault-tolerant, finite-time, and chatter-free approach. Entropy 2022, 24, 33. [Google Scholar] [CrossRef] [PubMed]
- Huo, Y.; Lv, Y.; Wu, X.; Duan, Z. Fully distributed consensus for general linear multi-agent systems with unknown external disturbances. IET Control Theory Appl. 2019, 13, 2595–2609. [Google Scholar] [CrossRef]
- Shi, L.; Guo, W.; He, W. Distributed adaptive discontinuous consensus tracking control for disturbed multi-agent systems based on input-observers. Eur. Phys. J. Spec. Top. 2022, 231, 2401–2408. [Google Scholar] [CrossRef]
- Luo, Y.; Zhu, J. Finite-time average consensus control of multi-agent systems based on the aperiodically intermittent control. IEEE Access 2022, 10, 14959–14968. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. A new class of finite-time nonlinear consensus protocols for multi-agent systems. Int. J. Control 2014, 87, 363–370. [Google Scholar] [CrossRef]
- He, W.; Guo, W.; Shi, L.; Sun, W.; Jahanshahi, H. Stochastic fixed-time formation for nonlinear multi-agent systems under a discontinuous protocol. Int. J. Robust Nonlinear Control 2022, 32, 5881–5896. [Google Scholar] [CrossRef]
- Sharifi, A.; Pourgholi, M. Resilient fixed-time bipartite consensus of multi-agent systems with nonlinear dynamics and directed graphs. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2022, 236, 1755–1765. [Google Scholar] [CrossRef]
- Wang, L.; Zou, M.; Guo, W.; Alsubaie, H.; Alotaibi, A.; Taie, R.O.A.; Jahanshahi, H. Adaptive discontinuous control for fixed-Time consensus of nonlinear multi-agent systems. Electronics 2022, 11, 3545. [Google Scholar] [CrossRef]
- Kumar, V.; Srinivasan, S. A review of supply chain management using multi-agent system. Int. J. Comput. Sci. Issues 2010, 7, 198. [Google Scholar]
- Anne, K.; Chedjou, J.; Kyamakya, K. Bifurcation analysis and synchronisation issues in a three-echelon supply chain. Int. J. Logist. Res. Appl. 2009, 12, 347–362. [Google Scholar] [CrossRef]
- Huang, Z.; Nie, J.; Tsai, S. Dynamic collection strategy and coordination of a remanufacturing closed-loop supply chain under uncertainty. Sustainability 2017, 9, 683. [Google Scholar] [CrossRef]
- Xiao, J.; Huang, Z. A stochastic differential game in the closed-loop supply chain with third-party collecting and fairness concerns. Sustainability 2019, 11, 2241. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Altafini, C. Consensus problems on networks with antagonistic interactions. IEEE Trans. Autom. Control 2012, 58, 935–946. [Google Scholar] [CrossRef]
- Meng, D.; Jia, Y.; Du, J. Finite-time consensus for multiagent systems with cooperative and antagonistic interactions. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 762–770. [Google Scholar] [CrossRef]
- Hardy, G.; Littlewood, J.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Mao, X. Stochastic Differential Equations and Applications; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Guo, W.; He, W.; Shi, L.; Sun, W.; Lu, X. Fixed-time consensus tracking for nonlinear stochastically disturbed multi-agent systems via discontinuous protocols. Appl. Math. Comput. 2021, 400, 126046. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, J.; Liang, J.; Cao, J.; Perc, M. Pinning synchronization of nonlinear coupled lur’e networks under hybrid impulses. IEEE Trans. Circuits Syst. -Express Briefs 2019, 66, 432–436. [Google Scholar] [CrossRef]
- Wang, X.; Fang, J.; Zhou, W. Controller design for fixed-time synchronization of nonlinear coupled Cohen-Grossberg neural networks with switching parameters and time-varying delays based on synchronization dynamics analysis. Nonlinear Dyn. 2019, 98, 2079–2096. [Google Scholar] [CrossRef]
- Chen, T.; Zhu, Z. Exponential synchronization of nonlinear coupled dynamical networks. Int. J. Bifurc. Chaos 2007, 17, 999–1005. [Google Scholar] [CrossRef]
- Higham, D. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Filippove, A. Differential equations with discontinuous right-hand side. In Mathematics and Its Applications; Kluwer: Boston, MA, USA, 1998. [Google Scholar]
- Russo, G.; Wirth, F.; Shorten, R. On synchronization in continuous-time networks of nonlinear nodes with state-dependent and degenerate noise diffusion. IEEE Trans. Autom. Control 2018, 64, 389–395. [Google Scholar] [CrossRef]
- Burbano-L, D.A.; Russo, G.; di Bernardo, M. Pinning controllability of complex stochastic networks. IFAC-PapersOnLine 2017, 50, 8327–8332. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, L.; Guo, W.; Wang, L.; Bekiros, S.; Alsubaie, H.; Alotaibi, A.; Jahanshahi, H. Stochastic Fixed-Time Tracking Control for the Chaotic Multi-Agent-Based Supply Chain Networks with Nonlinear Communication. Electronics 2023, 12, 83. https://doi.org/10.3390/electronics12010083
Shi L, Guo W, Wang L, Bekiros S, Alsubaie H, Alotaibi A, Jahanshahi H. Stochastic Fixed-Time Tracking Control for the Chaotic Multi-Agent-Based Supply Chain Networks with Nonlinear Communication. Electronics. 2023; 12(1):83. https://doi.org/10.3390/electronics12010083
Chicago/Turabian StyleShi, Lili, Wanli Guo, Lu Wang, Stelios Bekiros, Hajid Alsubaie, Ahmed Alotaibi, and Hadi Jahanshahi. 2023. "Stochastic Fixed-Time Tracking Control for the Chaotic Multi-Agent-Based Supply Chain Networks with Nonlinear Communication" Electronics 12, no. 1: 83. https://doi.org/10.3390/electronics12010083
APA StyleShi, L., Guo, W., Wang, L., Bekiros, S., Alsubaie, H., Alotaibi, A., & Jahanshahi, H. (2023). Stochastic Fixed-Time Tracking Control for the Chaotic Multi-Agent-Based Supply Chain Networks with Nonlinear Communication. Electronics, 12(1), 83. https://doi.org/10.3390/electronics12010083






