ESMD-WSST High-Frequency De-Noising Method for Bridge Dynamic Deflection Using GB-SAR
Abstract
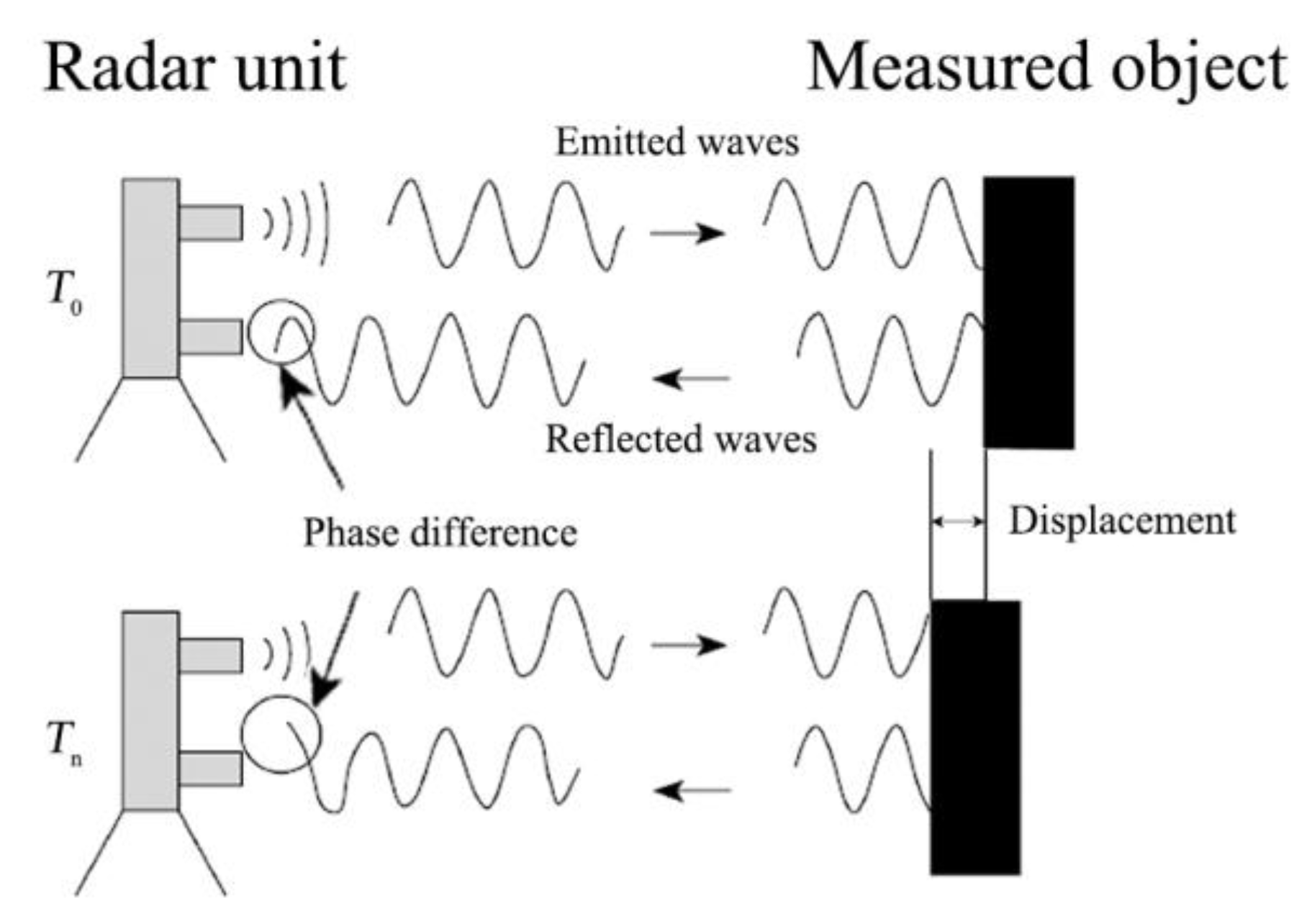
1. Introduction
2. Methodology
2.1. Mutual Information Entropy
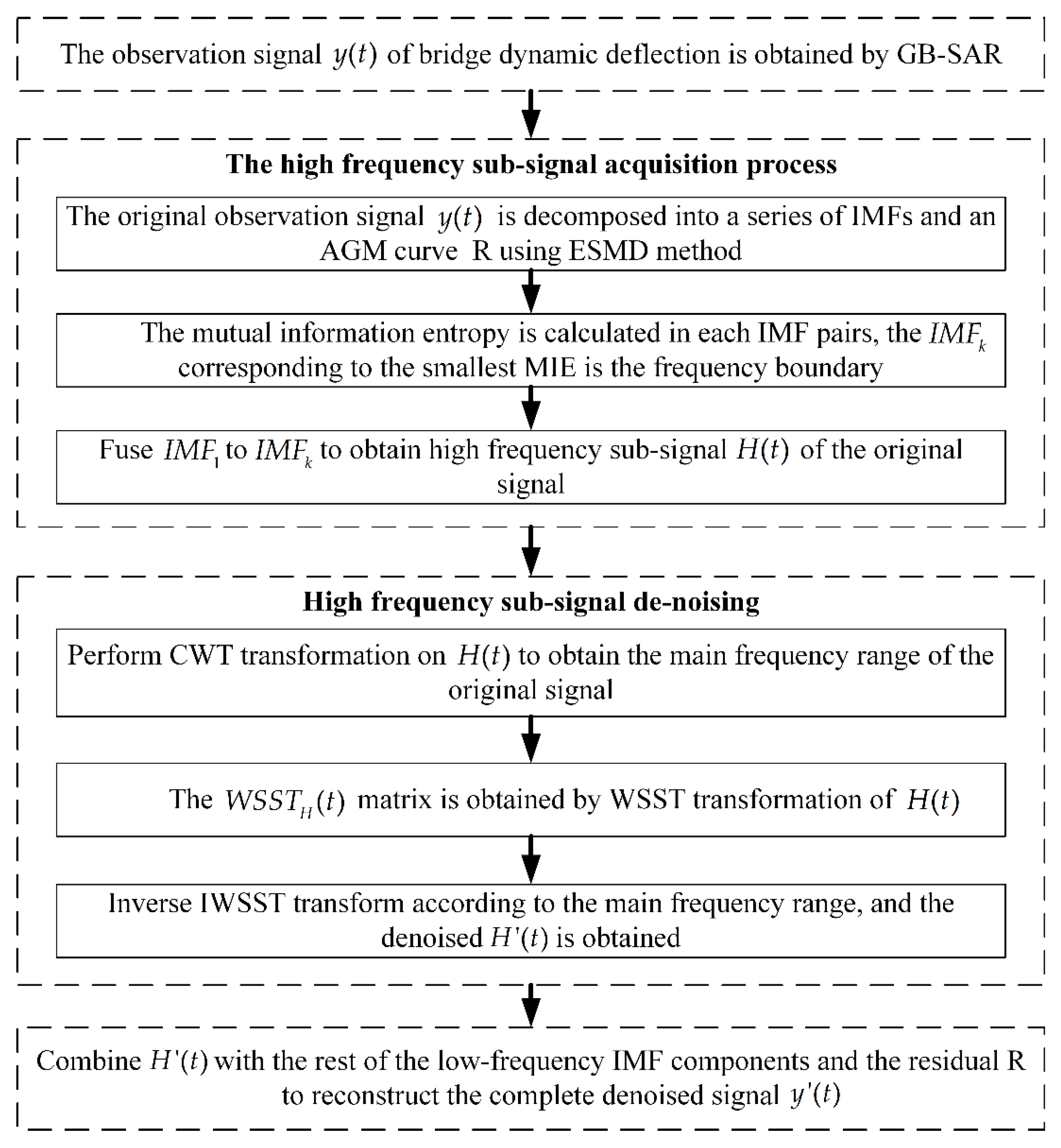
2.2. ESMD-WSST De-Noising Method
- Decompose the original signal into a series of IMFs and an AGM curve R.
- Use MIE to calculate the correlation of IMF pairs, where the search parameter represents the minimum value of MIE, and the corresponding IMF pair is the frequency boundary.
- The high-frequency sub-signal of the original signal is obtained by Equation (6).
- Perform continuous wavelet transform (CWT) on sub-signal to obtain the wavelet transform coefficients and instantaneous frequency using Equations (9) and (10),where is the wavelet basis, and when , the Fourier transform of is .
- Perform WSST on sub-signal ,where the range of satisfies the interval , is the lth discrete angular frequency, is the kth discrete scale, , and .
- Inverse transform is adopted to obtain the compressed de-noised signal using Equation (12),where takes a finite value, and is the conjugate Fourier transform of the basic wavelet function .
- Combine with the remaining to obtain the de-noised dynamic deflection signal .
3. Experiments and Analysis
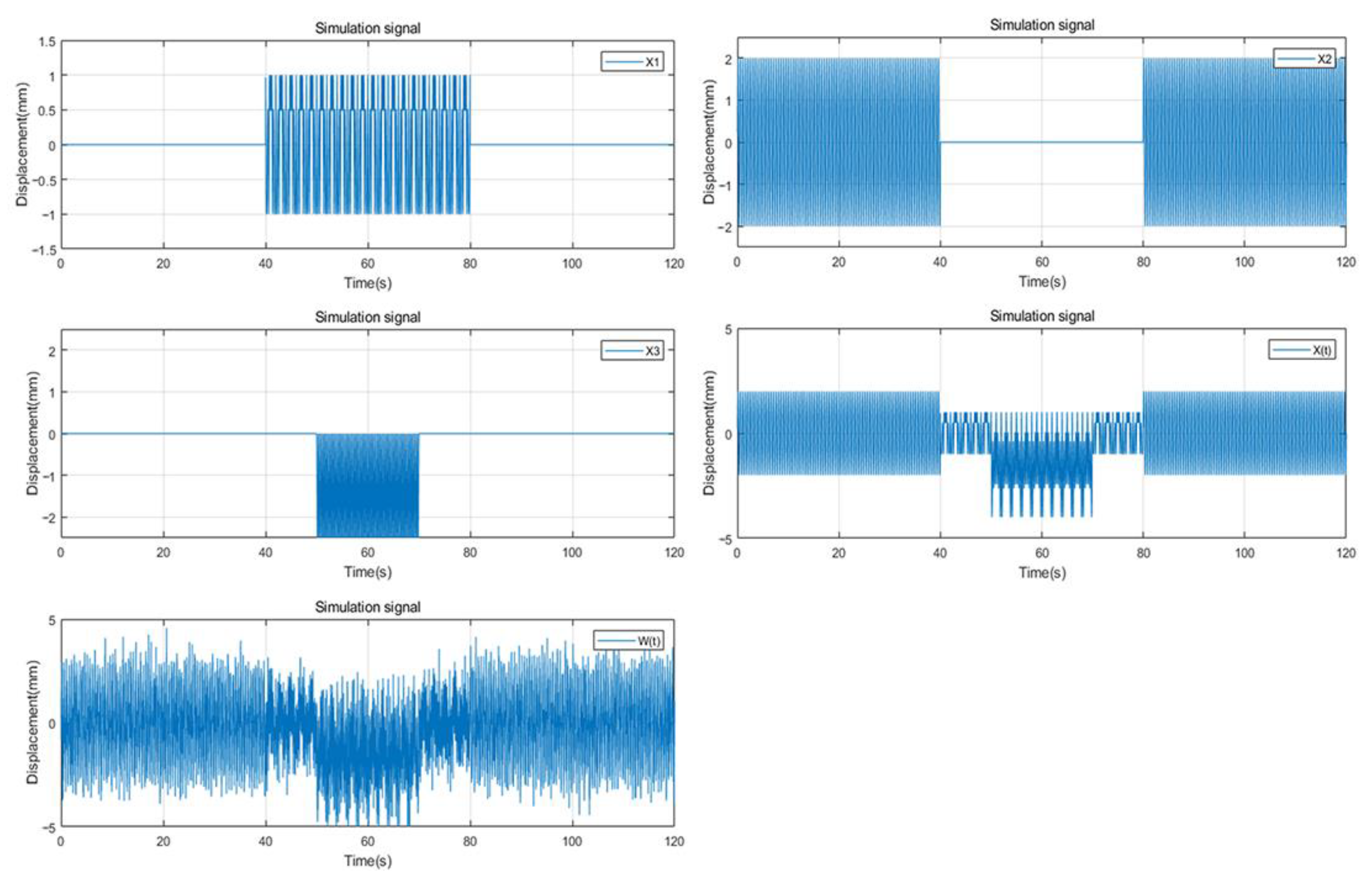
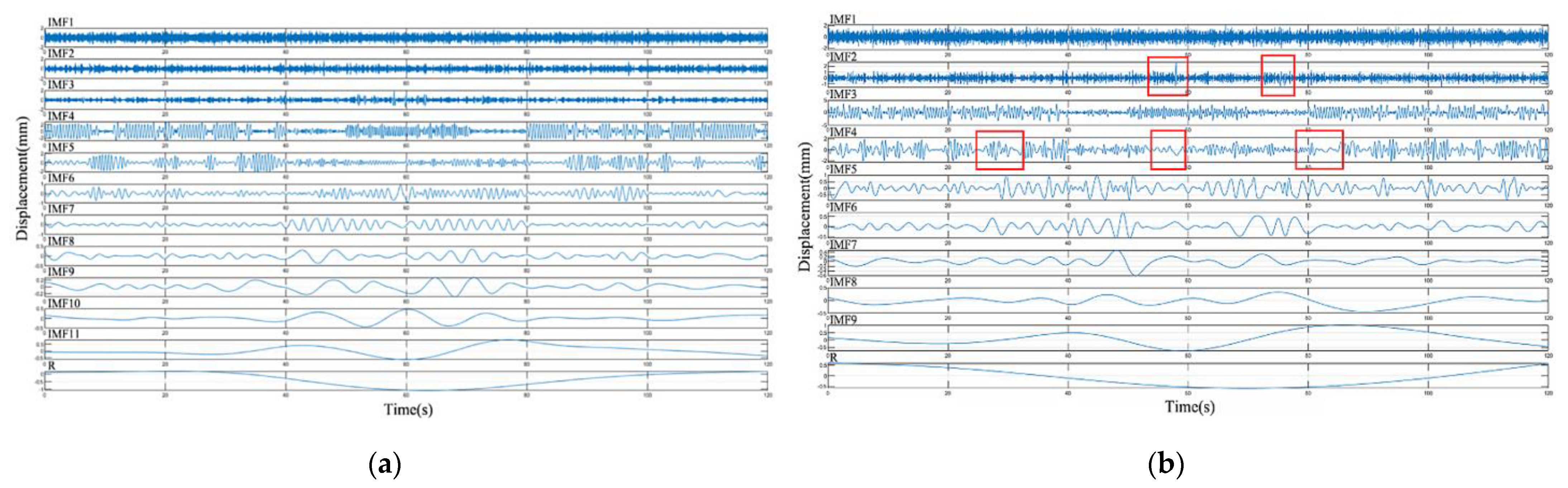
3.1. Simulated Experiment and Analysis
3.2. On-Site Experiment and Analysis
4. Conclusions
- The feasibility and accuracy of the proposed ESMD-WSST de-noising method are verified by simulation experiments. In the low signal-to-noise ratio (5 dB) environment, the SNR of the proposed method after noise reduction is 11.33 dB, and the RMSE value is 0.3049 mm, which is far superior to the traditional ESMD, WSST, and EMD-WSST methods.
- Considering the high-frequency noise content (low original SNR) and short-term high-frequency changes of bridge dynamic deflections collected by GB-SAR, the high-frequency IMF components decomposed by the ESMD method are fused by IME classification, and the high-frequency noise is compressed by the characteristics of WSST transform. It greatly preserves the effective information in the high frequency and improves the accuracy of the bridge dynamic deflection obtained by GB-SAR.
- The evaluation indicators in both the simulation experiment and the on-site bridge experiment show that the proposed ESMD-WSST de-noising method has a good noise reduction ability for the actual GB-SAR dynamic deflection, which not only reduces the impact of noise, but also retains more effective information.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ntotsios, E.; Papadimitriou, C.; Panetsos, P.; Karaiskos, G.; Perros, K.; Perdikaris, P.C. Bridge Health Monitoring System Based on Vibration Measurements. Bull. Earthq. Eng. 2009, 7, 469–483. [Google Scholar] [CrossRef]
- Marrongelli, G.; Gentile, C.; Saisi, A. Anomaly detection based on automated OMA and mode shape changes: Application on a historic arch bridge. In International Conference on Arch Bridges; Springer: Cham, Switzerland, 2019; pp. 447–455. [Google Scholar]
- Dabous, S.A.; Feroz, S. Condition monitoring of bridges with non-contact testing technologies. Autom. Constr. 2020, 116, 103224. [Google Scholar] [CrossRef]
- He, H.; Zhou, Y.; Cao, J.; Zhang, J. Calibration Method for Dynamic Deflection Measurement of Bridges by Photogrammetry. J. Phys. Conf. 2018, 1061, 012004. [Google Scholar] [CrossRef]
- Ye, X.; Sun, Z.; Cai, X.; Mei, L. An Improved Step-Type Liquid Level Sensing System for Bridge Structural Dynamic Deflection Monitoring. Sensors 2019, 19, 2155. [Google Scholar] [CrossRef] [PubMed]
- Tarchi, D.; Rudolf, H.; Pieraccini, M.; Atzeni, C. Remote monitoring of buildings using a ground-based SAR: Application to cultural heritage survey. Int. J. Remote Sens. 2000, 21, 3545–3551. [Google Scholar] [CrossRef]
- Granello, G.; Andisheh, K.; Palermo, A.; Waldin, J. Microwave radar interferometry as a cost-efficient method of monitoring the structural health of bridges in New Zealand. Struct. Eng. Int. 2018, 28, 518–525. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, S.; Wang, P.; Wang, R.; Huang, M. Improved Data-Driven Stochastic Subspace Identification with Autocorrelation Matrix Modal Order Estimation for Bridge Modal Parameter Extraction Using GB-SAR Data. Buildings 2022, 12, 253. [Google Scholar] [CrossRef]
- Makwana, G.; Gupta, L. De-Noising of Electrocardiogram (ECG) with adaptive filter using MATLAB. In Proceedings of the 2015 Fifth International Conference on Communication Systems and Network Technologies, Gwalior, India, 4–6 April 2015; pp. 511–514. [Google Scholar]
- Zhang, D.; Wang, S.; Li, F.; Wang, J.; Sangaiah, A.K.; Sheng, V.S.; Ding, X. An ECG signal de-noising approach based on wavelet energy and sub-band smoothing filter. Appl. Sci. 2019, 9, 4968. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Cexus, J.C. EMD-based signal filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Han, G.; Lin, B.; Xu, Z. Electrocardiogram signal denoising based on empirical mode decomposition technique: An overview. J. Instrum. 2017, 12, P03010. [Google Scholar] [CrossRef]
- Cohen, R. Signal Denoising Using Wavelets; Project Report; Department of Electrical Engineering Technion, Israel Institute of Technology: Haifa, Israel, 2012. [Google Scholar]
- Kumar, A.; Tomar, H.; Mehla, V.K.; Komaragiri, R.; Kumar, M. Stationary wavelet transform based ECG signal denoising method. ISA Trans. 2021, 114, 251–262. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Gaci, S. A new ensemble empirical mode decomposition (EEMD) denoising method for seismic signals. Energy Procedia 2016, 97, 84–91. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z. Extreme-point symmetric mode decomposition method for data analysis. Adv. Adapt. Data Anal. 2013, 5, 1350015. [Google Scholar] [CrossRef]
- Wang, J.; Fang, X. ESMD method for frequency distribution of tank surface temperature under wind effect. Int. J. Geosci. 2015, 6, 481. [Google Scholar] [CrossRef][Green Version]
- Liu, X.; Li, S.; Tong, X. Two-level W-ESMD denoising for dynamic deflection measurement of railway bridges by microwave interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4874–4883. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z. The ESMD method for climate data analysis. Clim. Chang. Res. Lett. 2014, 3, 1–5. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Yang, H. Statistical analysis of synchrosqueezed transforms. Appl. Comput. Harmon. Anal. 2018, 45, 526–550. [Google Scholar] [CrossRef]
- Herrera, R.H.; Han, J.; van der Baan, M. Applications of the synchrosqueezing transform in seismic time-frequency analysis. Geophysics 2014, 79, V55–V64. [Google Scholar] [CrossRef]
- Herrera, R.H.; Tary, J.B.; Van der Baan, M.; Eaton, D.W. Body wave separation in the time-frequency domain. IEEE Geosci. Remote Sens. Lett. 2014, 12, 364–368. [Google Scholar] [CrossRef]
- Thakur, G.; Brevdo, E.; Fučkar, N.S.; Wu, H.T. The synchrosqueezing algorithm for time-varying spectral analysis: Robustness properties and new paleoclimate applications. Signal Process. 2013, 93, 1079–1094. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S. The second-order wavelet synchrosqueezing transform. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 3994–3998. [Google Scholar]
- Auger, F.; Flandrin, P.; Lin, Y.T.; McLaughlin, S.; Meignen, S.; Oberlin, T.; Wu, H.T. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Process. Mag. 2013, 30, 32–41. [Google Scholar] [CrossRef]
- Qin, X.; Cai, J.C.; Liu, S.Y. Microseismic data denoising method based on EMD mutual information entropy and synchrosqueezing transform. Geophys. Prospect. Pet. 2017, 56, 658–666. (In Chinese) [Google Scholar]
- Toprak, A.; Güler, I. Impulse noise reduction in medical images with the use of switch mode fuzzy adaptive median filter. Digit. Signal Process. 2007, 17, 711–723. [Google Scholar] [CrossRef]
- Rödelsperger, S.; Läufer, G.; Gerstenecker, C.; Becker, M. Monitoring of displacements with ground-based microwave interferometry: IBIS-S and IBIS-L. J. Appl. Geod. 2010, 4, 41–54. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, T.; Liu, X.; Lu, Z.; Guo, T. Distance-restrained atmospheric parameters correction (DR-APC) model for GB-SAR transmission power attenuation compensation in bridges dynamic deflection measurement. Measurement 2022, 205, 112192. [Google Scholar] [CrossRef]
- Cai, J.; Xiao, Y.; Li, X. Nuclear magnetic resonance logging signal de-noising based on empirical mode decomposition threshold filtering in frequency domain. Prog. Geophys. 2019, 34, 509–516. [Google Scholar]






| Simulated Signal | ESMD | WSST | EMD-WSST | ESMD-WSST | |
|---|---|---|---|---|---|
| SNR (dB) | 5.03 | 10.16 | 7.24 | 9.99 | 11.33 |
| RMSE (mm) | 0.7799 | 0.4136 | 0.5601 | 0.4596 | 0.3049 |
| IMF Pairs | 1~2 | 2~3 | 3~4 | 4~5 | 5~6 | 6~7 | 7~8 | 8~9 | 9~10 | 10~11 | 11~R |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MIE | 0.8927 | 0.8658 | 0.8847 | 0.8974 | 0.8817 | 0.8903 | 0.8960 | 0.8982 | 0.8908 | 0.8924 | 0.9182 |
| IMF Pairs | 1~2 | 2~3 | 3~4 | 4~5 | 5~6 | 6~7 | 7~8 | 8~9 | 9~R |
|---|---|---|---|---|---|---|---|---|---|
| MIE | 0.8684 | 0.8735 | 0.8982 | 0.8965 | 0.8920 | 0.8642 | 0.8872 | 0.9188 | 0.9340 |
| IMF Pairs | 1~2 | 2~3 | 3~4 | 4~5 | 5~6 | 6~7 | 7~8 | 8~9 | 9~10 | 10~11 | 11~R |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MIE | 0.7137 | 0.6687 | 0.6894 | 0.7507 | 0.7942 | 0.8151 | 0.8371 | 0.8393 | 0.8628 | 0.8929 | 0.9061 |
| ESMD | WSST | EMD-WSST | Proposed Method | |
|---|---|---|---|---|
| NRR (dB) | 4.42 | 3.99 | 4.48 | 5.48 |
| RVR (mm) | 0.1471 | 0.1732 | 0.0732 | 0.0501 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhao, S.; Wang, R. ESMD-WSST High-Frequency De-Noising Method for Bridge Dynamic Deflection Using GB-SAR. Electronics 2023, 12, 54. https://doi.org/10.3390/electronics12010054
Liu X, Zhao S, Wang R. ESMD-WSST High-Frequency De-Noising Method for Bridge Dynamic Deflection Using GB-SAR. Electronics. 2023; 12(1):54. https://doi.org/10.3390/electronics12010054
Chicago/Turabian StyleLiu, Xianglei, Songxue Zhao, and Runjie Wang. 2023. "ESMD-WSST High-Frequency De-Noising Method for Bridge Dynamic Deflection Using GB-SAR" Electronics 12, no. 1: 54. https://doi.org/10.3390/electronics12010054
APA StyleLiu, X., Zhao, S., & Wang, R. (2023). ESMD-WSST High-Frequency De-Noising Method for Bridge Dynamic Deflection Using GB-SAR. Electronics, 12(1), 54. https://doi.org/10.3390/electronics12010054







