Research on Fractional-Order Global Fast Terminal Sliding Mode Control of MDF Continuous Hot-Pressing Position Servo System Based on Adaptive RBF Neural Network
Abstract
:1. Introduction
- (1)
- A FGFTSMC is constructed based on dynamics and mathematical model of the MDF hot-pressing position servo system, which ensures the rapid convergence of the system state and improves the tracking accuracy.
- (2)
- The adaptive law and the RBF neural network are introduced to estimate the upper bound of the parameter perturbation and approximate the external load disturbance, respectively. The results of them are fed back to FGFTSMC controller to avoid system performance degradation.
- (3)
- The Lyapunov theorem is utilized to prove the stability of system and analyze finite-time reachability of the sliding mode.
2. System Model and Theoretical Basis of Fractional-Order
2.1. Theoretical Basis of Fractional-Order Calculus
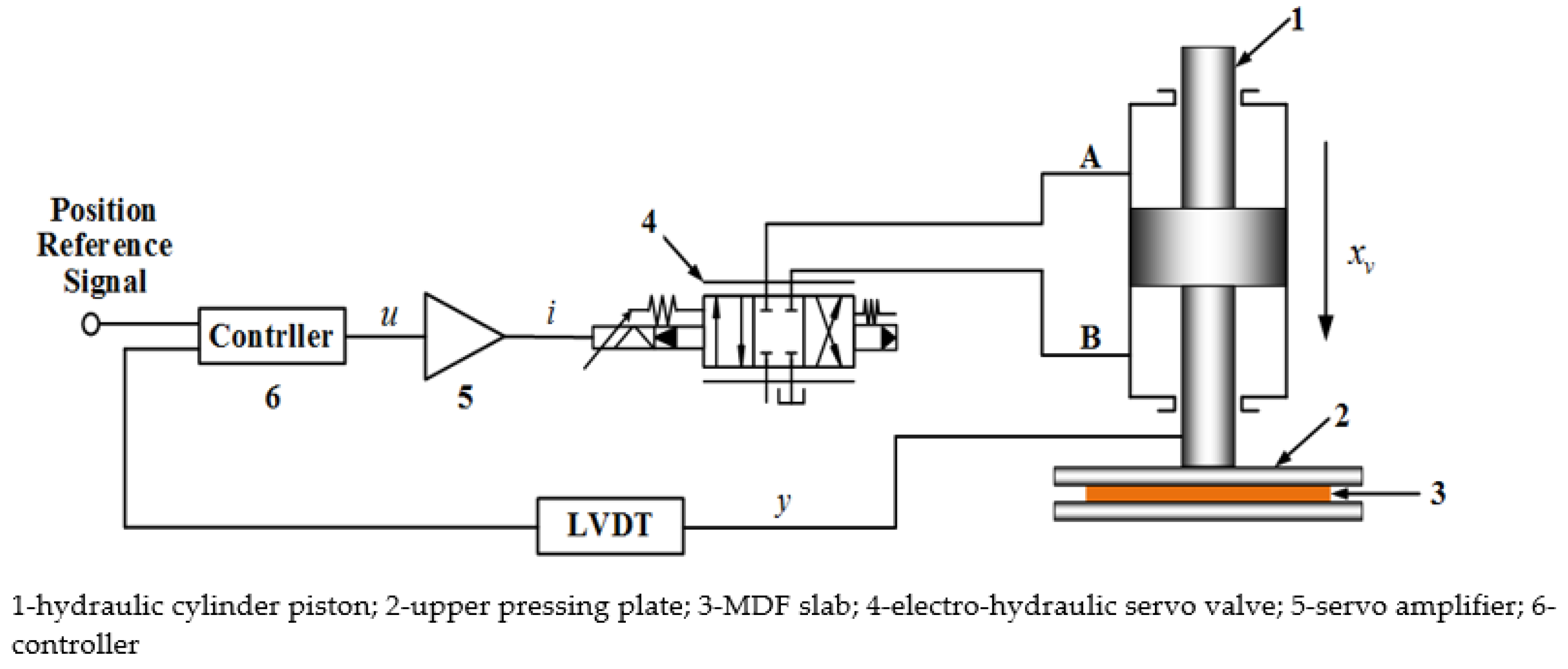
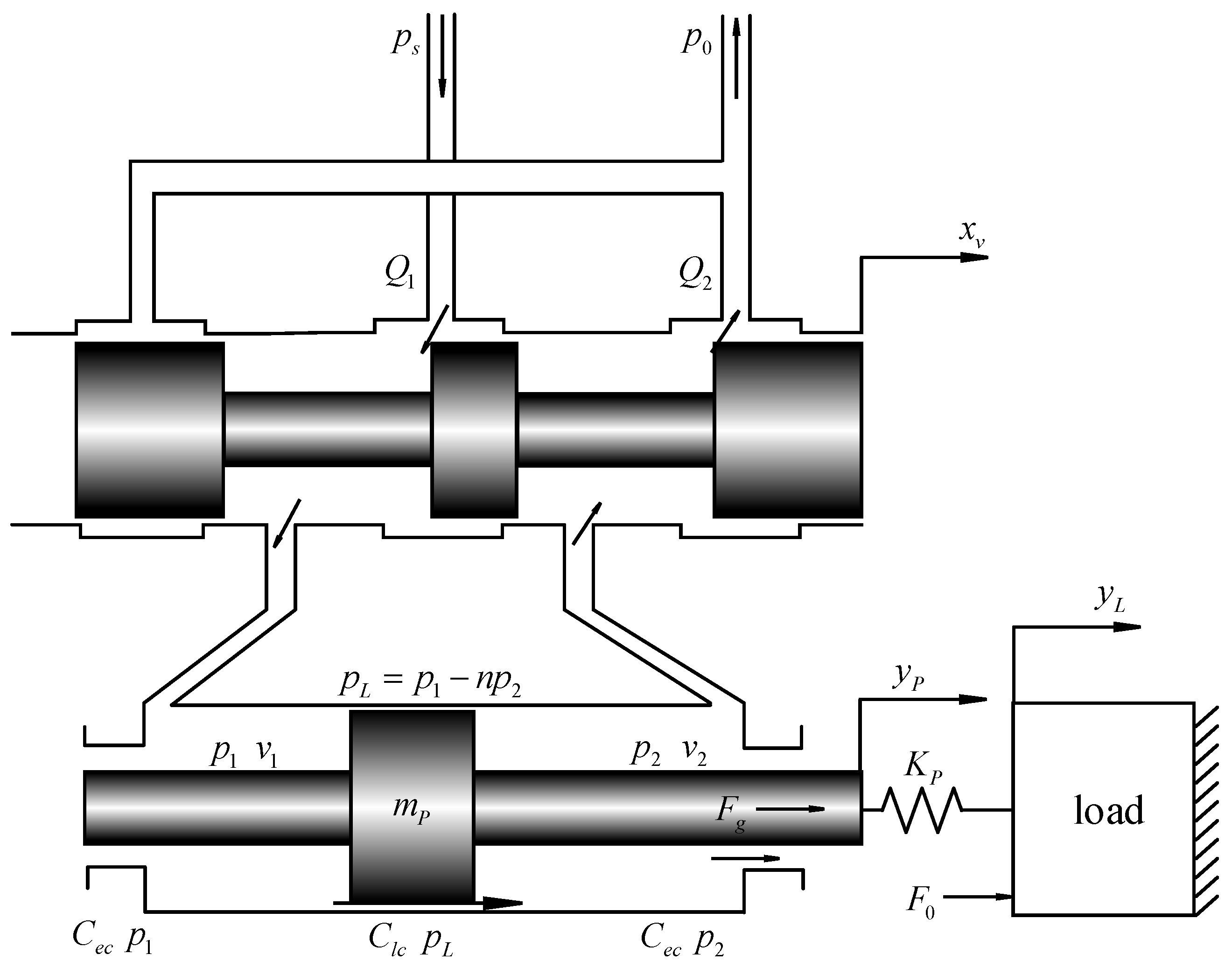
2.2. MDF Continuous Hot-Pressing Position Servo System Model
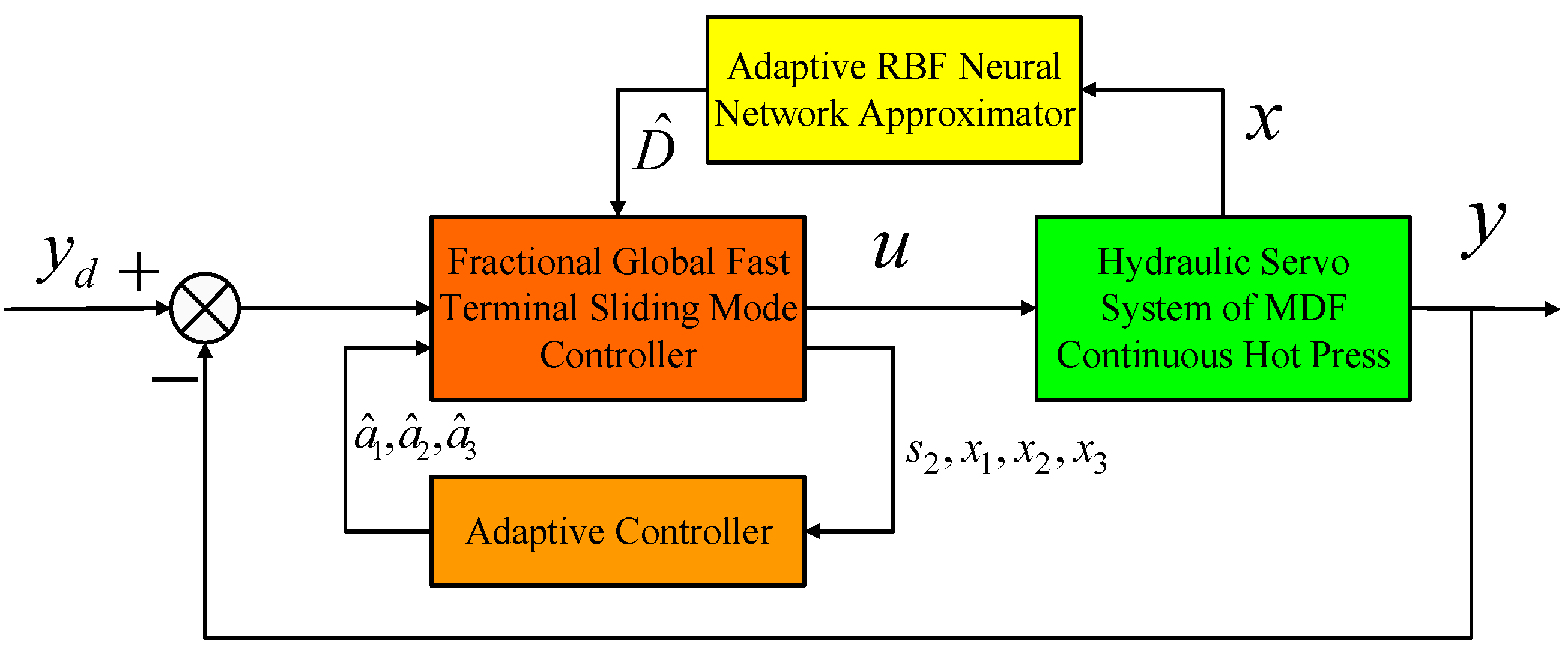
3. Design of FGFTSMC Controller Based on Adaptive RBF Neural Network
3.1. Subsection
3.2. Design of Adaptive Law with Unknown Parameters
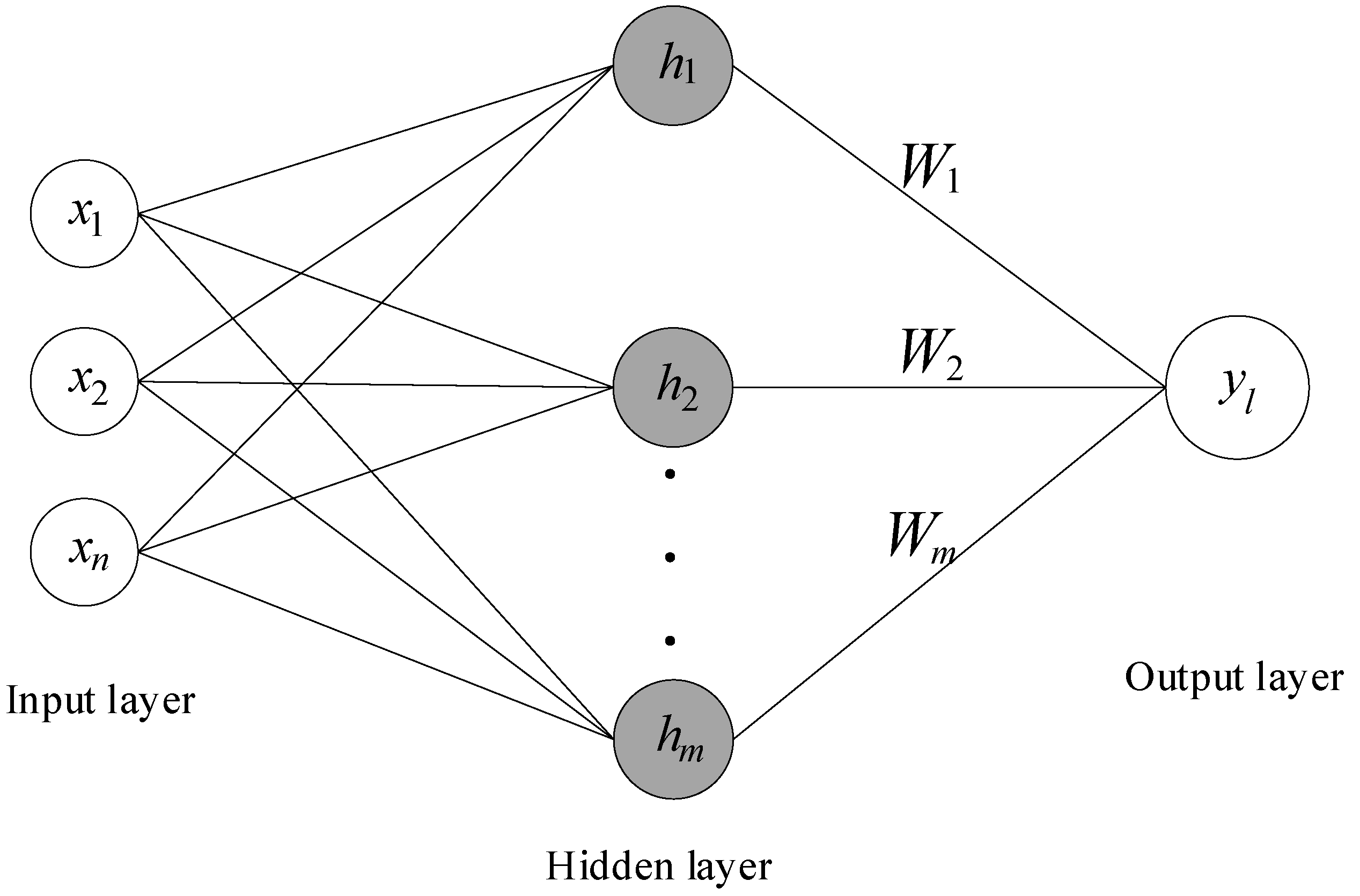
3.3. Design of Adaptive RBF Neural Network Approximator
4. Stability and Convergence Time Analysis
4.1. Stability Analysis
4.2. Analysis of Convergence Time
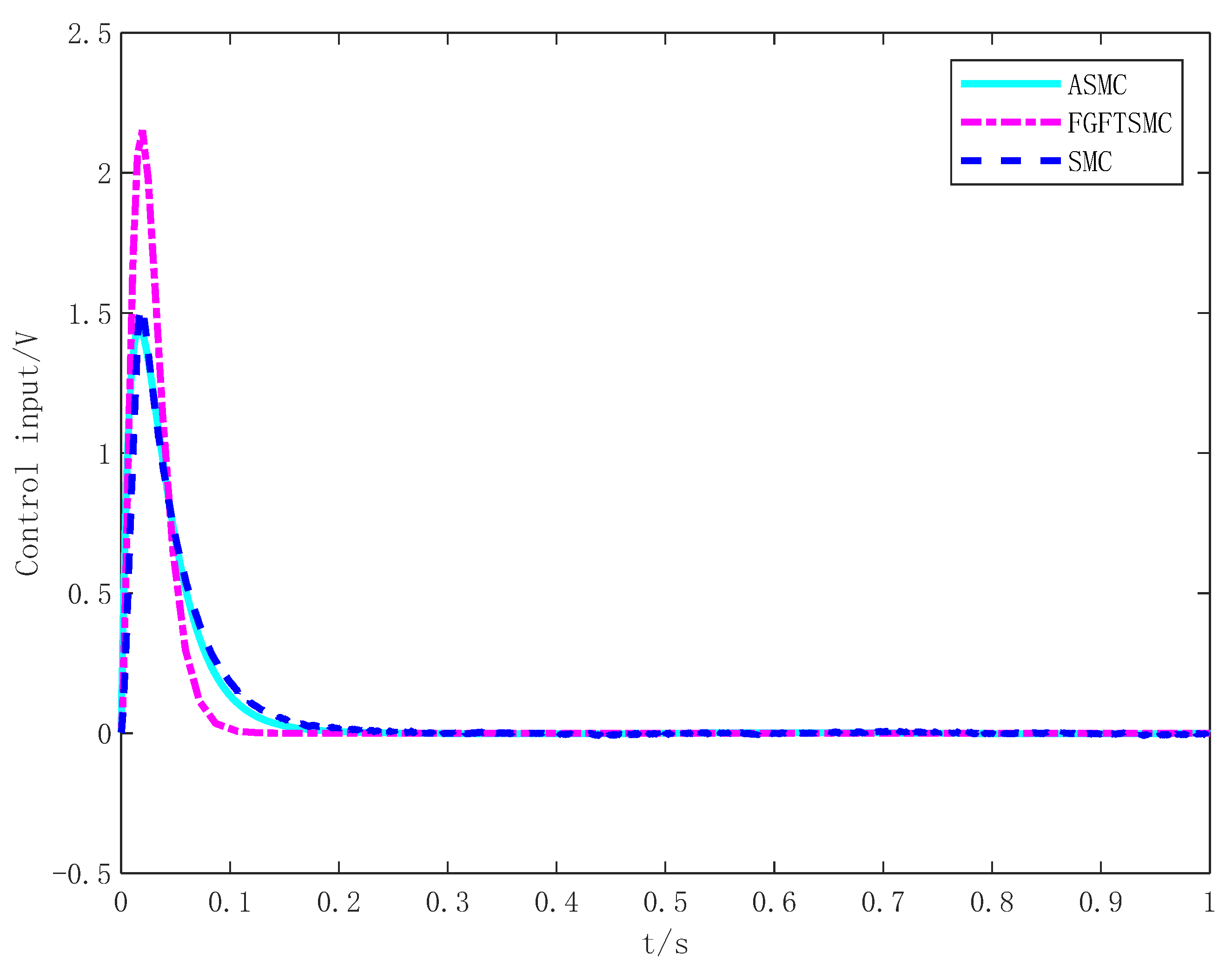
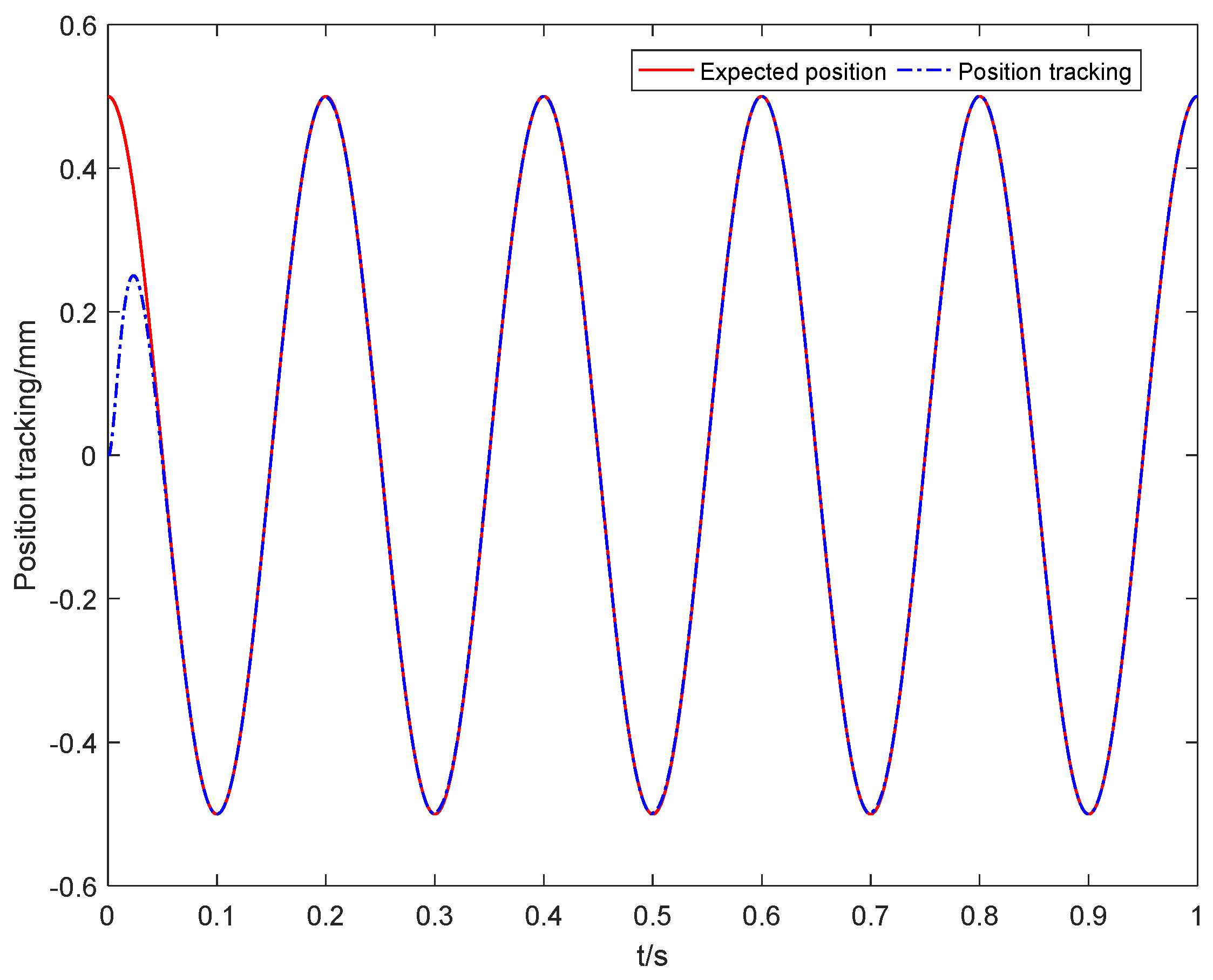
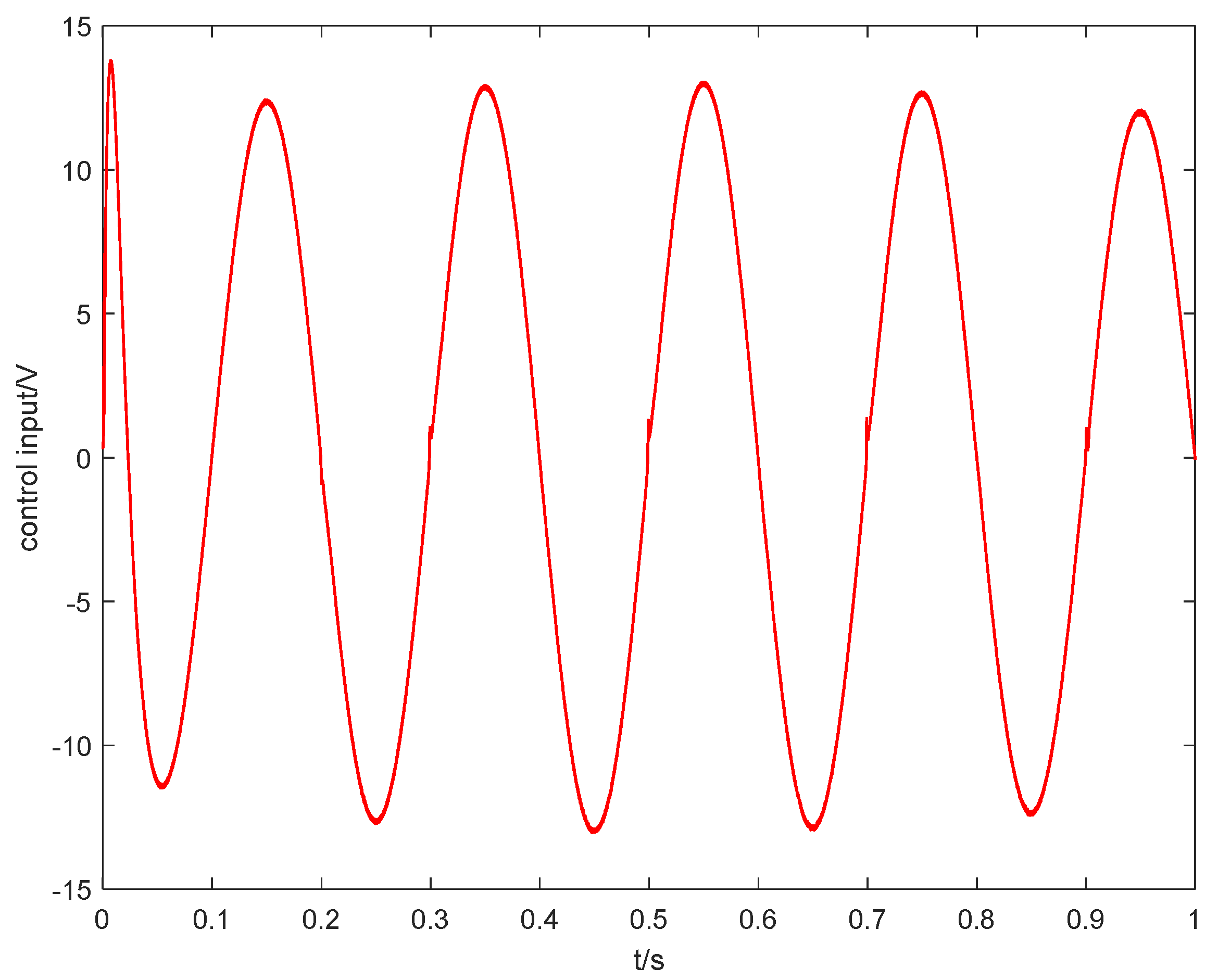
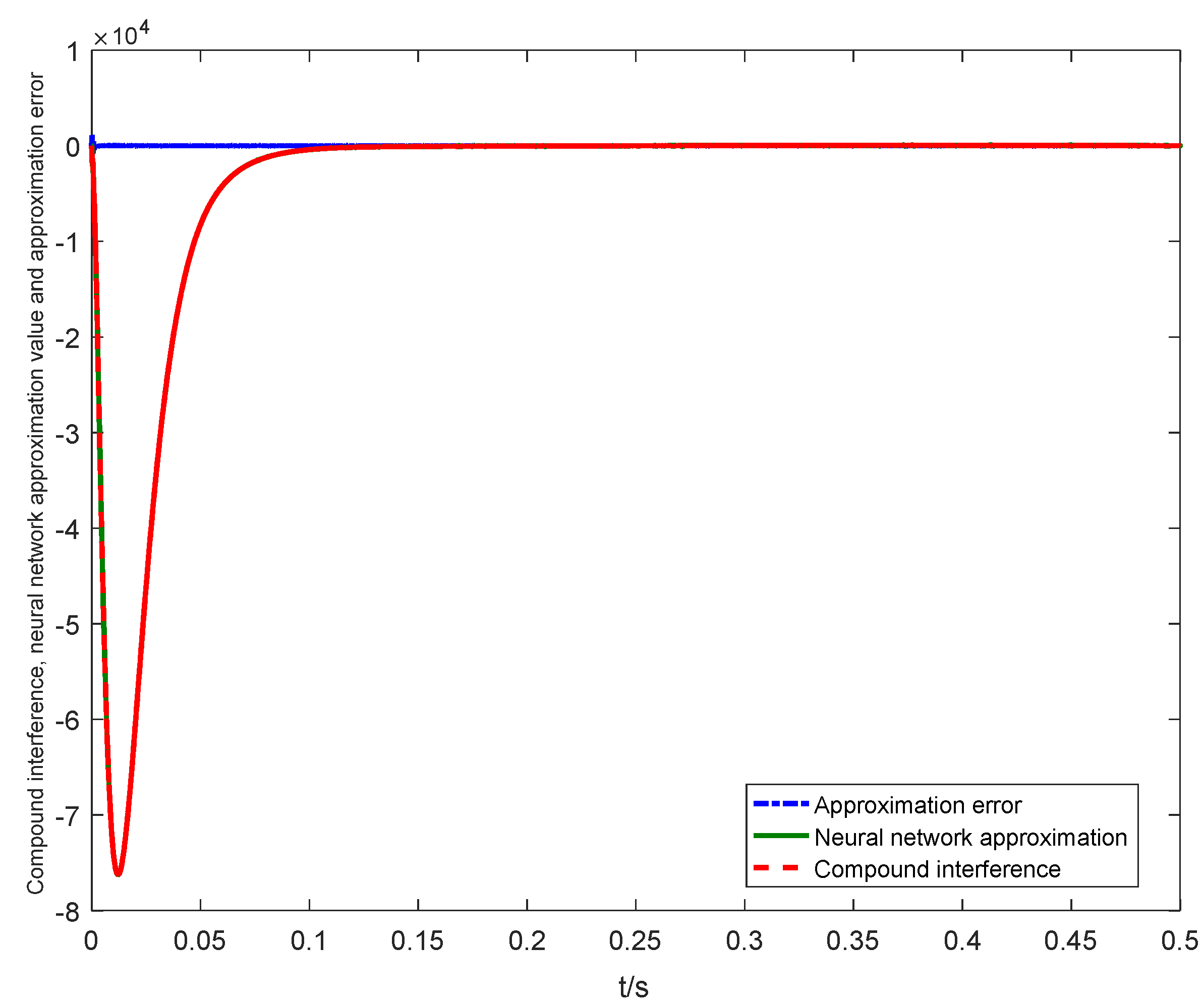
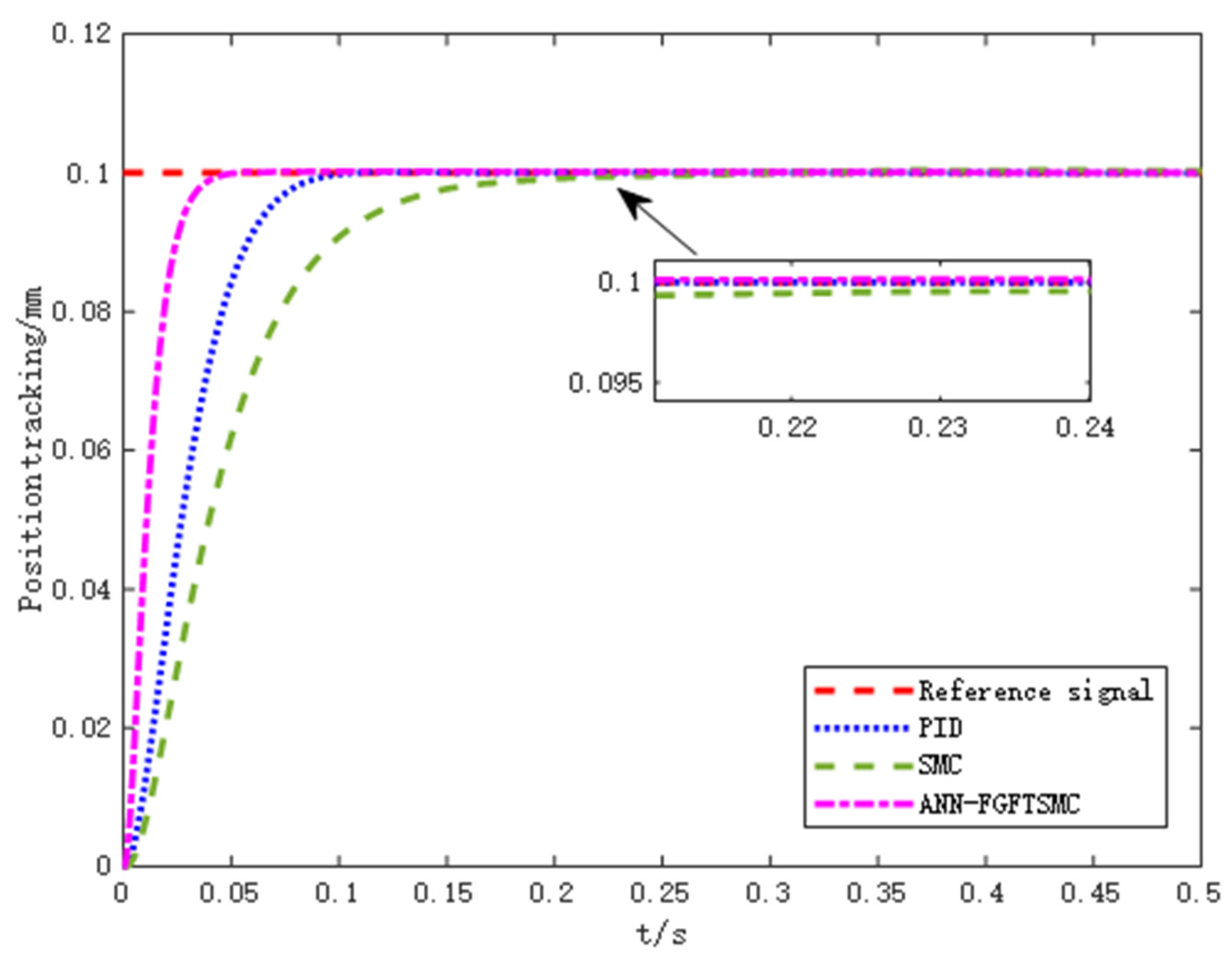
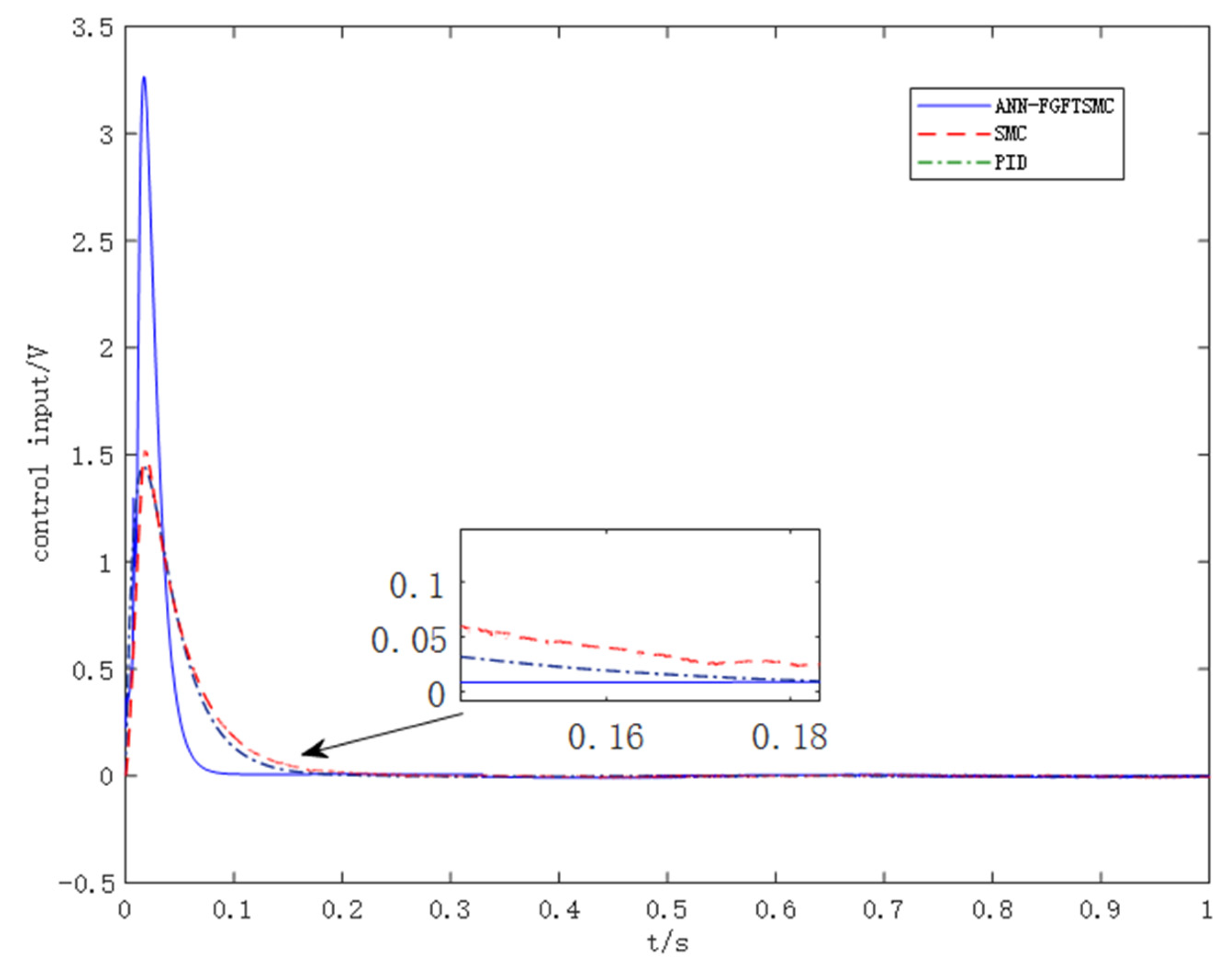
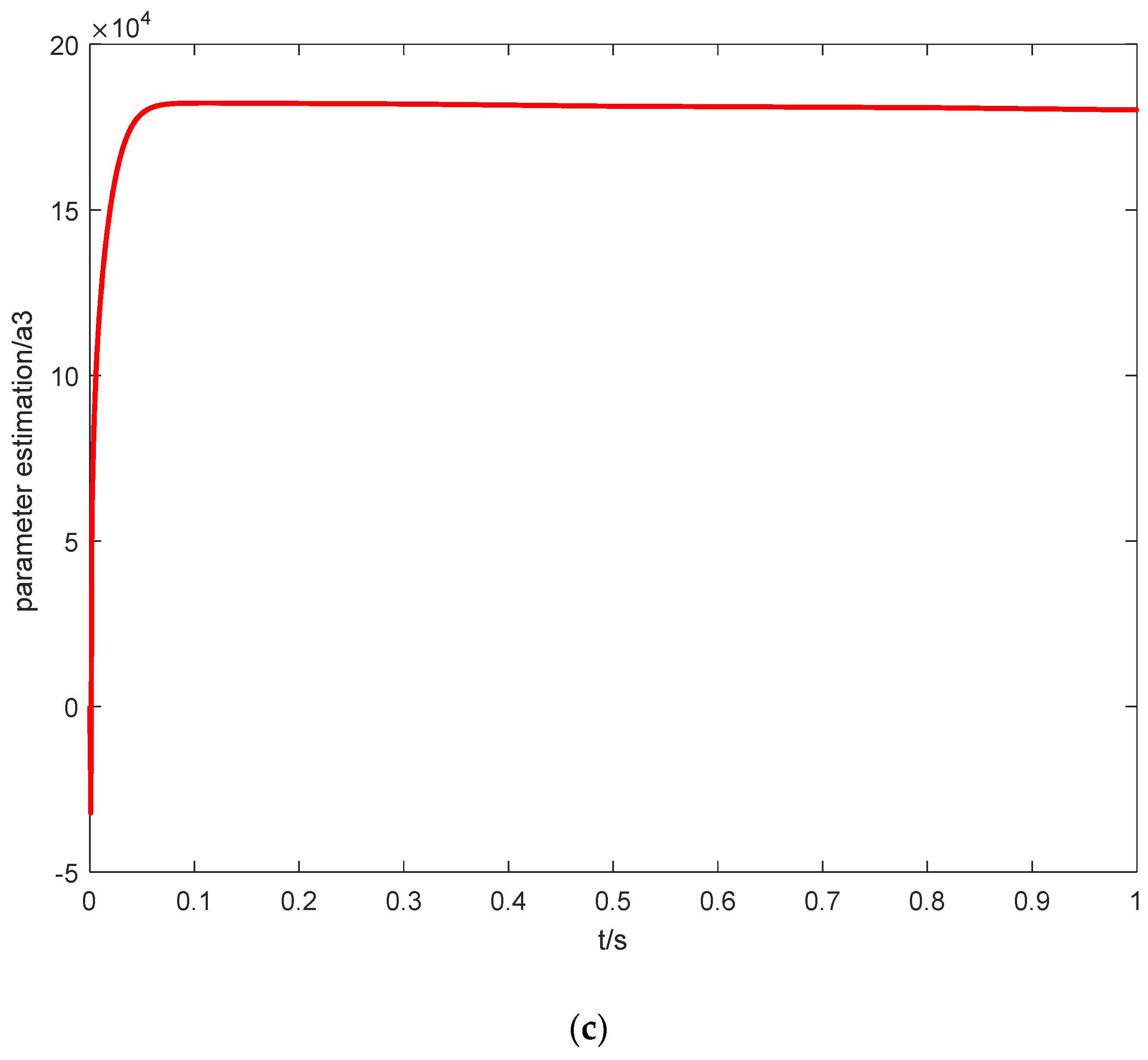
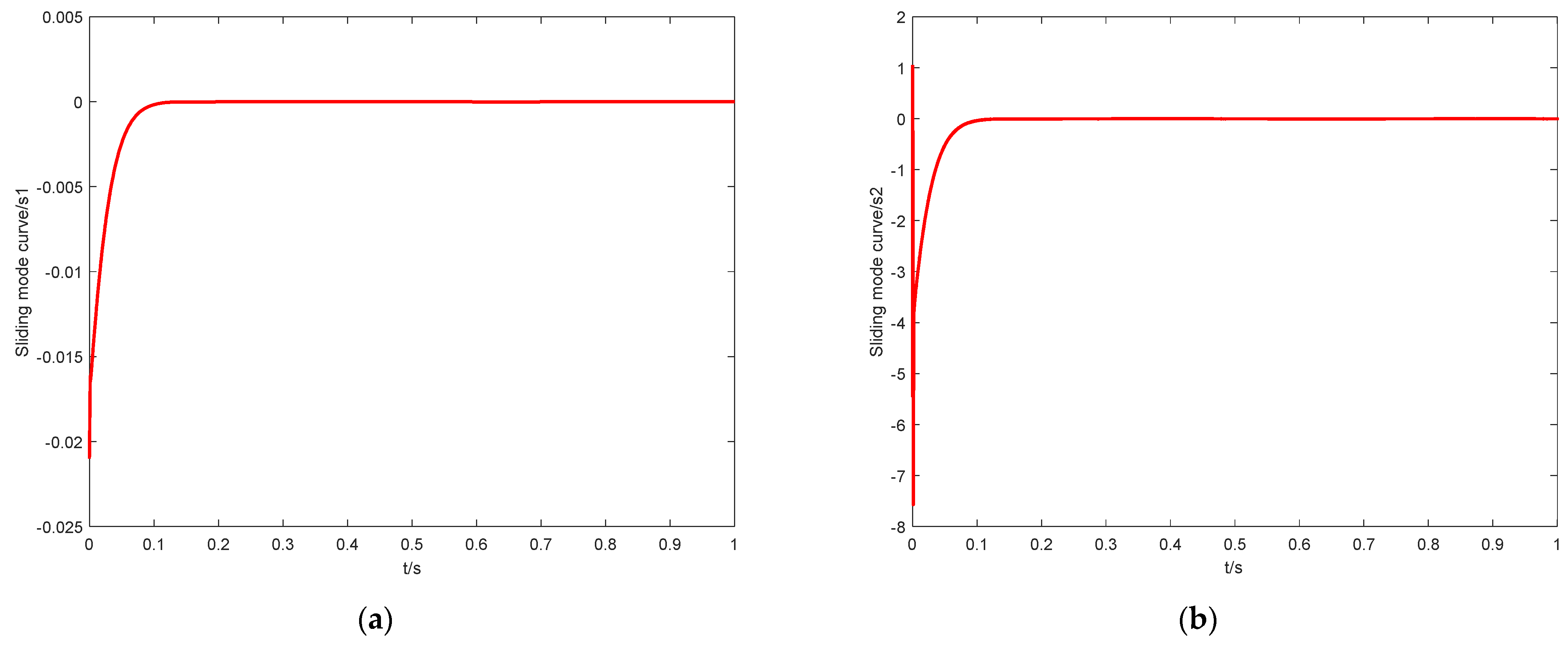
5. Simulation Analysis
- (1)
- The initial state is .
- (2)
- The reference output signal is .
- (3)
- The disturbance of unknown external load force is .
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, W. Current situation of MDF Industry and analysis of product quality. Sichuan Build. Mater. 2017, 43, 217–218. [Google Scholar]
- Ren, R. Analysis on quality problems of MDF products. Hebei Enterp. 2015, 8, 143–144. [Google Scholar]
- Li, G.; Ding, Y.; Feng, Y.; Li, Y. AMESim simulation and energy control of hydraulic control system for direct drive electro-hydraulic servo die forging hammer. Int. J. Hydromechatron. 2019, 2, 203–225. [Google Scholar] [CrossRef]
- Wiens, T. Engine speed reduction for hydraulic machinery using predictive algorithms. Int. J. Hydromechatron. 2019, 2, 16–31. [Google Scholar] [CrossRef]
- Togawa, T.; Tachibana, T.; Tanaka, Y.; Peng, J. Hydro-disk-type of electrorheological brakes for small mobile robots. Int. J. Hydromechatron. 2021, 4, 99–115. [Google Scholar] [CrossRef]
- Wang, L. PID Control System Design and Automatic Tuning Using MATLAB/Simulink; Wiley-IEEE Press Ltd.: Chichester, UK, 2020; pp. 1–30. [Google Scholar]
- Karami, M.; Tavakolpour-Saleh, A.R.; Norouzi, A. Optimal Nonlinear PID Control of a Micro-Robot Equipped with Vibratory Actuator Using Ant Colony Algorithm: Simulation and Experiment. J. Intell. Robot. Syst. 2020, 99, 773–796. [Google Scholar] [CrossRef]
- Fan, Y.; Shao, J.; Sun, G. Optimized PID Controller Based on Beetle Antennae Search Algorithm for Electro-Hydraulic Position Servo Control System. Sensors 2019, 19, 2727. [Google Scholar] [CrossRef] [Green Version]
- Caglar, C.; Mustafa, K. Fuzzy self-adaptive PID control technique for driving HHO dry cell systems. Int. J. Hydrogen Energy 2020, 45, 26059–26069. [Google Scholar]
- Wang, B.; Jahanshahi, H.; Volos, C.; Bekiros, S.; Aly, A.A. A New RBF Neural Network-Based Fault-Tolerant Active Control for Fractional Time-Delayed Systems. Electronics 2021, 10, 1501. [Google Scholar] [CrossRef]
- Al-Darraji, I.; Piromalis, D.; Kakei, A.A.; Khan, F.Q.; Stojmenovic, M.; Tsaramirsis, G.; Papageorgas, P.G. Adaptive robust controller design-based rbf neural network for aerial robot arm model. Electronics 2021, 10, 831. [Google Scholar] [CrossRef]
- Lopac, N.; Jurdana, I.; Lerga, J.; Wakabayashi, N. Particle-Swarm-Optimization-Enhanced Radial-Basis-Function-Kernel-Based Adaptive Filtering Applied to Maritime Data. J. Mar. Sci. Eng. 2021, 9, 439. [Google Scholar] [CrossRef]
- Luo, J.; Yuan, R.; Yuan, Y.; Ba, S.; Zhang, Z. Analysis of Speed Servo System of Pneumatic Manipulator Based RBF Neural Network PID Control. Appl. Mech. Mater. 2010, 41, 65–70. [Google Scholar] [CrossRef]
- Liu, C.; Wang, M.; Zhang, J. Research on RBF Neural Network PID Controller for Quadcopter ESO. Electro-Opt. Control. 2021, 28, 84. [Google Scholar]
- Meda-Campaña, J.A.; Escobedo-Alva, J.O.; Rubio, J.D.J.; Aguilar-Ibañez, C.; Perez-Cruz, J.H.; Obregon-Pulido, G.; Tapia-Herrera, R.; Orozco, E.; Cordova, D.A.; Islas, M.A. On the Rejection of Random Perturbations and the Tracking of Random References in a Quadrotor. Complexity 2022, 2022, 1–16. [Google Scholar] [CrossRef]
- de Jesús Rubio, J.; Orozco, E.; Cordova, D.A.; Islas, M.A.; Pacheco, J.; Gutierrez, G.J.; Zacarias, A.; Soriano, L.A.; Meda-Campaña, J.A.; Mujica-Vargas, D. Modified Linear Technique for the Controllability and Observability of Robotic Arms. IEEE Access 2022, 10, 3366–3377. [Google Scholar] [CrossRef]
- Aguilar-Ibanez, C.; Moreno-Valenzuela, J.; García-Alarcón, O.; Martinez-Lopez, M.; Acosta, J.Á.; Suarez-Castanon, M.S. PI-Type Controllers and Σ–Δ Modulation for Saturated DC-DC Buck Power Converters. IEEE Access 2021, 9, 20346–20357. [Google Scholar] [CrossRef]
- Soriano, L.A.; Rubio, J.D.J.; Orozco, E.; Cordova, D.A.; Ochoa, G.; Balcazar, R.; Cruz, D.R.; Meda-Campaña, J.A.; Zacarias, A.; Gutierrez, G.J. Optimization of Sliding Mode Control to Save Energy in a SCARA Robot. Mathematics 2021, 9, 3160. [Google Scholar] [CrossRef]
- Soriano, L.A.; Zamora, E.; Vazquez-Nicolas, J.M.; Hernández, G.; Barraza Madrigal, J.A.; Balderas, D. PD control compensation based on a cascade neural network applied to a robot manipulator. Front. Neurorobot. 2020, 78, 1–9. [Google Scholar] [CrossRef]
- Silva-Ortigoza, R.; Hernández-Márquez, E.; Roldán-Caballero, A.; Tavera-Mosqueda, S.; Marciano-Melchor, M.; García-Sánchez, J.R.; Hernández-Guzmán, V.M.; Silva-Ortigoza, G. Sensorless Tracking Control for a “Full-Bridge Buck Inverter–DC Motor” System: Passivity and Flatness-Based Design. IEEE Access 2021, 9, 132191–132204. [Google Scholar] [CrossRef]
- Kishore, B.; Rosdiazli, I.; Mohd, N.; Sabo, M.; Vivekananda, R. Fractional-Order Systems and PID Controllers; Springer: Berlin, Germany, 2020; pp. 1–20. [Google Scholar]
- Agila, A.; Baleanu, D.; Eid, R.; Irfanoglu, B. A freely damped oscillating fractional dynamic system modeled by fractional Euler–Lagrange equations. J. Vib. Control 2018, 24, 1228–1238. [Google Scholar] [CrossRef]
- Delavari, H.; Senejohnny, D.; Baleanu, D. Sliding observer for synchronization of fractional order chaotic systems with mismatched parameter. Open Phys. 2012, 10, 1095–1101. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Yuan, X.; Ji, B.; Wang, P.; Tian, H. Design of a fractional order PID controller for hydraulic turbine regulating system using chaotic non-dominated sorting genetic algorithm II. Energy Convers. Manag. 2014, 84, 390–404. [Google Scholar] [CrossRef]
- Trivedi, R.; Padhy, P.K. Design of Indirect Fractional Order IMC Controller for Fractional Order Processes. IEEE Trans. Circuits Syst. II Express Briefs 2020, 68, 968–972. [Google Scholar] [CrossRef]
- Zhao, H.; Li, D.; Deng, W.; Yang, X. Research on Vibration Suppression Method of Alternating Current Motor Based on Fractional Order Control Strategy. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2017, 231, 786–799. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, B.; Lu, J.; Cao, J.; Lu, G. Event-triggered sliding mode control for attitude stabilization of a rigid spacecraft. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3290–3299. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, L.; Tan, M.; Hou, Z.G. Exponential finite-time consensus of fractional-order multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 1549–1558. [Google Scholar] [CrossRef]
- Wang, H.; Liu, P.X.; Zhao, X.; Liu, X. Adaptive fuzzy finite-time control of nonlinear systems with actuator faults. IEEE Trans. Cybern. 2019, 50, 1786–1797. [Google Scholar] [CrossRef]
- Lopac, N.; Bulic, N.; Vrkic, N. Sliding mode observer-based load angle estimation for salient-pole wound rotor synchronous generators. Energies 2019, 12, 1609. [Google Scholar] [CrossRef] [Green Version]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Adaptive sliding mode trajectory tracking control for unmanned surface vehicle with modeling uncertainties and input saturation. Appl. Sci. 2019, 9, 1240. [Google Scholar] [CrossRef] [Green Version]
- Song, S.; Zhang, B.; Xia, J.; Zhang, Z. Adaptive Backstepping Hybrid Fuzzy Sliding Mode Control for Uncertain Fractional-Order Nonlinear Systems Based on Finite-Time Scheme. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1559–1569. [Google Scholar] [CrossRef]
- Ying, L.; Tao, Z.; Lee, B.J.; Kang, C.; Chen, Y. Fractional-Order Proportional Derivative Controller Synthesis and Implementation for Hard-Disk-Drive Servo System. IEEE Trans. Control. Syst. Technol. 2014, 22, 281–289. [Google Scholar]
- Ullah, N.; Shao, W.; Khattak, M.I.; Shafi, M. Fractional order adaptive fuzzy sliding mode controller for a position servo system subjected to aerodynamic loading and nonlinearities. Aerosp. Sci. Technol. 2015, 43, 381–387. [Google Scholar] [CrossRef]
- Trieu, P.V.; Cuong, H.M.; Dong, H.Q.; Tuan, N.H.; Le, A.T. Adaptive fractional-order fast terminal sliding mode with fault-tolerant control for underactuated mechanical systems: Application to tower cranes. Autom. Constr. 2021, 123, 103533. [Google Scholar] [CrossRef]
- Aghaeinezhad, S.M.; Taghizadeh, M.; Mazare, M.; Kazemi, M. Individual Pitch Angle Control of a Variable Speed Wind Turbine Using Adaptive Fractional Order Non-Singular Fast Terminal Sliding Mode Control. Int. J. Precis. Eng. Manuf. 2021, 22, 511–522. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Adaptive Fractional-Order Nonsingular Fast Terminal Sliding Mode Based Robust Tracking Control of Quadrotor UAV With Gaussian Random Disturbances and Uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2265–2277. [Google Scholar] [CrossRef]
- Anjum, Z.; Guo, Y.; Yao, W. Fault tolerant control for robotic manipulator using fractional-order backstepping fast terminal sliding mode control. Trans. Inst. Meas. Control 2021, 43, 3244–3254. [Google Scholar] [CrossRef]
- Le, A.T. Neural Observer and Adaptive Fractional-Order Backstepping Fast-Terminal Sliding-Mode Control of RTG Cranes. IEEE Trans. Ind. Electron. 2020, 68, 434–442. [Google Scholar]
- Zhang, W. Research on Permanent Magnet Synchronous Motor Control Based on Fractional Order Sliding Mode Observer. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2019. [Google Scholar]
- Wu, Z. Hydraulic Control System, 1st ed.; Higher Education Press: Beijing, China, 2008; pp. 14–43. [Google Scholar]
- Shao, X. Research on Position Tracking Control of MDF Continuous Hot Press Plate Thickness Control Hydraulic System. Master’s Thesis, Northeast Forestry University, Harbin, China, 2015. [Google Scholar]
- Wang, H.; Lu, Y.; Tian, Y.; Christov, N. Fuzzy sliding mode based active disturbance rejection control for active suspension system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 449–457. [Google Scholar] [CrossRef]



| Physical Parameter | Numerical Value | Physical Parameter | Numerical Value |
|---|---|---|---|
| 0.01 | 5 | ||
| 0.0125 | 25 | ||
| 0.61 | 6.85 | ||
| 850 | 2.4 | ||
| 0.1256 | 2.356 | ||
| 0.025 | 1000 | ||
| 6.85 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Chen, X.; Qi, X.; Zhang, J. Research on Fractional-Order Global Fast Terminal Sliding Mode Control of MDF Continuous Hot-Pressing Position Servo System Based on Adaptive RBF Neural Network. Electronics 2022, 11, 1117. https://doi.org/10.3390/electronics11071117
Zhu L, Chen X, Qi X, Zhang J. Research on Fractional-Order Global Fast Terminal Sliding Mode Control of MDF Continuous Hot-Pressing Position Servo System Based on Adaptive RBF Neural Network. Electronics. 2022; 11(7):1117. https://doi.org/10.3390/electronics11071117
Chicago/Turabian StyleZhu, Liangkuan, Xinrui Chen, Xing Qi, and Jian Zhang. 2022. "Research on Fractional-Order Global Fast Terminal Sliding Mode Control of MDF Continuous Hot-Pressing Position Servo System Based on Adaptive RBF Neural Network" Electronics 11, no. 7: 1117. https://doi.org/10.3390/electronics11071117
APA StyleZhu, L., Chen, X., Qi, X., & Zhang, J. (2022). Research on Fractional-Order Global Fast Terminal Sliding Mode Control of MDF Continuous Hot-Pressing Position Servo System Based on Adaptive RBF Neural Network. Electronics, 11(7), 1117. https://doi.org/10.3390/electronics11071117






