A Low-Complexity Detector for Uplink SCMA by Exploiting Dynamical Superior User Removal Algorithm

Abstract

Sparse Code Multiple Access (SCMA) is capable of ameliorating the performance of wireless communication systems for massive connectivity. The sparsity of the codeword allows SCMA to employ the message-passing algorithm (MPA) at the receiver to address the connection overload. The detection complexity of traditional MPA, on the other hand, is exponentially exploding with the increasing number of connected devices. In this paper, a low-complexity MPA scheme is developed with the threshold and dynamical user removal algorithm (TB-RMPA) based on shuffled MPA (SMPA). By introducing the concept of Iterative Elimination of Dominated Strategies (IEDS) in game theory, a novel method of assigning different dominance levels to users is proposed hereby, and a threshold criterion is discussed to judge the reliability of user decoding. Inspired by this, users with reliable decoding in the iterative process will be dynamically eliminated in each iteration. The numerical analysis revealed that the new TB-RMPA detector’s implementation complexity decreases significantly compared with SMPA, while the symbol error ratio performance degrades unnoticeably.

1. Introduction

Communication resources have become scarce treasures due to the unprecedented expansion of access users. Multiple access technology is regarded as a critical technology to circumvent the problem. However, orthogonal multiple access technology (OMA) normally cannot meet the requirements of massive connection, ultra-high data transmission rate, and low latency for future mobile communications. A new multiple access technology, namely non-orthogonal multiple access (NOMA), has been developed for providing high spectrum utilization and massive connections [1,2]. By overlapping user data information to increase the system capacity, NOMA supports the non-orthogonal transmission of signals, albeit with increasing the computational complexity.

Sparse Code Multiple Access (SCMA) is an emerging NOMA technology based on multidimensional codebooks that is theoretically derived from low-density signature code division multiple access (LDS-CDMA) [3,4,5]. CDMA applies spread spectrum technology and distinguishes different users by assigning different code sequences. The transmitter in the CDMA system performs quadrature amplitude modulation (QAM) on the bit data stream after forwarding error correction. Thereafter, the wide-bandwidth spreading sequence generated by the spreading sequence generator will spread the modulated signal. After adding the inverse fast Fourier transform (IFFT), the user information is superimposed and sent through the channel. SCMA integrates the QAM modulator and the spread spectrum part of the LDS-CDMA system at the transmitting end, directly mapping the incoming bits to the complex multidimensional codeword after channel coding. Different users hold dedicated codebooks, and the spreading coding part selects a codeword from each codebook for transmission according to user data.

For SCMA, the received signal is a mixed superposition of codewords of each user, and there is a certain degree of interference among different users. Ordinary orthogonal separation methods cannot distinguish user information, and joint multi-user detection is required for data separation. The key challenges for multi-user detection (MUD) are serious multiple access interference and considerable processing complexity. To tackle this, sophisticated methods have been designed to save computing resources [6,7,8]. An improved MUD scheme is advocated by employing maximum joint posterior probability (MAP) detection and over-searching. However, this algorithm incurs significant additional complexity. By leveraging the sparse structure, theoretically, SCMA can obtain multi-user detection with close to maximum likelihood (ML) performance by utilizing a less complex message-passing algorithm (MPA) detector.

Multiple compelling decoders modified from MPA have been proposed to approximate the optimal performance [9,10,11]. Unfortunately, the detection complexity of traditional MPA grows exponentially as the the number of access devices grows. Hence, some plausible approaches are developed to simplify the MPA calculation. By removing all exponential operations, MAX-Log-MPA and Log-MPA have reasonably low complexity, albeit with slightly sacrificed performance [12,13,14]. In [15], MPA and the compressed sensing (CS) technique are combined, and a compressive sampling matching algorithm is introduced to correct the error code. Additionally, refs. [16,17] reclassify the information transmitted in factor graphs as strong edges and interference. The unselected edges are processed by Gaussian approximation (ESGA). In reference [18], a modified ESGA scheme is proposed, and a threshold selection method is introduced to define a strong neighbor edge group. The method devised in [19] adopts the expectation propagation algorithm (EPA) in a massive MU-MIMO SCMA system. QR decomposition and decentralized function nodes are employed to improve the performance. Codebook optimization methods are also applied to reduce the complexity by utilizing different codebook structures and design approaches [20,21,22,23]. Moreover, a partial marginalization (PM) MPA algorithm is investigated to further simplify the iterative processing [24]. However, the parallel technique is ineffective in terms of convergence rate. To address this issue, shuffled MPA (SMPA), a novel multi-user detection approach for uplink SCMA systems that employs a dissimilar message update method, has been developed [25].

Specifically, the essence of the MPA algorithm is to utilize the iterative update of the information between the factor nodes to obtain the optimal solution. Unfortunately, reducing the algorithm’s computing complexity remains a challenging task due to the iterative process’s intricacy. Recent studies demonstrate that game theory is capable of studying the act of association and interaction of different autonomous nodes thanks to its excellent processing and optimization capabilities for mathematical problems [26,27]. In recent years, game theory models have been widely used as an analysis tool to circumvent problems such as congestion control, power control, decoding, and algorithm optimization [28,29,30,31]. In the game process, participants always hope to continuously eliminate inferior strategies, and they finally obtain a dominant strategy to maximize their own benefits, which is the definition of Iterative Elimination of Dominated Strategies (IEDS). From the game theory perspective, each iteration process in the MPA algorithm can be regarded as a game, and each user can be regarded as a strategy in the game.

Inspired by [25], we amalgamate IEDS in game theory with an SMPA detection scheme to conceive a low-complexity MUD for uplink SCMA. Specifically, we develop a novel threshold-based SCMA detection scheme with a dynamical user removal algorithm (TB-RMPA). We provide substantial analysis and numerical simulations to study the decoding performance of the proposed algorithm. The main contributions of this paper are summarized as follows.

• An improved low-complexity MPA receiver for SCMA is proposed. This scheme, of sequential nature, was further generalized to the SMPA scheme imposing a threshold-based criterion for dynamically weeding out users.
• An advantage user-ranking method is introduced based on the factor graph, and users are sorted in descending order before searching so that reliable nodes can be pruned in subsequent iterations. Additionally, we combine the idea of repeatedly eliminating disadvantages in game theory with the iterative serial message algorithm, and we treat every user whose information has been reliably decoded as a strict inferior strategy that can be eliminated.
• The threshold is set to determine the reliability and stability of the signal. In the iterative process, the current optimal user will be judged in each iteration. Once the threshold condition is met, the current optimal user will be deleted. Meanwhile, we use the parameter $\beta$ to balance the system error performance and complexity.

The remainder of this paper is structured as follows. We first elaborate on the system model of SCMA in Section 2. Furthermore, the original MPA detection algorithm and SMPA scheme are presented. In Section 3, we put forward the concept of superior users, and the proposed TB-RMPA scheme is presented. The decoding complexity and performance comparison are discussed in Section 4. Finally, our conclusions are provided in Section 5.

The notations in this paper are as follows. The uppercase boldface letter $\mathbf{X}$ stands for matrices, the lowercase boldface letter $\mathbf{x}$ denotes vectors, and normal letters are scalar quantities. $\left|x\right|$ denotes the absolute value of scalar x. The n-th unit of the vector $\mathbf{x}$ is expressed as ${\mathbf{x}}_{\mathbf{n}}$. ${\mathbf{x}}^T$ denotes the transpose of $\mathbf{x}$.

Especially, the abbreviations employed in this paper are illustrated in Table 1 for ease of access.

Table 1. Summary of abbreviations.

Acronyms	Full Form	Acronyms	Full Form
MPA	Message-Passing Algorithm	IEDS	Iterative Elimination of Dominated Strategies
SER	Symbol Error Ratio	NOMA	Non-Orthogonal Multiple Access
OMA	Orthogonal Multiple Access	LDS-CDMA	Low-Density Signature Code Division Multiple Access
QAM	Quadrature Amplitude Modulation	MUD	Multi-User Detection
MAP	Maximum Joint Posterior Probability	ML	Maximum Likelihood
CS	Compressed Sensing	EPA	Expectation Propagation Algorithm
SMPA	Shuffled MPA	PM	Partial Marginalization
FN	Function Nodes	VN	Variable Nodes
ES-MPA	Edge Selected MPA	DMPA	Discretized MPA
LOS	Line-of-Sigh	LDPC	Low-Density Parity Check Code

2. System Model

2.1. Principle of SCMA

In the SCMA system, J and K denote the number of access users and physical resources orthogonal to each other, respectively. In a non-orthogonal system, the channel can be overloaded, and the number of J is usually greater than K. The overloading factor is defined as the ratio of users to physical resources. Table 2 presents the definitions and key points of the parameters in the uplink SCMA system [32,33].

Table 2. The parameters in the uplink SCMA system.

Parameter	Definition	Remarks
K	Number of resources	Orthogonal to each other
J	Number of users	Transformed on the resources simultaneously
$\lambda$	Overloading factor, $\lambda =J/K$	Show the overload performance of the system
M	Size of codebook	Data rate is proportional to ${log}_{2}M$
N	Amount of resource occupied by a user	Diversity is proportional to N
$d_f$	Collision degree, amount of the neighbors on a resource. $d_f=\lambda \times N$	MPA complexity order increases exponentially with $d_f$

Figure 1 illustrated an uplink SCMA system. The initial information bits are coded into ${\mathbf{b}}_j={[{\mathbf{b}}_1,{\mathbf{b}}_2,...,{\mathbf{b}}_J]}^T$ in the channel encoding section by utilizing a Low-Density Parity Check Code (LDPC) represented by a check matrix ${\mathbf{H}}_{\mathbf{C}}$ [34]. Thereafter, the system users select corresponding codewords from the codebook at the transmitter, and the coded bitstreams ${\mathbf{b}}_j$ are directly mapped to the K-dimensional plural codewords ${\mathbf{x}}_j$. The K-dimensional codewords comprise N non-zero elements, and each codebook contains M codewords. The mapped codeword will be superimposed and sent on each physical resource. The mapping relationship can be expressed as $f:B^{{log}_{2}M}\to \chi$, for user j, where $\chi \in C^K$.

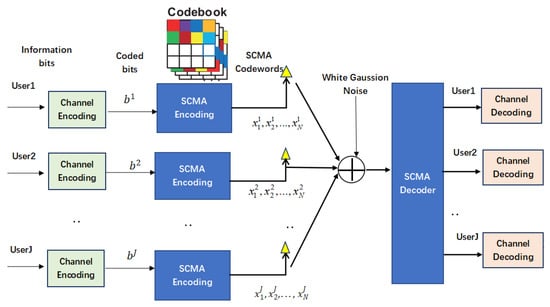
Figure 1. SCMA multiplexing scheme.

The transmitted signal at the receiver can be expressed as

$$\mathbf{y}={\sum }_{j=1}^{J}diag\left({\mathbf{h}}_j\right){\mathbf{x}}_j+\mathbf{n},$$

(1)

where ${\mathbf{x}}_j={[{\mathbf{x}}_1,{\mathbf{x}}_2,...,{\mathbf{x}}_J]}^T$ represents the SCMA codeword sent by the j-th user, and ${\mathbf{h}}_j={[{\mathbf{h}}_1,{\mathbf{h}}_2,...,{\mathbf{h}}_J]}^T$ stands for the channel coefficient vector between the base station and user j. In this paper, the channels are modeled as an independent Rayleigh channel and Rician channel. $\mathbf{n}$ is the white noise vector, which obeys the Gaussian distribution of $CN\left(0,{\sigma }^{2}I\right)$. ${\sigma }^2$ indicates the variance of each element of $\mathbf{n}$, and $\mathbf{I}$ is the identity matrix. The factor graph matrix $\mathbf{F}$ reflects the user’s usage of transmission resources. The total number of “1” in each row and column of $\mathbf{F}$ are denoted by $d_f=\left(d_{f1},...,d_{fK}\right)$ and $d_v=\left(d_{v1},...,d_{fJ}\right)$, respectively. The received signal is subjected to multi-user detection in the SCMA decoder, and the detected LDPC signal is decoded by a belief propogation algorithm [35].

2.2. Original MPA Multi-User Detection for Uplink SCMA

Assuming that the receiving signal $\mathbf{y}$ and the user channel gain ${\mathbf{h}}_j$ are all known conditions, we can use the MAP algorithm to detect the user’s codeword combination. The joint optimal MAP detection will estimate the joint posterior probability function that maximizes the transmitted symbols, which can be expressed as

$$\widehat{\mathbf{X}}=\underset{\mathbf{X}\in \left\{{\mathbf{X}}_{j=1}^J\right\}{\chi }_j}{argmax}P\left(\mathbf{X}|\mathbf{y}\right).$$

(2)

Although MAP is the optimal multi-user detection algorithm, its complexity is too high. Therefore, MPA, a message-passing algorithm with close performance but low computational complexity, has become the focus of research in the industry at this stage. MPA uses the idea of iteration based on bipartite factor graph modeling. Function nodes (FNs) and variable nodes (VNs) represent the transmission layers and users, respectively [36]. Iteration is repeated feedback, and the result obtained each time will become the initial value of the next iteration. The MPA algorithm obtains a performance close to the maximum likelihood through continuous iterative updates of the information transmitted between the nodes. When the number of iterations meets the maximum number of iterations set initially, the user codeword is judged and output. The following optimal detection criterion is admitted.

$${\widehat{\mathbf{x}}}_j=\underset{a\in \chi }{argmax}{\sum }_{\left\{{\mathbf{x}}_j\right\}\in {\chi }^J}p\left({\mathbf{x}}_1,...,{\mathbf{x}}_J|\mathbf{y}\right),$$

(3)

$${\widehat{\mathbf{x}}}_j=\underset{a\in \chi }{argmax}{\sum }_{\left\{{\mathbf{x}}_j\right\}\in {\chi }^J}{\prod }_{k\in R\left(j\right)}p\left({\mathbf{y}}_k|{\mathbf{x}}_l,l\in N\left(K\right)\right).$$

(4)

The posterior probabilities are calculable with the factor graph known. For ease of notation, we define $M_{V_j\to F_k}^t$ as the probability that user node $V_j$ transfers codeword information to resource node $F_k$ during the t-th iteration. $M_{F_k\to V_j}^t$ denotes the probability that resource node $F_k$ transfers codeword information to user node $V_j$ during the t-th iteration, and t represents the number of the current iteration. The update of information is divided into two steps. (1) Resource nodes use external information from user nodes to update information. (2) User nodes use external information from resource nodes to update information [37,38]. The two processes are expressed by mathematical formulas as

$$\begin{array}{cc}\hfill M_{F_K\to V_j}^t\left({\mathbf{x}}_j\right)=& \sum \left\{exp\left(-\frac{1}{2{\sigma }^2}\Vert {\mathbf{y}}_k-{\sum }_{j\in {\xi }_k}{\mathbf{h}}_{k,j}{\mathbf{x}}_{k,j}{\Vert }^2\right)\right.\hfill \\ \hfill & \left.\times {\prod }_{l\in {\xi }_k/\left[j\right]}{M}_{V_l\to F_k}^{t-1}\left({\mathbf{x}}_j\right)\right\},\hfill \end{array}$$

(5)

$$M_{V_j\to F_k}^t\left({\mathbf{x}}_j\right)={\prod }_{m\in {\xi }_j/\left[k\right]}{M}_{F_m\to V_j}^t\left({\mathbf{x}}_j\right),$$

(6)

where ${\xi }_k/\left[j\right]$ represents all elements in ${\xi }_k$ except j, and ${\xi }_j/\left[k\right]$ represents all elements in ${\xi }_j$ except k. The algorithm will continue to repeat the two steps of the iterative process until the maximum number of iteration is reached and then execute the decision output. A posterior probability for the corresponding codeword can be represented as

$$Pr\left({\mathbf{x}}_j\right)=\frac{1}{M}{\prod }_{k\in R\left(j\right)}{M}_{F_K\to V_j}^T\left({\mathbf{x}}_j\right).$$

(7)

The binary log-likelihood ratios (LLRs) to decide the ${log}_{2}M$ bits are

$$\mathrm{LLR}\left({\mathbf{b}}_j\right)=log\frac{{\sum }_{\left\{{\mathbf{x}}_j\in \chi |{\mathbf{b}}_i=0\right\}}Pr\left({\mathbf{x}}_j\right)}{{\sum }_{\left\{{\mathbf{x}}_j\in \chi |{\mathbf{b}}_i=1\right\}}Pr\left({\mathbf{x}}_j\right)}.$$

(8)

2.3. SMPA Multi-User Detection Scheme

In the traditional MPA algorithm, the new messages generated in the current iteration will not be used until the next iteration. The SMPA algorithm does not update the function node and the variable node sequentially. It updates a function node and then updates the related variable node, so that the function node information updated in the current iteration can be used for other function node updates in the same round [25]. Different from the traditional MPA algorithm, the update of the variable node in the SMPA algorithm is immediately after the update of each function node. The update of information iteration in the SMPA algorithm can be modified as

$$\begin{array}{cc}\hfill M_{F_K\to V_j}^t\left({\mathbf{x}}_j\right)=& \sum \left\{exp\left(-\frac{1}{2{\sigma }^2}\Vert {\mathbf{y}}_k-{\sum }_{j\in {\xi }_k}{\mathbf{h}}_{k,j}{\mathbf{x}}_{k,j}{\Vert }^2\right)\right.\hfill \\ \hfill & \left.\times {\prod }_{l\in {\xi }_k/\left[j\right]}^{l<j}{M}_{V_l\to F_k}^t\left({\mathbf{x}}_j\right){\prod }_{l\in {\xi }_k/\left[j\right]}^{l>j}{M}_{V_l\to F_k}^{t-1}\left({\mathbf{x}}_j\right)\right\},\hfill \end{array}$$

(9)

$$M_{V_j\to F_k}^t\left({\mathbf{x}}_j\right)={\prod }_{m\in {\xi }_j/\left[k\right]}{M}_{F_m\to V_j}^t\left({\mathbf{x}}_j\right).$$

(10)

It can be seen from Equation (9) that the message of the variable node updated in this round of iteration has been used when some function nodes are updated in this round of iterations. Obviously, the updated variable node messages in this round are more reliable than the previous round variable node messages; that is, the message propagation in the SMPA algorithm is more timely, which makes the convergence speed faster.

In order to further simplify the complexity of the algorithm, we give priority to preprocessing the algorithm by moving the iterative process into the logarithmic domain, which follows the Jacobian logarithm formula.

$$log\left(exp\left({\mathbf{x}}_1\right)+...+exp\left({\mathbf{x}}_n\right)\right)\approx max\left({\mathbf{x}}_1,...,{\mathbf{x}}_n\right).$$

(11)

Equations (9) and (10) are applied in log-domain as

$$\begin{array}{cc}\hfill M_{F_K\to V_j}^t\left({\mathbf{x}}_j\right)=& max\left\{-\frac{1}{2{\sigma }^2}\Vert {\mathbf{y}}_k-{\sum }_{j\in {\xi }_k}{\mathbf{h}}_{k,j}{\mathbf{x}}_{k,j}{\Vert }^2\right.\hfill \\ \hfill & \left.+{\sum }_{l\in {\xi }_k/\left[j\right]}^{l<j}{M}_{V_l\to F_k}^t\left({\mathbf{x}}_j\right)+{\sum }_{l\in {\xi }_k/\left[j\right]}^{l>j}{M}_{V_l\to F_k}^{t-1}\left({\mathbf{x}}_j\right)\right\},\hfill \end{array}$$

(12)

$$M_{V_j\to F_k}^t\left({\mathbf{x}}_j\right)={\sum }_{m\in {\xi }_j/\left[k\right]}{M}_{F_m\to V_j}^t\left({\mathbf{x}}_j\right).$$

(13)

3. Proposed Detection Schemes for UPLINK SCMA

The traditional MPA algorithm and the S-MPA algorithm both detect the user signals uniformly after the algorithm is executed to the maximum number of iterations, and each user will participate in the process of each iteration, so the execution complexity of the algorithm is very high. In this section, we propose a new low-complexity decoder based on confidence stability and dynamic user culling, called TB-RMPA, to reach equilibrium between error rate performance and complexity.

3.1. Iterative Elimination of Dominated Strategies

In game theory, the ideal goal is to obtain the maximum benefit at the minimum cost [26,27]. Participants in each game are independent decision-makers, and their benefits depend on the actions of other participants. Convergence of the game to a steady state is the Nash equilibrium. The usual way to identify a game Nash equilibrium is to do an exhaustive search, but this is very complicated, and we hope to reduce the search process as much as possible.

There is a definition of a disadvantageous strategy in game theory, where it shows that participants can always recognize bad strategies based on rational assumptions, and these strategies definitely can be avoided. If $u_i\left(b_i,a_{-i}\right)\ge u_i\left(a_i,a_{-i}\right)$ holds for all $a_{-i}\in A_{-i}$, and for a certain $b_{-i}\in A_{-i}$, $u_i\left(b_i,b_{-i}\right)>u_i\left(a_i,b_{-i}\right)$, then the strategy $a_i$ is inferior to $b_i$.

If all participants actually understand the strict bad strategies that every participant will not adopt, then they can effectively ignore the strict bad strategies that their opponents will not adopt. If the initial game has some players with strict inferior strategies, then all the players know that they are facing a small-scale restricted game because the number of total strategies is reduced.

We introduce this idea into the decoding algorithm to further reduce the algorithm complexity. Each iteration process can be regarded as a game, and each user can be regarded as a strategy in the game. When the user’s decoding reaches the optimal level, it becomes an inferior strategy that can be eliminated in the restricted game. After removing the strictly inferior strategy, the new game will not include the strictly inferior strategy that has been removed.

Inspired by this, we can continuously detect and eliminate users with reliable decoding in the iterative process. At this time, we need to deal with two new key issues: first, how to define the user’s decoding reliability to ensure that the elimination of users will not increase the bit error rate and reduce the system performance; second, whether the sequence of multi-user elimination has an impact on the system performance and complexity. Moreover, we also need to determine a good elimination strategy.

3.2. User Ranking

In the traditional parallel message passing algorithm, each VN node is an independent unit. During the iterative update, each VN node searches for the FN node connected to it in the factor graph to update the message. Take the SCMA system whose factor matrix is Equation (14) as an example. Among them, the rows of the sparse matrix represent the number of physical resources, and the columns of the matrix represent the number of users. The content of the matrix contains two elements: ‘0’ and ‘1’; ‘0’ means that the user does not occupy this physical resource, and ‘1’ means that user data occupies this orthogonal resource for transmission.

$${\mathbf{F}}_{4,6}=\left\{\begin{array}{cccccc}0& 1& 1& 0& 1& 0\\ 1& 0& 1& 0& 0& 1\\ 0& 1& 0& 1& 0& 1\\ 1& 0& 0& 1& 1& 0\end{array}\right\}.$$

(14)

Figure 2 shows the information iteration update factor graph structure of the traditional parallel message passing algorithm. The user node VN1 uses the resource nodes FN2 and FN4 connected to it to update information, and then, the new VN1 is used as external information to update the information values of FN2 and FN4. According to this rule, each iteration will be updated in the order of the user nodes. The information value of FN will not be calculated until all the messages from FN to VN have been propagated, so that the external information of FN that can be used in time is not fully utilized.

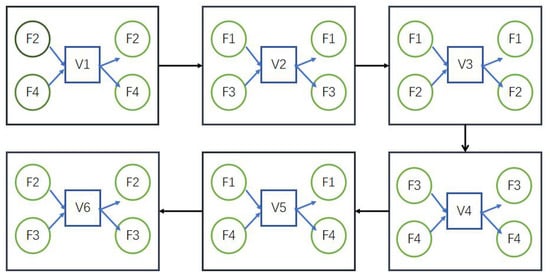
Figure 2. Information iteration update factor graph structure of traditional parallel message passing algorithm for an SCMA system with $J=6$, $K=4$.

Figure 3 displays the information iteration update factor graph structure of the serial message passing algorithm. In an iteration process, we can use the updated VN1 information value as external information to indirectly update VN4 and then use the updated information from VN4 to indirectly update VN2. Once the order of VN nodes is reasonably chosen, an update to the current user node can be synchronously transmitted to other user nodes, so that users can receive more external information and converge faster.

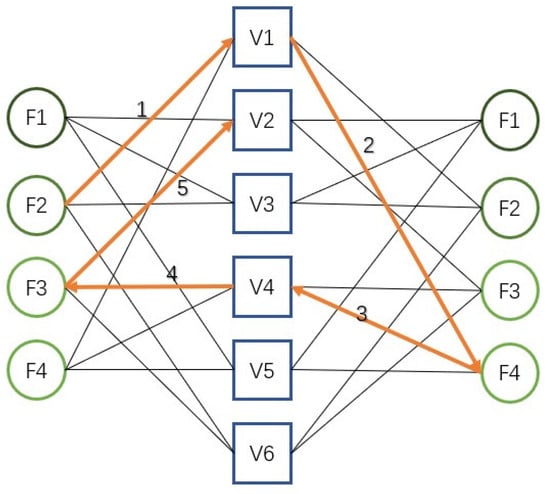
Figure 3. Information iteration update factor graph structure of the serial message passing algorithm.

In the iterative process, the convergence speed of different user nodes is different. The nodes that converge slowly need more iterations to get a sufficiently reliable decoding. We reasonably choose the order of the VN nodes and sort the user nodes; then, the convergent nodes can be eliminated from the original factor graph, effectively reducing the complexity of the algorithm.

In the process of iterative update of information, the more external information a user iteratively generates, the more reliable his decoding is after this iteration. In other words, this user enjoys a high level of advantage. Since the threshold condition is met, the effect of eliminating the user in the next iteration process on the signal decoding recovery will become minor.

According to the order in which the time-frequency resources are processed, we can assign different initial coefficients $a_k$ to the time-frequency resources. Information decoding on post-processing physical resources is more reliable. Under this principle, for the SCMA system with J = 6 and K = 4, the coefficient of the time-frequency resource can be set to $a_k=1,2,...,6$. User ranking level $r_j$ can be jointly expressed by sparse matrix $f_{kj}$ and resource coefficient $a_k$.

$$r_j=\sum a_k\times f_{kj}.$$

(15)

For the SCMA system whose sparse matrix is Formula (15), the order of the dominant users is

$$u_4>u_1>u_6=u_5>u_2>u_3.$$

(16)

3.3. Confidence Stability Based on a Threshold

The algorithm dynamically removes users based on the confidence stability judgment. In each iteration process, the current user with the highest level is judged. We develop a residual-based threshold criterion, which includes two parts: initial threshold and parameter $\beta$. The threshold is initially set to one-twentieth of the updated information in this iteration, and the final criterion is adjusted by parameter $\beta$. If the user satisfies Formula (17), the user signal judgment is determined to be sufficiently reliable. The user will be eliminated from the next iteration, and the eliminated user will no longer participate in subsequent iterations processes.

$$\left(sqrt{\sum }_{m=1}^M{\left(I_{k\to j}^t\left({\mathbf{x}}_{jm}\right)-I_{k\to j}^{t-1}\left({\mathbf{x}}_{jm}\right)\right)}^2\right)\le \beta \times threshold.$$

(17)

where $threshold{\displaystyle =0.05\times \sum _{m=1}^M}{I}_{k\to j}^{t-1}\left({\mathbf{x}}_{jm}\right)$ and coefficient $\beta$ have a value range of (0, 1) .

3.4. TB-RMPA Multiuser Detection Scheme

To address the problem of excessive complexity of the algorithm, we transfer the SMPA algorithm to the logarithmic domain initially and apply the above-mentioned advantageous user dynamic elimination strategy to this algorithm, which is named the TB-RMPA algorithm. Equations (12) and (13) are modified to

$$\begin{array}{cc}\hfill M_{F_K\to V_j}^t\left({\mathbf{x}}_j\right)=& max\left\{-\frac{1}{2{\sigma }^2}\Vert {\mathbf{y}}_k-{\sum }_{j\in {\xi }_k}{\mathbf{h}}_{k,j}{\mathbf{x}}_{k,j}{\Vert }^2\right.\hfill \\ \hfill & \left.+{\sum }_{l\in {\xi }_k/\left[j\right]/\left[j_s\right]}^{l<j}{M}_{V_l\to F_k}^t\left({\mathbf{x}}_j\right)+{\sum }_{l\in {\xi }_k/\left[j\right]/\left[j_s\right]}^{l>j}{M}_{V_l\to F_k}^{t-1}\left({\mathbf{x}}_j\right)\right\},\hfill \end{array}$$

(18)

$$M_{V_j\to F_k}^t\left({\mathbf{x}}_j\right)={\sum }_{m\in {\xi }_j/\left[k\right]/\left[j_s\right]}{M}_{F_m\to V_j}^t\left({\mathbf{x}}_j\right).$$

(19)

The value of the coefficient $\beta$ will affect the overall result of the threshold, which determines the range of signal reliability judgment. We can find the best parameter $\beta$ suitable for the current system through a dynamically selected procedure. Initialize $\beta$ = 1; in this case, the complexity of the system is the lowest. Set an appropriate step size S and target SER to simulate a system over a fixed signal-to-noise ratio. If the simulation performance fails to reach the target, reduce the value of $\beta$ by the step size and repeat the above process until the simulation results meet the expected requirements. If the $\beta$ value is reduced to 0 and SER is still greater than the target, it means that the current signal-to-noise ratio is not suitable. Repeat the process after increasing the signal-to-noise ratio appropriately.

If before the arrival of the maximum number of iterations $t_{max}$, then all users have been decoded and eliminated, indicating that the algorithm does not require so many iterations. If the operation reaches the maximum number of iterations $t_{max}$, then all remaining undecoded users will be decoded uniformly. It is foreseeable that the more users are eliminated after each iteration, the lower the overall complexity of the decoding algorithm. When $\beta$ = 0, the proposed TB-RMPA scheme is the original serial logSMPA scheme. According to this idea, users are dynamically identified in iterations, and factor graphs are deleted.

Table 3 illustrates the key notations and descriptions of the TB-RMPA algorithm while Algorithm 1 demonstrates the detailed procedure including threshold selection and user dynamic elimination.

Algorithm 1 TB-RMPA

Input:$\mathbf{y}$,$\mathbf{CB}$,$\mathbf{H}$,${\mathrm{t}}_{max}$,$N0$, S

Output:$Q\left({\mathbf{x}}_j\right)$

1: Preliminary THRESHOLD SELECTION 2: Initialization $\beta =1$, S , $SE{R}^0$ 3: while $SER>SE{R}^0$do 4:   $\beta =\beta -S$ 5:   Run a SER simulation of TB-RMPA with fixed $Eb/N0$ 6:   if $beta=0$ and $SER>SE{R}^0$ then 7:    Declare failure. Eb/N0 needs to be raised. 8:   end if 9: end while 10: Return $\beta$ 11: for all$k=1,\dots ,K$ and $j=1,\dots ,J$ do 12:   $M_{V_j\to F_k}^0\left({\mathbf{x}}_j\right)=\frac{1}{M}$ for all ${\mathbf{x}}_j\in {\chi }_j$ 13: end for 14: Generate user ranking using (8) 15: while $t<t_{max}$ do 16:   for all $k\in {\xi }_j$ do 17:    Generate and propagate $M_{F_k\to V_j}^t\left({\mathbf{x}}_j\right)$ using (18) 18:   end for 19:   for all $j\in {\xi }_k$ do 20:    Generate and propagate $M_{V_j\to F_k}^t\left({\mathbf{x}}_j\right)$ using (19) 21:   end for 22:   if $U>0$ then 23:    Determine whether the current best user meets the conditions using (9) 24:    Elimate the user if the answer is yes 25:   end if 26:   $t=t+1$ 27: end while 28: Calculate the LLR of each Bit 29: for alljdo 30:   $Q\left({\mathbf{x}}_j\right){\displaystyle =\prod _{k\in {\xi }_j}}{M}_{F_k\to V_j}^{t_{max}}\left({\mathbf{x}}_j\right)$ 31: end for 32: return$Q\left({\mathbf{x}}_j\right)$

Table 3. The notation list of the TB-RMPA algorithm.

Notations	Description	Notations	Description
$\mathbf{y}$	Received signal	$t_{max}$	The maximum number of iterations
$\beta$	Current threshold	S	The dynamic adjustment step size of $\beta$
J	Number of system users	U	Number of remaining users

For the SCMA system in the previous example with $\beta$ = 0.4, the number of eliminated users is 3 after T iterations. User nodes VN4, VN1, and VN6 are judged to be trusted nodes, and the factor graph is updated as shown in Figure 4.

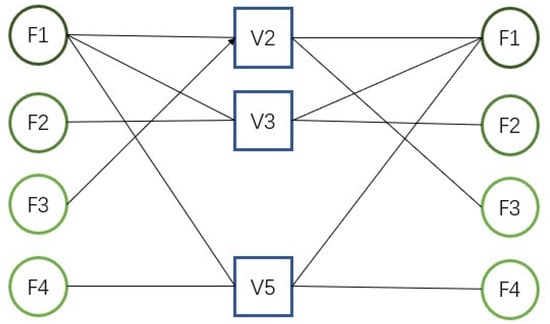
Figure 4. Updated factor graph structure using TB-RMPA.

3.5. Computational Complexity Analysis

In this subsection, the computational complexities of TB-RMPA are analyzed in detail. SMPA, log-SMPA, edge-selected MPA (ES-MPA) [17], and discretized message passing algorithm (DMPA) [39] are also compared as baselines. The detailed calculation complexity comparison of different detection schemes is shown in Table 4, where the symbol set size for each user is M, the number of physical resources is K, the user number is J, and the maximum iteration number is T. $d_f$ and $d_v$ denote the amount of users hosted by a physical resource and amount of resources occupied by a user. S stands for the number of users that have been eliminated until this iteration. Since the proposed TB-RMPA scheme eliminates users in the iterative process, it is obvious that the number of real-time users and the $d_f$ values corresponding to different resources in FN-to-VN are dynamically changing during each iteration. The proposed scheme can immediately add message propagation in the current iteration and timely eliminate user signals whose decoding is sufficiently reliable to speed up the convergence speed. Therefore, the overall computational complexity can be greatly reduced.

Table 4. Simulation scenarios with fixed parameters.

	Addition	Multiplication	Exponentiation
SMPA	$\begin{array}{c}TK{d}_f\left\{M^{df}(1+d_f)\right\}-TK{d}_{f}M\hfill \end{array}$	$\begin{array}{c}TM{d}_{v}J(d_v-2)\hfill \\ +TK{d}_f{M}^{df}(1+2d_f)\hfill \end{array}$	$TK{d}_f{M}^{d_f}$
LOG-SMPA	$TK{d}_f+2KT{d}_{f}M+TK{d}_f\left\{M^{df}\left(2df-1\right)\right\}$	$TK{M}^{df}d{f}^2$	0
ES-MPA	$TK{d}_f\left\{M^{d_s+1}(3+d_s)\right\}+TK{d}_f(d_f-d_s-2)-KT{d}_{f}M$	$TK{d}_f{M}^{d_s+1}(3+2d_s)+TK{d}_f(d_f-d_s-1)+TK{d}_{v}M(d_v-2)$	$TK{d}_f{M}^{d_v+1}$
DMPA	$J{d}_v(M-1)(T-1)+J(2M-1)+2T{d}_{f}K(M+2N^2{log}_{2}N)$	$TK{d}_f{N}^2\times (2{log}_{2}N+d_f-2)+MJ{d}_v(\left(T-1\right)\left(d_v-2\right)+1)$	0
TB-RMPA	$\begin{array}{c}{M}^{d_f}K\left\{{\displaystyle \sum _{t=1}^T}\left(d_f\left(d_f-1\right)\right.\right.\left.\left.-d_{v}S\right)+d_f\right\}\\ +M{d}_{v}J+{\displaystyle \sum _{t=1}^T}\left(J-S\right)M\left(d_v-1\right)+\\ {\displaystyle \sum _{t=1}^T}M\left\{d_f\left(K+1\right)-d_{v}S\right\}\end{array}$	$TK\times M^{df}d{f}^2$	0

4. Simulations

In this section, numerical simulations are presented to validate the analytical results as well as the proposed TB-RMPA scheme. In order to investigate the proposed scheme under different configurations, the computational complexity, SER, and the convergence performances are taken into consideration. In the SCMA system, the number of transmitted stream is J = 6, and the number of resources is K = 4. The channel coding adopts LDPC codes with rate $R=0.5$ and length $n=128$. In all simulations, the coded two-dimensional data flow of each user is modulated by a group of four-dimensional complex constellation points, and the channel settings are modeled as independent Rayleigh channel and Rician channel [40].

Figure 5 depicts the computational complexity comparison of the detection schemes with six iterations. To facilitate observation, we have normalized the mathematical operations of the complexity derived in Table 4. Addition is normalized by a ratio of one to one, while multiplication and comparison are normalized by a ratio of one to ten and one to twenty, respectively. Here, we set $\beta$ = 0.2, 0.5, and 0.8 in the TB-RMPA algorithm.

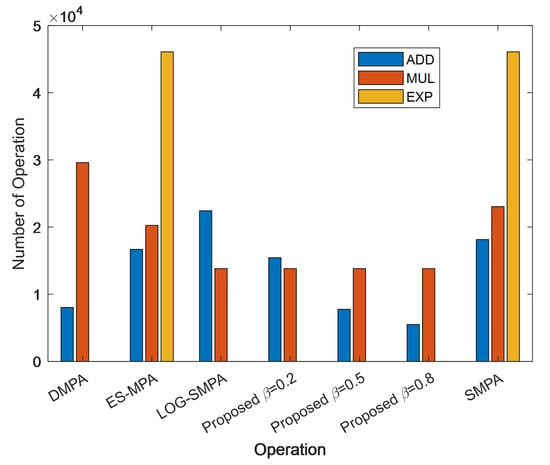
Figure 5. Complexity comparison of different detection schemes.

As shown, the proposed TB-RMPA has significantly lower computational complexity than the SMPA, Log-SMPA, DMPA, and ES-MPA algorithms. After the iterative user elimination scheme is applied, the TB-RMPA algorithm can save varying degrees of the computational complexity (with different $\beta$ apllied) compared to that of the Log-SMPA receiver. This result demonstrates the superiority of the proposed TB-RMPA scheme.

In Figure 6, we present the result of numerical evaluation complexity of the proposed TB-RMPA for the scenarios in Table 5. From the complexity order prediction above, the value of $\beta$ can be chosen to reduce the average complexity with respect to TB-RMPA. It is inspired that the larger the value of $\beta$ is, the greater complexity reduction ratio can be achieved, which is meaningful for high-efficiency transmission.

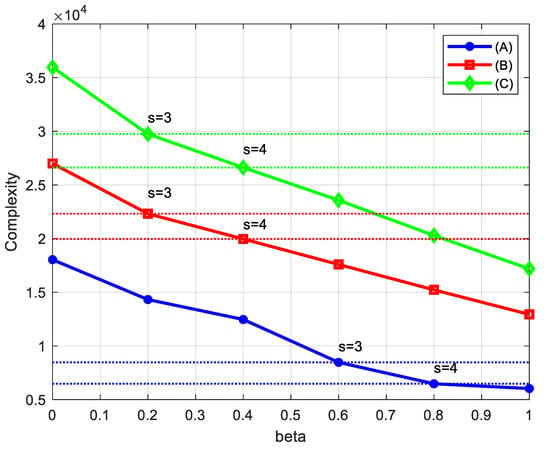
Figure 6. Complexity of proposed TB-RMPA scheme for scenarios in Table 5. Markers stand for the results of excluded users s = 3 and s = 4 in numerical simulation.

Table 5. Parameters of different simulation scenarios.

Scenario	(J,K)	$\mathit{df}$	$\mathit{\lambda }$
(A)	(6,4)	3	$150\%$
(B)	(9,6)	3	$150\%$
(C)	(12,6)	4	$200\%$

To evaluate the convergence performance of the TB-RMPA detector more intuitively, we demonstrate the SER vs. SNRs at different numbers of outer loop iterations in Figure 7. In our simulation, the basic parameters are set as follows: the number of users is J = 6, the number of subcarriers is $K=4$, the degrees of the factor graph are $df$ = 3 and $dv$ = 2, and the threshold is $\beta$ = 0.5. As shown, the performance of the receivers improves as iterations increase. After several iterations, the performance gains become marginal. It can be seen that the proposed scheme converges after four outer iterations. The BER curves of the algorithm suffer only negligible BER performance degradation and almost coincide with the optimal curve. Similar results can be obtained for other scenarios, which demonstrate the good convergence of the TB-RMPA receiver.

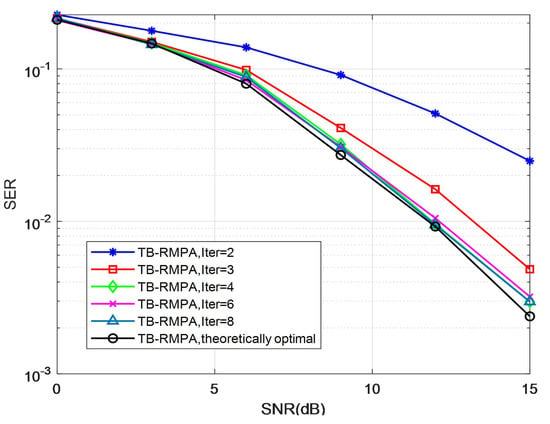
Figure 7. Convergence performance of TB-RMPA with $\beta$ = 0.5 in the Rayleigh channel.

Figure 8 compares the SER performance versus SNR for the proposed TB-RMPA, SMPA, classic MPA, ES-MPA, and PM-MPA schemes on the Rayleigh channel, respectively. The TB-RMPA decoder has nearly the same SER as the SMPA method, which has a nearly 3 dB performance loss compared to the classic MPA method when iteration = 3. This can be explained that a sufficient number of users cannot be eliminated and the decoding is not reliable enough due to the insufficient iteration of information. The figure illustrates that the proposed scheme has about 3 dB gain over PM-MPA (iteration = 6) and suffers only negligible BER performance degradation compared with the SMPA schemes at SNR = 15. It can be explained that the proposed TB-RMPA can utilize more effective messages to achieve convergence. Compared with other detection algorithms, TB-RMPA achieves similar bit error performance while maintaining low complexity.

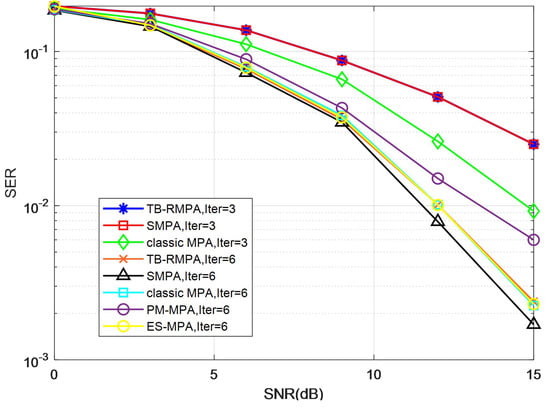
Figure 8. SER performance comparison of different detection schemes in the Rayleigh channel.

Figure 9 illustrates the SER performance of the proposed TB-RMPA decoder for various numbers of $\beta$ on the Rayleigh channel. It demonstrates that there is a slight performance loss when beta changes. Hence, a comprehensive consideration is supposed to be made between the computational complexity and system performance. Furthermore, the threshold $\beta$ must be revised for different scenarios. Applying the proper threshold to the algorithm allows the system to achieve the desired performance at the lowest accomplishable complexity.

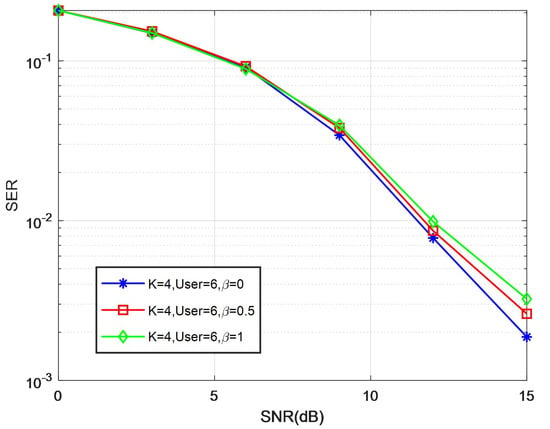
Figure 9. SER performance comparison of different $\beta$ on the Rayleigh channel.

To illustrate the superior performance of the proposed algorithm, the above simulations are also performed on the Rician channel. Rayleigh distribution is a specific scenario of Rician distribution. Multipath transmission occurs during the transmission of the transmitted signal, which leads to amplitude degradation of the received signal due to the superposition of multiple signals. The distribution of the received signal amplitude can be Rayleigh distribution or Rician distribution. When a path does not have a dominant scattering path, we term it a Rayleigh fading channel. If a path in the multipath is dominant (with only a line-of-sight (LOS) component), that is a Rician fading channel.

In a Rician channel, parameter k is the essential parameter. The link-level simulations adopt k = 10 with other settings same as the preliminary. Figure 10, Figure 11 and Figure 12 show the SER performance on a Rician channel for the TB-RMPA scheme. As Rayleigh fading has a greater impact on the signal, the overall bit error rate of the simulation results in the Rician channel has dropped significantly, but the trend of the curve remains basically unchanged. We can get the same conclusion as the previous simulation.

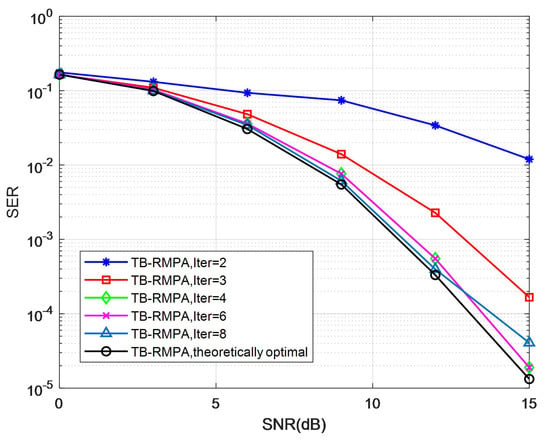
Figure 10. Convergence performance of TB-RMPA with $\beta$ = 0.5 in a Rician channel.

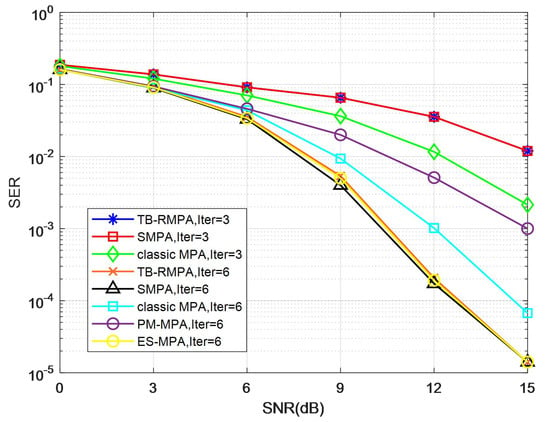
Figure 11. Comparisonof different detection schemes in a Rician channel.

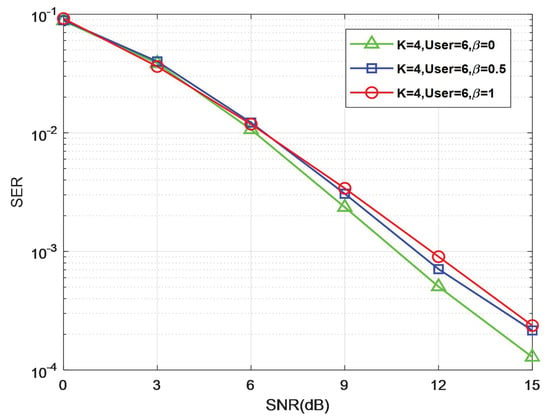
Figure 12. SER performance comparison of different $\beta$ in a Rician channel.

5. Conclusions

In this paper, we propose a novel low-complexity detection scheme derived from SMPA, and we term our approach TB-RMPA. The modification to SMPA considers a threshold-based confidence stability criterion to weed out users. Specifically, we combine the idea of IEDS in game theory with the SMPA algorithm, assigning different dominance levels to system users based on the factor matrix, and dynamically eliminating the dominant users, which has met the threshold standard in the iterative process. Threshold $\beta$, as a parameter that can be dynamically adjusted, becomes an effective means to balance the system complexity and bit error rate. Numerical analysis revealed that the proposed algorithm can achieve a significant reduction in computational complexity with a small compromise on BER performance loss.