Abstract
In this paper, more efficient allocation of forces is analyzed in the future air confrontation among unmanned aerial vehicle swarms. A novel method is proposed for swarm confrontation based on the Lanchester law and Nash equilibrium. Due to the huge number of unmanned aerial vehicles, it is not beneficial to deploy UAV forces in swarm confrontation. Moreover, unmanned aerial vehicles do not have high maneuverability in collaboration. Therefore, we propose to divide the swarms of unmanned aerial vehicles into groups, so that swarms of both sides can fight in different battlefields, which could be considered as a Colonel Blotto Game. Inspired by the double oracle algorithm, a Nash equilibrium solving method is proposed to searched for the best force allocation of the swarm confrontation. In addition, this paper proposes the concept of the boundary contact rate and carries out quantitative numerical analysis with the Lanchester law. Experiments reveal the relationship between the boundary contact rate and the optimal strategy of swarm confrontation, which could guide the force allocation in future swarm confrontation. Furthermore, the effectiveness of the division method and the double oracle-based equilibrium solving algorithm proposed in this paper is verified.
1. Introduction
With the continuous improvement of current unmanned aerial vehicles’ (UAVs) communication technology, endurance and anti-jamming capability, it is possible for UAV swarms to perform tasks of saturation attacks. UAV swarm confrontation is likely to be a new operation mode in the future. As far as we know, in terms of defending against swarm attacks by UAVs, there are several options, including missiles, anti-aircraft artillery, laser weapons [1] and electronic countermeasures (ECM) [2]. The cost of missile defense is too expensive, and the anti-aircraft artillery and laser energy weapons are also unaffordable. Moreover, when dealing with a UAV swarm with strong self-organization ability, the ECM are not completely reliable. Meanwhile, using a UAV swarm to fight another UAV swarm is full of potential. Therefore, the swarm confrontation between UAV swarms has practical significance.
Among research on UAV swarms versus UAV swarms, algorithms of deep reinforcement learning are mostly used, such as Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [3], Multiagent Bidirectionally-Coordinated Nets(MBCN) [4] and other algorithms. They control swarms from the perspective of micro-manipulation. Though collaborative behaviors such as teamwork can be trained, it requires a very high cost of calculation. Training a single agent to adapt to more complex environments is relatively economical and practical. The MBCN algorithm, which is improved based on actor-critic, successfully coordinates multiple agents as a team with a trained swarm confrontation network and defeats opponents in StarCraft (a real-time strategy game). The actor-critic framework of centralized learning and decentralized execution is also adopted by MADDPG in non-StarCraft cases. In [5], a deep reinforcement learning platform MAgent is used to develop multi-agent confrontation strategies for swarms, which is highly scalable and can enclose one million agents. These studies focus on confrontation from the perspective of deep reinforcement learning, which has strong real-time performance. However, swarm confrontation does not emphasize strong real-time performance from a macro perspective. Therefore, this paper proposes a swarm confrontation game method based on the division approach and Lanchester law instead of the deep reinforcement learning method.
As the swarm confrontation involves numerous UAVs, target allocation methods are essential for guaranteeing the scalability of the swarm system. In Xing’s paper [6], an auction algorithm is used to allocate targets from the perspective of attack and defense. The individual flight and attack are controlled according to the method of biological attraction. A comparison of some algorithms for UAV swarm confrontation is shown in Table 1.

Table 1.
Algorithms for UAV swarm confrontation.
The method of swarm confrontation proposed by Xing has greatly inspired our research work on swarm confrontation. However, unlike Xing’s work, we consider division in swarm confrontation. Division in swarm confrontation is to divide the swarm into several groups. Two advantages of applying the division approach to swarm confrontation can be obtained. Under the condition that the current collision avoidance control ability is limited, group confrontation provides better conditions for both sides to design confrontation methods. In the case of reducing the scale of the confrontation, more complex interaction logic and more advanced countermeasures can be designed. In addition, the computational effort for decision-making will be greatly reduced with the number of UAVs coming down.
Division in swarm confrontation can be thought of as a game of force allocation. The Colonel Blotto Game is a kind of force allocation game. In [7], the Colonel Blotto game provides an ideal framework for the allocation of the Mosaic force, where the limited military resources of two opposing parties are allocated to a corresponding battlefield. The result of the confrontation is reflected in the comprehensive results of each battlefield. However, the model is too simplified to be in line with reality because the victory or defeat on a single battlefield is determined only by the number of soldiers on each battlefield. In historical battlefield confrontation, the Lanchester law [8] is an effective model reflecting the force attrition, which has played an important role in predicting force loss. The introduction of the Lanchester law will make our swarm confrontation model closer to reality.
In the field of game, fictitious play [9] and the double oracle algorithm [10] are designed to select good strategies iteratively in the game. The numerical experiments in [11] showed that the double oracle algorithm converges faster than fictitious play. This inspires us to use the double oracle algorithm to improve the performance of force allocation.
In general, this paper constructed the UAV swarm confrontation model based on the classic Colonel Blotto Game, which is widely used in the training of military commanders to the UAV swarm confrontation scenario. We reformed the Colonel Blotto Game model and made innovations in several aspects. For example, we take advantage of the Lanchester law to calculate the battle loss of swarm confrontation in each battlefield. We introduced the concept of space constraints for a certain space, which can only meet the confrontation needs of a limited number of UAVs. Based on this concept, the swarm confrontation is divided into groups, which greatly reduces the control burden of the swarm. We combined the concepts of battlefields and swarms, making the Colonel Blotto Game model also suitable for UAV swarm confrontation. Then, we designed the double oracle(DO)-based [12] equilibrium solving algorithm based on the concept of the Nash equilibrium of game theory [13] to calculate the strategy of groups against each other. Contributions of our paper are listed as follows:
- We innovatively abstract swarm confrontation into a force allocation model, which greatly eases the control difficulty of the swarm confrontation. The concept of space constraint and the Lanchester law is creatively introduced into the UAV swarm confrontation model. Compared with the simple force comparison method to judge the result of the confrontation, the application of the Lanchester law makes the model closer to the actual confrontation scenario.
- We introduce the concept of approximate Nash equilibrium, and propose an equilibrium solving method based on the DO algorithm that can solve the equilibrium of the game more efficiently.
- Our analysis of the experimental results provides valuable guidance for the strategy design of swarm confrontation. In particular, as the confrontation space constraints change, the optimal strategy will vary between preferring an even allocation of force to different battlefields and preferring to concentrate the force on one or two battlefields.
The organization of this paper is as follows. In Section 2, we formulate the problem and illustrate the Lanchester law and the concept of constraints in the confrontation scenarios. We introduce the concept of the swarm game and Nash equilibrium. Section 3 presents the simulations and experimental evaluation. Section 4 presents the discussion. Section 5 concludes the paper briefly.
2. Problem Formulation and Scheme Design
This section constructs a model of the swarm confrontation. It mainly combines the Lanchester law and boundary contact rate to modify the Colonel Blotto Game model. At the same time, we also design a game solving method for the Colonel Blotto Game. The structure of this section is illustrated in Figure 1.
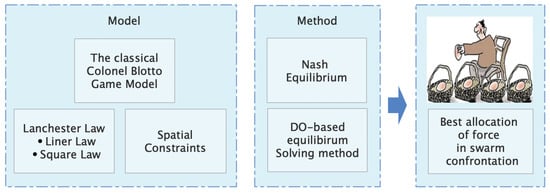
Figure 1.
Modeling and equilibrium solving of UAV swarm confrontation.
2.1. Problem Formulation
In actual swarm confrontation, considering the distribution of individuals in the swarm, three situations in the swarm confrontation can be considered according to whether the swarms are divided into groups or the cooperation is amenable. The three situations can be seen in Figure 2. Firstly, when the two groups enter into a melee and the cooperation between UAVs is amenable, a link indicates that there is cooperation between two UAVs. This situation is mostly solved by researchers through deep reinforcement learning methods. The adversarial advantage function and the cooperation between individuals are considered to improve the adversarial ability. However, this situation is not prevalent in the current confrontational environment since it is difficult to avoid collisions and obtain a good angle of attack in a melee. Secondly, in the case of complete distribution, individuals of one team fight the adversarial team independently. No combat power bonus is obtained since there is no cooperation between individuals. Thirdly, the swarms are divided into several groups. In the group consisting of a small number of UAVs, it is easier and less expensive to control the UAV swarm. In this paper, we consider the third situation, where swarms are divided into multi-groups and UAVs could cooperate in each group. In this subsection, we will sequentially introduce the Lanchester law for force loss prediction and the concept of space constraints in swarm confrontation. Finally, a swarm game model is constructed based on the Lanchester law in Section 2.1.3.

Figure 2.
Three situations of swarm confrontation.
2.1.1. Attrition with Lanchester Law
The Lanchester law is a mathematical formula for calculating the attrition of military forces, which was first proposed by FW Lanchester in 1914 [8] and has become one of the basic sources of the development of modern combat simulation. The Lanchester law includes the Lanchester linear law and Lanchester square law. They are suitable for different scenarios.
A. Lanchester Linear Law
On the ancient battlefield, spearmen between phalanxes could only fight against one other soldier at a time. If each soldier kills or is killed by another soldier, assuming the same weapons, then the number of remaining soldiers at the end is exactly the difference between the large phalanxes and the small phalanxes. Assume that the initial strength of the red side is when . is the strength of the red side at time t. Assume that the initial strength of the blue side is when . is the strength of the blue side at time t. Let a be the number of UAVs that the red team loses per unit time and b be the number of UAVs that the blue team loses per unit time, which represent the attack power of both sides. Then, the Lanchester law could be denoted as
The Lanchester linear law is suitable for calculating the attrition of military forces with identical weapons. The kill rate of the two sides will not change due to the attrition.
B. Lanchester Square Law
Firearms engage directly with each other in long-range aiming shots; they can strike multiple targets, and receive fire from multiple directions. The attrition rate now only depends on the number of weapons that corresponds to the number of units. The power of such a force is proportional to the square of the number of units.
In the Lanchester square law, the rate of loss of personnel depends entirely on the enemy’s lethality and the number of enemies, such as
In this case, the Lanchester square law could be denoted as
The Lanchester linear law and square law are utilized in our model to predict the attrition. According to the spatial constraints of swarm confrontation, we adopt the corresponding Lanchester law. The Lanchester linear law is used when spatial constraints are strict, while the Lanchester square law is used when spatial constraints are relaxed.
2.1.2. Constraints of the Confrontation Scenarios
In swarm confrontation, subject to the constraints of the confrontation scenario, such as space constraints, individual size and safe distance between individuals, the fourth frontier between swarms will be different. It is assumed that only individuals in the front of the swarm can attack each other due to the size of the UAV when two groups meet, as in Figure 3. For easier explanation, we give the definition of the fourth frontier.
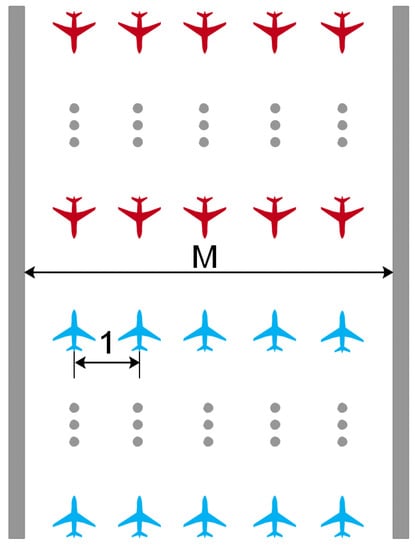
Figure 3.
Two swarms fight head-on over a narrow passage.
Definition 1.
Assuming that two swarms are flying head-on over a narrow passage with a width of M and the minimum safe distance between individuals is 1, then the maximum fourth frontier is M. In special cases when the number N of UAVs in the swarm is less than M, the fourth frontier is N.
The fourth frontier is particularly important since it determines the application of the Lanchester law. The increase in the fourth frontier can enhance the intensity of confrontation and end the battle early. For example, in ancient combat, if the two sides can line up, the battle can be quickly ended. On the contrary, in urban warfare, which differs from combat in an open area, you will not be able to decide the outcome for a long time. In modern air combat, the blitzkrieg effect is outstanding, and it is necessary to emphasize the intensity of confrontation.
Definition 2.
Assuming that the fourth frontier of the swarm is M and the number of units is N, then the boundary contact rate is .
Assuming that N isomorphic UAVs of each side confront on a passage with a width of M, the distance between the individual is 1. When , the two sides can line up in a line, and the boundary contact rate is 1. When , the maximum fourth frontier is M, and the boundary contact rate is . The formation here is an queue. An attrition speed is proportional to the fourth frontier M, and then the confrontation time is . The larger the fourth frontier, the faster the battle ends under the same conditions. It is assumed that all conditions are ideal, and the attrition speed conforms to the Lanchester law in the analysis. The enlargement of the fourth frontier can improve combat efficiency when the total number is determined.
If N UAVs are divided into k small groups, each group has UAVs. The width of the passage is M. When , they can line up, the boundary contact rate is 1, and the combat efficiency is improved. If , the formation is , the boundary contact rate is , and the fourth frontier is increased by k times, which contributes to the process of confrontation. As shown in the example in Figure 4, when 15 UAVs on both sides are evenly distributed to 3 battlefields, the boundary contact rate increases from to 1.
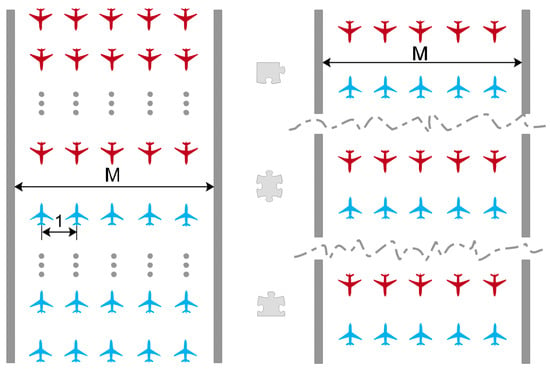
Figure 4.
UAVs in swarms are evenly distributed to 3 battlefields.
In special cases, when and the formation of the phalanx is formed, the boundary contact rate is . The larger the N, the lower the combat efficiency. An excessive number of UAVs in swarm confrontation can easily affect the progress of confrontation.
However, sometimes, the length of the fourth frontier of the two sides is different, such as in the case in Figure 5. There are two groups of identical UAVs, where one group of UAVs surrounds the other group. The perimeter of the enclosing circle is S. It is assumed that each UAV occupies a hexagonal area of a fixed size and the distance between adjacent UAVs is equal. As shown in Figure 5, 36 blue UAVs surround 36 red UAVs. The blue side’s fourth frontier is 36, and the red side’s fourth frontier is 24. The boundary contact rate of blue is 1 and 0.67 for red.
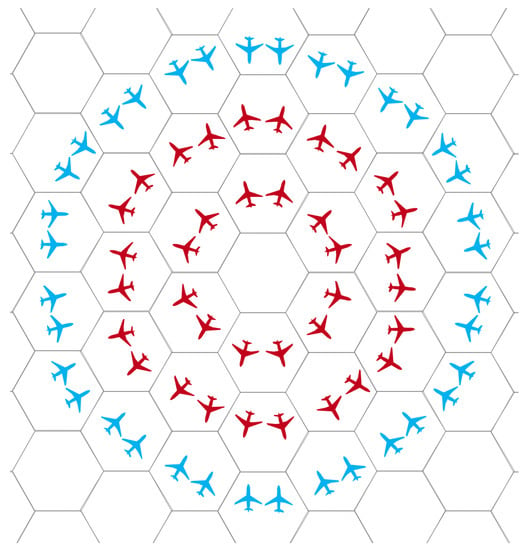
Figure 5.
One group of UAVs surrounds the other group.
In this subsection, a space constraint is introduced. The width of the passage or the circumference of the enclosing circle result in a different fourth frontier. The corresponding boundary contact rate and calculation method are given. It can be concluded that dispersing the swarm into small groups to fight against each other can improve the battlefield attrition speed and thus speed up the battle process. A partial siege of the opponent can be formed and an advantage over the boundary contact rate is gained. We mainly adopt the form of urban warfare in Figure 4 to verify the performance of the Lanchester law.
2.1.3. UAV Swarm Game
We consider UAV swarm confrontation as a UAV swarm game and we integrate the Lanchester law into the UAV swarm game. The construction of the model of the UAV swarm game is based on the Colonel Blotto Game. In the UAV swarm game, we assume that opposite swarm 1 and swarm 2 choose strategies through nonempty compact sets and . The utility function for swarm 1 is illustrated by . is the utility function for swarm 2. Then, triple constitute a UAV swarm game.
The concept of a mixed strategy allows each swarm to distribute any probability on the strategy set. A mixed strategy of swarm 1 is a Borel probability p over strategy set X. All mixed strategies for swarm 1 constitute . The support of a mixed strategy p is
There are three types of mixed strategy p.
1. Pure strategy p, when for some .
2. Finitely supported mixed strategy p when spt p is finite.
3. Mixed strategy p when spt p is infinite.
We construct the model of the UAV swarm game based on the Colonel Blotto Game, where two players simultaneously allocate UAVs into n battlefields. The strategy sets of swarm 1 and swarm 2 are X and Y.
The utility function,
describes the utility of swarm 1 over swarm 2. is the result on a battlefield j; is the corresponding weight. measures the performance of swarm 1 on a battlefield j.
Assuming that swarm 1 and swarm 2 have and UAVs, respectively, we designed the function based on the Lanchester law in Section 2.1.1 to upgrade .
In order to make it convenient to calculate the value of , we transform it as:
However, it is found that in actual confrontation, the attrition of the two sides usually does not strictly conform to the Lanchester linear law or the square law. The attrition can be illustrated by a combination of the Lanchester linear law and square law in most cases. Finally, we set the attrition in the formula below, which is a combination of the linear law and square law. The power exponent of is between 1 and 2.
where is a constant small variable greater than 0. M is the passage width.
Assuming that swarm 2 employs strategies , the corresponding probabilities are , where . The best response strategy of swarm 1 can be solved by
Since the Lanchester function contains the max term, we use the mixed integer programming method [14] to solve the extremum. We can transform into the computation of
where , , and
In the experiment, the SciPy optimize solver is used to solve the optimal strategy of swarm 1. Thus far, the calculation of the Lanchester function is finished. The rewards of both sides are calculated by the Lanchester law. The construction of the model of the UAV swarm game is completed.
2.2. The Equilibrium Solving Algorithm for Swarm Confrontation
A DO-based equilibrium solving algorithm is proposed for swarm confrontation. Based on the Lanchester law, we constructed a game model of swarm confrontation. The game model has equilibrium in which neither side can achieve greater rewards through unilateral strategic changes. Since the search for equilibrium has a large computational burden, we propose to find an -equilibrium that is an approximate solution to the confrontation.
2.2.1. Game Equilibrium
Equilibrium is pervasive in our day-to-day decisions. There is also equilibrium [15] in games based on the Colonel Blotto Game. A mixed strategy profile is a Nash equilibrium if
for . Define the lower value of by
and the upper value of by
holds for every continuous game , and is called the value of [11].
The -equilibrium for some satisfies
for . An -equilibrium is sufficient for our performance needs and it can reduce the burden of calculation.
2.2.2. DO-Based Equilibrium Solving Algorithm
Fictitious play and the double oracle algorithm could be used to solve the game. Numerical experiments in [11] showed that the double oracle algorithm converges faster than fictitious play. We design the equilibrium solving method based on the double oracle algorithm.
The best response of Player 1 for every mixed strategy of Player 2 is
Analogously, the best response of Player 2 for of Player 1 is
The DO-based equilibrium solving algorithm is shown in Algorithm 1. We set the initial strategy sets and in the first place. During each iteration i, strategy sets and are upgraded. Equilibrium of the subgame is calculated. Then, the best responses and to and are added to the strategy sets and if they do not exist in the current strategy sets. The calculation process would not end until . Then, an -equilibrium of the game is found.
| Algorithm 1 DO-based Equilibrium Solving Algorithm. |
| Input: game , , , M, , nonempty subsets , , and Output: -equilibrium of game
|
3. Experiments
Experiments were performed to verify the game model, which was constructed based on the Lanchester law. The performance of the DO-based equilibrium solving algorithm was also verified. Simulations were performed on a platform with 2.20 GHz Intel Core i7 CPU, 16 GB RAM. The algorithm that we proposed was implemented in Python.
3.1. Experimental Settings
We focus on the numerical analysis of the situation in Figure 4, where the UAVs swarm confronts on narrow passages. Several settings are made as follows:
- Both sides of the game deploy force on three battlefields;
- Each battlefield has equal weights, which means ;
- Both sides are flying head-on on a 2D narrow passage with a width of M;
- Safe distance between UAVs is 1 and UAV swarm stays in neat formation in Figure 4;
- The attrition of the confrontation is calculated by the Lanchester law in Equation (3).
Each side has 100 identical UAVs, which means that the attack power of both sides is equal (). UAVs are constrained to fly on the same plane. An attack can only take place between unobstructed UAVs. The model that we constructed based on the Colonel Blotto Game is a continuous game. We cannot exhaust all strategies, so we discretize the sub-strategies with the interval of .
The sub-strategies of X and Y are discretized into
There are a total of 145 sub-policies.
We initialize the initial policy of X and Y over all 145 sub-strategies. The weights for all sub-strategies are the same and equal to . Battlefield passage width M is set to be 15, 20, 25, 30, 35, 40, 50, 60, 70, 80, 90 in the experiment.
3.2. Experimental Results
Through the implementation of the DO-based equilibrium solving method, we draw the equilibrium results of UAV swarm confrontation. Points contained in the figure are the sub-strategies. The 3D coordinates of the sub-strategies correspond to the force allocation on three battlefields. The colors of the sub-strategies denote their weights. All the points (sub-strategies) and their weights formed an equilibrium of the UAV swarm confrontation. Sub-strategies are symmetric in the figure because the weights of the three battlefields are equal. Since the solution is an approximate equilibrium, some sub-strategies are symmetric but the weights of the sub-strategies are not equal.
In Figure 6, when M is in the range of 15 to 40, as M increases, the sub-strategies distributed in the middle of the triangle account for a smaller proportion of the support sub-strategies. More sub-strategies in the middle of the triangle means that the strategy prefers to equally allocate force to three different battlefields. We can make the conclusion that the UAV swarms tend to be distributed in three battlefields and gradually come to concentrate on two battlefields as M increases.
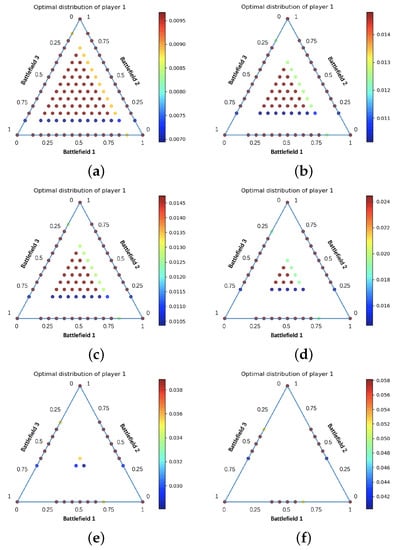
Figure 6.
Optimal distribution of Player 1 corresponding to different M. Each point is a sub-strategy, and its 3D coordinates represent the proportion of force allocated on the three battlefields. Its color denotes the weight of this sub-strategy among all sub-strategies. If more sub-strategies are located in the middle of the triangle, both sides of the confrontation tend to allocate their force equally across the three battlefields. If more sub-strategies are allocated on the axis of the triangle, both sides prefer to allocate force on only one or two battlefields. (a) ; (b) ; (c) ; (d) ; (e) ; (f) .
In Figure 7, when M is in the range of 40 to 90, the equilibrium of UAV swarm confrontation is extremely different. All sub-strategies are located on the axis and vertices of the coordinate plane. Both sides prefer to concentrate their forces in one or two battlefields. A conclusion can be drawn that as M increases, the sub-strategies located on the axis begin to move toward the vertices. There is a tendency to concentrate all forces on a single battlefield.
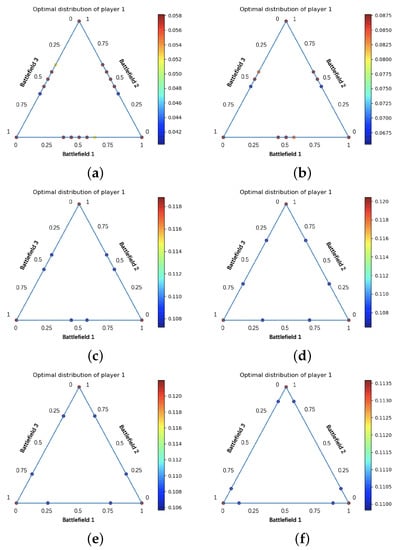
Figure 7.
Optimal distribution of Player 1 corresponding to different M. (a) ; (b) ; (c) ; (d) ; (e) ; (f) .
The number of UAVs on both sides is 100. It can be found that the larger M, the larger the boundary contact rate, and the more sub-strategies are located on the axis. When the passage width M is large, the attrition of the confrontation is determined by the Lanchester square law. When M is small, the confrontation attrition is decided by the Lanchester linear law.
4. Discussion
The equilibrium of the UAV swarm confrontation was intuitive in Figure 6. Points denote the sub-strategies and the color is the weight. Readers can easily understand the details of the strategies. Compared with the neural network trained by the deep reinforcement learning algorithm to guide the confrontation, our results are easier to understand and more appropriate for humans. Therefore, the UAV confrontation model that we propose can greatly ease the control in human–computer interaction. When we construct the confrontation model with Lanchester law, the environmental constraints M are introduced. In our experimental analysis, M is closely related to the boundary contact rate. The environmental constraints M introduced in the Colonel Blotto Game make our model closer to reality.
The DO-based equilibrium solving method that we propose was used to solve the approximate Nash equilibrium of UAV swarm confrontation. The calculation time in the experiments is short since the method is efficient.
We found the relationship between the equilibrium solution and M. This could help to guide the strategy design of UAV swarm confrontation. Since the number of UAVs of both sides is 100, the larger M, the greater the boundary contact rate. Therefore, the higher the boundary contact rate, the higher the expectation of confrontation rewards can be obtained by concentrating the force on a small number of battlefields. However, when M is small, which means that the constraints are strict, more UAVs are allocated to multiple battlefields to obtain a higher expectation of reward. Just as the UAV swarm confined in forests or urban warfare, where M and the boundary contact rate is small, UAVs should be assigned to more smaller swarms into the corresponding space.
5. Conclusions
In this paper, we have designed a new swarm confrontation mode to address the limitations of current single UAV performance. In this mode, UAV swarms are divided into smaller swarms and fight in different battlefields. UAV swarm confrontation is transformed into a force allocation game. This greatly eases the control of the swarm confrontation. During the construction of the game model, space constraints and the Lanchester law are creatively introduced, which make the model closer to the actual confrontation scenario.
In the process of searching for the approximate Nash equilibrium of UAV swarm confrontation, the combination of the Lanchester law and DO-based equilibrium solving method proposed in this paper has been verified to be efficient.
The boundary contact rate that we propose is verified to have a significant impact on force allocation. The higher the boundary contact rate, the more forces should be concentrated to fewer battlefields to gain a higher expectation of confrontation rewards. The relationship revealed between the boundary contact rate and the optimal strategy would have a great impact on UAV swarm confrontation in the future.
Author Contributions
X.J. and W.Z. proposed the method; J.C. and X.J. designed and performed the experiments; X.J., F.X. and W.Y. analyzed the experimental data and wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant No. 61806212 and the Natural Science Foundation of Hunan Province under Grant No. 2021JJ40693.
Data Availability Statement
The data presented in this study are available in the article.
Conflicts of Interest
The authors declare that there are no conflict of interest regarding the publication of this paper.
Abbreviations
The following abbreviations are used in this manuscript:
| UAV | unmanned aerial vehicle |
| ECM | electronic countermeasure |
| MADDPG | Multi-Agent Deep Deterministic Policy Gradient |
| MBCN | Multi-Agent Bidirectionally Coordinated Nets |
| DO | double oracle |
References
- Coffey, V. High-energy lasers: New advances in defense applications. Opt. Photonics News 2014, 25, 28–35. [Google Scholar] [CrossRef]
- Hartmann, K.; Giles, K. UAV exploitation: A new domain for cyber power. In Proceedings of the 2016 8th International Conference on Cyber Conflict (CyCon), Tallinn, Estonia, 31 May–3 June 2016; pp. 205–221. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. arXiv 2017, arXiv:1706.02275. [Google Scholar]
- Peng, P.; Wen, Y.; Yang, Y.; Yuan, Q.; Tang, Z.; Long, H.; Wang, J. Multiagent bidirectionally-coordinated nets: Emergence of human-level coordination in learning to play starcraft combat games. arXiv 2017, arXiv:1703.10069. [Google Scholar]
- Zheng, L.; Yang, J.; Cai, H.; Zhou, M.; Zhang, W.; Wang, J.; Yu, Y. Magent: A many-agent reinforcement learning platform for artificial collective intelligence. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Xing, D.; Zhen, Z.; Gong, H. Offense–defense confrontation decision making for dynamic UAV swarm versus UAV swarm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 5689–5702. [Google Scholar] [CrossRef]
- Grana, J.; Lamb, J.; O’Donoughue, N.A. Findings on Mosaic Warfare from a Colonel Blotto Game; Technical Report; RAND Corp.: Santa Monica, CA, USA, 2021. [Google Scholar]
- Bauer, H. Mathematical Models: The Lanchester Equations and the Zombie Apocalypse. Bachelor’s Thesis, University of Lynchburg, Lynchburg, VA, USA, April 2019. [Google Scholar]
- Brown, G.W. Iterative solution of games by fictitious play. Act. Anal. Prod. Alloc. 1951, 13, 374–376. [Google Scholar]
- McMahan, H.B.; Gordon, G.J.; Blum, A. Planning in the presence of cost functions controlled by an adversary. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 536–543. [Google Scholar]
- Adam, L.; Horcík, R.; Kasl, T.; Kroupa, T. Double oracle algorithm for computing equilibria in continuous games. arXiv 2020, arXiv:2009.12185. [Google Scholar]
- Bosansky, B.; Kiekintveld, C.; Lisy, V.; Pechoucek, M. An exact double-oracle algorithm for zero-sum extensive-form games with imperfect information. J. Artif. Intell. Res. 2014, 51, 829–866. [Google Scholar] [CrossRef] [Green Version]
- Vu, D.Q. Models and Solutions of Strategic Resource Allocation Problems: Approximate Equilibrium and Online Learning in Blotto Games. Ph.D. Thesis, Sorbonne Universites, UPMC University of Paris 6, Paris, France, 2020. [Google Scholar]
- Bixby, R.E.; Fenelon, M.; Gu, Z.; Rothberg, E.; Wunderling, R. Mixed-integer programming: A progress report. In The Sharpest Cut: The Impact of Manfred Padberg and His Work; SIAM: Philadelphia, PA, USA, 2004; pp. 309–325. [Google Scholar]
- Benazzoli, C.; Campi, L.; Di Persio, L. ε-Nash equilibrium in stochastic differential games with mean-field interaction and controlled jumps. Stat. Probab. Lett. 2019, 154, 108522. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).