Abstract
In recent years, multi-objective cuckoo search (MOCS) has been widely used to settle the multi-objective (MOP) optimization issue. However, some drawbacks still exist that hinder the further development of the MOCS, such as lower convergence accuracy and weaker efficiency. An improved MOCS (IMOCS) is proposed in this manuscript by investigating the balance between development and exploration to obtain more accurate solutions while solving the MOP. The main contributions of the IMOCS could be separated into two aspects. Firstly, a dynamic adjustment is utilized to enhance the efficiency of searching non-dominated solutions in different periods utilizing the Levy flight. Secondly, a reconstructed local dynamic search mechanism and disturbance strategy are employed to strengthen the accuracy while searching non-dominated solutions and to prevent local stagnation when solving complex problems. Two experiments are implemented from different aspects to verify the performance of the IMOCS. Firstly, seven different multi-objective problems are optimized using three typical approaches, and some statistical methods are used to analyze the experimental results. Secondly, the IMOCS is applied to the obstacle avoidance problem of multiple unmanned aerial vehicles (UAVs), for seeking a safe route through optimizing the coordinated formation control of UAVs to ensure the horizontal airspeed, yaw angle, altitude, and altitude rate are converged to the expected level within a given time. The experimental results illustrate that the IMOCS can make the multiple UAVs converge in a shorter time than other comparison algorithms. The above two experimental results indicate that the proposed IMOCS is superior to other algorithms in convergence and diversity.
1. Introduction
Engineering design optimization could be considered as an NP-hard problem, which often faces various conflicting factors and constraints under complex high-dimensional nonlinear constraints. Moreover, it is challenging to find the best solution while inter-conflicts exist among different goals. Therefore, an appropriate method to find the relative optimal compromise solution is to transform the engineering design optimization problem into a multi-objective (MOP) optimization issue due to the specific conflict factors and constraints.
Due to the low cost and high convergence accuracy, the heuristic algorithm has been applied to settle the MOP issues and obtain fruitful achievements. Sinivas [1] proposed a non-dominated sorting genetic algorithm (NSGA) to solve the MOP in 1994. To overcome the shortage of the NSGA, such as the high time complexity of NSGA dominated sorting, lack of elite mechanism, and the need to formulate shared parameters, Deb et al. [2] proposed a fast elitist multi-objective genetic algorithm (NSGAII) utilizing a fast non-dominated sorting strategy. Experimental results revealed that the NSGAII can improve the accuracy of optimization results and reduce the complexity of solving non-dominated sorting. Zhang and LI et al. [3] discussed a multi-objective evolutionary algorithm based on decomposition (MOEA/D) to divide a MOP into several small-dimensional goals using Chershev and weight sum. The MOEA/D can reduce the difficulty of solving the MOP and improve the algorithm’s convergence efficiency for selecting the best solution set. Wang et al. [4] proposed a multi-objective self-adaptive difference evolution (MOSADE) algorithm to control the optimization direction of differential evolution algorithms by variation parameters and crossover probability adaption, and to further optimize the calculation for gaining the Pareto solution through introducing the external elite archiving and the crowded entropy density strategy. Cui et al. [5] proposed a multi-stage multi-objective Particle Swarm optimization algorithm (MSMOPSO) to improve the convergence performance and population diversity due to the leader selection strategy and mutation operator. Mahalingam et al. [6] used the harmony search (HS) algorithm and technique for order preference by similarity to the ideal solution (TOPSIS) to find the best drilling parameters of a horizontal ABRASIVE water jet. The primary thinking is to convert multiple goals into single goals based on the TOPSIS and to adjust the drilling parameters of abrasive water injection using the HS, respectively. The experimental results show that the characteristic error of the abrasive water injection hole predicted by the proposed method in the die steel model is less than 6%. Wang et al. [7] proposed an enhanced competitive swarm optimizer with a strongly convex Sparse operator (S-ECSO). The modifications could be classified into three aspects. Firstly, the strong convex sparse operator is used to optimize the vital convergence function for generating sparse solutions. Then, the tripartite competition mechanism is introduced to update the worst position searched by the L1 and L2 paradigm, respectively, for ensuring the generated solutions are distributed on the front surface of the Pareto. The results show that the neural network optimized by the S-ECSO has relatively high precision in feature selection extraction and can obtain a better sparse solution. To obtain a satisfying distribution of Pareto optimal solutions, Hu et al. proposed a niching backtracking search algorithm with adaptive local search to simultaneously locate and maintain all Pareto optimal solutions in the decision space [8]. Yue et al. propose a multimodal multi-objective differential evolution algorithm to investigate the mapping mechanism from more than one Pareto Set (PS) to the same Pareto Fronts (PF) for maintaining multiple PSs of multimodal multi-objective optimization problems and improve the diversity in both decision and objective space. Experiments indicate that the proposed method can gain high comprehensive performance [9]. Zouache and Abdelaziz extended the Manta Ray foraging optimization (MOMRFO) to address the multi-objective problem. In the proposed MOMRFO, a population archive is employed to store the non-dominated solutions generated. The leader’s solutions are selected to lead the Manta Rays’ population towards promising search regions. Meanwhile, a crowding distance and ε-dominance are utilized to provide a good compromise between diversity and convergence of the obtained potential Pareto set. The experimental results demonstrate that the MOMRFO algorithm outperforms and can provide better convergence and diversity of solutions [10].
Except for the mentioned heuristic algorithms, the cuckoo search (CS) algorithm has gone deep into various disciplines and gained fruitful achievements, such as engineering design [11,12,13], parameter estimation [14,15], prediction recognition [16,17], power energy [18], image processing [19]. Recently, an extension of CS, namely multi-objective cuckoo search (MOCS), has also been proposed and widely used to settle the MOP issues due to the remarkable advantages, such as simple algorithm framework, easy implementation, and good global convergence, in recent years [20]. To obtain genes with high correlation with cancer with the minimum number of genes from the high-dimensional cancer microarray dataset, Othman et al. [21] proposes a hybrid multi-objective CS and evolutionary operators (MOCS-EO) to optimize the DNN classifier to extract genes with high correlation. Experimental results illustrate that the MOCS-EO can extract genes associated with cancer and obtain very high classification accuracy under the condition of selecting fewer cancer genes. Hanoun et al. [22] presented a Pareto archived multi-objective CS (PAMOCS) to address the multi-objective shop scheduling issue by introducing the pairwise interchange perturbation scheme for replacing the Levy flight mode and utilizing the external archives for storing all non-dominated solutions. The results demonstrate that the PAMOCS can reduce the computational overhead to a large extent and improve the scheduling efficiency. Chen et al. [23] propose a decomposition-based multi-objective CS (MOEA/D-CS). The amendments could be summarized into the following points. Firstly, the global and local random walk operators are reconstructed to enhance searchability. Then, the bandit adaptive operator decision is used to select different operators in the evolution process. Next, the Cherchev strategy is employed to transform multiple objectives into a series of subproblem aspects. The optimization results of a series of numerical functions show that the MOEA/D-CS has the advantages of fast convergence speed, high precision, and low CPU consumption. Paul et al. [24] used MOCS to optimize individual-based stream feature selection (I-SFS) and group-based stream feature selection (G-SFS), respectively. The optimization results using the I-SFS and G-SFS show that the MOCS HAS high classification according to feature a selection of different multi-label datasets. Other industrial optimization cases using MOCS and related variants could be found in references [25,26,27,28,29].
To guide the optimization operation towards a better direction in the whole optimization process, an improved MOCS (IMOCS) is discussed in this manuscript for exploring the balance between development and exploration. The main contributions of the IMOCS could be concluded into the following three strategies.
Firstly, the parameters of MOCS influence the solution quality and search efficiency of the global migration. An automatic adjustment mechanism of the step factor of Levy flight is used in the IMOCS to enhance the adaptive ability of global walk. With the increase in the number of iterations, the step factor decreases linearly to adjust the search range at different stages and improve the population’s density.
Secondly, because of the weak random migration of the MOCS, a strengthened local search mechanism is employed in the IMOCS to dynamically change the random migration mode using the characteristics of uniform distribution and to refine the accuracy of non-dominated solutions after fully tapping the potential individuals around the current individual.
Finally, to prevent the convergence accuracy of MOCS from deteriorating, a disturbance operator is added to the local search mechanism of the IMOCS for maintaining the differences among individuals and leading the direction of population evolution.
The experiments are executed from two aspects. Firstly, seven classical functions with different objective constraints are selected to compare with the other three multi-objective algorithms (NSGAII [2], SPEAII [9], MOCS [20]) to verify the effectiveness of the proposed IMOCS. The experimental results are analyzed from three aspects: convergence, diversity, and robustness, using different indicators (Wilcoxon rank-sum test, hypervolume, inverted general distance, and general distance). The results reveal that the proposed IMOCS is superior to other algorithms in convergence and diversity. Secondly, the IMOCS algorithm is applied to the model of cooperative obstacle avoidance of multiple UAVs to broaden the application prospect of the MOCS algorithm for verifying the feasibility and practicability of settling the real-world problem using the proposed method.
The remaining sections are organized as follows. Section 2 recalls the basic concepts of the MOP and MOCS. The modifications of the IMOCS from different aspects are introduced in Section 3. Section 4 highlights the performance and feasibility of the IMOCS through optimizing seven classical functions with different objective constraints. Section 5 employs the IMOCS to optimize the model of cooperative obstacle avoidance of multiple UAVs. Section 6 summarizes the entire manuscript.
2. Multi-Objective Optimization and MOCS
This section discusses the basic notions of multi-objective optimization and MOCS.
2.1. Multi-Objective Optimization
The MOP could be considered as a set of objectives. Hence, the optimal solution of MOP is not a single solution, but a set of intermediate solutions. Assume that the mathematical definition of MOP’s minimization problem is given as shown in Equation (1):
where M represents the number of objective functions and x is a solution vector or decision variable.
The core task of the multi-objective optimization is to find a set of non-dominant solutions with good diversity and convergence.
Furthermore, one decision variable x is called strictly dominated, and the other decision variable Y can be expressed as x < y, if x dominates y or x is superior to y, as shown in Equation (2):
In the MOP, a Pareto optimal solution could be achieved when a solution is not dominated by any other solution.
2.2. MOCS
The cuckoo search (CS) algorithm is a kind of natural heuristic algorithm by analyzing the parasitic behavior of cuckoo brood and including the Levy flight behavior of birds. The female cuckoo will find the best nest and lay multiple eggs into it by the Levy flight mechanism, and the host bird will inadvertently incubate cuckoo chicks. If the host bird finds an alien bird’s egg in the nest, it will kick out the egg or discard the current nest, build a new nest, and start breeding its own chicks. Hence, the parasitic reproduction strategy is employed in the CS method to find the optimal solution. In the implementation processing of the CS algorithm, the location of cuckoo’s parasitic nests will be mapped to the solution in the population space, and the advantages and disadvantages of the location of the parasitic nest will be designed as the optimal fitness value to evaluate the solution. The MOCS is proposed to further broaden the application field of CS from single-objective problem optimization to MOP solving, while preserving the population renewal strategy using Levy flight and the principle of discovery probability.
In MOCS, each cuckoo generates a new variant vector (nest position) by Levy flight by using Equation (3) to enhance the global search ability of the population.
In Equation (3), and respectively represent the position of nest i of (t+1)-th and t-th generation, represents the point-to-point multiplication, and represents the random search path of Levy’s flight, whose flight direction obeys the uniform distribution and the walking step obeys the Levy distribution. is the step size scaling factor in the update process. The could be calculate by the Equation (4).
In the Equation (4), represents the location of next j in the t-th generation.
In addition, the probability indicates the possibility that an egg could be found by the host bird. Once the cuckoo egg is found, the cuckoo will lay eggs in another nest. Then, the new nest position calculation formula is illustrated in Equation (5).
In the Equation (5), and represent two randomly selected individuals from the population. r and r1 are random numbers within the range of [0, 1].
3. The Proposed Improved Cuckoo Search Algorithm
In the standard MOCS algorithm, the step size generated by Levy flight lacks adaptability in the later iterations of the algorithm, resulting in low population density in the search. Secondly, in the process of local search, the moving direction of is determined by and two individuals, which reduces the local optimization ability of MOCS, the accuracy of obtaining non-dominated solutions is not high when optimizing complex problems. Therefore, this paper proposes an improved multi-objective cuckoo algorithm to solve the above problems.
3.1. Improvements
The main modifications of the IMOCS could be summarized into following two aspects.
To begin with, to amend the search range automatically in different periods and improve the accuracy in the solution space, Equation (6) is used to make the step factor α linearly decrease when the number of iterations increase.
In the Equation (6), and are the maximum and minimum step size factors, respectively. t is the current number of iterations, and T is the maximum number of iterations.
Secondly, to enhance the random migration ability of the local search and find the best Pareto solution, the uniform distribution characteristics and random disturbance are used to prevent falling into the local extremum. Thereby, a new random migration operator is reconstructed, as shown in Equation (7), to fully explore the potential individuals around the current individual and improve the accuracy of the non-dominated solution.
In the Equation (7), , , and are uniformly distributed numbers in the range [0, 1]. and satisfies the condition . is introduced as a disturbance to prevent falling into a stagnant state.
3.2. IMOCS Implementation steps
Due to the above improvement ideas, IMOCS could be divided into eight implementation steps as follows.
Step 1: Initialization. Define objective function f(x), population number N, set problem dimension D, discovery probability Pa, step size α, maximum number of iterations T, lower and upper bounds (LB, UB), and new dynamic search domain upper and lower limits.
Step 2: Initialize the MOCS population. Randomly create N sets of solution vectors in the search space and generate the bird’s nest solution vector using Equation (8), and calculate the corresponding fitness value.
where rand(D) represents the 0–1 random number of D dimension and x0 is the initial nest position.
Step 3: Non-dominated sorting (I). To realize the stratification of the population due to the dominance relationship between each individual in the population. Then, the individual with the best Pareto front level will be selected as the optimal solution.
Step 4: Population update. A certain number of offspring will be produced from the parent population under the combined action of three different strategies, which are Levy flight strategy, the adaptive step-length factor is calculated by the Equation (6) and the best individual selected from the elite selection as the learning object. The population update formula is as follows as shown in Equation (9).
In the Equation (9), represents the best individual selected from the elite; and respectively represent the position of nest i of (t+1)-th and t-th generation; represents the random search path of Levy’s flight.
Step 5: Random migration. To obtain a random number , when the host bird finds cuckoo chicks (), it will abandon the current nest and build a new nest using Equation (5). Otherwise, keep the original position unchanged.
Step 6: Population merger. The initial population and the progeny population are merged to produce 2N populations, which expands the sampling space.
Step 7: Non-dominated sorting (II). The merged population is processed into layers to obtain the level information of each individual using the dominance relationship between individuals.
Step 8: Crowding distance calculation. Allocate the crowding distance for each individual using normalization due to the projection of adjacent individuals at the same level. The crowding distance could be calculated using Equation (10).
In the Equation (10), and respectively denote the mth objective function value of the i + 1 and i − 1 individuals. and denote the maximum and minimum function values of the mth objective function.
Step 9: Elite selection. According to the evaluation of all non-dominated solution sets in the same level, individuals with a larger crowding distance are selected to be retained until the population size reaches N. If the number of individuals who have joined the next generation in a certain level exceeds N, the layer is sorted according to the crowding distance, and a better solution is selected to join until the next generation population is N.
Step 10: Termination. Record the historical Pareto optimal solution and check whether the current algorithm iteration fulfills the termination condition. If fulfilled, output the Pareto optimal solution. Otherwise, go to Step 4.
According to the above implementation steps, the entire flowchart of the IMOCS algorithm is as shown in Figure 1:
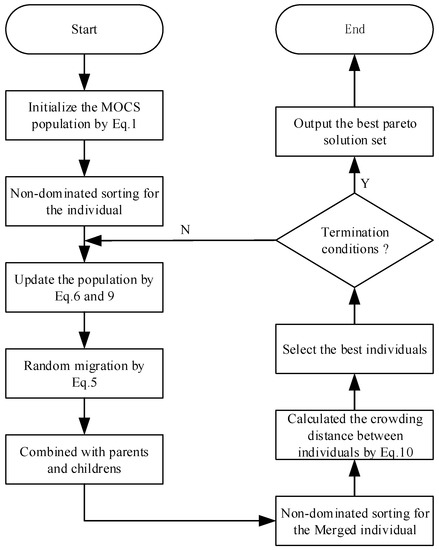
Figure 1.
Flowchart of the IMOCS.
3.3. Time Complexity Analysis
In the IMOCS algorithm, the calculation of the objective function takes up most of the time of the whole algorithm. Therefore, the use of asymptotic time complexity to evaluate algorithm performance is one of the important theoretical criteria.
Assuming that the dimension of the objective function f is Dim, the number of populations is N, and the number of objective functions is M, the detailed analysis of the implementation steps of the IMOCS algorithm is as follows:
- (1)
- The time complexity of IMOCS population initialization is O(N × Dim). The time complexity of each individual evaluation objective function of the population is O(f(Dim)).
- (2)
- The calculation of the non-dominant solution is divided into two parts. The first part is used to obtain the number of dominant individuals and the set of dominated individuals, and the time required is O(M × N2). The second part is used to solve individual computation except the first Pareto front, and its time complexity is O(N2). Thus, the algorithm time complexity of this process is O(M × N2).
- (3)
- In the Equation (9), the time complexity of the update stage of Levy flight population is O(N × (Dim + O(Levy)), where O(Levy) is a random number subject. Hence, its computational complexity is of a constant order. Therefore, the time complexity of population renewal process is O(N × Dim).
- (4)
- In the Equation (5), the time complexity of random migration operator optimization is O(N × Dim).
- (5)
- The worst time complexity after merging parent and child is O(2N).
- (6)
- The worst time complexity of stratification by using non-dominated sorting method after population merging is O(M × 4N2).
- (7)
- Before calculating the crowding distance of each individual, descending order is required for each sub-target whose time complexity is O(M × 2N × log(2N)), and the time for calculating the crowding distance of each individual is O(M × 2N). Therefore, the worst time complexity of the algorithm is O(M × 2N × log(2N)).
- (8)
- After calculating the non-dominated ordering and crowding degree, the crowding degree of all individuals at the same level is compared, and the worst time complexity required by the pose constructed is O(2N × log(2N)).
- (9)
- According to the above analysis, when T = 1, the worst time complexity is:
O(N × Dim)+O(N × (Dim + f(Dim)) + O(N × (Dim + f(Dim)) + O(N × (Dim + f(Dim)) + O(M×N2) + O(2N) + O(M×4N2) + O(M × 2N × log(2N)) + O(2N × log(2N)) ≈ O(M × 4N2) ≈ O(M × N2)
Therefore, when T = Maxgen, the worst time complexity is O(Maxgen × M × N2).
4. Numerical Experiment and Analysis
To verify the effectiveness, a numerical experiment is designed below to reveal the feasibility of the IMOCS. First, the related characteristics of the seven classic multi-objective test functions and the quality indicators used to evaluate the frontier performance of Pareto are introduced. Secondly, the algorithm parameter design and operating environment of NSGAII [2], SPEAII [4], MOCS [20], and IMOCS are described and analyzed. Finally, the performance of the proposed algorithm is compared with the other three algorithms to optimize the classical function. All the experiments are run under the environment of Intel® Core™ i5-10200H CPU @ 2.40 GHz, 16 G memory, Windows 10 operating system. The programming language is Python 3.7.
4.1. Multi-Objective Benchmark Functions
Table 1 shows the parameter settings of seven classic multi-objective benchmark functions, which are widely used to verify the effectiveness of heuristic algorithms. Among them, Dim, M, Characteristics, Space Search, and other parameters respectively represent the dimension of the problem, the number of targets, Pareto frontier feature attributes, and the search domain range.

Table 1.
Seven classic multi-objective benchmark functions.
4.2. Quality Indicators
The purpose of the MOO problem is to obtain a set of optimal solutions that are uniformly distributed and close to the true Pareto front. Therefore, seven classic performance evaluation methods, which are hypervolume indicator (HV), generation distance (GD), Inverted generational distance (IGD), Wilcoxon rank sum-test, mean, and standard deviation (Std), are used to verify the performance of the proposed IMOCS.
The above seven evaluation methods are selected because they are frequently used for performance comparison in most literatures of multi-objective swarm intelligence algorithms and have the advantages of strong interpretability and easy calculation. For example, HV, IGD, and GD can all measure the convergence of multi-objective algorithms, but only HV and IGD indicators can quickly obtain the corresponding results when measuring the diversity of multi-objective algorithms. In addition, mean and Std results were calculated using four heuristic algorithms in different environments (HV, IGD, GD), and the stability of each algorithm was analyzed. Secondly, Wilcoxon rank-sum test was used to evaluate algorithm performance based on mean value, which effectively demonstrated the strong competitiveness of the algorithm.
- HV: This indicator is used to calculate the volume surrounded by the non-dominated solution set S of all target minimization problems and a set of pre-set reference points distributed in the target space. If any solution is satisfied, there is . The definition of HV is as shown in Equation (11).where represents Lebesgue measure. The larger the value of HV is, the closer the non-dominated solution set S obtained by the algorithm optimization is to the true Pareto frontier, and the better the convergence and uniformity of the algorithm are reflected from the side. This metric evaluates convergence and diversity without knowing the reference set. However, the computational complexity is high, especially for high-dimensional multi-objective optimization (MOO) issues.
- IGD: This indicator is mainly calculated by calculating the minimum distance and between each point (individual) on the true Pareto front surface and the set of individuals obtained by the algorithm. The algorithm is used to evaluate the proximity and distribution of the true Pareto frontier to the optimal non-dominated solution set, and the convergence and diversity of the algorithm are comprehensively measured. Let PF be the true Pareto frontier and S be the best non-dominated solution set obtained through multi-objective algorithm. The definition of IGD is as shown in (12):
The is the number of individuals of the point set distributed on the true Pareto front surface; is the individual on the real PF; and is the minimum Euclidean distance between an individual on the PF to the population S, which is calculated by Equation (13).
According to Equations (12) and (13), the smaller the IGD value, the closer the non-dominated solution obtained by the algorithm is to the true Pareto front, the better the convergence of the algorithm, and the better the diversity of the non-dominated solution set. It can be found that the GD method can only evaluate the convergence of the algorithm, while the IGD can evaluate the convergence and diversity at the same time, and the calculation cost is small. The disadvantage is that a reference set is required.
- 3.
- GD: This indicator is used to measure the distance between the optimal non-dominated solution set obtained by the algorithm and the true Pareto front, and is a measure of the convergence of the algorithm. GD indicator is defined as shown in Equation (14):
The represents the number of optimal non-dominated solutions discovered by the algorithm; represents the minimum Euclidean distance between the non-dominant solution Y and all points of PF, and its calculation is shown in Equation (15).
It can be seen from the Equations (14) and (15) that the smaller the GD value, the smaller the distance between the non-dominated solution set obtained by the algorithm and the true Pareto front, and the better the convergence of the algorithm. If , it indicates that the generated non-dominated solution set is on the true Pareto frontier, and the two completely coincide. Compared with HV, the computational cost of GD is lightweight, but only the convergence of the solution set is measured, and the diversity cannot be assessed.
- 4.
- Wilcoxon rank-sum test: This statistical method is a non-parametric statistical test used to detect whether two or more datasets are from the same distributed population, and its confidence level is 0.05. In order to conduct an in-depth analysis of the superiority of the algorithm, the performance of the algorithm is judged according to the mean value in the Wilcoxon rank-sum check. The symbols ‘−’, ‘+’, and ‘=‘, respectively, indicate that the algorithm proposed in this article compares with other algorithms. The performance of the algorithm is poor, significantly better than that, and there is no significant difference.
- 5.
- Mean and Std:Mean and Std are used to evaluate the stability of each algorithm and analyze the results obtained in different operating environments. The mean and Std are calculated as shown in Equations (16) and (17):
The is the optimal solution obtained under the current operating environment, Num is the total number of optimal solutions (times of independent operation of the algorithm).
4.3. Numerical Parameter Design
In this experiment, to reduce the influence of the randomness, these four algorithms are independently run Num = 30 times. In addition, each algorithm uses an iterative calculation scheme to solve the MOO problems and considers the fairness of the algorithm. All the population size and the maximum number of iterations are set to 100 and 1000, respectively. The design of other parameters is designed with reference to the existing literature. The specific parameter design is listed in Table 2.

Table 2.
Parameters setting of examined algorithm.
4.4. Analysis of Simulation Results
Four algorithms are used to calculate seven classic test functions (ZDT1-ZDT4, ZDT6, DTLZ2, DTLZ4), and statistical results are obtained. Different convergence curves and the mean and standard deviation of GD, IGD, and HV are obtained. In the convergence result graph (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8), there are curves with different colors to represent different algorithms. For example, the solid red line represents the true Pareto optimal front, the purple scattered points represent the IMOCS, the cyan scattered points represent SPEAII, the green scattered points Represents NSGAII, and the blue scattered dots represent MOCS. As the number of iterations increases, the algorithm continuously searches for the best non-dominated solutions so that all non-dominated solutions can approach the true PF frontier and finally obtain a higher convergence accuracy.
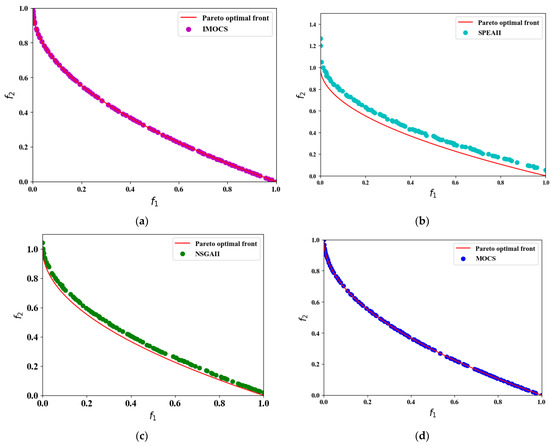
Figure 2.
The convergence results of ZDT1 test problem over all algorithms. (a) IMOCS, (b) SPEAII, (c) NSGAII, and (d) MOCS.
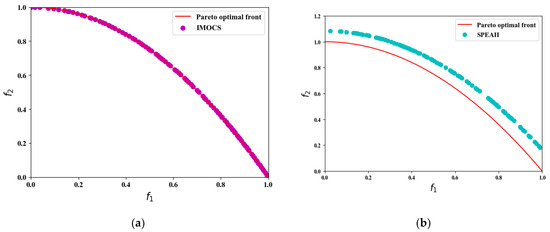
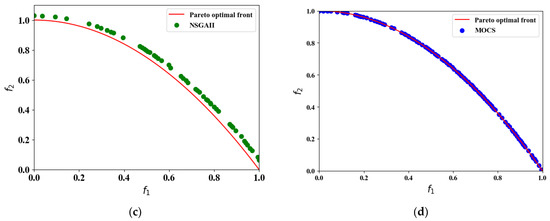
Figure 3.
The convergence results of ZDT test problem over all algorithms. (a) IMOCS, (b) SPEAII, (c) NSGAII, and (d) MOCS.
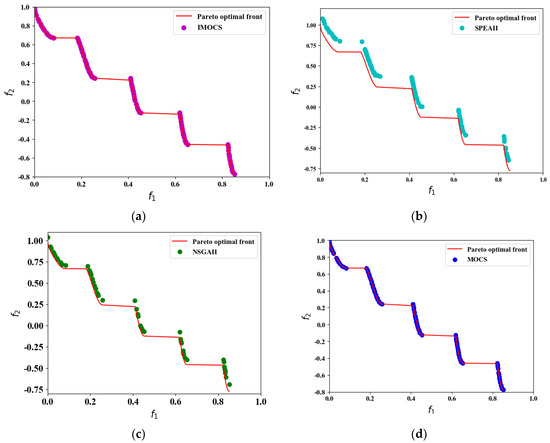
Figure 4.
The convergence results of ZDT3 test problem over all algorithms. (a) IMOCS, (b) SPEAII, (c) NSGAII, and (d) MOCS.
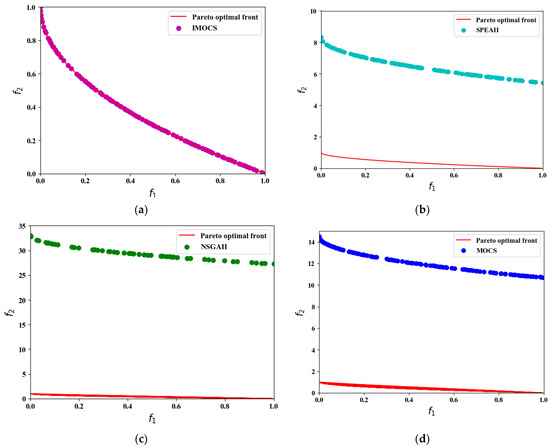
Figure 5.
The convergence results of ZDT4 test problem over all algorithms. (a) IMOCS, (b) SPEAII, (c) NSGAII, and (d) MOCS.
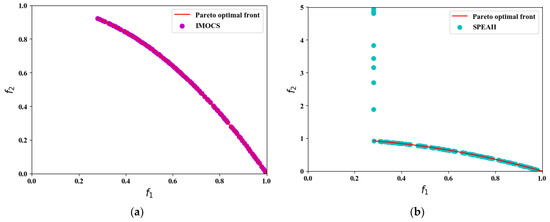
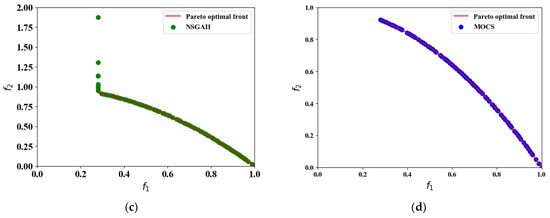
Figure 6.
The convergence results of ZDT6 test problem over all algorithms. (a) IMOCS, (b) SPEAII, (c) NSGAII, and (d) MOCS.
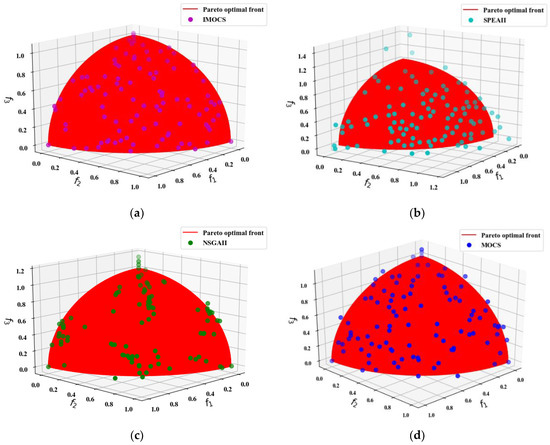
Figure 7.
The convergence results of DTLZ2 test problem over all algorithms. (a) IMOCS, (b) SPEAII, (c) NSGAII, and (d) MOCS.
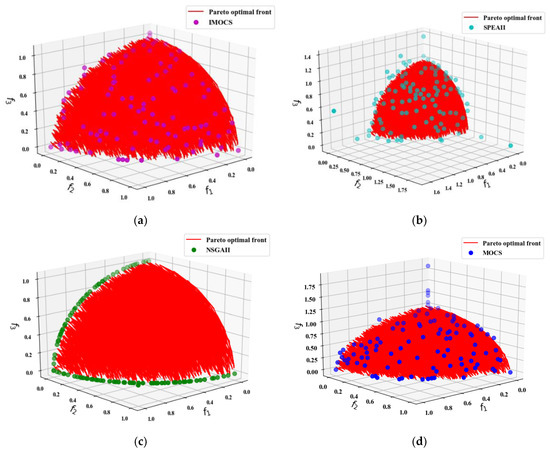
Figure 8.
The convergence results of DTLZ4 test problem over all algorithms. (a) IMOCS, (b) SPEAII, (c) NSGAII, and (d) MOCS.
It can be seen from Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 that the four algorithms are in the process of solving the MOO problems. The IMOCS is far superior to the other three comparison algorithms in terms of non-dominated density and accuracy.
In the ZDT1 function problem, Figure 2a–d show that the non-dominated solutions found by the IMOCS and MOCS are uniformly covered on the true Pareto front surface, but the solution of the MOCS on the front surface is relatively sparse compared to IMOCS; the spacing is large. The non-dominated solutions obtained by the SPEAII and NSGAII are close to the true Pareto front, but they are not distributed on the true Pareto front.
When optimizing the non-convex function ZDT2, IMOCS shows a high optimization accuracy in Figure 3a, and all the solutions can be evenly distributed on the Pareto front surface. In Figure 3b, the non-dominated solutions obtained by the SPEAII do not cover the entire true Pareto front surface, and the accuracy of the obtained solutions is very poor, much higher than the real solution. When the NSGAII optimizes ZDT2, the solution obtained is much better than that of the SPEAII and is closer to the true Pareto front. However, it can be seen from Figure 3c that the non-dominated solution is sparsely distributed, which indicates that most of the solutions searched by the NSGAII algorithm are relatively low. Moving in a small area results in poorer accuracy of the later iterative search than the IMOCS and MOCS. In Figure 3d, the MOCS solutions are all on the real Pareto, but the distribution of IMOCS solutions is denser than that of the MOCS, SPEAII, and NSGAII. In the process of optimizing ZDT3 for the four algorithms, the performance of the IMOCS and MOCS after 1000 iterations is almost the same as when solving ZDT2. The density distribution of non-dominated solutions obtained by the NSGAII is far worse than that of the SPEAII.
It can be seen from Figure 5 that in the later search process of IMOCS, the local minimum function can be better escaped through disturbance, and the global optimal non-dominated solution can be found quickly. While SPEAII uses external archiving technology to optimize complex multimodal functions, it can be seen from Figure 5b that the disturbance capability of external archiving technology is relatively weak and cannot make the SPEAII algorithm jump out of the local extreme state. In the later stage of the iteration, the NSGAII and MOCS have no disturbance mechanism and external archiving schemes, and both of them have fallen into a partial stagnation state and cannot search for the best non-dominated solution.
In Figure 6a–d, it can be seen that both the SPEAII and NSGAII can cover the true Pareto front surface. Due to the insufficient ability of later optimization, some non-inferior solutions cannot converge to the real PF. All non-inferior solutions found by the IMOCS and MOCS can fall on PF, but there is a big gap in particle uniformity distribution.
When optimizing the three-dimensional multi-objective function DTLZ2, the non-inferior solutions obtained by the IMOCS can be uniformly distributed on the PF, and the solutions obtained by the NSGAII can also be scattered on the PF, but most of the solutions are concentrated in a certain area, resulting in uneven particle distribution. In addition, Figure 7b shows that most of the solutions generated by SPEAII dealing with the DTLZ2 problem are beyond the optimal PF frontier, which indicates that the convergence accuracy of the SPEAII optimization is poor. However, the MOCS algorithm achieves a non-inferior solution (Figure 7d) that is the uniform distribution on the PF, but the parts of the non-inferior solution that are not closely of the PF. Figure 7 shows that IMOCS obtained by the four algorithms are superior to that of MOCS, NSGAII, and SPEAII in terms of uniformity and diversity of non-dominated solutions, and describes that the IMOCS can effectively find non-inferior solutions distributed on true PF in the case of 1000 iterations, and it can quickly converge to the optimal PF.
In optimizing the DTLZ4 problem, NSGAII shows poor convergence performance due to most of the non-dominated solutions being linearly distributed at the real PF (Figure 8c), and all non-inferior solutions have not covered the PF. It is also implied that the NSGAII cannot handle the high-dimensional problems effectively, so the solution fails to cover the entire PF. Meanwhile, the NSGAII also has a low convergence accuracy due to the poor solution diversity. Figure 8b reveals that the non-dominated solutions generated by SPEAII are similar to the optimization DTLZ2 problem. Most of the non-inferior solutions fail to find the best frontier, resulting in low convergence accuracy of the SPEAII. However, the non-inferior solution obtained by the MOCS algorithm is better than the former (NSGAII and SPEAII), but compared with the convergence diagram of the IMOCS in Figure 8a, the uniformity of the obtained solution is slightly worse than the IMOCS, and there are some solutions beyond the range of true PF.
According to the convergence results of the above four heuristic algorithms to optimize the multi-objective benchmark functions, it can be seen that the non-dominated solutions obtained by IMOCS algorithm can uniformly cover the optimal Pareto frontier. In addition to the ZDT4 function, the MOCS algorithm can find solutions that converge to the Pareto front, but the distribution of the solutions is relatively sparse compared to that of the IMOCS. However, the non-inferior solutions obtained by the NSGAII and SPEAII have poor convergence accuracy compared with that of the IMOCS and cannot converge to the optimal Pareto front surface. It can be seen that the IMOCSs are highly competitive in the convergence measure and have the ability to deal with complex problems. They can quickly jump out of local extreme values by perturbation and adjustment of Levy flight strategy, showing high convergence accuracy.
To further analyze the performance of the IMOCS, the indicators including GD, IGD, and HV are used to analyze the convergence and diversity and the records of the mean, std, and optimal value of the four algorithms, which are running 30 times independently under different indicators. Numerical experimental data such as the worst solution and the results of Wilcoxon rank-sum test, GD, IGD, and HV numerical statistics are shown in Table 3, Table 4 and Table 5, respectively. From the data in these tables, the IMOCS can successfully deal with ZDT, DTLZ2, and DTLZ4 in GD, IGD, HV, and other measures and obtain the optimal value on the Pareto frontier.

Table 3.
Related statistical data based on the GD.

Table 4.
Related statistical data based on the IGD.

Table 5.
Related statistical data based on the HV.
For the ZDT1 problem, it is found from Table 3, Table 4 and Table 5 that the MOCS and IMOCS are similar in convergence measures (GD, IGD, HV), but the mean and variance of IMOCS are slightly better than MOCS and significantly better than SPEAII and NSGAII. In terms of density indicators (IGD, HV), the density indicators of IMOCS and MOCS are not much different, and the obtained non-dominated solutions are evenly distributed on the Pareto front, indicating that the diversity of IMOCS and MOCS solutions is better. However, algorithms such as NSGAII and SPEAII, especially in the IGD indicators in Table 4, have significantly worse solution diversity than IMOCS, indicating that the solutions they find are not all on the true Pareto frontier.
In the ZDT2, the IMOCS ranks first among the GD, IGD, HV, and other indicators, followed by MOCS ranking second, and NSGAII and SPEAII are ranking third and fourth, respectively.
ZDT3 is a convex optimization problem containing a large number of non-continuous Pareto frontiers. The IMOCS has obtained the best non-inferior solution in the GD, IGD, and HV, compared with the other three algorithms, and reached the optimal GD-standard deviation, IGD-standard deviation, and HV-standard deviation. It indicates that the IMOCS can obtain stable convergence performance when optimizing the ZDT3 problem. Secondly, in the HV indicators, the mean values of IMOCS and MOCS are the same, but the standard deviation of IMOCS is smaller, reflecting that the population diversity obtained by IMOCS after 1000 iterations is relatively denser than that of the MOCS, SPEAII, and NSGAII.
Focusing on the ZDT4, all evaluation indicators can obtain the best solution. It is difficult to find the global optimal Pareto front for algorithms with weak adaptive ability and weak external disturbance ability because the ZDT4 contains 219 different local optimal Pareto fronts in the search domain. Therefore, the MOCS, NSGAII, and SPEAII are stuck in different local Pareto fronts when iterating 1000 times and cannot jump out of the local extremes. Although the ZDT6 has a non-uniform search domain, it can be seen from the evaluation data of GD, IGD, and HV that the IMOCS algorithm can obtain the best non-inferior solution in terms of convergence and solution density. In contrast, the MOCS obtains non-inferior solutions in solution density indicators (IGD, HV), followed by the IMOCS, SPEAII, and NSGAII.
The results of DTLZ2 optimization by four algorithms that can be seen from the data are the IMOCS has obtained good non-inferior solutions in both convergence indicator and density indicator, and its stability is much better than that of the MOCS, SPEAII, and NSGAII. Although the average value obtained by MOCS in the diversity indicator is not much different from that of the IMOCS, some non-inferior solutions are dissociated on the true Pareto front surface, resulting in the diversity of non-inferior solutions obtained by the MOCS being far worse than that of the IMOCS.
For the optimization DTLZ4 problem, the convergence and diversity indicators of the four algorithms are evaluated. As shown in the statistical results in Table 3, Table 4 and Table 5, the non-inferior solution obtained by the NSGAII in the GD indicator is smaller than that of IMOCS, and then its convergence is better than the IMOCS. However, the comprehensive evaluation of indicators (such as IGD and HV) shows that the diversity of non-inferior solutions of the NSGAII is far worse than the IMOCS. Therefore, when NSGAII addresses the high-dimensional and complex DTLZ4 problems, most solutions are closely distributed in a small area at the bottom of the true PF surface. As a result, the GD indicator is considered to coincide with the true Pareto frontier in evaluating the convergence, which leads to its convergence in the GD indicator being better than other algorithms. Second, in Table 4 and Table 5, IMOCS is far superior to the other three algorithms in both convergence and diversity evaluation, and the ranking remains the first, while the MOCS ranks the second and SPEAII and NSGAII are the third and fourth position, respectively.
According to the above experimental statistics, the optimization problems (ZDT1-4, ZDT6, DTLZ2, and DTLZ4) of the IMOCS in GD, IGD, and HV indicators can obtain reasonable solutions, and the rank-sum test W+/W− obtained by Wilcoxon rank-sum test are 28/0. It demonstrates that the strong performance of the IMOCS is superior to other comparison algorithms in terms of convergence and diversity, and the ranking remains the first.
To enhance the conclusions of the previous experimental results, mean analysis is used to test the performance of the entire algorithm in an environment of 30 independent runs, and the overall performance of different algorithms to optimize different functions is shown through boxplots as shown in Figure 9, Figure 10 and Figure 11. In the box chart, the yellow dotted line represents the median, the horizontal line below the graph is the minimum value, the horizontal line above the graph is the maximum value, and the open circle indicates that the current algorithm optimizes a problem for 30 independent runs. The resulting data exceed the maximum the abnormal value of the range of the value and the minimum value.
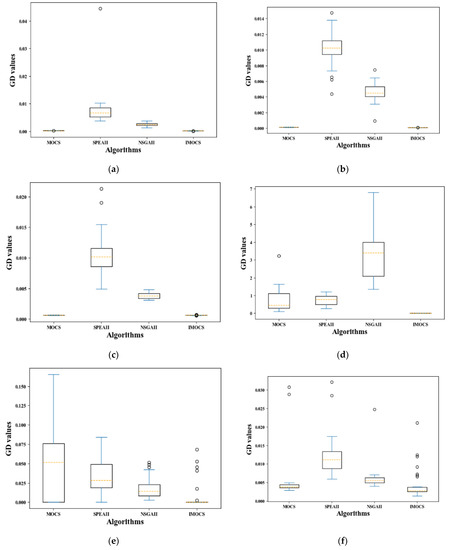
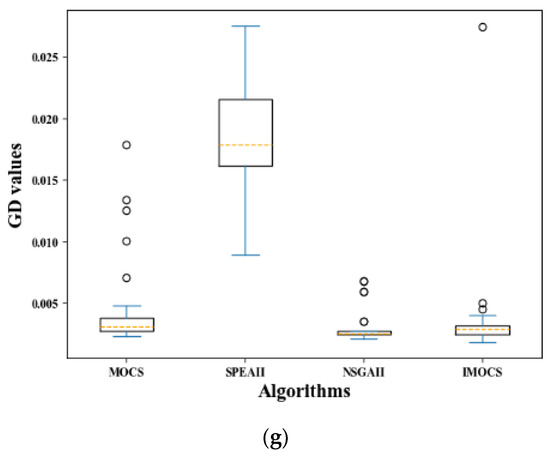
Figure 9.
Boxplot of GD values achieved by different algorithms. (a) ZDT1, (b) ZDT2, (c) ZDT3, (d) ZDT4, (e) ZDT6, (f) DTLZ2, and (g) DTLZ4.
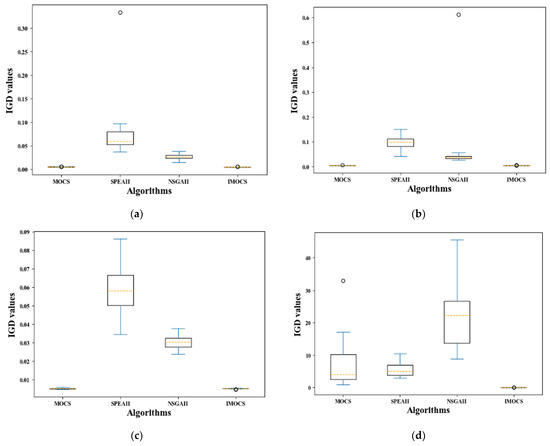
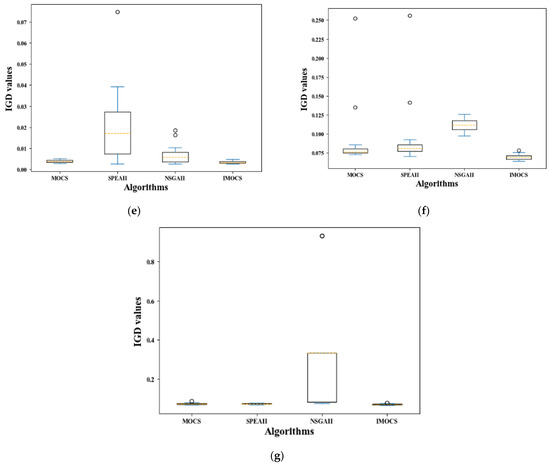
Figure 10.
The results of IGD test problem over all algorithms. (a) ZDT1, (b) ZDT2, (c) ZDT3, (d) ZDT4, (e) ZDT6, (f) DTLZ2, and (g) DTLZ4.
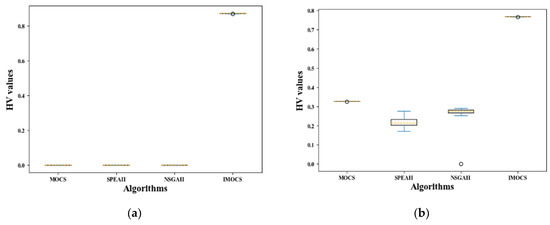
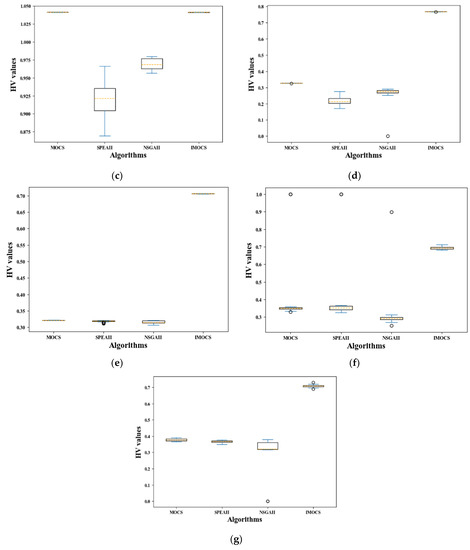
Figure 11.
The results of HV test problem over all algorithms. (a) ZDT1, (b) ZDT2, (c) ZDT3, (d) ZDT4, (e) ZDT6, (f) DTLZ2, and (g) DTLZ4.
Based on the characteristics analysis of the boxplot, the boxplot of IMOCS occupies the smallest area (except Figure 9c), and they are all in the range of 0.001–0.005, indicating that IMOCS has the best convergence performance in the GD indicator relative to the other comparison algorithms. Secondly, the occupied area of the boxplot obtained by the NSGAII is much smaller than the other three algorithms in optimizing the DTLZ4 problem. Moreover, Figure 9a–f show that the area of the boxplot is larger than IMOCS and MOCS and the convergence of NSGAII is worse than IMOCS and MOCS. However, in the process of GD indicator evaluation, the boxplot occupied area obtained by the SPEAII optimization function is the largest of the other three algorithms, implying that the SPEAII algorithm is the worst in terms of convergence. In addition, the MOCS can also get a smaller graph area in the GD indicator, but when optimizing functions such as ZDT4-ZDT6, the graph occupies a larger space (0–1.5, 0–0.17), indicating that the MOCS has relatively poor convergence performance when solving complex problems. It can be seen that the convergence of the IMOCS algorithm has been further improved. It can be seen from Figure 10 that the space occupied by the box diagram of IMOCS and MOCS is roughly similar, while the maximum and minimum values on the box diagram of IMOCS are smaller than those of the MOCS and the number and value of outliers generated by the MOCS in DTLZ2 are larger than those of the IMOCS. While the SPEAII and NSGAII have a large graph span space, it can be seen from the characteristics of IGD that the convergence performance and non-inferior solution diversity of SPEAII and NSGAII are worse than that of the IMOCS and MOCS, but the SPEAII is better than NSGAII. In addition, in Figure 10, the MOCS, SPEAII, and NSGAII obtained corresponding box diagrams on ZDT1-2, ZDT4-5, and DTLZ2, occupying a small HV value, and the abnormal points generated by the three in DTLZ2 can be close to 1, but relative to the entire algorithm, their convergence and diversity are weaker than IMOCS. The HV value corresponding to the position of the IMOCS box diagram is larger than the other three algorithms, which shows that the non-inferior solution searched by the IMOCS algorithm is closer to the true Pareto frontier, and the convergence performance is obviously improved.
Through the above numerical experiment analysis and discussion, it can be noted that the proposed IMOCS can better deal with different types of MOPs. On the one hand, it adjusts the exploration range and changes the random migration mechanism according to iterative growth to ensure jumping out of the complex local optimal region, improving the population density, enhancing the convergence of the MOCS, and finding the global optimal Pareto non-inferior solution quickly. On the other hand, the demonstration of experimental results also implies that the improved ideas of this algorithm have good feasibility.
5. Collaborative Obstacle Avoidance Task of Multiple UAVs Using IMOCS
In the section, to further verify the practically of the proposed method, the IMOCS is used to optimize the collaborative obstacle avoidance task of multiple UAVs within an appropriate time.
5.1. UAV Model
It is necessary to consider the relative position between UAVs, and the UAV is regarded as a particle for addressing the cooperative obstacle avoidance problem of multiple UAVs in the obstacle environment. The single-UAV model can be simplified into a UAV kinematic model and an autopilot model by considering six parameters (including speed, yaw angle, altitude, and three types of autopilots) [29,30,31]. The formula is illustrated as shown in Equation (18).
where represents the position coordinates of the i-th UAV in the x, y, and z direction under the inertial coordinate system, respectively; are the horizontal speed, yaw angle, and altitude rate of the i-th UAV, respectively; are the time constants of Mach channel, heading channel, altitude rate channel, and altitude channel, respectively; are the control inputs of the i-th UAV Mach-hold autopilot, heading-hold autopilot, and altitude-hold autopilot, respectively, and the three control inputs of autopilot [31], those specific calculation are shown in Equation (19):
where represents the control inputs components in the x, y, and z directions, respectively. In addition, the flight constraints also need to be considered in the UAV model, as shown in Equation (20):
In the formula, represent the maximum horizontal velocity, minimum horizontal velocity, maximum lateral overload, maximum altitude rate, and gravity acceleration, respectively. The values of these variables are greater than 0, and the gravity acceleration g = 10 m/s2; is the minimum altitude rate, and the corresponding value is marked less than 0 ().
5.2. Simulation Experiments
The experiment is designed based on the references [30,31]. In the subsection, NSGAII, MOCS, IMOCS, and multi-objective pigeon-inspired optimization (MPIO) [30] are used to optimize UAVs’ formation obstacle avoidance control. In order to ensure the normal operation of these algorithms, the parameters are designed as follows.
The population numbers of the NSGAII, MOCS, and IMOCS are set as 20, but the population number of the MPIO is set as 58 [30].
The maximum number of iterations are set to 20 times.
In addition, we selected five UAVs to fly in the three-dimensional space, and the related parameters are listed in Table 6; the initial position value of UAVs are given in Table 7. Other initial state parameters of UAVs are also set, which include horizontal airspeed , yaw angle , altitude rate , and expected altitude . However, when five UAVs fly in formation through the area of seven obstacles in the horizontal direction and the radius parameters of obstacles, as shown in Table 8, the maximum running time required by UAVs to fly over different obstacles is set at 42 s, and the sampling time interval is set at 0.5 s.

Table 6.
Parameter setting of UAVs.

Table 7.
Initial position parameters of five UAVs.

Table 8.
Position and radius parameters of seven obstacles.
Figure 12 displays the simulation results of the proposed method in this paper. The circle graph represents obstacles, the triangle represents UAVs, the yellow curve, the magenta curve, the red curve, the black curve, and the green curve, respectively, represent the flight routes of the first, second, third, fourth, and fifth UAVs.
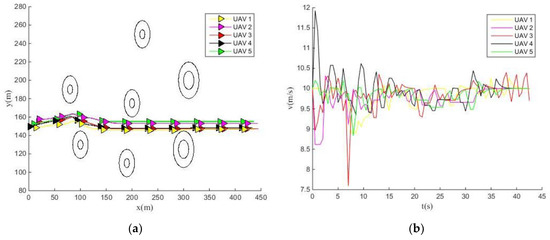
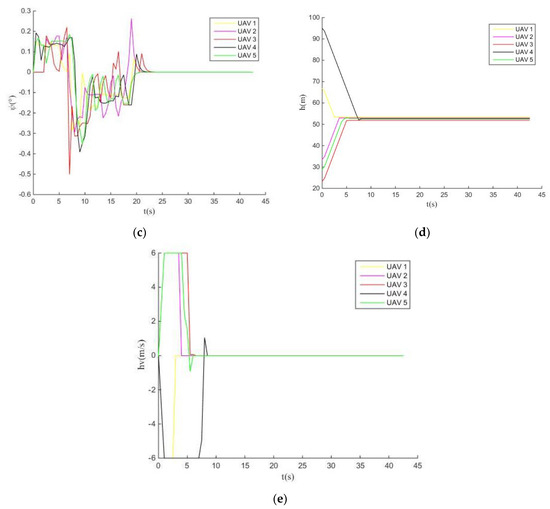
Figure 12.
IMOCS optimizes the flight change curves of UAVs. (a) Obstacle avoidance curve of UAVs; (b) Horizontal airspeed change curves of UAVs; (c) Yaw angle change curves of UAVs; (d) Flight altitude change curves of UAVs; (e) Altitude rate change curves of UAVs.
Figure 12a shows that the five UAVs smoothly pass through the obstacles’ information while the obstacles are very closely arranged. Moreover, the five UAVs that failed to detour from the top obstacle were controlled by the control strategy of the UAV to find the shortest safe route and easily pass through the obstacle area. Figure 12b illustrates the horizontal airspeed change curves of the UAVs 1–2, and UAVs 4–5 are converged to 10 m/s at the 38 s, while the UAV3 has fluctuated after 42 s. Since the amplitude of oscillation is within the allowable range, it was also considered consistent with the horizontal airspeed of the other four UAVs. Meanwhile, all UAVs converged to 0rad within 25 s in Figure 12c and remained the same until 42 s. This indicates that the five UAVs flying in the exact directions after 25 s can effectively avoid the obstacle. When the UAV reaches the expected altitude in the vertical direction, the UAVs start from the preset altitude and slowly through the obstacle area during the iterations. Its vertical altitude tends to the expected altitude. Figure 12d exhibits that all UAVs converge to the expected altitude and remain consistent in 10 s, and the altitude rate also is changed. In addition, both UAV1 and UAV4 descended from a height to a position with a vertical altitude of 50 m, and their altitude rate curves (Figure 12e) show an extremely rapid decline from 0 m/s to −6 m/s within 0–2 s. However, the altitude of the UAV1 was relatively lower than the UAV4, and then there was a rapid rise to the expected speed of 0m/s after 3 s. On the contrary, the UAV4 kept a constant decline from 2 s to 7 s until it rose rapidly after 7 s, and finally reached the expected altitude rate converged to 0m/s at 10 s. At the same time, the vertical altitude of UAV2–3 and UAV5 is lower than the expected vertical altitude. It rose rapidly to a constant speed and then changed from a constant speed to a rapid decline, until the altitude rate of all UAVs converged to the expected level at 10 s in this process
Figure 13, Figure 14 and Figure 15 display the experimental results of cooperative obstacle avoidance of multiple UAVs using MPIO, MOCS, and NSGAII.
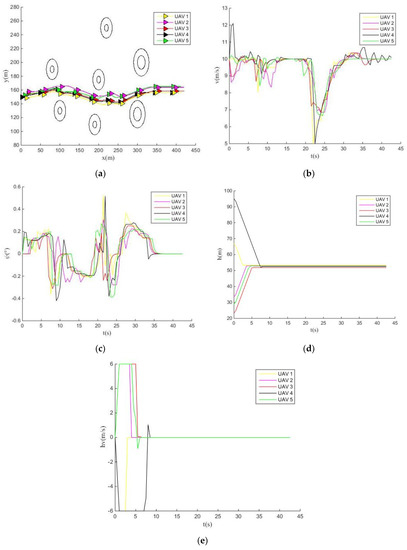
Figure 13.
MPIO optimizes the flight change curves of UAVs. (a) Obstacle avoidance curve of UAVs; (b) Horizontal airspeed change curves of UAVs; (c) Yaw angle change curves of UAVs; (d) Flight altitude change curves of UAVs; (e) Altitude rate change curves of UAVs.
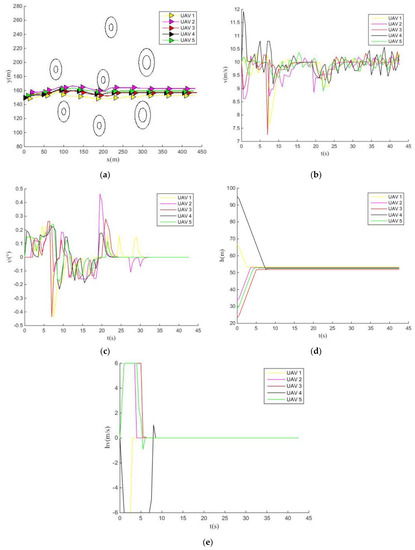
Figure 14.
MOCS optimizes the flight change curves of UAVs. (a) Obstacle avoidance curve of UAVs; (b) Horizontal airspeed change curves of UAVs; (c) Yaw angle change curves of UAVs; (d) Flight altitude change curves of UAVs; (e) Altitude rate change curves of UAVs.
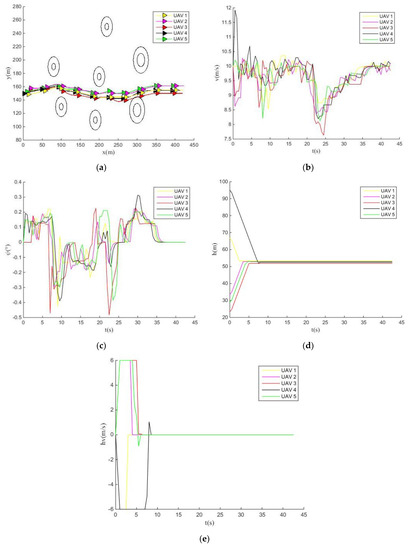
Figure 15.
NSGAII optimizes the flight change curves of UAVs. (a) Obstacle avoidance curve of UAVs; (b) Horizontal airspeed change curves of UAVs; (c) Yaw angle change curves of UAVs; (d) Flight altitude change curves of UAVs; (e) Altitude rate change curves of UAVs.
In Figure 13a, the MPIO also obtained the best safe route. It makes multiple deflections and finally passes through the obstacle area when the UAVs cross obstacles. Due to the multiple deflections of UAVs, the yaw angle also changes (Figure 13c), which makes the UAVs unable to converge consistently within 35 s, and the overall yaw angle convergence efficiency of UAVs is worse than the IMOCS’. Meanwhile, only the horizontal velocity of the UAV4 is fluctuated after the execution of the maximum running time and is also regarded as convergence within the allowable range.
It can be seen from Figure 14 that the horizontal velocity convergence curves of the five UAVs obtained by the MOCS are in a state of fluctuation within 42 s, and the expected convergence has not been achieved. In addition, the MOCS optimized the yaw angle of UAVs, but some UAVs still adjusted their flight direction between 25–35 s until they reached the expected yaw angle at 35 s.
When the NSGAII optimized the multiple UAVs obstacle avoidance process in Figure 15, the UAV3 was very close to the curve of the outer edge of the seventh obstacle and made a quick turn to avoid hitting this obstacle in the later iteration stage. It further caused the yaw angle to change until all UAVs’ yaw angles converged to the same at 35 s. However, the horizontal velocity of the NSGAII was also consistent with the MOCS, and none of all UAVs reached the expected speed within the specified time. Finally, all UAVs have the same initial altitude in the vertical direction and enter the expected altitude in the obstacle area. Therefore, only IMOCS has the altitude change and altitude rate change in the vertical direction.
In this section, different simulation results are obtained by using different algorithms to optimize the problem of multiple UAVs’ cooperative obstacle avoidance with a given maximum running time. In the horizontal direction, the speed of all UAVs is only the IMOCS, and MPIO arrives within 42 s. However, when the yaw angle converges to the expected yaw angle, the time spent by the IMOCS is less than MPIO. This is better than the MOCS and NSGAII. Meanwhile, the convergence speed of IMOCS is also the fastest.
6. Conclusions
An improved multi-objective cuckoo search algorithm (IMOCS) is discussed in this manuscript to solve MOO problems. The step size factor of Levy’s flight was used to adjust the search range adaptively. Secondly, a new local search method was constructed using dynamic random migration and disturbance factors to develop search space. Two types of experiments are employed to verify the effectiveness of the IMOCS. On the one hand, three classic multi-objective algorithms (MOCS, NSGAII, SPEAII) and the IMOCS are used to test five kinds of ZDT and DTLZ2 multi-objective benchmark issues. Meanwhile, the diversity and convergence are effectively evaluated based on the GD, IGD, HV, and other indicators. The results show that the IMOCS can solve different MOPs (such as convexity, concavity, discontinuity, etc.), and the calculated non-inferior solution sets are all uniformly covered on the true Pareto front surface. Secondly, to reflect the performance of the IMOCS algorithm, the Wilcoxon rank-sum test is used to compare and analyze the experimental data of different indicators, which proves that the IMOCS has significant performance in terms of convergence and diversity. Next, the analysis of the visualization of obtained data from the evaluation indicators of GD, IGD, HV, etc. shows that the graph occupancy area obtained by the IMOCS is relatively small, and the accuracy of obtaining the evaluation solution is better than other comparison algorithms. On the other hand, the IMOCS is also applied to solve the real-world problem of multiple UAVs’ cooperative obstacle avoidance. The IMOCS and the other three algorithms can quickly cross the obstacle area, but while the horizontal airspeed of the MOCS and NSGAII cannot achieve convergence to the expected velocity, the MPIO and IMOCS can converge to the expected level within a given time. However, the MPIO took longer than the IMOCS with more yaw angle deflections. The IMOCS is better than the comparison algorithms in applying multiple UAVs’ obstacle avoidance. Hence, the proposed IMOCS could achieve the best performance.
The proposed IMOCS is mainly aimed at extending the adaptive search mechanism and obtaining more accurate optimization results of MOCS. There are still has some disadvantages which need to be overcome. First, the IMOCS may lack searchability in solving high-dimensional MOO problems. Secondly, the parameters are difficult to set for various MOO problems. Hence, the future work could be executed from two aspects. First, our uppermost priority is to enhance the adaptive searchability while solving the high-dimensional MOO problems. Second, studies that design an adaptive adjustment strategy of the parameters due to the population’s current status are also needed.
Author Contributions
Conceptualization, K.-Q.Z.; methodology, S.-Q.Y.; formal analysis, S.-Q.Y.; investigation, S.-Q.Y., Y.O. and C.-X.Z.; writing—original draft preparation, A.M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 62066016 and in part by the Natural Science Foundation of Hunan Province, China, under Grant 2020JJ5458.
Acknowledgments
The authors would like to extend our sincere thanks to Haibin Duan from Beihang University for his guidance and support in this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Srinivas, N.; Deb, K. Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Wang, Y.-N.; Wu, L.-H.; Yuan, X.-F. Multi-objective self-adaptive differential evolution with elitist archive and crowding entropy-based diversity measure. Soft Comput. 2010, 14, 193–209. [Google Scholar] [CrossRef]
- Cui, Y.; Qiao, J.; Meng, X. Multi-stage multi-objective particle swarm optimization algorithm based on the evolutionary information of population. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 3412–3417. [Google Scholar]
- Mahalingam, S.; Kuppusamy, B.; Natarajan, Y. Multi-objective Soft Computing Approaches to Evaluate the Performance of Abrasive Water Jet drilling Parameters on Die Steel. Arab. J. Sci. Eng. 2021, 46, 7893–7907. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wang, J.; Jin, Y. An Enhanced Competitive Swarm Optimizer with Strongly Convex Sparse Operator for Large-Scale Multi-Objective Optimization. IEEE Trans. Evol. Comput. 2021, 1. [Google Scholar] [CrossRef]
- Hu, Z.; Zhou, T.; Su, Q.; Liu, M. A niching backtracking search algorithm with adaptive local search for multimodal multiobjective optimization. Swarm Evol. Comput. 2022, 69, 101031. [Google Scholar] [CrossRef]
- Yue, C.; Suganthan, P.; Liang, J.; Qu, B.; Yu, K.; Zhu, Y.; Yan, L. Differential evolution using improved crowding distance for multimodal multiobjective optimization. Swarm Evol. Comput. 2021, 62, 100849. [Google Scholar] [CrossRef]
- Zouache, D.; Abdelaziz, F.B. Guided Manta Ray foraging optimization using epsilon dominance for multi-objective optimization in engineering design. Expert Syst. Appl. 2022, 189, 116126. [Google Scholar] [CrossRef]
- Marichelvam, M.K.; Prabaharan, T.; Yang, X.-S. Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan. Appl. Soft Comput. 2014, 19, 93–101. [Google Scholar] [CrossRef]
- Karthik, G.; Deb, S. A methodology for assembly sequence optimization by hybrid Cuckoo-Search Genetic Algorithm. J. Adv. Manuf. Syst. 2018, 17, 47–59. [Google Scholar] [CrossRef]
- Yildiz, A.R. Cuckoo search algorithm for the selection of optimal machining parameters in milling operations. Int. J. Adv. Manuf. Technol. 2013, 64, 55–61. [Google Scholar] [CrossRef]
- Zhang, C.-X.; Zhou, K.-Q.; Ye, S.-Q.; Zain, A.M. An improved cuckoo search algorithm utilizing nonlinear inertia weight and differential evolution for function optimization problem. IEEE Access 2021, 9, 161352–161373. [Google Scholar] [CrossRef]
- Peng, H.; Zeng, Z.; Deng, C.; Wu, Z. Multi-strategy serial cuckoo search algorithm for global optimization. Knowl.-Based Syst. 2021, 214, 106729. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Minh, H.-L.; Khatir, S.; Wahab, M.A.; Tran, M.T.; Mirjalili, S. A novel version of Cuckoo search algorithm for solving optimization problems. Expert Syst. Appl. 2021, 186, 115669. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Shen, X.; Zhang, J. A comprehensive wind speed prediction system based on Monte Carlo and artificial intelligence algorithms. Appl. Energy 2022, 305, 117815. [Google Scholar] [CrossRef]
- Niveditha, C.; Ashok, K. ACNN Based Speech Emotion Recognition and Noise Suppression Using Modified Cuckoo Search Algorithm. In Proceedings of the 2nd International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 5–6 July 2019; Volume 1, pp. 79–86. [Google Scholar]
- Kamoona, A.M.; Patra, J.C. A novel enhanced cuckoo search algorithm for contrast enhancement of gray scale images. Appl. Soft Comput. 2019, 85, 105749. [Google Scholar] [CrossRef]
- He, X.; Li, N.; Yang, X.S. Non-dominated sorting cuckoo search for multiobjective optimization. In Proceedings of the IEEE Symposium on Swarm Intelligence, Orlando, FL, USA, 9–12 December 2014; pp. 1–7. [Google Scholar]
- Othman, M.S.; Kumaran, S.R.; Yusuf, L.M. Gene Selection Using Hybrid Multi-Objective Cuckoo Search Algorithm with Evolutionary Operators for Cancer Microarray Data. IEEE Access 2020, 8, 186348–186361. [Google Scholar] [CrossRef]
- Hanoun, S.; Nahavandi, S.; Creighton, D.; Kull, H. Solving a multiobjective job shop scheduling problem using Pareto Archived Cuckoo Search. In Proceedings of the 17th International Conference on Emerging Technologies & Factory Automation (ETFA 2012), Krakow, Poland, 17–21 September 2012; pp. 1–8. [Google Scholar]
- Chen, L.; Gan, W.; Li, H.; Cheng, K.; Pan, D.; Chen, L.; Zhang, Z. Solving multi-objective optimization problem using cuckoo search algorithm based on decomposition. Appl. Intell. 2021, 51, 143–160. [Google Scholar] [CrossRef]
- Paul, D.; Kumar, R.; Saha, S.; Mathew, J. Multi-objective Cuckoo Search-based Streaming Feature Selection for Multi-label Dataset. ACM Trans. Knowl. Discov. Data 2021, 15, 1–24. [Google Scholar] [CrossRef]
- Zainal, M.I.; Yasin, Z.M.; Zakaria, Z. Optimizing Voltage Profile and Loss Minimization using Multi Objective Cuckoo Search Algorithm. In Proceedings of the 11th IEEE Symposium on Computer Applications & Industrial Electronics (ISCAIE), Penang, Malaysia, 3–4 April 2021; pp. 116–122. [Google Scholar]
- Yamany, W.; El-Bendary, N.; Hassanien, A.E.; Emary, E. Multi-Objective Cuckoo Search Optimization for Dimensionality Reduction. Procedia Comput. Sci. 2016, 96, 207–215. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.; Li, Y. Irreversibility analysis for optimization design of plate fin heat exchangers using a multi-objective cuckoo search algorithm. Energy Convers. Manag. 2015, 101, 126–135. [Google Scholar] [CrossRef]
- Rao, N.T.; Sankar, M.M.; Rao, S.P.; Rao, B.S. Comparative study of Pareto optimal multi objective cuckoo search algorithm and multi objective particle swarm optimization for power loss minimization incorporating UPFC. J. Ambient Intell. Humaniz. Comput. 2021, 12, 1069–1080. [Google Scholar] [CrossRef]
- Valasek, J. Small Unmanned Aircraft: Theory and Practice. J. Guid. Control. Dyn. 2013, 36, 344–345. [Google Scholar] [CrossRef]
- Qiu, H.; Duan, H. A multi-objective pigeon-inspired optimization approach to UAV distributed flocking among obstacles. Inf. Sci. 2020, 509, 515–529. [Google Scholar] [CrossRef]
- Ruan, W.-Y.; Duan, H.-B. Multi-UAV obstacle avoidance control via multi-objective social learning pigeon-inspired optimization. Front. Inf. Technol. Electron. Eng. 2020, 21, 740–748. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).