Tutorial on the Use of Deep Learning in Diffuse Optical Tomography
Abstract
:1. Introduction
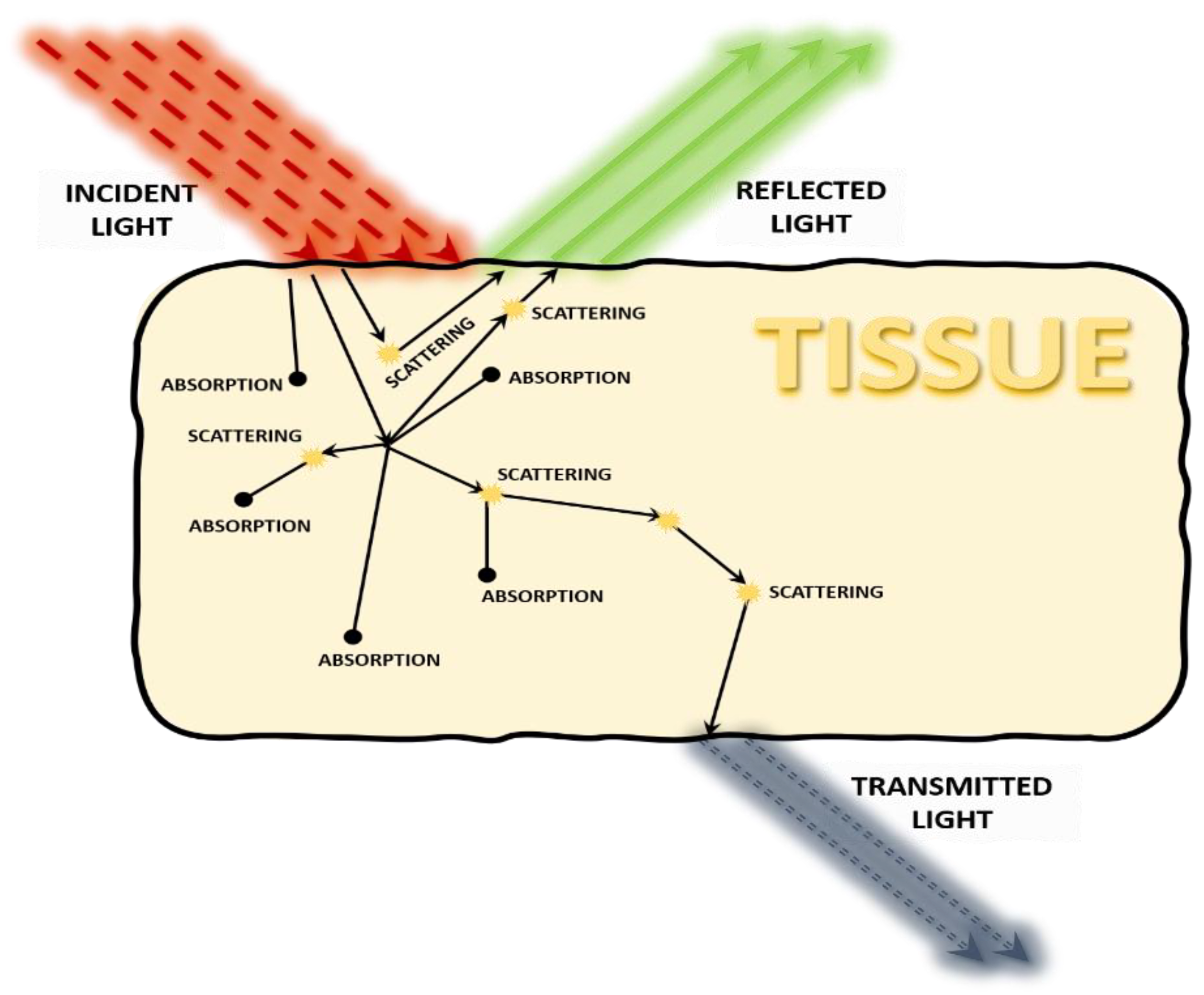
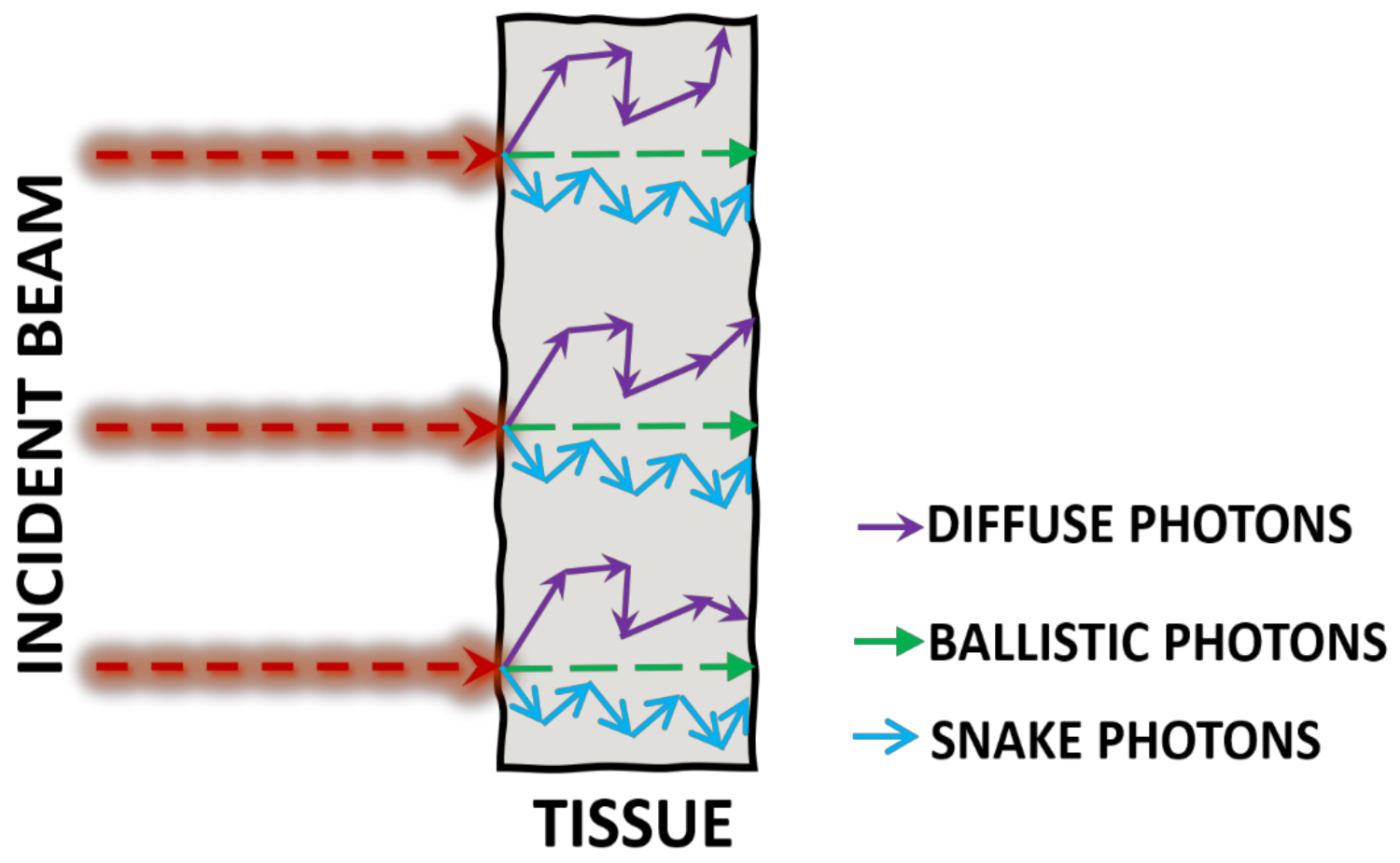
2. Photon Propagation through Tissue
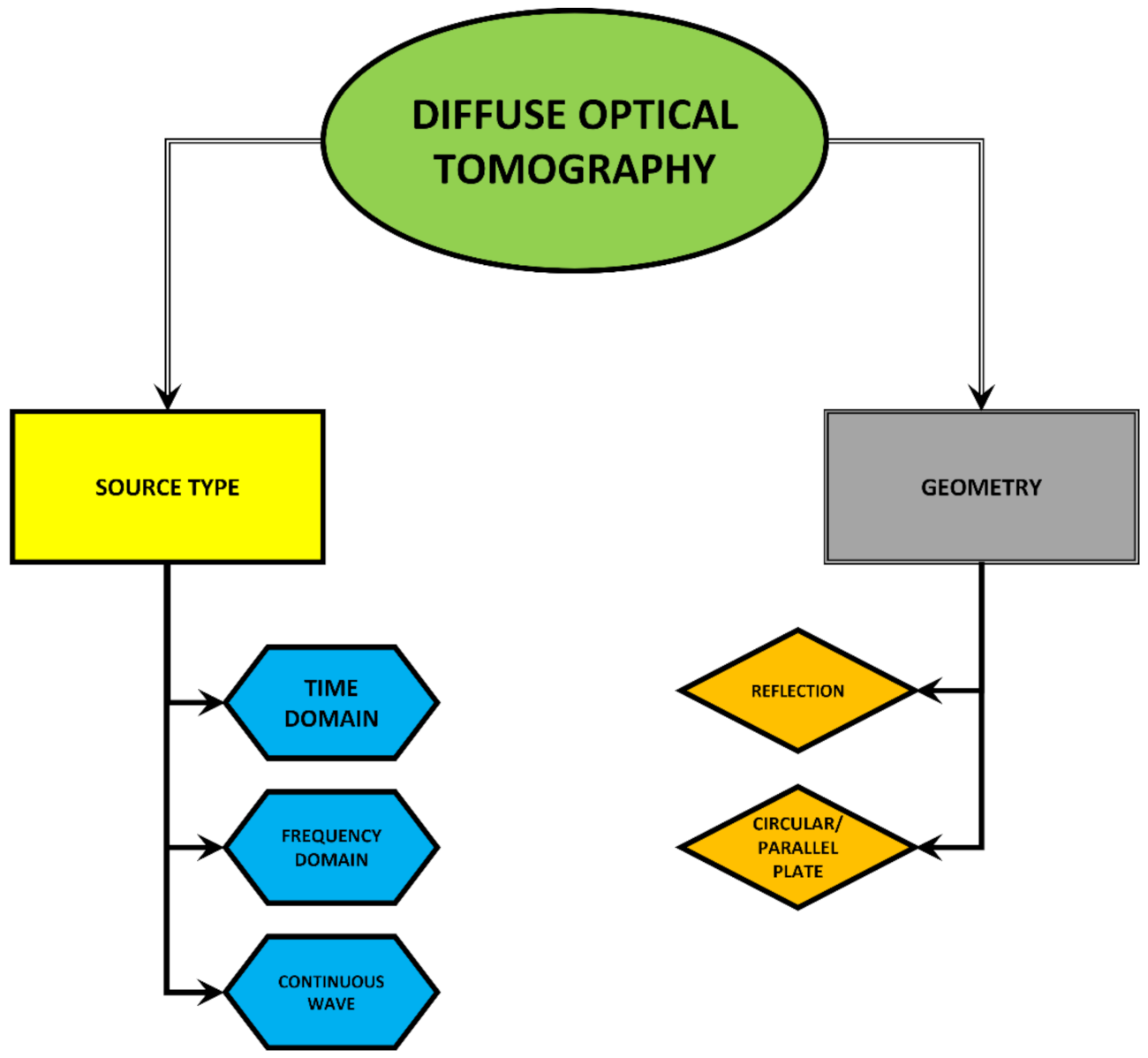
3. Diffuse Optical Tomography (DOT)
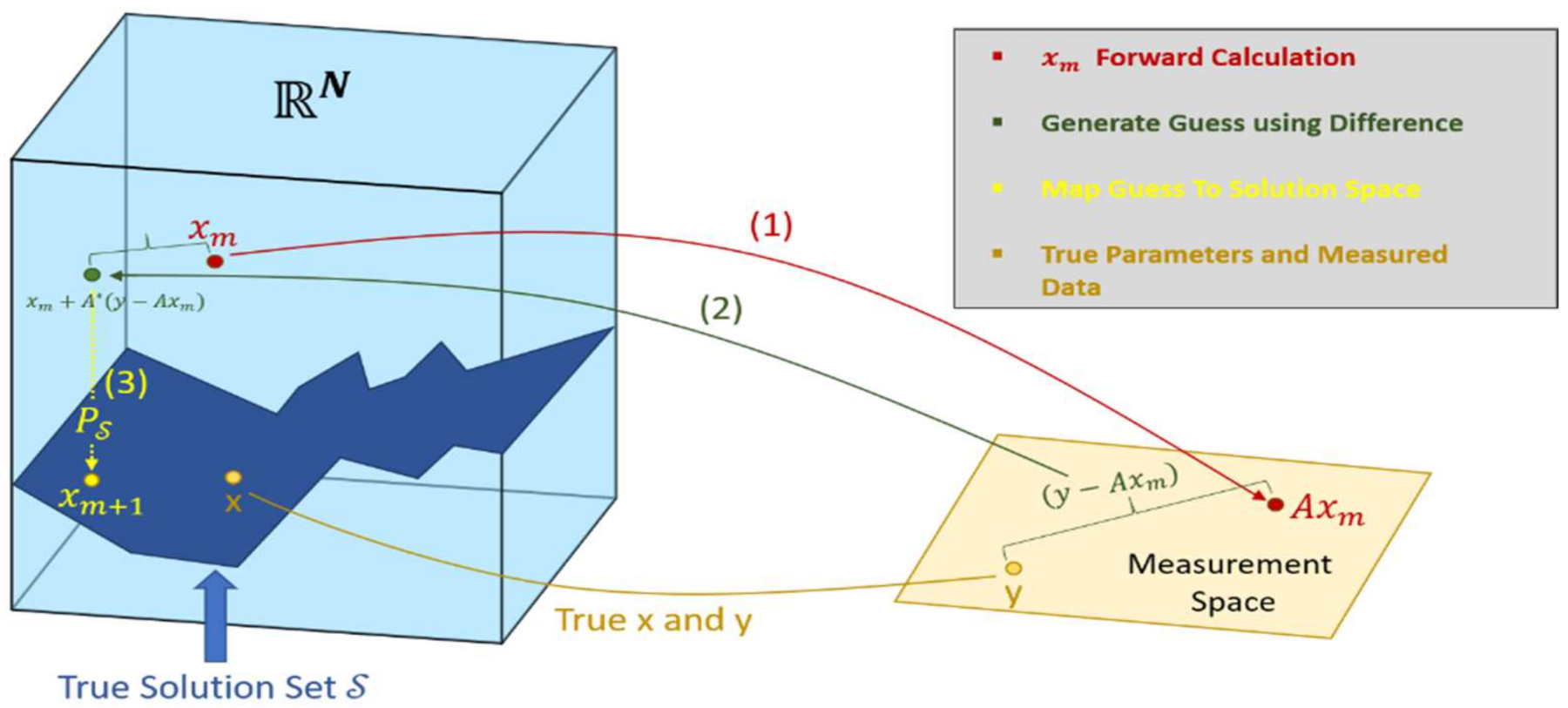
4. Inverse Problems in DOT
5. Deep Learning
6. Deep Learning Diffuse Optical Tomography
7. Deep Learning as a Tool to Solve Inverse Problems
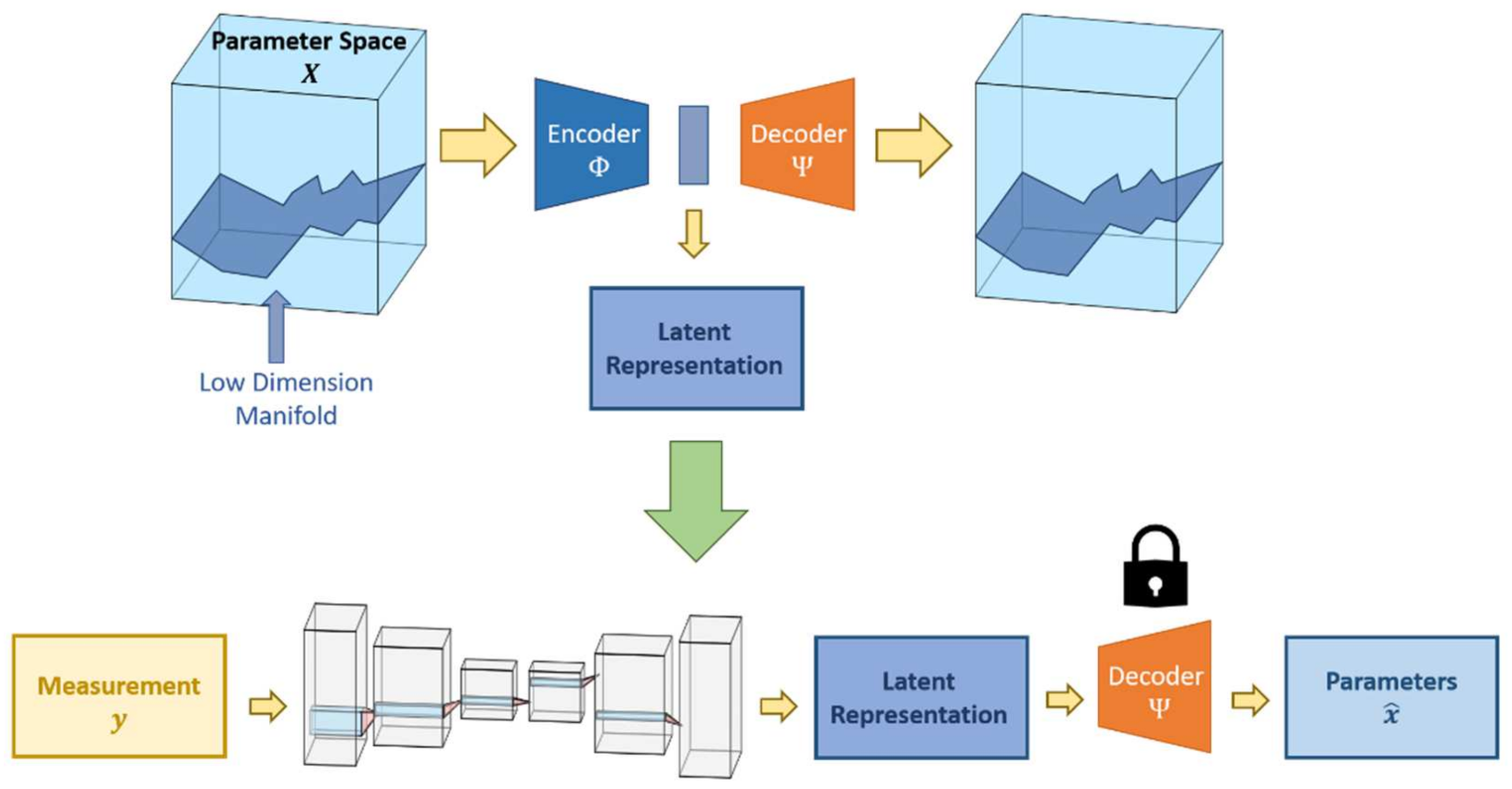
7.1. Feed-Forward Networks
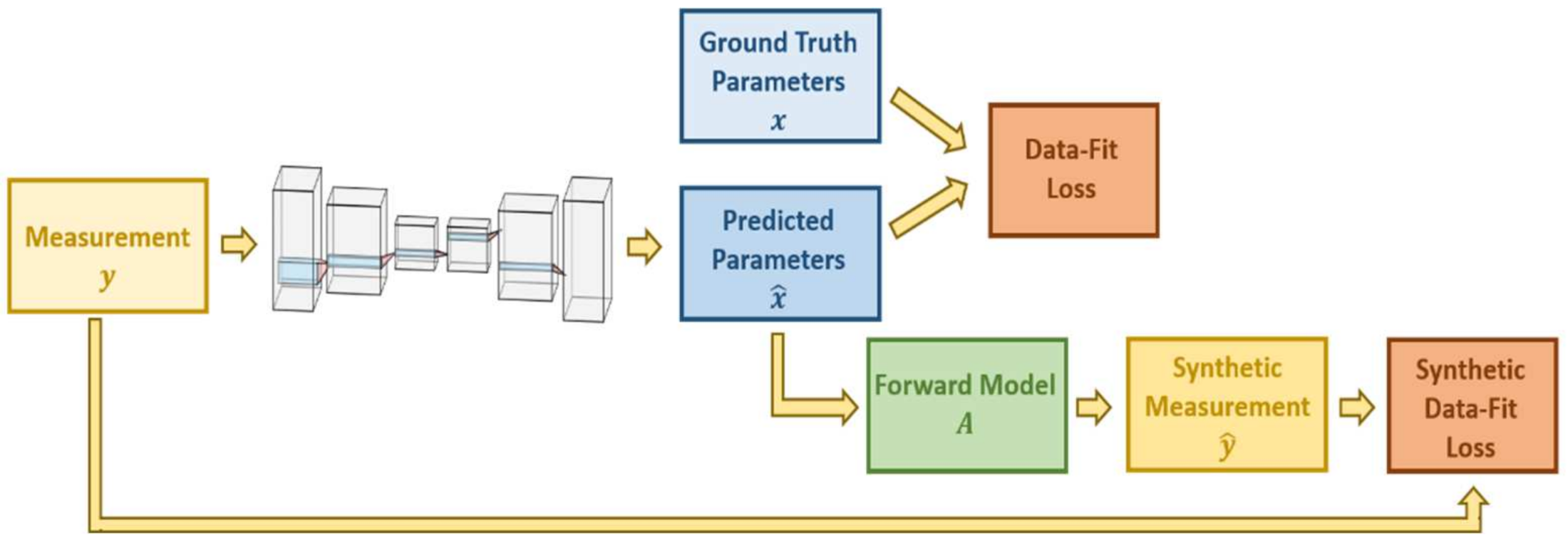
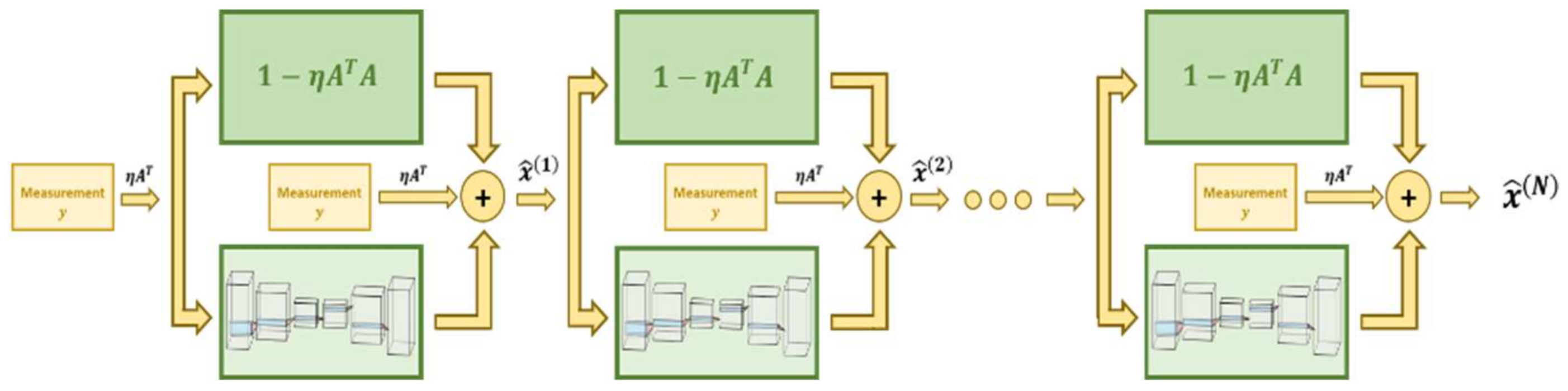
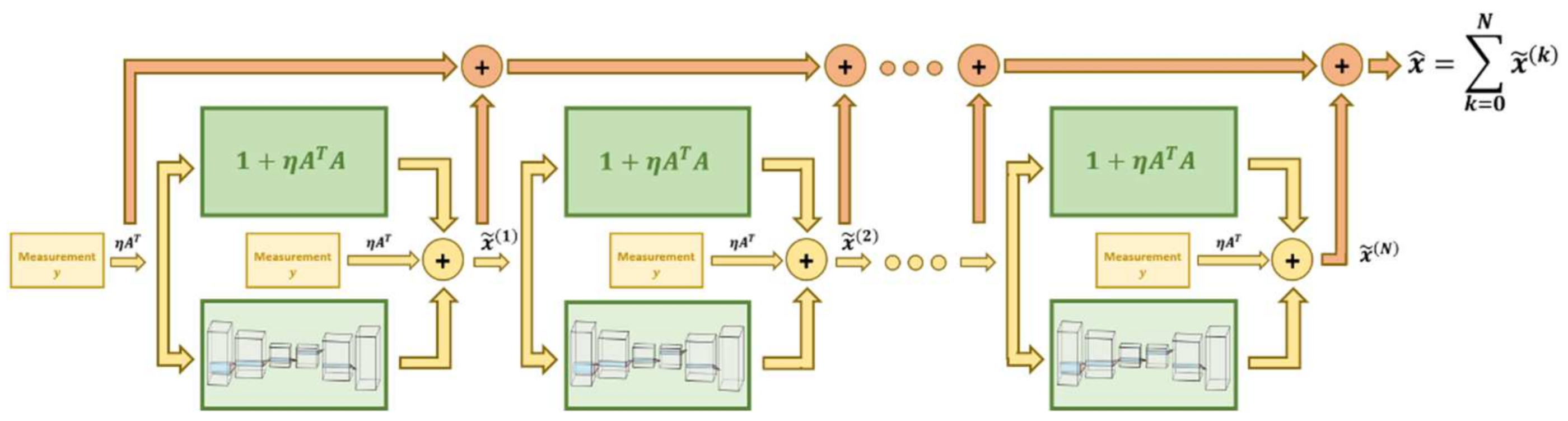
7.2. Regularization Networks
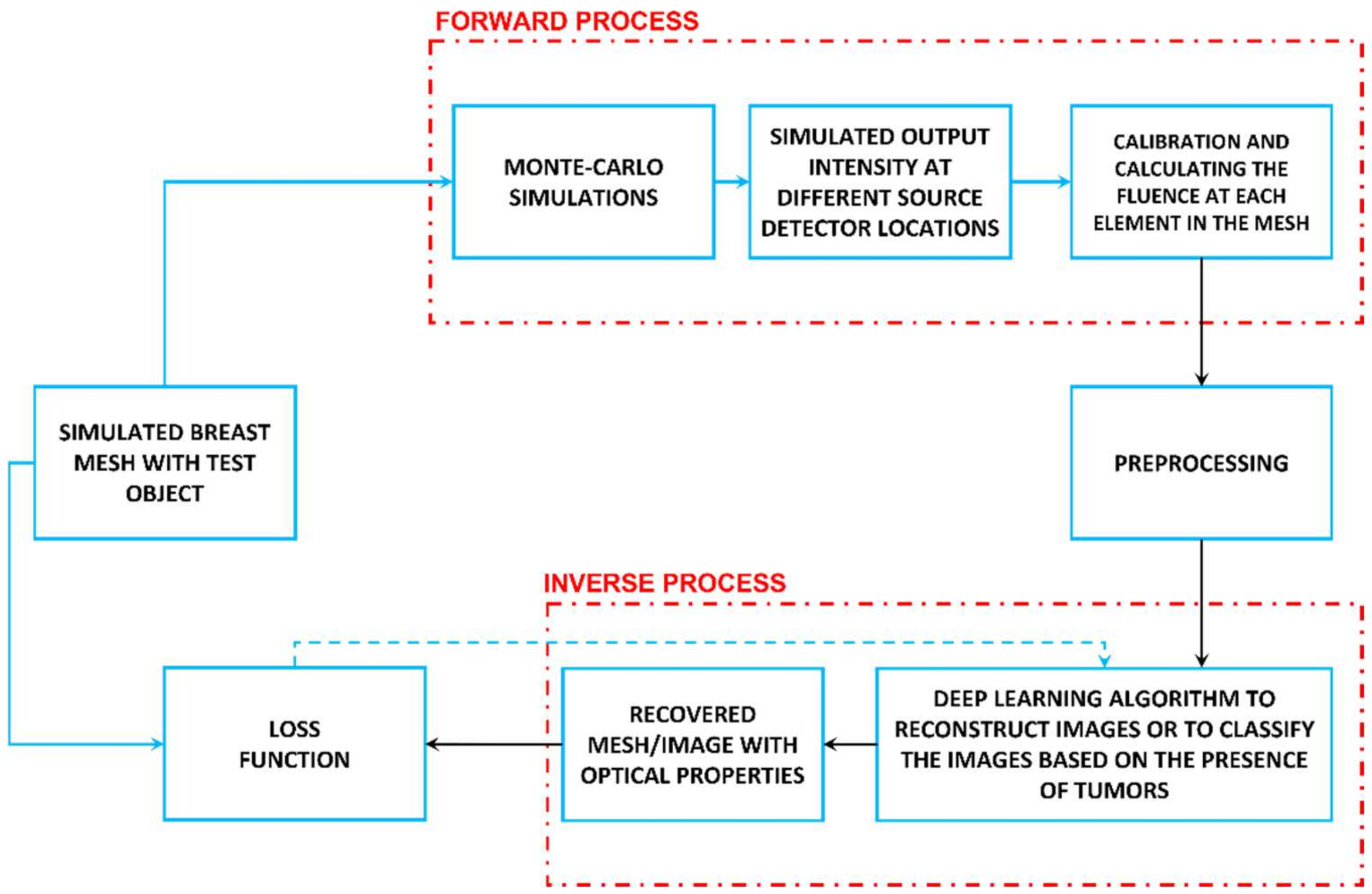
8. Tutorial on the Use of Deep Learning for Diffuse Optical Tomography
- (1)
- Optical property estimation and mesh creation:
- (2)
- Forward process and data creation:
- (3)
- Solving the inverse problem and designing the network architecture:
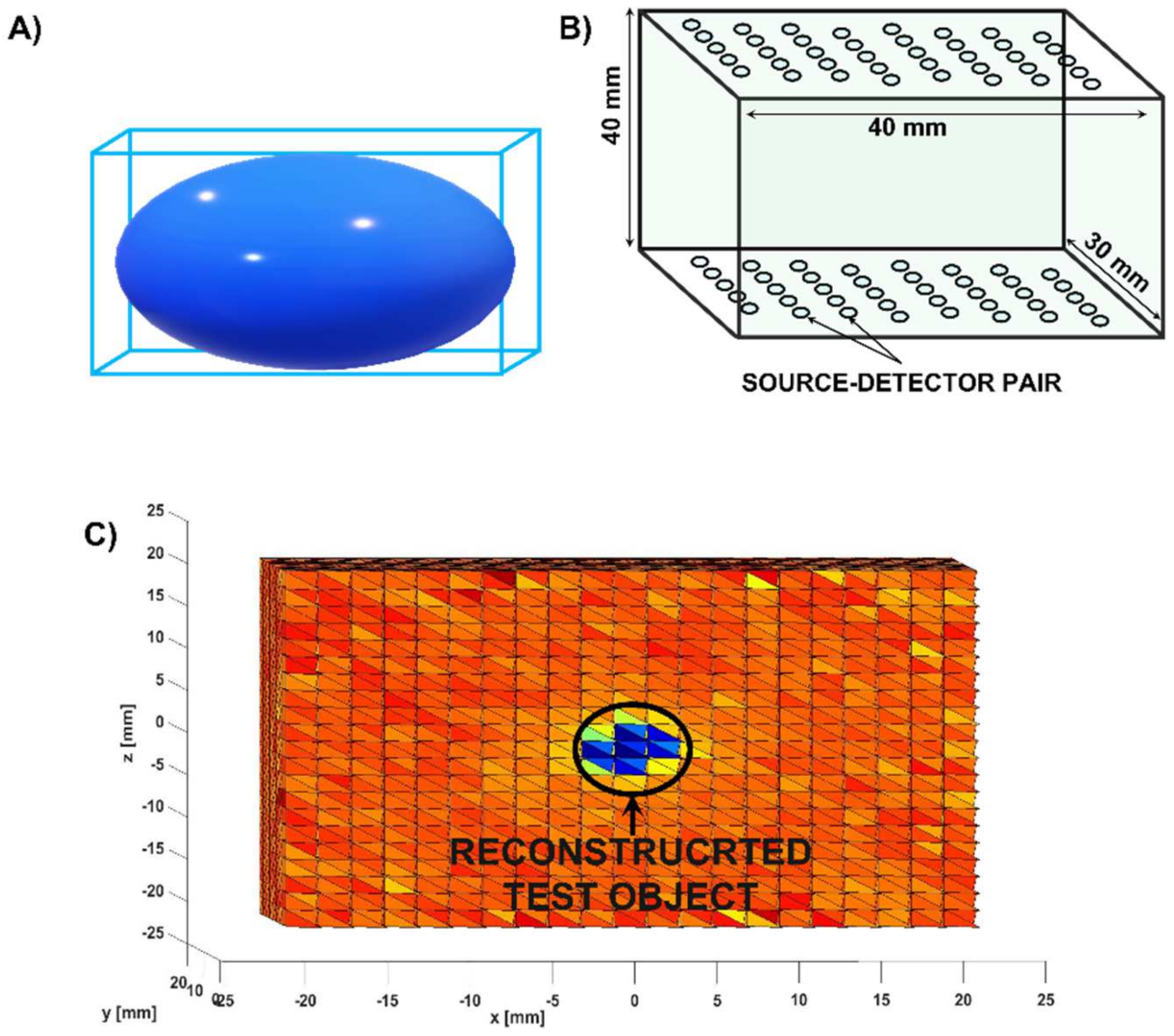
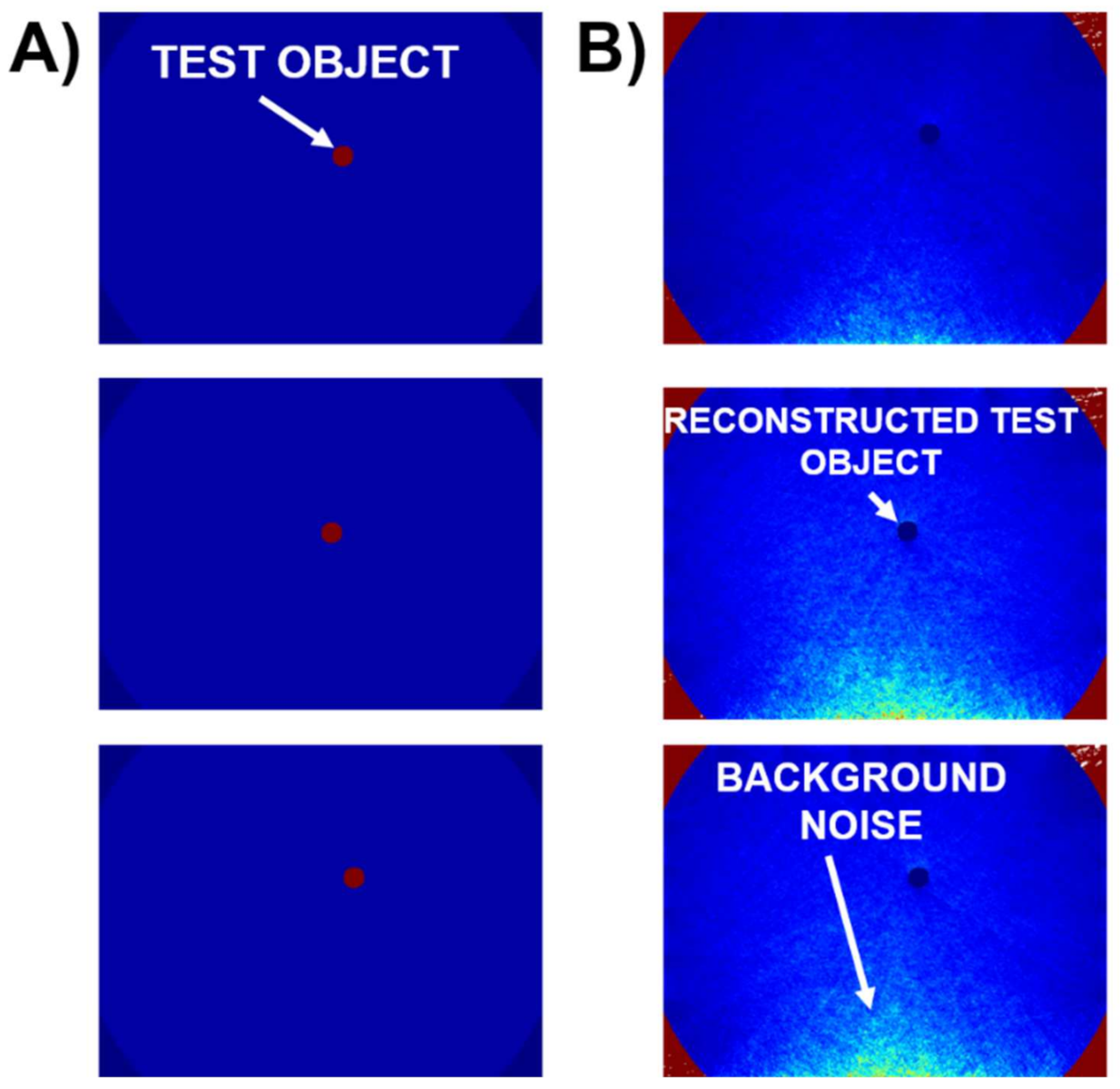
9. Deep-Learning Diffuse Optical Tomography Using Digital Phantoms: An Example
- (1)
- Optical property estimation and mesh creation: Creating the digital breast phantom
- (2)
- Forward process: Propagation of light through the digital phantom:
- (3)
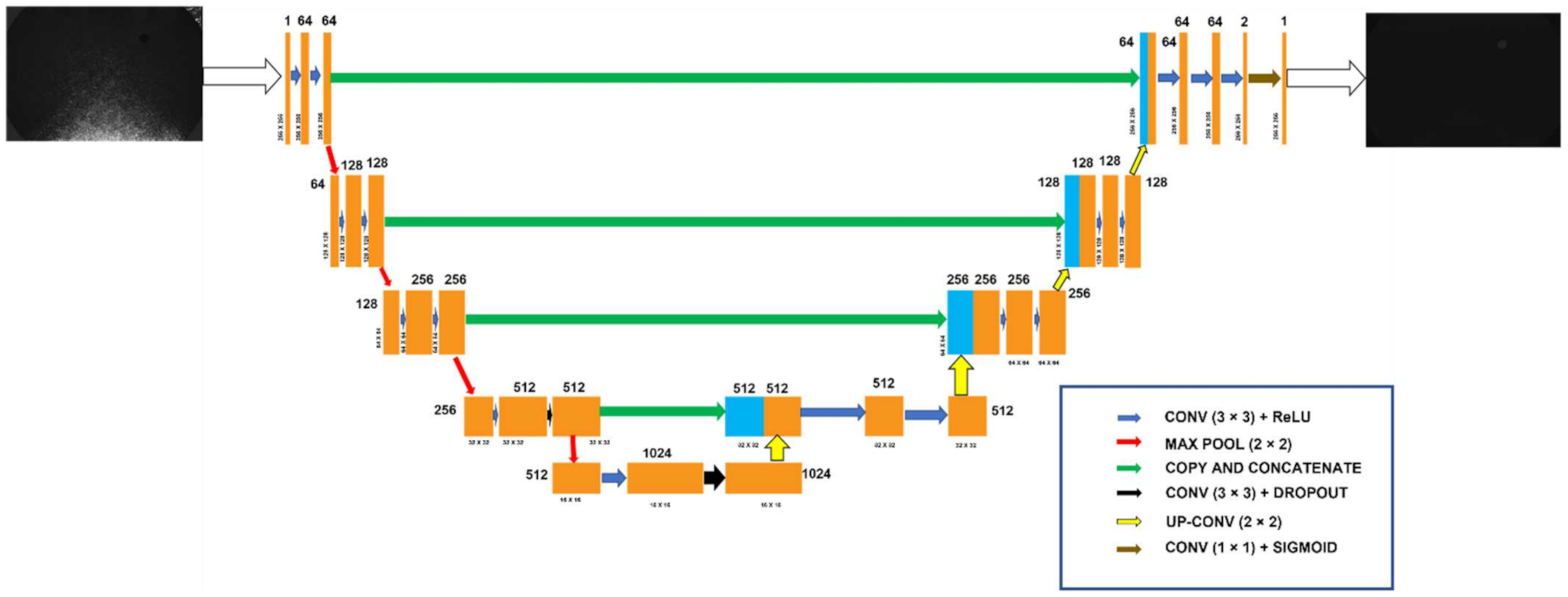
- The neural network architecture used for image reconstruction:
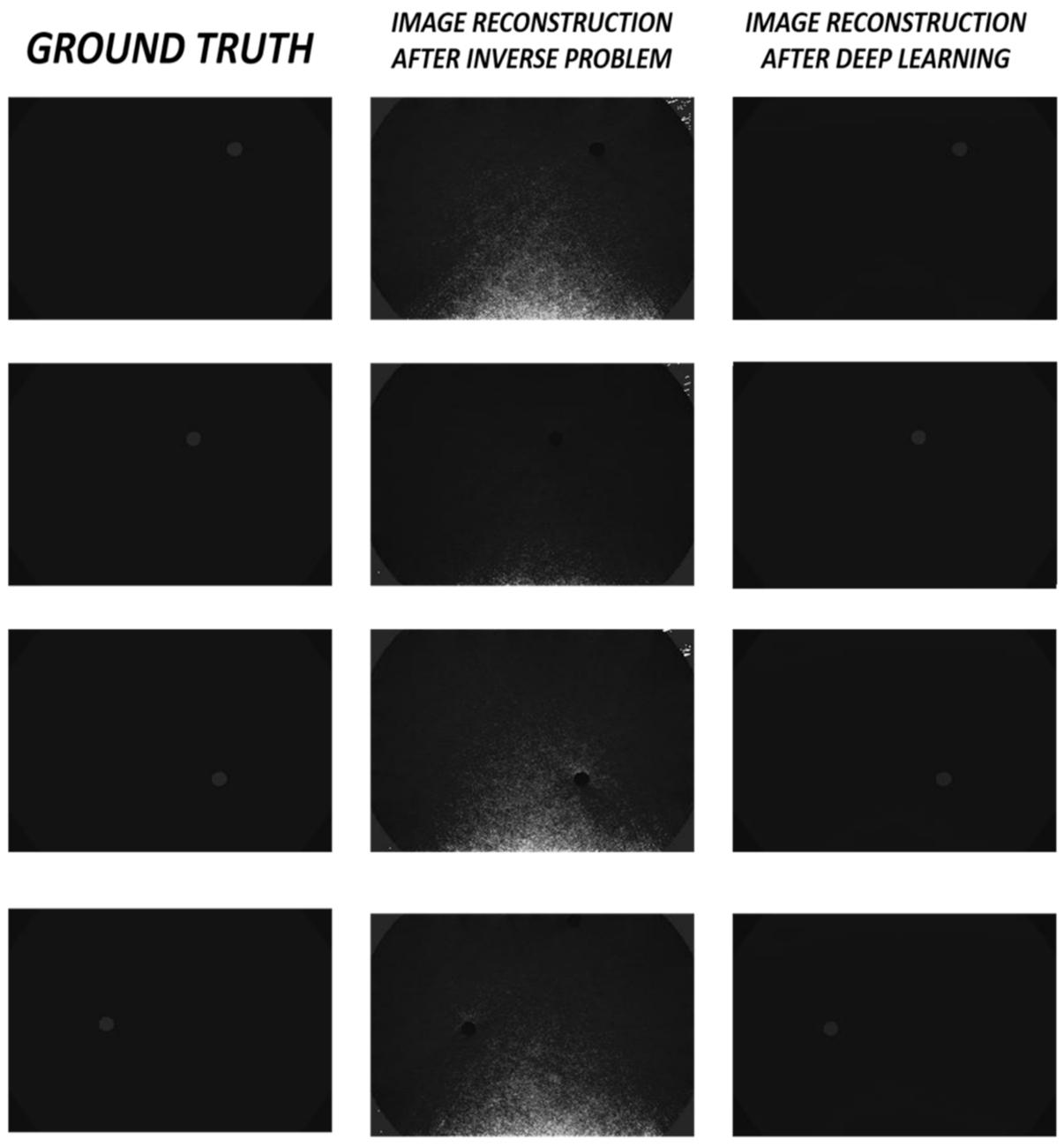
10. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Drukteinis, J.S.; Mooney, B.P.; Flowers, C.I.; Gatenby, R.A. Beyond mammography: New frontiers in breast cancer screening. Am. J. Med. 2013, 126, 472–479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taroni, P. Diffuse optical imaging and spectroscopy of the breast: A brief outline of history and perspectives. Photochem. Photobiol. Sci. 2012, 11, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Santarelli, M.F.; Giovannetti, G.; Hartwig, V.; Celi, S.; Positano, V.; Landini, L. The core of medical imaging: State of the art and perspectives on the detectors. Electronics 2021, 10, 1642. [Google Scholar] [CrossRef]
- Tuchin, V.V. Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis, 3rd ed.; SPIE: Bellingham, WA, USA, 2015; ISBN 9781628415179. [Google Scholar]
- Dehghani, H.; Eames, M.E.; Yalavarthy, P.K.; Davis, S.C.; Srinivasan, S.; Carpenter, C.M.; Pogue, B.W.; Paulsen, K.D. Near infrared optical tomography using NIRFAST: Algorithm for numerical model and image reconstruction. Commun. Numer. Methods Eng. 2009, 25, 711–732. [Google Scholar] [CrossRef]
- Yoo, J.; Sabir, S.; Heo, D.; Kim, K.H.; Wahab, A.; Choi, Y.; Lee, S.I.; Chae, E.Y.; Kim, H.H.; Bae, Y.M.; et al. Deep Learning Diffuse Optical Tomography. IEEE Trans. Med. Imaging 2020, 39, 877–887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ban, H.Y.; Schweiger, M.; Kavuri, V.C.; Cochran, J.M.; Xie, L.; Busch, D.R.; Katrašnik, J.; Pathak, S.; Chung, S.H.; Lee, K.; et al. Heterodyne frequency-domain multispectral diffuse optical tomography of breast cancer in the parallel-plane transmission geometry. Med. Phys. 2016, 43, 4383–4395. [Google Scholar] [CrossRef] [Green Version]
- Survarachakan, S.; Pelanis, E.; Khan, Z.A.; Kumar, R.P.; Edwin, B.; Lindseth, F. Effects of enhancement on deep learning based hepatic vessel segmentation. Electronics 2021, 10, 1165. [Google Scholar] [CrossRef]
- Ben Yedder, H.; BenTaieb, A.; Shokoufi, M.; Zahiremami, A.; Golnaraghi, F.; Hamarneh, G. Deep learning based image reconstruction for diffuse optical tomography. Proceedings of Internal workshop on Machine Learning for Medical Image Reconstruction Conference, Granada, Spain, 16 September 2018; Volume 11074, pp. 112–119. [Google Scholar]
- Applegate, M.B.; Istfan, R.E.; Spink, S.; Tank, A.; Roblyer, D. Recent advances in high speed diffuse optical imaging in biomedicine. APL Photonics 2020, 5. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Gao, C.; Li, Y.; Li, T. Solving heterogenous region for diffuse optical tomography with a convolutional forward calculation model and the inverse neural network. In Advanced Optical Imaging Technologies III; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; p. 18. [Google Scholar]
- Kabe, G.K.; Song, Y.; Liu, Z. Optimization of firenet for liver lesion classification. Electronics 2020, 9, 1237. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, G.; Jiang, Y.; Wang, B.; Soleimani, M. Application of Deep Neural Network to the Reconstruction of Two-Phase Material Imaging by Capacitively Coupled Electrical Resistance Tomography. Electronics 2021, 10, 1058. [Google Scholar] [CrossRef]
- Cho, C.; Lee, Y.H.; Park, J.; Lee, S. A self-spatial adaptive weighting based u-net for image segmentation. Electronics 2021, 10, 348. [Google Scholar] [CrossRef]
- Blondel, W.; Delconte, A.; Khairallah, G.; Marchal, F.; Gavoille, A.; Amouroux, M. Spatially-resolved multiply-excited autofluorescence and diffuse reflectance spectroscopy: Spectrolive medical device for skin in vivo optical biopsy. Electronics 2021, 10, 243. [Google Scholar] [CrossRef]
- Feng, Y.; Lighter, D.; Lei, Z.; Yan, W.; Dehghani, H. Application of deep neural networks to improve diagnostic accuracy of rheumatoid arthritis using diffuse optical tomography. Quantum Electron. 2020, 50, 21–32. [Google Scholar] [CrossRef]
- Balasubramaniam, G.M.; Arnon, S. Deep-Learning Algorithm To Detect Anomalies In Compressed Breast: A Numerical Study. In Proceedings of the Bio-Optics: Design and Application 2021, Washington, DC, USA, 12–16 April 2021. [Google Scholar]
- Saikia, M.J.; Kanhirodan, R.; Mohan Vasu, R. High-speed GPU-based fully three-dimensional diffuse optical tomographic system. Int. J. Biomed. Imaging 2014, 2014, 376456. [Google Scholar] [CrossRef] [Green Version]
- Altini, N.; Cascarano, G.D.; Brunetti, A.; De Feudis, I.; Buongiorno, D.; Rossini, M.; Pesce, F.; Gesualdo, L.; Bevilacqua, V. A deep learning instance segmentation approach for global glomerulosclerosis assessment in donor kidney biopsies. Electronics 2020, 9, 1768. [Google Scholar] [CrossRef]
- Binzoni, T.; Leung, T.S.; Gandjbakhche, A.H.; Rüfenacht, D.; Delpy, D.T. The use of the Henyey-Greenstein phase function in Monte Carlo simulations in biomedical optics. Phys. Med. Biol. 2006, 51. [Google Scholar] [CrossRef]
- Bloembergen, N. Laser-material interactions, fundamentals and applications. In AIP Conference Proceedings, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-662-04717-0. [Google Scholar]
- Wang, L.V.; Wu, H.I. Biomedical Optics: Principles and Imaging; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 9780471743040. [Google Scholar]
- Tran, A.P.; Jacques, S.L. Modeling voxel-based Monte Carlo light transport with curved and oblique boundary surfaces. J. Biomed. Opt. 2020, 25, 1. [Google Scholar] [CrossRef]
- Zhu, C.; Liu, Q. Review of Monte Carlo modeling of light transport in tissues. J. Biomed. Opt. 2013, 18, 050902. [Google Scholar] [CrossRef] [Green Version]
- Keller, M.D.; Wilson, R.H.; Mycek, M.A.; Mahadevan-Jansen, A. Monte cario model of spatially offset raman spectroscopy for breast tumor margin analysis. Appl. Spectrosc. 2010, 64, 607–614. [Google Scholar] [CrossRef]
- Alerstam, E.; Andersson-Engels, S.; Svensson, T. White Monte Carlo for time-resolved photon migration. J. Biomed. Opt. 2008, 13, 041304. [Google Scholar] [CrossRef]
- Gardner, A.R.; Venugopalan, V. Accurate and efficient Monte Carlo solutions to the radiative transport equation in the spatial frequency domain. Opt. Lett. 2011, 36, 2269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, N.; Liang, J.; Qu, X.; Li, J.; Lu, B.; Tian, J. GPU-based Monte Carlo simulation for light propagation in complex heterogeneous tissues. Opt. Express 2010, 18, 6811. [Google Scholar] [CrossRef] [PubMed]
- Hu, D.; Sun, T.; Yao, L.; Yang, Z.; Wang, A.; Ying, Y. Monte Carlo: A flexible and accurate technique for modeling light transport in food and agricultural products. Trends Food Sci. Technol. 2020, 102, 280–290. [Google Scholar] [CrossRef]
- Mavaddat, N.; Ahderom, S.; Tiporlini, V.; Alameh, K. Simulation of biomedical signals and images using Monte Carlo methods for training of deep learning networks. In Deep Learning Techniques for Biomedical and Health Informatics; Springer: Berlin/Heidelberg, Germany, 2020; pp. 213–236. ISBN 9780128190616. [Google Scholar]
- Kaiser, W.; Göwein, M.; Gagliardi, A. Acceleration scheme for particle transport in kinetic Monte Carlo methods. J. Chem. Phys. 2020, 152. [Google Scholar] [CrossRef]
- Kwon, K.; Son, T.; Lee, K.J.; Jung, B. Enhancement of light propagation depth in skin: Cross-validation of mathematical modeling methods. Lasers Med. Sci. 2009, 24, 605–615. [Google Scholar] [CrossRef]
- Anderson, R.R.; Parrish, J.A. The optics of human skin. J. Invest. Dermatol. 1981, 77, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Young, A.R. Chromophores in human skin. Phys. Med. Biol. 1997, 42, 789–802. [Google Scholar] [CrossRef]
- Jacques, S.L. Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58. [Google Scholar] [CrossRef]
- Cheong, W.F.; Prahl, S.A.; Welch, A.J. A Review of the Optical Properties of Biological Tissues. IEEE J. Quantum Electron. 1990, 26, 2166–2185. [Google Scholar] [CrossRef] [Green Version]
- Frijia, E.M.; Billing, A.; Lloyd-Fox, S.; Vidal Rosas, E.; Collins-Jones, L.; Crespo-Llado, M.M.; Amadó, M.P.; Austin, T.; Edwards, A.; Dunne, L.; et al. Functional imaging of the developing brain with wearable high-density diffuse optical tomography: A new benchmark for infant neuroimaging outside the scanner environment. Neuroimage 2021, 225. [Google Scholar] [CrossRef]
- Sherafati, A.; Snyder, A.Z.; Eggebrecht, A.T.; Bergonzi, K.M.; Burns-Yocum, T.M.; Lugar, H.M.; Ferradal, S.L.; Robichaux-Viehoever, A.; Smyser, C.D.; Palanca, B.J.; et al. Global motion detection and censoring in high-density diffuse optical tomography. Hum. Brain Mapp. 2020, 41, 4093–4112. [Google Scholar] [CrossRef]
- Lavaud, J.; Henry, M.; Gayet, P.; Fertin, A.; Vollaire, J.; Usson, Y.; Coll, J.L.; Josserand, V. Noninvasive monitoring of liver metastasis development via combined multispectral photoacoustic imaging and fluorescence diffuse optical tomography. Int. J. Biol. Sci. 2020, 16, 1616–1628. [Google Scholar] [CrossRef] [Green Version]
- Tromberg, B.J.; Zhang, Z.; Leproux, A.; O’Sullivan, T.D.; Cerussi, A.E.; Carpenter, P.M.; Mehta, R.S.; Roblyer, D.; Yang, W.; Paulsen, K.D.; et al. Predicting responses to neoadjuvant chemotherapy in breast cancer: ACRIN 6691 trial of diffuse optical spectroscopic imaging. Cancer Res. 2016, 76, 5933–5944. [Google Scholar] [CrossRef] [Green Version]
- Uddin, K.M.S.; Zhang, M.; Anastasio, M.; Zhu, Q. Optimal breast cancer diagnostic strategy using combined ultrasound and diffuse optical tomography. Biomed. Opt. Express 2020, 11, 2722. [Google Scholar] [CrossRef]
- Zhao, Y.; Raghuram, A.; Kim, H.; Hielscher, A.; Robinson, J.T.; Veeraraghavan, A.N. High Resolution, Deep Imaging Using Confocal Time-of-flight Diffuse Optical Tomography. IEEE Trans. Pattern Anal. Mach. Intell. 2021. [Google Scholar] [CrossRef]
- Sabir, S.; Cho, S.; Kim, Y.; Pua, R.; Heo, D.; Kim, K.H.; Choi, Y.; Cho, S. Convolutional neural network-based approach to estimate bulk optical properties in diffuse optical tomography. Appl. Opt. 2020, 59, 1461. [Google Scholar] [CrossRef]
- Arridge, S.R.; Schotland, J.C. Optical tomography: Forward and inverse problems. Inverse Probl. 2009, 25, 123010. [Google Scholar] [CrossRef]
- Tarvainen, T.; Cox, B.T.; Kaipio, J.P.; Arridge, S.R. Reconstructing absorption and scattering distributions in quantitative photoacoustic tomography. Inverse Probl. 2012, 28. [Google Scholar] [CrossRef]
- Arridge, S.R. Optical tomography in medical imaging. Inverse Probl. 1999, 15, R41. [Google Scholar] [CrossRef] [Green Version]
- Abdoulaev, G.S.; Ren, K.; Hielscher, A.H. Optical tomography as a PDE-constrained optimization problem. Inverse Probl. 2005, 21, 1507–1530. [Google Scholar] [CrossRef]
- Bal, G. Inverse transport theory and applications. Inverse Probl. 2009, 25. [Google Scholar] [CrossRef] [Green Version]
- Arridge, S.R.; Lionheart, W.R.B. Nonuniqueness in diffusion-based optical tomography. Opt. Lett. 1998, 23, 882. [Google Scholar] [CrossRef] [Green Version]
- Venugopal, V.; Fang, Q.; Intes, X. Multimodal diffuse optical imaging for biomedical applications. In Biophotonics for Medical Applications; Elsevier: Amsterdam, The Netherlands, 2015; pp. 3–24. ISBN 9780857096746. [Google Scholar]
- Wang, X.; Xie, X.; Ku, G.; Wang, L.V.; Stoica, G. Noninvasive imaging of hemoglobin concentration and oxygenation in the rat brain using high-resolution photoacoustic tomography. J. Biomed. Opt. 2006, 11, 024015. [Google Scholar] [CrossRef] [Green Version]
- Siegel, A.; Marota, J.J.; Boas, D. Design and evaluation of a continuous-wave diffuse optical tomography system. Opt. Express 1999, 4, 287. [Google Scholar] [CrossRef]
- Vo-Dinh, T. Biomedical Photonics: Handbook; CRC Press: Boca Raton, FL, USA, 2003; ISBN 9780203008997. [Google Scholar]
- Haskell, R.C.; Svaasand, L.O.; Tsay, T.-T.; Feng, T.-C.; Tromberg, B.J.; McAdams, M.S. Boundary conditions for the diffusion equation in radiative transfer. J. Opt. Soc. Am. A 1994, 11, 2727. [Google Scholar] [CrossRef] [Green Version]
- Shah, N.; Cerussi, A.; Eker, C.; Espinoza, J.; Butler, J.; Fishkin, J.; Hornung, R.; Tromberg, B. Noninvasive functional optical spectroscopy of human breast tissue. Proc. Natl. Acad. Sci. USA 2001, 98, 4420–4425. [Google Scholar] [CrossRef] [Green Version]
- Leino, A.A.; Pulkkinen, A.; Tarvainen, T. ValoMC: A Monte Carlo software and MATLAB toolbox for simulating light transport in biological tissue. OSA Contin. 2019, 2, 957. [Google Scholar] [CrossRef]
- Yun, S.; Tearney, G.; de Boer, J.; Iftimia, N.; Bouma, B. High-speed optical frequency-domain imaging. Opt. Express 2003, 11, 2953. [Google Scholar] [CrossRef] [Green Version]
- Cuccia, D.J.; Bevilacqua, F.; Durkin, A.J.; Tromberg, B.J. Modulated imaging: Quantitative analysis and tomography of turbid media in the spatial-frequency domain. Opt. Lett. 2005, 30, 1354. [Google Scholar] [CrossRef] [PubMed]
- O’Leary, M.A.; Boas, D.A.; Chance, B.; Yodh, A.G. Experimental images of heterogeneous turbid media by frequency-domain diffusing-photon tomography. Opt. Lett. 1995, 20, 426. [Google Scholar] [CrossRef] [PubMed]
- Nissilä, I.; Hebden, J.C.; Jennions, D.; Heino, J.; Schweiger, M.; Kotilahti, K.; Noponen, T.; Gibson, A.; Järvenpää, S.; Lipiäinen, L.; et al. Comparison between a time-domain and a frequency-domain system for optical tomography. J. Biomed. Opt. 2006, 11, 064015. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.T.N.; Raymond, S.B.; Bacskai, B.J.; Boas, D.A. Comparison of frequency-domain and time-domain fluorescence lifetime tomography. Opt. Lett. 2008, 33, 470. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joshi, A.; Rasmussen, J.C.; Sevick-Muraca, E.M.; Wareing, T.A.; McGhee, J. Radiative transport-based frequency-domain fluorescence tomography. Phys. Med. Biol. 2008, 53, 2069–2088. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stillwell, R.A.; Kitsmiller, V.J.; O’Sullivan, T.D. Towards a high-speed handheld frequency-domain diffuse optical spectroscopy deep tissue imaging system. In Proceedings of the Optics InfoBase Conference Papers, Washington, DC, USA, 20–23 March 2020; Volume Part F178. [Google Scholar]
- Kitsmiller, V.J.; Campbell, C.; O’Sullivan, T.D. Optimizing sensitivity and dynamic range of silicon photomultipliers for frequency-domain near infrared spectroscopy. Biomed. Opt. Express 2020, 11, 5373. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, Y.; Yue, S.; Wang, M.; Song, B.; Fan, Y. Direct mapping from diffuse reflectance to chromophore concentrations in multi-fx spatial frequency domain imaging (SFDI) with a deep residual network (DRN). Biomed. Opt. Express 2021, 12, 433. [Google Scholar] [CrossRef]
- Hu, D.; Lu, R.; Ying, Y. Spatial-frequency domain imaging coupled with frequency optimization for estimating optical properties of two-layered food and agricultural products. J. Food Eng. 2020, 277. [Google Scholar] [CrossRef]
- Hillman, E. Experimental and Theoretical Investigations of Near Infrared Tomographic Imaging Methods and Clinical Applications. Ph.D. Thesis, University College London, London, UK, 2002. [Google Scholar]
- Culver, J.P.; Choe, R.; Holboke, M.J.; Zubkov, L.; Durduran, T.; Slemp, A.; Ntziachristos, V.; Chance, B.; Yodh, A.G. Three-dimensional diffuse optical tomography in the parallel plane transmission geometry: Evaluation of a hybrid frequency domain/continuous wave clinical system for breast imaging. Med. Phys. 2003, 30, 235–247. [Google Scholar] [CrossRef]
- Cubeddu, R.; Musolino, M.; Pifferi, A.; Taroni, P.; Valentini, G. Time-Resolved Reflectance: A Systematic Study for Application to The Optical Characterization of Tissues. IEEE J. Quantum Electron. 1994, 30, 2421–2430. [Google Scholar] [CrossRef]
- Taroni, P.; Pifferi, A.; Torricelli, A.; Comelli, D.; Cubeddu, R. In vivo absorption and scattering spectroscopy of biological tissues. Photochem. Photobiol. Sci. 2003, 2, 124–129. [Google Scholar] [CrossRef]
- Jacques, S.L. Time resolved propagation of ultrashort laser pulses within turbid tissues. Appl. Opt. 1989, 28, 2223. [Google Scholar] [CrossRef]
- Zevallos, M.E.; Liu, F.; Alfano, R.R. Time-resolved pulse propagation in tissue tubular structures. In Proceedings of the Lasers and Electro-Optics Society Annual Meeting-LEOS, Baltimore, MD, USA, 18–23 May 1997; Volume 11, pp. 148–149. [Google Scholar]
- Piron, V.; L’Huillier, J.P.; Mansouri, C. Object localization within turbid slab media using time-resolved transillumination contrast functions: A finite element approach. In Proceedings of the European Conferences on Biomedical Optics, Munich, Germany, 17–21 June 2007. paper 6628_32. [Google Scholar]
- Patterson, M.S.; Chance, B.; Wilson, B.C. Time resolved reflectance and transmittance for the noninvasive measurement of tissue optical properties. Appl. Opt. 1989, 28, 2331. [Google Scholar] [CrossRef]
- Wilson, B.C.; Jacques, S.L. Optical Reflectance and Transmittance of Tissues: Principles and Applications. IEEE J. Quantum Electron. 1990, 26, 2186–2199. [Google Scholar] [CrossRef]
- Pifferi, A.; Swartling, J.; Chikoidze, E.; Torricelli, A.; Taroni, P.; Bassi, A.; Andersson-Engels, S.; Cubeddu, R. Spectroscopic time-resolved diffuse reflectance and transmittance measurements of the female breast at different interfiber distances. J. Biomed. Opt. 2004, 9, 1143. [Google Scholar] [CrossRef] [Green Version]
- Cubeddu, R.; Pifferi, A.; Taroni, P.; Torricelli, A.; Valentini, G. Noninvasive absorption and scattering spectroscopy of bulk diffusive media: An application to the optical characterization of human breast. Appl. Phys. Lett. 1999, 74, 874–876. [Google Scholar] [CrossRef]
- Mozumder, M.; Tarvainen, T. Evaluation of temporal moments and Fourier transformed data in time-domain diffuse optical tomography. J. Opt. Soc. Am. A 2020, 37, 1845. [Google Scholar] [CrossRef]
- Di Sieno, L.; Dalla Mora, A.; Ferocino, E.; Pifferi, A.; Tosi, A.; Conca, E.; Sesta, V.; Giudice, A.; Ruggeri, A.; Tisa, S.; et al. SOLUS project: Bringing innovation into breast cancer diagnosis and in the time-domain diffuse optical field. In Proceedings of the Optics InfoBase Conference Papers, Washington, DC, USA, 20–23 March 2020; Volume Part F179. [Google Scholar]
- Samaei, S.; Sawosz, P.; Kacprzak, M.; Pastuszak, Ż.; Borycki, D.; Liebert, A. Time-domain diffuse correlation spectroscopy (TD-DCS) for noninvasive, depth-dependent blood flow quantification in human tissue in vivo. Sci. Rep. 2021, 11. [Google Scholar] [CrossRef]
- Takamizu, Y.; Umemura, M.; Yajima, H.; Abe, M.; Hoshi, Y. Deep Learning of Diffuse Optical Tomography based on Time-Domain Radiative Transfer Equation. arXiv 2020, arXiv:2011.12520. [Google Scholar]
- Kalyanov, A.; Jiang, J.; Lindner, S.; Ahnen, L.; di Costanzo, A.; Pavia, J.M.; Majos, S.S.; Wolf, M. Time domain near-infrared optical tomography with time-of-flight SPAD camera: The new generation. In Proceedings of the Optical Tomography and Spectroscopy 2018, Hollywood, FL, USA, 3–6 April 2018; Volume Part F90-O. [Google Scholar]
- Mimura, T.; Okawa, S.; Kawaguchi, H.; Tanikawa, Y.; Hoshi, Y. Imaging the human thyroid using three-dimensional diffuse optical tomography: A preliminary study. Appl. Sci. 2021, 11, 1–13. [Google Scholar] [CrossRef]
- Uddin, K.M.S.; Mostafa, A.; Anastasio, M.; Zhu, Q. Two step imaging reconstruction using truncated pseudoinverse as a preliminary estimate in ultrasound guided diffuse optical tomography. Biomed. Opt. Express 2017, 8, 5437. [Google Scholar] [CrossRef] [Green Version]
- Bertero, M.; Boccacci, P. Introduction to Inverse Problems in Imaging; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Ben Yedder, H.; Cardoen, B.; Hamarneh, G. Deep learning for biomedical image reconstruction: A survey. Artif. Intell. Rev. 2021, 54, 215–251. [Google Scholar] [CrossRef]
- Ben Yedder, H.; Shokoufi, M.; Cardoen, B.; Golnaraghi, F.; Hamarneh, G. Limited-angle diffuse optical tomography image reconstruction using deep learning. In Proceedings of the Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Shenzhen, China, 13–17 October 2019; Volume 11764 LNCS, pp. 66–74. [Google Scholar]
- Guo, Y.; Liu, Y.; Oerlemans, A.; Lao, S.; Wu, S.; Lew, M.S. Deep learning for visual understanding: A review. Neurocomputing 2016, 187, 27–48. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, S.; Li, H.; Su, C.; Yu, J.; Jin, F. Evolutionary artificial neural networks: A review. Artif. Intell. Rev. 2013, 39, 251–260. [Google Scholar] [CrossRef]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep Learning for Computer Vision: A Brief Review. Comput. Intell. Neurosci. 2018. [Google Scholar] [CrossRef]
- Deng, L.; Hinton, G.; Kingsbury, B. New types of deep neural network learning for speech recognition and related applications: An overview. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8599–8603. [Google Scholar]
- Doulamis, N.; Doulamis, A. Semi-supervised deep learning for object tracking and classification. In Proceedings of the 2014 IEEE International Conference on Image Processing, ICIP, Paris, France, 27–30 October 2014; pp. 848–852. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386–408. [Google Scholar] [CrossRef] [Green Version]
- Nievergelt, J. R69-13 Perceptrons: An Introduction to Computational Geometry. IEEE Trans. Comput. 1969, C-18, 572. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Van Esesn, B.C.; Awwal, A.A.S.; Asari, V.K. The History Began from AlexNet: A Comprehensive Survey on Deep Learning Approaches. arXiv 2018, arXiv:1803.01164. [Google Scholar]
- Goodfellow, I.B.Y. Courville A-Deep learning-MIT (2016); Nature MIT Press, 2016; Available online: http://www.deeplearningbook.org (accessed on 24 August 2021).
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Chen, H.; Engkvist, O.; Wang, Y.; Olivecrona, M.; Blaschke, T. The rise of deep learning in drug discovery. Drug Discov. Today 2018, 23, 1241–1250. [Google Scholar] [CrossRef]
- Min, S.; Lee, B.; Yoon, S. Deep learning in bioinformatics. Brief. Bioinform. 2017, 18, 851–869. [Google Scholar] [CrossRef] [Green Version]
- Gawehn, E.; Hiss, J.A.; Schneider, G. Deep Learning in Drug Discovery. Mol. Inform. 2016, 35, 3–14. [Google Scholar] [CrossRef]
- Lee, J.G.; Jun, S.; Cho, Y.W.; Lee, H.; Kim, G.B.; Seo, J.B.; Kim, N. Deep learning in medical imaging: General overview. Korean J. Radiol. 2017, 18, 570–584. [Google Scholar] [CrossRef] [Green Version]
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Cui, C.; Corrado, G.; Thrun, S.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef]
- Antholzer, S.; Haltmeier, M.; Schwab, J. Deep learning for photoacoustic tomography from sparse data. Inverse Probl. Sci. Eng. 2019, 27, 987–1005. [Google Scholar] [CrossRef] [Green Version]
- Araya-Polo, M.; Jennings, J.; Adler, A.; Dahlke, T. Deep-learning tomography. Lead. Edge 2018, 37, 58–66. [Google Scholar] [CrossRef]
- Shaul, R.; David, I.; Shitrit, O.; Riklin Raviv, T. Subsampled brain MRI reconstruction by generative adversarial neural networks. Med. Image Anal. 2020, 65. [Google Scholar] [CrossRef]
- Ben Wiesel and Shlomi Arnon Anomaly Detection Inside Diffuse Media using Deep Learning Algorithm. In Proceedings of the European Conferences on Biomedical Optics 2021 (ECBO), Munich, Germany, 20–24 June 2021. paper ETu2A.8.
- Schweiger, M.; Arridge, S. The Toast++ software suite for forward and inverse modeling in optical tomography. J. Biomed. Opt. 2014, 19, 040801. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Ying, L. Solving Traveltime Tomography with Deep Learning. arXiv 2019, arXiv:1911.11636. [Google Scholar]
- Feng, T.; Edström, P.; Gulliksson, M. Levenberg-Marquardt methods for parameter estimation problems in the radiative transfer equation. Inverse Probl. 2007, 23, 879–891. [Google Scholar] [CrossRef] [Green Version]
- Emmert-Streib, F.; Yang, Z.; Feng, H.; Tripathi, S.; Dehmer, M. An Introductory Review of Deep Learning for Prediction Models With Big Data. Front. Artif. Intell. 2020, 3. [Google Scholar] [CrossRef] [Green Version]
- Dhillon, A.; Verma, G.K. Convolutional neural network: A review of models, methodologies and applications to object detection. Prog. Artif. Intell. 2020, 9, 85–112. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. In Proceedings of the 2nd International Conference on Learning Representations (ICLR 2014), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Wang, D.; Gu, J. VASC: Dimension Reduction and Visualization of Single-cell RNA-seq Data by Deep Variational Autoencoder. Genom. Proteom. Bioinform. 2018, 16, 320–331. [Google Scholar] [CrossRef]
- Lin, E.; Mukherjee, S.; Kannan, S. A deep adversarial variational autoencoder model for dimensionality reduction in single-cell RNA sequencing analysis. BMC Bioinform. 2020, 21. [Google Scholar] [CrossRef] [Green Version]
- Seo, J.K.; Kim, K.C.; Jargal, A.; Lee, K.; Harrach, B. A learning-based method for solving ill-posed nonlinear inverse problems: A simulation study of lung EIT. SIAM J. Imaging Sci. 2019, 12, 1275–1295. [Google Scholar] [CrossRef]
- Gupta, H.; Jin, K.H.; Nguyen, H.Q.; McCann, M.T.; Unser, M. CNN-Based Projected Gradient Descent for Consistent CT Image Reconstruction. IEEE Trans. Med. Imaging 2018, 37, 1440–1453. [Google Scholar] [CrossRef] [Green Version]
- Ye, D.H.; Buzzard, G.T.; Ruby, M.; Bouman, C.A. Deep back projection for sparse-view CT reconstruction. In Proceedings of the 2018 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Anaheim, CA, USA, 26–29 November 2018; pp. 1–5. [Google Scholar]
- Koneripalli, K.; Lohit, S.; Anirudh, R.; Turaga, P. Rate-Invariant Autoencoding of Time-Series. In Proceedings of the ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 3732–3736. [Google Scholar]
- Lohit, S.; Turaga, P.; Veeraraghavan, A. Invariant Methods in Computer Vision. In Computer Vision; Ikeuchi, K., Ed.; Springer: Cham, Switzerland, 2020; pp. 1–7. [Google Scholar]
- Lohit, S.; Kulkarni, K.; Kerviche, R.; Turaga, P.; Ashok, A. Convolutional Neural Networks for Noniterative Reconstruction of Compressively Sensed Images. IEEE Trans. Comput. Imaging 2018, 4, 326–340. [Google Scholar] [CrossRef] [Green Version]
- Liang, D.; Cheng, J.; Ke, Z.; Ying, L. Deep MRI Reconstruction: Unrolled Optimization Algorithms Meet Neural Networks. arXiv 2019, arXiv:1907.11711. [Google Scholar]
- Jin, Y.; Shen, Q.; Wu, X.; Chen, J.; Huang, Y. A physics-driven deep-learning network for solving nonlinear inverse problems. Petrophysics 2020, 61, 86–98. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2242–2251. [Google Scholar]
- Lunz, S.; Öktem, O.; Schönlieb, C.B. Adversarial regularizers in inverse problems. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 8507–8516. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning, ICML, Sydney, Australia, 6–11 August 2017; Volume 1, pp. 298–321. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Bora, A.; Jalal, A.; Price, E.; Dimakis, A.G. Compressed sensing using generative models. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 2, pp. 822–841. [Google Scholar]
- Gilton, D.; Ongie, G.; Willett, R. Learning to Regularize Using Neumann Networks. In Proceedings of the 2019 IEEE Data Science Workshop (DSW), Minneapolis, MN, USA, 2–5 June 2019; pp. 201–207. [Google Scholar]
- Mardani, M.; Sun, Q.; Vasawanala, S.; Papyan, V.; Monajemi, H.; Pauly, J.; Donoho, D. Neural proximal gradient descent for compressive imaging. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 9573–9583. [Google Scholar]
- Yang, Y.; Sun, J.; Li, H.; Xu, Z. ADMM-Net: A Deep Learning Approach for Compressive Sensing MRI. arXiv 2017, arXiv:1705.06869. [Google Scholar]
- Schmidt, U.; Roth, S. Shrinkage fields for effective image restoration. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2774–2781. [Google Scholar]
- Gohberg, I.; Goldberg, S. Basic Operator Theory; Birkhauser: Boston, MA, USA, 1981. [Google Scholar]
- Pogue, B.W.; McBride, T.O.; Osterberg, U.L.; Paulsen, K.D. Comparison of imaging geometries for diffuse optical tomography of tissue. Opt. Express 1999, 4, 270. [Google Scholar] [CrossRef]
- Weng, Y.; Zhou, T.; Li, Y.; Qiu, X. NAS-Unet: Neural architecture search for medical image segmentation. IEEE Access 2019, 7, 44247–44257. [Google Scholar] [CrossRef]
- Pinto, M.; Egging, R.; Rodríguez-Ruiz, A.; Michielsen, K.; Sechopoulos, I. Compressed breast shape characterization and modelling during digital breast tomosynthesis using 3D stereoscopic surface cameras. In Proceedings of the 15th International Workshop on Breast Imaging (IWBI2020), Leuven, Belgium, 25–27 May 2020; p. 38. [Google Scholar]
- Yuan, Y.; Yan, S.; Fang, Q. Light transport modeling in highly complex tissues using the implicit mesh-based Monte Carlo algorithm. Biomed. Opt. Express 2021, 12, 147. [Google Scholar] [CrossRef]
- Fang, Q.; Boas, D.A. Monte Carlo Simulation of Photon Migration in 3D Turbid Media Accelerated by Graphics Processing Units. Opt. Express 2009, 17, 20178. [Google Scholar] [CrossRef] [Green Version]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Durduran, T.; Choe, R.; Baker, W.B.; Yodh, A.G. Diffuse optics for tissue monitoring and tomography. Rep. Prog. Phys. 2010, 73, 76701. [Google Scholar] [CrossRef] [Green Version]
- Chance, B. Optical method. Annu. Rev. Biophys. Biophys. Chem. 1991, 20, 1–28. [Google Scholar] [CrossRef]
- Sood, B.G.; McLaughlin, K.; Cortez, J. Near-infrared spectroscopy: Applications in neonates. Semin. Fetal Neonatal Med. 2015, 20, 164–172. [Google Scholar] [CrossRef]

| S. No. | Function | Use | Value |
|---|---|---|---|
| 1 | vmcmedium.absorption_coefficient | Function used to impart absorption coefficient to the medium. | |
| 2 | vmcmedium.scattering_coefficient | Function used to impart scattering coefficient to the medium. | |
| 3 | vmcmedium.refravtive_index | Function used to impart refractive index to the medium. | N (glass box) = 1.013 n (compressed breast) = 1.37 n (anomaly) = 1.4 |
| 4 | vmcmedium.scattering_anisotropy | Function used to impart scattering anisotropy to the medium. | G (glass box) = 1 g (compressed breast) = 0.9 g (anomaly) = 0.85 |
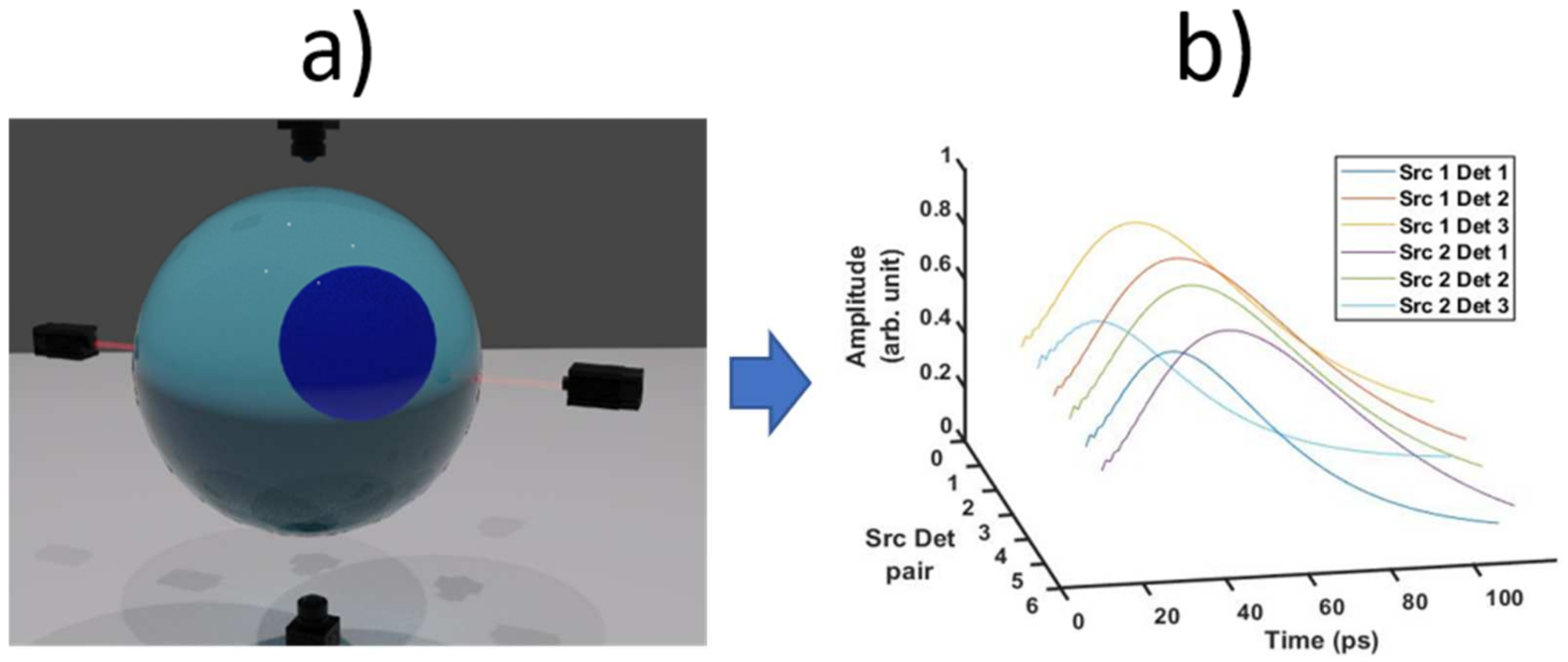
| 5 | vmcboundary.lightsource | Define the type of light source and the location of the light source. | Light source and detector locations are set according to Figure 4. |
| 6 | vmcboundary.exterior_refractive_index | Define the refractive index of the external medium. | Exterior refractive index is set at 1.5 to create a mismatch between the glass box and surrounding environment. |
| S. No. | Function | Use |
|---|---|---|
| 1 | Solution.element_fluence | Function that outputs the fluence at each element. |
| 2 | Solution.boundary_fluence | Function that outputs the excitance at each boundary element. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasubramaniam, G.M.; Wiesel, B.; Biton, N.; Kumar, R.; Kupferman, J.; Arnon, S. Tutorial on the Use of Deep Learning in Diffuse Optical Tomography. Electronics 2022, 11, 305. https://doi.org/10.3390/electronics11030305
Balasubramaniam GM, Wiesel B, Biton N, Kumar R, Kupferman J, Arnon S. Tutorial on the Use of Deep Learning in Diffuse Optical Tomography. Electronics. 2022; 11(3):305. https://doi.org/10.3390/electronics11030305
Chicago/Turabian StyleBalasubramaniam, Ganesh M., Ben Wiesel, Netanel Biton, Rajnish Kumar, Judy Kupferman, and Shlomi Arnon. 2022. "Tutorial on the Use of Deep Learning in Diffuse Optical Tomography" Electronics 11, no. 3: 305. https://doi.org/10.3390/electronics11030305
APA StyleBalasubramaniam, G. M., Wiesel, B., Biton, N., Kumar, R., Kupferman, J., & Arnon, S. (2022). Tutorial on the Use of Deep Learning in Diffuse Optical Tomography. Electronics, 11(3), 305. https://doi.org/10.3390/electronics11030305








