Abstract
A planar current is generally divided into a radiating part that mainly generates propagation fields and a non-radiating part that mainly generates evanescent fields. This paper proposes a direct method to reconstruct the radiating part of a planar source from its far-fields based on their explicit relationships. A standard reconstruction process is provided in which the far-fields are sampled at the peaks of their propagation modes. An analysis shows that the achievable reconstruction resolution of the source distribution is about half a wavelength. The paper also demonstrates that it is possible to reconstruct the source by sampling the far-fields on a plane or along a linear path. The performance of the reconstruction algorithm is illustrated with numerical examples.
1. Introduction
In many practical applications, such as in antenna synthesis and diagnosis [1,2,3,4,5], imaging of defects [6], and radar imaging [7], it is required to reconstruct the source from its fields. These kinds of problems are referred to as inverse electromagnetic source problems. Unlike in the inverse electromagnetic scattering problems [8,9], it is not necessary to recover the property of the media, but only the source distributions. Inverse source problems are usually linear problems. However, they are generally ill-posed and have to be solved with some kinds of optimization algorithms or regularization techniques, or with the help of priori information [10,11,12,13,14,15,16,17,18]. The introduction of the concept of the number of degrees of freedom (NDF) of the fields helps to overcome the ill-posedness of the problem [19,20,21,22]. Although the NBF of a practical inverse source problem can be effectively obtained by performing singular value decomposition (SVD) to the corresponding operator, the calculation is time-consuming. The point spread function (PSF) has been applied successfully in solving inverse source problems [23,24,25]. However, it is very complicated to find the exact evaluation of the PSF. For most geometries, PSF can only be performed numerically, or with an approximate analytical assessment.
It is well known that a source can be divided into a radiating part and a non-radiating part [26,27,28,29,30]. The radiating source mainly generates propagation fields and contributes to the far-fields of the source, while the non-radiating part mainly generates evanescent fields. Therefore, from the far-fields of a source, we can only effectively reconstruct its radiating part with achievable spatial resolution subject to the Rayleigh diffraction limit, typically half a wavelength [31,32,33]. If additional information, like the near fields of the source, is available, the diffraction limit may be broken and super resolution can be obtained using the proper algorithm [34,35,36,37].
By expanding the sources with Fourier series, a linear source or a planar source on a rectangular sheet can be expressed with superposition of its harmonic components. These components were further divided into two groups based on the property of the fields generated by them. The propagation group consists of all harmonic components that mainly generate propagation fields, and the evanescent group includes all other components that mainly generate evanescent fields. The first group is apparently the main radiating part of the source, while the latter one is the non-radiating part. Each component of the source in the propagation group generates a propagation mode in the space. The far-field mainly consists of the contributions from the propagation modes. Hence, the relationship between the far-fields and the radiating part of the current can be derived and is found to be very efficient for the synthesis of large-scale antenna arrays. This paper shows that the relationship can also be applied for efficiently and accurately reconstructing the radiating part of the source from its far-fields. The achievable spatial resolution is about half a wavelength, the same as the Rayleigh diffraction limit.
The main contribution of this paper is as follows: (1) an efficient algorithm is proposed to separately recover the two polarization components of the radiating part of a planar current source, in which the far-fields of the source are sampled on the constellation of the propagation modes; (2) it is verified that, using only part of the propagation modes and sampling on a planar grid or linear grid, the radiating part of the current source can be recovered with moderate accuracy; and (3) the performance of the algorithm with the presence of noise is revealed with examples.
This paper is organized as follows. In Section 2, the standard reconstruction process is described and numerical examples are provided to show the reconstruction performance of the algorithm. The non-standard reconstruction method by sampling on a plane or along a linear path is discussed in Section 3, including the modified algorithm using part of the propagation modes, and a brief conclusion is provided in Section 4.
2. Standard Reconstruction Algorithm
Consider a current source , , in free space. The electric field at the position in far region can be generally expressed as
where is the wave vector, is the radial unit vector, and is the identity operator. Consider a current source on a rectangular sheet in the xoy plane with a size of and centered at the origin, its far-field can be separated into two polarizations:
The primes for the source coordinates in the integrands are omitted for the sake of simplicity. In the spherical coordinate system, , , and . In Equation (2), is the angle between the position vector and the x-axis, and is that with the y-axis. and are the corresponding unit vectors, respectively, as shown in Figure 1. The factors and come from the x-polarized infinitesimal dipole and the y-polarized infinitesimal dipole composing the current sheets, respectively.
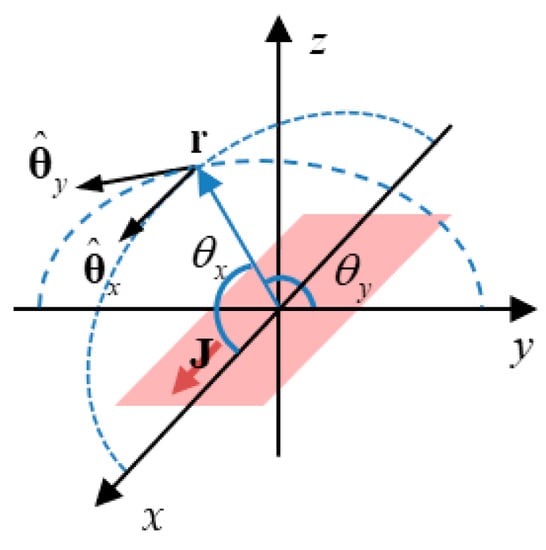
Figure 1.
Current sheet and the unit vectors in the coordinate system.
The x-component of the current is related to the x-polarized far-field alone:
We deliberately put the minus sign on the right-hand side of Equation (3) and ignore the coefficient . Similarly, the y-component of the current can be equated to its y-polarized far-field alone. Therefore, it is possible for us to reconstruct the two components of the current separately.
At first, we consider the problem of reconstructing the x-component of the source current from the x-polarization field. Discarding the factor relating to distance , the x-polarized far-field of the current sheet can be expressed as follows:
Expanding the currents with 2D Fourier series, we obtain
where and . Substituting Equation (5) into Equation (4) gives
where the 2D mode function is the product of two sinc functions:
Each mode function describes a beam in the space with its peak at the direction of and , which can be determined with equations
The wave vector of the mode at its peak direction is denoted as , and
In order to analyze the property of these modes in a simple way, we choose , where is the wavelength and and are two integers. It can be shown that only those modes belong to the propagation set can contribute significantly to the far-field, where is defined as
A typical constellation of the propagation group in k-space is shown in Figure 2, where each circle denotes the wave vector of a propagation mode. As all propagation modes are mirror symmetrical with respect to the current sheet, only the upper half of the constellation is illustrated in Figure 2.
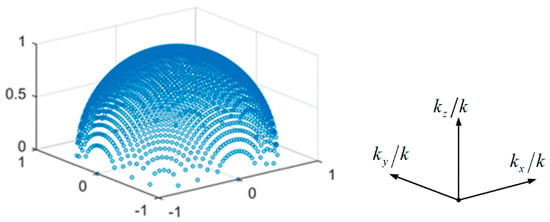
Figure 2.
Constellation of the propagation group in the k-space.
The far-field of the current sheet is mainly determined by the associated propagation modes:
with . It is worthwhile to emphasize that, for a spatial band-limited current source, Equation (11) is a rigorous relationship between the radiating part of the source current and its far-fields.
Note that, at the peak of a mode function, all other mode functions are zeroes, or explicitly, we can write
This property enables us to directly determine the coefficients of the current by sampling the far-fields at in the upper half space. From Equation (11) we obtain
The reconstructed x-component of the current can then be calculated with
where , , and is given by Equation (12). Note that a qualified far-field must be zero at the direction of . We may simply exclude this mode from the propagation group to avoid possible abnormal data at this direction.
In a practical reconstruction task, it is neither necessary nor easy to know the exact sizes of the source area. We can estimate the source area at first, and then choose a proper reconstruction area to cover it. The dimensions of the reconstruction area must be selected as .
It can be seen from Equation (13) that the spatial frequency of the highest radiating component is . Therefore, the spatial resolution in both directions is , which agrees with the Rayleigh diffraction limit. In other words, we cannot expect to obtain a higher spatial resolution than with the proposed reconstruction algorithm.
To demonstrate the effectiveness of the method, we reconstruct the pattern of a digit array formed by 364 Hertzian dipoles, as shown in Figure 3. All dipoles have unit amplitudes and are located on a uniform grid with spacing in the xoy plane. Four cases of source distributions are examined. They all have the same patterns as shown in Figure 3, but the spacings and the source areas are changed, as listed below:
- Case 1:
- , resulting in a source area of ,
- Case 2:
- , source area is ,
- Case 3:
- , source area is ,
- Case 4:
- , source area is .
The numerical experiments are carried out at first in an ideal situation that all far-fields are accurately calculated at the required sampling directions. No noises are included.
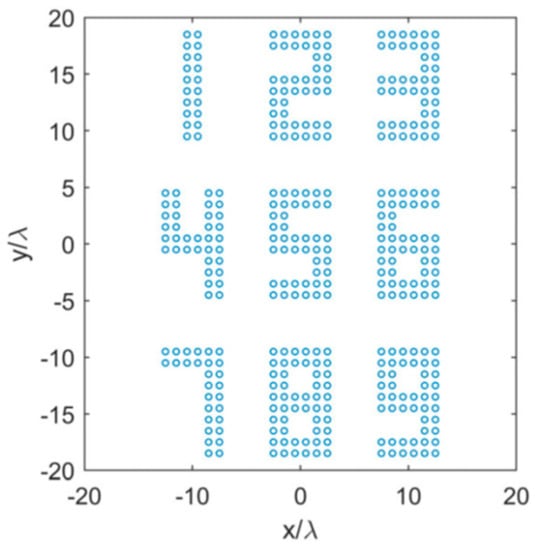
Figure 3.
Source picture to reconstruct. Here, 364 Hertzian dipoles locate on the xoy plane. Each dot represents a dipole.
Firstly, we assume all dipoles are x-polarized and choose the reconstruction area as for all four source cases. The center of the reconstruction area is placed at the origin, the same as that of the source area. As , we can count using (10) that there are 5025 modes in total in the propagation group. Their peak directions and the corresponding wave vectors are calculated with Equations (8) and (9). The far-fields at these directions in the upper half space are calculated with
where and the number of the dipoles is . All Hertzian dipoles have unitary amplitude.
The reconstructed radiating part of the x-component of the source currents can be calculated with Equation (13). The results are plotted in Figure 4. The nine digits can be recognized in all four of these cases. In Case 1 and Case 2, almost all dipoles can be distinguished as the smallest spacing between them is larger than the achievable spatial resolution (). However, in Case 3 and Case 4, the dipoles cannot be distinguished anymore because their small spacings obviously exceed the range of the achievable spatial resolution.
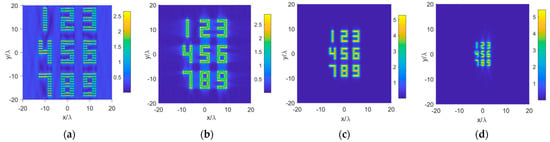
Figure 4.
The reconstructed pictures of the four sources: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
From Equation (10), we observe that a larger reconstruction area generates a larger number of propagation modes and requires more sampling data of the far-fields. As a result, more information can be recovered. However, it is not necessary to use a reconstruction area much larger than the estimated source area. As shown in Figure 4c,d, there is almost no useful information in the blue area outside the source region.
To exploit the effect of the reconstruction area, we choose for Case 3 and for Case 4, which are in proportion to their source area. The number of the corresponding propagation modes is then reduced to 1257 and 317, respectively. The reconstructed results are shown in Figure 5. It can be seen that the resolution of the reconstructed source pictures is almost the same as that in Figure 4c,d. The reconstruction area mainly affects the range of the reconstructed picture, but has little effect on the spatial resolution. We may use a smaller reconstruction area to alleviate the requirement for a large amount of sampling data.
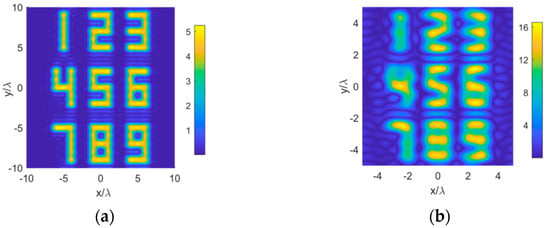
Figure 5.
The results with smaller reconstruction areas. (a) Case 3; (b) Case 4.
In many situations, there may be no priori information that we can use to choose the direction and the center of the reconstruction area. However, their choices have an inevitable impact on the reconstruction results. We will use Case 3 to reveal this effect. First, we rotate the source area with an angle of and in the xoy plane, respectively. The polarization of all dipoles is rotated in the same way. Assume that we still reconstruct the x-component with the reconstruction area of . The resultant pictures are shown in Figure 6a,b. As the polarization of the far-fields rotates with the sources, the x-polarization component of the far-fields decreases with the increase in the rotation angle. Therefore, the effective information for the reconstruction decreases and the definition of the reconstructed source picture deteriorates. The recovered source picture begins to blur when the rotation angle is larger than , as shown in Figure 6b.
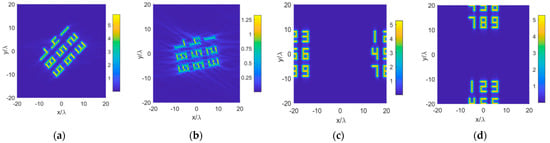
Figure 6.
The reconstructed currents when the source area rotates with an angle of (a) and (b) , and shifts by in the (c) x-direction and (d) y-direction.
Next, we shift the center of the source area to , while the reconstruction area is unchanged. The center of the current expressed by Equation (13) will also shift to . As is shown in Equation (13), is a 2D periodic function with periodicity of and in x- and y-direction, respectively. We can truncate in the reconstruction area to obtain the reconstructed current distribution. We have examined two cases in which the center of the source is shifted to and , respectively. The recovered source pictures are shown in Figure 6c,d. The spatial periodicity of the reconstructed pictures is clearly demonstrated.
Generally, it is required to reconstruct both the x-component and the y-component of the planar current in order to recover the total radiating part of the source. We still use Case 3 as the source to recover, but the polarization of the middle raw of digits, i.e., “456”, is changed from x-polarization to y-polarization. The reconstructed x-component source picture and y-component source picture are shown in Figure 7a,b, respectively. Each reconstruction process can accurately reconstruct the corresponding polarization component of the source current. However, we have to combine them together to obtain a complete source picture.
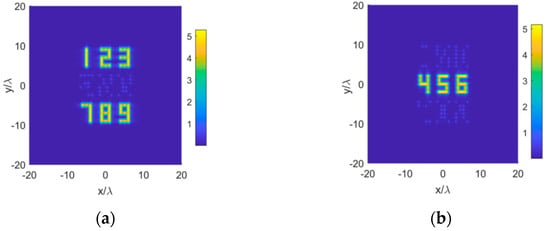
Figure 7.
The reconstructed pictures of a source with two polarizations. (a) x-component and (b) y-component.
Noises inevitably exist in measurements. In order to evaluate the performance of the reconstruction method with the presence of noise, we add white Gaussian noises (WGNs) with different levels into the sampled far-field data. The signal-to-noise ratio (SNR) in the first case is about 30 dB and the SNR in the second case is about 0 dB. The source type Case 3 listed previously is used as the source to recover and the reconstruction area is selected to be . The results are shown in Figure 8. Although the resolution of the recovered image becomes lower with a larger noise level, the nine digits can all be clearly identified even when the SNR decreases to 0 dB.
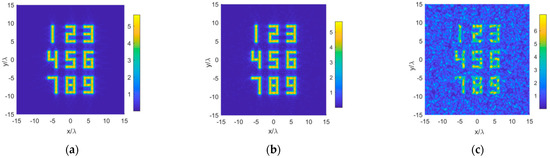
Figure 8.
The reconstructed pictures of source Case 3. (a) no noise; (b) SNR = 30 dB WGN; (c) SNR = 0 dB WGN.
3. Sampling on a Plane
In the standard reconstruction process discussed in Section II, the spatial samplings are performed at the peak directions of all propagation modes. We will show in this section that it is possible to reconstruct the source picture by sampling at other directions with the same number of sampling data. As the sampling points are not necessarily at the peaks of the mode functions, the coefficients of the current cannot be determined directly with Equation (12). Instead, they have to be calculated by solving a matrix equation. For the sake of convenience, we reorder the coefficients of the current to form a single column vector
and number them from 1 to , where is the number of the total radiating harmonic components of the current and is also the number of the total propagation modes. The sampled far-fields are arranged as a column vector in the same order with . Then, the current vector can be obtained by solving the following matrix equation:
The entries of the impedance matrix and that of the far-field vector are, respectively, expressed as follows:
It is assumed to sample the far-field at , as shown in Figure 9a.
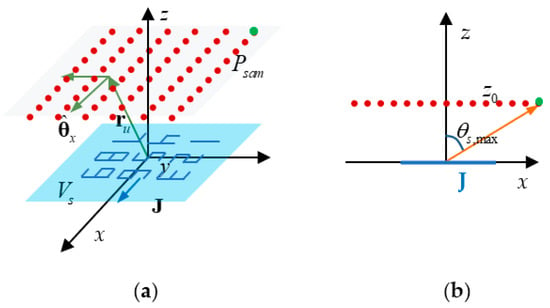
Figure 9.
Sample the far-field on a plane. Dots are the sampling points. (a) Perspective view; (b) side view with .
The plane is in the upper half space and is parallel to the source plane with a center at . A convenient strategy is to sample the far-fields at a uniform grid with a spacing of . The number of the sampling points has to be exactly equal to . In order to indicate the sampling area intuitively, we use a parameter to represent the largest polar angle of the sampling points.
We use a reconstruction area of to reconstruct the source Case 3, where all Hertzian dipoles are x-polarized and the smallest spacing is . The far-field is sampled on a uniform grid within a square region at the plane with . By varying from to , the sampling spacing can be adjusted. The recovered source distributions are shown in Figure 10. Although the quality of the recovered source pictures are different, the nine digits can be distinguished when equals , , , and , respectively. In this example, the source picture cannot be correctly reconstructed when or .
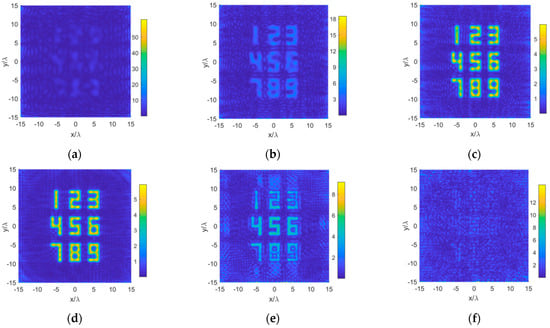
Figure 10.
Reconstructed results for Case 3. Sample on a planar grid above the source with different : (a) ; (b) ; (c) ; (d) ; (e) ; and (f) .
It is not necessary to arrange the sampling grid within a square-shaped area. In practical applications like remote sensing, we may sample the far-field using aircraft along a linear path , as shown in Figure 11. In this situation, the information in the transversal direction will be lost and only the source distribution in the direction along the sampling path can be reconstructed. We again take the source Case 3 as an example, and all dipoles are x-polarized. The far-fields are sampled right above the source area, along a linear path in the x-direction and the y-direction, respectively. The reconstructed results are shown in Figure 12a,b. Actually, they are 1D pictures. They are uniform in the transversal direction. In the direction of the sampling path, the reconstructed source distribution at a certain point includes the contributions from all of the sources on the transversal line.
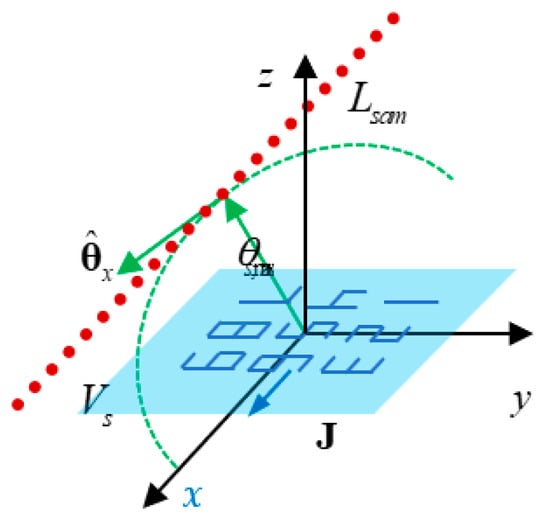
Figure 11.
Sample on a linear grid right above the source.
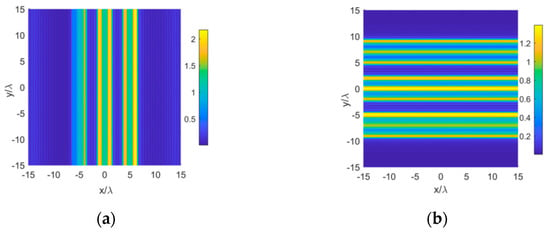
Figure 12.
Reconstructed pictures for Case 3. Sample on a linear grid right above the source along the (a) x-direction and (b) y-direction.
However, we have checked that these two algorithms are quite sensitive to noises. They may fail for even a very small noise level. A better choice is to sample the far-fields on the plane exactly at the grids corresponding to the propagation modes that fall in the specified planar sampling area, as shown in Figure 13. Each grid corresponds to the peak direction of a propagation mode. Note that the grid is also uniform. The spacing between two adjacent grids can be determined by the constellation and the distance between the source plane and the sampling plane. As only parts of the propagation modes are used in the reconstruction, the spatial resolution of the recovered images will inevitably deteriorate. However, as can be seen in Figure 14, all nine digits can be recognized even in the case when , in which only about 1/6 of the total propagation modes are used.

Figure 13.
The propagation modes in the sampling plane (red grids).
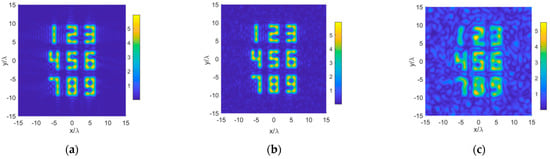
Figure 14.
Reconstructed results for Case 3. Sampling on a plane grid. Only propagation modes within are used. (a) No noise; (b) SNR = 20 dB WGN; (c) SNR = 0 dB WGN.
The performance with the presence of noise is also largely improved. As shown in Figure 14b, when the SNR is 20 dB, the deterioration of the recovered picture is not severe. The nine digits can still be recognized even for an SNR of 0 dB, as shown in Figure 14c. The loss of definition of the picture is mainly caused by the reduction in the number of the sampling data.
4. Conclusions
A direct algorithm for reconstructing the radiating part of a current source is proposed in this paper. After choosing a proper reconstruction area, a constellation can be created for the propagating modes. The two polarization components of the current are then recovered separately using far electric field data sampled on the corresponding constellation grids. Numerical examples have demonstrated that the radiating part of the source can be effectively reconstructed even if the far-field data are contaminated by a white Gaussian noise with a low SNR of 0 dB.
It has been shown that the source image can be recovered by sampling on a plane or along a linear path over the source region. However, the algorithm is found to be sensitive to noise. This drawback can be overcome by sampling the far-fields exactly at the constellation dots on the plane. Therefore, only part of the propagation modes contributes to the reconstruction. The resolution of the recovered image may deteriorate accordingly.
Basically, the proposed method can be applied in situations where the far electric fields can be sampled on the corresponding constellation grids. In order to achieve the finest resolution, it is required to acquire the far-fields on the whole upper half constellation grids, including information of the amplitudes, phases, polarizations of the fields, as well as the positions of the grids. As the method is proposed for recovering the radiating part of a current source on a plane, it provides no information on the non-radiating part of the source.
In future work, we will try to do achieve the following: (i) Find effective methods to avoid significant deterioration of the recovered source images in the situations of using only part of the propagation modes when planar sampling strategy is adopted. (ii) Extend the method to reconstructing sources on a spherical surface, multilayer sources, and volume current distributions. In these cases, the NDF is still important information for developing stable algorithms. (iii) Try to find or apply denoising techniques [38] to improve the reconstruction results with the presence of background or measurement noises. As it is always not an easy task to measure the phase of fields, it is of great significance if the radiating part of the current source can be reconstructed with phaseless data [39].
Author Contributions
Conceptualization, methodology, original draft, funding acquisition, calculation, G.X.; Verification, review and editing, R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (61831016) and the National Natural Science Foundation of China (Grant 62188102). The National Key R&D Program of China, China, (Grant 2019YFB2204703).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Napier, P.J.; Thompson, A.R.; Ekers, R.D. The very large array: Design and performance of a modern synthesis radio telescope. Proc. IEEE 1983, 71, 1295–1320. [Google Scholar] [CrossRef]
- Ares, F.; Elliott, R.S.; Moreno, E. Design of planar arrays to obtain efficient footprint patterns with an arbitrary footprint boundary. IEEE Trans. Antennas Propag. 1994, 42, 1509–1514. [Google Scholar] [CrossRef]
- Bucci, O.M.; D’Elia, G.; Mazzarella, G.; Panariello, G. Antenna pattern synthesis: A new general approach. Proc. IEEE 1994, 82, 358–371. [Google Scholar] [CrossRef]
- Massa, A.; Rocca, P.; Oliveri, G. Compressive sensing in electromagnetics—A review. IEEE Antennas Propag. Mag. 2015, 57, 224–238. [Google Scholar] [CrossRef]
- Xiong, C.; Xiao, G.B. A diagnosing method for phased antenna array element excitation amplitude and phase failures using random binary matrices. IEEE Access 2020, 8, 33060–33071. [Google Scholar] [CrossRef]
- Persson, K.; Gustafsson, M.; Kristensson, G.; Widenberg, B. Source reconstruction by far-field data for imaging of defects in frequency selective radomes. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 480–483. [Google Scholar] [CrossRef]
- Xu, X.; Narayanan, R.M. Three-dimensional interferometric ISAR imaging for target scattering diagnosis and modeling. IEEE Trans. Image Proc. 2001, 10, 1094–1102. [Google Scholar]
- Joachimowicz, N.; Pichot, C.; Hugonin, J.P. Inverse scattering: An iterative numerical method for electromagnetic imaging. IEEE Trans. Antennas Propag. 1991, 39, 1742–1753. [Google Scholar] [CrossRef]
- Chen, X. Subspace-based optimization method for solving inverse scattering problems. IEEE Trans. Geosci. Remote Sens. 2010, 48, 42–49. [Google Scholar] [CrossRef]
- Johnson, J.M.; Rahmat-Samii, V. Genetic algorithms in engineering electromagnetics. IEEE Antennas Propag. 1997, 39, 7–21. [Google Scholar] [CrossRef]
- Fuchs, B. Synthesis of sparse arrays with focused or shaped beam pattern via sequential convex optimizations. IEEE Trans. Antennas Propag. 2012, 60, 3499–3503. [Google Scholar] [CrossRef]
- Meijer, C.A. Simulated annealing in the design of thinned arrays having low sidelobe levels. In Proceedings of the 1998 South African Symposium on Communications and Signal Processing-COMSIG’98, Rondebosch, South Africa, 7–8 September 1998; pp. 361–366. [Google Scholar]
- Prisco, G.; D’Urso, M. Maximally sparse arrays via sequential convex optimizations. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 192–195. [Google Scholar] [CrossRef]
- Boeringer, D.; Werner, D. Particle swarm optimization versus genetic algorithms for phased array synthesis. IEEE Trans. Antennas Propag. 2004, 52, 771–779. [Google Scholar] [CrossRef]
- Mojabi, P.; LoVetri, J. Overview and classification of some regularization techniques for the Gauss-Newton inversion method applied to inverse scattering problems. IEEE Trans. Antennas Propag. 2009, 57, 2658–2665. [Google Scholar] [CrossRef]
- Wang, L.; Zhong, Y.; Chen, L.; He, Z.; Zhou, J.; Liu, Q.H. Radiation diagnosis of PCBs and ICs using array probes and phaseless inverse source method with a joint regularization. IEEE Trans. Microw. Theory Techn. 2022, 70, 1442–1453. [Google Scholar] [CrossRef]
- Kumar, B.P.; Branner, G.R. Generalized analytical technique for the synthesis of unequally spaced arrays with linear, planar, cylindrical or spherical geometry. IEEE Trans. Antennas Propag. 2005, 53, 621–633. [Google Scholar] [CrossRef]
- Haupt, R.L. Thinned arrays using genetic algorithms. IEEE Trans. Antennas Propag. 1994, 42, 993–999. [Google Scholar] [CrossRef]
- Bucci, O.M.; Genearelli, C.; Savarese, C. Representation of electromagnetic fields over arbitrary surfaces by a finite and nonredundant number of samples. IEEE Trans. Antennas Propag. 1998, 46, 351–359. [Google Scholar] [CrossRef]
- Miller, E.K. The incremental far field and degrees of freedom of the sinusoidal current filament. IEEE Antennas Propag. Mag. 2007, 49, 13–21. [Google Scholar] [CrossRef]
- Pizzo, A.; Marzetta, T.L.; Sanguinetti, L. Degrees of freedom of holographic MIMO channels. In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, Georgia, 26–29 May 2020; pp. 1–5. [Google Scholar]
- Sekehravani, E.A.; Leone, G.; Pierri, R. NDF and PSF analysis in inverse source and scattering problems for circumference geometries. Electronics 2021, 10, 2157. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698. [Google Scholar] [CrossRef]
- Panin, V.Y.; Kehren, F.; Michel, C.; Casey, M. Fully 3-D PET reconstruction with system matrix derived from point source measurements. IEEE Trans. Med. Imaging 2006, 25, 907–921. [Google Scholar] [CrossRef]
- Sekehravani, E.A.; Leone, G.; Pierri, R. PSF analysis of the inverse source and scattering problems for strip geometries. Electronics 2021, 10, 754. [Google Scholar] [CrossRef]
- Devaney, A.J.; Wolf, E. Radiating and nonradiating classical current distributions and the field they generate. Phys. Rev. D 1973, 8, 1044–1047. [Google Scholar] [CrossRef]
- Chen, X.D. Computational Methods for Electromagnetic Inverse Scattering; John Wiley & Sons: Singapore, 2018. [Google Scholar]
- Devaney, A.J. Mathematical Foundations of Imaging, Tomography and Wavefield Inversion; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Chew, W.C.; Wang, Y.M.; Otto, G.; Lesselier, D.; Bolomey, J.C. On the inverse source method of solving inverse scattering problems. Inverse Probl. 1994, 10, 547–553. [Google Scholar] [CrossRef]
- Marengo, E.A.; Ziolkowski, R.W. Nonradiating and minimum energy sources and their fields: Generalized source inversion theory and applications. IEEE Trans. Antennas Propag. 2000, 48, 1553–1562. [Google Scholar] [CrossRef]
- Rosenbaum-Raz, S. On scatterer reconstruction from far-field data. IEEE Trans. Antennas Propag. 1976, 24, 66–70. [Google Scholar] [CrossRef]
- Tsitsas, N.L.; Athanasiadis, C. Point source excitation of a layered sphere: Direct and far-field inverse scattering problems. Quarter. J. Mech. Appl. Math. 2008, 61, 549–580. [Google Scholar] [CrossRef][Green Version]
- Yang, J.; Sarkar, T.K. Reconstructing a nonminimum phase response from the far-field power pattern of an electromagnetic system. IEEE Trans. Antennas Propag. 2005, 53, 833–841. [Google Scholar] [CrossRef]
- Otto, G.P.; Chew, W.C. Microwave inverse scattering-local shape function imaging for improved solution of strong scatterers. IEEE Trans. Microw. Theory Techn. 1994, 42, 137–141. [Google Scholar] [CrossRef]
- Cui, T.J.; Chew, W.C.; Yin, X.X.; Hong, W. Study of resolution and super resolution in electromagnetic imaging for half-space problems. IEEE Trans. Antennas Propag. 2004, 52, 1398–1411. [Google Scholar]
- Lopez, Y.A.; Las-Heras Andres, F.; Pino, M.R.; Sarkar, T.K. An improved super-resolution source reconstruction method. IEEE Trans. Instrum. Meas. 2009, 58, 3855–3866. [Google Scholar] [CrossRef]
- Szameit, A.; Shechtman, Y.; Osherovich, E.; Bullkich, E.; Sidorenko, P.; Dana, H.; Steiner, S.; Kley, E.B.; Gazit, S.; Cohen-Hyams, T.; et al. Sparsity-based single-shot subwavelength coherent diffractive imaging. Nat. Mater. 2012, 11, 455–459. [Google Scholar] [CrossRef]
- Schimmack, M.; Mercorelli, P. An on-line orthogonal wavelet denoising algorithm for high-resolution surface scans. J. Frankl. Inst. 2018, 355, 9245–9270. [Google Scholar] [CrossRef]
- Ji, X.; Liu, X.; Zhang, B. Phaseless inverse source scattering problem: Phase retrieval, uniqueness and direct sampling methods. J. Comput. Phys. X 2019, 1, 100003. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).