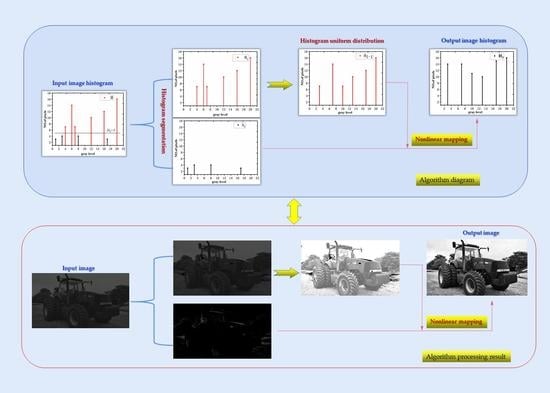
Contrast-Controllable Image Enhancement Based on Limited Histogram
Abstract
1. Introduction
- We devised a histogram segmentation mechanism for the grey-level probability parameter which splits the input images into two sub-images: the main histogram and the restricted histogram. The grey-scale probability parameter is composed of the number of grey-scale pixels among all pixels in the original histogram, and the effects of this varying parameter on the two metrics of contrast and information entropy of the output histogram are elaborated.
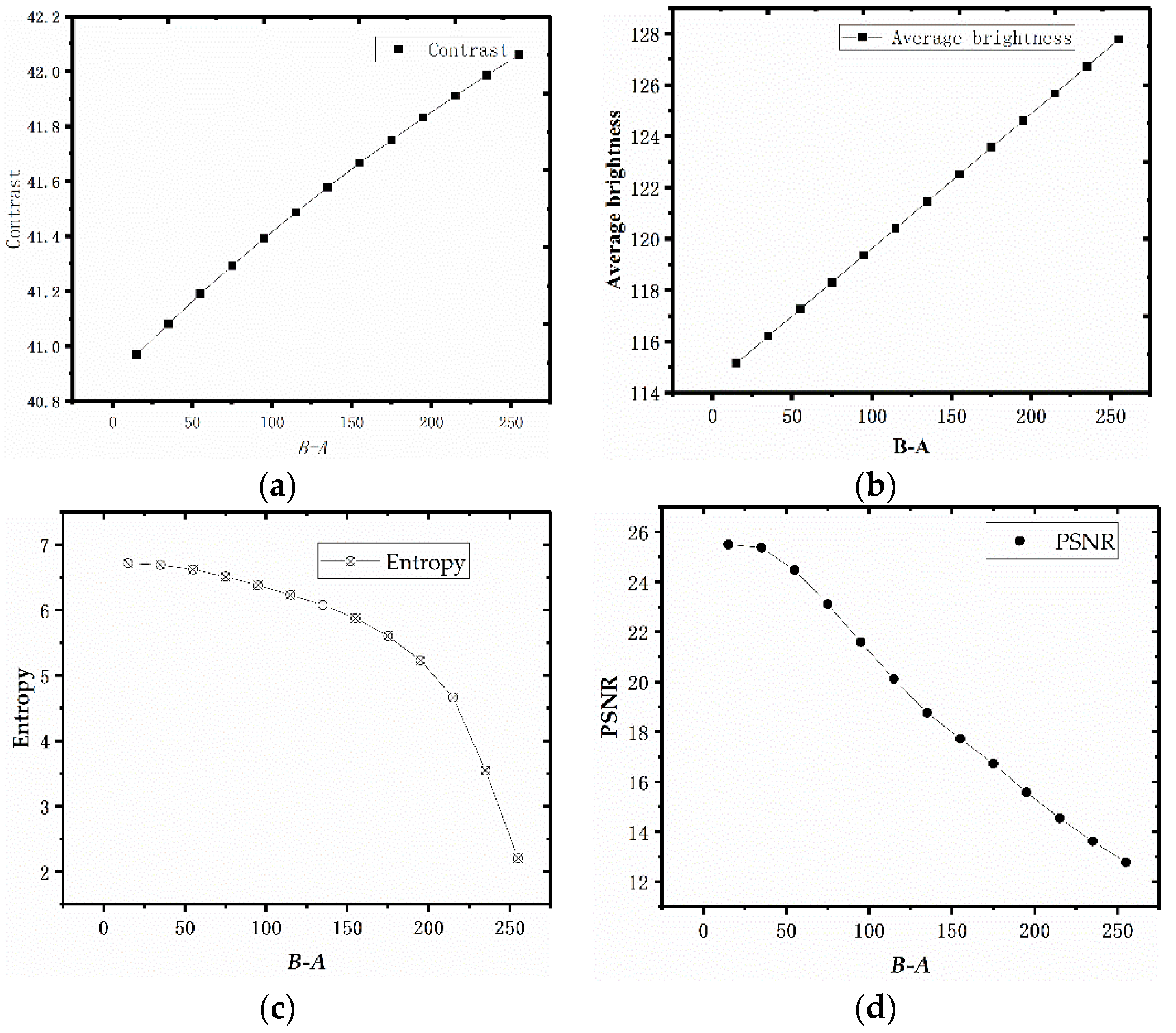
- The main histograms are evenly distributed between A and B. Adjusting the size of A and B also changes the output image contrast and average brightness index values. By modifying the main histogram with a uniformly distributed histogram, there will be very few artifacts in the final output image and the brightness of the histogram will become more natural.
- Using the non-linear mapping method given in this paper, the constrained histogram is mapped into the modified master histogram. This aims to reduce the detail loss in the output image, making the main viewing of the enhanced histogram look more detailed and natural.
2. Research Objective and Method
2.1. Research Objective
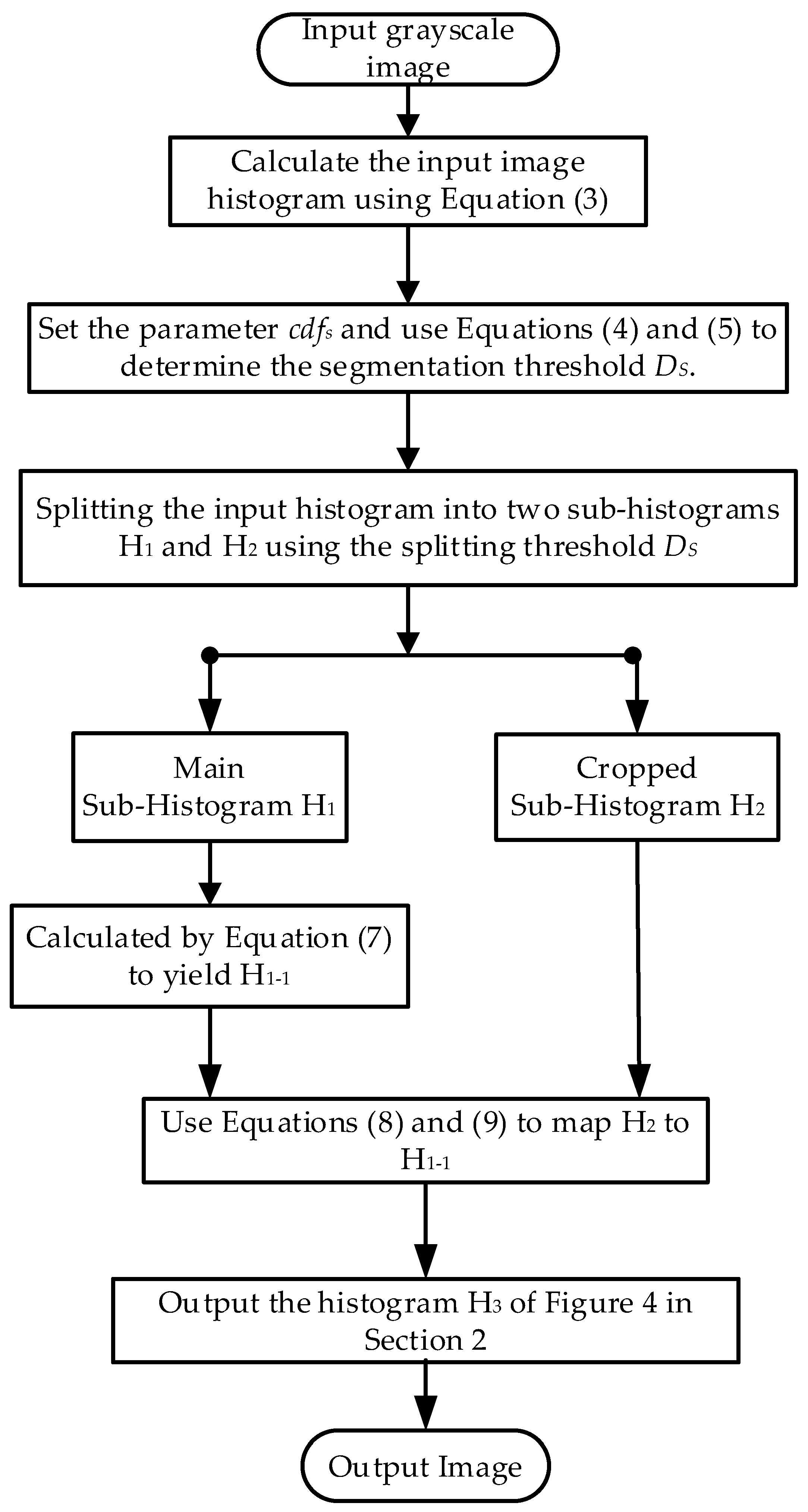
2.2. Proposed Method
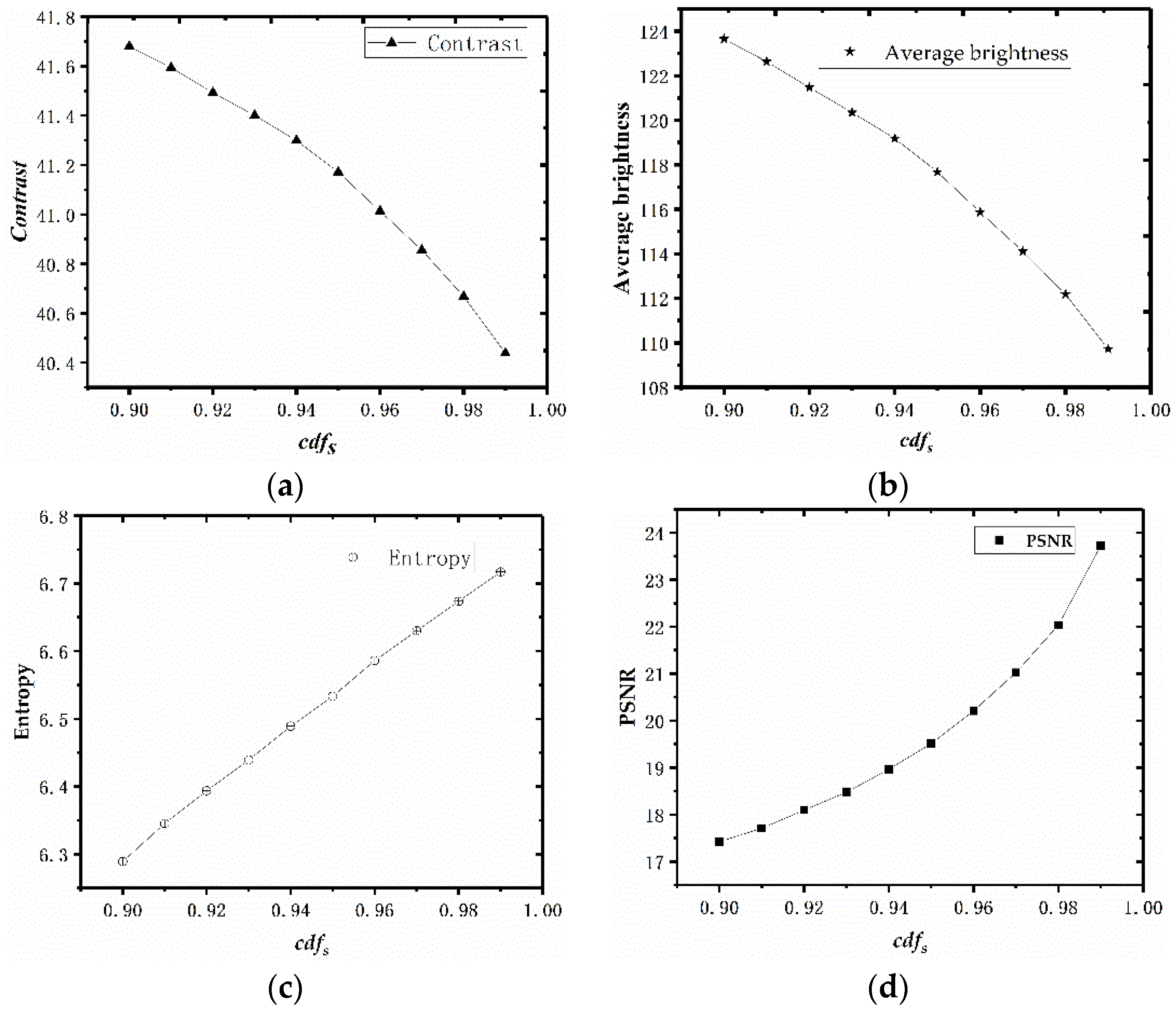
- The first part is the segmentation of the original histogram. Assuming cdfs is the set to a cumulative probability partition value, the corresponding histogram number partition value Ds is calculated cyclically according to Equation (4). For the actual calculation, the initial value DS = 0 is set first, and whether cdf(j) ≥ cdfS is satisfied is judged after cdf(j) is calculated by Equation (5). If the condition is satisfied, then DS = DS + 1; otherwise, the value of DS remains unchanged.
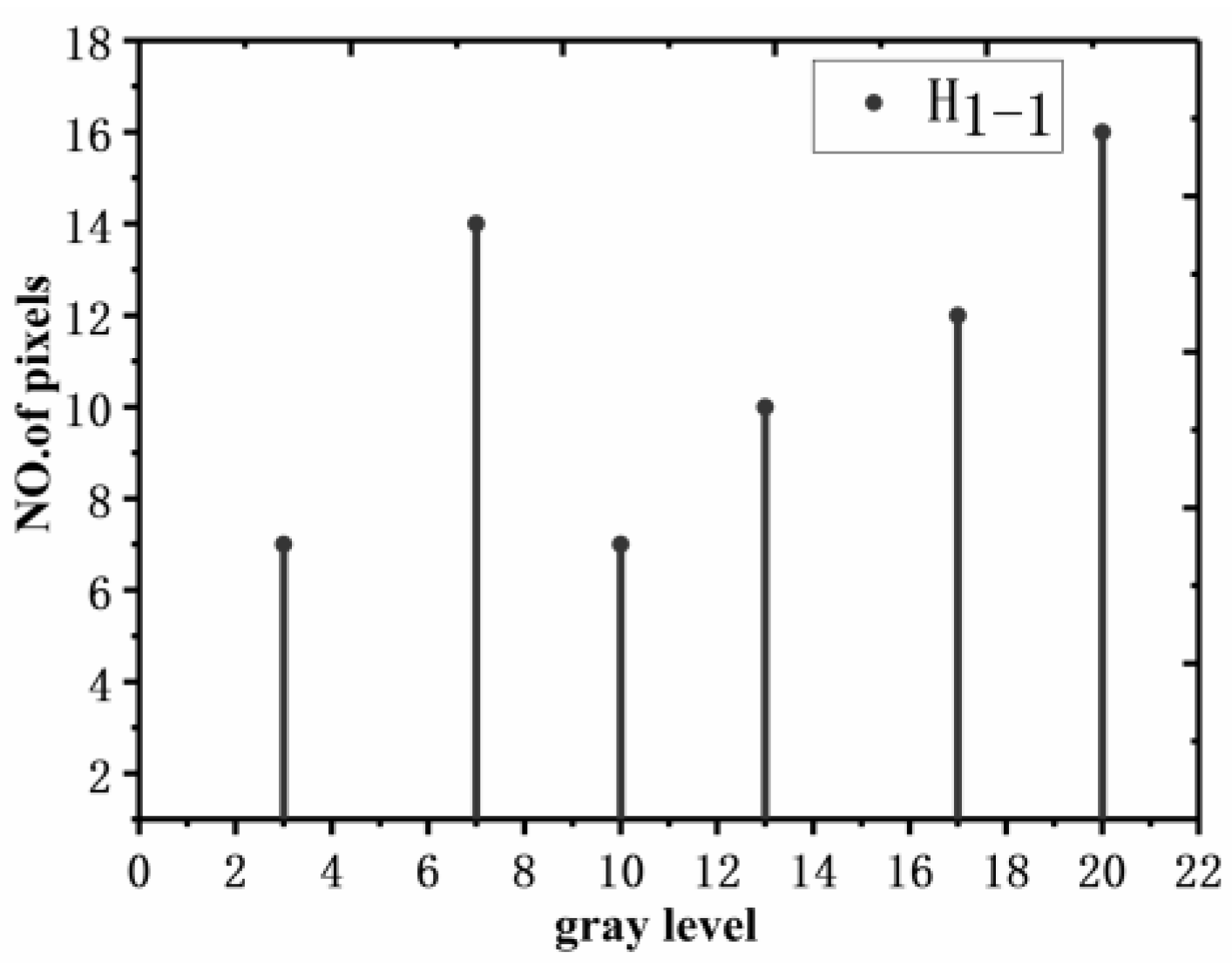
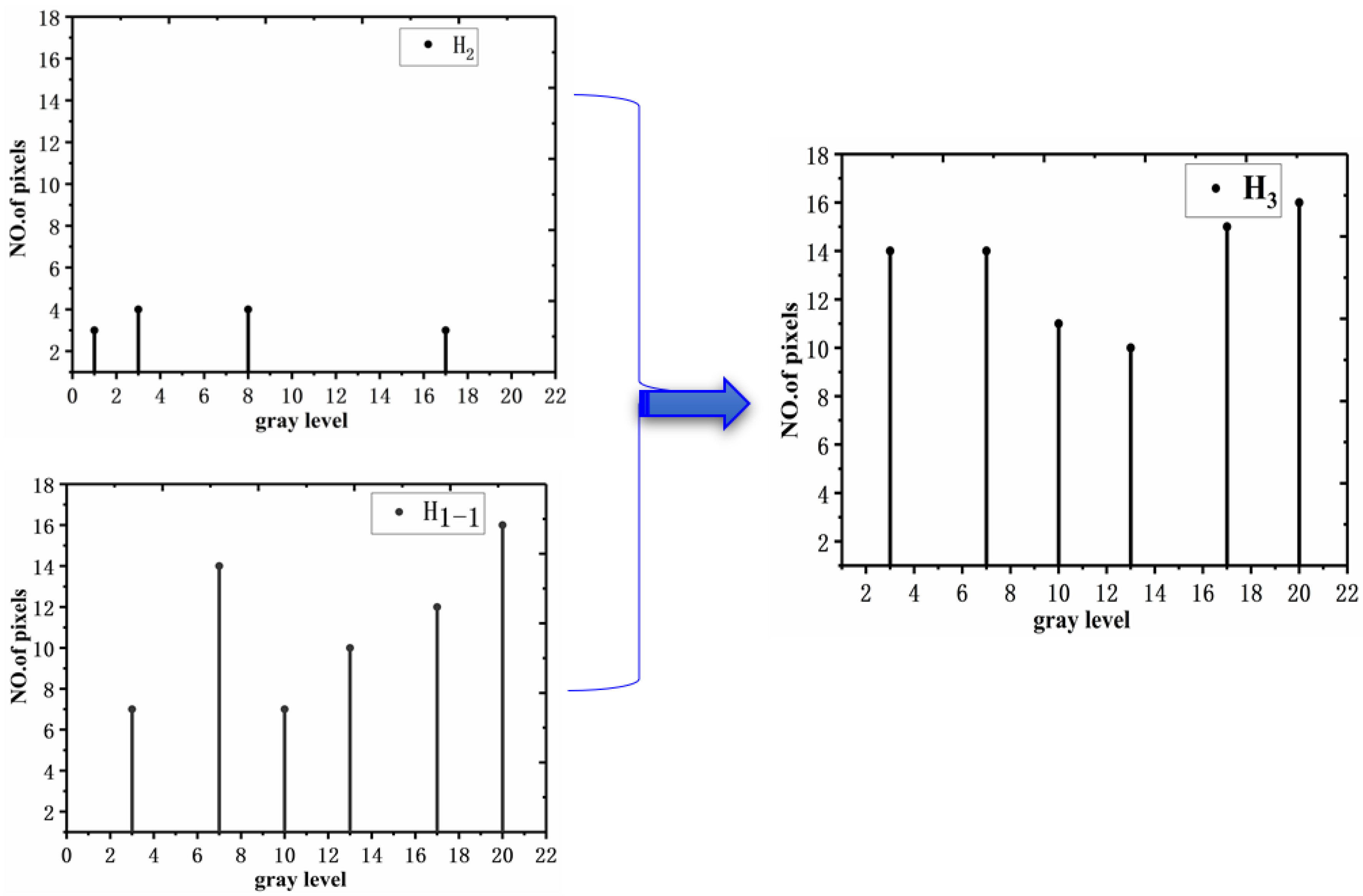
- The second part is the uniform distribution of sub-histogram H1. Suppose [A B] is the histogram grayscale range of the input image, in our schematic A = 0, B = 20; then, the sub-histogram H1 is uniformly distributed in this range; the uniformly distributed histogram is recorded as H1-1. The uniform distribution diagram is shown in Figure 3, and the uniform distribution equation of the histogram is defined as the Equation (7).
- The third part is to map the restricted sub-histogram H2 into the sub-histogram H1-1. Assume i is the index gray value variable of the main histogram H1 and I is the index gray value of restricted histogram H2. The non-linear mapping process consists of 3 main steps. First, to find the grey value DI with the smallest difference in value and its corresponding index value t, we select the grey value I from the sub-histogram H2 and compare it with all the grey values in the H1 histogram, in turn, calculated as shown in Equation (8). Taking the input image histogram H as an example, if we choose I = 3, we find that only the grey value 4 in H1 is closest to 3. At this point, we can determine DI = 4, t = 1. Secondly, we calculate the new grey value It in H1-1 after uniform distribution of grey values according to Equation (9). After the calculation, we find that DI = 4 in H2 has become the new grey value 3 in H1-1. Finally, all DI grey values of the restricted sub-histogram H1 are mapped to the sub-histogram H1-1. In this example, DI = 4 is mapped to It = 3, and Figure 4 represents the final mapping process and results.
3. Evaluation Metrics
- (i)
- Information entropy [31]
- (ii)
- (iii)
- (iv)
- MS-SSIM
4. Experiment Results and Analysis
4.1. Impacts of the Parameters A and B on Brightness and Contrast
4.2. Impacts of cdfs Parameters on Algorithm Performance Metrics
4.3. Comparison of Algorithms
4.3.1. Narrow-Dynamic-Range Image “Tractor” with Low Grayscale
4.3.2. Narrow-Dynamic-Range Image “fish” with Medium Grayscale
4.3.3. Narrow-Dynamic-Range Image “Bridge” with High Grayscale
4.3.4. Average Performance Metric for All Algorithms
5. Experimental Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, W.; Gao, F.; Zhang, P.; Li, Y.; An, Y.; Zhong, X.; Lu, Q. Research on Multiview Stereo Mapping Based on Satellite Video Images. IEEE Access 2021, 9, 44069–44083. [Google Scholar] [CrossRef]
- He, Z.; Li, J.; Liu, L.; He, D.; Xiao, M. Multiframe Video Satellite Image Super-Resolution via Attention-Based Residual Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5605015. [Google Scholar] [CrossRef]
- Cheng, L.; Wang, J.; Li, Y. ViTrack: Efficient Tracking on the Edge for Commodity Video Surveillance Systems. IEEE Trans. Parallel Distrib. Syst. 2022, 33, 723–735. [Google Scholar] [CrossRef]
- Fu, C.; Wu, X.; Hu, Y.; Huang, H.; He, R. DVG-Face: Dual Variational Generation for Heterogeneous Face Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 2938–2952. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Liu, J.; Liu, Y.; Fu, H.; Hu, Y.; Cheng, J.; Qi, H.; Wu, Y.; Zhang, J.; Zhao, Y. Structure and Illumination Constrained GAN for Medical Image Enhancement. IEEE Trans. Med. Imaging 2021, 40, 3955–3967. [Google Scholar] [CrossRef] [PubMed]
- Mozaffarzadeh, M.; Minonzio, C.; de Jong, N.; Verweij, M.D.; Hemm, S.; Daeichin, V. Lamb Waves and Adaptive Beamforming for Aberration Correction in Medical Ultrasound Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 84–91. [Google Scholar] [CrossRef]
- Priya, S.; Santhi, B.A. Novel Visual Medical Image Encryption for Secure Transmission of Authenticated Watermarked Medical Images. Mob. Netw. Appl. 2021, 26, 2501–2508. [Google Scholar] [CrossRef]
- Xie, Y.B. Research on Application of Ultrasound Medical Imaging Technology in Big Data Mining of Regional Medical Imaging. J. Med. Imaging Health Inform. 2021, 11, 930–937. [Google Scholar] [CrossRef]
- Wang, X.W.; Chen, L.X. An effective histogram modification scheme for image contrast enhancement. Signal Process. Image Commun. 2017, 58, 187–198. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Z.B. Image contrast enhancement using adjacent-blocks-based modification for local histogram equalization. Infrared Phys. Technol. 2017, 86, 59–65. [Google Scholar] [CrossRef]
- Liu, S.L.; Rahman, M.A.; Lin, C.F.; Wong, C.Y.; Jiang, G.N.; Liu, S.C.; Kwok, N.; Shi, H.Y. Image contrast enhancement based on intensity expansion-compression. J. Vis. Commun. Image 2017, 48, 169–181. [Google Scholar] [CrossRef]
- Xiao, B.; Tang, H.; Jiang, Y.J.; Li, W.S.; Wang, G.Y. Brightness and contrast controllable image enhancement based on histogram specification. Neurocomputing 2018, 275, 2798–2809. [Google Scholar] [CrossRef]
- Kim, Y.T. Contrast enhancement using brightness preserving bi-histogram equalization. IEEE Trans. Consum. Electron. 1997, 43, 1–8. [Google Scholar]
- Wang, Y.; Zhang, B. Image enhancement based on equal area dualistic sub image histogram equalization method. IEEE Trans. Consum. Electron. 1999, 45, 68–75. [Google Scholar] [CrossRef]
- Chen, S.D.; Ramli, R. Contrast enhancement using recursive mean-separate histogram equalization for scalable brightness preservation. IEEE Trans. Consum. Electron. 2003, 49, 1301–1309. [Google Scholar] [CrossRef]
- Sim, K.S.; Tso, C.P.; Tan, Y.Y. Recursive sub-image histogram equalizationapplied to gray scale images. Pattern Recogn. Lett. 2007, 28, 1209–1221. [Google Scholar] [CrossRef]
- Huang, S.; Cheng, F.; Chiu, Y. Efficient contrast enhancement using adaptive gamma correction with weighting distribution. IEEE Trans. Image Process 2012, 22, 1032–1041. [Google Scholar] [CrossRef]
- Chen, S.D.; Ramli, A.R. Minimum mean brightness error bi-histogram equalization in contrast enhancement. IEEE Trans. Consum. Electron. 2003, 49, 1310–1319. [Google Scholar] [CrossRef]
- Lu, C.H.; Hsu, H.Y.; Wang, L. A new contrast enhancement technique by adaptively increasing the value of histogram. In Proceedings of the IST 2009—International Workshop on Imaging Systems and Techniques, Shenzhen, China, 11–12 May 2009. [Google Scholar]
- Tang, J.R.; Mat Isa, N.A. Bi-histogram equalization using modified histogram bins. Appl. Soft Comput. 2017, 55, 31–43. [Google Scholar] [CrossRef]
- Zuiderveld, K. Contrast limited adaptive histogram equalization. In Graphic Gems IV; Academic Press Professional: San Diego, CA, USA, 1994; pp. 474–485. [Google Scholar]
- Ooi, C.H.; Kong, N.S.P.; Ibrahim, H. Bi-histogram equalization with a plateau limit for digital image enhancement. IEEE Trans. Consum. Electron. 2009, 55, 2072–2080. [Google Scholar] [CrossRef]
- Ooi, C.H.; Mat Isa, N.A. Adaptive contrast enhancement methods with brightness preserving. IEEE Trans. Consum. Electron. 2010, 56, 2543–2551. [Google Scholar] [CrossRef]
- Singh, K.; Kapoor, R. Image enhancement using exposure-based sub-image histogram equalization. Pattern Recogn. Lett. 2014, 36, 10–14. [Google Scholar] [CrossRef]
- Santhi, K.; Wahida Banu, R.S.D. Adaptive contrast enhancement using modified histogram equalization. Opt.—Int. J. Light Electron Opt. 2015, 126, 1809–1814. [Google Scholar] [CrossRef]
- Li, S.; Jin, W.Q.; Li, L.; Li, Y.Y. An improved contrast enhancement algorithm for infrared images based on adaptive double plateaus histogram equalization. Infrared Phys. Technol. 2018, 90, 164–174. [Google Scholar] [CrossRef]
- Ashiba, H.I. Cepstrum adaptive plateau histogram for dark IR night vision images enhancement. Multimed. Tools Appl. 2020, 79, 2543–2554. [Google Scholar] [CrossRef]
- Acharya, K. Central Moment and Multinomial Based Sub Image Clipped Histogram Equalization for Image Enhancement. Int. J. Image Graph. Signal Process. 2021, 1, 1–12. [Google Scholar] [CrossRef]
- Paul, A. Adaptive tri-plateau limit tri-histogram equalization algorithm for digital image enhancement. Vis. Comput. 2021. [CrossRef]
- Paul, A.; Bhattacharya, P.; Maity, S.P. Histogram modification in adaptive bi-histogram equalization for contrast enhancement on digital images. Optik 2022, 259, 168899. [Google Scholar] [CrossRef]
- Wan, M.J.; Gu, G.H.; Qian, W.X.; Ren, K.; Chen, Q.; Maldague, X. Infrared image enhancement using adaptive histogram partition and brightness correction. Remote Sens. 2018, 10, 682. [Google Scholar] [CrossRef]
- Liang, K.; Ma, Y.; Xie, Y.; Zhou, B.; Wang, R. A new adaptive contrast enhancement algorithm for infrared images based on double plateaus histogram equalization. Infrared Phys. Technol. 2012, 55, 309–315. [Google Scholar] [CrossRef]
- Chaudhry, H.; Rahim, M.S.M.; Khalid, A. Multi scale entropy based adaptive fuzzy contrast image enhancement for crowd images. Multimed. Tools Appl. 2018, 77, 15485–15504. [Google Scholar] [CrossRef]
- Kanmani, M.; Narsimhan, V. An image contrast enhancement algorithm for grayscale images using particle swarm optimization. Multimed. Tools Appl. 2018, 77, 23371–23387. [Google Scholar] [CrossRef]
- Wang, Z.; P, S.E.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
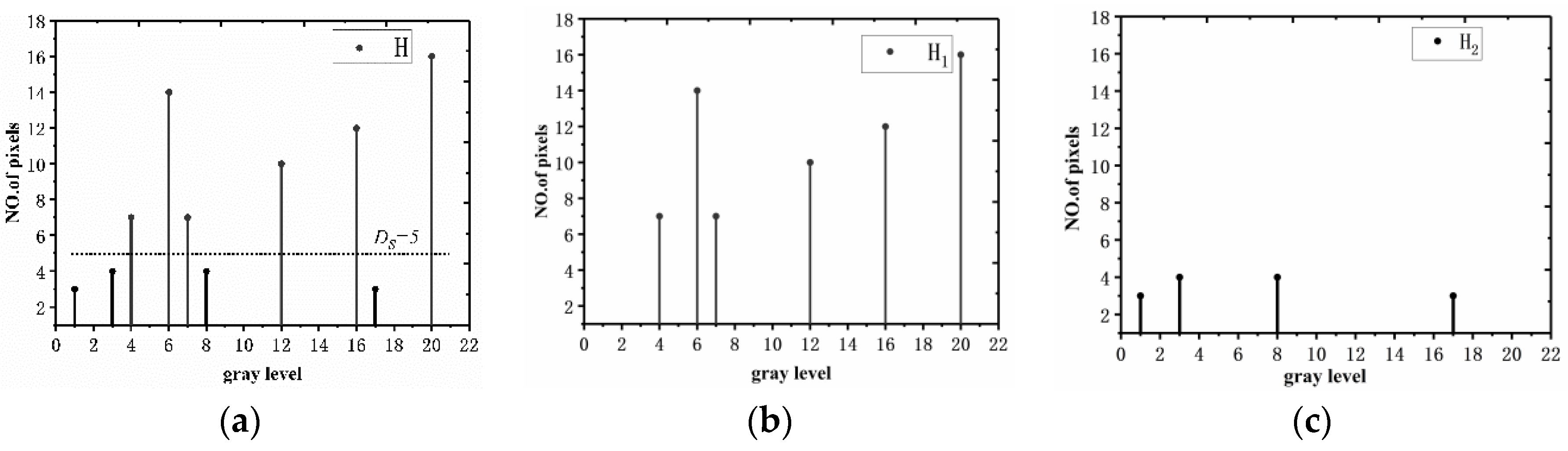






| Variable | Histogram Values | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Gray level | 1 | 3 | 4 | 6 | 7 | 8 | 12 | 16 | 17 | 20 |
| Number of pixels | 3 | 4 | 7 | 14 | 7 | 4 | 10 | 12 | 3 | 16 |
| Techniques | Entropy (bit) | PSNR (dB) | C (dB) | MS-SSIM |
|---|---|---|---|---|
| Input image | 5.6278 | — | 31.19 | 1 |
| BHEMHE | 5.6254 | 23.97 | 32.07 | 0.8768 |
| RMSHE | 5.5856 | 15.92 | 33.81 | 0.8364 |
| DSIHE | 5.4967 | 28.21 | 32.43 | 0.9389 |
| AGCWD | 5.3453 | 23.58 | 34.34 | 0.9377 |
| BHEPL | 5.5817 | 13.44 | 35.84 | 0.6624 |
| Ref. [30] | 5.6268 | 12.49 | 38.00 | 0.6477 |
| Proposed | 5.6272 | 11.49 | 39.19 | 0.6546 |
| Techniques | Entropy (bit) | PSNR (dB) | C (dB) | MS-SSIM |
|---|---|---|---|---|
| Input image | 5.8827 | — | 42.13 | 1 |
| BHEMHE | 5.5462 | 11.79 | 42.29 | 0.4937 |
| RMSHE | 5.8231 | 16.86 | 42.14 | 0.6749 |
| DSIHE | 5.7467 | 24.62 | 42.66 | 0.8972 |
| AGCWD | 5.7231 | 20.30 | 43.56 | 0.9397 |
| BHEPL | 5.7756 | 14.71 | 42.69 | 0.5952 |
| Ref. [30] | 5.8789 | 16.55 | 43.47 | 0.7744 |
| Proposed | 5.8821 | 15.82 | 42.37 | 0.7309 |
| Techniques | Entropy (bit) | PSNR (dB) | C (dB) | MS-SSIM |
|---|---|---|---|---|
| Input image | 5.8731 | ― | 46.76 | 1 |
| BHEMHE | 3.8784 | 10.03 | 45.06 | 0.6085 |
| RMSHE | 5.7085 | 13.58 | 45.82 | 0.7787 |
| DSIHE | 5.6787 | 32.11 | 46.69 | 0.9756 |
| AGCWD | 5.4201 | 24.89 | 47.27 | 0.9785 |
| BHEPL | 5.5614 | 12.81 | 45.36 | 0.7131 |
| Ref. [30] | 5.8470 | 20.95 | 46.60 | 0.9214 |
| Proposed | 5.8725 | 8.46 | 42.66 | 0.7899 |
| Techniques | Entropy (bit) | PSNR (dB) | C (dB) | MS-SSIM |
|---|---|---|---|---|
| Input images | 7.1273 | ― | 40.35 | 1 |
| BHEMHE | 6.4441 | 18.13 | 40.51 | 0.8358 |
| RMSHE | 6.9712 | 24.66 | 40.56 | 0.9272 |
| DSIHE | 6.9189 | 19.61 | 41.39 | 0.8653 |
| AGCWD | 6.8224 | 14.61 | 43.45 | 0.8872 |
| BHEPL | 5.9408 | 16.80 | 41.12 | 0.8164 |
| Ref. [30] | 7.1151 | 31.27 | 40.68 | 0.9873 |
| Proposed | 7.1266 | 30.90 | 40.74 | 0.9905 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Wang, J.; Wang, H.; Xia, C. Contrast-Controllable Image Enhancement Based on Limited Histogram. Electronics 2022, 11, 3822. https://doi.org/10.3390/electronics11223822
Fan X, Wang J, Wang H, Xia C. Contrast-Controllable Image Enhancement Based on Limited Histogram. Electronics. 2022; 11(22):3822. https://doi.org/10.3390/electronics11223822
Chicago/Turabian StyleFan, Xin, Junyan Wang, Haifeng Wang, and Changgao Xia. 2022. "Contrast-Controllable Image Enhancement Based on Limited Histogram" Electronics 11, no. 22: 3822. https://doi.org/10.3390/electronics11223822
APA StyleFan, X., Wang, J., Wang, H., & Xia, C. (2022). Contrast-Controllable Image Enhancement Based on Limited Histogram. Electronics, 11(22), 3822. https://doi.org/10.3390/electronics11223822