Abstract
Traditional monopulse radar cannot resolve two closely spaced targets present in one resolution cell (range and Doppler) by means of the monopulse ratio. This study presents a closed-form solution to resolve the directions of arrival of two unresolved targets using a single snapshot of four independent channels in phase comparison monopulse radar. If both targets have the same elevation or same azimuth direction, the proposed scheme cannot estimate their directions. To estimate the direction of such targets, an extra antenna is required. The impact of input noise power, the targets’ direction, and phase difference of the targets’ signal on the accuracy of angle estimation are also explained. The numerical simulation result validates the effectiveness of the presented scheme.
1. Introduction
Monopulse radar systems represent a practical and fast technique to determine the direction of targets. Monopulse radar can detect the target angle by using multiple antennas and comparing the phases of the signals in phase comparison monopulse radar (PCM), as well as comparing the amplitudes of the signals in amplitude comparison monopulse. They require a single pulse to compare the received signals, and estimate the azimuth and elevation directions of a target. Nonetheless, the basic monopulse technique is suitable when there is only one target in each resolution cell (range and Doppler); however, when there are two or more targets in a resolution cell and when it suffers from multi-path effect, their complex amplitudes will interfere with each other; thus, the indicated angles of the targets wander wildly and the estimated angle can have a huge error [1,2,3]. Radars are limited in terms of improving the range, beam width, and Doppler resolution [1]. Furthermore, in an electronic counter measure condition, an active jammer’s signal is present in all the range cells; therefore, range-resolving techniques would not be useful. To overcome this limitation of monopulse radars, several studies have been conducted; the methods fall into two categories: statistical and deterministic. Although the statistical methods can reach more accurate solutions than the deterministic methods, they are not appropriate for tight-time scenarios, because these methods generally use several pulses to extract the statistical features and have limitations depending on the target model [4,5]. Deterministic methods use one or two pulses and are not limited by the target model; they are mostly based on Sherman’s method [6,7], in which he used a complex difference/sum ratio and two pulses to separate two unresolved targets. However, Sherman’s method and the other two pulse methods have two drawbacks: first, the amplitude coefficient of the sum signals from the two targets should be steady between pulses and second, the relative phase should be different; these are called Sherman’s conditions [8]. To estimate the angle of ambiguous targets in radar cells, different methods such as beamforming, STAP, subspace rejection [4,9,10], MIMO radar, and two polarization radar [6,11] have been presented in the literature. However, these methods require additional equipment and different types of signal transmissions for monopulse radars [12]. In [8,13], to solve the drawback of Sherman’s method, instead of graphical (or numerical) ones, exact algebraic solutions are proposed; however, this method is applicable for non-fluctuating or slowly fluctuating targets. Papers [14,15,16] present a practical method for estimating the angle of two targets in a radar cell for angle comparison monopulse radar. This solution provides ways to avoid both drawbacks; however, it fails to estimate the angles of targets when the two targets are positioned at the same azimuth or same elevation angle. In [17] and [18], two additional antennas have been used to detect targets located at the same elevation or same azimuth angle, which are applicable at certain antenna configurations, but not for all configurations. In this paper, we present the closed-form method for angle estimation of two unresolved targets whose signals overlap in both frequency and time domains by using only one pulse in PCM for rapidly fluctuating targets, which enables us to solve the drawbacks of Sherman’s method. The solution is mathematically similar to that of [17] and [19]; however, it has less computational complexity and better performance. Furthermore, our method can estimate the angles of two targets that are positioned at the same azimuth or same elevation angle by adding an extra antenna; in addition, the impact of SNR, the targets’ direction, and the phase difference of targets on the accuracy of angle estimation is also described.
In Section 2, the characteristics of two target signals in PCM will be described and the presented direction estimation method for two targets for PCM is described; in Section 3, the exact solutions for the same azimuth and same elevation targets angle estimation are derived; in Section 4, the effect of SNR, phase difference, and angle difference between the targets on the accuracy of angles’ estimation of the targets will be examined; and eventually, in Section 5, the simulation results of the proposed methods for the two targets for several values of the SNR and relative positions of the two targets are shown.
2. Closed-Form Solutions to Resolve the Direction of Two Targets
A four-channel PCM consists of four antenna feeders located on the corners of a rectangle. In this section, we formulate an exact two-target solution for a phase comparison configuration, which is essentially a two-by-two array shown in Figure 1 [14].
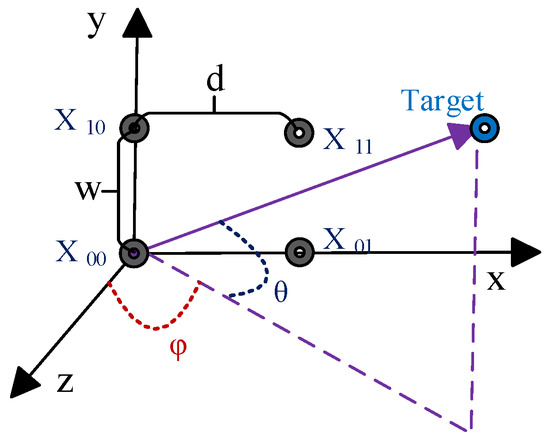
Figure 1.
Configuration of a four-channel PCM antenna.
For a single target, the phase relationships of the four-channel noiseless signal, denoted x00, x01, x10, and x11, give the target direction [14].
where , , and φ and θ are the azimuth and elevation angles of the target; while ‘d’ and ‘w’ are the X and Y spacing between elements; and λ is the received signal wavelength. For the two targets, Equation (1) can be written as below [14]:
where αa, αb, βa, and βb are the corresponding phase angles; and ga, gb, γa, and γb target amplitude and phase (indices ‘a’ and ‘b’ mean two separate targets). In Equation (2), we have eight real unknowns for four equations; thus, the unknowns cannot be obtained by numerical methods. If , the signal will be received from a single target; otherwise, the received signal will be from two separate targets with different angles [14].
We can write ; thus, the expressions of the four-antenna receiver signals from (2) directly as follows:
Therefore, we can obtain from the same equation:
Define , so Equation (4) can be expressed as:
By multiplying (5) through with H, the Equation (5) converts to (6):
Therefore, the two solutions for the desired H (Ha and Hb) are:
If |H|2 = 1, the solutions are valid. Assuming that the square root provides a real solution, we can deduce:
For the real solution, both A and B must be real; then, the only possible solution is in the limit as A→0. If B2 < 4|A|2; then, the magnitude of (8) is [19]:
So, |H|2 = 1; whether B2 < 4|A|2, the existence of the solutions is verified. ℑ(B) = 0 (ℑ(.) mean the imaginary part); then, we can extract the values of αa and αb as follows:
The function ‘f’ is determined as:
To determine the elevation angle, we can write the expressions of the four-antenna receive signals directly as follows:
Therefore, we can obtain from the same equation:
Define ; so, the same as (4) and (5), which can be expressed as:
Therefore, the two solutions for the desired ρ are:
We can extract the values of βa and βb from (10) and (11) as follows:
The function ‘f’ is determined as (11). From (7), the amplitude of the targets are:
From (1), we can calculate θx and φx from βa and βb, and αa and αb. Generally, the decoy (deception target) signal power is greater than the real target signal power. So, based on the signal amplitude after separation, it is possible to distinguish the real target from the decoy.
3. Estimate the Direction of Two Targets Located at Same Azimuth or Same Elevation Angle Due to Angular Ambiguity
Whenever two targets are at the same azimuth or same elevation angle (if αa = αb, then AE = 0; and if βa = βb, then A = 0), the derived algorithm fails to estimate the angular location of the targets. To overcome this limitation, the paper [17] has used two extra antennas to detect such targets; it is applicable to certain antenna configurations where , and not applicable to other antenna configurations. The paper [20] proposes a subarray-based four-channel monopulse method to achieve an efficient, unambiguous, and fast two-target resolution to estimate the angle of same direction targets. We used an extra antenna (xz antenna) to overcome the limitation of the above derived algorithm and improve its angle estimation performance; it is applicable for all the antenna configurations. The xz antenna (extra antenna) is located in the center of antennas; the location of the xz antenna shown in Figure 2.
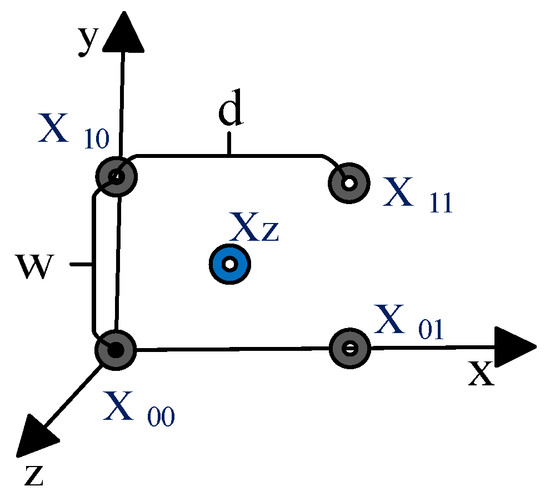
Figure 2.
Location of the xz antenna.
For the two targets case, the xz antenna’s received signal can be written as below:
If the two targets are located at the same elevation angle (βa = βb), then ; and if the two targets are located at the same azimuth angle (αa = αb), then . So, we can calculate and . During target tracking mode in monopulse radars, the angle error tends to zero; so, at the same elevation angle targets, the elevation angle tends to zero (β = 0); and at the same azimuth angle targets, the azimuth angle tends to zero (α = 0). From (3) and (4), if β = 0 (if β ≠ 0, then ), we can write:
Therefore, we can obtain from the same equation:
Define ; so, from (6) we can write:
We can calculate αa/2 and αb/2 the same as (10). From (12) and (13), we can write:
Define ; so, from (6) we can write:
We can calculate βa/2 and βb/2 the same as (16). By calculating the value of βa/2 and βb/2, it is possible to calculate the value of αx, βx, θx, and φx.
4. Accuracy Analysis of Direction Estimation
From (14), (6) we can write:
We can deduce:
where is the phase differences between the two targets; so:
We can write B as follows:
We can deduce:
If , we can write (6) as follows:
So, we have:
To investigate the effect of phase difference and azimuth angle on the accuracy of elevation angle estimation:
From (30), if , we can write (14) as follows:
From (24)–(28) and (29), A, B, and C are a function of sin(βb − βa), sinψ, ga, and gb (SNR); and from (30) and (31), AE, BE, and CE are a function of sin(αb − αa), sinψ, ga, and gb (SNR). The angle estimation error is inversely proportional to the targets’ SNR and for the azimuth angle, and inversely proportional to the targets’ SNR and for the elevation angle. If the phase difference between the two targets’ echoes zero or 180 degrees, the noise is infinite; and if two targets have the same elevation angle or same azimuth angle, the noise is infinite and the proposed method will not work; so, we cannot obtain the expected solutions from (7) and (15). If , SNR increased, and = MAX at the elevation angle estimation and = MAX at the azimuth angle estimation are satisfied; the proposed algorithm will have smallest error and best accuracy.
5. Simulation Results and Discussion
We simulated the ability of the proposed method to estimate two target angles due to angular ambiguity in the phase comparison monopulse radar. The 3 dB width of the sum beam is 6 deg and the two targets have different amplitudes (ga = 2gb), with uniformly distributed random phases. Using these conditions, simulations were performed for various SNRs and the relative positions of the two targets. For the simulations, the deception target positioned at [+1°, +1°] (the towed decoy ‘a’ amplitude is bigger than the real target ‘b’) and the real target positioned at [−1.6°, −1.6°] (azimuth angles and elevation angles, respectively). The simulations were performed for 20 pulses with SNR = 20 dB and SNR = 30 dB. Without the proposed method for unresolved targets’ angle estimation, the estimated angle by typical monopulse radar is shown in Figure 3.
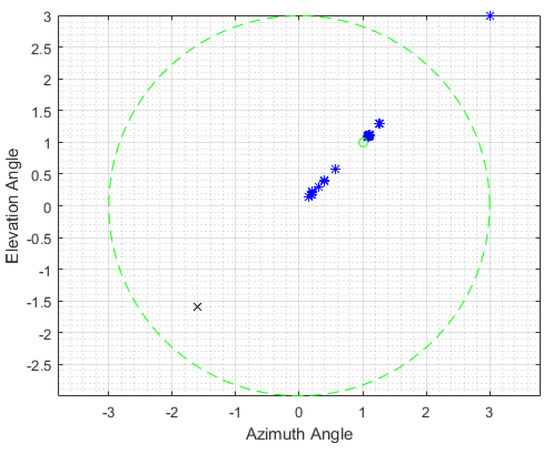
Figure 3.
The estimated angle of two unresolved targets by typical monopulse radar (the green circle is 3 dB width of the sum beam; truth locations: decoy (O), real target (x), and estimated angle (*)).
The accuracy of the proposed angle estimation method is shown in Figure 4 for SNR = 20 dB and SNR = 30 dB (20 times).
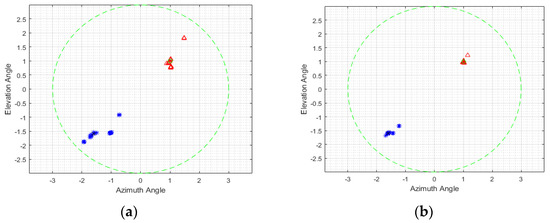
Figure 4.
Scatter plot of angle estimation of real target (*) and decoy (Δ) The green circle is 3 dB width of the sum beam (ground truth locations of decoy (O) and real target (x)). (a) SNR = 20 dB; (b) SNR = 30 dB.
We simulated the ability of proposed method to estimate the angles of two targets that are positioned at the same azimuth or elevation angle (Figure 5); in this case, the same elevation targets are positioned at [−1.8, 0] degree for the real target (‘b’) and [1.2, 0] degree for the decoy (azimuth and elevation angles). The same azimuth targets are positioned at [0, 1.6] degree for the real target (‘b’) and [0, −1] degree for the decoy (azimuth and elevation angles). The two targets have different amplitudes (ga = 2gb) and uniformly distributed random phases. The simulations were performed for 20 pulses, with SNR = 22 dB. We showed the simulation results of the estimated angle of two unresolved targets by typical phase comparison monopulse radar in Figure 5.
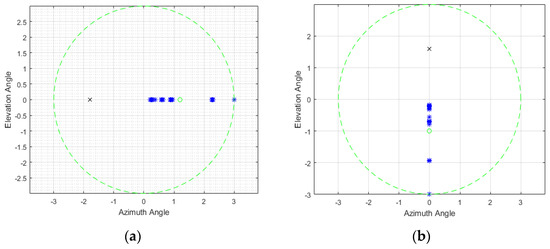
Figure 5.
The estimated angle of two unresolved targets by typical phase comparison monopulse radar; ground truth locations of decoy (O) and real target (x), and estimated angle (*). (a) same elevation; (b) same azimuth.
The accuracy of the proposed angle estimation method (20 times) for the targets located at same azimuth angle or at the same elevation angle is shown in Figure 6.
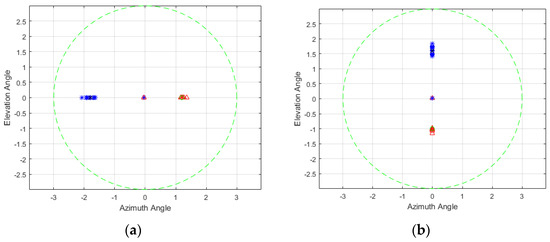
Figure 6.
Scatter plot of angle estimates of real target and decoy (decoy (Δ) and real target (*); ground truth locations of decoy (O) and real target (x)). (a) same elevation; (b) same azimuth.
In our simulations, we use two targets with random phases and place them randomly inside the 3 dB beam. We then add white Gaussian noises that correspond to various levels of SNR. Simulation results demonstrate that the angle estimation is approximately accurate when the SNR is 30 dB and that the two targets are distinguishable when the SNR is 20 dB. Figure 7 shows the root mean square errors (RMSEs) of αa. In this case, the ψ varies from 15° to 165° (when ψ gets closer to zero, the performance will become worse). We can see that the algorithm has the best performance when ψ is close to 90°.
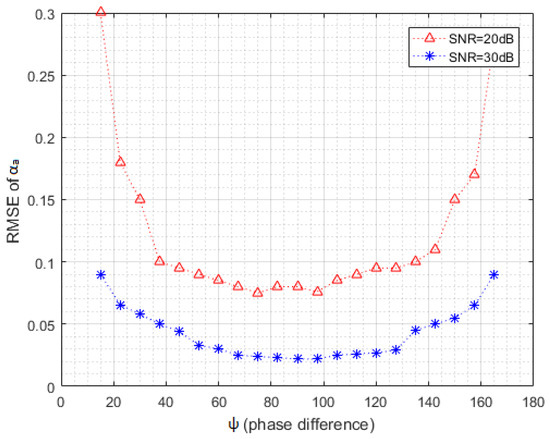
Figure 7.
RMSE of αa versus ψ for SNR = 30 dB and SNR = 20 dB (Δφ = 0.7°).
Figure 8 represents the RMSE of αa; in this case, Δφ = φa − φb varies from 0.2° to 6° (when φa gets closer to φb, the performance will become worse). We can see that the algorithm has a better performance when Δφ increases (Δφ is proportional to Δβ = βb − βa).
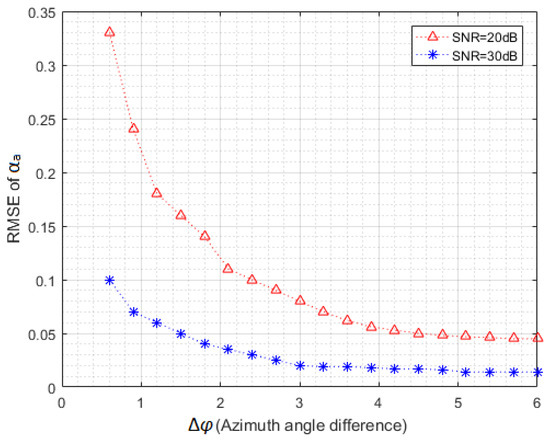
Figure 8.
RMSE of αa versus Δφ = φa − φb for SNR = 30 dB, SNR = 20 dB, and ψ = 45°.
Figure 9 represents the RMSE of αa; in this case, SNR varies from 20 dB to 30 dB.
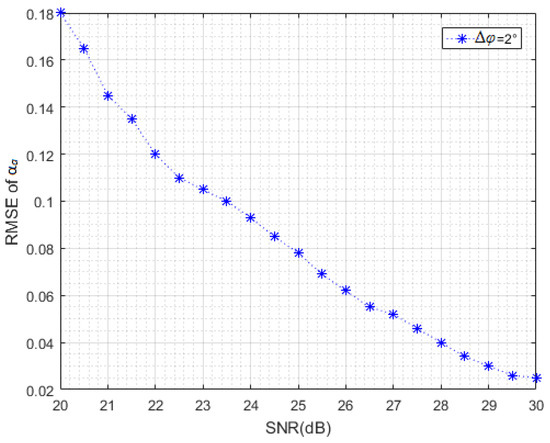
Figure 9.
RMSE of αa versus SNR for ψ = 45°and Δφ = 2°.
The shape of the plot in Figure 9 is obvious; thus, the algorithm has the best performance when SNR increased.
6. Conclusions
In this study, a practical method for the angle estimating of two targets that are located in the same radar resolution cell was presented. By solving the equation group of four antennas, it is possible to use only one pulse to perform angle discrimination of the target and the decoy in the main beam. The same amplitude of the targets will not affect the proposed method for the angle estimating of two targets, and it enjoys high simplicity and high efficiency. If both targets have the same elevation or azimuth angle, the proposed scheme cannot resolve them; thus, we used an extra antenna to detect such targets in the phase comparison monopulse. It is demonstrated that the RMSE of the direction estimation is inversely proportional to the SNR, and the angle difference and phase difference between the two targets. If three or more targets are located in one resolution cell, the estimated angles by the proposed method will be close to the angles of the targets with a larger amplitude. More antennas and more complex algorithms will be needed to detect the angle of three ambiguous targets and the proposed scheme cannot resolve them. The performance of the proposed algorithm was verified by numerical simulation.
Author Contributions
Conceptualization, H.R. and M.A.S.; methodology, H.R.; software, H.R.; validation, H.R., M.A.S. and N.Z.; formal analysis, H.R.; investigation, H.R.; resources, N.Z.; data curation, H.R.; writing—original draft preparation, H.R.; writing—review and editing, M.A.S.; visualization, N.Z.; supervision, M.A.S. and G.S.M.; project administration, M.A.S.; funding acquisition, H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sherman, S.M.; Barton, D.K. Monopulse Principles and Techniques, 2nd ed.; Artech House: Boston, MA, USA, 2011; pp. 187–223. [Google Scholar]
- Gogineni, S.; Nehorai, A. Monopulse MIMO radar for target tracking. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 755–768. [Google Scholar] [CrossRef]
- Wang, Z.; Sinha, A.; Willett, P. Angle estimation for two unresolved targets with monopulse radar. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 998–1019. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Z.; Liu, X.; Dong, W.; Wang, G. Estimation of unresolved targets number based on Gerschgorin disks. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–5. [Google Scholar]
- Sherman, S.M. Complex indicated angles applied to unresolved radar targets and multipath. IEEE Trans. Aerosp. Electron. Syst. 1971, AES-7, 160–170. [Google Scholar] [CrossRef]
- Ma, J.; Shi, L.; Liu, J. Improved two-targets resolution using dual-polarization radar with interlaced subarray partition. In Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Yangzhou, China, 20–22 October 2017; pp. 397–400. [Google Scholar]
- Gorji, A.A.; Tharmarasa, R.; Blair, W.D.; Kirubarajan, T. Multiple unresolved target localization and tracking using colocated MIMO radars. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2498–2517. [Google Scholar] [CrossRef]
- Seung, P.L.; Byung, L.; Cho, S.; Min, L. Unambiguous Angle Estimation of Unresolved Targets in Monopulse Radar. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1170–1177. [Google Scholar]
- Bosse, J.; Rabaste, O. Subspace rejection for matching pursuit in the presence of unresolved targets. IEEE Trans. Signal Process. 2018, 66, 1997–2010. [Google Scholar] [CrossRef]
- Shengbin, L.; Wang, Z.; Hai, X.; Xinghua, L.; Wei, D.; Guoyu, W. A Novel Scheme for Detection and Estimation of Unresolved Targets With Stepped-Frequency Waveform. IEEE Access 2019, 7, 129018–129028. [Google Scholar]
- Zhao, Y.N.; Zhou, Z.Q.; Qiao, X.L. Angle estimation for two closely spaced targets with polarization monopulse radar. In Proceedings of the 2005 Asia-Pacific Microwave Conference Proceedings, Suzhou, China, 4–7 December 2005; pp. 3–8. [Google Scholar]
- Zhiyong, S.; Fei, C.; Qiang, F. A Joint Detection and Tracking Algorithm for Unresolved Target and Radar Decoy. Prog. Electromagn. Res. 2019, 83, 43–60. [Google Scholar]
- Zhenxing, L.; Yunjie, L.; Meiguo, G. Direction estimation for two steady targets in monopulse radar. J. Syst. Eng. Electron. 2015, 26, 61–68. [Google Scholar]
- Zheng, Y.; Shu, T.; Kai, Y. Closed-form four-channel monopulse two-target Resolution. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1083–1089. [Google Scholar] [CrossRef]
- Song, Z.; Xiao, H. Detection of presence of towed radar active decoys based on angle glint. Signal Process 2011, 27, 522–528. [Google Scholar]
- Wang, J.; Xu, X.; Dai, H.; Sun, D.; Qiao, H. Method for four-channel monopulse radar to resist dual-source angle deception jamming. J. Eng. 2019, 2019, 7493–7497. [Google Scholar]
- Seifallah, J.; Ahmed, S.; Mohamed, A. Generalised two target localisation using passive monopulse radar. IET Radar Sonar Navig. 2017, 11, 932–936. [Google Scholar]
- Seifallah, J.; Ahmed, S.; Mohamed, A. Two Target Localization Using Passive Monopulse Radar. In Proceedings of the 2015 IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015. [Google Scholar]
- David, F. Comments on Closed-Form Four-Channel Monopulse Two-Target Resolution. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 913–916. [Google Scholar]
- Shengbin, W.; Zhen, X.; Xiao, Y.; Zhongren, L.; Guoyu, W. Efficient and Unambiguous Two-Target Resolution via Subarray-Based Four-Channel Monopulse. IEEE Trans. Signal Process. 2020, 68, 885–900. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).