Performance Improvement of Polar Codes via UEP Product Coding

Abstract

Aiming to improve the error correction performance of polar codes, researchers have proposed employing the product coding structure involving RS codes of different rates in the horizontal direction and the short polar codewords along the vertical direction. However, there is no efficient algorithm optimizing the rate allocation of RS codes. In order to address this problem, this paper provides an analytical formulation by maximizing the number of correctly decoded information bits. The proposed rate allocation formulation takes the channel statistics into consideration, and we further find that the number of different RS code rates could be limited to a small value. By doing so, the complexities of both the rate allocation optimization and the iterative product decoding could be reduced. Simulation results demonstrate the superiority of RS-polar product codes with the proposed rate allocation method over both additive white Gaussian noise channels and Gilbert–Elliott channels. When the inner polar codes of rate $1/2$ are utilized, the optimized RS-polar product codes of low-to-medium rates significantly outperform the successive cancellation decoding of long polar codes, in the regime of a frame error rate $\ge {10}^{-3}$.

1. Introduction

Polar codes [1] are the first provably capacity-achieving codes for the class of binary-input symmetric discrete memoryless channels. Although the polarized bit-channels are completely noisy or noiseless when the code length approaches infinity, polar codes of short to moderate lengths usually have limited error-correction performance under successive cancellation (SC) decoding. However, for ultra reliable and low-latency communications (URLLC) using polar codes, the constraints on transmission reliability, fast decoding, and limited code lengths have to be satisfied simultaneously. Therefore, the performance of polar codes of limited lengths needs to be improved.

Compared with SC decoding, the successive cancellation list (SCL) decoding provides an improved performance at the cost of a higher decoding complexity and latency. Nevertheless, both SC and SCL algorithms run sequentially, i.e., the decoding of the current bit depends on the correct decoding of all previous bits. Consequently, this will cause severe error propagation and increase the decoding failure probability of those less reliable positions.

One promising solution is to concatenate short polar codes with other block codes [2]; thus, more protection could be introduced to bit-channels of less reliability. For instance, serial coding structures concatenating low-density parity-check codes and simple parity-check codes are discussed in [3,4], respectively. Taking advantage of parallel decoding, parallel concatenation structures of polar codes have also been broadly investigated [5,6,7,8], among which the product coding schemes play major roles. Due to their low-complexity and high parallelism, product coding structures have been widely used for optical communications [9,10,11,12].

To further improve the performance of product codes over wireless channels, product coding systems utilizing unequal error protection (UEP) have been extensively investigated. One of the common approaches is to use Reed–Solomon (RS) codes of progressively weaker strengths. Taking the image transmission scenario as an example, a product code employing horizontal RS codes and vertical rate-compatible punctured convolutional codes (RCPC) is proposed in [13]. In this setting, for those packets that are not correctly decoded by a vertical RCPC decoder, the horizontal RS decoding could still recover part of the information bits by viewing the erroneous packets as erasures. The RS decoding performs only once in the scheme of [13], and the authors of [14,15,16] find that more information bits could be recovered when an iterative decoding is exploited between the horizontal RS codes and vertical channel codes. This is based on the fact that the decoding performance of vertical channel codes could be improved, with some of the information bits already being known from the previous RS decoding. As a result, more corrupted packets could be decoded and, thus, more information could be recovered. This iterative decoding of product codes has been studied for various vertical channels, such as Turbo codes [14], low-density parity-check (LDPC) codes [15] and convolutional codes [16]. Additionally, the product codes with UEP have also been combined with joint source-channel coding [17] and multiple description coding [18].

Following the success of UEP-based product codes, the concept of product coding has also been applied to boost the performance of polar codes. Work [6] utilizes two non-systematic polar codes in both horizontal and vertical directions, and proposes a two-step decoding method to improve the throughput and error correction performance. However, locating errors using the two-step decoder is time-consuming and the resultant product code is still a polar code. Therefore, the problem of protecting less reliable bit-channels is not fully addressed. To solve this problem, the authors of [7] employ interleaved RS codes along the horizontal direction, for the implementation of UEP, and the corresponding error decay rate of the RS-polar product code is analyzed. Nevertheless, the UEP scheme of [7] needs to calculate the code rate of each RS codeword, which requires a high-complexity code rate allocation. Furthermore, the authors of [8] allocate the rates of different RS codes in terms of the error patterns of an SCL decoder. In addition, both [9,10] involve the soft decoding of RS codes, which is too complicated for practical low-latency scenarios.

Despite the fact that the usefulness of UEP-RS-polar product codes has been validated in the aforementioned work, there is still no analytical formulation addressing the rate assignment of different RS codes. Therefore, it would be extremely difficult to find an optimal rate allocation via an exhaustive search. To address this difficulty, we formulate the rate allocation of RS codes as an integer optimization problem, aiming to maximize the amount of correctly decoded information in the RS-polar product codes. In addition, we show that the number of different RS code rates could be limited, considering the channel statistics. In this case, a solution to the proposed rate allocation problem is flexible even with an exhaustive search.

To summarize, the main contributions of this paper are listed as follows.

• The optimal code rate allocation scheme of UEP-RS-polar code is proposed. The rate allocation of RS codes is analytically formulated and efficiently solved, as mentioned before, which could flexibly optimize the RS code rates given the number of desired UEP levels and the channel statistics. To reduce the overhead of extra RS parity symbols, the bit-channels of high reliability are not protected by RS codes. In addition, a judgment module is introduced into the UEP-RS-polar product code, counting the number of correctly decoded polar codewords. This could be achieved by adding 16 cyclic redundancy check (CRC) bits at the end of each polar code. If the number of erasures exceeds the correction ability of RS codes, then the corresponding incorrect polar codewords will be kept as final outputs to prevent more errors caused by RS decoding.
• In order to reduce the decoding latency and iterative decoding complexity of the UEP-RS-polar codes, we propose using a hard decoding for RS codes and SC decoding for polar codes, and both RS decoding and polar decoding could run in parallel. Specifically, if a polar codeword is not correctly decoded, then the whole codeword will be viewed as erased and sent to the RS hard decoder for erasure recovery.
• The proposed UEP-RS-polar scheme is evaluated over additive white Gaussian noise (AWGN) channels and Gilbert–Elliott (GE) channels. By examining different rates of inner polar codes, we find that the proposed “RS(32)-polar(256)” scheme with inner polar codes of rate $1/2$ outperforms the SC decoding of long polar codes. Moreover, it achieves a performance gain of $0.25$ dB compared with the counterpart of [8] at frame error rate ${10}^{-3}$ (the corresponding bit error rate is as low as ${10}^{-6}$) when the overall product code rate is around $1/4$ and the inner polar code rate is $0.5$.

The remainder of this work is organized as follows. Section 2 describes the background of polar codes and the proposed UEP-RS-polar product structure. Section 3 explicitly presents the optimal rate allocation of RS codes. Simulation results and comparisons are reported in Section 4 and finally Section 5 concludes the paper.

2. Proposed UEP-RS-Polar Product Coding Scheme

2.1. Polar Codes

A polar codeword of length $N=2^n,n\ge 1$, is generated by $x_1^N=u_1^{N}G$, where $u_1^N$ is a length-N source block and $x_1^N$ is the codeword. The generation matrix of dimension $N\times N$ is denoted by $G=B_N{F}_2^{\otimes n}$, where $B_N$ and $F_2=\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]$ are the bit-reversal permutation matrix and the core matrix, respectively. The channel polarization theorem [1] states that bit-channels will become noise-free or completely noisy as N reaches infinity.

This paper estimates the reliability of each bit-channel using Gaussian approximation (GA). Further, an information set $\mathcal{F}$ includes the K most reliable bit-channels and a frozen set ${\mathcal{F}}^c$ consists of the remaining $N-K$ bit-channels. Consequently, the polar codes of rate $R_{polar}=\frac{K}{N}$ are constructed by transmitting K information bits over the bit-channels from $\mathcal{F}$, and sending frozen bits (usually zeros) over the bit-channels in ${\mathcal{F}}^c$. Note that both the encoder and decoder know the sets $\mathcal{F}$ and ${\mathcal{F}}^c$.

The SC decoder sequentially determines each information bit using the following rule [1]:

$${\widehat{u}}_i=\left\{\begin{array}{cc}0,& if\frac{W_N^{\left(i\right)}\left(y_1^N,{\widehat{u}}_1^{i-1}|0\right)}{W_N^{\left(i\right)}\left(y_1^N,{\widehat{u}}_1^{i-1}|1\right)}\ge 1\\ 1,& \mathrm{otherwise}\end{array},\right.$$

(1)

where $y_1^N$ is a received block with channel noise. It is easy to notice that the decoding of the i-th bit depends on the correct decoding of all previous $i-1$ bits, calling for a UEP scheme, as described next.

2.2. Proposed Product Code Structure

Since the frozen bits and positions are known at the decoder; thus, no protection is required for them. Figure 1 illustrates the packetization of the proposed UEP-RS-polar product codes, involving only the input bits (i.e., information bits and CRC bits), where each row denotes an RS code and each column is a polar codeword, and the CRC check bits of polar codes are located at the end of each column. Using M and S, respectively, we denote the total number of RS codewords and polar codewords, where each rectangle represents a symbol of $l_{rs}$ bits. Let $(T+1)$ be the number of UEP levels of the UEP-RS-polar scheme, such that all source symbols within the same layer are protected by the same $\left(S,r_t\right)$ RS code, where $r_t$ is the number of RS source symbols at the t-th layer ($1\le r_1\le r_2\le \cdots \le r_T\le r_{T+1}=S$). As a consequence, all symbols of the t-th layer could be successfully recovered if any $r_t$ polar codewords are correctly decoded. Moreover, each polar codeword is appended 16 CRC bits to check if the polar code is successfully decoded, and we assume that the CRC code can detect all erroneous packets.

Considering that the bit-channels of very high reliability could already provide sufficient protection, these corresponding information bits are put at the $(T+1)$-th layer with no extra RS encoding. In addition, the CRC bits generated from the corresponding polar packet are not protected by RS codes. Accordingly, the other information bits are sequentially put in each UEP level, as depicted in Figure 1.

Additionally, let $M_t$ be the number of RS codewords in the first t UEP levels; then, the number of RS codes at the t-th layer is $(M_t-M_{t-1})$, and $M_0=0$ by default. Therefore, by counting the CRC bits as part of source bits (this is commonly used in existing CRC-aided SCL (CA-SCL) decoders [19]), the overall code rate of the UEP-RS-polar product scheme is

$$R_{tx}=\frac{{\sum }_{t=1}^{T+1}{r}_t\left(M_t-M_{t-1}\right)l_{rs}+16S}{NS}.$$

(2)

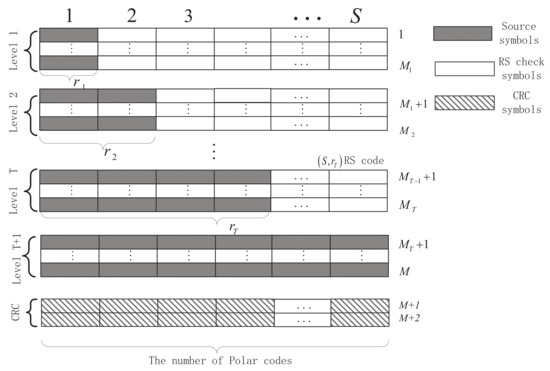
Figure 1. Structure of the proposed UEP-RS-polar product coding scheme.

Figure 2 depicts the block diagram of the proposed UEP-RS-polar scheme, where the SC decoding of polar codes and hard RS decoding are performed iteratively. At the encoding side, the information bits are first encoded by RS encoders of different strengths, and then the RS codewords go through an interleaving block, as described in [7]. Next, CRC bits are generated from the interleaved RS codewords, followed by the polar encoding. At the decoder, S polar packets are decoded in parallel and checked by the corresponding CRC bits. To this end, some polar packets will be correctly decoded while the others are marked as erased. Subsequently, hard RS decoding is performed to decode these erasures. At the t-th decoding iteration $\left(0<t\le T\right)$, if the number of erased polar packets is within the erasure correction ability of the RS codes at level t, then the RS decoders will successfully recover all bits of the polar packets within level t. Consequently, all bits before the t-th level are marked as known in the next decoding iteration. Note that if the number of incorrect polar codewords exceeds the correction ability of RS codes, then the RS decoding will not be triggered and the iterative decoding stops. Therefore, the symbols output by the hard RS decoding are known to be correct, due to the nature of maximum-distance separable codes. At the subsequent iteration, the performance of SC decoding could be improved, taking advantage of the correctly decoded bits from previous RS decoding. This decoding process repeats until no more bits can be recovered.

The motivation of the iterative decoding procedure is described as follows. The polar encoding could be expressed by

$$\begin{array}{cc}\hfill x_1^N& =u_1^{N}G\hfill \\ \hfill & =[u_1,u_2,\cdots ,u_N]G\hfill \\ \hfill & =[u_1,\cdots ,u_n|u_{n+1},\cdots ,u_N]\left[\begin{array}{c}G(1:n)\hfill \\ G(n+1:N)\hfill \end{array}\right]\hfill \\ \hfill & =[u_1,\cdots ,u_n]G(1:n)+[u_{n+1},\cdots ,u_N]G(n+1:N)\hfill \\ \hfill & =\left[x_1^n{x}_{n+1}^N\right],\hfill \end{array}$$

where $G(1:n)$ is an $n\times N$ submatrix and $G(n+1:N)$ is an $\left(N-n\right)\times N$ submatrix of G. Now, the codeword $x_1^N$ can be divided into two parts: the first part $x_1^n$ corresponds to the correctly decoded information bits from prior RS decoding, and $x_{n+1}^N$ can be viewed as a short codeword to be decoded at the next iteration. Therefore, the error propagation of the SC decoding is alleviated, and the successful decoding probability of the next information bit could be improved, since all previous information bits have been correct.

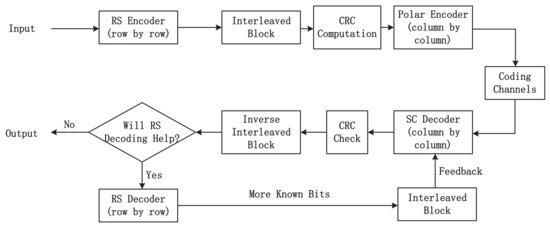
Figure 2. System diagram of the proposed UEP-RS-polar scheme.

2.3. Decoding Complexity

Due to the nature of parallel decoding, the decoding complexity of multiple codewords is the same as that of one codeword. It is known that the complexity of SC decoding is $O(NlogN)$. In addition, the complexity of decoding RS codes is less than $O(Slog{r}_t)<O(SlogS)$, using the low-complexity hard-decision algorithm of [20]. Further, as the maximum number of product decoding iterations is T, the total decoding complexity amounts to $O(TSlogS+TNlogN)$. In practice, it is sufficient to use a small value of T, e.g., this paper takes $T=4$.

On the other hand, if a long polar code of length $SN$ is utilized, then the SC decoding complexity would be $O(SNlog(SN\left)\right)$, which is larger than the complexity of the proposed product scheme.

3. Optimal Rate Allocation of RS Codes

Before proceeding to the formulation of optimal rate allocation, let us first discuss how to select the number of UEP levels T, as shown in Figure 1. The determination of T is significant to the proposed UEP-RS-polar scheme. By taking a large value of T, the error-correction performance would be improved, but at the cost of more product decoding iterations, so the decoding complexity should be comprehensively considered when choosing the value of T. In addition, we note that if all RS codewords within the t-th UEP level are correctly decoded, then the SC decoding performance in terms of frame error rate (FER) could be greatly improved. Inspired from this observation, FERs of SC decoding versus different number of known bits could be calculated, and then the UEP levels are partitioned so that an FER sees a significant decline. In this way, the number $(T+1)$ of total UEP levels and the T-tuple $(M_1,M_2,\dots ,M_T)$ could be flexibly determined, depending on the channel statistics and the affordable decoding complexity, etc.

As an example, Figure 3 shows the FER performance over the Gilbert–Elliott (GE) channels versus the number of known symbols in a polar codeword, where we take the polar code information bits rate to be $0.5$, and $N=512,l_{rs}=8$, and, thus, $M=32$. Each dashed line represents a bound of a UEP level, and the solid line marks the start of the last level with no extra RS protection. Using the notations in Figure 1, we have $T=4$, $M_1=8,M_2=17,M_3=20,M_4=24$ and the last UEP level starts from the 25-th RS codeword.

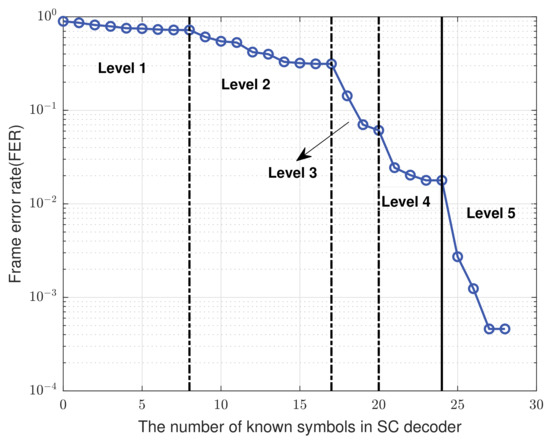
Figure 3. FER over GE channels versus the number of known symbols in a polar codeword, with $M=32$ and $N=512$.

Given the partition of UEP levels, the optimal rate allocation of RS codes is formulated as follows. Let $P_t$ denote the number of source symbols in the first t UEP levels, i.e.,

$$P_t=\sum _{i=1}^t\left(M_i-M_{i-1}\right)\times r_i,1\le t\le T+1,$$

(3)

where $M_0=0$ by default, and the number of information symbols at the t-th layer is $(P_t-P_{t-1})$. Accordingly, the expected number of decoded source symbols of the UEP-RS-polar product scheme can be expressed by

$$\begin{array}{c}\hfill \phi =\sum _{t=1}^{T+1}\left(P_t-P_{t-1}\right)\times D_t,\end{array}$$

(4)

where $D_t$ is the probability of successfully decoding the t-th UEP level.

Next, we define an event ${\mathcal{E}}_t$, where a polar codeword can be successfully decoded when only the first $t\left(1\le t\le T\right)$ UEP levels are known, but cannot be correctly decoded when knowing only the first $t-1$ levels. Additionally, let $F\left(j\right),1\le j\le M$, which denotes the probability of successfully decoding a polar codeword when only the first j symbols (i.e., the first j rows or RS codewords in Figure 1) are already known. Then, we have $\mathbb{P}\left({\mathcal{E}}_t\right)=F\left(M_t\right)-F\left(M_{t-1}\right)$.

Therefore, the probability of decoding the t-th UEP level, for $1\le t\le T+1$, can be given by

$$\begin{array}{c}{D}_t={\displaystyle \sum _{k_1=r_1}^N}{\displaystyle \sum _{k_2=r_2-r_1}^{N-k_1}}{\displaystyle \sum _{k_t=r_t-r_{t-1}\cdots -r_1}^{N-r_{t-1}\cdots -r_1}}\hfill \\ \times \left(\begin{array}{c}N\\ k_1\end{array}\right)\left(\begin{array}{c}N-k_1\\ k_2\end{array}\right)\cdots \left(\begin{array}{c}N-r_{t-1}\cdots -r_1\\ k_t\end{array}\right)\hfill \\ \times {F\left(M_0\right)}^{k_1}{\left(F\left(M_1\right)-F\left(M_0\right)\right)}^{k_2}\cdots \hfill \\ {\left(F\left(M_{t-1}\right)-F\left(M_{t-2}\right)\right)}^{k_t}{\left(1-F\left(M_{t-1}\right)\right)}^{N-r_{t-1}\cdots -r_1}.\hfill \end{array}$$

Based on the above expression, the problem of optimal rate allocation of RS codes is finding the T-tuple $(r_1,r_2,\cdots ,r_T)$ that maximizes the expected number of source symbols, i.e.,

$$\begin{array}{cc}\hfill & \underset{\left(r_1,\cdots ,r_T\right),\left(M_1,\cdots ,M_T\right)}{max}\phi \hfill \\ \hfill s.t.& 1\le r_1<r_2<\cdots <r_T<r_{T+1}=S\hfill \\ \hfill & 1\le M_1<M_2<\cdots <M_T\le M\hfill \end{array}.$$

(5)

Note that the value of T and the vector $\left(M_1,\cdots ,M_T\right)$ are predetermined in terms of the channel statistics and the iterative product decoding by simulations, as described at the beginning of this section. Finally, the desired rate allocation vector, $(r_1,r_2,\cdots ,r_T)$, is optimized by exhaustive search.

4. Simulation Results and Discussion

This section examines the error-correction performance of the proposed UEP-RS-polar product scheme compared to AWGN and GE channels, utilizing the binary phase shift keying (BPSK) modulation. The RS codes used in this section are defined on $GF\left(2^8\right)$, i.e., $l_{rs}=8$, and we set the number of UEP levels as $T=4$. In addition, we took polar code rates of $R_{polar}=0.5$ and $0.67$, and the values of M and S were selected, such that the total codeword length of the proposed product code was 8192 bits. In this section, we utilized the overall code rate $R_{tx}\approx 1/3$ and $1/4$ for the UEP-RS-polar product code. Note that, given an inner polar code rate, both the number of RS codewords within each UEP level and the RS code rates need to be reallocated for a target overall rate $R_{tx}$, as shown in Equation (2). Further, Table 1 lists more parameters, including the optimal rate allocation of RS codes, when $R_{polar}=0.5$ and $0.67$. Moreover, the corresponding overall code rate $R_{tx}$ is also given in Table 1.

It is worth noting that the proposed RS rate allocation depends on the channel statistics of a given $E_b/N_0$, and we named this “design $E_b/N_0$” in this section. Figure 4 plots the number of recoverable symbols versus different values of $E_b/N_0$, where the smallest value achieving the maximum number of recovered symbols is selected as the design $E_b/N_0$.

As shown in Figure 4, the design $E_b/N_0$ for rate around $1/4$ and $1/3$, respectively, is 0.5 dB and 1.0 dB, when $S=32$ and $N=256$. Note that the design $E_b/N_0$ plays an important role in optimizing the rate allocation of RS codes. A high design $E_b/N_0$ reduces the extra overhead of RS codes but leads to performance degradation in low-SNR regimes, while a low design $E_b/N_0$ improves the error-correction performance at the cost of too many RS parity symbols. Consequently, the connection between a target FER and its design $E_b/N_0$ needs to be established in a future work.

Next, let us discuss the rationality for choosing $T=4$ in this section. Using $H_T$, we denote the maximum number of symbols that can be recovered by employing $(T+1)$ UEP levels. Figure 5 quantitatively compares the maximum number recoverable symbols with respect to $T=3,4$ and 5, respectively. It can be seen that $\frac{H_4}{H_5}=97.9\%$ and $\frac{H_3}{H_5}=65.7\%$ in the case of design $E_b/N_0=1$ dB, and when design $E_b/N_0=1.5$ dB, we obtain $\frac{H_4}{H_5}=98.3\%$ and $\frac{H_3}{H_5}=89.9\%$. Considering this empirical observation and the complexity of iterative product decoding, we used $T=4$ in this paper. Note that the value of T could be flexibly selected in terms of the channel statistics and the decoding complexity.

Table 1. Parameters of the UEP-RS-polar Product Codes and the Corresponding Optimal Rate Allocation of RS Codes over AWGN Channels, for $R_{polar}=0.5$ and 0.67.

${\mathit{R}}_{\mathit{polar}}$	${\mathit{R}}_{\mathit{tx}}$	N (bits)	M (symbols)	S (symbols)	Design ${\mathit{E}}_{\mathit{b}}/{\mathit{N}}_0$ (dB)	$({\mathit{r}}_1,{\mathit{r}}_2,{\mathit{r}}_3,{\mathit{r}}_4)$	$({\mathit{M}}_1,{\mathit{M}}_2,{\mathit{M}}_3,{\mathit{M}}_4)$
0.5	0.270	256	16	32	0.5	(2,8,12,18)	(3,5,10,14)
	0.255	512	32	16	0.5	(1,3,7,12)	(5,15,20,28)
	0.267	1024	64	8	1	(1,2,4,6)	(10,25,40,56)
	0.361	256	16	32	1	(6,12,20,25)	(3,5,10,14)
	0.361	512	32	16	1.5	(5,9,11,13)	(5,15,20,28)
	0.338	1024	64	8	1.5	(2,3,6,7)	(10,25,40,56)
0.67	0.263	256	21	32	0.5	(1,2,5,21)	(3,7,13,16)
	0.262	512	42	16	0.5	(1,3,4,8)	(4,15,27,34)
	0.280	1024	85	8	1	(1,1,3,5)	(19,39,54,69)
	0.332	256	21	32	1	(1,7,11,25)	(3,7,13,16)
	0.347	512	42	16	1.5	(1,4,8,12)	(4,15,27,34)
	0.348	1024	85	8	1.5	(1,3,4,6)	(19,39,54,69)

Table 1. Parameters of the UEP-RS-polar Product Codes and the Corresponding Optimal Rate Allocation of RS Codes over AWGN Channels, for $R_{polar}=0.5$ and 0.67.

${\mathit{R}}_{\mathit{polar}}$	${\mathit{R}}_{\mathit{tx}}$	N (bits)	M (symbols)	S (symbols)	Design ${\mathit{E}}_{\mathit{b}}/{\mathit{N}}_0$ (dB)	$({\mathit{r}}_1,{\mathit{r}}_2,{\mathit{r}}_3,{\mathit{r}}_4)$	$({\mathit{M}}_1,{\mathit{M}}_2,{\mathit{M}}_3,{\mathit{M}}_4)$
0.5	0.270	256	16	32	0.5	(2,8,12,18)	(3,5,10,14)
	0.255	512	32	16	0.5	(1,3,7,12)	(5,15,20,28)
	0.267	1024	64	8	1	(1,2,4,6)	(10,25,40,56)
	0.361	256	16	32	1	(6,12,20,25)	(3,5,10,14)
	0.361	512	32	16	1.5	(5,9,11,13)	(5,15,20,28)
	0.338	1024	64	8	1.5	(2,3,6,7)	(10,25,40,56)
0.67	0.263	256	21	32	0.5	(1,2,5,21)	(3,7,13,16)
	0.262	512	42	16	0.5	(1,3,4,8)	(4,15,27,34)
	0.280	1024	85	8	1	(1,1,3,5)	(19,39,54,69)
	0.332	256	21	32	1	(1,7,11,25)	(3,7,13,16)
	0.347	512	42	16	1.5	(1,4,8,12)	(4,15,27,34)
	0.348	1024	85	8	1.5	(1,3,4,6)	(19,39,54,69)

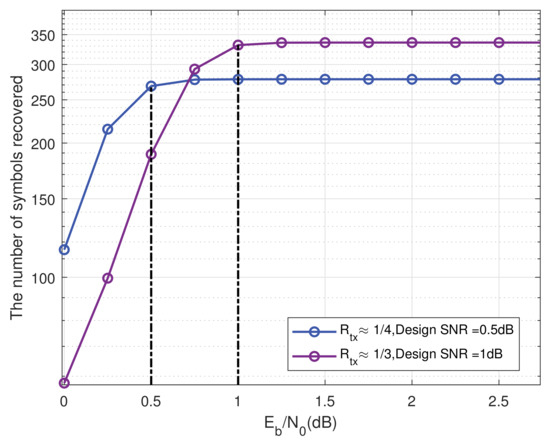
Figure 4. The impact of different SNRs on the number of symbols recovered, when $S=32,N=256$.

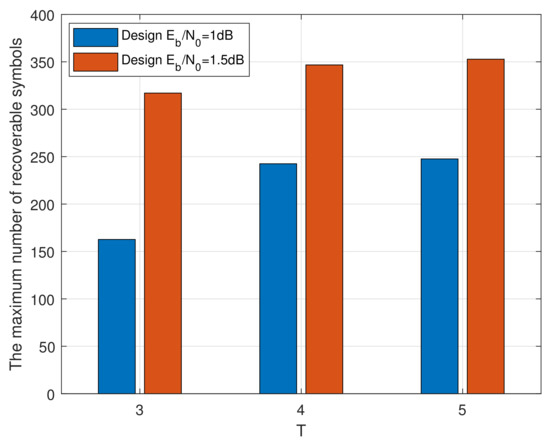
Figure 5. The maximum number of recoverable symbols over AWGN channels with different values of T, for $N=1024$ and design $E_b/N_0=1$ and $1.5$ dB.

4.1. Performance Evaluation over AWGN Channels

Figure 6 and Figure 7 compares the proposed UEP-RS-polar product scheme against the SC decoding and SCL decoding of long polar codewords when the transmission code rate is around $1/4$ and $1/3$, respectively. For a fair comparison, the rates of the long polar codewords are $1/4$ and $1/3$, which are no larger than the corresponding transmission rates $R_{tx}$. It can be seen from Figure 6 that the “RS(32)-polar(256)” scheme significantly outperforms the SC decoding of a polar codeword of 8192 bits at FER = $1\times {10}^{-3}$, and an improvement of 0.75 dB is obtained when $R_{polar}=0.5$. Moreover, a coding gain of 0.15 dB is achieved when compared with the SCL decoding with four survival paths (“SCL4” in Figure 6) at FER = $1\times {10}^{-3}$. In the case of $R_{polar}=0.67$, the “RS(32)-polar(256)” scheme performs close to the SC decoding at FER = $1\times {10}^{-3}$. In addition, when $R_{tx}\approx 1/3$ and FER $\ge {10}^{-3}$, the “RS(32)-polar(256)” scheme is comparable to the “SCL4” decoding with $R_{polar}=0.5$, and outperforms the SC decoding of long polar codes in the case of $R_{polar}=0.67$. Notably, a peak coding gain of $0.8$ dB and $0.7$ dB is achieved for $R_{tx}\approx 1/4$ at FER = $4.13\times {10}^{-4}$, and for $R_{tx}\approx 1/3$ at FER = $1.45\times {10}^{-3}$, respectively, compared with the SC decoding. We note that the target FER = ${10}^{-3}$ already meets the requirements of practical wireless communications.

Figure 6 and Figure 7 show that, for a fixed overall rate $R_{tx}$, the FER performance of the UEP-RS-polar product code with $R_{polar}=0.5$ is significantly better than that with $R_{polar}=0.67$. The reason for this is that the FER of component polar codes of rate $R_{polar}=0.67$ is larger than that of rate $R_{polar}=0.5$, and then more polar packets would be viewed as erased, possibly leading to an early termination of the iterative product decoding. Additionally, for a fixed overall product code rate $R_{tx}$, the optimized “RS(32)-polar(256)” scheme with $R_{polar}=0.5$ can outperform the SC decoding of a long polar code. However, practical techniques need to be developed to further improve the performance of the “RS(32)-polar(256)” scheme with $R_{polar}=0.67$.

In addition, Figure 8 compares the proposed UEP-RS-polar codes with the RS-polar product scheme of [8] when the transmission rates are around $1/4$ and $1/3$, for $R_{polar}=0.5$. The RS rate allocation parameters of [8] are specified by $\left(r_1,r_2,r_3,r_4\right)=\left(3,5,7,9\right)$ rate 1/4, and $\left(r_1,r_2,r_3,r_4\right)=\left(7,9,11,13\right)$ (this is taken from [8]) for rate 1/3, and the same values of $(M_1,M_2,M_3,M_4)$, as in Table 1. It can be observed that the proposed UEP-RS-polar scheme consistently outperforms the counterpart of [8], by about 0.2 dB and 0.1dB, respectively, when $R_{tx}\approx 1/4$ and $1/3$, at FER = $1\times {10}^{-3}$.

Furthermore, we evaluate the decoding complexity in terms of the single average decoding running time, i.e., the single runtime consumed when decoding a long polar code and the proposed product code, when the total code length is 8192 bits. Each value reported in Figure 9 is averaged by performing ${10}^5$ independent simulation trails. The source codes are executed by the MATLAB R2021a software running on a computer with Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz. Figure 9 shows that the decoding time of UEP-RS-polar scheme decreases when $E_b/N_0\ge 1$ dB. The reason for this is that with the increasing channel reliability, more polar packets could be correctly decoded, thus triggering the early stopping of the iterative product decoding. On the other hand, the decoding time of a long polar code is always constant, and it is more time-consuming compared with the UEP-RS-polar scheme.

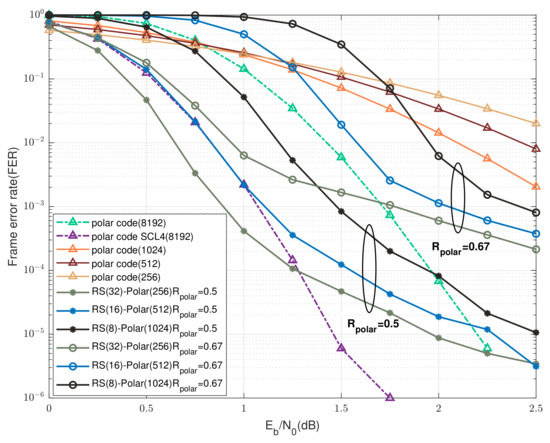
Figure 6. Performance comparison of the UEP-RS-polar product codes, the SC decoding and SCL decoding of long polar codewords over AWGN channels when $R_{tx}\approx 1/4$ and $R_{polar}=0.5,0.67$.

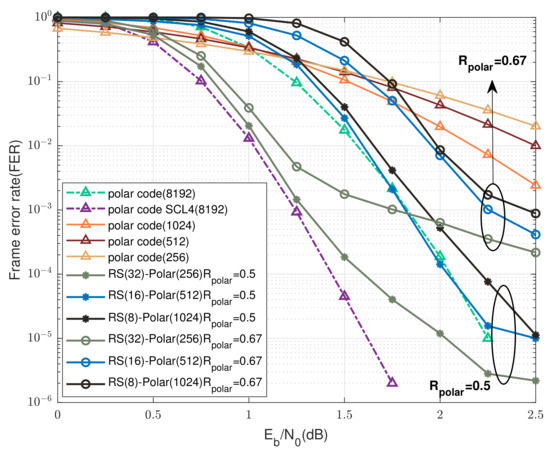
Figure 7. Performance comparison of the UEP-RS-polar product codes, the SC decoding and SCL decoding of long polar codewords over AWGN channels when $R_{tx}\approx 1/3$ and $R_{polar}=0.5,0.67$.

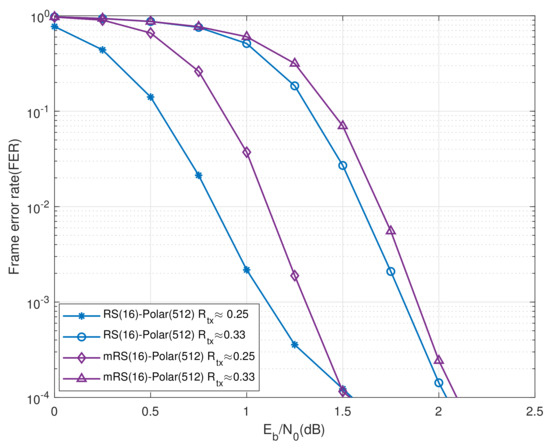
Figure 8. Performance comparison between the proposed UEP-RS-polar product scheme and the UEP-RS-polar product scheme of [8], (referred to as “mRS-polar” in the figure), for $R_{tx}\approx 1/4,1/3$ and $R_{polar}=0.5$ over AWGN channels.

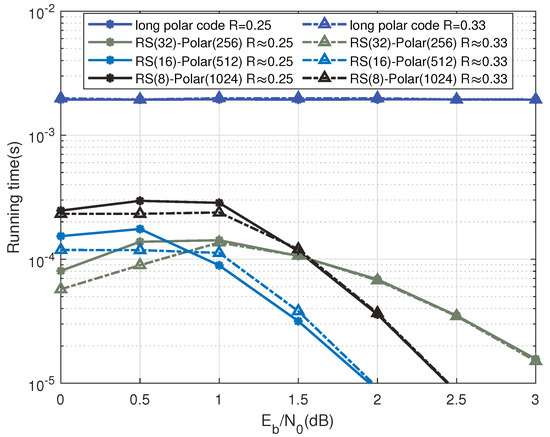
Figure 9. Single average running time when decoding the UEP-RS-polar scheme and long polar codes over AWGN channels with a code length og 8192 bits. Each runtime is averaged by ${10}^5$ trails, executed on the MATLAB R2021a software with an Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz.

4.2. Performance Evaluation over Gilbert–Elliott Channels

Since RS codes could correct burst errors or erasures, this section examines the proposed UEP-RS-polar codes over a two-state Gilbert–Elliott (GE) channel. The corresponding channel model is depicted in Figure 10, where G and B denote the good and bad states, respectively. Moreover, $P_{VW}$ represents the transition probability from state V to state W. Specifically, the GE channel used in this section is expressed by

$$y_1^N=h{x}_1^N+n,h\in \left\{0,1\right\},$$

(6)

where n is the AWGN, and $h=1$ and 0 for good and bad state, respectively. In other words, the GE channel becomes a deletion channel of deletion probability 1 when it falls into the bad state.

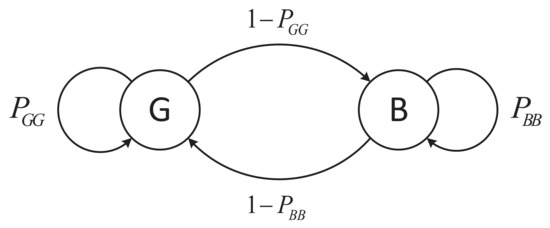
Figure 10. A GE channel model with good (G) and bad (B) states.

This section fixes $P_{BB}=0.1$ and considers the cases of $P_{GG}=0.9$ and $0.99$, and the corresponding FER versus SNR curves are plotted in Figure 11 and Figure 12 for $R_{tx}\approx 1/4$, and Figure 13 and Figure 14 for $R_{tx}\approx 1/3$, respectively. In the case of $P_{GG}=0.99$, i.e., the channel would be in good state with high probability; it can be seen from Figure 12 and Figure 14 that the proposed “RS(32)-polar(256)” scheme consistently outperforms the SC decoding of length-8192 polar codes when $E_b/N_0\le 1.7$ dB, for both $R_{polar}=0.5$ and $0.67$. Particularly, the “RS(32)-polar(256)” scheme with $R_{tx}\approx 1/4$ and $R_{polar}=0.5$ achieves an improvement of around 0.8 dB at FER $=1\times {10}^{-3}$, as shown in Figure 12. When the component polar code rate increases to $R_{polar}=0.67$, the performance of “RS(32)-polar(256)” scheme is expected to become worse, but almost the same performance as the SC decoding still could be obtained at FER $=1\times {10}^{-3}$.

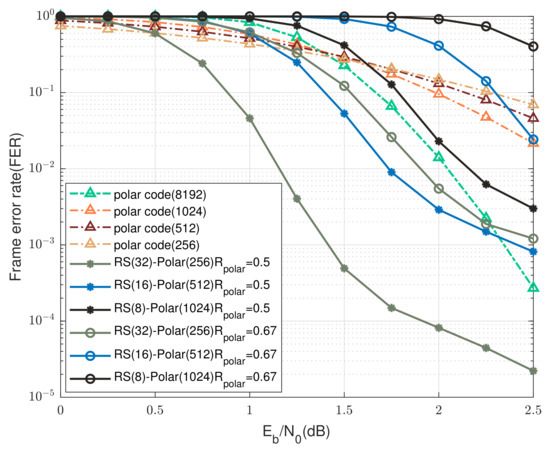
Figure 11. Comparison between the UEP-RS-polar product codes and the SC decoding of single polar codewords over GE channels for $R_{tx}\approx 1/4$, $P_{GG}=0.9$ and $R_{polar}=0.5,0.67$.

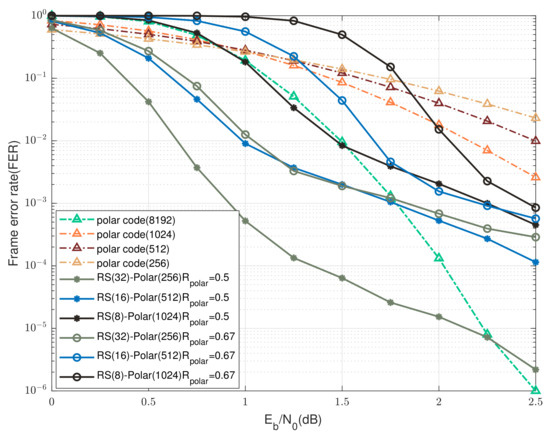
Figure 12. Comparison between the UEP-RS-polar product codes and the SC decoding of single polar codewords over GE channels for $R_{tx}\approx 1/4$, $P_{GG}=0.99$ and $R_{polar}=0.5,0.67$.

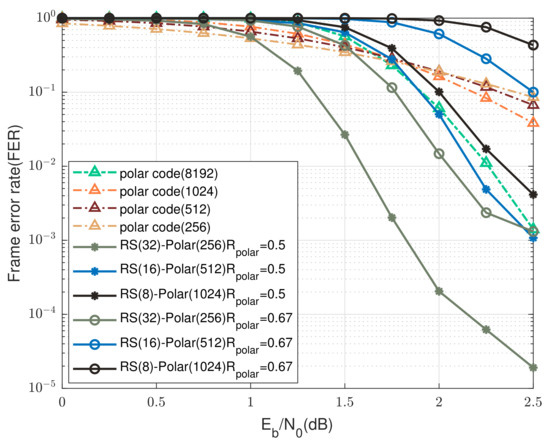
Figure 13. Comparison between the UEP-RS-polar product codes and the SC decoding of single polar codewords over GE channels for $R_{tx}\approx 1/3$, $P_{GG}=0.9$ and $R_{polar}=0.5,0.67$.

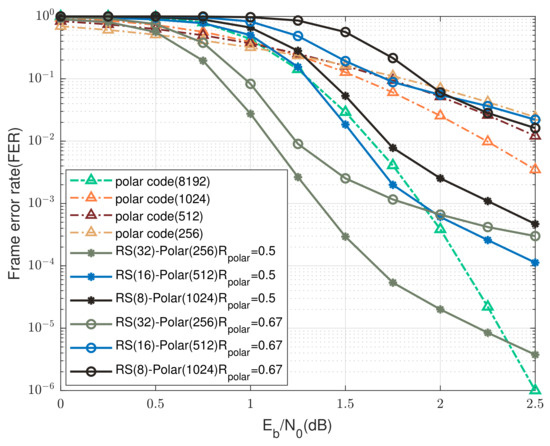
Figure 14. Comparison between the UEP-RS-polar product codes and the SC decoding of single polar codewords over GE channels, for $R_{tx}\approx 1/3$, $P_{GG}=0.99$ and $R_{polar}=0.5,0.67$.

When $P_{GG}$ decreases to 0.9, the probability of the channel being in a bad state becomes larger, and no information bits would be transmitted in this scenario. As a result, it is more likely that the number of unsuccessfully decoded polar packets will exceed the erasure correction ability of RS codes within the first UEP level, meaning that iterative product decoding could not be conducted (see Figure 1 and Figure 2). This explains the deteriorate performance, as shown in Figure 11 and Figure 13 for $P_{GG}=0.9$. Although the channel condition becomes more severe, the “RS(32)-polar(256)” scheme with $R_{polar}=0.5$ still achieves an improvement of $0.9$ dB and $0.7$ dB at FER $=1\times {10}^{-3}$, for $R_{tx}\approx 1/4$ and $1/3$, respectively. Finally, these observations demonstrate the superior performance of the UEP-RS-polar product codes in the low-to-medium regime of $E_b/N_0$.

In sum, when the overall product code rate $R_{tx}$ is fixed, the performance of “RS(32)-polar(256)” scheme with $R_{polar}=0.5$ is better than the SC decoding of long polar codes of the same rate. When we use the inner polar code rate $R_{polar}=0.67$, the “RS(32)-polar(256)” scheme outperforms the SC decoding in the low-to-medium $E_b/N_0$ regime. Moreover, the UEP-RS-polar product codes have a lower decoding latency than the SC decoding of long polar codes. However, further performance improvements are still required when inner polar codes of higher rates are involved.

5. Conclusions

This paper proposes an analytical rate allocation for the UEP-RS-polar product coding scheme to effectively improve the performance of polar codes with limited lengths. The proposed product coding scheme could be decoded in parallel to reduce the decoding complexity and latency. The purpose of the proposed rate allocation of RS codes is to maximize the number of correctly decoded information bits. The simulation results show the superiority of the UEP-RS(32)-polar(256) product coding scheme compared to the SC decoding and SCL decoding of a length-8192 polar code under the same channels and transmission rates. The UEP-RS-polar product codes would be more promising if inner polar codes of higher rates could be employed, which is an interesting direction requiring novel code design methods. Furthermore, problems such as the optimal configuration between the lengths of RS codewords and polar codes, and the optimal matching between the overall product code rate and the inner polar code rate, remain open.