LRSE-Net: Lightweight Residual Squeeze-and-Excitation Network for Stenosis Detection in X-ray Coronary Angiography
Abstract
1. Introduction
2. Related Work
- An LRSE-Net model is proposed by replacing vanilla convolutions with Depthwise Separable Convolutions, drastically reducing the number of parameters;
- Independent dilation ratios for each attention module are selected to enhance the network performance;
- Redundant kernels in the convolutional layers are removed to obtain a smaller model;
- A data augmentation policy is introduced to mitigate the imbalance of the dataset;
- A new patch-based dataset is released to validate the model performance.
3. Materials and Methods
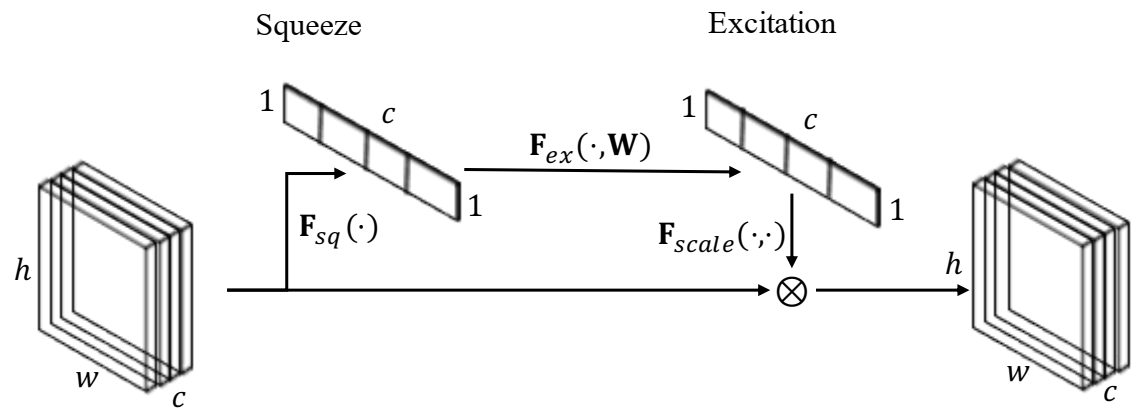
3.1. Squeeze-and-Excitation Attention Mechanism
3.1.1. Squeeze Operation
3.1.2. Excitation Operation
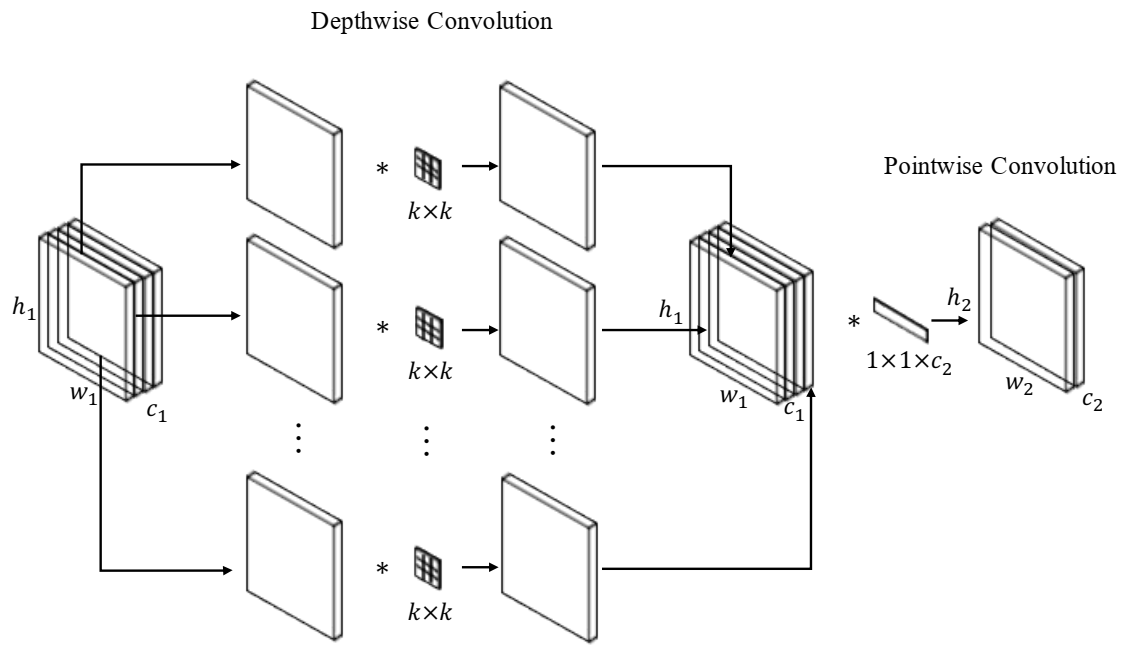
3.2. Depthwise Separable Convolution
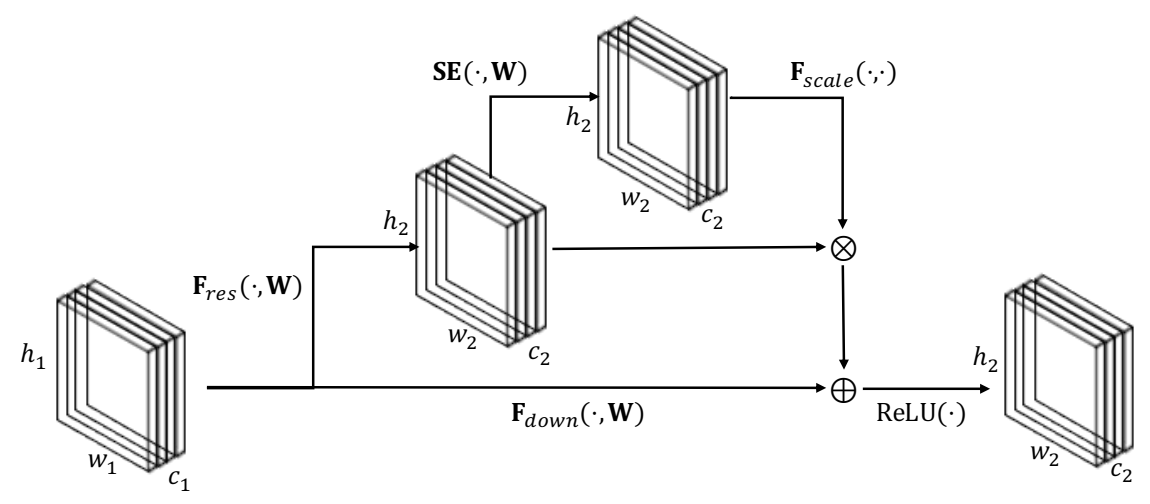
3.3. Lightweight Residual Squeeze-and-Excitation Network
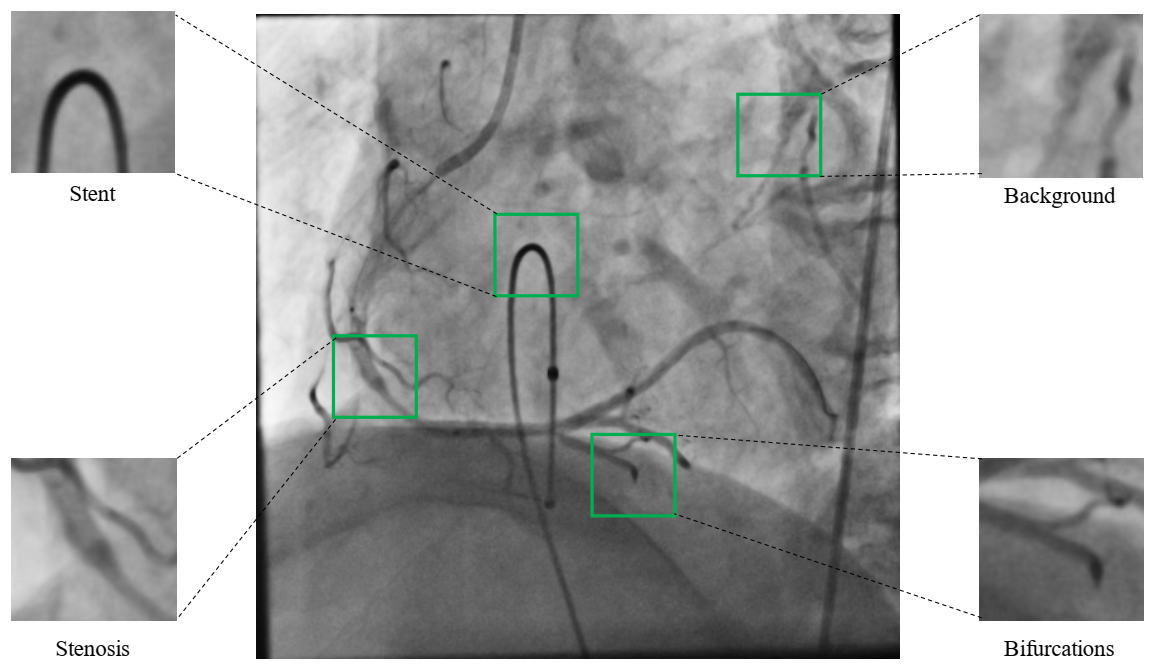
3.4. Datasets
4. Results
4.1. Evaluation Metrics
4.2. Implementation Details
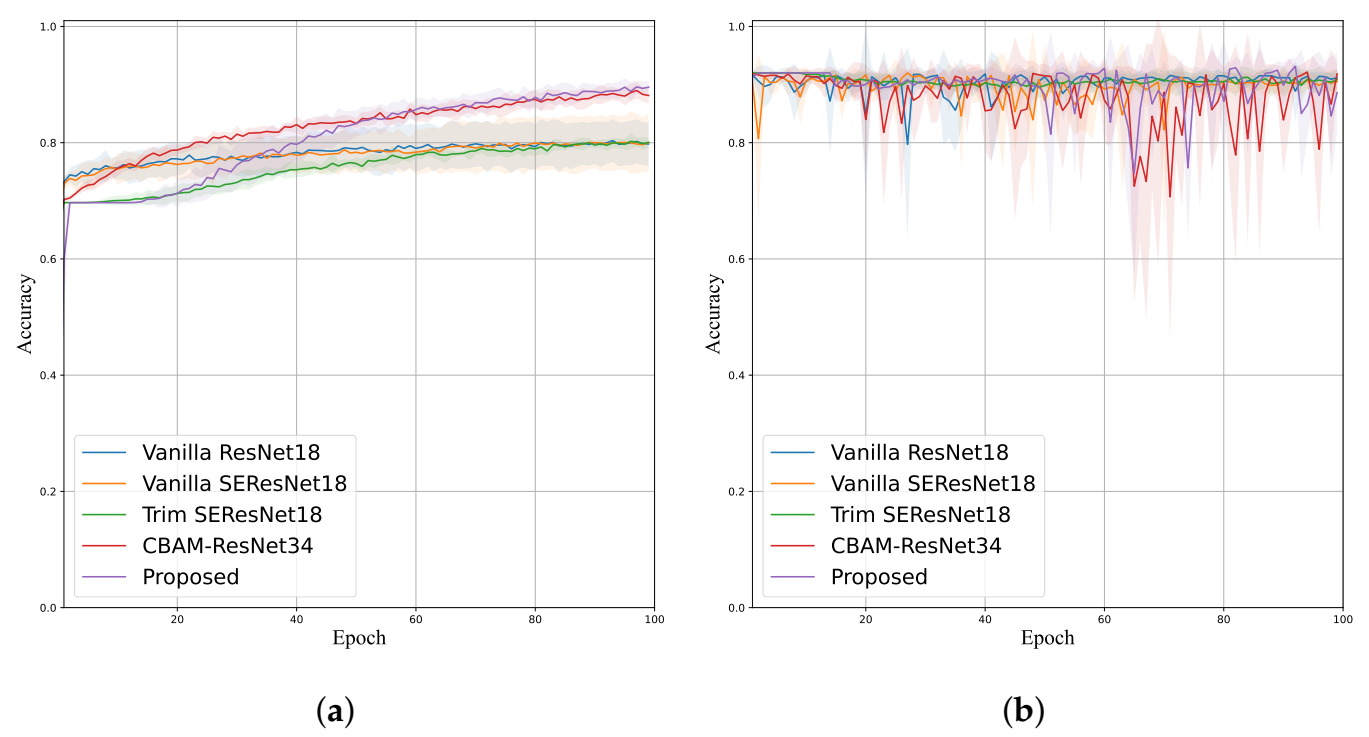
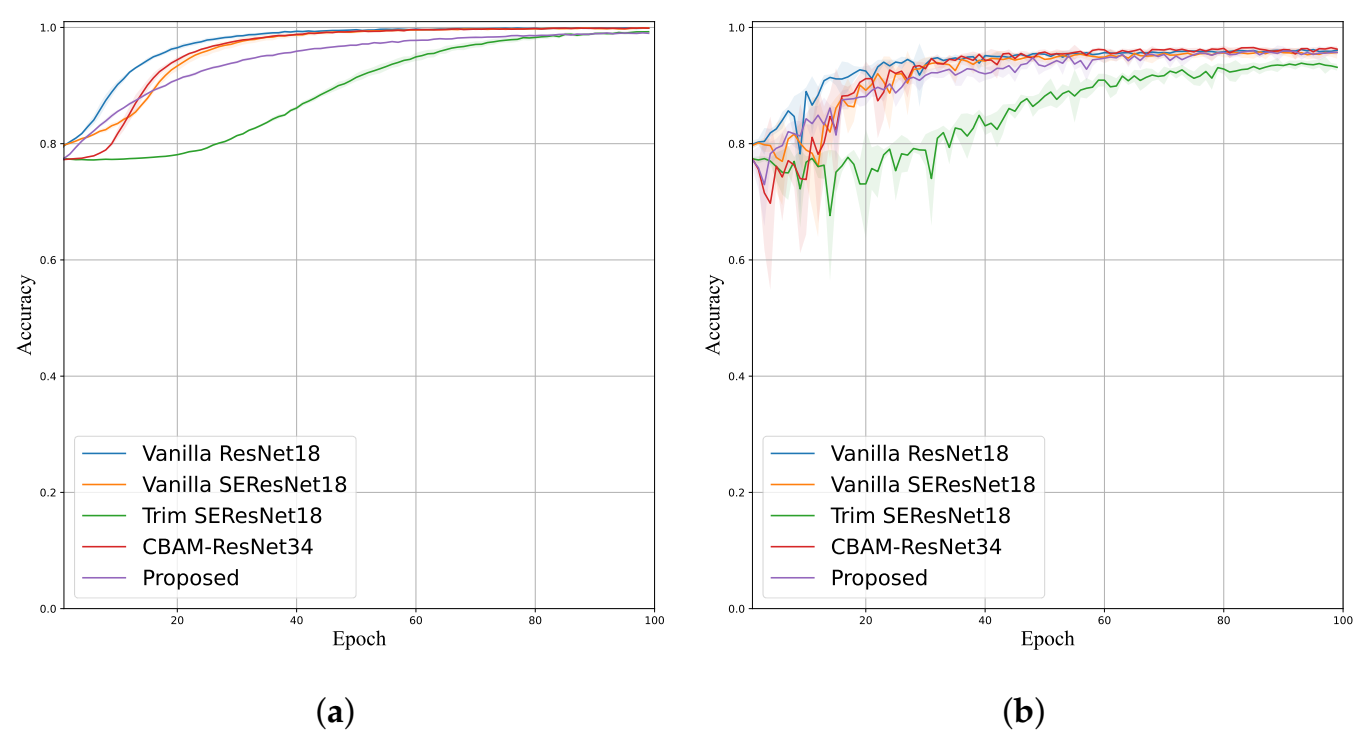
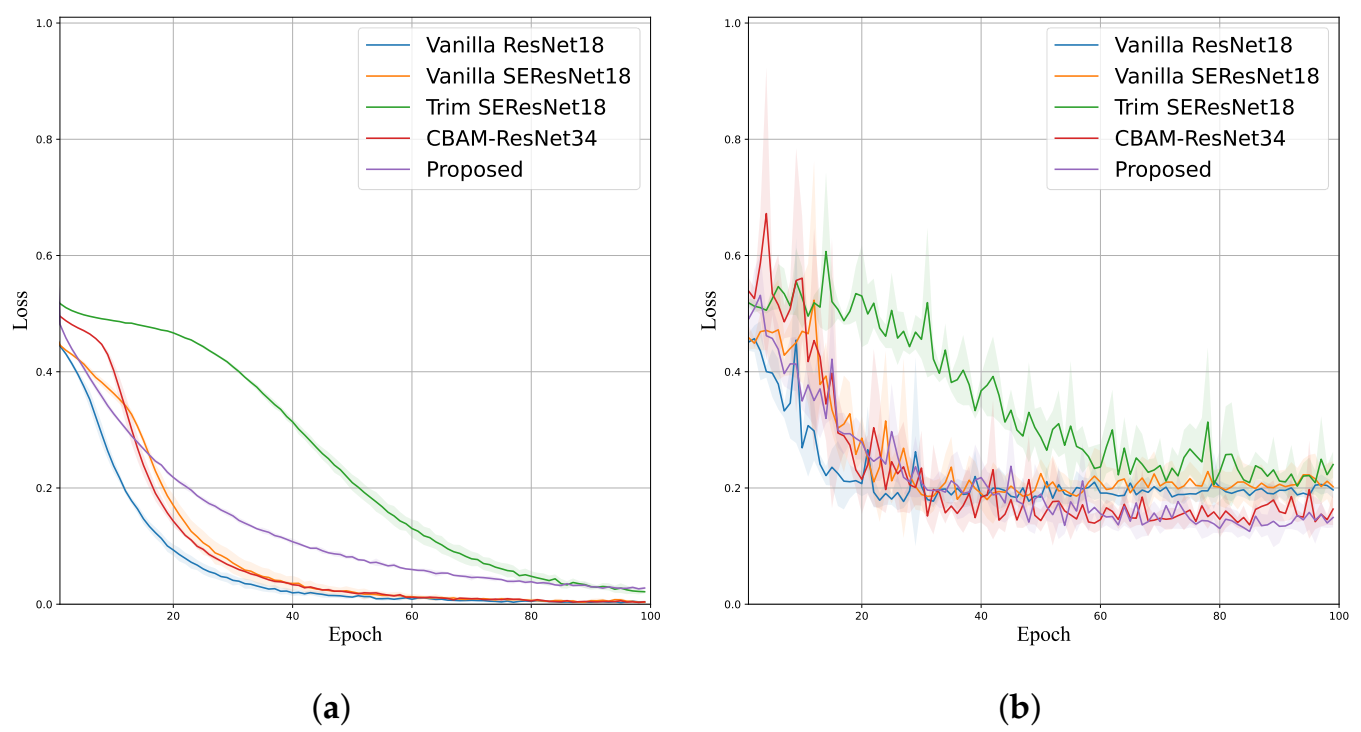
4.3. Ablation Study
4.4. Stenosis Classification Performance Comparison
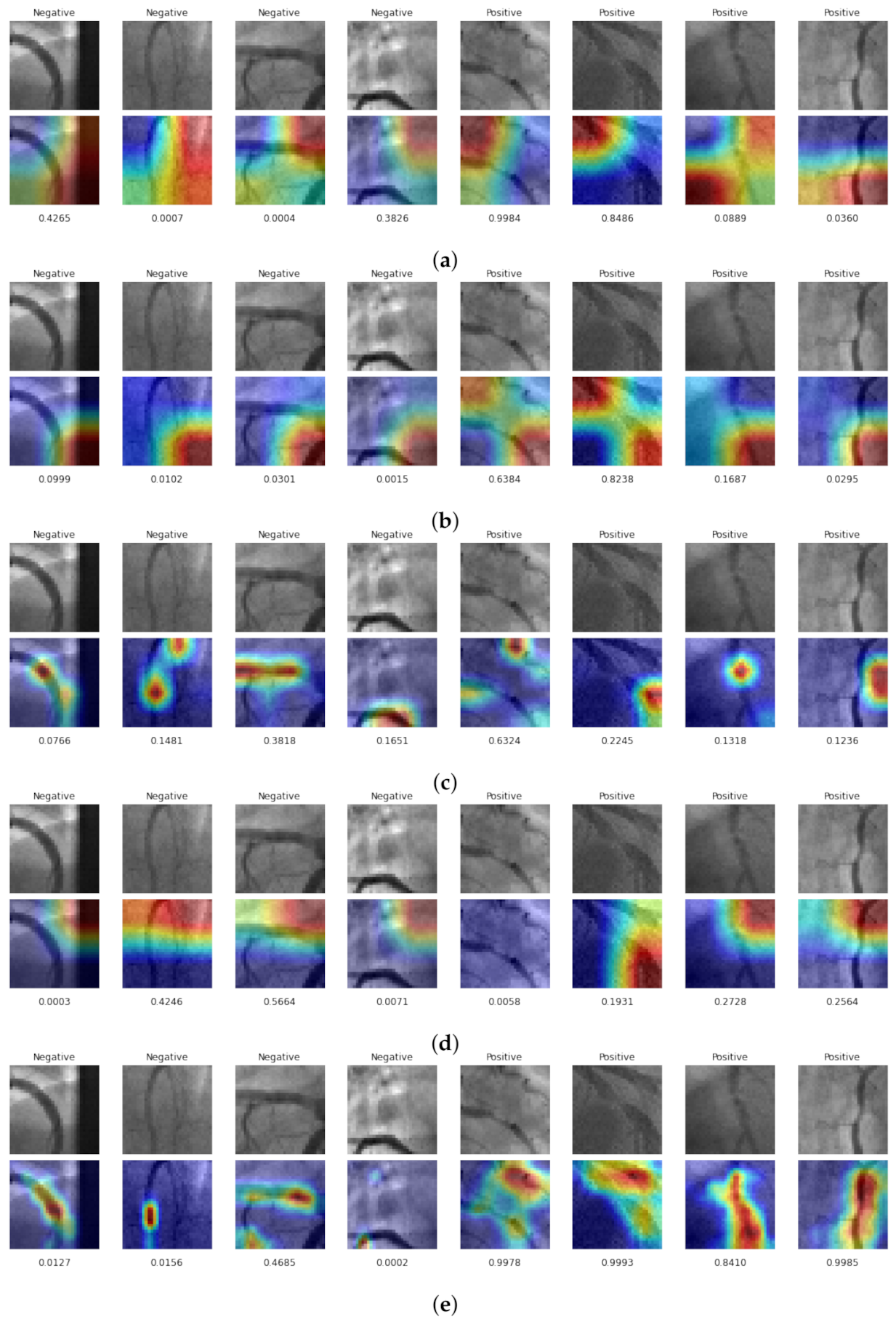
4.5. Class Activation Maps Compassion
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADSD | Angiographic Dataset for Stenosis Detection |
| CAD | Computer-Aided Diagnosis |
| CBAM | Convolutional Block Attention Module |
| CHD | Coronary Heart Disease |
| CNN | Convolutional Neural Network |
| DSC | Depthwise Separable Convolution |
| DSDD | Deep Stenosis Detection Dataset |
| ECA | Efficient Channel Attention |
| Faster-RDCNN | Faster-Region Based Convolutional Neural Networks |
| FN | False Negative |
| FP | False Positive |
| GAP | Global Average Pooling |
| GradCAM | Gradient-weighted Class Activation Map |
| ML | Machine Learning |
| ReLU | Rectified Linear Unit |
| ResNet | Residual Network |
| R-FCN | Region-based Fully Convolutional Networks |
| RSE | Residual Squeeze-and-Excitation |
| SE | Squeeze-and-Excitation |
| SENet | Squeeze-and-Excitation Network |
| SGDM | Stochastic Gradient Descent with Momentum |
| SSD | Single Shot multi-box Detector |
| TN | True Negative |
| TP | True Positive |
| TPE | Tree-structured Parzen Estimator |
| LRSE-Net | Lightweight Residual Squeeze-and-Excitation Network |
| VGG | Visual Geometry Group |
| XCA | X-ray Coronary Angiography |
References
- World Health Organization. Cardiovascular Diseases (CVDs). 2022. Available online: https://www.who.int/health-topics/cardiovascular-diseases (accessed on 30 October 2022).
- Britannica, The Editors of Encyclopaedia. Coronary Heart Disease. 2022. Available online: https://www.britannica.com/science/coronary-heart-disease (accessed on 30 October 2022).
- National Heart, Lung, and Blood Institute. Atherosclerosis. 2022. Available online: https://www.nhlbi.nih.gov (accessed on 30 October 2022).
- Nandalur, K.R.; Dwamena, B.A.; Choudhri, A.F.; Nandalur, M.R.; Carlos, R.C. Diagnostic Performance of Stress Cardiac Magnetic Resonance Imaging in the Detection of Coronary Artery Disease: A Meta-Analysis. J. Am. Coll. Cardiol. 2007, 50, 1343–1353. [Google Scholar] [CrossRef] [PubMed]
- Athanasiou, L.S.; Fotiadis, D.I.; Michalis, L.K. Atherosclerotic Plaque Characterization Methods Based on Coronary Imaging; Academic Press: New York, NY, USA, 2017. [Google Scholar]
- Johal, G.S.; Goel, S.; Kini, A. Coronary Anatomy and Angiography. In Practical Manual of Interventional Cardiology; Springer: Berlin/Heidelberg, Germany, 2021; pp. 35–49. [Google Scholar] [CrossRef]
- Chiastra, C.; Iannaccone, F.; Grundeken, M.J.; Gijsen, F.J.; Segers, P.; De Beule, M.; Serruys, P.W.; Wykrzykowska, J.J.; van der Steen, A.F.; Wentzel, J.J. Coronary fractional flow reserve measurements of a stenosed side branch: A computational study investigating the influence of the bifurcation angle. Biomed. Eng. Online 2016, 15, 1–16. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Manson, E.; Ampoh, V.A.; Fiagbedzi, E.; Amuasi, J.; Flether, J.; Schandorf, C. Image noise in radiography and tomography: Causes, effects and reduction techniques. Curr. Trends Clin. Med. Imaging 2019, 2, 555620. [Google Scholar] [CrossRef]
- Chang, C.F.; Chang, K.H.; Lai, C.H.; Lin, T.H.; Liu, T.J.; Lee, W.L.; Su, C.S. Clinical outcomes of coronary artery bifurcation disease patients underwent Culotte two-stent technique: A single center experience. BMC Cardiovasc. Disord. 2019, 19, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Sarvamangala, D.; Kulkarni, R.V. Convolutional neural networks in medical image understanding: A survey. Evol. Intell. 2021, 15, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Mohapatra, S.; Swarnkar, T.; Das, J. Deep convolutional neural network in medical image processing. In Handbook of Deep Learning in Biomedical Engineering; Elsevier: Berlin/Heidelberg, Germany, 2021; pp. 25–60. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar] [CrossRef]
- Sameh, S.; Azim, M.A.; AbdelRaouf, A. Narrowed coronary artery detection and classification using angiographic scans. In Proceedings of the 2017 12th International Conference on Computer Engineering and Systems (ICCES), Cairo, Egypt, 19–20 December 2017; pp. 73–79. [Google Scholar] [CrossRef]
- Wan, T.; Feng, H.; Tong, C.; Li, D.; Qin, Z. Automated Identification and Grading of Coronary Artery Stenoses with X-ray Angiography. Comput. Methods Programs Biomed. 2018, 167, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Kishore, A.N.; Jayanthi, V. Automatic stenosis grading system for diagnosing coronary artery disease using coronary angiogram. Int. J. Biomed. Eng. Technol. 2019, 31, 260–277. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, J.; Xie, H.; Zhao, Y.; Zhang, S.; Gu, L. Automatic detection of coronary artery stenosis by convolutional neural network with temporal constraint. Comput. Biol. Med. 2020, 118, 103657. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Conference Track Proceedings. Bengio, Y., LeCun, Y., Eds.; Cornell University: New York, NY, USA, 2015; pp. 1–14. [Google Scholar]
- Pang, K.; Ai, D.; Fang, H.; Fan, J.; Song, H.; Yang, J. Stenosis-DetNet: Sequence consistency-based stenosis detection for X-ray coronary angiography. Comput. Med. Imaging Graph. 2021, 89, 101900. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; IEEE Computer Society: Los Alamitos, CA, USA, 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Danilov, V.V.; Klyshnikov, K.Y.; Gerget, O.M.; Kutikhin, A.G.; Ganyukov, V.I.; Frangi, A.F.; Ovcharenko, E.A. Real-time coronary artery stenosis detection based on modern neural networks. Sci. Rep. 2021, 11, 1–13. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 21–37. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; MIT Press: Cambridge, MA, USA, 2015; Volume 28, pp. 91–99. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-FCN: Object detection via region-based fully convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Curran Associates Inc.: Red Hook, NY, USA, 2016; pp. 379–387. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning. In Proceedings of the Thirty-first AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Antczak, K.; Liberadzki, Ł. Stenosis Detection with Deep Convolutional Neural Networks. In Proceedings of the MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 210, p. 04001. [Google Scholar] [CrossRef]
- Ovalle-Magallanes, E.; Avina-Cervantes, J.G.; Cruz-Aceves, I.; Ruiz-Pinales, J. Improving convolutional neural network learning based on a hierarchical bezier generative model for stenosis detection in X-ray images. Comput. Methods Programs Biomed. 2022, 219, 106767. [Google Scholar] [CrossRef] [PubMed]
- Woo, S.; Park, J.; Lee, J.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar] [CrossRef]
- Ovalle-Magallanes, E.; Alvarado-Carrillo, D.E.; Avina-Cervantes, J.G.; Cruz-Aceves, I.; Ruiz-Pinales, J.; Contreras-Hernandez, J.L. Attention Mechanisms Evaluated on Stenosis Detection using X-ray Angiography Images. J. Adv. Appl. Comput. Math. 2022, 9, 62–75. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11531–11539. [Google Scholar] [CrossRef]
- Antczak, K.; Liberadzki, Ł. Deep Stenosis Detection Dataset. 2022. Available online: https://github.com/KarolAntczak/DeepStenosisDetection (accessed on 30 October 2022).
- Danilov, V.; Klyshnikov, K.; Kutikhin, A.; Gerget, O.; Frangi, A.; Ovcharenko, E. Angiographic Dataset for Stenosis Detection; Mendeley Data, V2; Data Archiving and Networked Services (DANS): The Hague, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–14 December 2011; Curran Associates Inc.: Red Hook, NY, USA, 2011; Volume 24. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. 115–123. [Google Scholar]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; IEEE Computer Society: Venecia, Italy, 2017; pp. 618–626. [Google Scholar] [CrossRef]
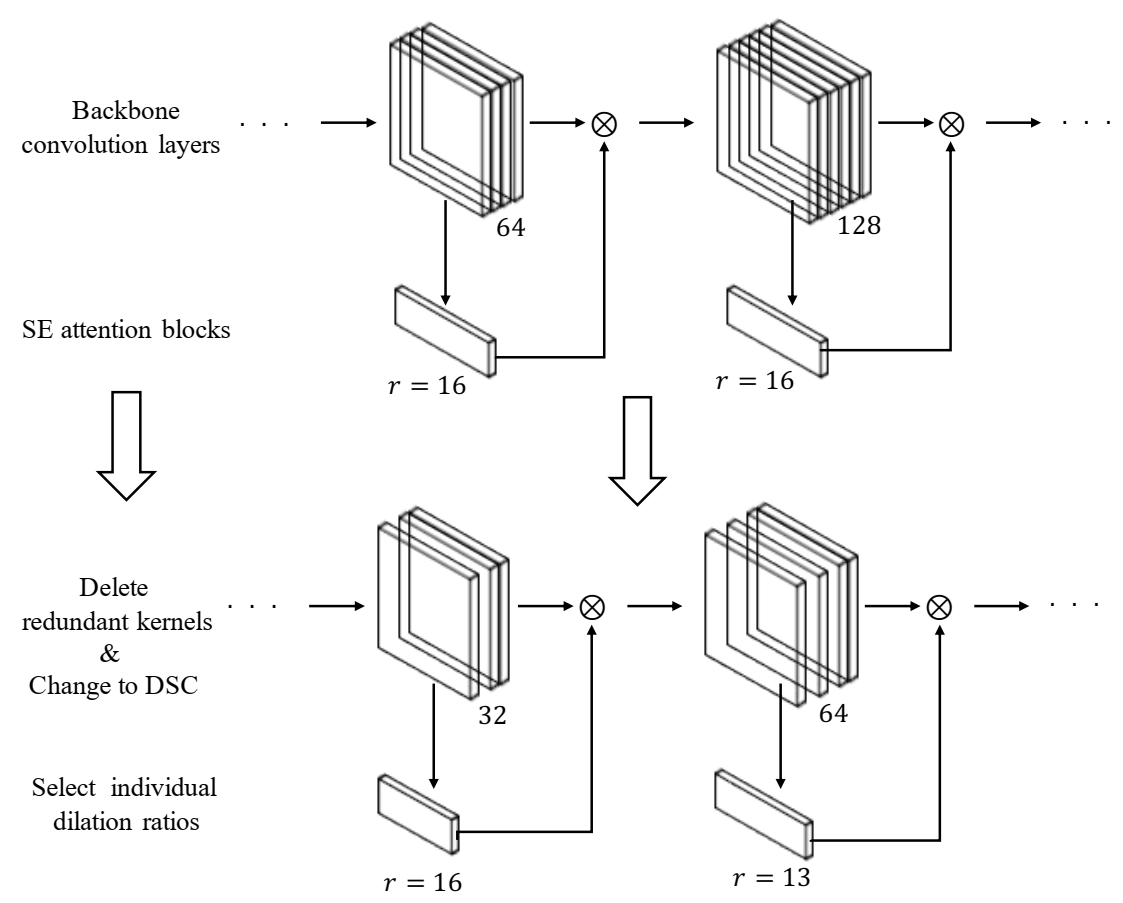


| Layer | Kernel Size | Stride | Output Size |
|---|---|---|---|
| Conv1 | 1 | / | |
| RSE 1 | 1 | / | |
| – | |||
| RSE 2 | 2 | / | |
| – | |||
| RSE 3 | 2 | / | |
| – | |||
| GAP | – | – | |
| SoftMax | – | – | 2 |
| Dataset | Train | Validation | Test | Size | |||
|---|---|---|---|---|---|---|---|
| Positive | Negative | Positive | Negative | Positive | Negative | ||
| P-ADSD | 4864 | 19,188 | 1216 | 4798 | 689 | 2713 | |
| A-DSSS | 385 | 892 | 20 | 223 | 25 | 279 | |
| DSC | SE | SE Ratios | Accuracy | Sensitivity | Specificity | Precision | F-Score | # Params |
|---|---|---|---|---|---|---|---|---|
| ✗ | ✗ | N/A | 0.9605 | 0.7600 | 0.9785 | 0.7600 | 0.7600 | 823,752 |
| ✗ | ✓ | 16, 13, 9 | 0.9605 | 0.7200 | 0.9821 | 0.7826 | 0.7500 | 829,128 |
| Default | 0.9507 | 0.7600 | 0.9677 | 0.6786 | 0.7170 | 832,200 | ||
| ✓ | ✗ | N/A | 0.9540 | 0.7600 | 0.9713 | 0.7037 | 0.7308 | 224,744 |
| ✓ | ✓ | 16, 13, 9 | 0.9638 | 0.8800 | 0.9713 | 0.7333 | 0.8000 | 230,120 |
| Default | 0.9638 | 0.7200 | 0.9857 | 0.8182 | 0.7660 | 233,192 |
| Method | Accuracy | Sensitivity | Specificity | Precision | F-Score | # Params |
|---|---|---|---|---|---|---|
| Vanilla ResNet18 [20] | 0.9152 (±0.0071) | 0.1360 (±0.0358) | 0.9850 (±0.0069) | 0.4661 (±0.1255) | 0.2081 (±0.0492) | 11,177,538 |
| Vanilla SE-ResNet18 [31] | 0.9172 (±0.0066) | 0.1840 (±0.0607) | 0.9828 (±0.0047) | 0.4874 (±0.1082) | 0.2652 (±0.0758) | 11,267,650 |
| Trim SE-ResNet18 [30] | 0.8914 (±0.0040) | 0.2000 (±0.0632) | 0.9534 (±0.0057) | 0.2729 (±0.0508) | 0.2585 (±0.0474) | 2,819,634 |
| CBAM-ResNet34 [28] | 0.9145 (±0.0062) | 0.1920 (±0.0769) | 0.9792 (±0.0069) | 0.4529 (±0.0922) | 0.2647 (±0.0817) | 8,209,870 |
| LRSE-Net (Proposed) | 0.9349 (±0.0233) | 0.6320 (±0.1820) | 0.9620 (±0.0151) | 0.5991 (±0.1161) | 0.6103 (±0.1405) | 230,120 |
| Method | Accuracy | Sensitivity | Specificity | Precision | F-Score | # Params |
|---|---|---|---|---|---|---|
| Vanilla ResNet18 [20] | 0.9357 (±0.0054) | 0.8139 (±0.0187) | 0.9666 (±0.0056) | 0.8614 (±0.0201) | 0.8368 (±0.0135) | 11,177,538 |
| Vanilla SE-ResNet18 [31] | 0.9403 (±0.0115) | 0.8316 (±0.0278) | 0.9679 (±0.0082) | 0.8682 (±0.0323) | 0.8494 (±0.0287) | 11,267,650 |
| Trim SE-ResNet18 [30] | 0.9267 (±0.0065) | 0.7913 (±0.0371) | 0.9611 (±0.0046) | 0.8380 (±0.0137) | 0.8134 (±0.0204) | 2,819,634 |
| CBAM-ResNet34 [28] | 0.9517 (±0.0046) | 0.8647 (±0.0110) | 0.9738 (±0.0035) | 0.8936 (±0.0133) | 0.8789 (±0.0113) | 8,209,870 |
| LRSE-Net (Proposed) | 0.9543 (±0.0074) | 0.8792 (±0.0246) | 0.9733 (±0.0086) | 0.8944 (±0.0301) | 0.8863 (±0.0177) | 230,120 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ovalle-Magallanes, E.; Avina-Cervantes, J.G.; Cruz-Aceves, I.; Ruiz-Pinales, J. LRSE-Net: Lightweight Residual Squeeze-and-Excitation Network for Stenosis Detection in X-ray Coronary Angiography. Electronics 2022, 11, 3570. https://doi.org/10.3390/electronics11213570
Ovalle-Magallanes E, Avina-Cervantes JG, Cruz-Aceves I, Ruiz-Pinales J. LRSE-Net: Lightweight Residual Squeeze-and-Excitation Network for Stenosis Detection in X-ray Coronary Angiography. Electronics. 2022; 11(21):3570. https://doi.org/10.3390/electronics11213570
Chicago/Turabian StyleOvalle-Magallanes, Emmanuel, Juan Gabriel Avina-Cervantes, Ivan Cruz-Aceves, and Jose Ruiz-Pinales. 2022. "LRSE-Net: Lightweight Residual Squeeze-and-Excitation Network for Stenosis Detection in X-ray Coronary Angiography" Electronics 11, no. 21: 3570. https://doi.org/10.3390/electronics11213570
APA StyleOvalle-Magallanes, E., Avina-Cervantes, J. G., Cruz-Aceves, I., & Ruiz-Pinales, J. (2022). LRSE-Net: Lightweight Residual Squeeze-and-Excitation Network for Stenosis Detection in X-ray Coronary Angiography. Electronics, 11(21), 3570. https://doi.org/10.3390/electronics11213570






