Abstract
Accurate model development and efficient representations of multivariate trajectories are crucial to understanding the behavioral patterns of pedestrian motion. Most of the existing algorithms use offline learning approaches to learn such motion behaviors. However, these approaches cannot take advantage of the streams of data that are available after training has concluded, and typically are not generalizable to data that they have not seen before. To solve this problem, this paper proposes two algorithms for learning incoherent dictionaries in an offline and online manner by extending the offline augmented semi-non-negative sparse coding (ASNSC) algorithm. We do this by adding a penalty into the objective function to promote dictionary incoherence. A trajectory-modeling application is studied, where we consider the learned atoms of the dictionary as local motion primitives. We use real-world datasets to show that the dictionaries trained by the proposed algorithms have enhanced representation ability and converge quickly as compared to ASNSC. Moreover, the trained dictionaries are well conditioned. In terms of pedestrian trajectory prediction, the proposed methods are shown to be on par (and often better) with the state-of-the-art algorithms in pedestrian trajectory prediction.
1. Introduction
With the advent of self-driving vehicles in urban environments, safe navigation via precise motion prediction of other moving agents such as motor vehicles, cyclists, and pedestrians is of utmost importance. Out of the three aforementioned agents, understanding and predicting the pedestrian mobility patterns poses the biggest challenge. This can be attributed not only to the mobility rules being less clear and their frequent violations, but also to the complicated interaction between pedestrians and other commuters.
Recently, many machine learning methods have been proposed to model the complex pedestrian mobility patterns by utilizing contextual features [1,2] and/or the interactions among other commuters [3,4]. In addition to these, the classical methods for trajectory modeling, i.e., Markovian-based [5] and clustering-based [6] methods have also been used to solve this problem. The aim of Markovian-based methods is to learn a state-transition model from the training trajectory samples. Once this model is trained, it can then be used to predict the motion trajectory by utilizing the current state and the agents’ latent intent (e.g., goal). On the other hand, clustering-based techniques group the training trajectories into a small group of clusters, fit a predictive motion model, e.g., a Gaussian Process [7] to each cluster, and make predictions by sampling from the model. As the Markovian methods make predictions using the current state only, it is much more affected by the ever present measurement noise. Although clustering-based methods have been shown to make comparatively accurate predictions, their ability to detect agents’ behavioral changes is rather slow [8]. Additionally, they (in accordance with [5]) also suffer from incomplete/occluded trajectory samples, typically found in real datasets. This causes issues with the trajectory clustering of the partial samples, frequently leading to the creation of similar clusters, resulting in repetitive predictions. Collecting datasets with fully un-occluded trajectories is difficult, as such collections are often made in crowded locations, e.g., traffic intersections, shopping centers, parks, and university campus areas; where a pedestrian trajectory can often be hidden behind other pedestrians, agents or immovable obstacles etc.
In another work [9], which is the inspiration for this paper, the authors proposed a pedestrian trajectory prediction model by combining the advantages of Markovian-based and clustering-based methods. They modeled the pedestrian trajectories using a Dictionary containing segmented trajectories (termed motion primitives), which are learned using a sparse representation-based dictionary learning algorithm (also known as embedding learning) [10]. Once the motion primitives have been learned, the transitions between these motion primitives are modeled via Gaussian Processes (GP). In comparison to [5], this method can be trained using partial trajectories and does not require estimation of the agents’ goal. Recently, this method has been extended by a number of research works towards solving the pedestrian trajectory estimation problem. As a dictionary learning algorithm, the key to its success is the ability of the learned dictionary to provide the best possible sparse representation of the training dataset. To achieve this, the motivation is to learn a dictionary whose column vectors (atoms) are minimally correlated, called incoherent dictionaries, which helps the sparse coding algorithms in finding sparser solutions [11]. Moreover, low coherence has been shown to result in dictionaries which are referred to as well-conditioned [12].
In most of the techniques discussed so far (except for [5]), learning is performed in an offline (batch) mode. However, with the popularity of big data, this offline setting becomes impractical in the scenario where the training samples are made available incrementally or when the autonomous agent moves to a new environment where it has not been trained before. As batch learning cannot be performed incrementally, in such scenarios, the pre-trained models lose their generalization ability when facing new pedestrian behaviors and environments. Here, the incremental learning models, often called online learning models, have the flexibility of capturing new behaviors by considering the newly available samples instead of having to train from scratch. This online paradigm is relevant for creating a system which is efficient and significantly better aligned towards autonomous driving applications where real-time learning is a necessity. Additionally, storing and relearning from old and newly available data, in the case of batch learning, could be detrimental to pedestrian privacy as well. However, an online learning agent can continue to improve the prediction model by training on new data examples without requiring the storage of past data. Moreover, online learning can enable systems with resource-constrained devices to learn using batches of big data gradually, whereas working with the entire dataset may be infeasible.
Based on the discussion presented so far and inspired by the work presented in [9], this paper presents two extensions of [9] aiming at improving it even further; first, we extend its framework to learn incoherent dictionaries which are a basic requirement for achieving efficient sparse representation. Second, we present an online learning algorithm to learn incoherent dictionaries which can update the learned model with new information whenever new pedestrian trajectory data are made available.
To summarize, the major contributions of this research are as follows: (i) A new incoherent dictionary learning algorithm for pedestrian motion prediction; (ii) a new online incoherent dictionary learning algorithm which can perform incremental training while maintaining knowledge from different environments; (iii) a detailed performance analysis of data representation ability of the learned dictionaries, highlighting the advantages of learning incoherent dictionaries; (iv) and a detailed comparison between the proposed algorithms and its contemporary methods in pedestrian trajectory estimation on benchmark datasets.
We begin by reviewing the relevant research works in Section 2, Section 3 provides some preliminary background of dictionary learning formulation and summarizes the augmented semi-non-negative sparse coding algorithm and the prediction model. The proposed incoherent dictionary learning algorithms are presented in Section 4; specifically, the batch dictionary update approach is presented in Section 4.2.1, followed by the online dictionary update approach in Section 4.2.2. A comprehensive performance evaluation of the proposed methods is given in Section 5. Finally, Section 6 concludes the manuscript.
2. Related Work
This section provides a summary of the related works falling under the pedestrian motion prediction class and methods that learn the motion primitives incrementally.
A number of research works have been presented recently in the domain of pedestrian motion prediction. In [13], authors use graph-attention networks to capture the spatio-temporal interactions among pedestrians. Similarly to [13], the authors in [14] model the pedestrian interactions with an attention graph and perform significantly better in terms of fewer learned model parameters and prediction accuracy. In [3], authors propose an LSTM-based model (conveniently called Social-LSTM) geared towards incorporating social interactions in the pedestrian trajectories. These social interactions were modeled using social pooling with predefined local grids. Instead, the authors in [15] use a multi-layer perceptron network to extend the social pooling technique and use the recurrent Generative Adversarial Networks (GAN) in place of LSTM. In [16], authors utilize a directed social graph to model the agent location and speed direction. Furthermore, they use a temporal stochastic method to model the uncertainty in social interactions to improve trajectory predictions in crowded scenarios. The authors in [4] modify the Info-GAN [17] architecture by replacing the loss term with an entropy-based loss function to improve networks’ generalization performance for the trajectory-prediction horizon of over several seconds. For a detailed review of deep learning-based techniques for pedestrian trajectory detection, the reader is referred to Section 3 in [18].
In [9], the authors proposed a dictionary learning algorithm, termed Augmented Semi Non-negative Sparse Coding (ASNSC), to represent the pedestrian trajectories in terms of motion primitives (atoms of a dictionary) and their pair-wise transitions. This work was extended in [19] called Transferable ASNSC (TASNSC) where the trajectories were projected into a normalized alternate environment independent coordinate system with the aim of learning a prediction model which can easily be generalized to different environmental geometries.
TASNSC was further extended as an incremental learning framework, SILA [20], where the model was incrementally updated when new trajectory samples/datasets were available. SILA used the TASNSC method to separately learn dictionaries/motion primitives on different datasets. These motion primitives were then combined together in a single model by fusing similar motion primitives together. This way, the model size was kept from growing linearly and better prediction performance was reported. Similarly to SILA, which could merge two sets of motion primitives at a time, the authors in [21] proposed a fusion framework which could fuse any number of models. An online learning method for motion patterns is proposed in [8] where GPs are used to compare newly learned behaviors with old ones and if considered novel enough, adding the new behavior into the model. Authors in [5] proposed a Growing Hidden Markov Model (GHMM) to perform incremental learning for pedestrian motion prediction. This method had a strict requirement of training on complete trajectories, which as discussed earlier, is difficult in crowded environments. An incremental learning model to predict full-body human motion is proposed in [22], where the authors use a pre-defined set of motion primitives and the relationship among them is incrementally extracted using HMMs.
The recently proposed incremental learning algorithms SILA [20] and SimFUSE [21] have been shown to generate high quality predictions when compared with other state-of-the-art algorithms. These methods learn the baseline motion primitives using the dictionary learning method ASNSC [9] and perform fusion of the learned motion primitives for performance improvement. However, as will be shown in the experimental Section 5.2.2, the dictionary extracted with the ASNSC method can contain atoms which are highly correlated, which affects the overall performance of the downstream methods when using such coherent dictionaries. To alleviate this issue, we extend the ASNSC method to learn incoherent dictionaries. When leveraging the post-processing methods such as SILA, our learned dictionaries lead to significant performance improvement as compared to ASNSC, (see Section 5.2.3). Furthermore, we present an online dictionary learning algorithm which has the flexibility to seamlessly update learned model when new samples are available. Detailed preliminary information about ASNSC [9], the agent trajectory model, and the used prediction model are provided in the next section.
3. Background
This section reviews the basics of the dictionary learning framework and sets the baseline for methods presented in this work. We further discuss the augmented semi-non-negative sparse coding (ASNSC) [9] method for the application of pedestrian trajectory modeling. In the upcoming sections, matrices will be represented as bold capital letters A, vectors as bold small letters a, scalars as small letters a, and subscripts/superscripts will be clarified according to the context.
3.1. Dictionary Learning-Based Sparse Signal Representations
Consider a data matrix consisting of N real-valued data vectors of size p. In order to generate a sparse signal representation of Y, dictionary learning (DL) algorithms aim to find an over-complete (fat) dictionary and a sparse representation matrix . In this framework, each sample is represented by a linear combination of a few dictionary columns (atoms), i.e., , with a sparse . These methods have been shown to work well in applications such as compressed sensing [23], image restoration [24], fMRI signal analysis [25], and face recognition [26], etc.
As natural data can take many different forms, e.g., non-negative image pixel values, further research has been conducted to find interpretable part-based representations. Examples include non-negative sparse coding (NSC) [27] and non-negative matrix factorization (NMF) [28] algorithms, where the non-negativity constraint is imposed on sparse coefficients and dictionary atoms . Similarly, the semi-non-negative sparse coding algorithm [29] constrains the sparse coefficients as non-negative, while allowing dictionary atoms to take on any value. Keeping the sparse codes non-negative simplifies their interpretation, i.e., the activation or absence of a basis function, however they bring other issue along with them. For example, two atoms with the same magnitude but opposite signs might cancel each other out [29], thus making the sparse coefficients’ interpretation difficult.
3.2. Augmented Semi-Non-Negative Sparse Coding
Consider the following optimization problem [9],
Here, the loss function is composed of two parts, the first is called the data fidelity term (a Frobenius norm of the residual) and the second is the sparsity penalty (-norm of the representation vector), is the sparsity controlling parameter, and is the feasible set containing atoms . The data fidelity term forces the model to learn a good signal approximation, while the sparsity penalty is used to promote the sparseness of the learned coefficients.
This optimization problem is linked with prior works in multiple important ways. For example, constraining in (1) results in the non-negative sparse coding (NSC) problem of [27]; furthermore, leads to the non-negative matrix factorization (NMF) problem [30]. Finally, with being unconstrained, a semi-non-negative matrix factorization (Semi-NMF) formulation is produced [29]. The main difference between the problem formulation in (1) and prior works is its flexibility to impose different constraints on different parts of the dictionary atom. This feature is the main use case of this formulation for trajectory prediction problem [9]. Suppose our signal vector is created by concatenating two different signals coming from some sensors measuring an event in different modalities, i.e., , where and are from different modalities and could have different lengths. As a result of such a formulation, the dictionary atoms can be similarly partitioned into , and can be constrained differently as well. Consequently, in (1) can be defined as [9]
here, and are the feasible sets and is a joint constraint. We can choose and to reflect the properties of the data under consideration, e.g., dynamic range, sampling rate, and discretization levels of the respective sensor measurements.
3.3. Agent Trajectory Model
Consider a two dimensional mobile agent trajectory, denoted as as a sequence of 2D positional measurements taken at a frequency of . At each location, we can approximate the agents’ velocity using the finite positional differences, i.e., . Here, we assume the mobile agents’ movement to be unconstrained, i.e., their velocities (speed and direction) can vary depending upon different environmental conditions, including traffic, signals, obstacles, and proximity to other agents. So, instead of speed, we are interested in the agents’ heading direction which can then be used to approximate the shape of a set of probable future paths. As a result of this formulation, our focus is on modeling the trajectory shape which will help us in predicting the agents’ future trajectory by using its current speed and the possible heading directions. To this end, we normalize the input velocities at each point to be of unit magnitude; .
In order to work with the motion trajectories s, we represent them as a column vectors and combine them in a matrix . This is achieved by dividing the entire environment where trajectories exist into a grid of size (number of rows and columns) blocks with width w. For each trajectory passing through a specific block , we compute their normalized x-y velocities . Similarly, if the trajectory does not pass through a block, its velocity is defaulted to zero. We keep track of an additional binary variable called activeness , which stores whether the trajectory passed through a specific grid block or not. Finally, following the formulation given in (2), the data vectors are established as
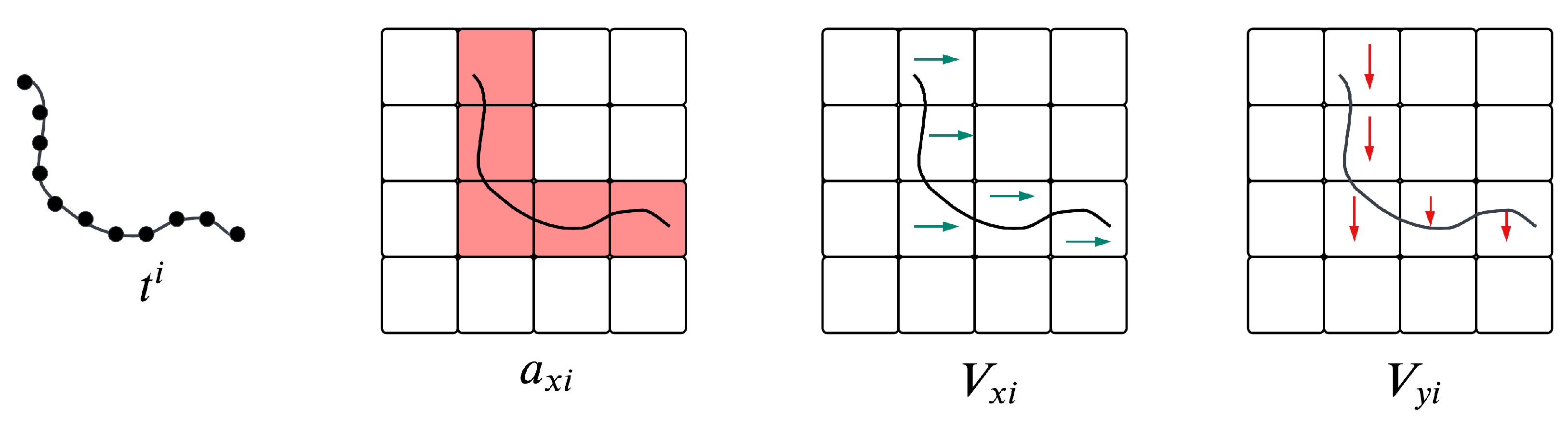
An example of a simple trajectory and its discrete representation is shown in Figure 1.
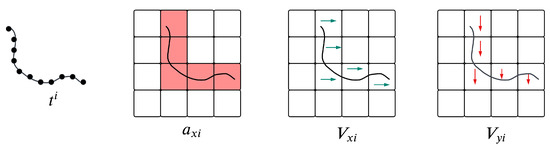
Figure 1.
Vectorized trajectory representation of a mobile agent [9]. is a sample trajectory which is represented in a discretized world with an grid size, and width w. The trajectory is represented as a vector , where normalized velocities are represented by , , with being the binary activeness variable.
The advantage of working with velocities instead of absolute positional values stems from enforcing the non-negativity constraint on the sparse coefficients , as a result of which, we are able to distinguish trajectories travelling in opposite directions, which is useful in the prediction stage. The issue of two identical but opposite moving trajectories is solved by incorporating the binary activeness variable, i.e., if the two atoms lower the sample error in the optimization problem, the addition of their binary activeness variables will increase it. This is further enforced by bounding the magnitude of velocity components by their respective activeness variable, i.e., , . Additionally, if we relax the binary assumption on the activeness variable and allow it to be a non-negative real variable, they can be interpreted as the degree of confidence that a learned motion primitive (atom) passes through some grid location [9].
3.4. Prediction Model
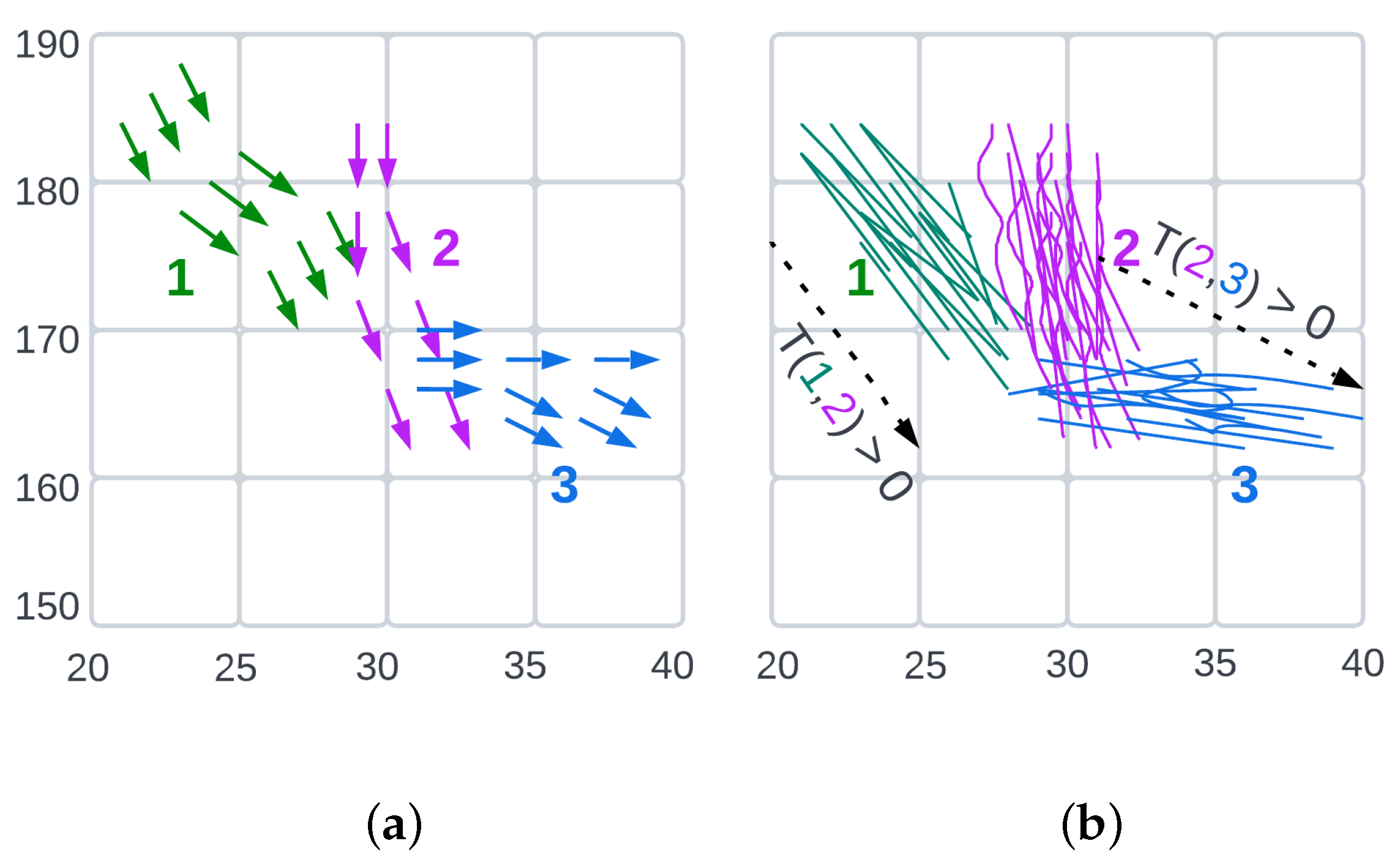
Once the ASNSC [9] learning process concludes, we receive a set of motion primitives (atoms) and their respective sparse code matrix X. An example of three learnt motion primitives is given in Figure 2a where each motion primitive has a designated color. These learnt motion primitives are then used to segment the training sample trajectories into clusters based on their similarity [9]. Figure 2b shows these clusters, color coded according to the motion primitive that best describes them. In order to perform motion predictions, a transition matrix is constructed from these clusters such that each entry denotes the number of training sample trajectories transitioning from the atom to atom.
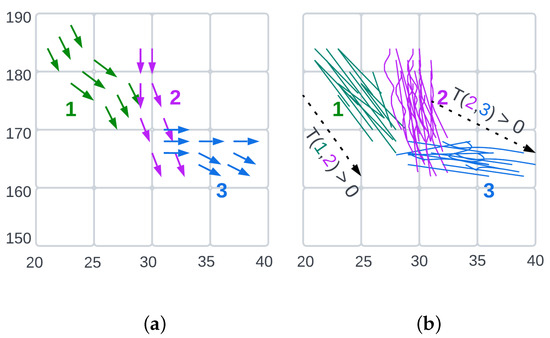
Figure 2.
An example of motion primitives learnt using ASNSC [9,20]. (a) Three sample motion primitives from the learned dictionary presented in discretized grid, each motion primitive is shown in different color. (b) Shows a number of training sample trajectories which have been segmented into three clusters using their similarity with the motion primitives given in (a). The black arrows signify the transition from cluster i to cluster j based on the Transition matrix T when their respective entry in non-zero, i.e., . The x and y axis are in meters.
Each sample trajectory is thus modeled as a concatenation of a set of dictionary atoms. Starting with a given path, we first locate the atom m which most likely generated this path; then, based on the transition matrix, we find the set of all possible subsequent atoms to make a prediction. Here each transition is modeled as a two-dimensional Gaussian Process flow field [6], leading to a set of transitions R such that . The final prediction is performed by sampling from this set.
4. Proposed Methods
One key requirement for the success of any dictionary learning algorithm is its ability to learn a dictionary which can provide the best possible sparse representation for the training dataset. In order to perform efficient sparse coding, the sparse coding algorithms require coherence between the given dictionary atoms to be as low as possible [31]. The coherence , called mutual coherence, is a property that characterizes the correlation (similarity) among dictionary atoms. For a dictionary of size K, it can be defined as [11]
Consider the following constrained optimization problem (Basis Pursuit) [31]
then, Theorem 3.1 in [31] provides a relationship between the sparsity of the representation vector x and the mutual coherence . It states that if (x is sparse enough), then the solution stability of (6) is bounded by
Here, is the approximated solution, is the -pseudo-norm which counts the number of non-zero entries of its argument, and is the representation error (signal noise) given in (6). (7) shows that for , the exact solution of (6) is guaranteed. Furthermore, authors in [11] have shown that a dictionary with low coherence requires less atoms to better represent the data, i.e., they improve signal sparsity [11], as their atoms are forced to be as discriminative as possible.
In this section, we present our proposed extensions to the ASNSC model [9] given in (1) by introducing an incoherence penalty into the optimization problem
here, is the set of all possible vectors adhering to the constraints given in (4). Similar to (1), the first term in the right side of our objective function is the data fidelity term, the second term is introduced to promote learning mutually incoherent dictionary atoms (incoherence penalty) [32], the third term is the sparsity penalty, and and are the incoherence and sparsity controlling parameters. In the incoherence penalty term, is the Gram matrix and contains the main diagonal of . The off diagonal entries of the gram matrix G are the inner products seen in (5) (ignoring denominator terms), with the highest off diagonal entry being the mutual coherence . The proposed penalty measures the Frobenius distance between the matrix G and , where can be considered as a Gram matrix of an orthogonal dictionary with zero . This method of enforcing incoherence between dictionary atoms has been shown to be effective as it is directly linked with the approximation accuracy of the objective function [32].
Although the objective in (8) is non-convex, it does admit a multi-convex structure in D and X, separately [33], and can be solved via an alternating optimization strategy that guarantees its convergence to a local minima. This approach is used in most dictionary learning algorithms to approximately solve (8) which consists of two alternating steps, a sparse coding step and a dictionary update step. These steps are alternated until some convergence criteria are satisfied. These steps are discussed next.
4.1. Sparse Coding Step
Keeping the dictionary D fixed, solving for X reduces (8) to
Since each sparse code vector corresponding to the signal vector is modeled independently from the others, the above problem can be solved for each individually. Furthermore, (9) can be written as a constrained quadratic program (QP) by considering the norm penalty as due to the non-negativity constraint on it. Thus, there are several off-the-shelf optimization algorithms available to solve (9). We chose to work with qpsolvers (https://pypi.org/project/qpsolvers/ accessed on 15 August 2022), a quadratic programming solvers library for the Python programming language, which contains a number of individual solvers optimized for different structured problems. From available solvers, we chose quadprog which uses a dual algorithm [34] to solve the sparse coding problem. This solver was found to be faster than the rest and provided fairly accurate results for our problem.
4.2. Dictionary Update Step
In this step, the sparse code matrix X is kept fixed, and the solution for D is found by solving the following reduced problem
Solutions to (10) generally follow two different avenues to solve the above dictionary update step, i.e., sequentially updating dictionary atoms [24,35], by breaking the global minimization problem of (10) into K sequential minimization problems or by solving for the entire dictionary at once [9].
We propose two different solutions to solve the problem given in (10);
- A1
- A batch learning approach, where the entire dictionary is updated at once, using the entire dataset.
- A2
- An online learning approach, where we train the dictionary atoms, one at a time, using a small batch from the entire dataset.
The batch learning approach is called A1, and the online learning approach is called A2 in the rest of the manuscript. The dictionary update rules under both approaches are given next.
4.2.1. A1: Batch Learning Approach
For the batch learning approach, taking the gradient of (10) with respect to dictionary D, we obtain
Let be the dictionary at the previous iteration; the updated dictionary is approximated by taking a step in the opposite direction of to perform the steepest gradient descent, i.e.,
where is the step size which should satisfy to guarantee convergence. So, we choose to set which has been found to achieve stable results. The reason for upper bounding stems from our dictionary initialization, which is initialized with random entries taken from a Normal distribution, followed by constraining its column entries according to (4). As a result of this, the initial sparse code matrix X contains very few small entries, as the initial dictionary used to compute it is not representative of the data. This leads to a small (low largest singular value) with a high inverse. Thus, upper bounding it with has been found to bring stability in the first few iterations.
In this dictionary update step, we did not consider the constraints given in (8). For the trajectory modeling application considered here, these constraints are given in (4), where each entry of the atom is constrained separately, so, following the dictionary update, we project all dictionary atoms into the feasible set according to (4). The stopping criteria for the overall process are set using the dictionary convergence rate (The dictionary convergence is computed as ) and a maximum number of iterations, whichever comes first. The pseudo-code of the proposed A1 algorithm is shown in Algorithm 1.
| Algorithm 1: A1: Incoherent dictionary learning algorithm |
 |
4.2.2. A2: Online Learning Approach
In this section, we present our online dictionary update strategy to solve (10). This strategy can be seen as an extension to the algorithm proposed in [35] to learn an incoherent dictionary in an online manner, called A2. The pseudo-code for this algorithm is outlined in Algorithm 2.
| Algorithm 2: A2: Online incoherent dictionary learning algorithm |
 |
Assuming the training data samples to be i.i.d. samples from some probability distribution , instead of using the entire dataset Y, we will work with a mini-batch taken from Y, denoted by at each iteration of the learning process (sparse coding and dictionary update). As the samples of mini-batch are i.i.d., the sparse coding step can be kept same as that used for algorithm A1 (Section 4.1), but instead of finding codes for the entire dataset, at each iteration, we only find codes for the mini-batch samples.
Similar to [35], our dictionary update step utilizes the block coordinate descent with warm restarts to update the dictionary for each new data batch. Starting from zero, the matrices and B are used to carry all the information from past sparse coefficients (see lines 9–10 in Algorithm 2). Their updates are tempered by using a leverage parameter , which starts out with a small value, and slowly increases towards unity, i.e., . This slope is controlled by parameter c, which is set as , where N is the size of the dataset (or a large number) and is the mini-batch size. This selection is observed to work well in our experiments. Moreover, this parameter can be reinitialized on the go if the new batch is considered slightly out of distribution or deemed more important during the online updates.
For the dictionary update step, we update each dictionary atom sequentially, using the atomic gradient of (10) as given below:
where is the kth atom, is the kth column of A, is the kth column of b, is the incoherence controlling parameter, and is vector of all zeros except its kth entry which is . The learning step is updated automatically using a similar strategy as for the A1 algorithm, i.e., , where is the kth diagonal entry of matrix A. Since the coefficients are sparse, and the learned dictionary is incoherent, most of the coefficients of A are concentrated along its main diagonal, making the block-coordinate descent even more efficient. This update step ensures that the learned atom is forced to have low coherence with all other dictionary atoms. Finally, the updated atom is projected back to the feasible set using (4). The entire procedure is repeated until convergence.
4.3. Convergence Analysis
Although the objective in (8) is non-convex, it admits a multi-convex structure in D and X separately [33], and can be solved via an alternating optimization strategy that guarantees its convergence to a local minima. We have used this approach in both of our methods to approximately solve (8), which consists of two alternating steps, a sparse coding stage and a dictionary update stage. The same sparse coding step is used in both A1 and A2 algorithms which we solve using a constrained quadratic problem which guarantees convergence to a local minima [34]. Similarly, the objective function for the dictionary update (10) is convex and is updated using gradient descent in the A1 algorithm and block-coordinate descent in the A2 algorithm, which guarantee the reduction in the objective towards a local minimum [35]. Additionally, the feasible set in (10) is shown to be convex as well [9].
5. Performance Evaluation
In this section, we perform two sets of experiments to evaluate our proposed algorithms. First, we compare the proposed methods in terms of the learned dictionary quality in the context of signal reconstruction, dictionary coherence, and average signal sparsity. Second, we present a performance comparison of the pedestrian trajectory prediction problem using real world pedestrian trajectory datasets in two additional settings, to be explained later in Section 5.2.2 and Section 5.2.3.
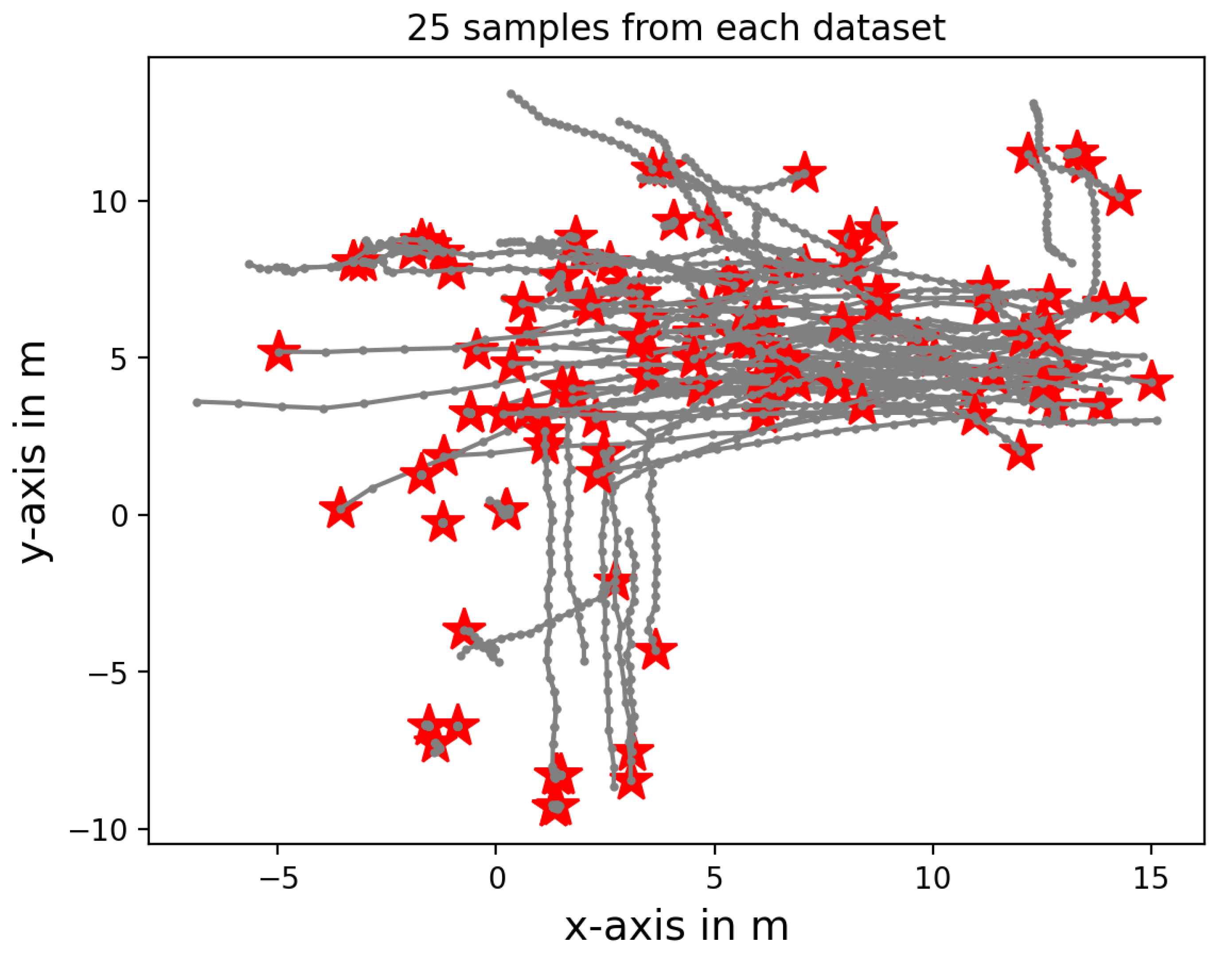
The datasets used in these sections are as follows: ETH [36] and UCY [37]. The ETH dataset contains two scenes, ETH-University (called ETH for short) and Hotel. The UCY dataset contains three scenes Zara01, Zara02, and Univ. The majority of trajectories in these datasets are in the horizontal direction except the Hotel scene, where the majority of the trajectories are vertical. The sampling rate for all measurements is Hz. For illustration purposes, 25 randomly chosen trajectories from each dataset are shown concurrently in Figure 3. For additional details, readers are referred to [36] for ETH, and [37] for UCY datasets.
Figure 3.
25 randomly sampled trajectories from each dataset. ⋆ represents the trajectory starting point.
All experiments were carried out on a Windows 10 laptop, equipped with 11th Gen Intel(R) Core(TM) i7 and 16 GB 4267 MHz RAM. The programming language used was Python v3.8.
5.1. Experiment 1: Dictionary Quality Assessment
In order to compare the quality of dictionaries learned by different algorithms, we consider the following three general metrics:
- Signal Representation Power: How well the dictionary can represent the given signals,
- Dictionary Condition: This relates to the dictionary atom coherence; a smaller value is better,which can be easily computed by summing the upper triangular part of the Gram matrix .
- Average Signal Sparsity: The number of atoms used to represent a given signal on average, a smaller number is better.
Here, is the Frobenius norm of a matrix, is the norm of a vector, is the pseudo-norm which counts the number of non-zero entries of the argument, and N is the dataset size. These metrics are not independent, i.e., increasing the number of dictionary atoms leads to a reduction in the reconstruction error at the expense of dictionary coherence. On the other hand, reducing the number of atoms, typically leads to an increase in the reconstruction error and average signal sparsity. In order to perform a fair comparison, in this experiment, we fix the size of the dictionaries to atoms.
The tests on all five datasets were performed separately. For each dataset, the data matrix is created as discussed in Section 3.3 with cm, containing all trajectories with length . In order to reduce the size of each vector , we omit those grid positions where no trajectory passes. This simple pre-processing step leads to . The spatial resolution (w) of the grid should be selected carefully as a small value will not only lead to a significantly large data vector, but will also result in empty grid slots between two trajectory sampled points for a relatively fast moving agent. On the other hand, setting a larger value could cause multiple sample points to end up in the same grid location. As the datasets under consideration contain pedestrian trajectories, a spatial resolution of 50–100 cm is considered sufficient.
Starting with a randomly initialized dictionary D, we use ASNSC [9], A1 and A2 algorithms to train the dictionaries. For each algorithm, the gradient descent step size is set to and maximum training iterations are upper bounded by 150. For ASNSC, A1 and A2, the incoherence controlling parameter and sparsity controlling parameter are chosen by performing a grid search, as discussed in Section 5.1.2. For A2, the batch size is set to 32. All experiments were repeated 10 times and the average scores for each algorithm and each dataset are reported in Table 1.

Table 1.
Performance comparison between dictionaries learned by ASNSC [9], and the proposed algorithms A1 and A2. Lower is better.
Looking at the reconstruction error scores in Table 1 for all algorithms, we find that their final scores are very similar, with A1 being slightly better on average, and that all algorithms were able to converge within 150 iterations. This is the consequence of keeping the dictionary size the same. This highlights the fact that all three algorithms are stable, as with everything else remaining the same, their performance (on average) is within a small margin of error. Moving on to dictionary coherence scores in Table 1, we see that on average, A1’s coherence score is and A2’s coherence score is lower than ASNSC. Furthermore, the average signal sparsity achieved by A1 and A2 is and lower than ASNSC’s scores, respectively. This shows that A1 and A2 algorithms were able to reach the error floor by using less atoms on average. Thus, the atom redundancy level in the dictionary recovered by ASNSC is much higher than that of A1 and A2’s dictionaries. Having a low coherence dictionary does lead to atoms with better generalization capabilities, which will be further highlighted in the next experiment of pedestrian trajectory prediction.
The run-times of a single iteration over the ETH dataset for the three algorithms is given in Table 2. We observe that the execution times for ASNSC and A1 are almost the same. This is expected as they both perform block dictionary updates and have similar complexities for the dictionary update step. Here, most of the time is taken by the non-negative sparse coding algorithm. On the other hand, A2 takes almost double the time for a single complete iteration which is attributed to the fact that it is an online learning algorithm and goes through the dataset one batch at a time. Thus, the sparse coding method is implemented for each batch separately. Additionally, the dictionary is updated sequentially, i.e., one atom at a time. These two loops contribute to the increase in execution time of the A2 algorithm.

Table 2.
Single iteration time (in seconds) for each algorithm for training a dictionary with 50 atoms on ETH dataset.
5.1.1. Dictionary Convergence
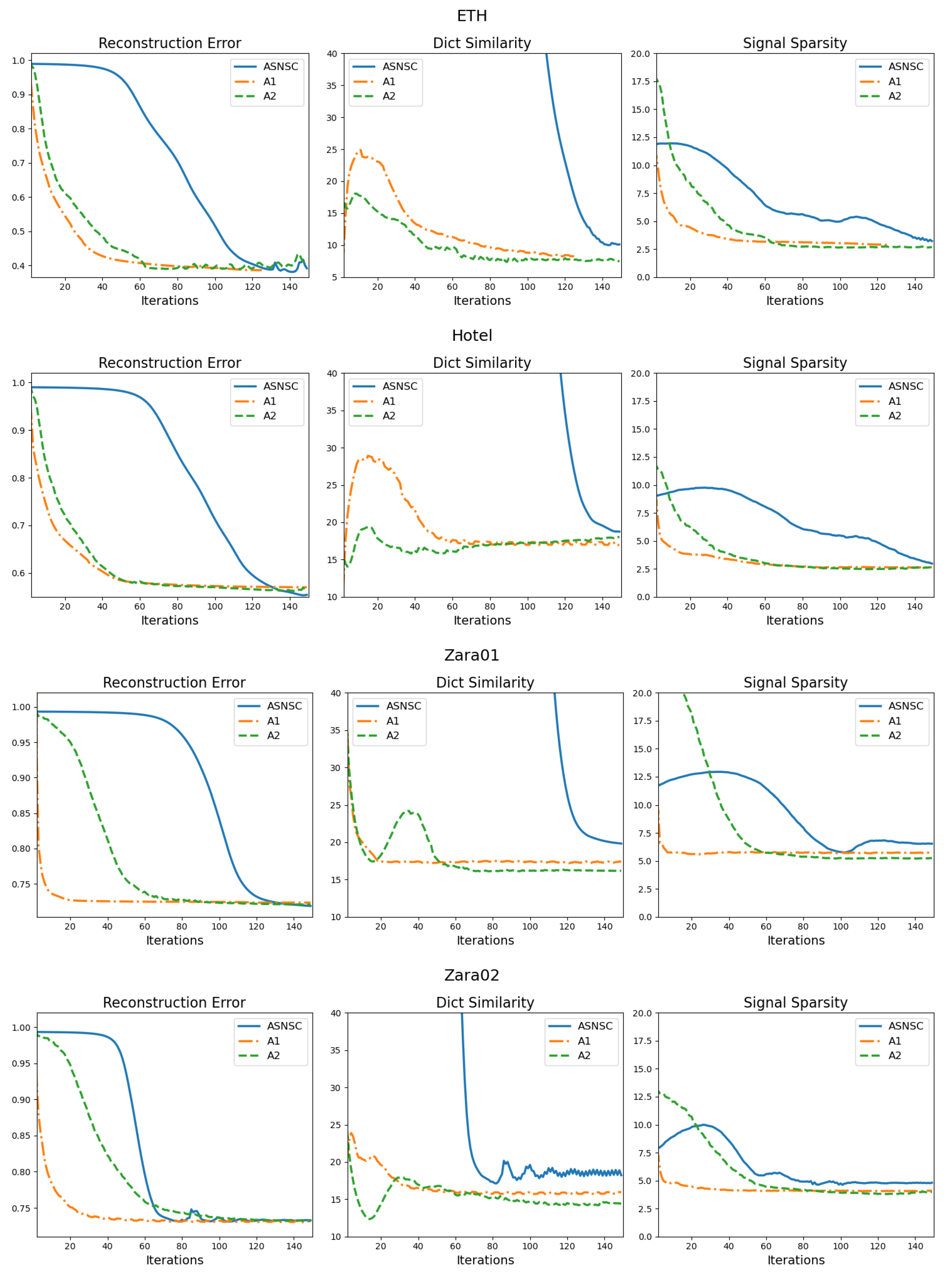
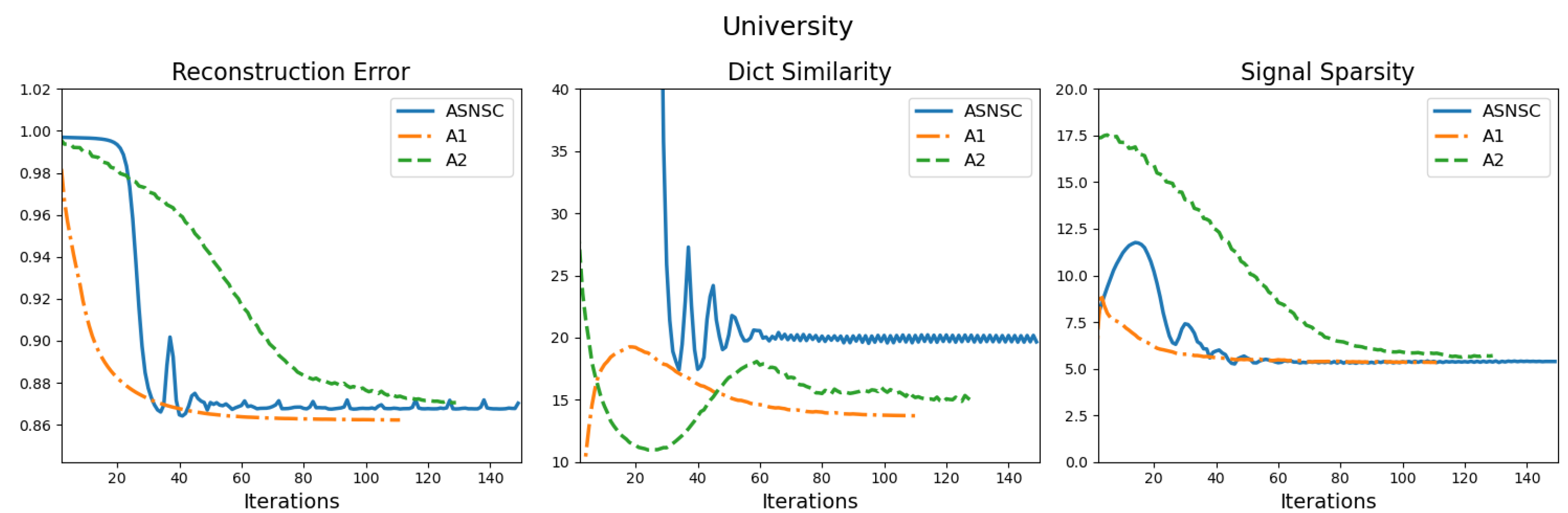
To visualize the convergence behaviour of the three algorithms, we present their convergence graphs for the three aforementioned metrics on all datasets in Figure 4. From the graphs, we observe that the convergence of the reconstruction error is directly linked with how incoherent the dictionary atoms are; the lower the coherence, the faster the reconstruction error convergence. This is especially true for ASNSC’s convergence graphs. Looking at the graphs for the Hotel dataset, we see that the coherence curve of ASNSC falls within range after 120 iterations, leading to a slower convergence of the reconstruction error as well. On the other hand, the reconstruction error and average sparsity graphs of A1 approach their respective floors much earlier than others. Furthermore, from the graphs of the University dataset, we see that A2’s reconstruction error graph converges last; this could be attributed to the fact that the University dataset has the highest number of sample trajectories, and during the accumulation phase of the A2 (see line 9 and 10) Algorithm 2, the growth rate of is low. This can be avoided by changing the scaling constant in line 7 of the Algorithm 2. Finally, for the Zara02 and Univ datasets, the oscillation frequency of the ASNSCs’ coherence curve is much higher than A1 or A2. This oscillation also manifests in its reconstruction error and signal sparsity graphs as well.
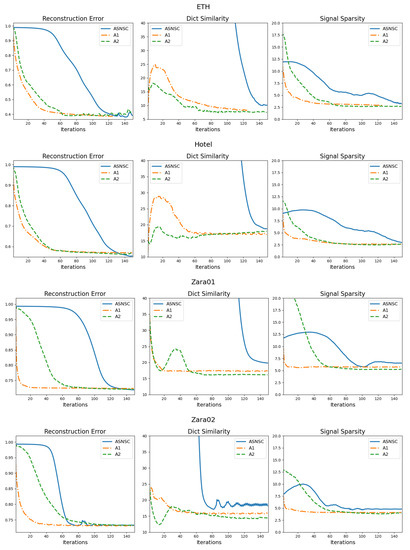
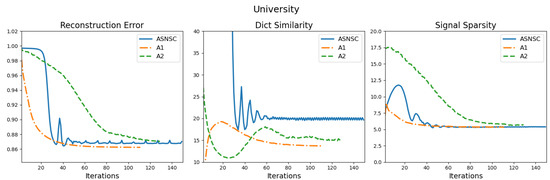
Figure 4.
Convergence graphs for the three metrics, for all algorithms and datasets. The reconstruction error, dictionary similarity (coherence), and signal sparsity metrics are computed using (14), (15) and (16), respectively. (For interpretation of the line colors, the reader is referred to the web version of this article).
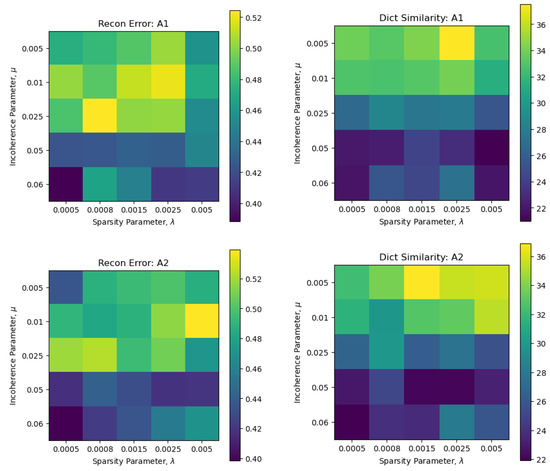
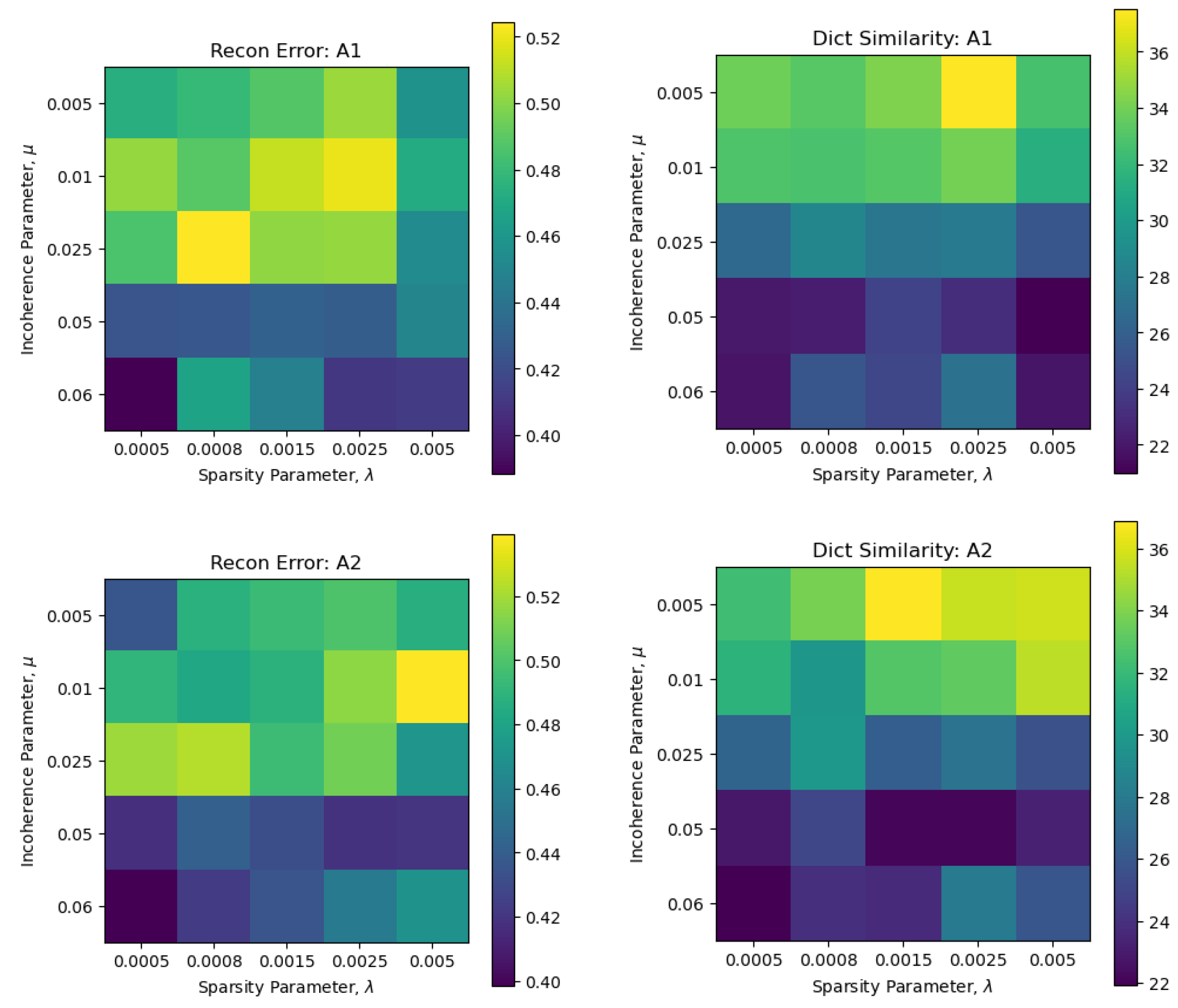
5.1.2. Parameter Selection
In addition to the sparsity-controlling parameter , the proposed algorithms also require selection of the incoherence controlling parameter . For the results reported in the previous section, for each dataset, we performed a grid search with and and selected the ones which gave us the lowest scores in terms of the reconstruction error. An example of such a search on the ETH dataset is shown in Figure 5, where we can see that a higher generally leads to a lower dictionary coherence and reconstruction error. Moreover, for A1, it is observed that for a low , increasing up to leads to an increase in the reconstruction error and dictionary coherence; however, for , the scores see a small dip. This effect, however, is not so visible in A2’s results, where increasing generally leads to slight increase in both metrics. Moreover, for , an increase in does not show any specific trend. On the other hand, for a fixed , increasing , on average, leads to a lower recon error and dictionary coherence.
5.2. Experiment 2: Pedestrian Trajectory Prediction
For this experiment, we follow the methodology of prior works [13,14,15,20] and use the following two metrics for prediction performance evaluation:
- Average Displacement Error (ADE) [15], which is the mean Euclidean distance between the true and predicted trajectory over a given time horizon H, given byhere, and are the samples at time t in the true and predicted trajectories, respectively. The last observed time sample is , after which the prediction starts.
- The final Displacement Error (FDE) is the final prediction error at the end of the time horizon H, given by
5.2.1. Prediction Method
Starting with an observed trajectory, we first find the dictionary atom (motion primitive) which most likely represents the given observed trajectory, referred to as the observed primitive. Then the transition set R is used to find all possible future directions the trajectory (of set ) might take from the observed primitive, i.e., all possible GPs. This gives us a set of Gaussian distributions, which are then sampled to obtain a set of predicted future trajectories.
5.2.2. Comparison with Baseline
In this section, we compare the raw prediction performance of ASNSC with the proposed A1 and A2 algorithms. Similar to [20], we use 4 out of 5 datasets for learning the dictionaries and evaluation is performed on the remaining dataset in a leave-one-out strategy. Two additional datasets (Zara03 and UCY uni examples) are also used for training, but not for testing [13,14,15,20].
For evaluation, we observe each trajectory for eight sample points (3.2 s) and predict the next twelve points (4.8 s). The methods compared are; a Linear model which assumes constant velocity as at the last observation point, ASNSC, A1, and A2 algorithms. ASNSC and A1 algorithms are offline, and A2 is an online learning algorithm. Apart from the Linear model, the rest perform trajectory predictions as summarized in Section 5.2.1. Similar to [13,14,15,20], we sample 20 trajectories from the predicted distributions and choose the one closest to the true trajectory for evaluation. The dataset feeding order for the online A2 algorithm is chosen in a similar way to [20], given in Table 3, which will also be used as the training order in Section 5.2.3. Similar to ASNSC, for A1 and A2 we set the initial dictionary size to and increase the dictionary size every 15 iterations, and the maximum learning iterations limit is set to 300. The final prediction results are outlined in Table 4.

Table 3.
Dataset feeding order for the online learning.

Table 4.
ADE/FDE scores for each evaluation dataset using the leave-one-out strategy.
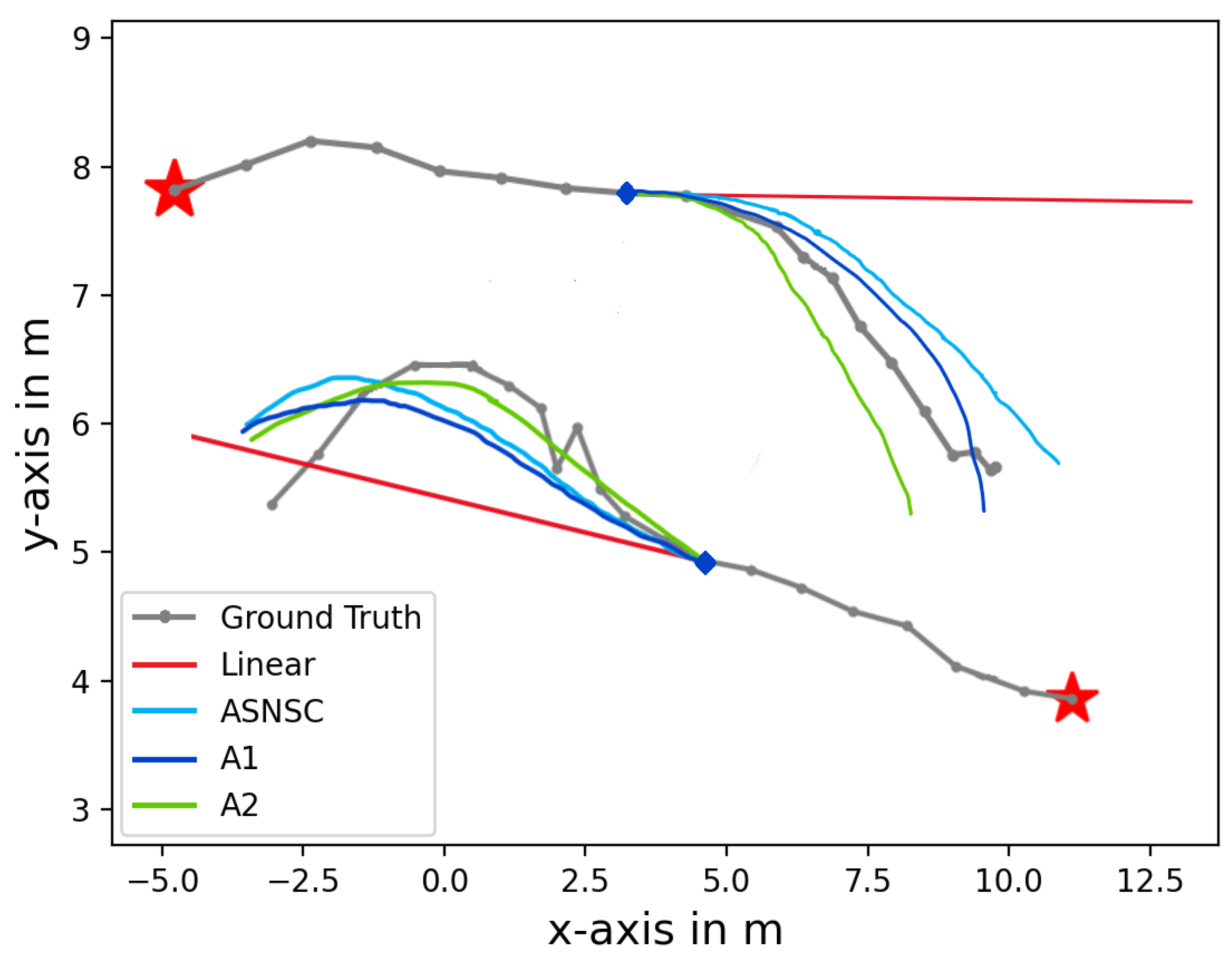
Looking at Table 4, we see that the prediction scores of A1 are slightly lower than ASNSC’s scores except for Zara01 where ASNSC’s ADE score is better than A1’s. However, the A2 algorithm is seen to perform better than its competition over all the testing datasets consistently. Moreover, the average final dictionary size of A2 algorithms was found to be less than A1 which was close to ASNSC, i.e., , respectively. This further highlights that the dictionary learned by the proposed algorithms are better conditioned and have fewer redundant atoms. For illustration, we show two example trajectories from the ETH dataset concurrently in Figure 6. Here, the first eight samples are the input and the next twelve are predictions of their respective methods. For the top example, the linear method fails as it predicts motion in the same direction as that of the final input sample, whereas ASNSC, A1, and A2 were able to follow the ground truth path much better. Here, in terms of ADE, A2 < A1 < ASNSC Linear, and for FDE, A1 < ASNSC < A2 Linear. A similar trend can be observed in the bottom example as well, where A2’s prediction was able to follow the ground truth much better than the other methods.
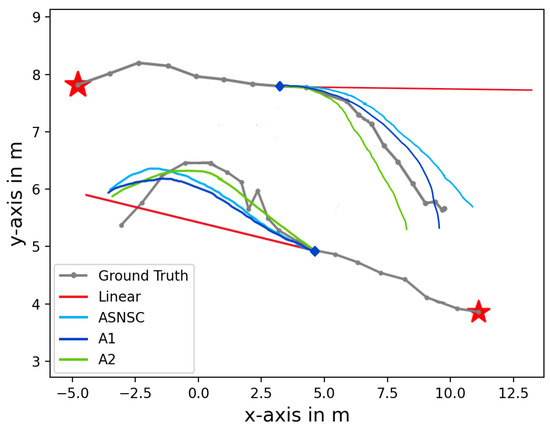
Figure 6.
Two example trajectories from the ETH dataset and their predicted trajectories. (For interpretation of the line colors, the reader is referred to the web version of this article).
5.2.3. Comparison with Recent Works
In this section, we use the motion primitive fusion algorithm SILA [20] as a post-processing method to obtain even better results as compared to the raw scores presented in Section 5.2.2. SILA is an incrementally learning algorithm which uses ASNSC to learn a dictionary from different datasets and incrementally fuses the learned dictionary atoms together using the atom coherence metric (5). Let (the fusion parameter) be the coherence metric between two motion primitives and ; if the coherence is greater than some threshold, SILA merges both primitives together by taking their average. This way, the SILA algorithm can update the learned dictionary when a new dataset is acquired and is shown to perform better than the naive batch learning approach [20].
Next, we augment our learning algorithms with SILA to leverage its performance extraction capabilities and compare them to recently presented works on interaction-aware pedestrian motion prediction algorithms like Social-STGCNN [14], STSGN [16], STGAT [13], GAT [38], and SGAN [15]. To this end, we use four SILA-based variants as described below:
- SILA-ASNSC: Here ASNSC [9] algorithm is used to train a dictionary (from random initialization) for each dataset in the training order given in Table 3, with each dictionary fused with the previous one using SILA [20].
- SILA-A1: Same as part 1, except the dictionaries are learned using A1 algorithm.
- SILA-A2-Simple: Here, we train a new dictionary (from random initialization) for each dataset using A2 algorithm. We reset accumulation variables A, B, and the dictionary for training over the next dataset. The resulting dictionaries are fused using SILA.
- SILA-A2-Snap: Here, after learning the dictionary from the first dataset, we keep the accumulation variables A and B, set the leverage parameter and keep a snapshot of the learned dictionary. Training over the next dataset leads to a warm restart using A, B, and the previously updated dictionary. Upon training completion, SILA is used to fuse the snapshot dictionary and updated dictionary together, resulting in a new fused dictionary.
For the above SILA-based algorithms, (similar to [20]), we set the threshold for fusion parameter as it was found to provide a good balance between the final dictionary size and prediction accuracy. All considered models, except the Linear model, are probabilistic, where we consider the best out of 20 sampled trajectories. The prediction results for all aforementioned algorithms are given in Table 5. The results for SGAN, STGAT, and Social-STGCNN were obtained using their code available in their respective repositories from github. The rest were taken from their respective papers.

Table 5.
ADE/FDE scores for each evaluation dataset under the leave-one-out strategy. Except the Linear model, all other models are probabilistic, where we consider the best out of 20 sampled trajectories.
The scores reported in Table 5 show that among the SILA-based algorithms, our proposed variants were able to beat SILA-ASNSC in all scenarios based on both FDE and ADE metrics. Furthermore, our A2-Snap variant ADE scores are very competitive as compared with other algorithms, as, on average, it achieves the lowest ADE for 4/5 scenarios as well. Furthermore, in terms of FDE, it is the second best based on the reported average scores, losing only to Social-STGCNN. This effect could be attributed to the pedestrian interactions, which are incorporated by Social-STGCNN but not by us. Additionally, compared to vanilla A2’s results, reported in Table 4, the A2-Snap variant scored and lower in terms of ADE and FDE scores, respectively, owing to SILA fusion algorithm [20]. On average, the final dictionary sizes for all SILA-based algorithms were similar.
5.2.4. Summary
In this section, we presented an in-depth performance review of the two proposed incoherent dictionary learning algorithms. The first experiment compared the proposed A1 (batch) and A2 (online) algorithms with ASNSC [9] by comparing the quality of the learned dictionaries in terms of their representation power. As discussed in Section 1 and Section 4, for an efficient sparse representation of some dataset, a dictionary with low coherence is desired; thus, the metrics selected for dictionary quality comparison were data reconstruction error, overall dictionary coherence, and the resulting average signal sparsity. The idea being that an incoherent dictionary will require less number of atoms to well represent the dataset. Using the 5 real-world datasets, in Table 1 we showed that the proposed algorithms not only achieved a lower reconstruction error (owing to better representation ability), but they achieved this by using, on average, fewer dictionary atoms (lower average signal sparsity). This effect was expected as the overall dictionary coherence metric for the dictionaries learned by proposed algorithms was much smaller than ASNSC.
Once the baseline assumption (incoherent > coherent dictionary) was validated, we compared the raw trajectory prediction performance of the proposed methods with ASNSC and presented the results in Table 4. In terms of both ADE and FDE, the proposed A2 algorithm performed better for all five datasets individually and on average as well. This validated our belief that an incoherent dictionary should perform better for the trajectory prediction application as well. Finally, we augmented the proposed algorithms with an incremental learning fusion-based algorithm SILA [20] to leverage its performance extraction capabilities and compared them with several interaction-aware and unaware pedestrian motion prediction algorithms. The overall results presented in Table 5 show that the proposed A2 variant SILA-A2-Snap was able to match the interaction-aware method Social-STGCNN and clearly outperformed other SILA-based algorithms including SILA-ASNSC.
6. Conclusions
In this paper, we presented two incoherent dictionary learning algorithms for the pedestrian trajectory prediction problem, using offline and online learning strategies. The offline training algorithm learns a dictionary using the entire training dataset, while online learning uses the warm restart strategy to learn on incrementally available data. The learned incoherent dictionaries were first compared against the dictionaries learned by the baseline ASNSC algorithm in terms of convergence rate, and representation power. We showed that the incoherent dictionaries were able to not only converge faster, but also led to lower reconstruction errors while utilizing fewer atoms from their respective dictionaries. Next, the pedestrian trajectory prediction performance analysis was presented, where we showed that the proposed algorithms consistently scored better than their baseline method and provided comparable performance with respect to other pedestrian interaction-aware prediction algorithms as well.
Under the framework used in this manuscript, the input trajectories were assumed to be independent, leading to independently learned motion primitives. This is a limiting assumption. Our next objective is to create a prediction framework where the temporal information of an agents’ trajectory is also taken into account during prediction. Furthermore, in real-world environments, the sampled trajectories are often correlated. Thus, an interesting research direction would be to augment the dictionary learning algorithm to capture such correlations, similar to [39], to further enhance the representation power of the learned dictionaries.
Author Contributions
Conceptualization, F.H. and A.I.; Formal analysis, F.H. and A.I.; Methodology, F.H., U.U.S. and M.N.A.; Supervision, U.U.S. and M.N.A.; Validation, M.N.A.; Visualization, A.I.; Writingg—original draft, F.H. and A.I.; Writing—review & editing, U.U.S. and M.N.A. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by the University of Nebraska-Lincoln.
Acknowledgments
The authors would like to acknowledge the facilities provided by Universiti Teknologi Malaysia for the accomplishment of this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schneemann, F.; Heinemann, P. Context-based detection of pedestrian crossing intention for autonomous driving in urban environments. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2243–2248. [Google Scholar]
- Bartoli, F.; Lisanti, G.; Ballan, L.; Del Bimbo, A. Context-aware trajectory prediction. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1941–1946. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Li, F.-F.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar]
- Amirian, J.; Hayet, J.B.; Pettré, J. Social ways: Learning multi-modal distributions of pedestrian trajectories with gans. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Vasquez, D.; Fraichard, T.; Laugier, C. Incremental learning of statistical motion patterns with growing hidden markov models. IEEE Trans. Intell. Transp. Syst. 2009, 10, 403–416. [Google Scholar] [CrossRef]
- Joseph, J.; Doshi-Velez, F.; Huang, A.S.; Roy, N. A Bayesian nonparametric approach to modeling motion patterns. Auton. Robot. 2011, 31, 383–400. [Google Scholar] [CrossRef]
- Ellis, D.; Sommerlade, E.; Reid, I. Modelling pedestrian trajectory patterns with gaussian processes. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1229–1234. [Google Scholar]
- Ferguson, S.; Luders, B.; Grande, R.C.; How, J.P. Real-time predictive modeling and robust avoidance of pedestrians with uncertain, changing intentions. In Algorithmic Foundations of Robotics XI; Springer: Berlin/Heidelberg, Germany, 2015; pp. 161–177. [Google Scholar]
- Chen, Y.F.; Liu, M.; How, J.P. Augmented dictionary learning for motion prediction. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2527–2534. [Google Scholar]
- Hou, C.; Nie, F.; Li, X.; Yi, D.; Wu, Y. Joint embedding learning and sparse regression: A framework for unsupervised feature selection. IEEE Trans. Cybern. 2013, 44, 793–804. [Google Scholar] [PubMed]
- Ubaru, S.; Seghouane, A.K.; Saad, Y. Improving the incoherence of a learned dictionary via rank shrinkage. Neural Comput. 2017, 29, 263–285. [Google Scholar] [CrossRef] [PubMed]
- Tropp, J.A. On the conditioning of random subdictionaries. Appl. Comput. Harmon. Anal. 2008, 25, 1–24. [Google Scholar] [CrossRef]
- Huang, Y.; Bi, H.; Li, Z.; Mao, T.; Wang, Z. Stgat: Modeling spatial-temporal interactions for human trajectory prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6272–6281. [Google Scholar]
- Mohamed, A.; Qian, K.; Elhoseiny, M.; Claudel, C. Social-stgcnn: A social spatio-temporal graph convolutional neural network for human trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 14424–14432. [Google Scholar]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social gan: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2255–2264. [Google Scholar]
- Zhang, L.; She, Q.; Guo, P. Stochastic trajectory prediction with social graph network. arXiv 2019, arXiv:1907.10233. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. Infogan: Interpretable representation learning by information maximizing generative adversarial nets. Adv. Neural Inf. Process. Syst. 2016, arXiv:1606.03657. [Google Scholar]
- Sighencea, B.I.; Stanciu, R.I.; Căleanu, C.D. A review of deep learning-based methods for pedestrian trajectory prediction. Sensors 2021, 21, 7543. [Google Scholar] [CrossRef]
- Jaipuria, N.; Habibi, G.; How, J.P. Learning in the curbside coordinate frame for a transferable pedestrian trajectory prediction model. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 3125–3131. [Google Scholar]
- Habibi, G.; Jaipuria, N.; How, J.P. SILA: An incremental learning approach for pedestrian trajectory prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 1024–1025. [Google Scholar]
- Habibi, G.; How, J.P. Human trajectory prediction using similarity-based multi-model fusion. IEEE Robot. Autom. Lett. 2021, 6, 715–722. [Google Scholar] [CrossRef]
- Kulić, D.; Takano, W.; Nakamura, Y. Incremental learning, clustering and hierarchy formation of whole body motion patterns using adaptive hidden markov chains. Int. J. Robot. Res. 2008, 27, 761–784. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Iqbal, A.; Seghouane, A.K. A dictionary learning algorithm for multi-subject fMRI analysis based on a hybrid concatenation scheme. Digit. Signal Process. 2018, 83, 249–260. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Yang, J.; Zhang, D. A Survey of Dictionary Learning Algorithms for Face Recognition. IEEE Access 2017, 5, 8502–8514. [Google Scholar] [CrossRef]
- Hoyer, P.O. Non-negative sparse coding. In Proceedings of the 12th IEEE workshop on Neural Networks for Signal Processing, Martigny, Switzerland, 6 September 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 557–565. [Google Scholar]
- Wang, Y.X.; Zhang, Y.J. Nonnegative matrix factorization: A comprehensive review. IEEE Trans. Knowl. Data Eng. 2012, 25, 1336–1353. [Google Scholar] [CrossRef]
- Ding, C.H.; Li, T.; Jordan, M.I. Convex and semi-nonnegative matrix factorizations. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 45–55. [Google Scholar] [CrossRef]
- Seung, D.; Lee, L. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2001, 13, 556–562. [Google Scholar]
- Donoho, D.L.; Elad, M.; Temlyakov, V.N. Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Trans. Inf. Theory 2005, 52, 6–18. [Google Scholar] [CrossRef]
- Ramírez, I.; Lecumberry, F.; Sapiro, G. Sparse Modeling with Universal Priors and Learned Incoherent Dictionaries. 2009. Available online: https://conservancy.umn.edu/bitstream/handle/11299/180327/2279.pdf?sequence=1 (accessed on 26 September 2022).
- Gorski, J.; Pfeuffer, F.; Klamroth, K. Biconvex sets and optimization with biconvex functions: A survey and extensions. Math. Methods Oper. Res. 2007, 66, 373–407. [Google Scholar] [CrossRef]
- Goldfarb, D.; Idnani, A. A numerically stable dual method for solving strictly convex quadratic programs. Math. Program. 1983, 27, 1–33. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online dictionary learning for sparse coding. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; ACM: New York, NY, USA, 2009; pp. 689–696. [Google Scholar]
- Pellegrini, S.; Ess, A.; Schindler, K.; Van Gool, L. You’ll never walk alone: Modeling social behavior for multi-target tracking. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–October 2009; pp. 261–268. [Google Scholar]
- Lerner, A.; Chrysanthou, Y.; Lischinski, D. Crowds by example. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2007; Volume 26, pp. 655–664. [Google Scholar]
- Kosaraju, V.; Sadeghian, A.; Martín-Martín, R.; Reid, I.; Rezatofighi, H.; Savarese, S. Social-bigat: Multimodal trajectory forecasting using bicycle-gan and graph attention networks. arXiv 2019, arXiv:1907.03395. [Google Scholar]
- Seghouane, A.K.; Iqbal, A. Sequential Dictionary Learning From Correlated Data: Application to fMRI Data Analysis. IEEE Trans. Image Process. 2017, 26, 3002–3015. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).