Out-of-Distribution (OOD) Detection Based on Deep Learning: A Review
Abstract
1. Introduction
2. Background
2.1. Development Background of OOD Detection
2.2. Datasets of Reference
2.2.1. MNIST
2.2.2. CIFAR-10
2.2.3. CIFAR-100
2.3. Evaluation Metrics
3. OOD Detection Based on Deep Learning
3.1. Definition
3.2. Related Works
3.2.1. Anomaly Detection
3.2.2. Novelty Detection
3.2.3. Outlier Detection
3.2.4. Discussion
3.3. Baseline Model
- (1)
- Use softmax probability values of model predicted samples to detect OOD samples effectively;
- (2)
- OOD detection tasks and new evaluation indicators are developed;
- (3)
- A novel approach is proposed: determining whether a sample is abnormal by combining the output of a neural network with the quality of reconstructed samples.
3.4. Categorization
- The machine learning paradigm used: supervised, semisupervised, or unsupervised;
- The different technical means: model, distance, or density.
4. Supervised Methods
4.1. Model-Based Methods
4.1.1. Structure-Based Methods
4.1.2. Threshold-Based Methods
4.2. Distance-Based Methods
4.3. Density-Based Methods
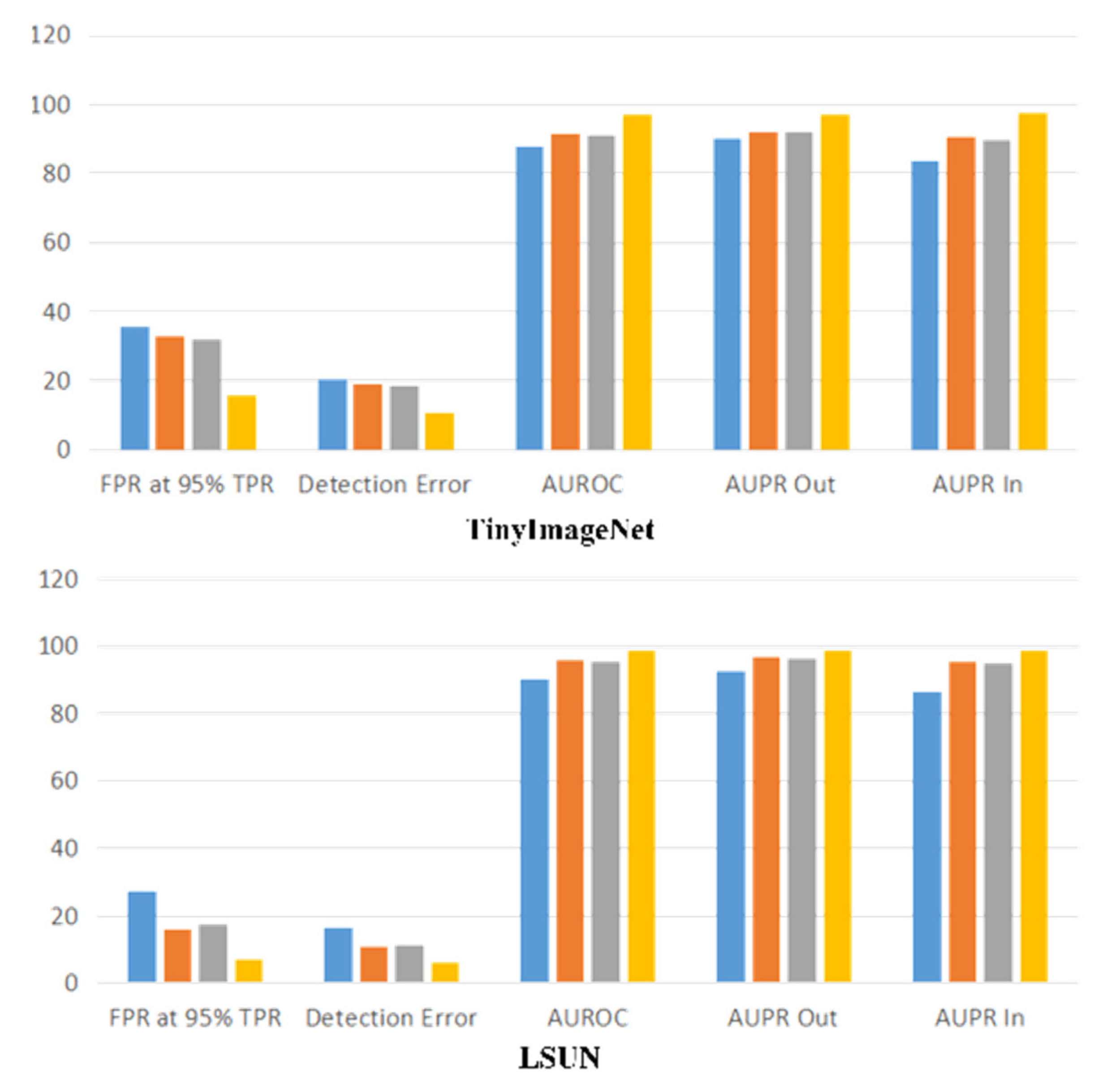
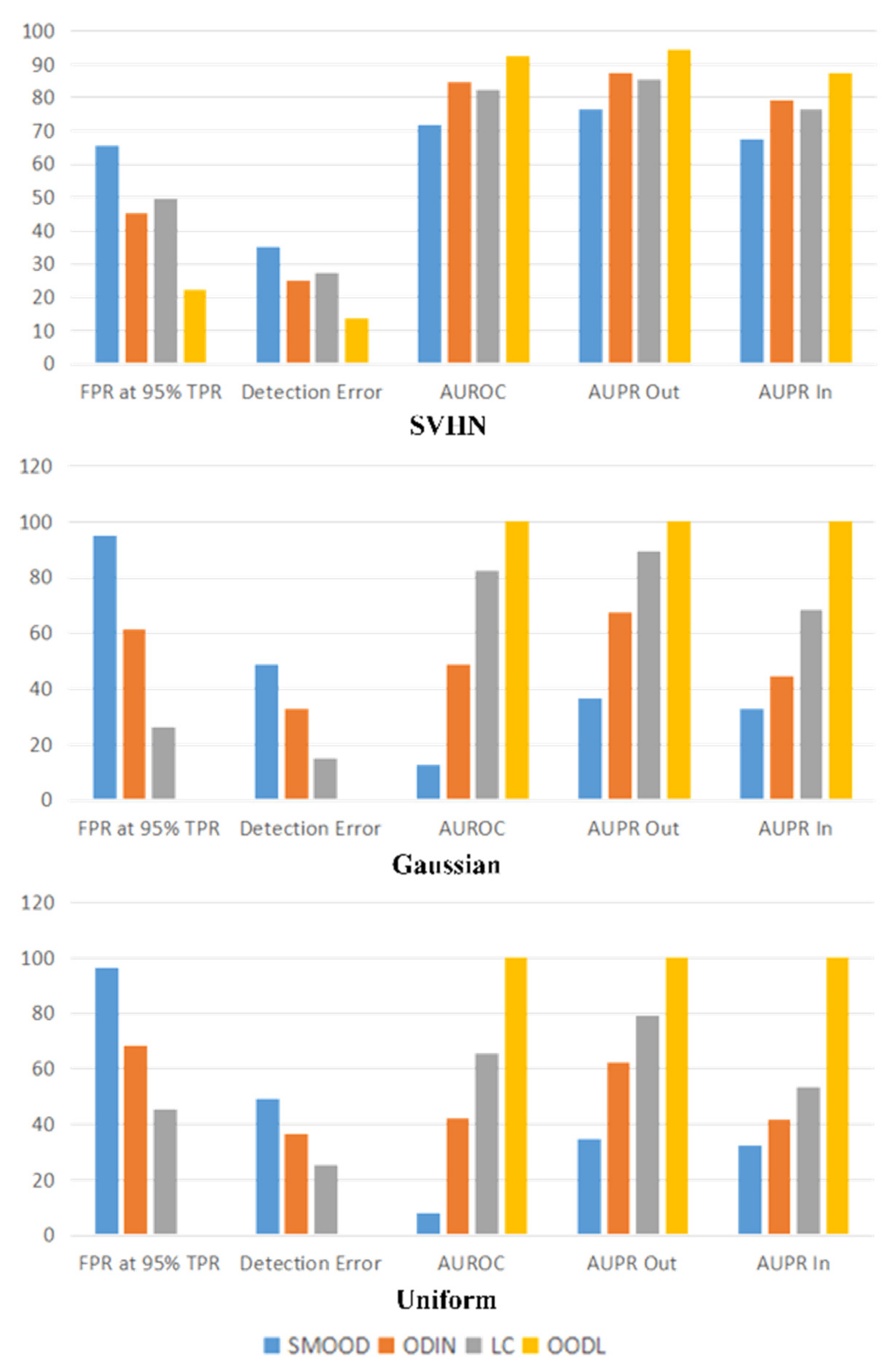
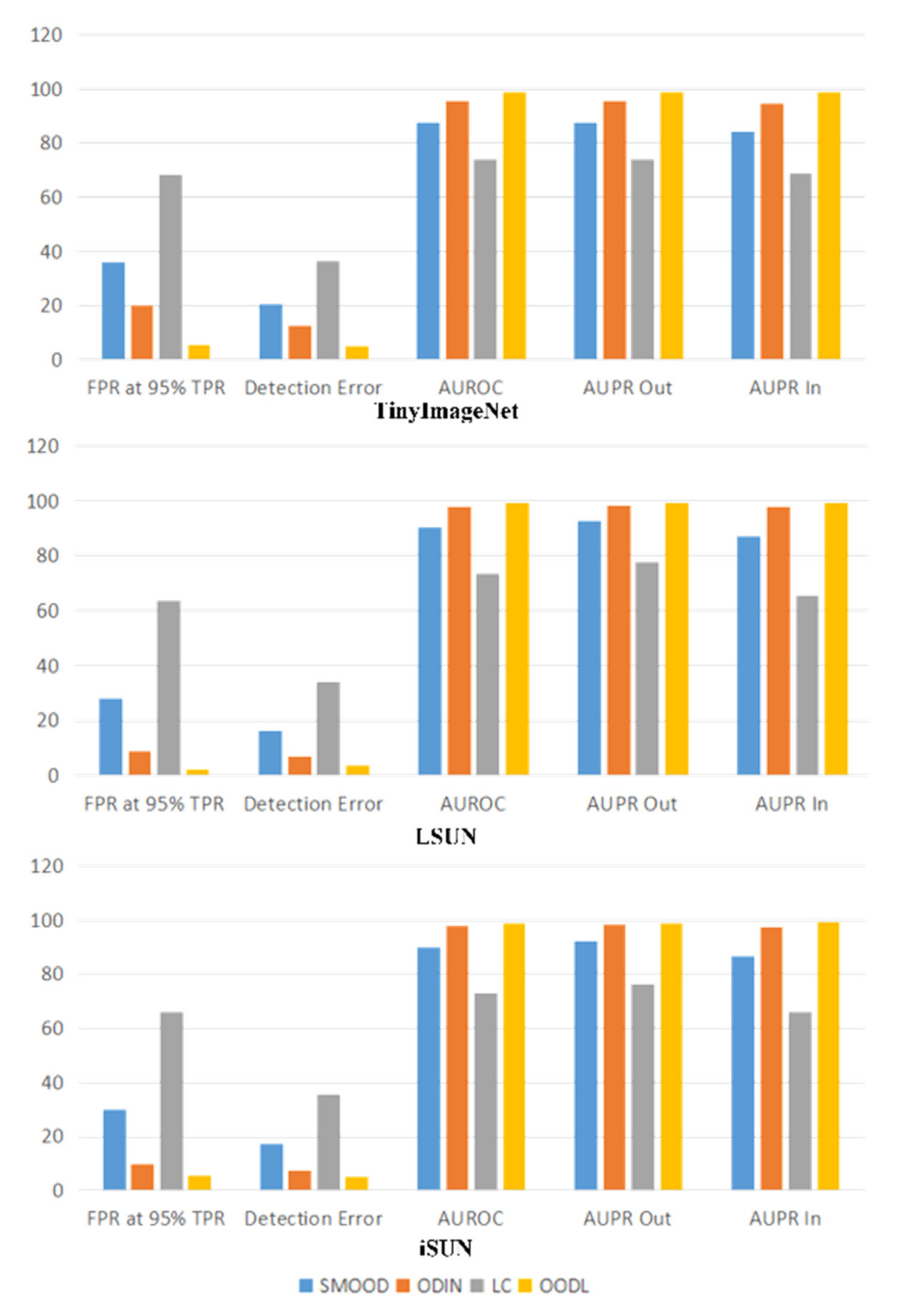
4.4. Performance Comparison
5. Semisupervised Methods
6. Generalization Detection
- (1)
- Determine the logits of the data, network, and subnetwork. Logit is a random distribution used to generate the mask. For example, if the network layer has parameters, then . The mask of this layer is obtained by sampling , and the mask transforms the complete network into a subnetwork;
- (2)
- Initialize the model and then use the ERM target to train steps;
- (3)
- Sample subnetworks from the entire network, combining cross-entropy and sparse regularization as a loss function to learn an effective subnetwork structure;
- (4)
- It is only necessary to use the weights in the obtained subnet to re-train and fix the other weights to zero.
7. Already Applied Fields
7.1. Data Migration
7.2. Fault Detection
7.3. Medical Image Processing
8. Challenges
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Geirhos, R.; Jacobsen, J.-H.; Michaelis, C.; Zemel, R.; Brendel, W.; Bethge, M.; Wichmann, F.A. Shortcut learning in deep neural networks. Nat. Mach. Intell. 2020, 2, 665–673. [Google Scholar] [CrossRef]
- Berend, D.; Xie, X.; Ma, L.; Zhou, L.; Liu, Y.; Xu, C.; Zhao, J. Cats Are Not Fish: Deep Learning Testing Calls for Out-Of-Distribution Awareness. In Proceedings of the 2020 35th IEEE/ACM International Conference on Automated Software Engineering (ASE), Melbourne, VIC, Australia, 24 December 2020; pp. 1041–1052. [Google Scholar] [CrossRef]
- Hsu, Y.C.; Shen, Y.; Jin, H.; Kira, Z. Generalized ODIN: Detecting Out-of-Distribution Image Without Learning from Out-of-Distribution Data. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 10948–10957. [Google Scholar] [CrossRef]
- Devries, T.; Taylor, G.W. Learning confidence for out-of-distribution detection in neural networks. arXiv 2018, arXiv:1802.04865. [Google Scholar] [CrossRef]
- Abdelzad, V.; Czarnecki, K.; Salay, R.; Denounden, T.; Vernekar, S.; Phan, B. Detecting Out-of-Distribution Inputs in Deep Neural Networks Using an Early-Layer Output. arXiv 2019, arXiv:1910.10307. [Google Scholar] [CrossRef]
- Denouden, T.; Salay, R.; Czarnecki, K.; Abdelzad, V.; Phan, B.; Vernekar, S. Improving reconstruction autoencoder out-of-distribution detection with mahalanobis distance. arXiv 2018, arXiv:1812.02765. [Google Scholar] [CrossRef]
- Dillon, B.M.; Favaro, L.; Plehn, T.; Sorrenson, P.; Krämer, M. A Normalized Autoencoder for LHC Triggers. arXiv 2022, arXiv:2206.14225. [Google Scholar] [CrossRef]
- Hoffman, S.C.; Wadhawan, K.; Das, P.; Sattigeri, P.; Shanmugam, K. Causal Graphs Underlying Generative Models: Path to Learning with Limited Data. arXiv 2022, arXiv:2207.07174. [Google Scholar] [CrossRef]
- Zhou, K.; Zhang, Y.; Zang, Y.; Yang, J.; Change Loy, C.; Liu, Z. On-Device Domain Generalization. arXiv 2022, arXiv:2209.07521. [Google Scholar] [CrossRef]
- Rosenfeld, E.; Ravikumar, P.; Risteski, A. Domain-Adjusted Regression or: ERM May Already Learn Features Sufficient for Out-of-Distribution Generalization. arXiv 2022, arXiv:2202.06856. [Google Scholar] [CrossRef]
- Krueger, D.; Caballero, E.; Jacobsen, J.-H.; Zhang, A.; Binas, J.; Zhang, D.; Le Priol, R.; Courville, A. Out-of-Distribution Generalization via Risk Extrapolation (REx). arXiv 2020, arXiv:2003.00688. [Google Scholar] [CrossRef]
- Arjovsky, M.; Bottou, L.; Gulrajani, I. Invariant Risk Minimization Games. In Proceedings of the International Conference on Machine Learning (ICML), Vienna, Austria, 12–18 July 2020. [Google Scholar] [CrossRef]
- Koyama, M.; Yamaguchi, S. When is invariance useful in an Out-of-Distribution Generalization problem? arXiv 2020, arXiv:2008.01883. [Google Scholar] [CrossRef]
- Adragna, R.; Creager, E.; Madras, D.; Zemel, R. Fairness and Robustness in Invariant Learning: A Case Study in Toxicity Classification. arXiv 2020, arXiv:2011.06485. [Google Scholar] [CrossRef]
- Auth, H.D.M. Identification of Outliers; Springer Dodrecht: Dodrecht, The Netherlands, 1980. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. In Chemometrics & Intelligent Laboratory Systems; Elsevier: Amsterdam, The Netherlands, 1987. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V.N. Support Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 1097–1105. [Google Scholar] [CrossRef]
- Kim, Y. Convolutional Neural Networks for Sentence Classification. arXiv 2014, arXiv:1408.5882. [Google Scholar] [CrossRef]
- Schlegl, T.; Seebck, P.; Waldstein, S.M.; Langs, G.; Schmidt-Erfurth, U. f-AnoGAN: Fast Unsupervised Anomaly Detection with Generative Adversarial Networks. Med. Image Anal. 2019, 54, 30–44. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimple, K. A Baseline for Detecting Misclassified and Out-of-Distribution Examples in Neural Networks. ICLR. April arXiv 2016, arXiv:1610.02136. [Google Scholar] [CrossRef]
- Liang, S.; Li, Y.; Srikant, R. Principled detection of out-of-distribution examples in neural networks. arXiv 2017, arXiv:1706.02690. [Google Scholar] [CrossRef]
- Shalev, G.; Adi, Y.; Keshet, J. Out-of-distribution Detection using Multiple Semantic Label Representations. Adv. Neural Inf. Process. Syst 2018, 31, 7375–7385. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, K.; Li, Y.; Liu, Z. Generalized Out-of-Distribution Detection: A Survey. arXiv 2021, arXiv:2110.11334. [Google Scholar] [CrossRef]
- Ye, H.; Xie, C.; Cai, T.; Li, R.; Li, Z.; Wang, L. Towards a Theoretical Framework of Out-of-Distribution Generalization. arXiv 2021, arXiv:2106.04496v2. [Google Scholar] [CrossRef]
- Liu, W.; Wang, X.; Owens, J.D.; Li, Y. Energy-based Out-of-distribution Detection. arXiv 2020, arXiv:2010.03759v4. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly Detection: A Survey. Acm Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Atha, D.J.; Jahanshahi, M.R. Evaluation of deep learning approaches based on convolutional neural networks for corrosion detection. Struct. Health Monit. 2018, 17, 1110–1128. [Google Scholar] [CrossRef]
- Patel, K.; Han, H.; Jain, A.K. Secure face unlock: Spoof detection on smartphones. IEEE Trans. Inf. Forensics Secur. 2016, 10, 2268–2283. [Google Scholar] [CrossRef]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. GANomaly: Semi-supervised Anomaly Detection via Adversarial Training. In Proceedings of the 14th Asian Conference on Computer Vision (ACCV), Perth, Australia, 2–6 December 2018; pp. 622–637. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, B.; Shen, C.; Liu, Y.; Lu, H.; Hua, X.S. Spatio-temporal autoencoder for video anomaly detection. In Proceedings of the 25th ACM International Conference on Multimedia, Mountain View, CA, USA, 23–27 October 2017; pp. 1933–1941. [Google Scholar] [CrossRef]
- Hodge, V.J.; Austin, J. A survey of outlier detection methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Pimentel, M.A.F.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Proces. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Idrees, H.; Shah, M.; Surette, R. Enhancing camera surveillance using computer vision: A research note. Polic. Int. J. 2018, 41, 292–307. [Google Scholar] [CrossRef]
- Kerner, H.R.; Wellington, D.F.; Wagstaff, K.L.; Bell, J.F.; Kwan, C.; Amor, H.B. Novelty detection for multispectral images with application to planetary exploration. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 8–12 October 2019; Volume 33, pp. 9484–9491. [Google Scholar] [CrossRef]
- Al-Behadili, H.; Grumpe, A.; Wohler, C. Incremental learning and novelty detection of gestures in a multi-class system. In Proceedings of the AIMS, Kota Kinabalu, Malaysia, 2–4 December 2015. [Google Scholar] [CrossRef]
- Liu, H.; Shah, S.; Jiang, W. On-line outlier detection and data cleaning. Comput. Chem. Eng. 2004, 28, 1635–1647. [Google Scholar] [CrossRef]
- Basu, S.; Meckesheimer, M. Automatic outlier detection for time series: An application to sensor data. Knowl. Inf. Syst 2007, 11, 137–154. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-mnist: A novel image dataset for benchmarking machine learning algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar] [CrossRef]
- Garitano, I.; Uribeetxeberria, R.; Zurutuza, U. A review of SCADA anomaly detection systems. In Proceedings of the 6th Springer International Conference on Soft Computing Models in Industrial and Environmental Applications, Berlin/Heidelberg, Germany, April 2011; pp. 357–366. [Google Scholar] [CrossRef]
- Pang, G.; Shen, C.; Cao, L.; Hengel, A.V.D. Deep learning for anomaly detection: A review. Acm Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Vernekar, S.; Gaurav, A.; Abdelzad, V.; Denouden, T.; Salay, R.; Czarnecki, K. Out-of-distribution Detection in Classifiers via Generation. arXiv 2019, arXiv:1910.04241. [Google Scholar] [CrossRef]
- Guénais, T.; Vamvourellis, D.; Yacoby, Y.; Doshi-Velez, F.; Pan, W. BaCOUn: Bayesian Classifers with Out-of-Distribution Uncertainty. arXiv 2020, arXiv:2007.06096. [Google Scholar] [CrossRef]
- Sedlmeier, A.; Muller, R.; Illium, S.; Linnhoff-Popien, C. Policy Entropy for Out-of-Distribution Classification. In Proceedings of the 29th International Conference on Artificial Neural Networks (ICANN), Bratislava, Slovakia, 15–18 September 2020; pp. 420–431. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, Y.; Qiao, Y.; Xiang, T. MixStyle Neural Networks for Domain Generalization and Adaptation. arXiv 2021, arXiv:2107.02053. [Google Scholar] [CrossRef]
- Dong, X.; Guo, J.; Li, A.; Ting, W.-T.; Liu, C.; Kung, H.T. Neural Mean Discrepancy for Efficient Out-of-Distribution Detection. arXiv 2021, arXiv:2104.11408v4. [Google Scholar]
- Moller, F.; Botache, D.; Huseljic, D.; Heidecker, F.; Bieshaar, M.; Sick, B. Out-of-distribution Detection and Generation using Soft Brownian Offset Sampling and Autoencoders. In Proceedings of the CVPRW, Electr Network, Virtual, 19–25 June 2021; pp. 46–55. [Google Scholar] [CrossRef]
- Lee, K.; Lee, H.; Lee, K.; Shin, J. Training Confidence-calibrated Classifiers for Detecting Out-of-Distribution Samples. arXiv 2017, arXiv:1711.09325. [Google Scholar] [CrossRef]
- Dong, X.; Guo, J.; Ting, W.T.; Kung, H.T. Lightweight Detection of Out-of-Distribution and Adversarial Samples via Channel Mean Discrepancy. arXiv 2021, arXiv:2104.11408v1. [Google Scholar]
- Zhang, X.; Cui, P.; Xu, R.; Zhou, L.; He, Y.; Shen, Z. Deep Stable Learning for Out-Of-Distribution Generalization. In Proceedings of the CVPR, Nashville, TN, USA, 20–25 June 2021; pp. 5368–5378. [Google Scholar] [CrossRef]
- Arjovsky, M. Out of Distribution Generalization in Machine Learning. arXiv 2021, arXiv:2103.02667. [Google Scholar] [CrossRef]
- Mundt, M.; Pliushch, I.; Majumder, S.; Ramesh, V. Open Set Recognition Through Deep Neural Network Uncertainty: Does Out-of-Distribution Detection Require Generative Classifiers? In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Korea, 27–28 October 2019; pp. 753–757. [Google Scholar] [CrossRef]
- Zaman, S.; Khandaker, M.; Khan, R.T.; Tariq, F.; Wong, K.K. Thinking Out of the Blocks: Holochain for Distributed Security in IoT Healthcare. IEEE Access. 2022, 10, 37064–37081. [Google Scholar] [CrossRef]
- Kuijs, M.; Jutzeler, C.R.; Rieck, B.; Bruningk, S. Interpretability Aware Model Training to Improve Robustness against Out-of-Distribution Magnetic Resonance Images in Alzheimer’s Disease Classification. arXiv 2021, arXiv:2111.08701. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Wu, X.; Liang, Y.; Jha, S. ATOM: Robustifying Out-of-distribution Detection Using Outlier Mining. arXiv 2020, arXiv:2006.15207. [Google Scholar] [CrossRef]
- Antonello, N.; Garner, P.N. At-Distribution Based Operator for Enhancing Out of Distribution Robustness of Neural Network Classifiers. IEEE Signal Proce. Lett. 2020, 27, 1070–1074. [Google Scholar] [CrossRef]
- Henriksson, J.; Berger, C.; Borg, M.; Tornberg, L.; Sathyamoorthy, S.R.; Englund, C. Performance Analysis of Out-of-Distribution Detection on Various Trained Neural Networks. In Proceedings of the 45th Euromicro Conference on Software Engineering and Advanced Applications (SEAA)/22nd Euromicro Conference on Digital System Design (DSD), Kallithea, Greece, 28–30 August 2019; pp. 113–120. [Google Scholar] [CrossRef]
- Haroush, M.; Frostig, T.; Heller, R.; Soudry, D. Statistical Testing for Efficient Out of Distribution Detection in Deep Neural Networks. arXiv 2021, arXiv:2102.12967. [Google Scholar]
- Baranwal, A.; Fountoulakis, K.; Jagannath, A. Graph Convolution for Semi-Supervised Classification: Improved Linear Separability and Out-of-Distribution Generalization. In Proceedings of the ICML, Virtual, 18–24 July 2021. [Google Scholar] [CrossRef]
- Vyas, A.; Jammalamadaka, N.; Zhu, X.; Das, D.; Kaul, B.; Willke, T.L. Out-of-Distribution Detection Using an Ensemble of Self Supervised Leave-Out Classifiers. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 560–574. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, P.; Liu, H.; Kiciman, E. Out-of-distribution Prediction with Invariant Risk Minimization: The Limitation and An Effective Fix. arXiv 2021, arXiv:2101.07732. [Google Scholar] [CrossRef]
- Techapanurak, E.; Okatani, T. Practical Evaluation of Out-of-Distribution Detection Methods for Image Classification. arXiv 2021, arXiv:2101.02447. [Google Scholar] [CrossRef]
- Sedlmeier, A.; Gabor, T.; Phan, T.; Belzner, L.; Linnhoff-Popien, C. Uncertainty-based Out-of-Distribution Classification in Deep Reinforcement Learning. In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART), Valletta, Malta, 22–24 February 2020; pp. 522–529. [Google Scholar] [CrossRef]
- Xie, S.M.; Kumar, A.; Jones, R.; Khani, F.; Ma, T.; Liang, P. In-N-Out: Pre-Training and Self-Training using Auxiliary Information for Out-of-Distribution Robustness. arXiv 2020, arXiv:2012.04550. [Google Scholar] [CrossRef]
- Ahuja, K.; Shanmugam, K.; Dhurandhar, A. Linear Regression Games: Convergence Guarantees to Approximate Out-of-Distribution Solutions. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 13–15 April 2021; pp. 1270–1278. [Google Scholar] [CrossRef]
- Bitterwolf, J.; Meinke, A.; Hein, M. Certifiably Adversarially Robust Detection of Out-of-Distribution Data. arXiv 2020, arXiv:2007.08473. [Google Scholar] [CrossRef]
- Morningstar, W.; Ham, C.; Gallagher, A.; Lakshminarayanan, B.; Alemi, A.; Dillon, J. Density of States Estimation for Out-of-Distribution Detection. In Proceedings of the 24th International Conference on Artificial Intelligence and Statistics, Electr Network, Virtual, 13–15 April 2021; pp. 232–3240. [Google Scholar] [CrossRef]
- Shao, Z.; Yang, J.; Ren, S. Calibrating Deep Neural Network Classifiers on Out-of-Distribution Datasets. arXiv 2020, arXiv:2006.08914. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, W.; Chen, Z.; Wang, J.; Liu, Z.; Li, K.; Wei, H. Towards Out-of-Distribution Detection with Divergence Guarantee in Deep Generative Models. arXiv 2020, arXiv:2002.03328. [Google Scholar]
- Chen, C.; Yuan, J.; Lu, Y.; Liu, Z.; Su, H.; Yuan, S.; Liu, S. OoDAnalyzer: Interactive Analysis of Out-of-Distribution Samples. IEEE Trans. Vis. Comput. Graph. 2021, 27, 3335–3349. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhu, S.; Li, Z.; Xu, C. Joint Distribution across Representation Space for Out-of-Distribution Detection. arXiv 2021, arXiv:2103.12344. [Google Scholar]
- Chen, X.; Lan, X.; Sun, F.; Zheng, N. A Boundary Based Out-of-Distribution Classifier for Generalized Zero-Shot Learning. In Proceedings of the Computer Vision—ECCV 2020, Lecture Notes in Computer Science, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzlerland, 2020; pp. 572–588. [Google Scholar] [CrossRef]
- Zisselman, E.; Tamar, A. Deep Residual Flow for Out of Distribution Detection. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 13991–14000. [Google Scholar] [CrossRef]
- Zong, B.; Song, Q.; Min, M.R.; Cheng, W.; Lumezanu, C.; Cho, D.; Chen, H. Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection. In Proceedings of the ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Ren, J.; Liu, P.J.; Fertig, E.A.; Snoek, J.R.; Poplin, R.; Depristo, M.; Dillon, J.; Lakshminarayanan, B. Likelihood Ratios for Out-of-Distribution Detection. In Proceedings of the Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Boutin, V.; Zerroug, A.; Jung, M.; Serre, T. Iterative VAE as a predictive brain model for out-of-distribution generalization. arXiv 2020, arXiv:2012.00557. [Google Scholar] [CrossRef]
- Ran, X.; Xu, M.; Mei, L.; Xu, Q.; Liu, Q. Detecting Out-of-distribution Samples via Variational Auto-encoder with Reliable Uncertainty Estimation. arXiv 2020, arXiv:2007.08128. [Google Scholar] [CrossRef]
- Zhang, D.; Ahuja, K.; Xu, Y.; Wang, Y.; Courville, A. Can Subnetwork Structure be the Key to Out-of-Distribution Generalization? arXiv 2021, arXiv:2106.02890. [Google Scholar] [CrossRef]
- Pan, S.J.; Qiang, Y. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Xu, Y.; Jaakkola, T. Learning Representations that Support Robust Transfer of Predictors. arXiv 2021, arXiv:2110.09940. [Google Scholar] [CrossRef]
- Jin, B.; Tan, Y.; Chen, Y.; Sangiovanni-Vincentelli, A. Augmenting Monte Carlo Dropout Classification Models with Unsupervised Learning Tasks for Detecting and Diagnosing Out-of-Distribution Faults. arXiv 2019, arXiv:1909.04202. [Google Scholar] [CrossRef]
- Zaida, M.; Ali, S.; Ali, M.; Hussein, S.; Saadia, A.; Sultani, W. Out of distribution detection for skin and malaria images. arXiv 2021, arXiv:2111.01505. [Google Scholar] [CrossRef]
- Kalantari, L.; Principe, J.; Sieving, K.E. Uncertainty quantification for multiclass data description. arXiv 2021, arXiv:2108.12857. [Google Scholar] [CrossRef]
- Li, X.; Wang, C.; Tang, Y.; Tran, C.; Auli, M. Multilingual Speech Translation from Efficient Finetuning of Pretrained Models. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers), Virtual, 1–6 August 2021. [Google Scholar]
- Yao, M.; Gao, H.; Zhao, G.; Wang, D.; Lin, Y.; Yang, Z.; Li, G. Semantically Coherent Out-of-Distribution Detection. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV) Montreal, QC, Canada, 10–17 October 2021; pp. 8281–8289. [Google Scholar] [CrossRef]
- Oberdiek, P.; Rottmann, M.; Fink, G.A. Detection and Retrieval of Out-of-Distribution Objects in Semantic Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Electr Network, Seattle, WA, USA, 14–19 June 2020; pp. 1331–1340. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Rahiminasab, Z.; Karsai, G.; Easwaran, A.; Dubey, A. Efficient Out-of-Distribution Detection Using Latent Space of β-VAE for Cyber-Physical Systems. arXiv 2021, arXiv:2108.11800. [Google Scholar] [CrossRef]
- Feng, Y.; Easwaran, A. WiP. Abstract: Robust Out-of-distribution Motion Detection and Localization in Autonomous CPS. arXiv 2021, arXiv:2107.11736. [Google Scholar] [CrossRef]
- Dery, L.M.; Dauphin, Y.; Grangier, D. Auxiliary Task Update Decomposition: The Good, The Bad and The Neutral. arXiv 2021, arXiv:2108.11346. [Google Scholar] [CrossRef]
- Chen, J.; Asma, E.; Chan, C. Targeted Gradient Descent: A Novel Method for Convolutional Neural Networks Fine-tuning and Online-learning. arXiv 2021, arXiv:2109.14729. [Google Scholar] [CrossRef]
- Gawlikowski, J.; Saha, S.; Kruspe, A.; Zhu, X.X. Out-of-distribution detection in satellite image classification. arXiv 2021, arXiv:2104.05442. [Google Scholar] [CrossRef]
- Asami, T.; Masumura, R.; Aono, Y.; Shinoda, K. Recurrent out-of-vocabulary word detection based on distribution of features. In Comput. Speech Lang. 2019, 58, 247–259. [Google Scholar] [CrossRef]
- Bayer, J.; Münch, D.; Arens, M. Image-Based Out-of-Distribution-Detector Principles on Graph-Based Input Data in Human Action Recognition. In Pattern Recognition. ICPR International Workshops and Challenges. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2021; Volume 12661, pp. 26–40. [Google Scholar] [CrossRef]
- Kim, Y.; Cho, D.; Lee, J.H. Wafer Map Classifier using Deep Learning for Detecting Out-of-Distribution Failure Patterns. In Proceedings of the 2020 IEEE International Symposium on the Physical and Failure Analysis of Integrated Circuits (IPFA), Singapore, 20–23 July 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Mensink, T.; Verbeek, J.; Perronnin, F.; Csurka, G. Distance-Based Image Classification: Generalizing to New Classes at Near-Zero Cost. Ieee Trans. Pattern Anal. Mach. Intell. 2013, 35, 2624–2637. [Google Scholar] [CrossRef]
- Yu, C.; Zhu, X.; Lei, Z.; Li, S.Z. Out-of-Distribution Detection for Reliable Face Recognition. IEEE Signal Process. Lett. 2020, 27, 710–714. [Google Scholar] [CrossRef]
- Dendorfer, P.; Elflein, S.; Leal-Taixé, L. MG-GAN: A Multi-Generator Model Preventing Out-of-Distribution Samples in Pedestrian Trajectory Prediction. arXiv 2021, arXiv:2108.09274. [Google Scholar] [CrossRef]
- Mandal, D.; Narayan, S.; Dwivedi, S.; Gupta, V.; Ahmed, S.; Khan, F.S.; Shao, L.; Soc, I.C. Out-of-Distribution Detection for Generalized Zero-Shot Action Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 9977–9985. [Google Scholar] [CrossRef]
- Srinidhi, C.L.; Martel, A.L. Improving Self-supervised Learning with Hardness-aware Dynamic Curriculum Learning: An Application to Digital Pathology. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Virtual, 11–17 October 2021; pp. 562–571. [Google Scholar] [CrossRef]
- Baltatzis, V.; Le Folgoc, L.; Ellis, S.; Manzanera, O.E.M.; Bintsi, K.-M.; Nair, A.; Desai, S.; Glocker, B.; Schnabel, J.A. The Effect of the Loss on Generalization: Empirical Study on Synthetic Lung Nodule Data; Springer: Cham, Switzerland, 2021; pp. 56–64. [Google Scholar] [CrossRef]
- Gao, L.; Wu, S.D. Response score of deep learning for out-of-distribution sample detection of medical images. J. Biomed. Inform. 2020, 107, 103442. [Google Scholar] [CrossRef]
- Martensson, G.; Ferreira, D.; Granberg, T.; Cavallin, L.; Oppedal, K.; Padovani, A.; Rektorova, I.; Bonanni, L.; Pardini, M.; Kramberger, M.G.; et al. The reliability of a deep learning model in clinical out-of-distribution MRI data: A multicohort study. Med. Image Anal. 2020, 66, 101714. [Google Scholar] [CrossRef]
- Nandy, J.; Hs, W.; Le, M.L. Distributional Shifts In Automated Diabetic Retinopathy Screening. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 255–259. [Google Scholar] [CrossRef]
- Gonzalez, C.; Gotkowski, K.; Bucher, A.; Fischbach, R.; Kaltenborn, I.; Mukhopadhyay, A. Detecting When Pre-trained nnU-Net Models Fail Silently for Covid-19 Lung Lesion Segmentation; Springer: Cham, Switzerland, 2021; pp. 304–314. [Google Scholar] [CrossRef]
- Yuhas, M.; Feng, Y.; Xian Ng, D.J.; Rahiminasab, Z.; Easwaran, A. Embedded out-of-distribution detection on an autonomous robot platform. arXiv 2021, arXiv:2106.15965. [Google Scholar] [CrossRef]
- Farid, A.; Veer, S.; Pachisia, D.; Majumdar, A. Task-Driven Detection of Distribution Shifts with Statistical Guarantees for Robot Learning. arXiv 2021, arXiv:2106.13703. [Google Scholar] [CrossRef]
- Caron, L.S.; Hendriks, L.; Verheyen, V. Rare and different: Anomaly scores from a combination of likelihood and out-of-distribution models to detect new physics at the LHC. SciPost Phys. 2022, 12, 77. [Google Scholar] [CrossRef]
- Jonmohamadi, Y.; Ali, S.; Liu, F.; Roberts, J.; Crawford, R.; Carneiro, G.; Pandey, A.K. 3D Semantic Mapping from Arthroscopy Using Out-of-Distribution Pose and Depth and In-Distribution Segmentation Training; Springer: Cham, Switzerland, 2021; pp. 383–393. [Google Scholar] [CrossRef]
- Lee, K.; Lee, K.; Lee, H.; Shin, J. A Simple Unified Framework for Detecting Out-of-Distribution Samples and Adversarial Attacks. In Proceedings of the 32nd Conference on Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Li, X.; Lu, Y.; Desrosiers, C.; Liu, X. Out-of-Distribution Detection for Skin Lesion Images with Deep Isolation Forest; Springer: Cham, Switzerland, 2020; pp. 91–100. [Google Scholar] [CrossRef]
- Kim, H.; Tadesse, G.A.; Cintas, C.; Speakman, S.; Varshney, K. Out-of-Distribution Detection In Dermatology Using Input Perturbation and Subset Scanning. In Proceedings of the 19th IEEE International Symposium on Biomedical Imaging (IEEE ISBI), Kolkata, India, 28–31 March 2022. [Google Scholar] [CrossRef]
- Pacheco, A.G.C.; Sastry, C.S.; Trappenberg, T.; Oore, S.; Krohling, R.A. On Out-of-Distribution Detection Algorithms with Deep Neural Skin Cancer Classifiers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Electr Network, Seattle, WA, USA, 14–19 June 2020; pp. 3152–3161. [Google Scholar] [CrossRef]
- Dohi, K.; Endo, T.; Purohit, H.; Tanabe, R.; Kawaguchi, Y. Flow-Based Self-Supervised Density Estimation for Anomalous Sound Detection. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Electr Network, Toronto, ON, Canada, 6–11 June 2021; pp. 336–340. [Google Scholar] [CrossRef]
- Iqbal, T.; Cao, Y.; Kong, Q.Q.; Plumbley, M.D.; Wang, W.W. Learning with Out-Of-Distribution data For Audio Classification. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 636–640. [Google Scholar] [CrossRef]
- Williams, D.S.W.; Gadd, M.; De Martini, D.; Newman, P. Fool Me Once: Robust Selective Segmentation via Out-of-Distribution Detection with Contrastive Learning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xian, China, 30 May–5 June 2021; pp. 9536–9542. [Google Scholar] [CrossRef]
- Liu, H.; Lai, V.; Tan, C. Understanding the Effect of Out-of-distribution Examples and Interactive Explanations on Human-AI Decision Making. arXiv 2021, arXiv:2101.05303. [Google Scholar] [CrossRef]
- Cai, F.; Koutsoukos, X. Real-time Out-of-distribution Detection in Learning-Enabled Cyber- Physical Systems. In Proceedings of the 2020 ACM/IEEE 11th International Conference on Cyber-Physical Systems (ICCPS), ACM, Sydney, NSW, Australia, 21–25 April 2020; pp. 174–183. [Google Scholar] [CrossRef]
- Kim, S.; Nam, H.; Kim, J.; Jung, K.; Association for the Advancement of Artificial Intelligence. Neural Sequence-to-grid Module for Learning Symbolic Rules. In Proceedings of the 35th AAAI Conference on Artificial Intelligence, Electr Network, 2–9 February 2021; pp. 8163–8171. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, C.; Dai, B. Understanding the Role of Self-Supervised Learning in Out-of-Distribution Detection Task. arXiv 2021, arXiv:2110.13435. [Google Scholar] [CrossRef]
- Nitsch, J.; Itkina, M.; Senanayake, R.; Nieto, J.; Schmidt, M.; Siegwart, R.; Kochenderfer, M.J.; Cadena, C. Out-of-Distribution Detection for Automotive Perception. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 2938–2943. [Google Scholar] [CrossRef]





| Number | Methodology | References |
|---|---|---|
| 1 | Generate OOD data by using ID data | [48,49] |
| 2 | Lightweight Detection of Out-of-Distribution and Adversarial Samples via Channel Mean Discrepancy | [50] |
| 3 | Learn the weights of training samples to eliminate the dependence between features and false correlations | [51] |
| 4 | The strong link between discovering the causal structure of the data and finding reliable features | [52,53] |
| 5 | Holochain-based security and privacy-preserving framework | [54] |
| 6 | Enhance robustness of Out-of-Distribution | [55,56,57,58] |
| 7 | The (OOD) detection problem in DNN as a statistical hypothesis testing problem | [59] |
| 8 | The linear classifier obtained by minimizing the cross-entropy loss after the graph convolution generalizes to out-of-distribution data | [45,60,61] |
| 9 | Invariant risk minimization (IRM) solves the prediction problem | [62] |
| 10 | The differences between scenarios and data sets will change the relative performance of the methods | [63,64] |
| 11 | pre-trains a model on OOD auxiliary outputs and fine-tunes this model with the pseudolabels | [65] |
| 12 | Nash equilibria of these games are closer to the ideal OOD solutions than the standard empirical risk minimization (ERM) | [66] |
| 13 | Interval bound propagation (IBP) is used to upper bound the maximal confidence in the l∞-ball and minimize this upper bound during training time | [67] |
| 14 | The density of states estimator is proposed | [68] |
| 15 | A new post-doc confidence calibration method is proposed, called CCAC (Confidence Calibration with an Auxiliary Class), for DNN classifiers on OOD datasets | [69] |
| 16 | The author proposes an easy-to-perform method both for group and point-wise anomaly detection via estimating the total correlation of representations in DGM | [70] |
| 17 | The author proposes OOD Analyzer, a visual analysis approach for interactively identifying OOD samples and explaining them in context | [71] |
| Number | Application Field | References |
|---|---|---|
| 1 | Avian note classification | [84] |
| 2 | Natural language processing (NLP) | [85,86,87] |
| 3 | Autonomous Vehicle | [88,89] |
| 4 | Text and Image classification | [90,91,92,93] [94,95,96,97] |
| 5 | Pedestrian trajectory prediction | [98,99] |
| 6 | Digital Pathology | [100] |
| 7 | Medical imaging | [101,102,103] |
| 8 | Automated Diabetic Retinopathy Screening | [104] |
| 9 | Lung lesion segmentation | [105] |
| 10 | Autonomous robot platform | [106] |
| 11 | Drone performing vision-based obstacle avoidance | [107] |
| 12 | Particle physics collider events | [108] |
| 13 | Minimally invasive surgery (MIS) | [109] |
| 14 | Adversarial attacks (AA) | [110] |
| 15 | Automated skin disease classification | [111,112,113] |
| 16 | Machine sound monitoring system | [114,115] |
| 17 | Scene segmentation | [116] |
| 18 | AI assistance | [117,118] |
| 19 | Logical reasoning over symbols | [119] |
| 20 | Self-supervised learning (SSL) | [120] |
| 21 | Automotive perception | [121] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, P.; Wang, J. Out-of-Distribution (OOD) Detection Based on Deep Learning: A Review. Electronics 2022, 11, 3500. https://doi.org/10.3390/electronics11213500
Cui P, Wang J. Out-of-Distribution (OOD) Detection Based on Deep Learning: A Review. Electronics. 2022; 11(21):3500. https://doi.org/10.3390/electronics11213500
Chicago/Turabian StyleCui, Peng, and Jinjia Wang. 2022. "Out-of-Distribution (OOD) Detection Based on Deep Learning: A Review" Electronics 11, no. 21: 3500. https://doi.org/10.3390/electronics11213500
APA StyleCui, P., & Wang, J. (2022). Out-of-Distribution (OOD) Detection Based on Deep Learning: A Review. Electronics, 11(21), 3500. https://doi.org/10.3390/electronics11213500





