Teaching–Learning-Based Optimization Algorithm Applied in Electronic Engineering: A Survey
Abstract
1. Introduction
- Algebraic methods: such as force summation and symmetric polynomial theory, among others.
- Numerical methods: such as Newton–Raphson, gradient optimization, and homotopy algorithm, among others.
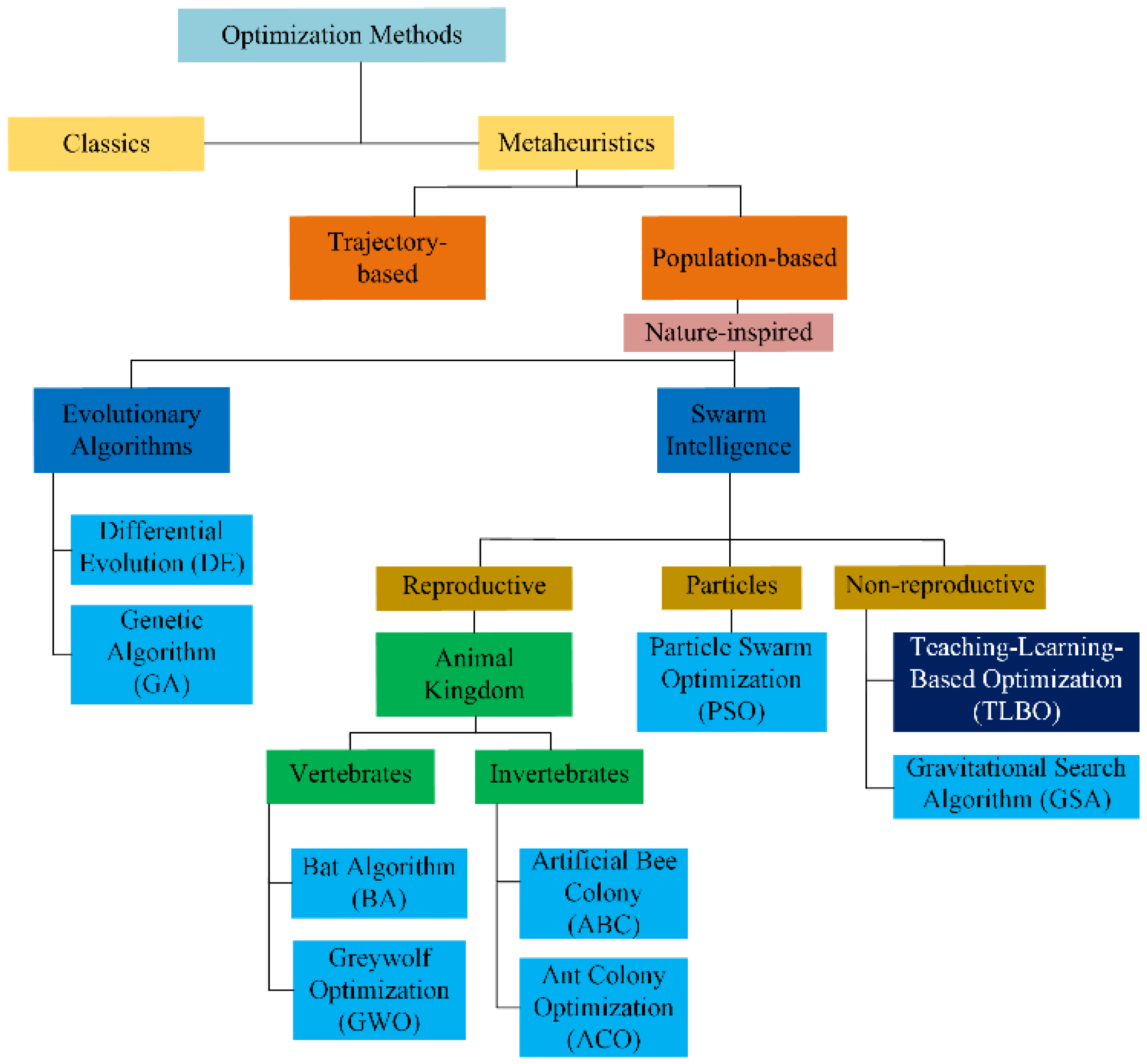
- Metaheuristic algorithms: such as genetic algorithm (GA), differential evolution (DE), particle swarm optimization (PSO), and teaching–learning-based optimization (TLBO) [5], among others.
- ▪
- The paper aims to provide a survey on the recent progress and application of the TLBO algorithm in the area of electronics. This is rarely found in previous works, allowing beginners to become familiar with the TLBO algorithm.
- ▪
- The article provides a taxonomy of the TLBO algorithm, which is useful for readers to understand and apply the TLBO algorithm.
- ▪
- The article describes the fields of application and the solutions obtained by the TLBO algorithm. All these are useful for understanding the algorithm and are expected to benefit both practical applications and future research.
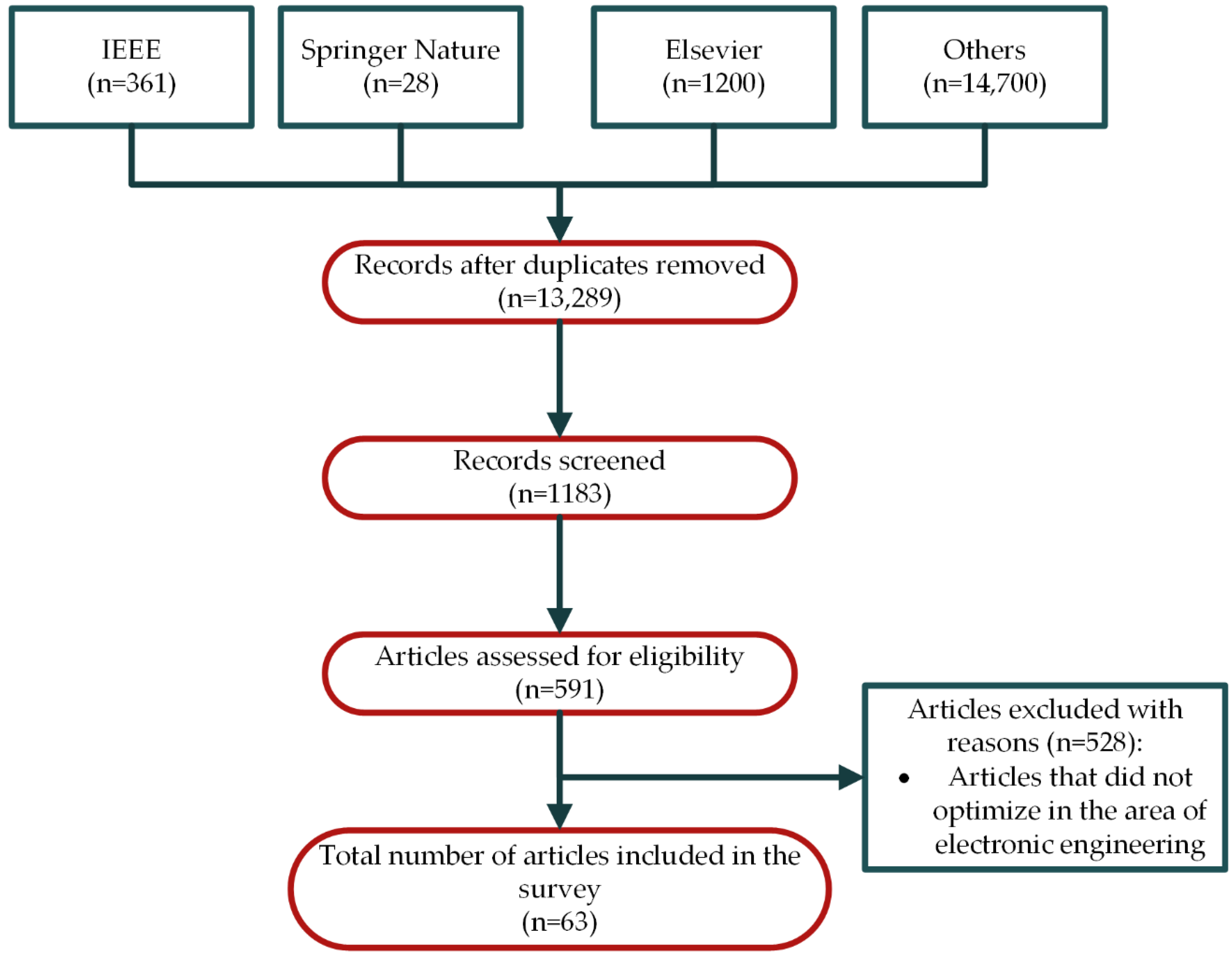
2. Methodology
3. Results
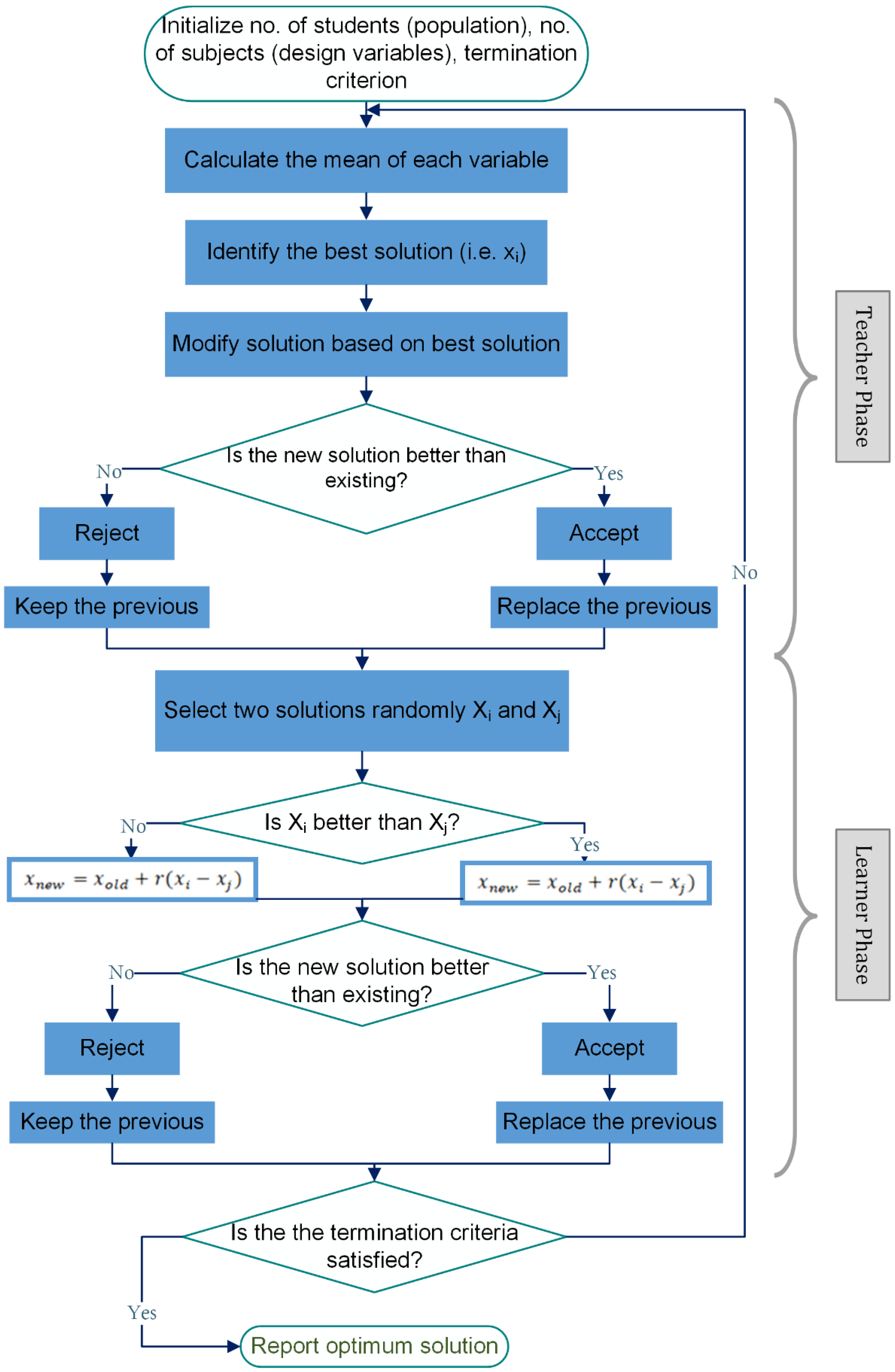
3.1. The Teaching–Learning-Based Optimization Algorithm
- Initialization: the user provides a population (number of students), the decision variables or design variables (number of topics), and the termination criteria is the maximum number of iterations.
- Teacher phase: This is the first part of the algorithm in which the students learn through the teacher. During this phase, the teacher tries to increase the average class score in the subject he/she teaches according to his/her ability. In any iteration i, assume there are “m” number of subjects (i.e., design variables), “n” number of students (i.e., population size, k = 1, 2, ..., n), and Mj,i is the average result of the students in a particular subject “j” (j = 1, 2, ..., m). The best overall result Xtotal-kbest,i considering all subjects together, obtained in the whole population of students, can be considered as the result of the best student kbest. However, as the teacher is usually considered to be a highly educated person who trains the students so that they can obtain better results, the algorithm considers that the best student identified is the teacher.
- Learner phase: This is the second part of the algorithm in which learners increase their knowledge by interacting with each other. A learner interacts randomly with other learners to improve his or her knowledge. A learner learns new things if the other learner has more knowledge than him/her. The one that provides the best result to the function is the one that will be chosen and will end the process when the termination criterion that was set in the initialization stage is met.
- a)
- Formulation of objective function or fitness function.
- b)
- Initialization of optimization parameters and the limits of the variables.
- c)
- Teacher phase: the mean for the particular variable can be calculated as the following equation:
- d)
- The best solution will be considered as a teacher for that iteration:
- e)
- Sort the grade point of each variable of each student and a new wean is calculated. The difference between two means can be calculated with next equation, TF may be considered as 1 or 2.
- f)
- Update the values by adding the difference to the old solution.
- g)
- Learner’s phase, in this second phase, the knowledge transfer takes place between the mutual interactions between the learners. The mathematical equations are as follows:
- h)
- The process will be finished only if the maximum generation is reached, otherwise repeat all the process.
3.2. The Teaching–Learning-Based Optimization Algorithm Applied in Electronic Engineering
3.3. The TLBO Algorithm in Power Electronics
- Overheating of the drivers.
- Malfunctioning electrical and electronic equipment.
- Overheating in motors.
| n-Level | Year | Load | Results (%THD) | Ref |
|---|---|---|---|---|
| CHMLI | ||||
| 5 | 2019 | R | Not specified | [44] |
| 7 | 2017 | R | Line = 11.53 Phase = 10.33 | [18] |
| 2018 | R | Case1 = 8.20 Case2 = 7.70 | [45] | |
| 2016 | R | NR = 8.86 TLBO = 6.95 | [46] | |
| 2020 | R | FLC = 7.77 TLBO = 2.13 ANFIS = 1.68 | [47] | |
| 2015 | R | Line = 9.45 Phase = 13.3 | [48] | |
| 2017 | R | Line = 5.98 Phase= 18.89 | [49] | |
| 2021 | R | TLBO = 8.2 MPA = 5.5 FPA = 6.1 PSOGWO = 8.2 | [50] | |
| 2020 | R | TLBO = 5.2 PSO = 6.22 | [51] | |
| 2017 | R | TLBO = 5.95 | [52] | |
| 27 | 2020 | R | ETLBO = 4.0 NR = 3.02 | [53] |
| DCMLI | ||||
| 5 | 2016 | RL | 41.13 | [54] |
| 7 | 2014 | RL | TLBO = 8.1 ETLBO = 9.0 NR = 14.3 | [55] |
| Modular | ||||
| 9 | 2020 | R | 7.3 | [56] |
3.4. The TLBO Algorithm in Control
3.5. The TLBO Algorithm in Electromagnetism
3.6. The TLBO Algorithm in Digital Electronics
3.7. The TLBO Algorithm in Analog Electronics
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rao, R.V. Teaching-learning-based optimization algorithm. In Teaching Learning Based Optimization Algorithm; Springer Nature: Berlin/Heidelberg, Germany, 2016; pp. 9–39. [Google Scholar]
- Malik, H. Metaheuristic and Evolutionary Computation; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Yang, X.-S. Engineering Optimization: An Introduction with Metaheuristic Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Memon, M.A.; Mekhilef, S.; Mubin, M.; Aamir, M.J.R. Selective harmonic elimination in inverters using bio-inspired intelligent algorithms for renewable energy conversion applications: A review. Renew. Sustain. Energy Rev. 2018, 82, 2235–2253. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A.; Alba, E. Parallel Metaheuristics: A New Class of Algorithms; Sons, J.W., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 47, p. 1. [Google Scholar]
- Machinery, A.F.C. Information and Guidelines for Reviewers. Available online: https://dl.acm.org/journal/trets/reviewers (accessed on 13 October 2022).
- Nayak, J.; Naik, B.; Chandrasekhar, G.; Behera, H. A survey on teaching–learning-based optimization algorithm: Short journey from 2011 to 2017. In Computational Intelligence in Data Mining; Springer: Berlin/Heidelberg, Germany, 2019; pp. 739–758. [Google Scholar]
- Kumar, M.S.; Gayathri, G. A short survey on teaching learning based optimization. In Emerging ICT for Bridging the Future-Proceedings of the 49th Annual Convention of the Computer Society of India CSI, Hyderabad, India, 11–15 December 2014; Springer: Berlin/Heidelberg, Germany, 2015; Volume 2, pp. 173–182. [Google Scholar]
- Zou, F.; Chen, D.; Xu, Q. A survey of teaching–learning-based optimization. Neurocomputing 2018, 335, 366–383. [Google Scholar] [CrossRef]
- Xue, R.; Wu, Z. A survey of application and classification on teaching-learning-based optimization algorithm. IEEE Access 2019, 8, 1062–1079. [Google Scholar] [CrossRef]
- Hamed, E.A. An improved teaching-learning-based optimization: Briefly survey. Turk. J. Comput. Math. Educ. 2021, 12, 2315–2319. [Google Scholar]
- Manda, K.; Satapathy, S.C.; Poornasatyanarayana, B. Population based meta-heuristic techniques for solving optimization problems: A selective survey. Int. J. Emerg. Technol. Adv. Eng. 2012, 2, 206–211. [Google Scholar]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Rao, R.V. Review of applications of TLBO algorithm and a tutorial for beginners to solve the unconstrained and constrained optimization problems. Decis. Sci. Lett. 2016, 5, 1–30. [Google Scholar]
- Tiwari, A.; Pradhan, M. Applications of TLBO algorithm on various manufacturing processes: A Review. Mater. Today Proc. 2017, 4, 1644–1652. [Google Scholar] [CrossRef]
- Kalra, S. Review of the teaching learning based optimization algorithm. Indian J. Comput. Sci. Eng. Sci. 2017, 8, 319–323. [Google Scholar]
- Olamaei, J.; Karimi, M. Total harmonic distortion minimisation in multilevel inverters using the teaching–learning-based optimisation algorithm. Int. J. Ambient. Energy 2018, 39, 264–269. [Google Scholar] [CrossRef]
- Alizadeh, M.; Rodriguez, R.; Bauman, J.; Emadi, A. Optimal design of integrated heat pipe air-cooled system using TLBO algorithm for SiC MOSFET converters. IEEE Open J. Power Electron. 2020, 1, 103–112. [Google Scholar] [CrossRef]
- Ortega, A.C.; Sutil, F.J.S.; Hernández, J.d. Power factor compensation using teaching learning based optimization and monitoring system by cloud data logger. Sensors 2019, 19, 2172. [Google Scholar] [CrossRef] [PubMed]
- Rao, D.; Kumar, N. Comparisional Investigation of Load Dispatch Solutions with TLBO. Int. J. Electr. Comput. Eng. 2017, 7, 3246. [Google Scholar] [CrossRef][Green Version]
- Rouhani, A.; Jabbari, M.; Honarmand, S. A teaching learning based optimization for optimal design of a hybrid energy system. Int. J. Energy Power Eng. 2015, 9, 896–903. [Google Scholar]
- Mohanty, B.; Tripathy, S. A teaching learning based optimization technique for optimal location and size of DG in distribution network. Electr. Syst. Inf. Technol. 2016, 3, 33–44. [Google Scholar] [CrossRef]
- Mishra, S.; Ray, P.K.; Dash, S.K. A TLBO optimized photovoltaic fed DSTATCOM for power quality improvement. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Chao, K.-H.; Wu, M.-C. Global maximum power point tracking (MPPT) of a photovoltaic module array constructed through improved teaching-learning-based optimization. Energies 2016, 9, 986. [Google Scholar] [CrossRef]
- Jabbari, M.; Moradlou, M.; Bigdeli, M. A TLBO Algorithm for Design Optimization of DVRs in an Interline DVR (IDVR). In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Turkey, 27 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 341–346. [Google Scholar]
- Nusair, K.N.; Alomoush, M.I. Optimal reactive power dispatch using teaching learning based optimization algorithm with consideration of FACTS device STATCOM. In Proceedings of the 2017 10th Jordanian International Electrical and Electronics Engineering Conference (JIEEEC), Amman, Jordan, 16–17 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–12. [Google Scholar]
- Fathy, A.; Rezk, H. A novel methodology for simulating maximum power point trackers using mine blast optimization and teaching learning based optimization algorithms for partially shaded photovoltaic system. J. Renew. Sustain. Energy 2016, 8, 023503. [Google Scholar] [CrossRef]
- Li, S.; Gong, W.; Yan, X.; Hu, C.; Bai, D.; Wang, L.; Gao, L. Parameter extraction of photovoltaic models using an improved teaching-learning-based optimization. Energy Convers. Manag. 2019, 186, 293–305. [Google Scholar] [CrossRef]
- Sharma, G.; Kumar, A. Modified energy-efficient range-free localization using teaching–learning-based optimization for wireless sensor networks. IETE J. Res. 2018, 64, 124–138. [Google Scholar] [CrossRef]
- Babu, B.S. TLBO based Power System Optimization for AC/DC Hybrid Systems. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1916, p. 012023. [Google Scholar]
- Kasaei, M.J.; Gandomkar, M.; Nikoukar, J. Optimal operational scheduling of renewable energy sources using teaching–learning based optimization algorithm by virtual power plant. J. Energy Resour. Technol. 2017, 139, 062003. [Google Scholar] [CrossRef]
- Tade, S.V.; Ghate, V.N.; Kalage, A.A. Economic Operation of Pumped Hydro Storage Plant using Teaching Learning based Optimization (TLBO) Algorithm. In Proceedings of the 2017 International Conference on Current Trends in Computer, Electrical, Electronics and Communication (CTCEEC), Mysore, India, 8–9 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 864–869. [Google Scholar]
- Das, K.C.; Sharma, V. Noble-TLBO MPPT Technique and its Comparative Analysis with Conventional Methods Implemented on Solar Photo Voltaic System; IOP Publishing Ltd.: Bristol, UK, 2017. [Google Scholar]
- Pasupulati, B.; Kumar, R.A.; Asokan, K. An effective methodology for short-term generation scheduling of hydrothermal power system using improved TLBO algorithm. In Proceedings of the 2017 International Conference on Innovations in Electrical, Electronics, Instrumentation and Media Technology (ICEEIMT), Coimbatore, India, 3–4 February 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 229–238. [Google Scholar]
- Kumar, D.; Gupta, V.K. Optimal reconfiguration of primary power distribution system using modified Teaching learning based optimization algorithm. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), New Delhi, India, 4–6 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Verma, S.; Saha, S.; Mukherjee, V. Optimal rescheduling of real power generation for congestion management using teaching-learning-based optimization algorithm. J. Electr. Syst. Inf. Technol. 2018, 5, 889–907. [Google Scholar] [CrossRef]
- Dastanian, R.; Abiri, E.; Salehi, M.R.; Akbari, A. A new approach based on TLBO for DC-DC converter in RFID tag. J. Intell. Fuzzy Syst. 2015, 29, 1827–1833. [Google Scholar] [CrossRef]
- Ahmed, A.S.; Attia, M.A.; Hamed, N.M.; Abdelaziz, A.Y. Modern optimization algorithms for fault location estimation in power systems. Eng. Sci. Technol. Int. J. 2017, 20, 1475–1485. [Google Scholar]
- Chatterjee, S.; Naithani, A.; Mukherjee, V. Small-signal stability analysis of DFIG based wind power system using teaching learning based optimization. Int. J. Electr. Power Energy Syst. 2016, 78, 672–689. [Google Scholar] [CrossRef]
- Rezk, H.; Fathy, A. Simulation of global MPPT based on teaching–learning-based optimization technique for partially shaded PV system. Electr. Eng. 2017, 99, 847–859. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Babu, R. Teaching Learning Based Optimization algorithm for reactive power planning. Int. J. Electr. Power Energy Syst. 2016, 81, 248–253. [Google Scholar] [CrossRef]
- Collins, E.D.; Ramachandran, B. Power management in a microgrid using teaching learning based optimization algorithm. In SoutheastCon 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Haghdar, K. Optimal DC source influence on selective harmonic elimination in multilevel inverters using teaching–learning-based optimization. IEEE Trans. Ind. Electron. 2019, 67, 942–949. [Google Scholar] [CrossRef]
- Manohar, V.J.; Jyothi, P. TLBO based Selection of Optimal Switching angles in SHE Control of CMLI with Unequal DC sources. In Proceedings of the 2018 2nd International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC) I-SMAC (IoT in Social, Mobile, Analytics and Cloud) (I-SMAC), Coimbatore, India, 30–31 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 393–398. [Google Scholar]
- Manohar, V.J.; Trinad, M.; Ramana, K.V. Comparative analysis of NR and TBLO algorithms in control of cascaded MLI at low switching frequency. Procedia Comput. Sci. 2016, 85, 976–986. [Google Scholar] [CrossRef][Green Version]
- Lakshmi, T.L.; Naik, M.G.; Prasad, S.R. TLBO Algorithm for Multi-Level Inverter-Based Multi-Terminal HVDC System in Grid-Tied Photovoltaic Power Plant. J. Inst. Eng. 2020, 101, 435–442. [Google Scholar] [CrossRef]
- Olamaei, J.; Karimi, M.; Khalilnasab, S.; Nikpour, S. Application of Teaching-Learning-Based Optimization in Solving Selective Harmonic Elimination Problem of Multilevel Inverters. Modares J. Electr. Eng. 2014. [Google Scholar]
- Olamaei, J.; Karimi, M.; Farhoudi, T. Solving line voltage THD minimization problem in multilevel inverter’s with constant dc voltage sources using teaching-learning-based optimization. UPB Sci. Bull. Ser. C Electr. Eng. Comput. Sci. 2017, 79, 197–210. [Google Scholar]
- Riad, N.; Anis, W.; Elkassas, A.; Hassan, A.E.-W. Three-Phase Multilevel Inverter Using Selective Harmonic Elimination with Marine Predator Algorithm. Electronics 2021, 10, 374. [Google Scholar] [CrossRef]
- Bhatt, K.; Chakravorty, S. A Comparative Study on Performance of Fitness Functions for Harmonic Profile Improvement using Parameter-less AI Technique in Multilevel Inverter for Electrical Drives. Int. J. Comput. Digit. Syst. 2020, 9, 1–14. [Google Scholar] [CrossRef]
- Karimi, M.; Oskuee, M.R.J.; Ravadanegh, S.N. Optimization of Line voltage THD in Multilevel Inverter’s with Alterable DC Links using TLBO. In Proceedings of the 2nd International Conference on Electrical Engineering, ICEE, Tehran, Iran, 21 September 2017. [Google Scholar]
- Kumar, S.S.; Nagarajan, C. Harmonic Analysis of Nr & Elitist Tlbo Algorithms in Control of Solar Fed Cascaded Multilevel Level Inverter. Int. J. Educ. Learn. Syst. 2020, 5, 31–39. Available online: https://www.iaras.org/iaras/home/caijps/harmonic-analysis-of-nr-elitist-tlbo-algorithms-in-control-of-solar-fed-cascaded-multilevel-level-inverter (accessed on 13 October 2022).
- Elkholy, M.M.; Fathy, A. Optimization of a PV fed water pumping system without storage based on teaching-learning-based optimization algorithm and artificial neural network. Solar Energy 2016, 139, 199–212. [Google Scholar] [CrossRef]
- Mardaneh, M.; Golestaneh, F. Harmonic optimization of diode-clamped multilevel inverter using teaching-learning-based optimization algorithm. IETE J. Res. 2013, 59, 9–16. [Google Scholar] [CrossRef]
- Xin, Y.; Yi, J.; Zhang, K.; Chen, C.; Xiong, J. Offline selective harmonic elimination with (2N+ 1) output voltage levels in modular multilevel converter using a differential harmony search algorithm. IEEE Access 2020, 8, 121596–121610. [Google Scholar] [CrossRef]
- Mishra, A.; Singh, N.; Yadav, S. Design of optimal PID controller for varied system using teaching–learning-based optimization. In Advances in Computing and Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 153–163. [Google Scholar]
- Prabu, R.G. Effect of Plug-in electric Vehicles on Load Frequency Control. In Proceedings of the 2018 8th IEEE India International Conference on Power Electronics (IICPE), Jaipur, India, 13–15 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Sahu, B.K.; Pati, S.; Mohanty, P.K.; Panda, S. Teaching–learning based optimization algorithm based fuzzy-PID controller for automatic generation control of multi-area power system. Appl. Soft Comput. 2015, 27, 240–249. [Google Scholar] [CrossRef]
- Hosseini, S.M.H.; Rezvani, A. Modeling and simulation to optimize direct power control of DFIG in variable-speed pumped-storage power plant using teaching–learning-based optimization technique. Soft Comput. 2020, 24, 16895–16915. [Google Scholar] [CrossRef]
- Barisal, A. Comparative performance analysis of teaching learning based optimization for automatic load frequency control of multi-source power systems. Int. J. Electr. Power Energy Syst. 2015, 66, 67–77. [Google Scholar] [CrossRef]
- Gorripotu, T.S.; Samalla, H.; Rao, C.J.M.; Azar, A.T.; Pelusi, D. TLBO algorithm optimized fractional-order PID controller for AGC of interconnected power system. In Soft Computing in Data Analytics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 847–855. [Google Scholar]
- Rajinikanth, V.; Satapathy, S.C. Design of controller for automatic voltage regulator using teaching learning based optimization. Procedia Technol. 2015, 21, 295–302. [Google Scholar] [CrossRef]
- Badis, A.; Boujmil, M.H. Cascade Control Based on TLBO-FOPID for Grid-Connected PV Systems. In Proceedings of the International Conference on the Sciences of Electronics, Technologies of Information and Telecommunications, Maghreb, Tunisia, 18–20 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 156–166. [Google Scholar]
- Basit, S.A.; Abido, M. Design of STATCOM Damping Controller Using Teaching Learning Based Optimization. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Khalghani, M.R.; Khooban, M.H. A novel self-tuning control method based on regulated bi-objective emotional learning controller’s structure with TLBO algorithm to control DVR compensator. Appl. Soft Comput. 2014, 24, 912–922. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Rout, U.K.; Sahoo, D.K. Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller. Int. J. Electr. Power Energy Syst. 2016, 77, 287–301. [Google Scholar] [CrossRef]
- Sahu, R.K.; Gorripotu, T.S.; Panda, S. Automatic generation control of multi-area power systems with diverse energy sources using teaching learning based optimization algorithm. Eng. Sci. Technol. Int. J. 2016, 19, 113–134. [Google Scholar] [CrossRef]
- Elkholy, M.M. Steady state and dynamic performance of self-excited induction generator using FACTS controller and teaching learning-based optimization algorithm. In COMPEL-The International Journal for Computation Mathematics in Electrical Electronic Engineering; Emerald Publishing: Bingley, UK, 2018. [Google Scholar]
- Bouchekara, H.; Nahas, M. Optimization of electromagnetics problems using an improved teaching-learning-based-optimization technique. Appl. Comput. Electromagn. Soc. J. 2015, 30, 1341–1347. [Google Scholar]
- Radmanesh, H.; Sharifi, R. Elimination of sub-synchronous resonance via doubly-fed induction generator based on teaching-learning-based optimization (TLBO) algorithm. In Proceedings of the 2019 27th Iranian Conference on Electrical Engineering (ICEE), Yazd, Iran, 30 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 748–752. [Google Scholar]
- Kheireddine, B.; Zoubida, B.; Tarik, H.; Imed, A. Application of PSO and TLBO algorithms with neural network for optimal design of electrical machines. In COMPEL-The International Journal for Computation Mathematics in Electrical Electronic Engineering; Emerald Publishing: Bingley, UK, 2018. [Google Scholar]
- Singh, D.; Dhillon, J. Teaching-Learning based optimization technique for the design of LP and HP digital IIR filter. Recent Adv. Electr. Eng. Electron. Devices 2013, 14, 203–208. [Google Scholar]
- Gunen, M.A.; Besdok, E.; Civicioglu, P.; Atasever, U.H. Camera calibration by using weighted differential evolution algorithm: A comparative study with ABC, PSO, COBIDE, DE, CS, GWO, TLBO, MVMO, FOA, LSHADE, ZHANG and BOUGUET. Neural Comput. Appl. 2020, 32, 17681–17701. [Google Scholar] [CrossRef]
- Chilamkurthi, D.P.; Tirupatipati, G.C.; Sulochanarani, J.; Pamula, V.K. Design of optimal digital FIR filters using TLBO and Jaya algorithms. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 0538–0541. [Google Scholar]
- Karampatea, A.; Boursianis, A.D.; Goudos, S.K.; Siakavara, K. Triple-band Inverted-F Antenna Using QR-OBL TLBO Algorithm for RF Energy Harvesting Applications. In Proceedings of the 2020 9th International Conference on Modern Circuits and Systems Technologies (MOCAST), Bremen, Germany, 7–9 September 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar]
- Cui, Z.; Li, C.; Dai, W.; Zhang, L.; Wu, Y. A Hierarchical Teaching-Learning-Based Optimization Algorithm for Optimal Design of Hybrid Active Power Filter. IEEE Access 2020, 8, 143530–143544. [Google Scholar] [CrossRef]
- Jamal, H.; Albatran, S.; Smadi, I.A. Optimal design of output LC filter and cooling for three-phase voltage-source inverters using teaching-learning-based optimization. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Perusquía, H.A.; Sánchez, J.R. Metodología Para el Análisis de Propagación y Filtrado de Armónicas en Sistemas Eléctricos. Master’s Thesis, ESIME-IPN, Mexico City, Mexico, 2010. [Google Scholar]
- Sharma, P.; Gupta, R. Tuning of PID controller for a linear BLDC motor using TLBO technique. In Proceedings of the International Conference on Computational Intelligence and Communication Networks, Bhopal, India, 16 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1224–1228. [Google Scholar]
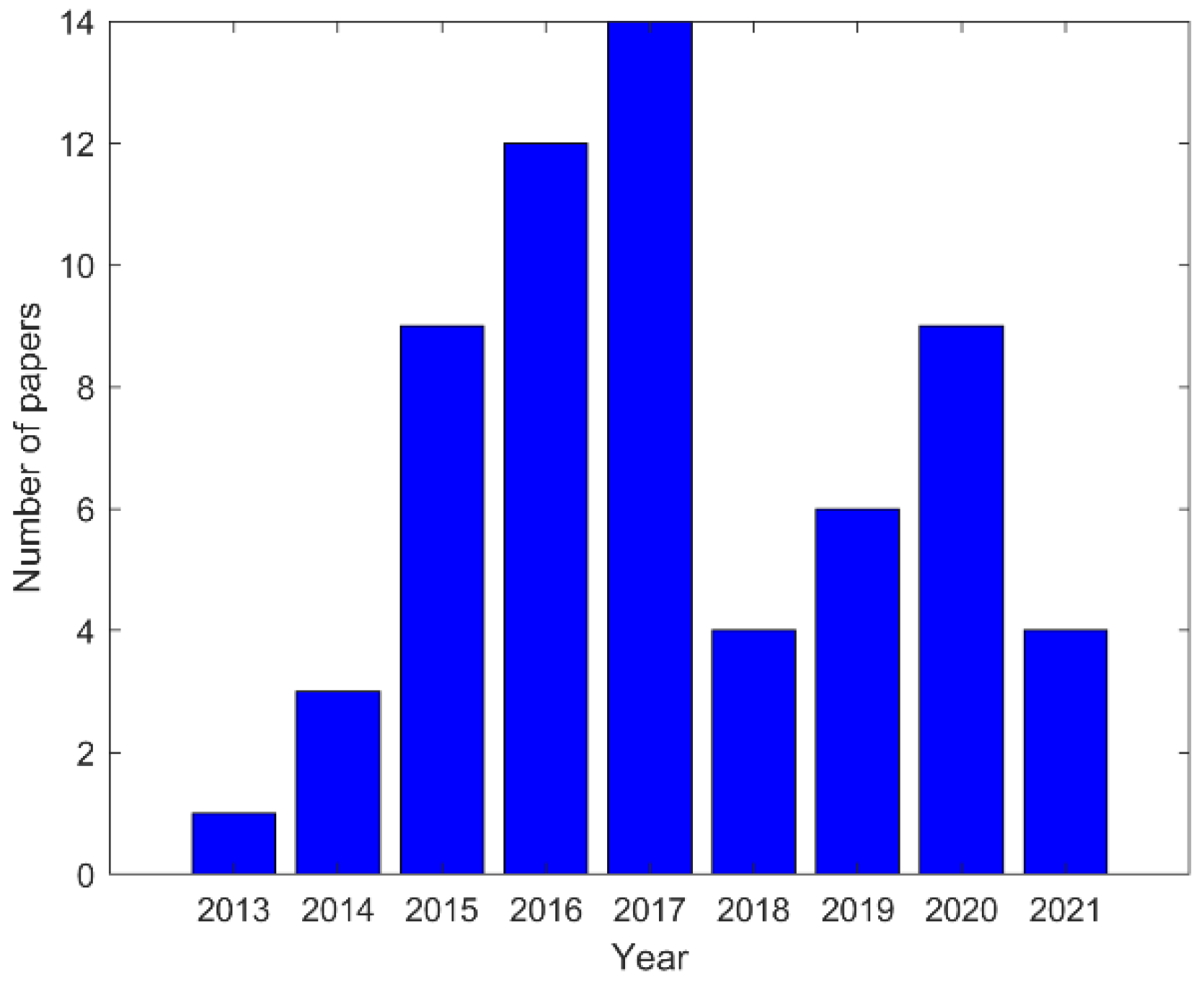
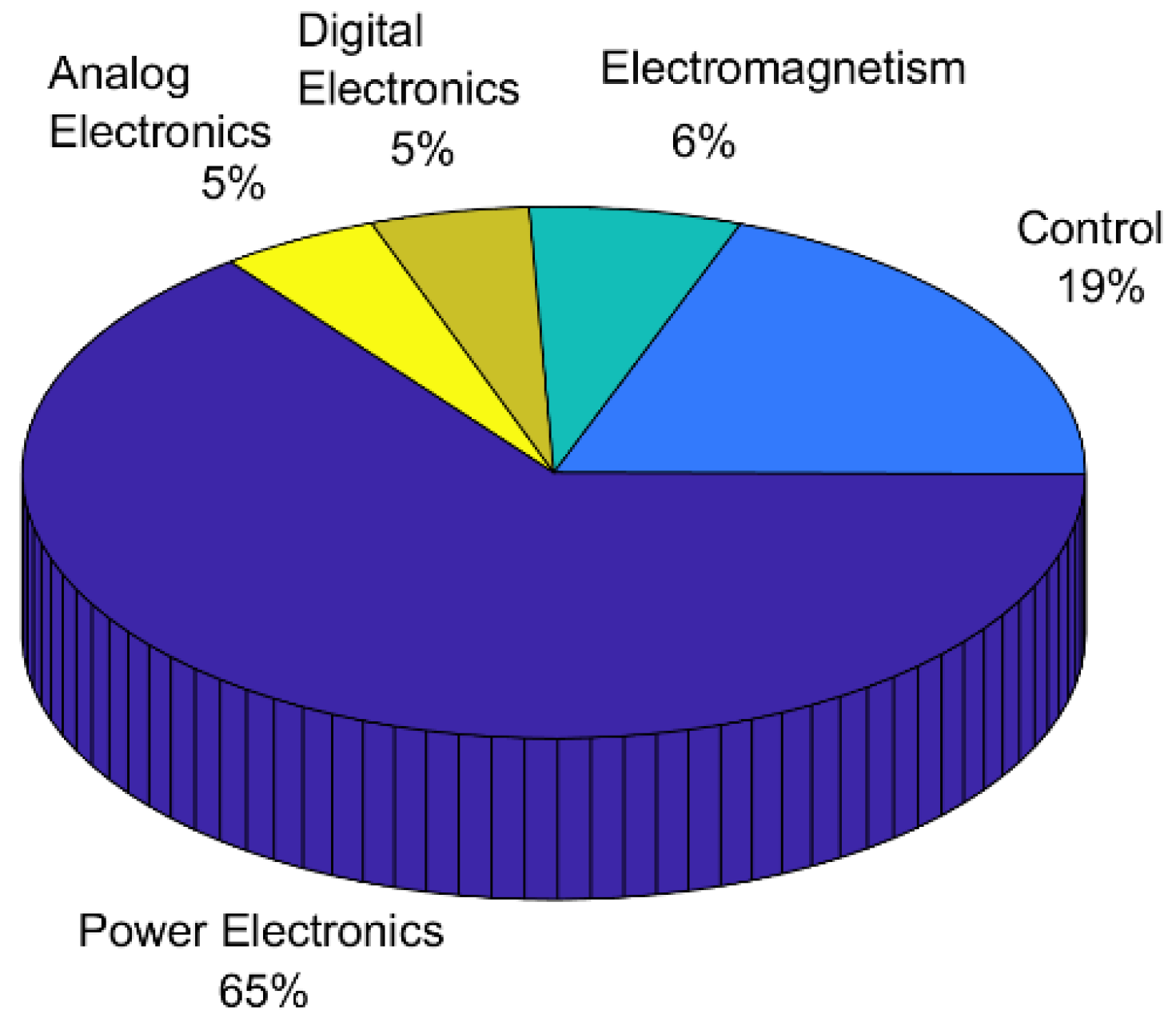

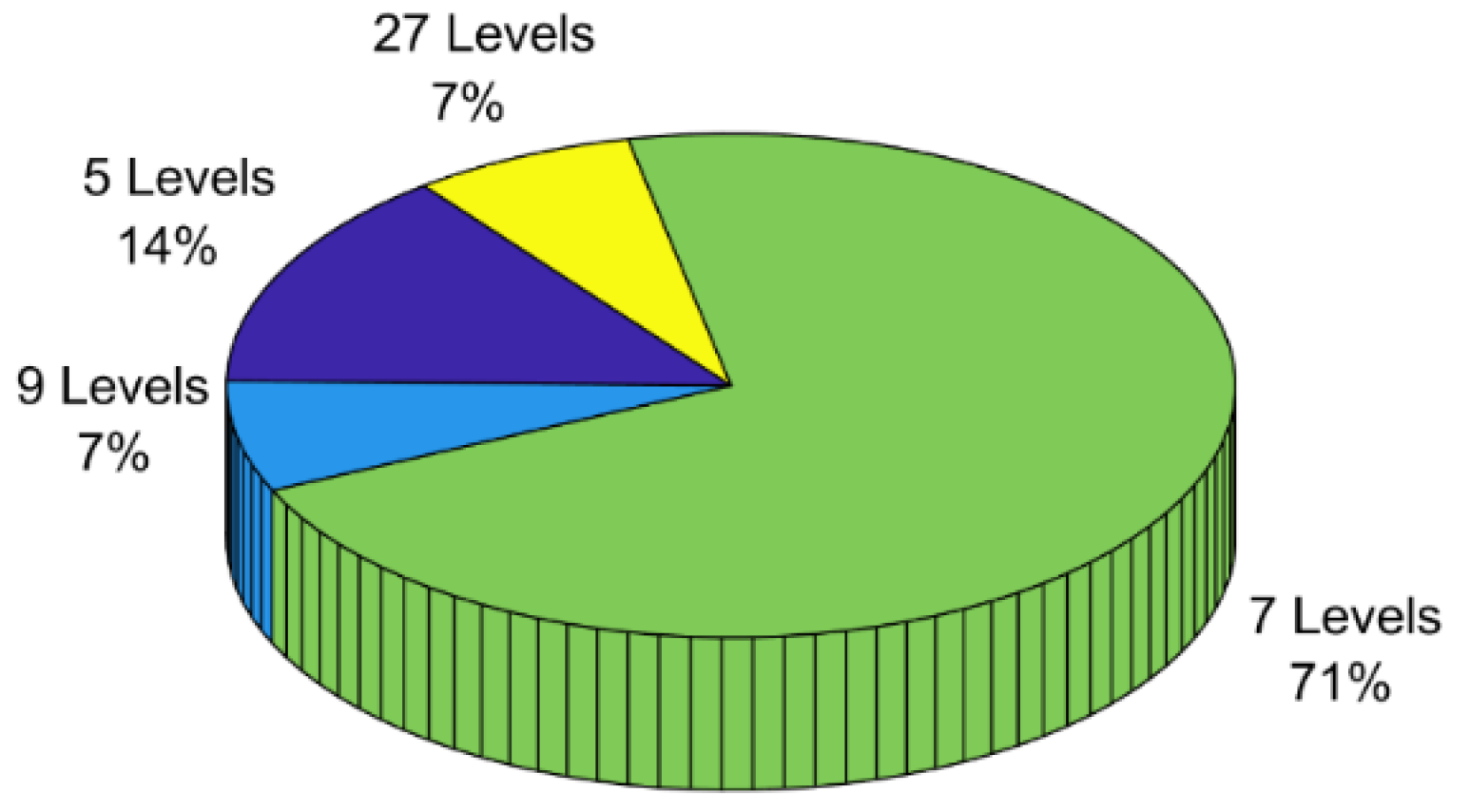
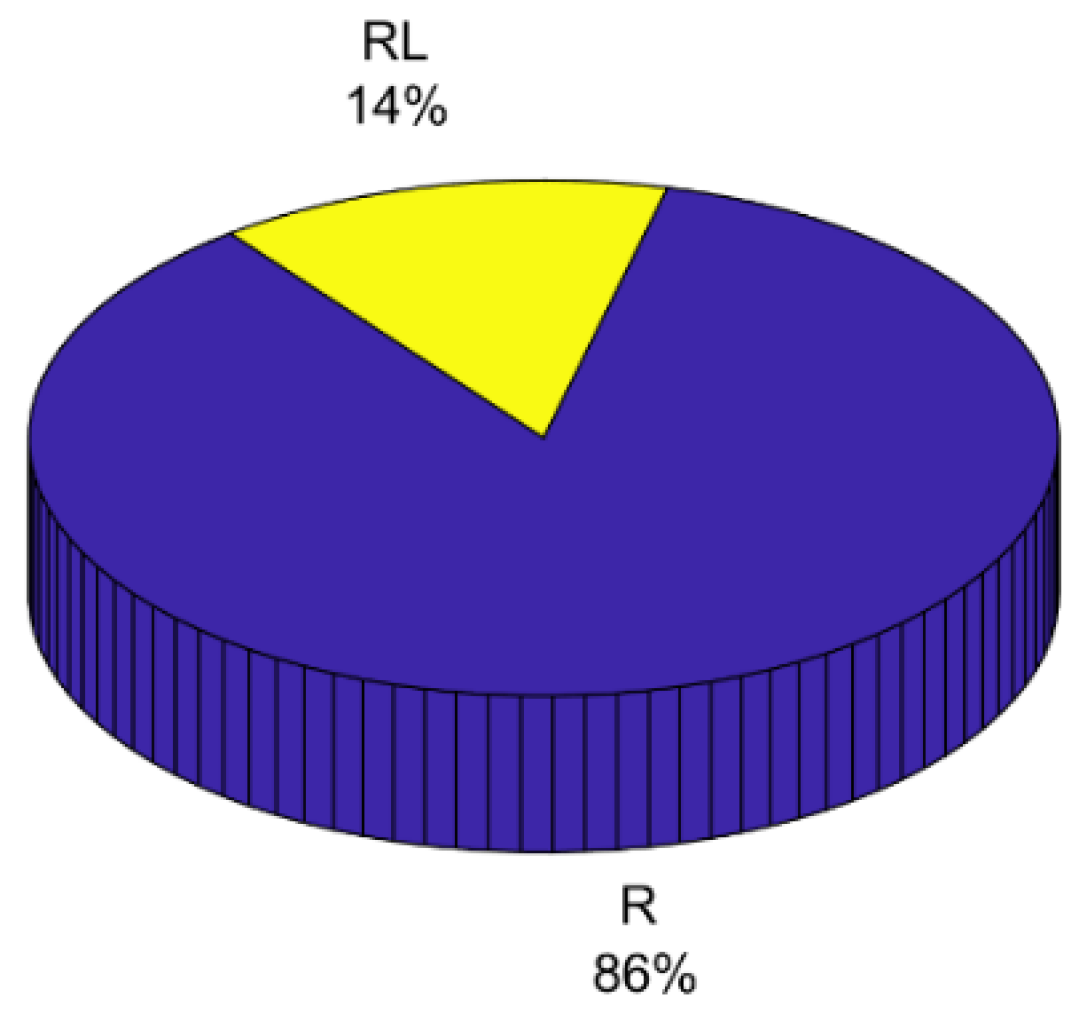
| Reference | Year | Article | Area |
|---|---|---|---|
| [8] | 2019 | A survey on teaching–learning-based optimization algorithm: short journey from 2011 to 2017 | Electrical engineering, data mining, optimization, and other applications |
| [9] | 2015 | A Short Survey on Teaching Learning Based Optimization | Optimization method for continuous non-linear large-scale problems constrained and unconstrained real parameter optimization problems shape and size optimization of truss structures with dynamic frequency constraints |
| [10] | 2018 | A survey of teaching–learning-based optimization | Manufacturing and operation research, mechanical and electrical engineering, civil engineering, electronics and control engineering, pattern recognition and image processing, other areas |
| [11] | 2019 | A Survey of Application and Classification on Teaching-Learning-Based Optimization Algorithm | General: Shop Scheduling, power systems, truss structures, multi-objective optimal, two-sided assembly line, others |
| [12] | 2015 | An improved teaching-learning-based optimization: briefly survey | Economic Load Dispatch Problems |
| [13] | 2012 | Population based meta-heuristic techniques for solvingoptimization problems: A selective survey | Location of automatic voltage regulators in distributed systems, integer programming for generation maintenance scheduling in power systems, data clustering, economic load dispatch problema with incommensurable objectives |
| [14] | 2019 | A survey on new generation metaheuristic algorithms | Data classification, quadratic assignment problems, design procedure, size and shape of structures |
| [15] | 2016 | Review of applications of TLBO algorithm and a tutorial for beginners to solve the unconstrained and constrained optimization problems | Encompasses many areas |
| [16] | 2017 | Applications of TLBO algorithm on various manufacturingprocesses: A Review | Machining processes: ultrasonic, electro chemical, electrical discharge, aser beam, electron beam, water jet, abrasive jet |
| [17] | 2017 | Review of the Teaching Learning Based Optimization Algorithm | Term hydrothermal scheduling problema, dynamic economic dispatch, flow shop and job shop scheduling, and others |
| Area | References | Applications | Years |
|---|---|---|---|
| Power Electronics | [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56] | Power generation and distribution, multilevel inverters, other | 2014–2021 |
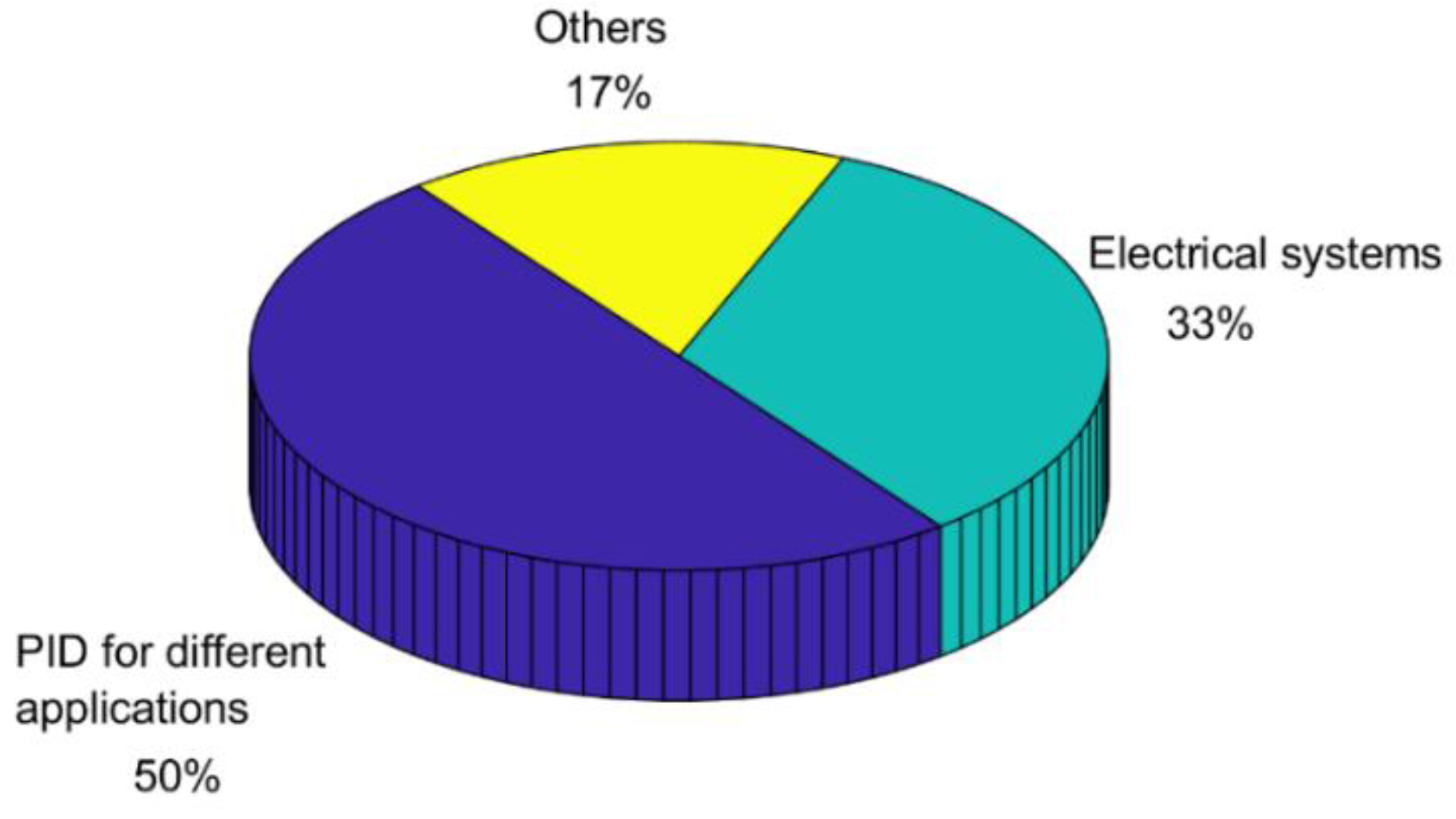
| Control | [57,58,59,60,61,62,63,64,65,66,67,68] | PID, other | 2014–2020 |
| Electromagnetism | [69,70,71,72] | Electrical machines and other | 2016–2019 |
| Digital Electronics | [73,74,75] | Filters and cameras | 2013–2020 |
| Analog Electronics | [76,77,78] | Antenna and filters | 2016–2020 |
| Area | Ref | Year | Application | Description | Author’s Conclusion |
|---|---|---|---|---|---|
| Power Electronics | [19] | 2020 | DAB converter | TLBO used to design the system with a minimum volume inverter and achieve maximum power efficiency | TLBO has better results and a faster convergence rate |
| [20] | 2019 | PFC and cloud data logger monitoring | TLBO used to optimize the capacitor bank and compensate power factor | TLBO reduced the time to find the best solution and obtained the power factor near the desired level | |
| [21] | 2017 | Load dispatch with TLBO | TLBO used to reduce energy production costs in power plants through economical load dispatching | TLBO provides lower-cost and high-quality solutions to the problem of economical freight forwarding | |
| [22] | 2015 | Design of a hybrid energy system | TLBO is used to design a hybrid system that can supply a typical household load. | TLBO was able to find the optimal design parameters and the system can provide power at an acceptable cost | |
| [23] | 2016 | Distribution network | Optimize system performance, such as real power loss, voltage profile, and voltage stability index | TLBO has shown good performance and efficiency, compared to the PSO and GA method | |
| [24] | 2016 | A DSTATCOM | Optimize the PI controller gains and filter parameters and compare the efficiency of the algorithms (TLBO and GEM) | TLBO performs better and converges faster than the GEM. The current THD is below the IEEE 519 standard. | |
| [25] | 2016 | Maximum power point global tracking (MPPT) | Improve TLBO algorithm for use in PV modules, compare results with other algorithms | I-TLBO allows to automatically adjust the teacher’s values, but it takes longer than the TLBO, but it does increase its power by 0.6 W | |
| [26] | 2019 | Dynamic voltage recloser (DVR) design | TLBO for the design to select the optimum nominal voltage values of the DVRs used in an IDVR to compensate for balanced voltage drops | Both methods lead to the optimal solution. However, the accuracy of TLBO is higher than GA and in less time | |
| [27] | 2017 | Flexible alternating current transmission systems “STATCOM” | Minimize transmission losses, determine the optimum value of control variables (real and reactive power) | TLBO has the efficiency to reduce the active power loss reasonably without violating any restrictions. It also has excellent convergence characteristics | |
| [28] | 2016 | Maximum power point trackers (MPPT) | The TLBO algorithm seeks to optimize the output power of the PV array as a function of the duty cycle of the DC-DC converter | The TLBO algorithm converges slower than the MBA, so it is less efficient | |
| [29] | 2019 | Parameter extraction from photovoltaic models | Extract the parameters of photovoltaic models using ITLBO and compare their performance with TLBO and others | ITLBO can provide more accurate and reliable parameter values, but the tables show that in some categories it has the same result as TLBO | |
| [30] | 2017 | Modified energy-efficient localization | Application of TLBO in MDV-Hop, Calculation and modification of the hop size, Optimal selection of anchor nodes, Updating the location | TLBO achieves higher localization accuracy. The results show that it has better positioning coverage and high location accuracy with lower power consumption | |
| [31] | 2021 | AC/DC hybrid power system | The evaluation function examines the suitability of the degree point as a solution to the optimization problem | It is tested on IEEE14, 30, and 57 bus systems, and it is observed in the tables that TLBO is the reduction in TFC, TRPL, and HVSI | |
| [32] | 2017 | Operational scheduling of renewable energy sources | TLBO aims to optimize the search for the lowest total cost of operation for 24 h | The results showed that TLBO is an effective method and achieves a lower cost (7–11%) than the other methods | |
| [33] | 2017 | Operation of the pumped-storage hydroelectric power plant | TLBO seeks to minimize the operating cost of the hydroelectric power plant | TLBO obtains the optimal generation considering the wind farm and the PHS unit | |
| [34] | 2017 | MPPT technology in the solar photovoltaic system | TLBO aims to obtain at any time the maximum power from a photovoltaic panel and to design an efficient DC–DC converter | The proposed TLBO-MPPT method gives more efficient results in the designed DC–DC converter, compared to conventional techniques | |
| [35] | 2017 | Hydrothermal energy system | TLBO aims to determine the optimal power generation from hydro and thermal power plants to minimize the total operating cost of thermal power plants | The results have been obtained for water discharge, reservoir storage volume, and optimal MW values of real hydroelectric and thermal power | |
| [36] | 2016 | Reconfiguration of the primary power distribution system | Aims to develop a TLBO-based bit relocation controller for simultaneous reconfiguration of primary PDSs | The best-reconfigured system has an active power loss of 0.130 MW, which is reduced by 30.10%, with respect to the base network | |
| [37] | 2018 | Real power generation for congestion | TLBO aims to minimize congestion cost while satisfying the network constraint | Total congestion cost (USD/h) = 494.66 | |
| [38] | 2015 | DC-DC converter on the RFID tag | TLBO aims to increase the voltage conversion ratio and also reduce the size of the charge transfer capacitor | The output voltage and voltage conversion ratio of the 4-stage DC–DC converter are 7.741 V and 86.01% | |
| [39] | 2017 | Electrical systems troubleshooting | TLBO aims to estimate the location of faults in electrical systems and also to obtain the error rate | TLBO achieves almost the same accuracy in a very short time, which is 7 s and can detect and locate any type of fault | |
| [40] | 2015 | Small-signal stability of a wind system with DFIG | TLBO aims to formulate state space model of DFIG, investigation of fault passage capability | Using TLBO is much better than PSO for the power system model | |
| [41] | 2016 | Simulation of global MPPT for photovoltaic systems | TLBO aims to track the global MPP (maximum power points) of PV power system under partial shading condition (PSC) | Simulations performed under varying shading patterns reveal that the performance of the TLBO-based tracker is better than PSO and fuzzy logic control (FLC) | |
| [42] | 2016 | Reactive power planning | TLBO is applied to determine the size of reactive power sources | From the results obtained, it is found that the active power loss is minimal in the TLBO method | |
| [43] | 2017 | Microgrid energy management | TLBO aims to develop an energy management infrastructure for sources and loads such that the total cost required is reduced | TLBO can achieve very accurate results in virtually any circumstance. Compared to others, it is the best solution finder. |
| Area | Ref | Year | Application | Description | Author’s Conclusion |
|---|---|---|---|---|---|
| Control | [57] | 2014 | PID controller tuning for linear BLDC motor | TLBO aims to determine the parameters of the PID controller | TLBO manages to find the controller parameters efficiently |
| [58] | 2018 | Electric vehicles | TLBO and PSO are used to optimize the integral controller gains and a comparison is made between the two-area hydrothermal unit with and without PEVs | The simulation shows that TLBO converges to the global minimum of the objective function | |
| [59] | 2015 | Fuzzy-PID controller for automatic generation control of a multi-area power system | TLBO aims to optimize the governor, turbine, load, and machine | Gives better performance, shorter settling time, less undershoot, less overshoot, and less frequency oscillation | |
| [60] | 2020 | Modelling and simulation to optimize direct power control of DFIGs in variable speed pumping power plants | TLBO aims to design and simulate a doubly fed induction generator | TLBO improves power quality by reducing stator active and reactive power ripple. THD of rotor and stator currents is lower | |
| [80] | 2020 | Design of optimal PID controller for varied systems using teaching–learning-based optimization | Design a PID controller to control the speed of a DC motor | The maximum percentage of over triggering is higher than with a typical PID controller; however, the rise and settling time is shorter | |
| [61] | 2015 | Charging frequency of multisource electrical systems | Optimize the gains of the PID controller and study its dynamic performance for the power system and compare it with the DE | It is more robust and stable to wide changes of system load, parameters, size, and location of load disturbance and various cost functions | |
| [62] | 2019 | Fractional-order PID controller optimized for the AGC (automatic generation control) of an interconnected power system | The thermal power system consists of a reheat turbine and power systems incorporated with GDBs and GRCs | The proposed FOPID controller using TLBO gives better results, compared to the PID controller | |
| [63] | 2015 | Control for an automatic voltage regulator | The objective function used is the integral absolute error multiplied by time (ITAE) and also ITSE | The controller parameters obtained are roughly similar and all show approximately similar Jmin values | |
| [64] | 2018 | Fractional order PID photovoltaic systems (FOPID) | All strategies are designed to control all cascading loops in the conversion chain in order to eliminate harmonics in the mains current | Simulations were performed to validate the functionality, robustness, and simplicity of the algorithm | |
| [65] | 2021 | Damping controller design of the STATCOM | TLBO aims to improve the dynamic stability of the power system under various operating conditions | The designed controller is robust and shows satisfactory performance to improve the dynamic stability of the power system | |
| [66] | 2014 | Auto-tuning control for a DVR compensator | TLBO aims to improve the THD and voltage drop rates of a sensitive load in the network | Simulation results show that TLBO is more efficient in its convergence speed and in the proposed optimal solution | |
| [67] | 2015 | Control of the generation of a power system using a 2DOF (2-degree freedom) PID controller | Demonstrate the advantages of TLBO over other techniques and the superiority of the 2DOF PID controller over the conventional PID | It is observed that the TLBO controller based on the 2DOF-PID controller is very effective and gives better performance, compared to others | |
| [68] | 2015 | Automatic control of the generation of multi-area electrical systems with various energy sources | Conduct a methodical simulation study to evaluate the performance of the proposed PID controller with the TLBO algorithm | The superiority of the proposed design approach has been demonstrated by comparing the results with some other techniques |
| Area | Ref | Year | Application | Description | Author’s Conclusion |
|---|---|---|---|---|---|
| Electromagnetism | [69] | 2018 | The behavior of a self-excited induction generator | TLBO aims to minimize the error between load voltage and nominal value and compare the results with other algorithms | TLBO guarantees the choice of the best solution to produce an optimal capacitor excitation to obtain the rated voltage at different loads |
| [70] | 2016 | Electromagnetic problems | The proposed technique is applied to two benchmarks related to the brushless DC wheel motor problem | The TLBO and ITLBO algorithms proved to be efficient in solving the problem with the advantage of not requiring control parameters | |
| [71] | 2019 | Sub-synchronous resonance elimination | An integral of time multiplied by the absolute value of the velocity deviation is taken as the objective function | When adequate additional transient power is supplied from DFIGs placed close to the power plants, the damping of torsional oscillations can be significant | |
| [72] | 2017 | Optimal design of electrical machines | Optimizing the equipment shop problem and switched reluctance motor (SRM) with flux barriers | In the solution of both problems, it was concluded that they are as efficient as other often-used algorithms |
| Area | Ref | Year | Application | Description | Author’s Conclusion |
|---|---|---|---|---|---|
| Digital Electronics | [73] | 2013 | LP and HP digital IIR filter design | TLBO aims to obtain the optimum values for the design of low-pass or high-pass filters | TLBO has a lower margin of error, compared to the other optimization methods |
| [74] | 2020 | Camera calibration | Optimize the calibration of a camera and find the rotation coordinates and compare it with the efficiency with other algorithms | The TLBO algorithm was one of the four slowest algorithms in obtaining the values, however, it was one of the four that found the best results | |
| [75] | 2017 | Design of optimal FIR digital filters | Optimization algorithms were considered for the optimal design perspective of the linear phase digital FIR filter for better control of filter parameters | Jaya is better than the TLBO algorithm in terms of stopband attenuation and error values that can be observed in the simulation results |
| Area | Ref | Year | Application | Description | Author’s Conclusion |
|---|---|---|---|---|---|
| Analog Electronics | [76] | 2020 | Triple-band inverted F-antenna | TLBO aims to design an inverted F antenna that operates at certain specified frequencies | The antenna works satisfactorily in the EGSM-900, GSM-1800, and LTE-2600 frequency bands |
| [77] | 2020 | Hybrid active power filter | A new clustering strategy is proposed to dynamically adjust the hierarchy of all individuals | This paper proposes a novel hierarchical TLBO (HTLBO) algorithm to accurately estimate the parameters of the hybrid active power filter | |
| [78] | 2016 | Optimal LC filter design | TLBO aims to minimize the total cost of the filter and heat sink | The measured TDD was 3.2% and the THDV was around 1%. The deviation of THDV value between calculation and measurement is mainly due to the effect of dead time |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez Díaz, K.Y.; De León Aldaco, S.E.; Aguayo Alquicira, J.; Ponce-Silva, M.; Olivares Peregrino, V.H. Teaching–Learning-Based Optimization Algorithm Applied in Electronic Engineering: A Survey. Electronics 2022, 11, 3451. https://doi.org/10.3390/electronics11213451
Gómez Díaz KY, De León Aldaco SE, Aguayo Alquicira J, Ponce-Silva M, Olivares Peregrino VH. Teaching–Learning-Based Optimization Algorithm Applied in Electronic Engineering: A Survey. Electronics. 2022; 11(21):3451. https://doi.org/10.3390/electronics11213451
Chicago/Turabian StyleGómez Díaz, Kenia Yadira, Susana Estefany De León Aldaco, Jesus Aguayo Alquicira, Mario Ponce-Silva, and Víctor Hugo Olivares Peregrino. 2022. "Teaching–Learning-Based Optimization Algorithm Applied in Electronic Engineering: A Survey" Electronics 11, no. 21: 3451. https://doi.org/10.3390/electronics11213451
APA StyleGómez Díaz, K. Y., De León Aldaco, S. E., Aguayo Alquicira, J., Ponce-Silva, M., & Olivares Peregrino, V. H. (2022). Teaching–Learning-Based Optimization Algorithm Applied in Electronic Engineering: A Survey. Electronics, 11(21), 3451. https://doi.org/10.3390/electronics11213451









