Meta Classification Model of Surface Appearance for Small Dataset Using Parallel Processing
Abstract
1. Introduction
2. Literature Review
3. Research Methodology
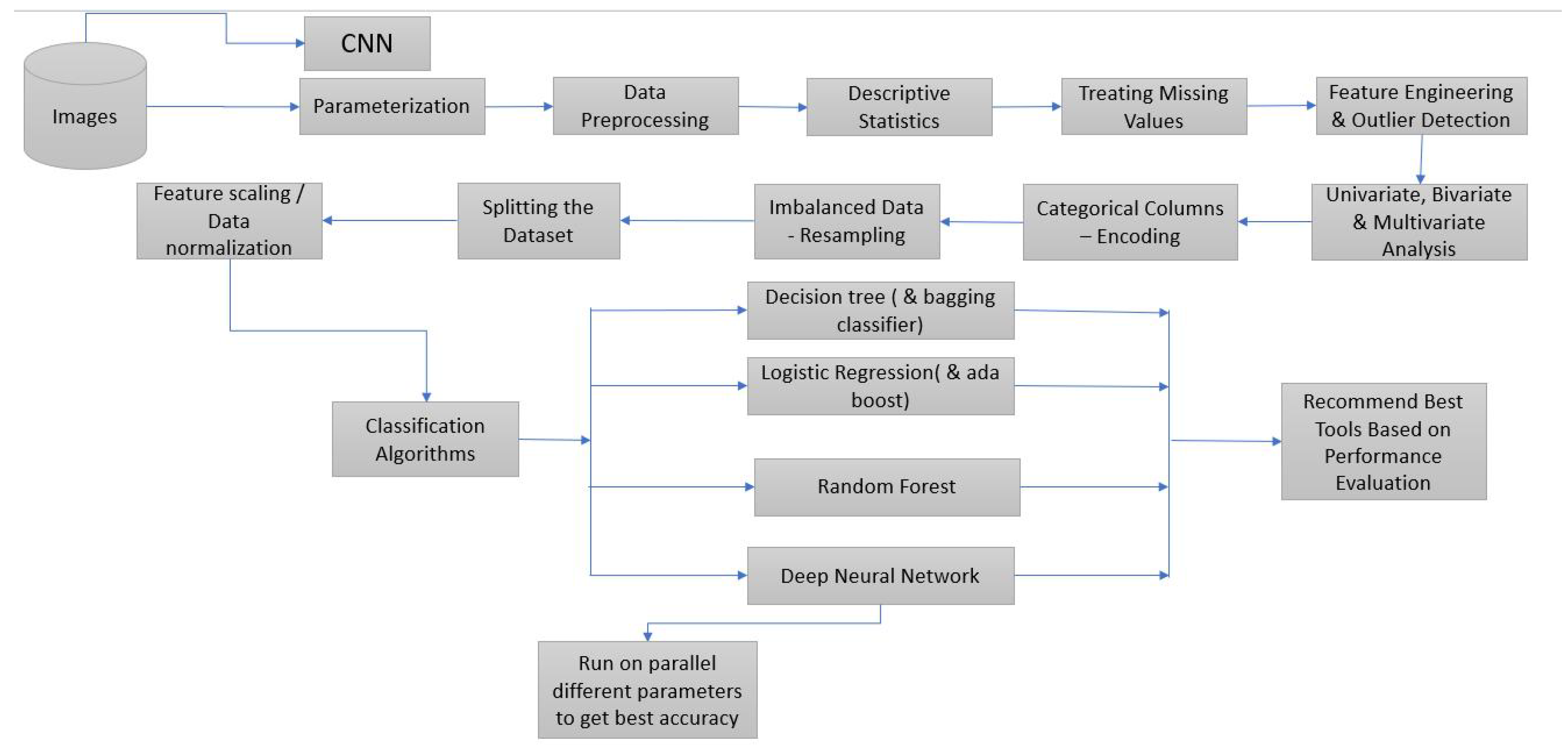
3.1. System Overview
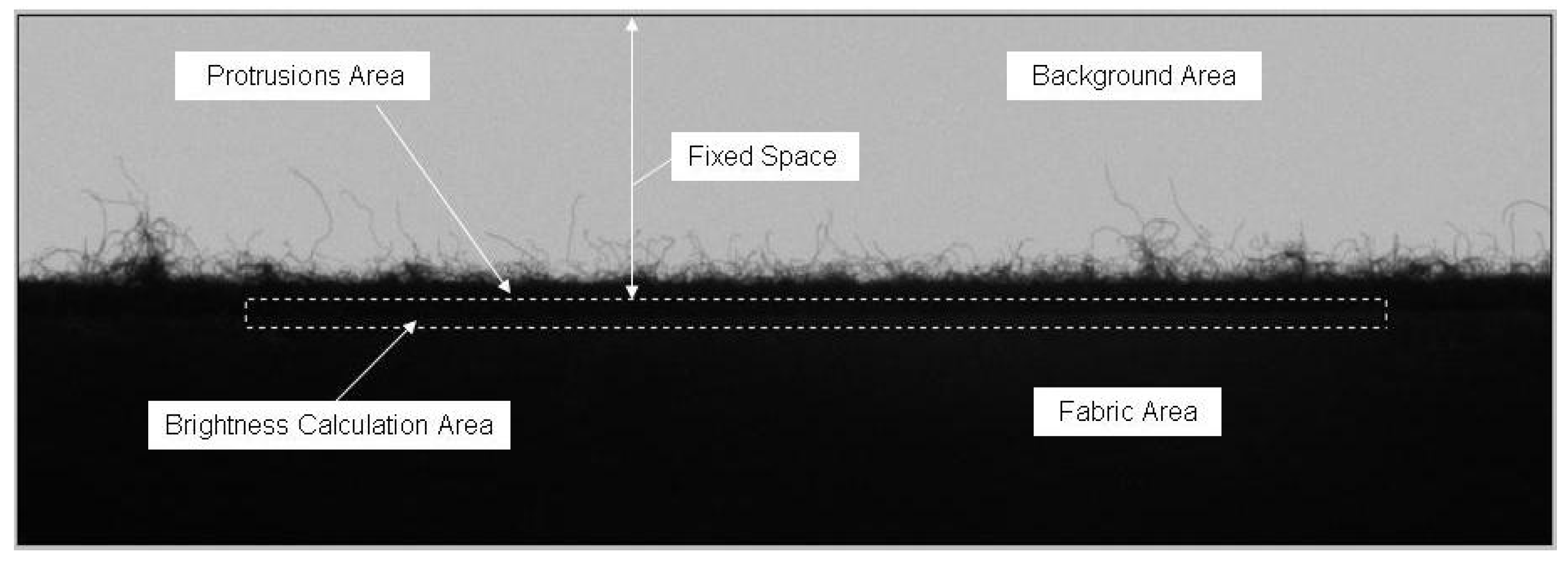
3.2. Hypothesis for Images—Low-Level Image Processing
3.3. Evaluation Criteria on Performance Measure Indices
3.4. Tool and Language
4. Dataset Preprocessing
4.1. Dataset Overview
4.2. Dataset Processing and Preparation
4.2.1. Missing Values and Outliers Detection
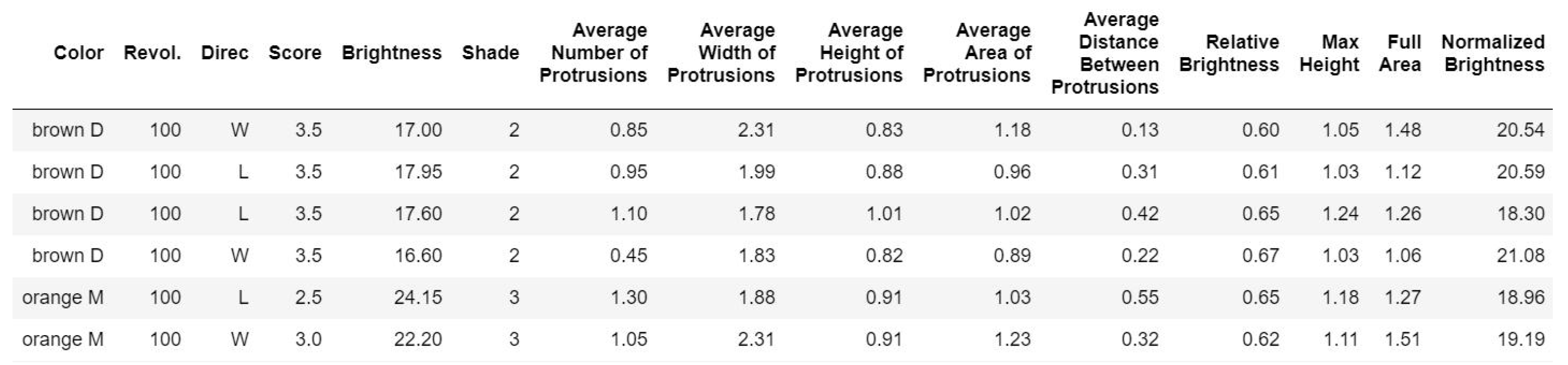
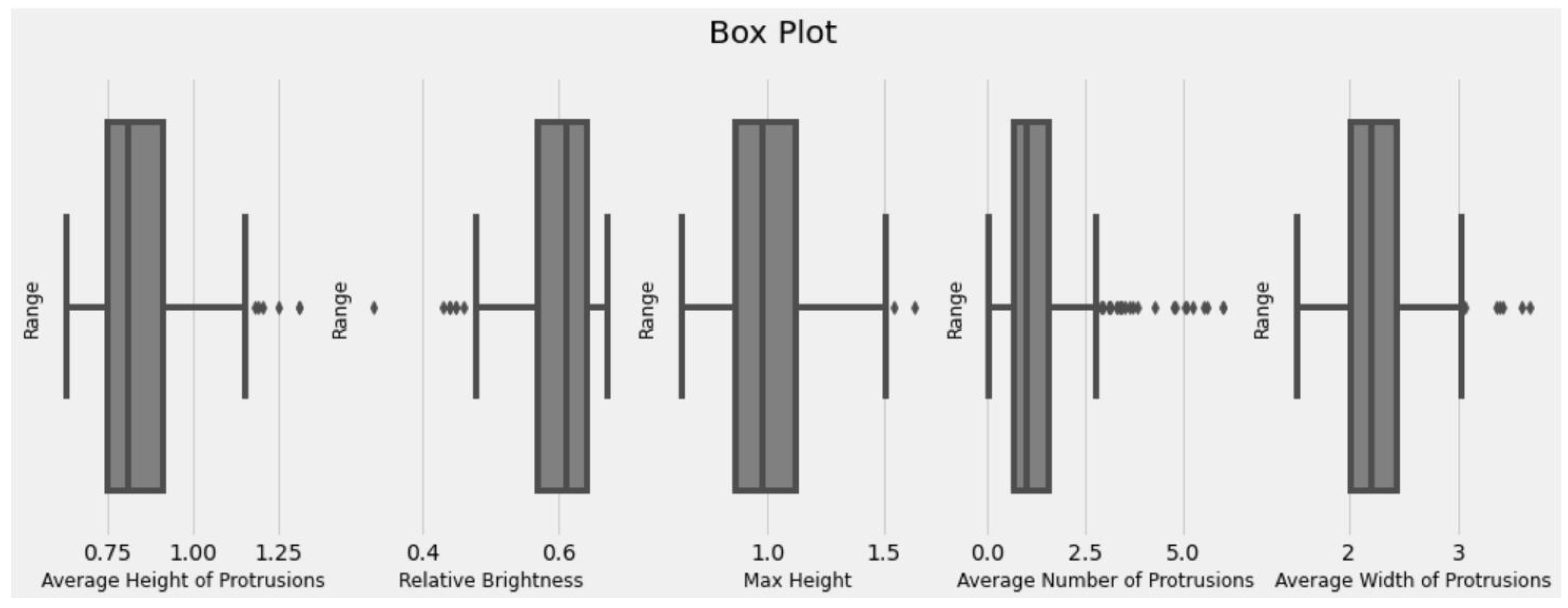
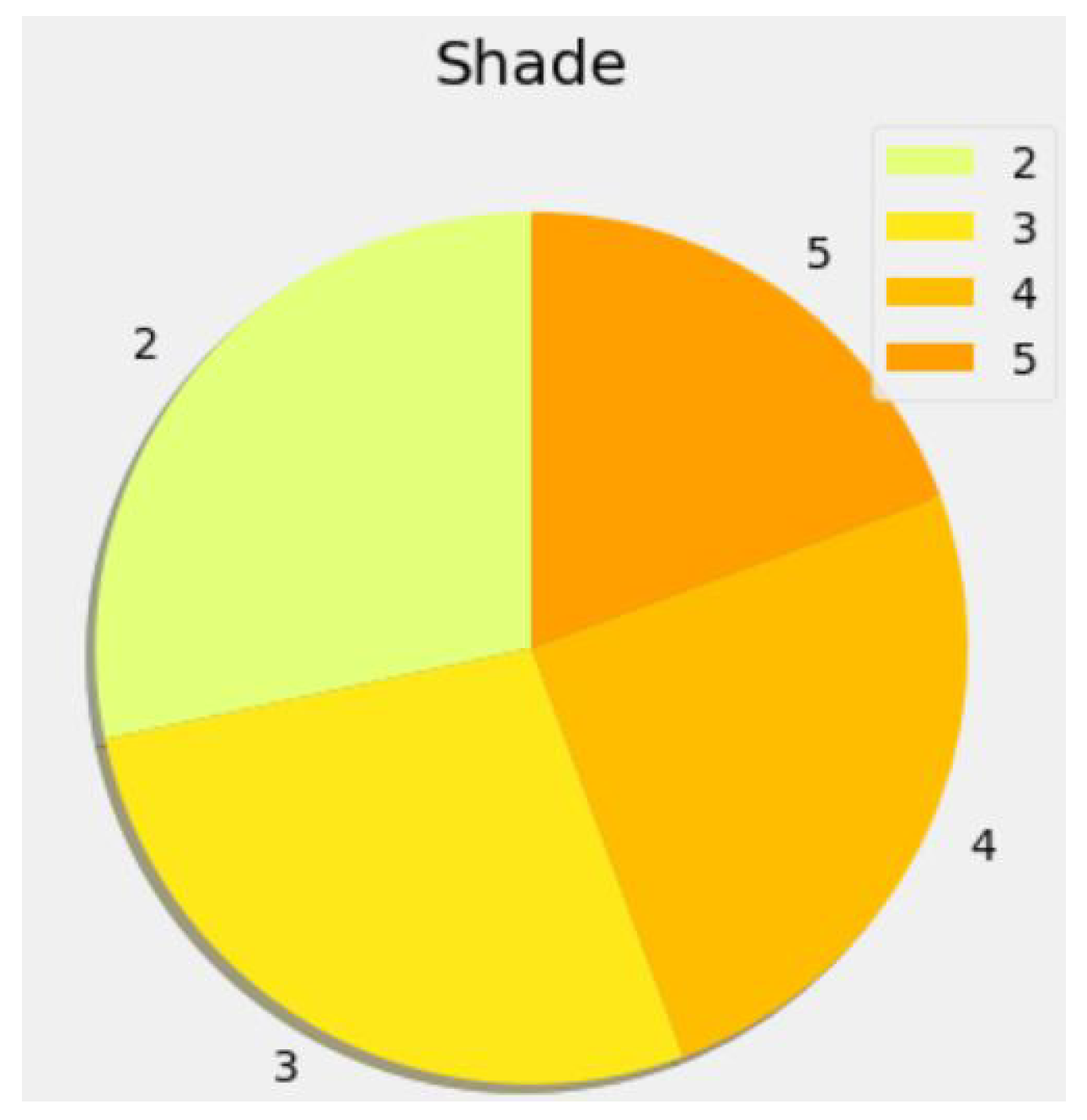
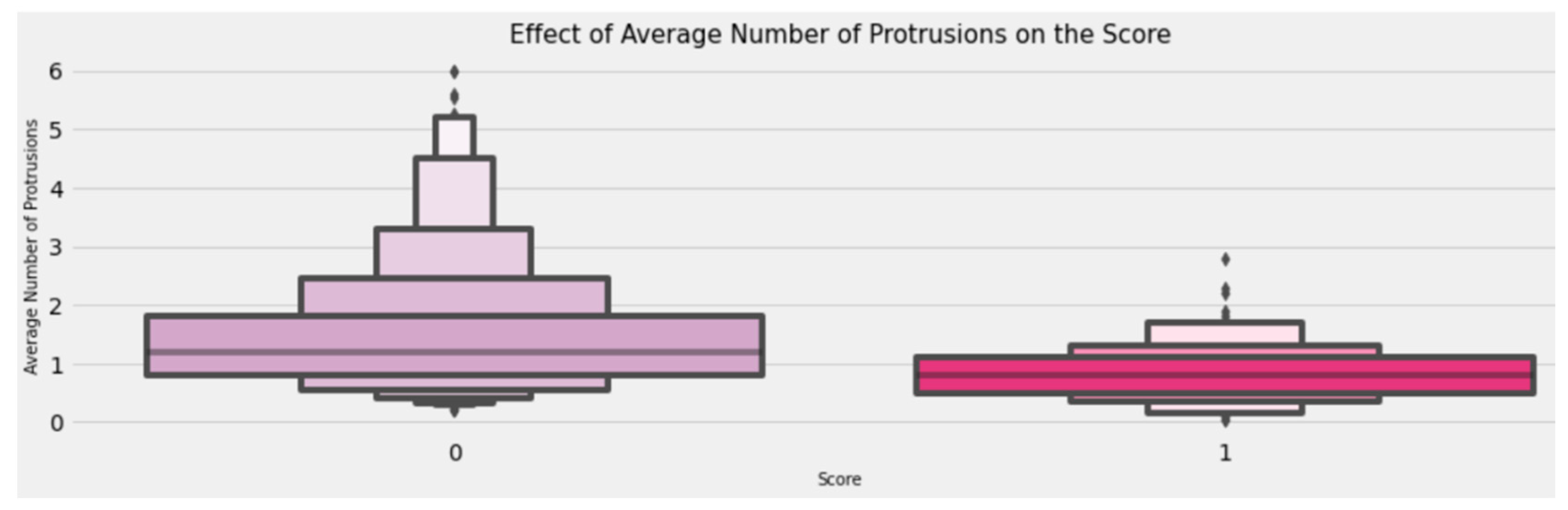
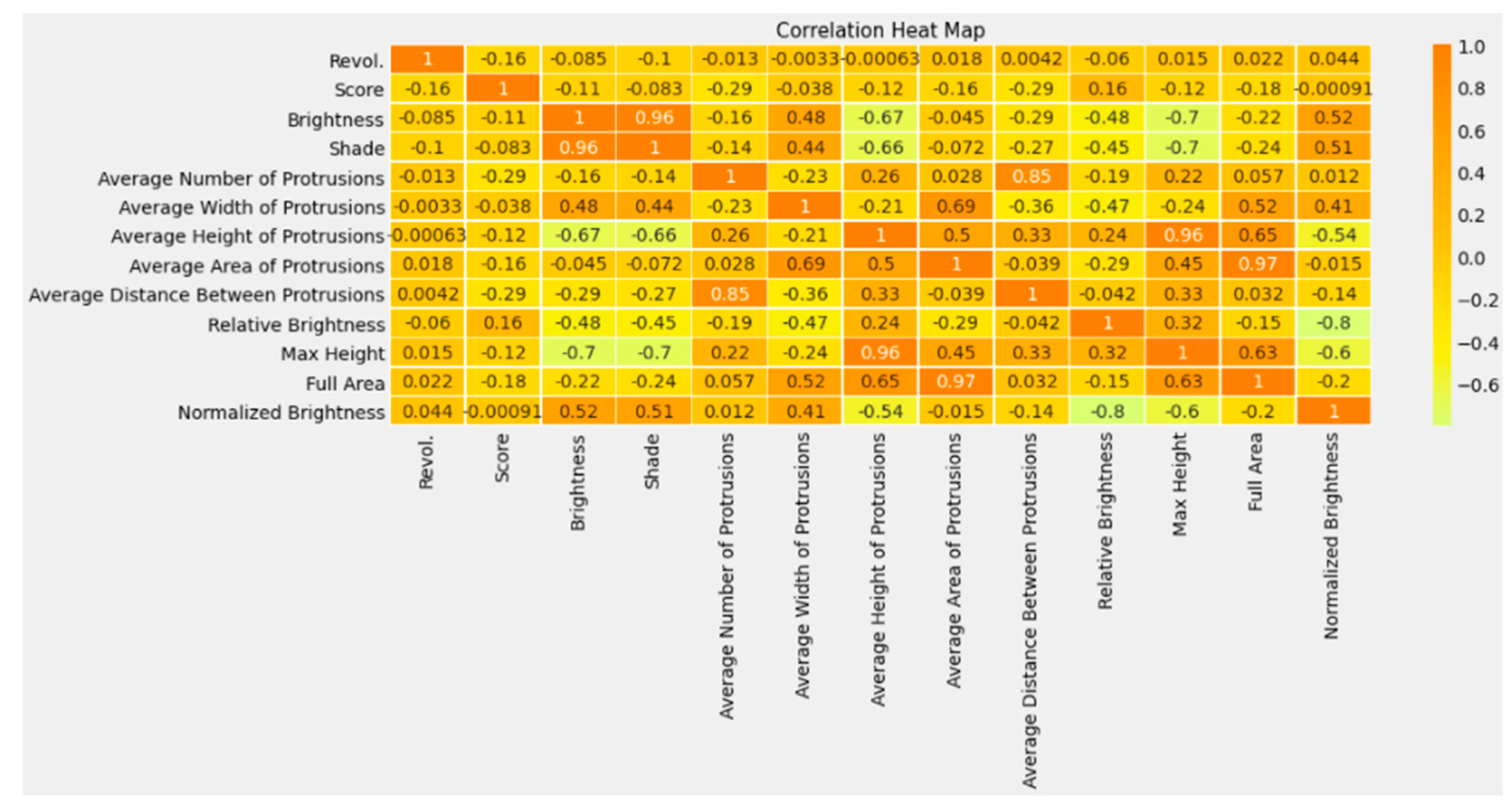
4.2.2. Univariate, Bivariate, and Multivariate Analysis
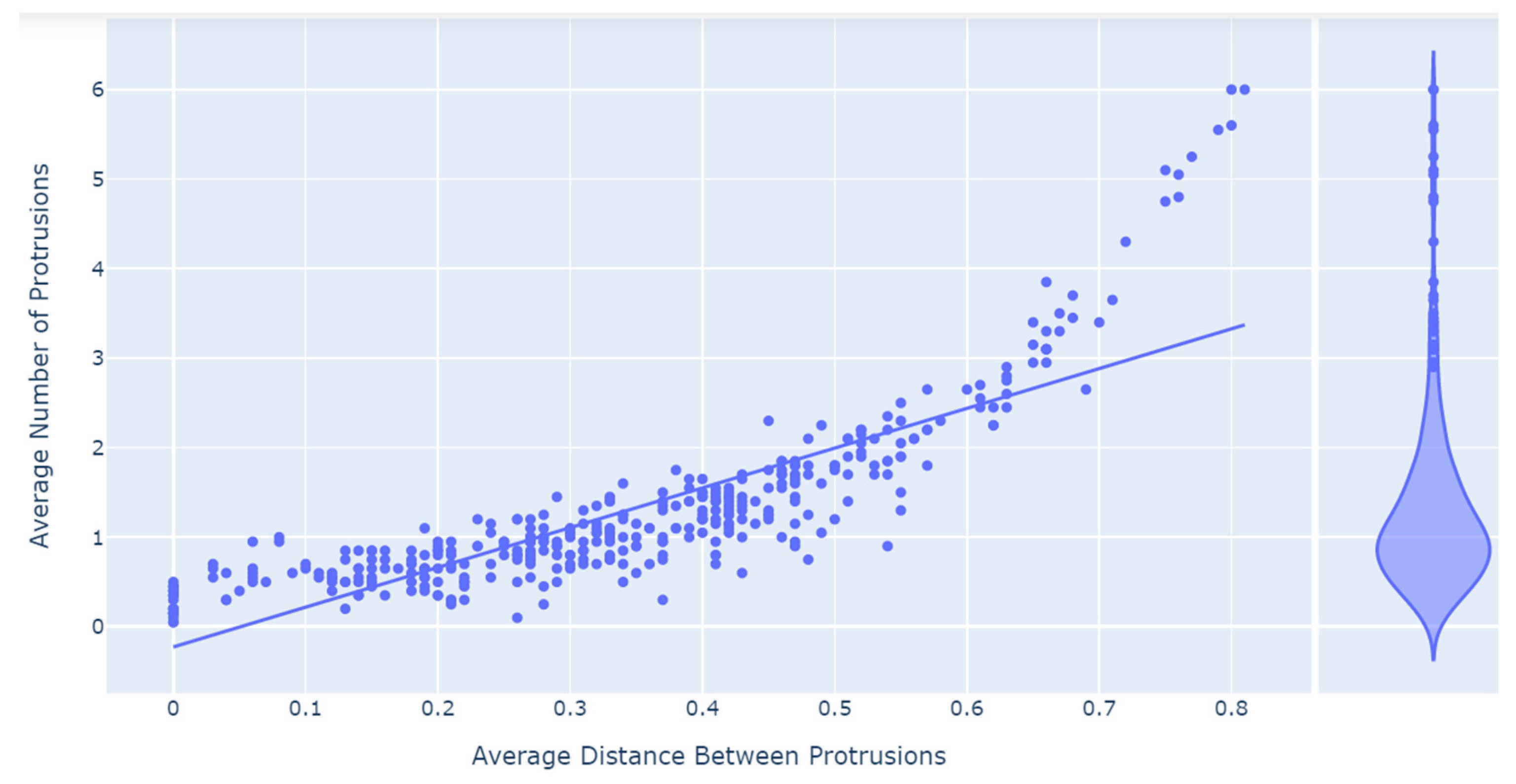
- The average distance between protrusions and the average number of protrusions are highly correlated (0.85).
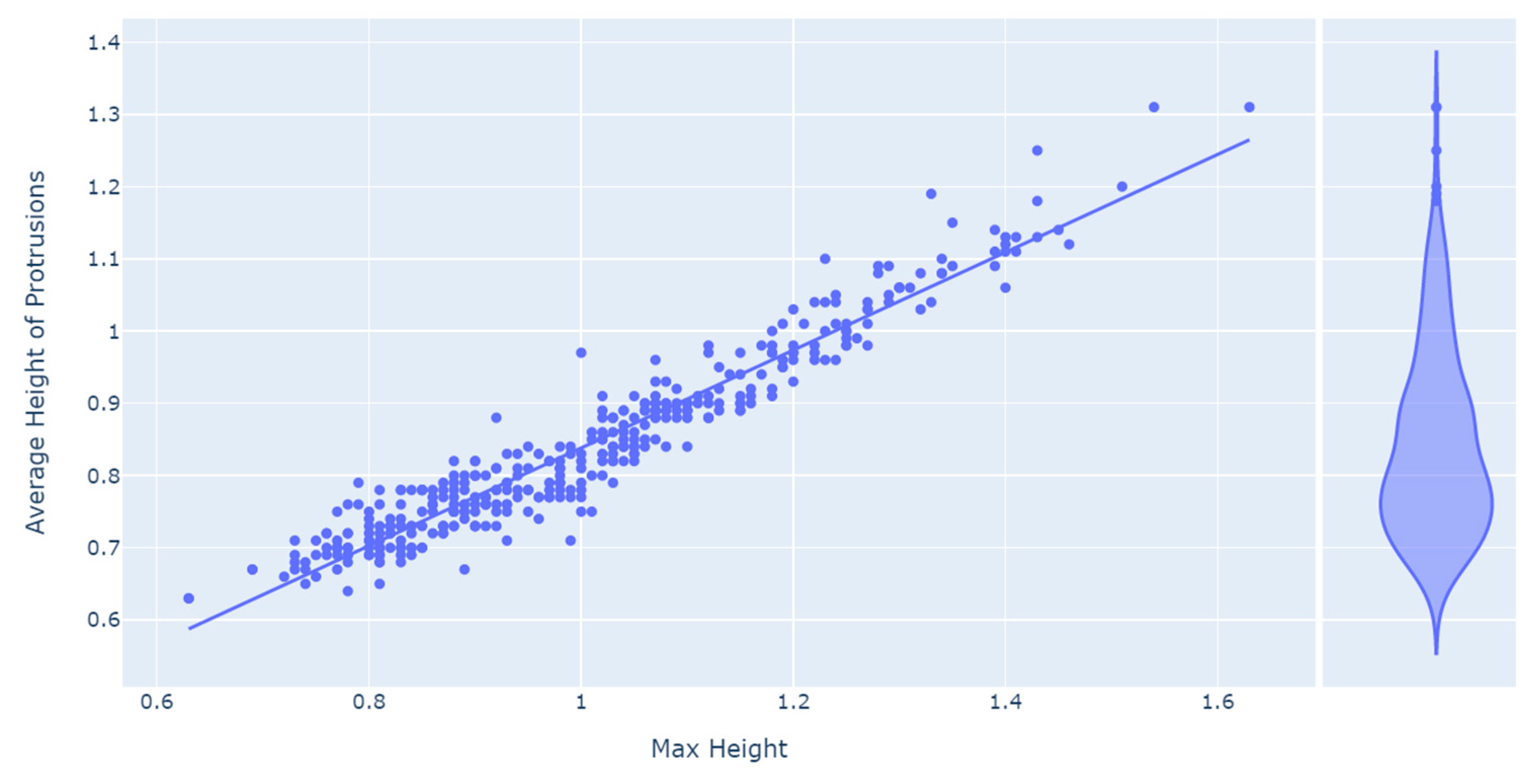
- Max height and average height of protrusions are correlated as well (0.96).
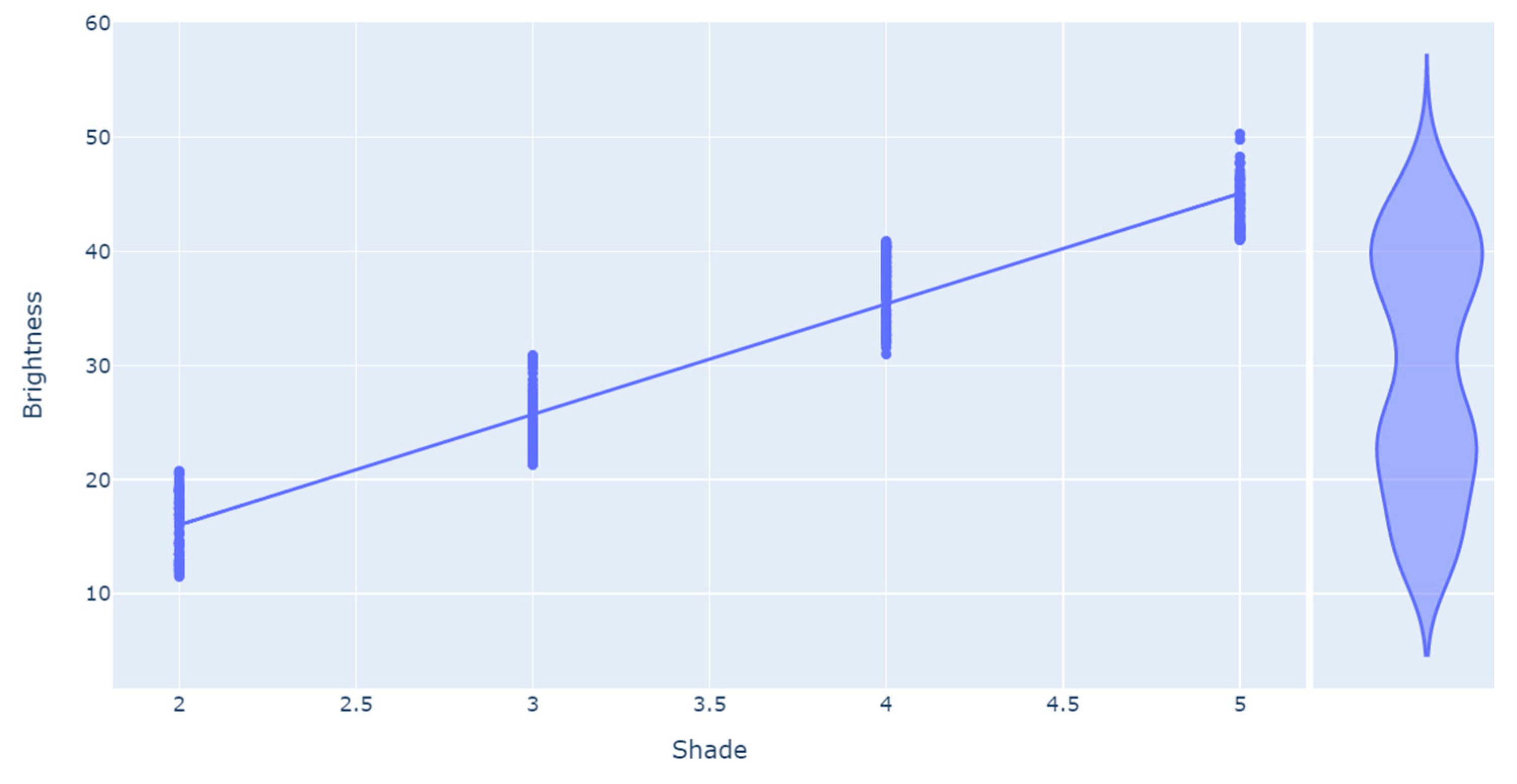
- Shade and brightness are highly correlated (0.96).
4.2.3. Categorical Columns (One-Hot Encoding)
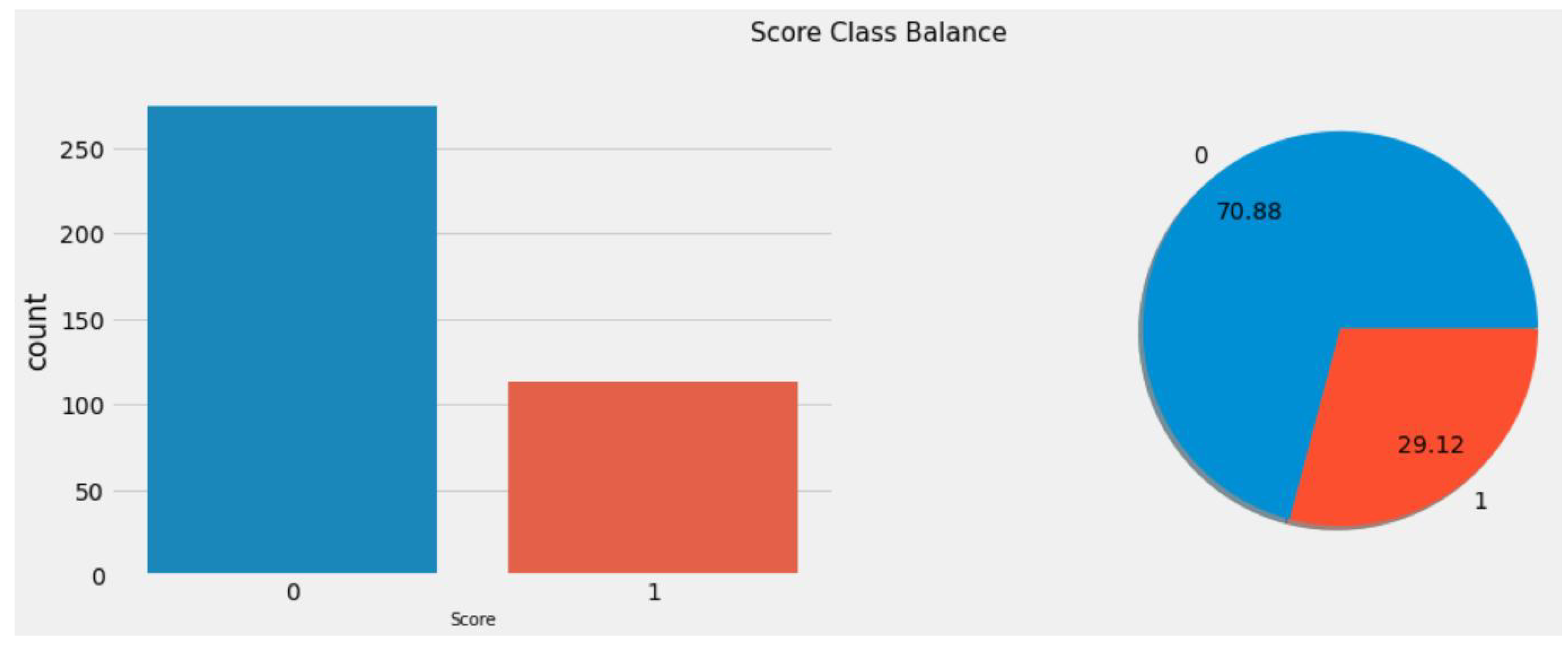
4.2.4. Imbalanced Data (Resampling)
4.2.5. Splitting the Dataset
4.2.6. Feature Scaling
5. Classification Algorithms
5.1. Decision Tree, Logistic Regression, and Adaboost Classifiers
5.2. Deep Learning Model (Neural Networks) Classifier
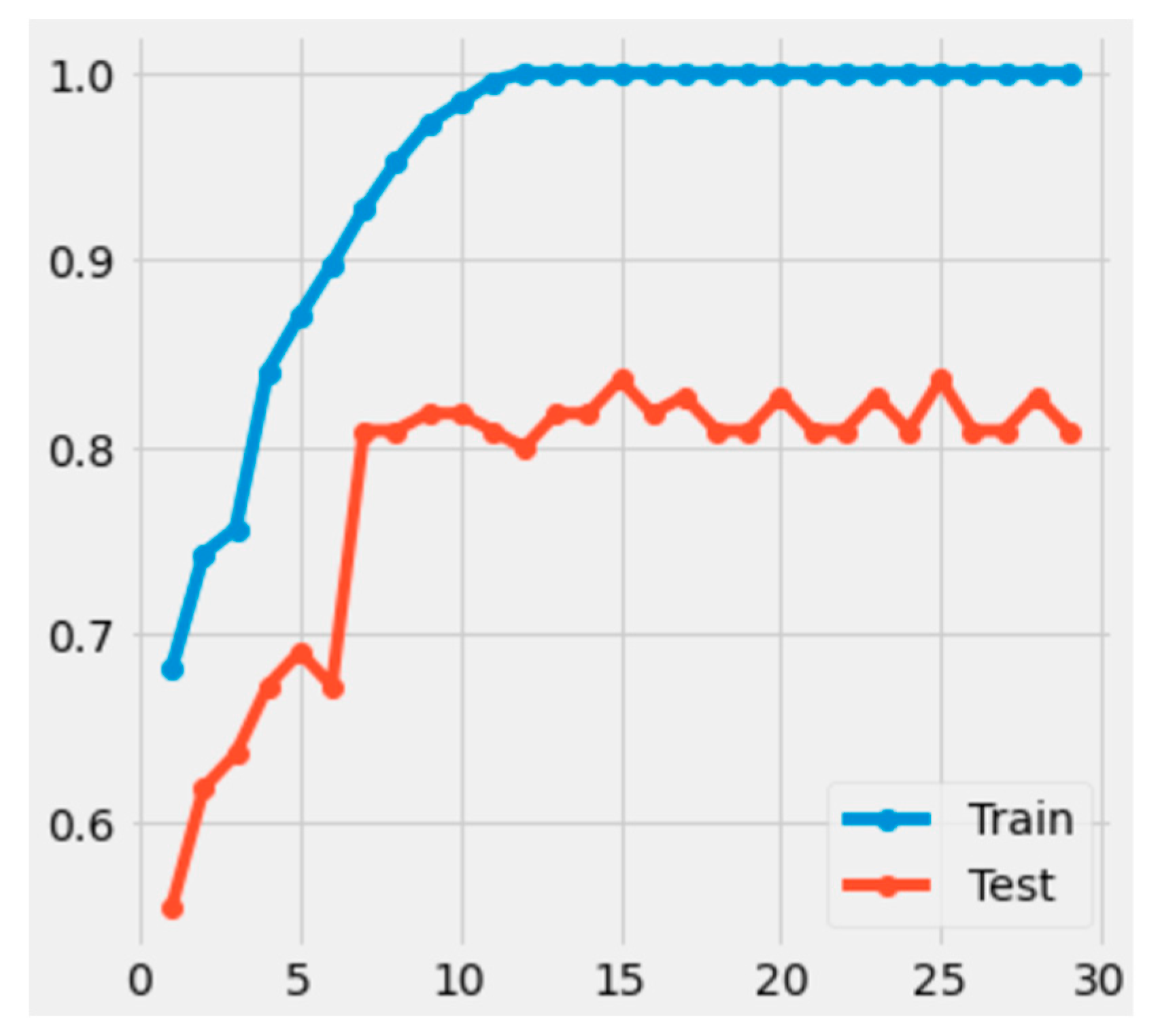
5.2.1. Neural Network Architecture
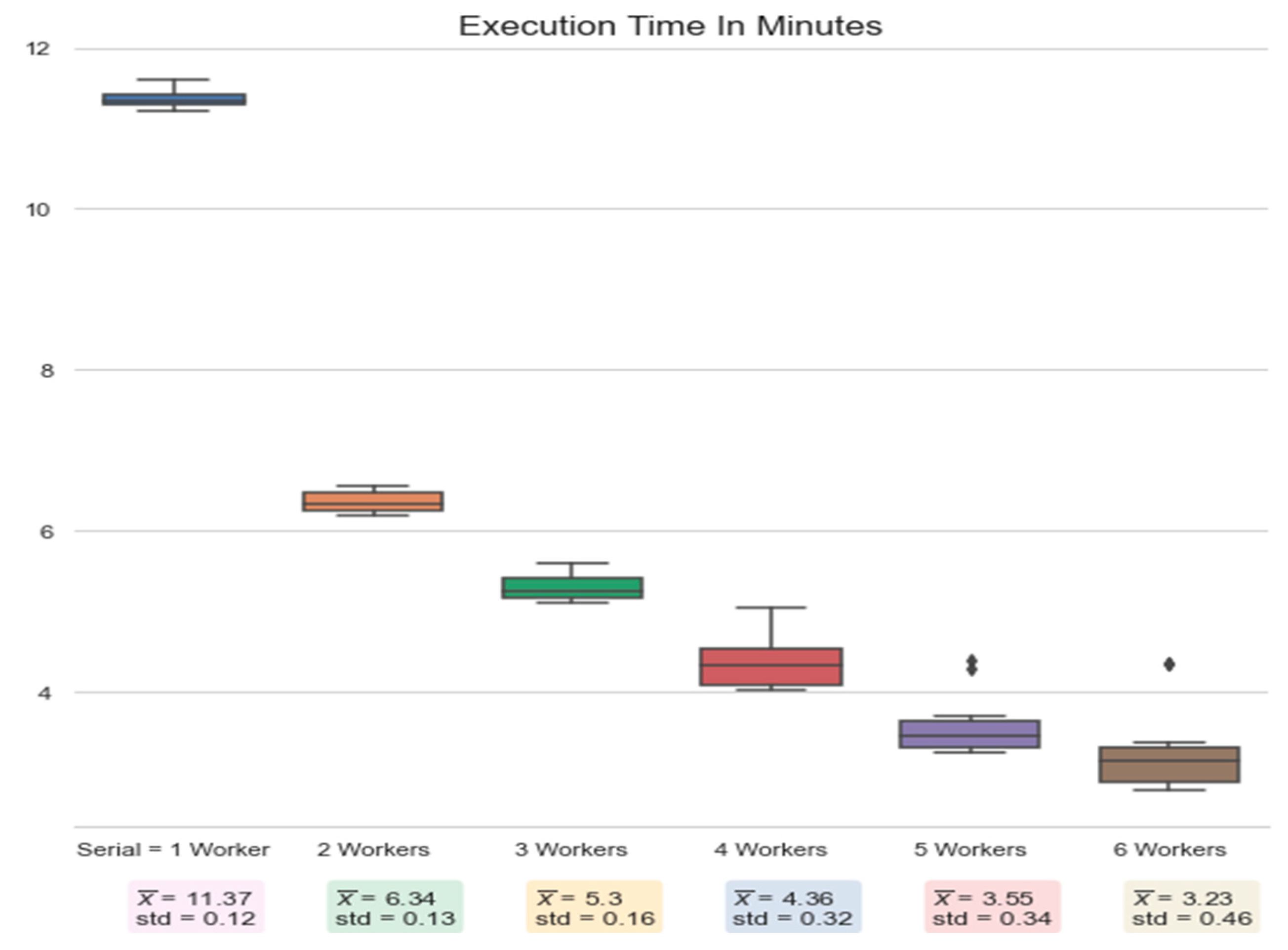
5.2.2. Hyperparameter Optimization Using Parallel Processing with Shared Memory
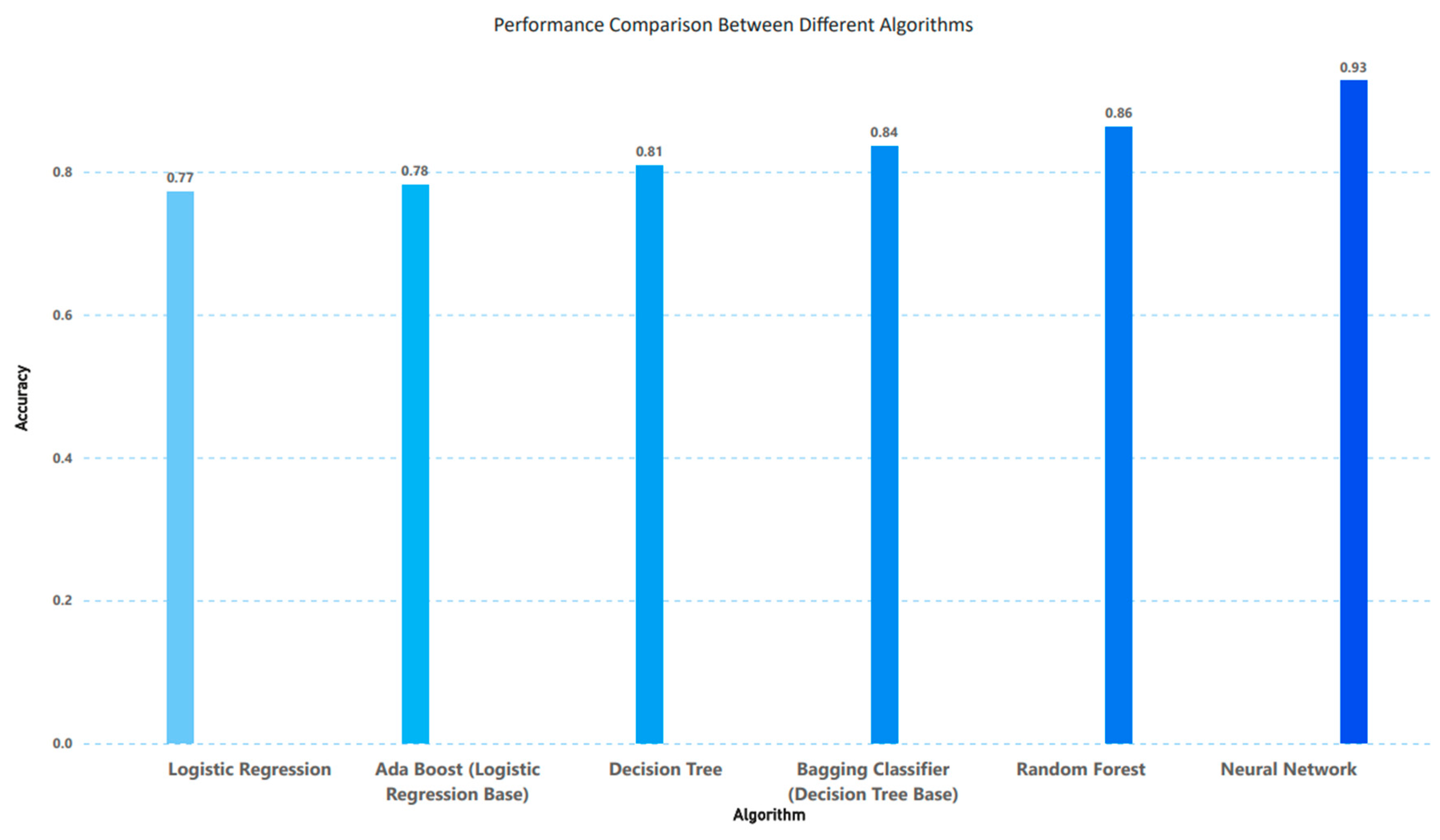
6. Performance Results
7. Discussion
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Skansi, S. Introduction to Deep Learning: From Logical Calculus to Artificial Intelligence; Springer: New York, NY, USA, 2018. [Google Scholar]
- Reitermanova, Z. Data splitting. In WDS’10 Proceedings of Contributed Papers; Matfyzpress: Prague, Czech Republic, 2010; Volume 10, p. 10. [Google Scholar]
- Cherkassky, A.; Weinberg, A. Objective evaluation of textile fabric appearance part 1: Basic principles, protrusion detection, and parameterization. Textile Res. J. 2010, 80, 226–235. [Google Scholar] [CrossRef]
- Cherkassky, A.; Weinberg, A. Objective Evaluation of Textile Fabric Appearance. Part 2: SET Opti-grade Tester, Grading Algorithms, and Testing. Textile Res. J. 2010, 80, 135–144. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Bresee, R.R. Fabric defect detection and classification using image analysis. Textile Res. J. 1995, 65, 1–9. [Google Scholar] [CrossRef]
- Dar, I.M.; Mahmood, W.; Vachtsevanos, G. Automated pilling detection and fuzzy classification of textile fabrics. In Machine Vision Applications in Industrial Inspection V; SPIE: Bellingham, WA, USA, 1997; Volume 3029, pp. 26–36. [Google Scholar]
- Abril, H.C.; Garcia-Verela MS, M.; Moreno YM, T.; Navarro, R.F. Automatic method based on image analysis for pilling evaluation in fabrics. Optical Eng. 1998, 37, 2937–2947. [Google Scholar] [CrossRef][Green Version]
- Konda, A.; Xin, L.C.; Takadera, M. Evaluation of Pilling by Computer Image Analysis. J. Textile Machin. Soc. Jpn. 1988, 36, 96–107. [Google Scholar] [CrossRef]
- Ramgulam, R.B.; Amirbayat, J.; Porat, I. The Objective Assessment of Fabric Pilling, Part 1: Methodology. J. Textile Inst. 1993, 84, 221–226. [Google Scholar] [CrossRef]
- Xu, B. Instrumental Evaluation of Fabric Pilling. J. Textile Inst. 1997, 88, 488–500. [Google Scholar] [CrossRef]
- His, C.H.; Bresee, R.R.; Annis, P.A. Characterizing Fabric Pilling by Using Image Analysis Techniques, Part 1: Pill Detection and Description. J. Textile Inst. 1997, 88, 80–95. [Google Scholar]
- Xin, B.; Hu, J. Objective Evaluation of Fabric Pilling Using Image Analysis Techniques. Textile Res. J. 2002, 72, 1057–1064. [Google Scholar]
- Jensen, K.L.; Carstensen, J.M. Fuzz and Pills Evaluated on Knitted Textiles by Image Analysis. Textile Res. J. 2002, 72, 34–38. [Google Scholar] [CrossRef]
- Behera, B.K.; Madan Mohan, T.E. Objective Measurement of Pilling by Image Processing Technique. Internat. J. Clothing Sci. Technol. 2005, 17, 279–291. [Google Scholar] [CrossRef]
- Behera, B.K.; Mishra, R. Objective Measurement of Fabric Appearance Using Digital Image Processing. J. Textile Inst. 2006, 97, 147–153. [Google Scholar] [CrossRef]
- Xu, B. Identifying Fabric Structures with Fast Fourier Transform Techniques. Textile Res. J. 1996, 66, 496–506. [Google Scholar]
- Kuo CF, J.; Lee, C.J.; Tsai, C.C. Using a Neural Network to Identify Fabric Defects in Dynamic Cloth Inspection. Textile Res. J. 2003, 73, 238–244. [Google Scholar]
- Tilocca, A.; Borzone, P.; Carosio, S.; Durante, A. Detecting Fabric Defects with a Neural Network Using Two Kinds of Optical Patterns. Textile Res. J. 2002, 72, 545–550. [Google Scholar] [CrossRef]
- Park, S.W.; Hwang, Y.G.; Kang, R.C. Applying Fuzzy Logic and Neural Networks to Total Hand Evaluation of Knitted Fabric, Textile Res. J. 2000, 70, 675–681. [Google Scholar]
- Rajasekaran, S. Training-free Counter Propagation Neural Network for Pattern Recognition of Fabric Defects. Textile Res. J. 1997, 67, 401–405. [Google Scholar] [CrossRef]
- Palmer, S. Objective Classification of Fabric Pilling Based on the Two-dimensional Discrete Wavelet Transform. Textile Res. J. 2003, 73, 713–720. [Google Scholar] [CrossRef]
- Barrett, G.; Clapp, T.G.; Titus, K. An On-Line Fabric Classification Technique Using a Wavelet-based Neural Network Approach. Textile Res. J. 1996, 66, 521–528. [Google Scholar] [CrossRef]
- Kim, S.C.; Kang, T.J. Image Analysis of Standard Pilling Photographs Using Wavelet Reconstruction. Textile Res. J. 2005, 75, 801–811. [Google Scholar] [CrossRef]
- Palmer, S.; Wang, X. Evaluating the Robustness of Objective Pilling Classification with the Two-dimensional Discrete Wavelet Transform. Textile Res. J. 2004, 74, 140–145. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Palmer, S. Objective grading of fabric pilling with wavelet texture analysis. Textile Res. J. 2007, 77, 871–879. [Google Scholar]
- Shamrat, F.J.M.; Ghosh, P.; Sadek, M.H.; Kazi, M.A.; Shultana, S. Implementation of machine learning algorithms to detect the prognosis rate of kidney disease. In Proceedings of the 2020 IEEE International Conference for Innovation in Technology (INOCON), Bangalore, India, 6–8 November 2020; pp. 1–7. [Google Scholar]
- Mohammed, R.; Rawashdeh, J.; Abdullah, M. Machine learning with oversampling and undersampling techniques: Overview study and experimental results. In Proceedings of the 2020 11th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 7–9 April 2020; pp. 243–248. [Google Scholar]
- Pietersma, D.; Lacroix, R.; Lefebvre, D.; Wade, K.M. Performance analysis for machine-learning experiments using small data sets. Comput. Electron. Agric. 2003, 38, 1–17. [Google Scholar] [CrossRef]
- Gros, C.; Lemay, A.; Cohen-Adad, J. SoftSeg: Advantages of soft versus binary training for image segmentation. Medical Image Anal. 2021, 71, 102038. [Google Scholar] [CrossRef] [PubMed]
- Visa, S.; Ramsay, B.; Ralescu, A.L.; Van Der Knaap, E. Confusion matrix-based feature selection. MAICS 2011, 710, 120–127. [Google Scholar]
- Yu, L.; Zhou, R.; Chen, R.; Lai, K.K. Missing data preprocessing in credit classification: One-hot encoding or imputation? Emerg. Markets Finance Trade 2022, 58, 472–482. [Google Scholar] [CrossRef]
- Elreedy, D.; Atiya, A.F. A comprehensive analysis of synthetic minority oversampling technique (SMOTE) for handling class imbalance. Inform. Sci. 2019, 505, 32–64. [Google Scholar] [CrossRef]
- Thara, D.K.; PremaSudha, B.G.; Xiong, F. Auto-detection of epileptic seizure events using deep neural network with different feature scaling techniques. Pattern Recog. Lett. 2019, 128, 544–550. [Google Scholar]
- Charbuty, B.; Abdulazeez, A. Classification based on decision tree algorithm for machine learning. J. Appl. Sci. Technol. Trends 2021, 2, 20–28. [Google Scholar] [CrossRef]
- Ying, C.; Qi-Guang, M.; Jia-Chen, L.; Lin, G. Advance and prospects of AdaBoost algorithm. Acta Autom. Sinica 2013, 39, 745–758. [Google Scholar]
- Zareapoor, M.; Shamsolmoali, P. Application of credit card fraud detection: Based on bagging ensemble classifier. Procedia Comput. Sci. 2015, 48, 679–685. [Google Scholar] [CrossRef]
- Livingston, F. Implementation of Breiman’s random forest machine learning algorithm. ECE591Q Machine Learn. J. Paper 2005, 2005, 1–13. [Google Scholar]
- Kleinbaum, D.G.; Klein, M. Introduction to logistic regression. In Logistic Regression; Springer: New York, NY, USA, 2010; pp. 1–39. [Google Scholar]
- Jurtz, V.I.; Johansen, A.R.; Nielsen, M.; Almagro Armenteros, J.J.; Nielsen, H.; Sønderby, C.K.; Winther, O.; Sønderby, S.K. An introduction to deep learning on biological sequence data: Examples and solutions. Bioinformatics 2017, 33, 3685–3690. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Moraga, C. The influence of the sigmoid function parameters on the speed of backpropagation learning. In International Workshop on Artificial Neural Networks; Springer: Berlin/Heidelberg, Germany, 1995; pp. 195–201. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Machine Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Halgamuge, M.N.; Daminda, E.; Nirmalathas, A. Best optimizer selection for predicting bushfire occurrences using deep learning. Nat. Hazards 2020, 103, 845–860. [Google Scholar] [CrossRef]
- Bock, S.; Goppold, J.; Weiß, M. An improvement of the convergence proof of the ADAM-Optimizer. arXiv 2018, arXiv:1804.10587. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Machine Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Chandra, R.; Dagum, L.; Kohr, D.; Menon, R.; Maydan, D.; McDonald, J. Parallel Programming in OpenMP; Morgan Kaufmann: Burlington, MA, USA, 2001. [Google Scholar]
- Rosenthal, J.S. Parallel computing and Monte Carlo algorithms. Far East J. Theor. Stat. 2000, 4, 207–236. [Google Scholar]
- Drakopoulos, V.; Mimikou, N.; Theoharis, T. An overview of parallel visualisation methods for Mandelbrot and Julia sets. Comput. Graph. 2003, 27, 635–646. [Google Scholar] [CrossRef]
- Pacheco, P. An Introduction to Parallel Programming; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Rocklin, M. Dask: Parallel computation with blocked algorithms and task scheduling. In Proceedings of the 14th Python in Science Conference (SciPy), Austin, TX, USA, 6–12 July 2015; Volume 130. [Google Scholar]






| Dimension | Value | |||||
|---|---|---|---|---|---|---|
| Algorithm | Decision Tree | Bagging Classifier (Decision Tree Base) | Logistic Regression | Ada Boost (Logistic Regression Base) | Random Forest | Neural Network |
| Confusion Matrix | [52 12] [9 37] | [49 15] [3 43] | [45 19] [6 40] | [45 19] [5 41] | [55 9] [6 40] | [56 5] [3 46] |
| Accuracy | 0.809 | 0.836 | 0.772 | 0.782 | 0.863 | 0.927 |
| Precision | 0.81 | 0.86 | 0.8 | 0.81 | 0.87 | 0.92 |
| Recall | 0.81 | 0.84 | 0.77 | 0.78 | 0.86 | 0.95 |
| F1 Score | 0.81 | 0.84 | 0.77 | 0.78 | 0.86 | 0.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazoom, R.; Birman, R.; Hadar, O. Meta Classification Model of Surface Appearance for Small Dataset Using Parallel Processing. Electronics 2022, 11, 3426. https://doi.org/10.3390/electronics11213426
Kazoom R, Birman R, Hadar O. Meta Classification Model of Surface Appearance for Small Dataset Using Parallel Processing. Electronics. 2022; 11(21):3426. https://doi.org/10.3390/electronics11213426
Chicago/Turabian StyleKazoom, Roie, Raz Birman, and Ofer Hadar. 2022. "Meta Classification Model of Surface Appearance for Small Dataset Using Parallel Processing" Electronics 11, no. 21: 3426. https://doi.org/10.3390/electronics11213426
APA StyleKazoom, R., Birman, R., & Hadar, O. (2022). Meta Classification Model of Surface Appearance for Small Dataset Using Parallel Processing. Electronics, 11(21), 3426. https://doi.org/10.3390/electronics11213426








