Relative Knowledge Distance Measure of Intuitionistic Fuzzy Concept
Abstract
1. Introduction
2. Preliminaries
- (1)
- When U is continuous.
- (2)
- When U is discrete.where, , and denotes the membership degree of belongs to the intuitionistic fuzzy set I.
- (1)
- When U is continuous, the average information entropy of the rough granular space of I can be denoted by:
- (2)
- When U is discrete, the average information entropy of the rough granular space of I can be denoted by:where, , and denotes the membership degree of x belongs to the intuitionistic fuzzy set I, is the average step intuitionistic fuzzy set of .
- (1)
- Positive: ;
- (2)
- Symmetric: ;
- (3)
- Triangle inequality: .
- (1)
- ;
- (2)
- ;
- (3)
- .
3. Information-Entropy-Based Two-Layer Knowledge Distance Measure
4. Relative Macro-Knowledge Distance
5. Experiment and Analysis
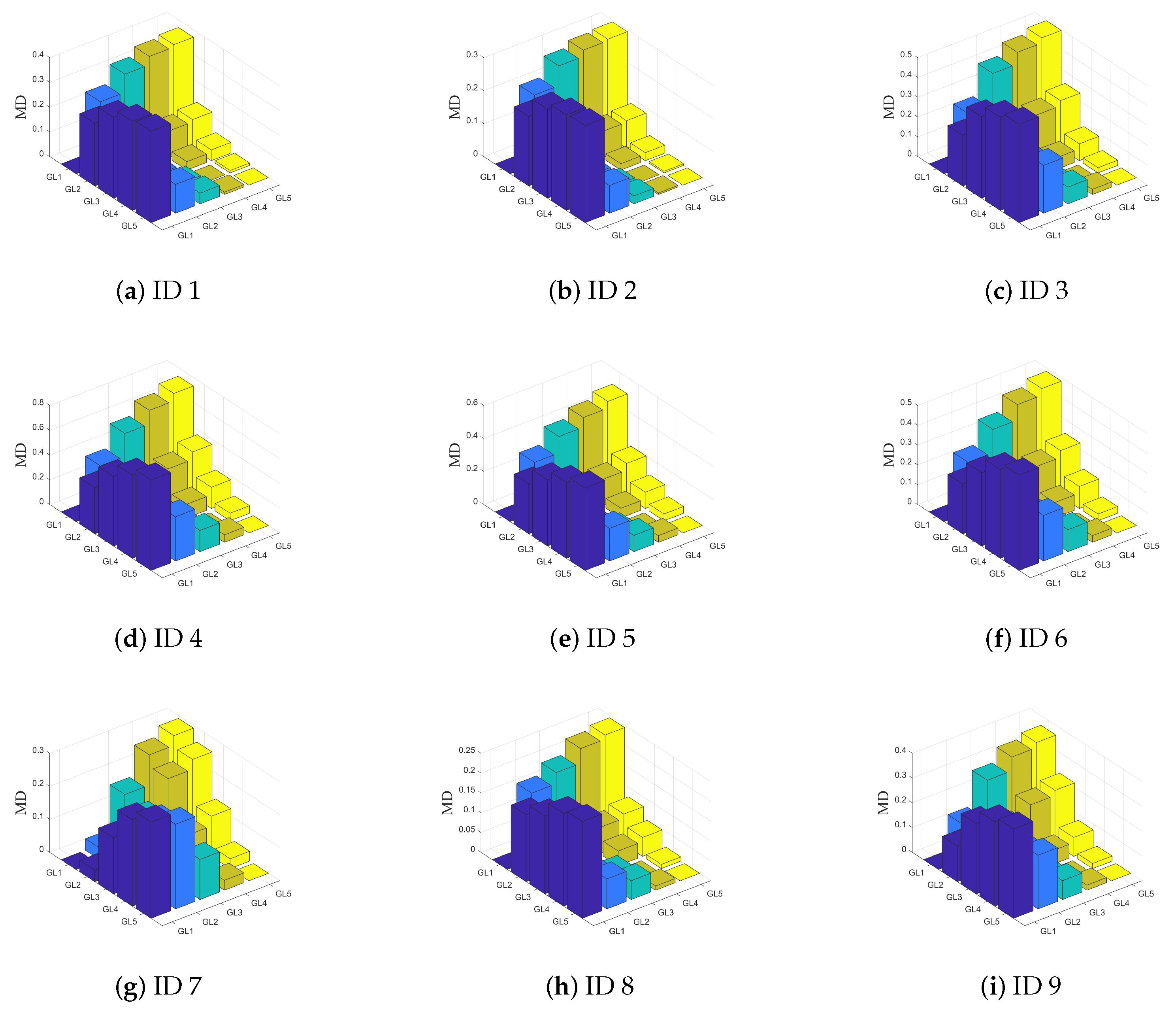
5.1. Monotonicity Experiment
5.2. Attribute Reduction
| Algorithm 1 Attribute reduction based on relative MD |
|
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, Y.Y. The art of granular computing. In Proceedings of the International Conference on Rough Sets and Intelligent Systems Paradigms, Warsaw, Poland, 28–30 June 2007; pp. 101–112. [Google Scholar]
- Bargiela, A.; Pedrycz, W. Toward a theory of granular computing for human-centered information processing. IEEE Trans. Fuzzy Syst. 2008, 16, 320–330. [Google Scholar] [CrossRef]
- Yao, J.T.; Vasilakos, A.V.; Pedrycz, W. Granular computing: Perspectives and challenges. IEEE Trans. Cybern. 2013, 43, 1977–1989. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.Y. Granular computing: Basic issues and possible solutions. In Proceedings of the 5th Joint Conference on Information Sciences, Atlantic City, NJ, USA, 27 February–3 March 2000; Volume 1, pp. 186–189. [Google Scholar]
- Yao, Y.Y. Set-theoretic models of three-way decision. Granul. Comput. 2021, 6, 133–148. [Google Scholar] [CrossRef]
- Yao, Y.Y. Tri-level thinking: Models of three-way decision. Int. J. Mach. Learn. Cybern. 2020, 11, 947–959. [Google Scholar] [CrossRef]
- Wang, G.Y.; Yang, J.; Xu, J. Granular computing: From granularity optimization to multi-granularity joint problem solving. Granul. Comput. 2017, 2, 105–120. [Google Scholar] [CrossRef]
- Wang, G.Y. DGCC: Data-driven granular cognitive computing. Granul. Comput. 2017, 2, 343–355. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Wang, C.Z.; Huang, Y.; Shao, M.W.; Hu, Q.H.; Chen, D.G. Feature selection based on neighborhood self-information. IEEE Trans. Cybern. 2019, 50, 4031–4042. [Google Scholar] [CrossRef]
- Li, Z.W.; Zhang, P.F.; Ge, X.; Xie, N.X.; Zhang, G.Q. Uncertainty measurement for a covering information system. Soft Comput. 2019, 23, 5307–5325. [Google Scholar] [CrossRef]
- Sun, L.; Wang, L.Y.; Ding, W.P.; Qian, Y.H.; Xu, J.C. Feature selection using fuzzy neighborhood entropy-based uncertainty measures for fuzzy neighborhood multigranulation rough sets. IEEE Trans. Fuzzy Syst. 2020, 29, 19–33. [Google Scholar] [CrossRef]
- Wang, Z.H.; Yue, H.F.; Deng, J.P. An uncertainty measure based on lower and upper approximations for generalized rough set models. Fundam. Informaticae 2019, 166, 273–296. [Google Scholar] [CrossRef]
- Qian, Y.H.; Liang, J.Y.; Dang, C.Y. Knowledge structure, knowledge granulation and knowledge distance in a knowledge base. Int. J. Approx. Reason. 2009, 50, 174–188. [Google Scholar] [CrossRef]
- Qian, Y.H.; Li, Y.B.; Liang, J.Y.; Lin, G.P.; Dang, C.Y. Fuzzy granular structure distance. IEEE Trans. Fuzzy Syst. 2015, 23, 2245–2259. [Google Scholar] [CrossRef]
- Li, S.; Yang, J.; Wang, G.Y.; Xu, T.H. Multi-granularity distance measure for interval-valued intuitionistic fuzzy concepts. Inf. Sci. 2021, 570, 599–622. [Google Scholar] [CrossRef]
- Yang, J.; Wang, G.Y.; Zhang, Q.H.; Wang, H.M. Knowledge distance measure for the multigranularity rough approximations of a fuzzy concept. IEEE Trans. Fuzzy Syst. 2020, 28, 706–717. [Google Scholar] [CrossRef]
- Yang, J.; Wang, G.Y.; Zhang, Q.H. Knowledge distance measure in multigranulation spaces of fuzzy equivalence relations. Inf. Sci. 2018, 448, 18–35. [Google Scholar] [CrossRef]
- Chen, Y.M.; Qin, N.; Li, W.; Xu, F.F. Granule structures, distances and measures in neighborhood systems. Knowl.-Based Syst. 2019, 165, 268–281. [Google Scholar] [CrossRef]
- Xia, D.Y.; Wang, G.Y.; Yang, J.; Zhang, Q.H.; Li, S. Local Knowledge Distance for Rough Approximation Measure in Multi-granularity Spaces. Inf. Sci. 2022, 605, 413–432. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Yang, C.C.; Zhang, Q.H.; Zhao, F. Hierarchical three-way decisions with intuitionistic fuzzy numbers in multi-granularity spaces. IEEE Access 2019, 7, 24362–24375. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Yang, C.C.; Wang, G.Y. A sequential three-way decision model with intuitionistic fuzzy numbers. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 51, 2640–2652. [Google Scholar] [CrossRef]
- Boran, F.E.; Genç, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Garg, H.; Rani, D. Novel similarity measure based on the transformed right-angled triangles between intuitionistic fuzzy sets and its applications. Cogn. Comput. 2021, 13, 447–465. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Duan, C.Y. An integrated approach for failure mode and effect analysis under interval-valued intuitionistic fuzzy environment. Int. J. Prod. Econ. 2019, 207, 163–172. [Google Scholar] [CrossRef]
- Akram, M.; Shahzad, S.; Butt, A.; Khaliq, A. Intuitionistic fuzzy logic control for heater fans. Math. Comput. Sci. 2013, 7, 367–378. [Google Scholar] [CrossRef]
- Atan, Ö.; Kutlu, F.; Castillo, O. Intuitionistic Fuzzy Sliding Controller for Uncertain Hyperchaotic Synchronization. Int. J. Fuzzy Syst. 2020, 22, 1430–1443. [Google Scholar] [CrossRef]
- Debnath, P.; Mohiuddine, S. Soft Computing Techniques in Engineering, Health, Mathematical and Social Sciences; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Mordeso, J.N.; Nair, P.S. Fuzzy Mathematics: An Introduction for Engineers and Scientists; Physica Verlag: Heidelberg, Germany, 2001. [Google Scholar]
- Zhang, X.H.; Zhou, B.; Li, P. A general frame for intuitionistic fuzzy rough sets. Inf. Sci. 2012, 216, 34–49. [Google Scholar] [CrossRef]
- Zhou, L.; Wu, W.Z. Characterization of rough set approximations in Atanassov intuitionistic fuzzy set theory. Comput. Math. Appl. 2011, 62, 282–296. [Google Scholar] [CrossRef]
- Jiang, Y.C.; Tang, Y.; Wang, J.; Tang, S.Q. Reasoning within intuitionistic fuzzy rough description logics. Inf. Sci. 2009, 179, 2362–2378. [Google Scholar] [CrossRef]
- Dubey, Y.K.; Mushrif, M.M.; Mitra, K. Segmentation of brain MR images using rough set based intuitionistic fuzzy clustering. Biocybern. Biomed. Eng. 2016, 36, 413–426. [Google Scholar] [CrossRef]
- Zheng, T.T.; Zhang, M.Y.; Zheng, W.R.; Zhou, L.G. A new uncertainty measure of covering-based rough interval-valued intuitionistic fuzzy sets. IEEE Access 2019, 7, 53213–53224. [Google Scholar] [CrossRef]
- Huang, B.; Guo, C.X.; Li, H.X.; Feng, G.F.; Zhou, X.Z. Hierarchical structures and uncertainty measures for intuitionistic fuzzy approximation space. Inf. Sci. 2016, 336, 92–114. [Google Scholar] [CrossRef]
- Zhang, Q.H.; Wang, J.; Wang, G.Y.; Yu, H. The approximation set of a vague set in rough approximation space. Inf. Sci. 2015, 300, 1–19. [Google Scholar] [CrossRef]
- Lawvere, F.W. Metric spaces, generalized logic, and closed categories. Rend. Del Semin. Matématico E Fis. Di Milano 1973, 43, 135–166. [Google Scholar] [CrossRef]
- Liang, J.Y.; Chin, K.S.; Dang, C.Y.; Yam, R.C. A new method for measuring uncertainty and fuzziness in rough set theory. Int. J. Gen. Syst. 2002, 31, 331–342. [Google Scholar] [CrossRef]
- Yao, Y.Y.; Zhao, L.Q. A measurement theory view on the granularity of partitions. Inf. Sci. 2012, 213, 1–13. [Google Scholar] [CrossRef]
- Du, W.S.; Hu, B.Q. Aggregation distance measure and its induced similarity measure between intuitionistic fuzzy sets. Pattern Recognit. Lett. 2015, 60, 65–71. [Google Scholar] [CrossRef]
- Du, W.S. Subtraction and division operations on intuitionistic fuzzy sets derived from the Hamming distance. Inf. Sci. 2021, 571, 206–224. [Google Scholar] [CrossRef]
- Ju, F.; Yuan, Y.Z.; Yuan, Y.; Quan, W. A divergence-based distance measure for intuitionistic fuzzy sets and its application in the decision-making of innovation management. IEEE Access 2019, 8, 1105–1117. [Google Scholar] [CrossRef]
- Jiang, Q.; Jin, X.; Lee, S.J.; Yao, S.W. A new similarity/distance measure between intuitionistic fuzzy sets based on the transformed isosceles triangles and its applications to pattern recognition. Expert Syst. Appl. 2019, 116, 439–453. [Google Scholar] [CrossRef]
- Wang, T.; Wang, B.L.; Han, S.Q.; Lian, K.C.; Lin, G.P. Relative knowledge distance and its cognition characteristic description in information systems. J. Bohai Univ. Sci. Ed. 2022, 43, 151–160. [Google Scholar]
- UCI Repository. 2007. Available online: Http://archive.ics.uci.edu/ml/ (accessed on 10 June 2022).
- Li, F.; Hu, B.Q.; Wang, J. Stepwise optimal scale selection for multi-scale decision tables via attribute significance. Knowl.-Based Syst. 2017, 129, 4–16. [Google Scholar] [CrossRef]
- Langeloh, L.; Seppälä, O. Relative importance of chemical attractiveness to parasites for susceptibility to trematode infection. Ecol. Evol. 2018, 8, 8921–8929. [Google Scholar] [CrossRef]
- Wang, J.W. Waterlow score on admission in acutely admitted patients aged 65 and over. BMJ Open 2019, 9, e032347. [Google Scholar] [CrossRef]
- Fidelix, T.; Czapkowski, A.; Azjen, S.; Andriolo, A.; Trevisani, V.F. Salivary gland ultrasonography as a predictor of clinical activity in Sjögren’s syndrome. PLoS ONE 2017, 12, e0182287. [Google Scholar] [CrossRef]
- Xing, H.M.; Zhou, W.D.; Fan, Y.Y.; Wen, T.X.; Wang, X.H.; Chang, G.M. Development and validation of a postoperative delirium prediction model for patients admitted to an intensive care unit in China: A prospective study. BMJ Open 2019, 9, e030733. [Google Scholar] [CrossRef]
- Combrink, L.; Glidden, C.K.; Beechler, B.R.; Charleston, B.; Koehler, A.V.; Sisson, D.; Gasser, R.B.; Jabbar, A.; Jolles, A.E. Age of first infection across a range of parasite taxa in a wild mammalian population. Biol. Lett. 2020, 16, 20190811. [Google Scholar] [CrossRef]





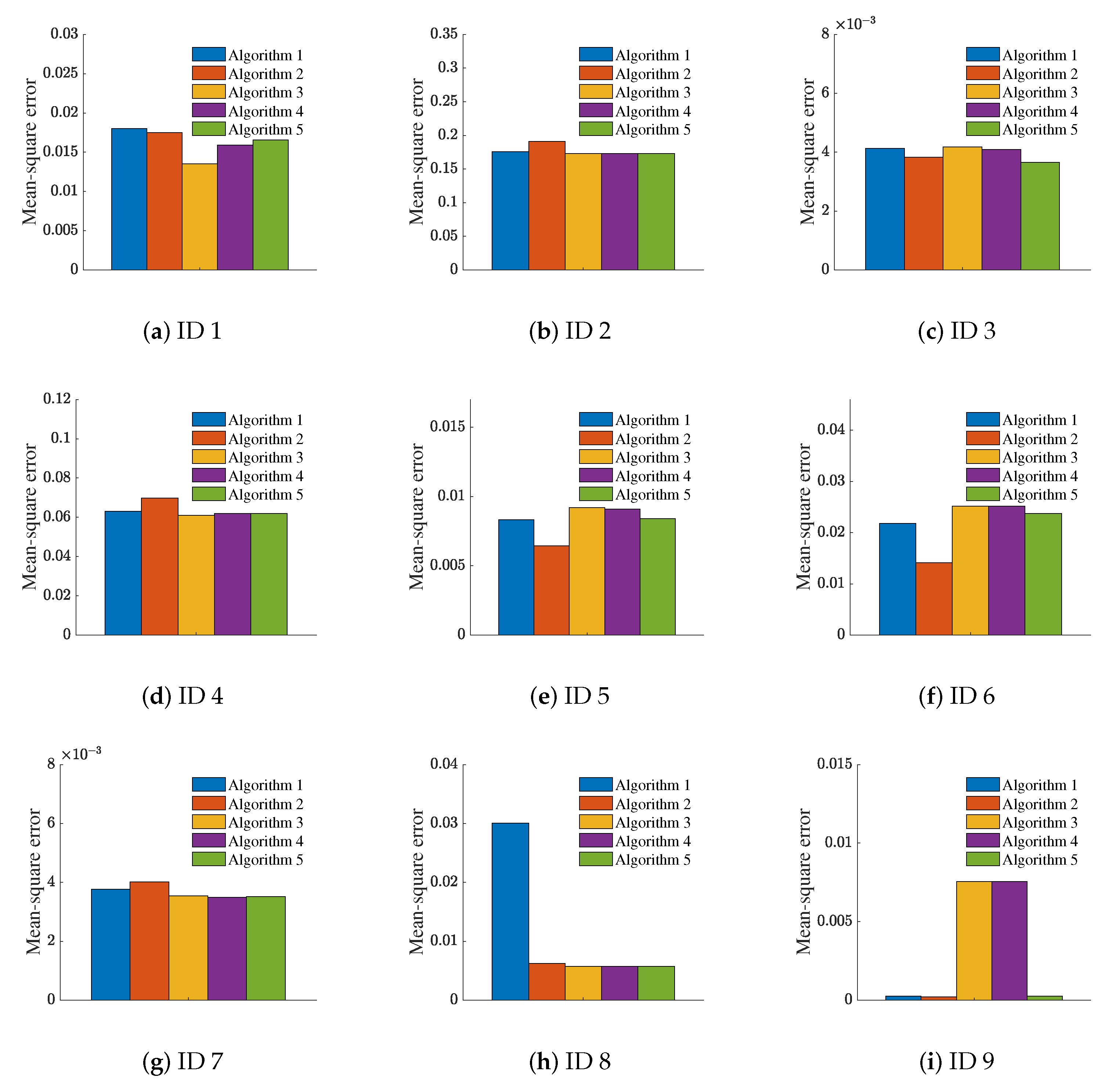
| ID | Dataset | Instances | Condition Attributes |
|---|---|---|---|
| 1 | Hungarian Chickenpox Cases Dataset | 521 | 19 |
| 2 | Data from: Relative importance of chemical attractiveness to parasites for susceptibility to trematode infection [49] | 67 | 7 |
| 3 | Waterlow score on admission in acutely admitted patients aged 65 and over [50] | 839 | 11 |
| 4 | Data from: Salivary gland ultrasonography as a predictor of clinical activity in Sjögren’s syndrome [51] | 70 | 10 |
| 5 | Data from: Development and validation of a postoperative delirium prediction model for patients admitted to an intensive care unit in China: a prospective study [52] | 300 | 13 |
| 6 | Data from: Age of first infection across a range of parasite taxa in a wild mammalian population [53] | 140 | 12 |
| 7 | Air Quality | 9538 | 10 |
| 8 | Concrete | 1030 | 8 |
| 9 | ENB2012 | 768 | 8 |
| ID (Dataset) | Measure | GL1 | GL2 | GL3 | GL4 | GL5 |
|---|---|---|---|---|---|---|
| 1 | Granularity measure | 0.4052 | 0.1523 | 0.0790 | 0.0453 | 0.0357 |
| Information measure | 0.5928 | 0.8458 | 0.9190 | 0.9528 | 0.9624 | |
| 2 | Granularity measure | 0.2952 | 0.0853 | 0.0253 | 0.0060 | 0.0012 |
| Information measure | 0.6899 | 0.8998 | 0.9598 | 0.9791 | 0.9839 | |
| 3 | Granularity measure | 0.5156 | 0.2604 | 0.1040 | 0.0451 | 0.0191 |
| Information measure | 0.4832 | 0.7384 | 0.8948 | 0.9537 | 0.9797 | |
| 4 | Granularity measure | 0.7516 | 0.3777 | 0.1916 | 0.0805 | 0.0199 |
| Information measure | 0.2341 | 0.6080 | 0.7942 | 0.9052 | 0.9658 | |
| 5 | Granularity measure | 0.5249 | 0.2229 | 0.1233 | 0.0653 | 0.0244 |
| Information measure | 0.4717 | 0.7737 | 0.8734 | 0.9314 | 0.9723 | |
| 6 | Granularity measure | 0.4975 | 0.2463 | 0.1267 | 0.0493 | 0.0155 |
| Information measure | 0.4954 | 0.7466 | 0.8661 | 0.9436 | 0.9773 | |
| 7 | Granularity measure | 0.3788 | 0.3438 | 0.2087 | 0.1170 | 0.0872 |
| Information measure | 0.6211 | 0.6561 | 0.7911 | 0.8828 | 0.9127 | |
| 8 | Granularity measure | 0.2557 | 0.0869 | 0.0588 | 0.0217 | 0.0112 |
| Information measure | 0.7433 | 0.9121 | 0.9402 | 0.9773 | 0.9878 | |
| 9 | Granularity measure | 0.3675 | 0.2237 | 0.0829 | 0.0271 | 0.0066 |
| information measure | 0.6312 | 0.7750 | 0.9157 | 0.9716 | 0.9921 |
| ID (Dataset) | The Original Attributes (Number) | Attribute Reduction Based on MD (In Parentheses Is the Number of Attributes after Attribute Reduction) | ||
|---|---|---|---|---|
| 1 | 6,16,11,13,4,3,19,15,2, 8,18,17,14,9,1,12,10 (17) | Absolute MD | 15,2,8,18,17,14,9,1,12,10 (10) | |
| 8,18,17,14,9,1,12,10 (8) | ||||
| Relative MD with attribute 7 as a prior condition | 15,2,8,18,17,14,9,1,12,10 (10) | |||
| 8,18,17,14,9,1,12,10 (8) | ||||
| Relative MD with attribute 5 as a prior condition | 2,8,18,17,14,9,1,12,10 (9) | |||
| 8,18,17,14,9,1,12,10 (8) | ||||
| 2 | 3,7,1,4,2 (5) | Absolute MD | 3,7,1,4,2 (5) | |
| 7,1,4,2 (4) | ||||
| Relative MD with attribute 6 as a prior condition | 7,1,4,2 (4) | |||
| 1,4,2 (3) | ||||
| Relative MD with attribute 5 as a prior condition | 7,1,4,2 (4) | |||
| 7,1,2 (3) | ||||
| 3 | 11,8,6,7,4,9,1,5,3 (9) | Absolute MD | 8,6,7,4,9,1,5,3 (8) | |
| 6,7,4,9,1,5,3 (7) | ||||
| Relative MD with attribute 10 as a prior condition | 8,6,7,4,9,1,5,3 (8) | |||
| 6,7,4,9,1,5,3 (7) | ||||
| Relative MD with attribute 2 as a prior condition | 6,7,4,9,1,5,3 (7) | |||
| 7,4,9,1,5,3 (6) | ||||
| 4 | 6,2,3,9,10,7,5,1 (8) | Absolute MD | 6,2,3,9,10,7,5,1 (8) | |
| 6,3,9,10,7,5,1 (7) | ||||
| Relative MD with attribute 4 as a prior condition | 6,3,9,10,7,5,1 (7) | |||
| 6,3,10,7,5,1 (6) | ||||
| Relative MD with attribute 8 as a prior condition | 3,9,10,7,5,1 (6) | |||
| 3,10,7,5,1 (5) | ||||
| 5 | 12,13,1,6,3,4,7,2,9, 5,11 (11) | Absolute MD | 1,6,3,4,7,2,9,5,11 (9) | |
| 6,3,4,7,2,9,5,11 (8) | ||||
| Relative MD with attribute 10 as a prior condition | 1,6,3,4,7,2,9,5,11 (9) | |||
| 3,4,7,2,9,5,11 (7) | ||||
| Relative MD with attribute 8 as a prior condition | 3,4,7,2,9,5,11 (7) | |||
| 3,4,2,9,5,11 (6) | ||||
| 6 | 7,9,8,11,5,10,6,3,4, 1 (10) | Absolute MD | 9,8,5,10,6,3,4,1 (8) | |
| 8,5,10,6,3,4,1 (7) | ||||
| Relative MD with attribute 12 as a prior condition | 8,11,5,10,6,3,4,1 (8) | |||
| 8,5,10,6,3,4,1 (7) | ||||
| Relative MD with attribute 2 as a prior condition | 11,5,10,6,3,4,1 (7) | |||
| 5,10,6,3,4,1 (6) | ||||
| 7 | 6,1,4,5,2,10,7,9 (8) | Absolute MD | 1,4,5,2,10,7,9 (7) | |
| 1,4,5,2,10,7,9 (7) | ||||
| Relative MD with attribute 3 as a prior condition | 1,4,5,2,10,7,9 (7) | |||
| 1,5,2,10,7,9 (6) | ||||
| Relative MD with attribute 8 as a prior condition | 1,5,2,10,7,9 (6) | |||
| 4,5,2,10,7,9 (6) | ||||
| 8 | 5,3,7,1,4,6 (6) | Absolute MD | 3,7,1,4,6 (5) | |
| 3,7,1,4,6 (5) | ||||
| Relative MD with attribute 2 as a prior condition | 3,7,1,4,6 (5) | |||
| 7,1,4,6 (4) | ||||
| Relative MD with attribute 8 as a prior condition | 3,7,1,4,6 (5) | |||
| 7,1,4,6 (4) | ||||
| 9 | 4,1,2,5,6 (5) | Absolute MD | 1,2,5,6 (4) | |
| 2,5,6 (3) | ||||
| Relative MD with attribute 3 as a prior condition | 2,5,6 (3) | |||
| 2,5,6 (3) | ||||
| Relative MD with attribute 7 as a prior condition | 2,5,6 (3) | |||
| 2,5,6 (3) | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Qin, X.; Wang, G.; Zhang, X.; Wang, B. Relative Knowledge Distance Measure of Intuitionistic Fuzzy Concept. Electronics 2022, 11, 3373. https://doi.org/10.3390/electronics11203373
Yang J, Qin X, Wang G, Zhang X, Wang B. Relative Knowledge Distance Measure of Intuitionistic Fuzzy Concept. Electronics. 2022; 11(20):3373. https://doi.org/10.3390/electronics11203373
Chicago/Turabian StyleYang, Jie, Xiaodan Qin, Guoyin Wang, Xiaoxia Zhang, and Baoli Wang. 2022. "Relative Knowledge Distance Measure of Intuitionistic Fuzzy Concept" Electronics 11, no. 20: 3373. https://doi.org/10.3390/electronics11203373
APA StyleYang, J., Qin, X., Wang, G., Zhang, X., & Wang, B. (2022). Relative Knowledge Distance Measure of Intuitionistic Fuzzy Concept. Electronics, 11(20), 3373. https://doi.org/10.3390/electronics11203373






