A Large Scale Evolutionary Algorithm Based on Determinantal Point Processes for Large Scale Multi-Objective Optimization Problems
Abstract
1. Introduction
- 1
- The balance between convergence and variety has been achieved by the reproduction process followed by the environmental selection process. A crossover with current parent individuals is performed using guiding solutions in the first reproduction, followed by a second reproduction with no guiding solutions involved in developing offspring individuals.
- 2
- We have used a kernel matrix to adapt to various LSMOEA-DPP. The kernel matrix defines the similarity measure as the angle’s cosine value among two solutions that measures solution quality using the L2 norm of an objective vector. By default, the MOP is divided into a collection of reference vectors, and each subproblem is chosen using both angle base and Euclidean distance.
- 3
- This study also suggests using a kernel matrix that searches for non-dominated solutions set to combine DPP selection with LSMOPs to choose a subset of the population.
2. Background
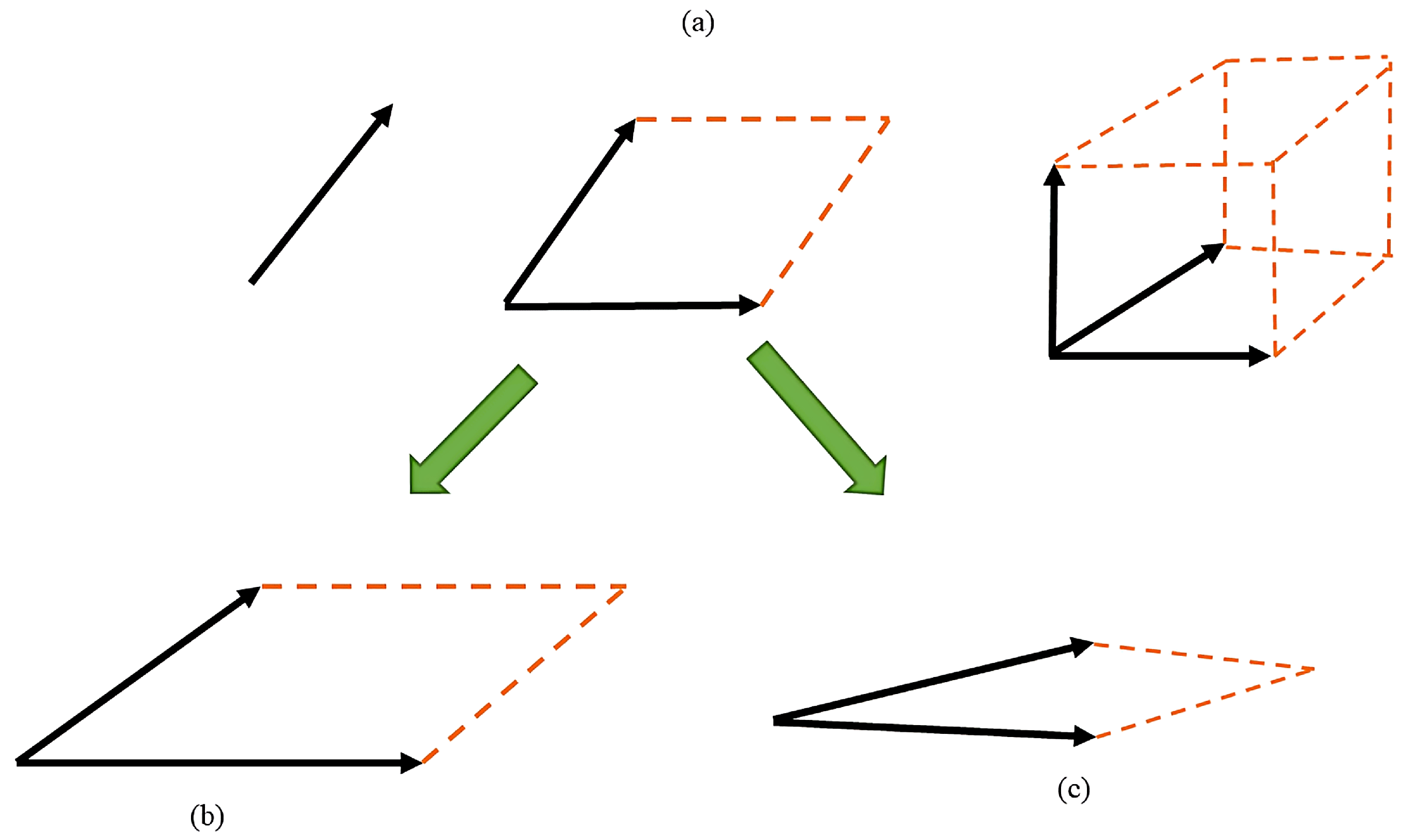
2.1. The Determinantal Point Process (DPP)
2.2. DPPs Geometry
2.3. Corner Solution
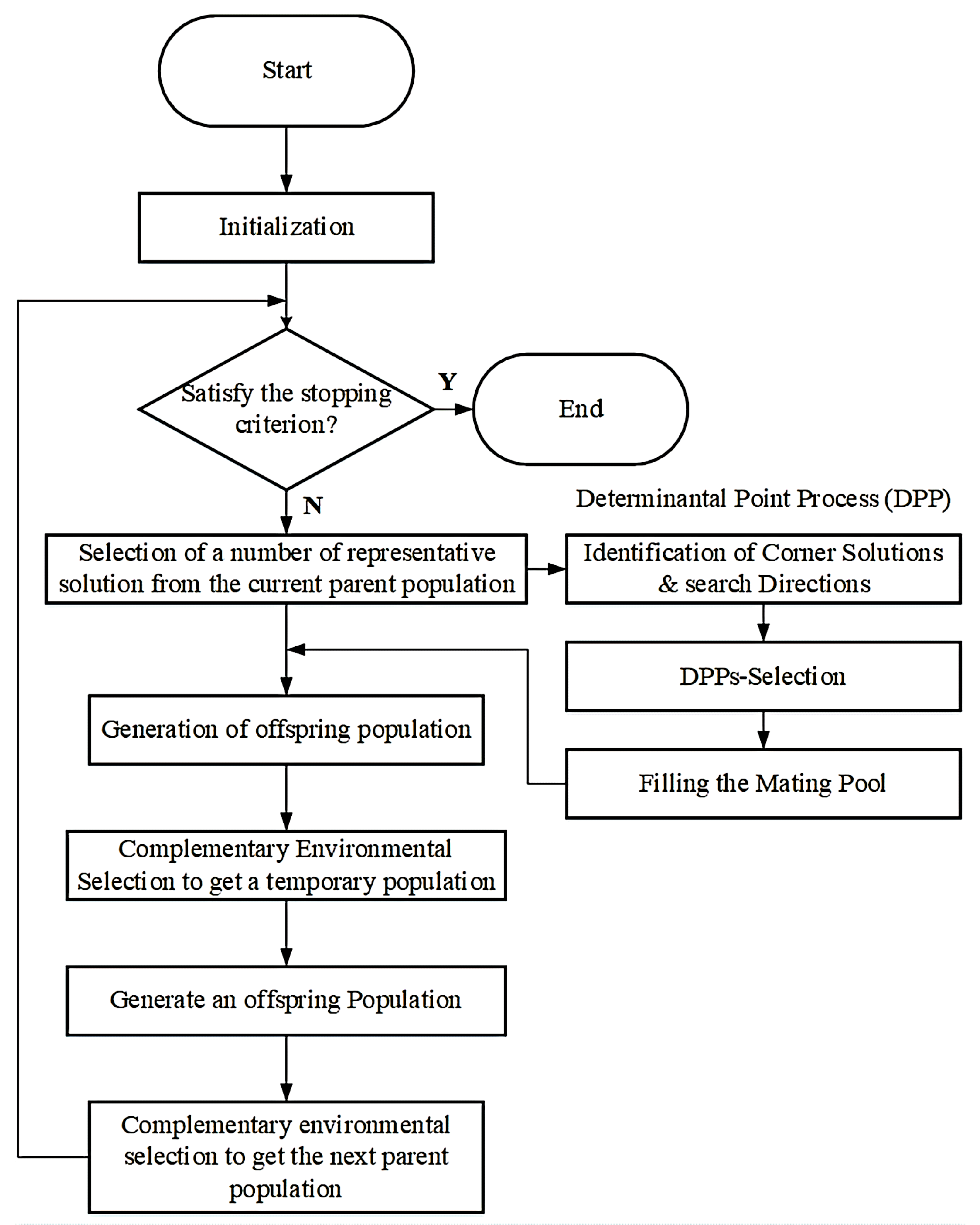
3. Proposed Innovative Global Optimization Algorithm
3.1. Framework of the LSMOEA-DPP
| Algorithm 1: Proposed LSMOEA-DPP Framework. |
| Input: M (The Size of Population) |
| 1 P← Initialization of population (M) |
| 2 |
| 3 |
| 4 |
| 5 while total function evaluations >= 80,000 do |
 |
3.2. Mating Pool
| Algorithm 2: Mating Pool filling. |
| Input: P (The size of Population) |
| 1 Normalization |
| 2 |
| 3 for do |
 |
3.3. Complementary Environmental Selection
| Algorithm 3: Environmental Selection. |
| Input: in initial selection and in 2nd selection |
| Selection; |
| : Sets of the reference vectors V; |
| M: Initial population size for LSMOEA-DPPs; |
| : Threshold to find respective method in Environmental selection. |
| Output: : Population for following generation |
| 1 Objective value Normalization in combined population; |
| 2 Allocation of particular individuals in population to the nearest reference vectors from ; |
| 3 if# of reference vector allocated to each individual !< |
| then |
 |
| Algorithm 4: The Kernel Matrix Computation. |
| Input: P (the size of population), CSA |
| 1 for the solution do |
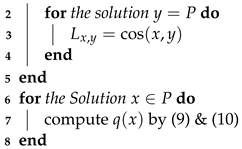 |
| 9 |
| 10 |
| Output: L |
| Algorithm 5: The selection of DPPs. |
| Input: L (The Kerne_Matrix), size of Subset = k |
| 1 whereas = Eigen decomposition |
| 2 Choose eigenvectors (k ) from in reference to max k eigen-values |
| 3 |
| 4 while do |
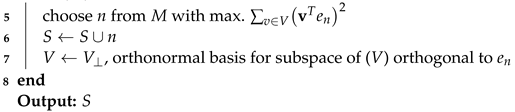 |
4. Experiment Settings and Result Analysis
4.1. Experimental Setup
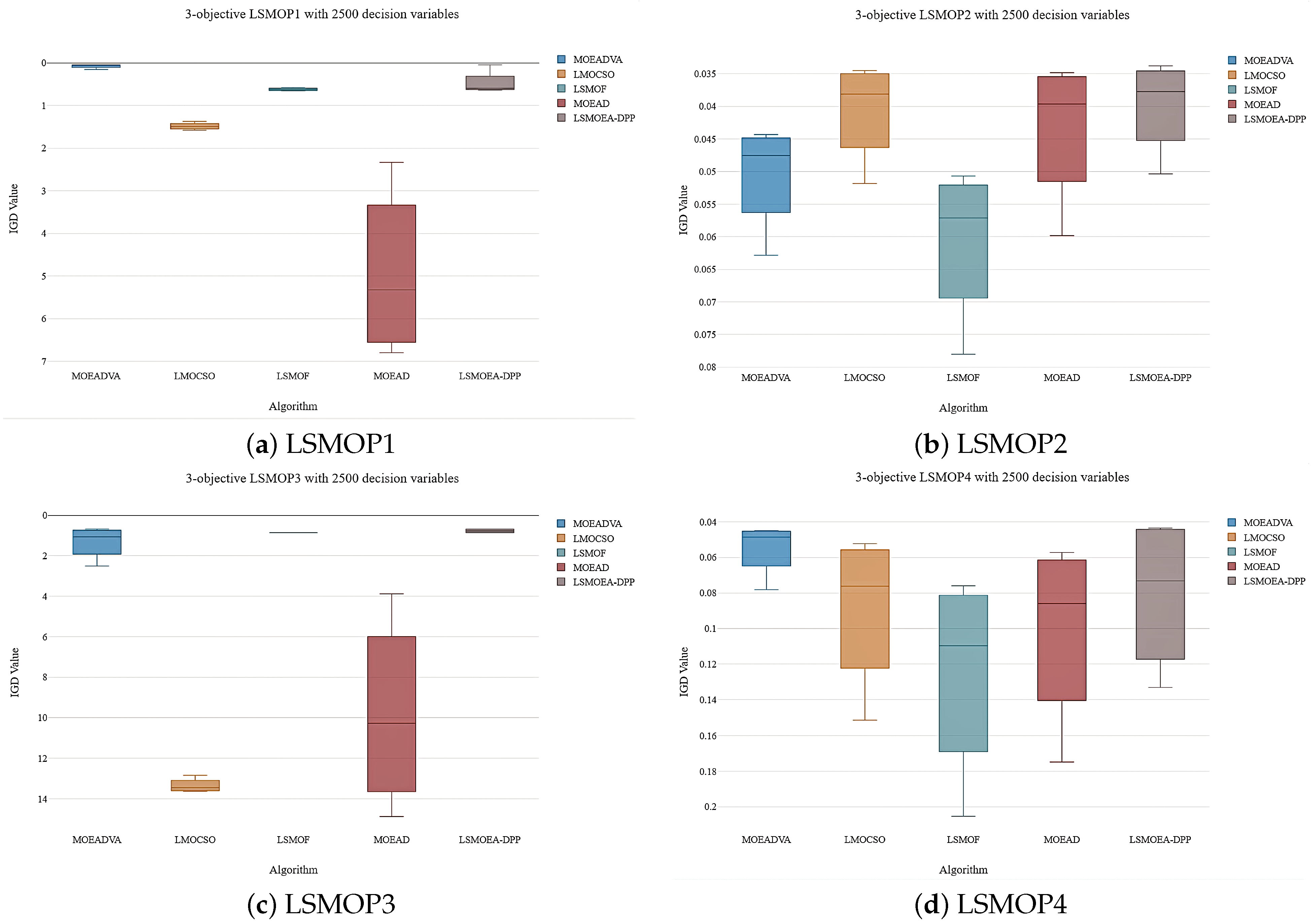
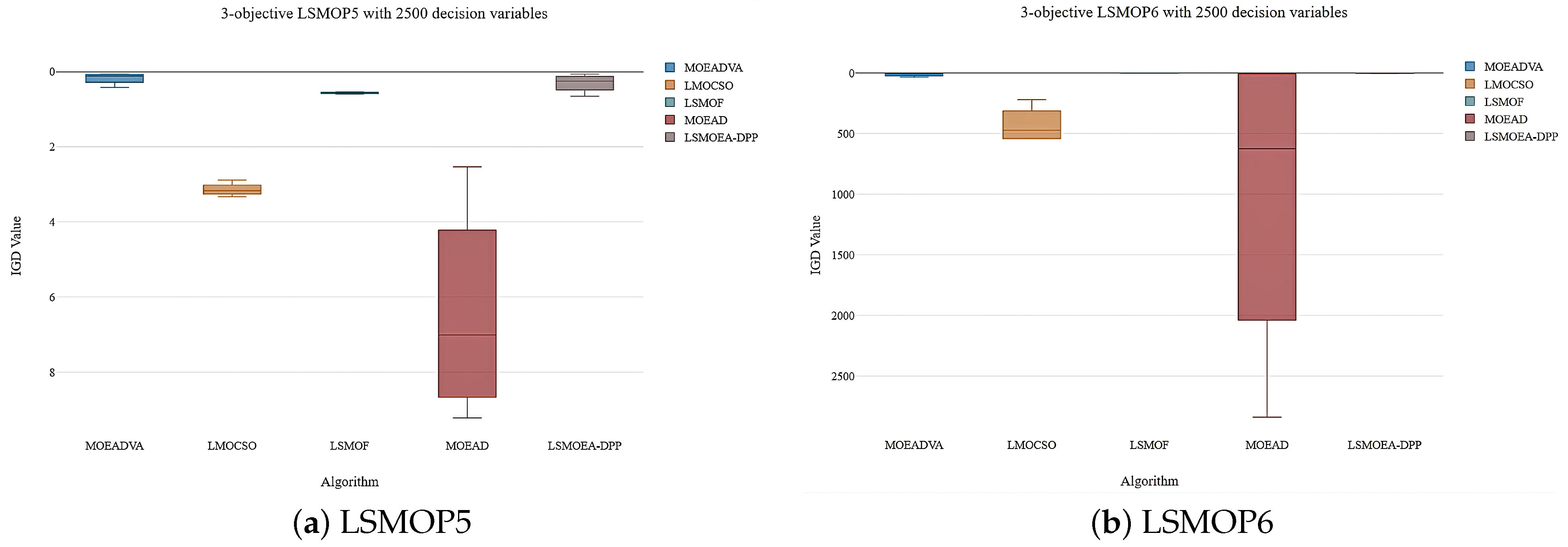
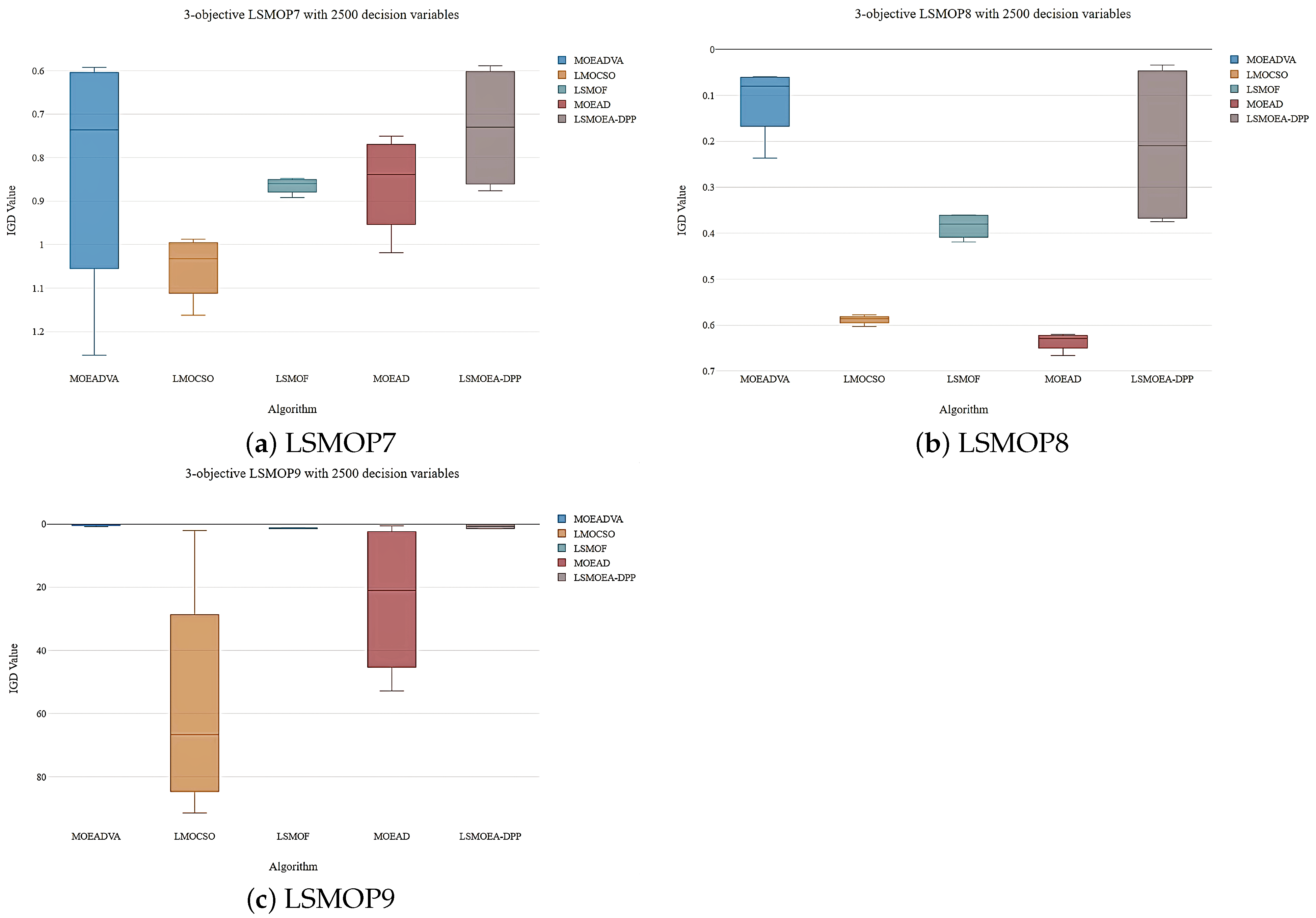
4.2. Analysis of the Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ishibuchi, H.; Tsukamoto, N.; Nojima, Y. Behavior of evolutionary many-objective optimization. In Proceedings of the Tenth International Conference on Computer Modeling and Simulation (uksim 2008), Cambridge, UK, 1–3 April 2008; pp. 266–271. [Google Scholar]
- He, Z.; Yen, G.G. Ranking many-objective evolutionary algorithms using performance metrics ensemble. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2480–2487. [Google Scholar]
- Ishibuchi, H.; Murata, T. A multi-objective genetic local search algorithm and its application to flowshop scheduling. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 1998, 28, 392–403. [Google Scholar] [CrossRef]
- Jin, Y.; Okabe, T.; Sendho, B. Adapting weighted aggregation for multiobjective evolution strategies. In International Conference on Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2001; pp. 96–110. [Google Scholar]
- Murata, T.; Ishibuchi, H.; Gen, M. Specification of genetic search directions in cellular multi-objective genetic algorithms. In International Conference on Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2001; pp. 82–95. [Google Scholar]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Liu, H.L.; Gu, F.; Zhang, Q. Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems. IEEE Trans. Evol. Comput. 2014, 18, 450–455. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Beume, N.; Naujoks, B.; Emmerich, M. SMS-EMOA: Multiobjective selection based on dominated hypervolume. Eur. J. Oper. Res. 2007, 181, 1653–1669. [Google Scholar] [CrossRef]
- Zitzler, E.; Künzli, S. Indicator-based selection in multiobjective search. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2004; pp. 832–842. [Google Scholar]
- Bringmann, K.; Friedrich, T. An efficient algorithm for computing hypervolume contributions. Evol. Comput. 2010, 18, 383–402. [Google Scholar] [CrossRef] [PubMed]
- Bader, J.; Zitzler, E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef] [PubMed]
- While, L.; Bradstreet, L.; Barone, L. A fast way of calculating exact hypervolumes. IEEE Trans. Evol. Comput. 2012, 16, 86–95. [Google Scholar] [CrossRef]
- Russo, L.M.; Francisco, A.P. Quick hypervolume. IEEE Trans. Evol. Comput. 2013, 18, 481–502. [Google Scholar] [CrossRef]
- Brockhoff, D.; Wagner, T.; Trautmann, H. On the properties of the R2 indicator. In Proceedings of the 14th Annual Conference on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; pp. 465–472. [Google Scholar]
- Gómez, R.H.; Coello, C.A.C. MOMBI: A new metaheuristic for many-objective optimization based on the R2 indicator. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2488–2495. [Google Scholar]
- Trautmann, H.; Wagner, T.; Brockhoff, D. R2-EMOA: Focused multiobjective search using R2-indicator-based selection. In International Conference on Learning and Intelligent Optimization; Springer: Berlin/Heidelberg, Germany, 2013; pp. 70–74. [Google Scholar]
- Tian, Y.; Cheng, R.; Zhang, X.; Cheng, F.; Jin, Y. An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility. IEEE Trans. Evol. Comput. 2017, 22, 609–622. [Google Scholar] [CrossRef]
- Corne, D.W.; Knowles, J.D.; Oates, M.J. The Pareto envelope-based selection algorithm for multiobjective optimization. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2000; pp. 839–848. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Li, K.; Deb, K.; Zhang, Q.; Kwong, S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans. Evol. Comput. 2015, 19, 694–716. [Google Scholar] [CrossRef]
- Gong, D.; Sun, J.; Ji, X. Evolutionary algorithms with preference polyhedron for interval multi-objective optimization problems. Inf. Sci. 2013, 233, 141–161. [Google Scholar] [CrossRef]
- Rong, M.; Gong, D.; Zhang, Y.; Jin, Y.; Pedrycz, W. Multidirectional prediction approach for dynamic multiobjective optimization problems. IEEE Trans. Cybern. 2019, 49, 3362–3374. [Google Scholar] [CrossRef] [PubMed]
- Hager, W.W.; Hearn, D.W.; Pardalos, P.M. Large Scale Optimization: State of the Art; Kluwer Academic Publishing: London, UK, 2013. [Google Scholar]
- Zhang, X.; Tian, Y.; Cheng, R.; Jin, Y. A decision variable clustering-based evolutionary algorithm for large-scale many-objective optimization. IEEE Trans. Evol. Comput. 2018, 22, 97–112. [Google Scholar] [CrossRef]
- Parsons, L.; Haque, E.; Liu, H. Subspace clustering for high dimensional data: A review. ACM Sigkdd Explor. Newsl. 2004, 6, 90–105. [Google Scholar] [CrossRef]
- Wang, H.; Liang, M.; Sun, C.; Zhang, G.; Xie, L. Multiple-strategy learning particle swarm optimization for large-scale optimization problems. Complex Intell. Syst. 2021, 7, 1–16. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, W.N.; Gu, T.; Zhang, H.; Deng, J.D.; Li, Y.; Zhang, J. Segment-based predominant learning swarm optimizer for large-scale optimization. IEEE Trans. Cybern. 2017, 47, 2896–2910. [Google Scholar] [CrossRef]
- Omidvar, M.N.; Li, X.; Yang, Z.; Yao, X. Cooperative co-evolution for large scale optimization through more frequent random grouping. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Cheng, R.; Jin, Y. A competitive swarm optimizer for large scale optimization. IEEE Trans. Cybern. 2015, 45, 191–204. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y. A social learning particle swarm optimization algorithm for scalable optimization. Inf. Sci. 2015, 291, 43–60. [Google Scholar] [CrossRef]
- He, C.; Cheng, R.; Zhang, C.; Tian, Y.; Chen, Q.; Yao, X. Evolutionary large-scale multiobjective optimization for ratio error estimation of voltage transformers. IEEE Trans. Evol. Comput. 2020, 24, 868–881. [Google Scholar] [CrossRef]
- Tian, Y.; Zheng, X.; Zhang, X.; Jin, Y. Efficient large-scale multiobjective optimization based on a competitive swarm optimizer. IEEE Trans. Cybern. 2019, 50, 3696–3708. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; He, C.; Cheng, R.; Pan, L. Large-scale Multiobjective Optimization via Problem Decomposition and Reformulation. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 2149–2155. [Google Scholar]
- Li, M.; Wei, J. A cooperative co-evolutionary algorithm for large-scale multi-objective optimization problems. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Kyoto, Japan, 15–19 July 2018; pp. 1716–1721. [Google Scholar]
- Chen, H.; Zhu, X.; Pedrycz, W.; Yin, S.; Wu, G.; Yan, H. PEA: Parallel evolutionary algorithm by separating convergence and diversity for large-scale multi-objective optimization. In Proceedings of the 2018 IEEE 38th International Conference on Distributed Computing Systems (ICDCS), Vienna, Austria, 2–6 July 2018; pp. 223–232. [Google Scholar]
- Ma, X.; Liu, F.; Qi, Y.; Wang, X.; Li, L.; Jiao, L.; Yin, M.; Gong, M. A multiobjective evolutionary algorithm based on decision variable analyses for multiobjective optimization problems with large-scale variables. IEEE Trans. Evol. Comput. 2016, 20, 275–298. [Google Scholar] [CrossRef]
- Miguel Antonio, L.; Coello Coello, C.A. Decomposition-based approach for solving large scale multi-objective problems. In International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2016; pp. 525–534. [Google Scholar]
- Song, A.; Yang, Q.; Chen, W.N.; Zhang, J. A random-based dynamic grouping strategy for large scale multi-objective optimization. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 468–475. [Google Scholar]
- Antonio, L.M.; Coello, C.A.C. Use of cooperative coevolution for solving large scale multiobjective optimization problems. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2758–2765. [Google Scholar]
- Liu, R.; Ren, R.; Liu, J.; Liu, J. A clustering and dimensionality reduction based evolutionary algorithm for large-scale multi-objective problems. Appl. Soft Comput. 2020, 89, 106120. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, R.; Wen, J.; Li, H.; Weng, J. Solving large-scale many-objective optimization problems by covariance matrix adaptation evolution strategy with scalable small subpopulations. Inf. Sci. 2020, 509, 457–469. [Google Scholar] [CrossRef]
- He, C.; Li, L.; Tian, Y.; Zhang, X.; Cheng, R.; Jin, Y.; Yao, X. Accelerating large-scale multiobjective optimization via problem reformulation. IEEE Trans. Evol. Comput. 2019, 23, 949–961. [Google Scholar] [CrossRef]
- Zille, H.; Ishibuchi, H.; Mostaghim, S.; Nojima, Y. A framework for large-scale multiobjective optimization based on problem transformation. IEEE Trans. Evol. Comput. 2018, 22, 260–275. [Google Scholar] [CrossRef]
- He, C.; Cheng, R.; Yazdani, D. Adaptive offspring generation for evolutionary large-scale multiobjective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 786–798. [Google Scholar] [CrossRef]
- Singh, H.K.; Isaacs, A.; Ray, T. A Pareto corner search evolutionary algorithm and dimensionality reduction in many-objective optimization problems. IEEE Trans. Evol. Comput. 2011, 15, 539–556. [Google Scholar] [CrossRef]
- Macchi, O. The coincidence approach to stochastic point processes. Adv. Appl. Probab. 1975, 7, 83–122. [Google Scholar] [CrossRef]
- Borodin, A.; Olshanski, G. Distributions on Partitions, Point Processes, and the Hypergeometric Kernel. Commun. Math. Phys. 2000, 211, 335–358. [Google Scholar] [CrossRef]
- Gartrell, M.; Paquet, U.; Koenigstein, N. Bayesian low-rank determinantal point processes. In Proceedings of the 10th ACM Conference on Recommender Systems, Boston, MA, USA, 15–19 September 2016; pp. 349–356. [Google Scholar]
- Kulesza, A.; Taskar, B. k-DPPs: Fixed-Size Determinantal Point Processes; ICML: 2011. Available online: https://openreview.net/forum?id=BJV9DjWuZS (accessed on 9 October 2022).
- Li, B.; Li, J.; Tang, K.; Yao, X. Many-objective evolutionary algorithms: A survey. ACM Comput. Surv. (CSUR) 2015, 48, 1–35. [Google Scholar] [CrossRef]
- Cheng, R.; Li, M.; Tian, Y.; Zhang, X.; Yang, S.; Jin, Y.; Yao, X. A benchmark test suite for evolutionary many-objective optimization. Complex Intell. Syst. 2017, 3, 67–81. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable test problems for evolutionary multiobjective optimization. In Evolutionary Multiobjective Optimization; Springer: London, UK, 2005; pp. 105–145. [Google Scholar]
- Cheng, R.; Jin, Y.; Olhofer, M. Test problems for large-scale multiobjective and many-objective optimization. IEEE Trans. Cybern. 2016, 47, 4108–4121. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Jin, Y.; Zhang, Q.; Sendhoff, B.; Tsang, E. Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 892–899. [Google Scholar]
- Czyzżak, P.; Jaszkiewicz, A. Pareto simulated annealing—A metaheuristic technique for multiple-objective combinatorial optimization. J. Multi-Criteria Decis. Anal. 1998, 7, 34–47. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- He, Z.; Yen, G.G. Many-objective evolutionary algorithms based on coordinated selection strategy. IEEE Trans. Evol. Comput. 2016, 21, 220–233. [Google Scholar] [CrossRef]
- Dufner, J.; Jensen, U.; Schumacher, E. Statistik mit SAS; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Tian, Y.; Si, L.; Zhang, X.; Cheng, R.; He, C.; Tan, K.C.; Jin, Y. Evolutionary large-scale multi-objective optimization: A survey. ACM Comput. Surv. (CSUR) 2021, 54, 1–34. [Google Scholar] [CrossRef]
| Problems | Characteristics | ||
|---|---|---|---|
| Modelity | Shape | Separability | |
| LSMOP-1 | Unimodal Modelity | Linear shape | Full separability |
| LSMOP-2 | Mixed Modelity | Linear shape | Partial separability |
| LSMOP-3 | Multi-modal Modelity | Linear shape | Mixed separability |
| LSMOP-4 | Mixed Modelity | Linear shape | Mixed separability |
| LSMOP-5 | Unimodal Modelity | Convex shape | Full separability |
| LSMOP-6 | Mixed Modelity | Convex shape | Partially separability |
| LSMOP-7 | Multimodal Modelity | Convex shape | Mixed separability |
| LSMOP-8 | Mixed Modelity | Convex | Mixed separability |
| LSMOP-9 | Mixed Modelity | Disconnected | Full separability |
| Reference No | Optimization Techniques Used | Accuracy | Complexity Level |
|---|---|---|---|
| [2] | Performance Metrics Ensemble | Fair | Very complex |
| [25] | Global Optimization | Low | Average |
| [26] | Decision Variable clustering & Non-dominated Sorting | High | Average |
| [28] | Multiple-strategy learning particle swarm optimization & Two-stage searching mechanism | High | Less Complex |
| [29] | Particle Swarm Optimization, Segment Predominant learning Optimization | High | Average |
| [62] | Decision variable grouping, Decision space reduction, & Novel Search strategies. | High | Very Complex |
| Problem | M | D | MOEADVA | LMOCSO | LSMOF | MOEAD | LSMOEADPP |
|---|---|---|---|---|---|---|---|
| LSMOP1 | 2 | 500 | 1.4062e-1 (5.42e-3) + | 1.3372e+0 (1.00e-1) − | 5.9889e-1 (5.47e-2) = | 6.3180e-1 (1.18e-1) − | 6.0395e-1 (4.18e-2) |
| 1000 | 4.2611e-2 (3.28e-4) + | 1.5183e+0 (5.45e-2) − | 6.3999e-1 (2.14e-2) − | 6.7100e+0 (6.04e-1) − | 6.2794e-1 (4.75e-2) | ||
| 2000 | 1.2933e-2 (3.66e-4) + | 1.5644e+0 (2.75e-2) − | 6.5257e-1 (2.21e-2) = | 6.9393e+0 (8.28e-1) − | 6.4003e-1 (2.67e-2) | ||
| 2500 | 9.2551e-3 (2.88e-4) − | 1.5796e+0 (3.45e-2) − | 6.5101e-1 (1.85e-2) − | 4.2072e+0 (3.79e-1) − | 9.0791e-3 (3.07e-4) | ||
| LSMOP2 | 2 | 500 | 6.2621e-2 (3.30e-4) − | 4.5700e-2 (5.84e-4) − | 1.9279e-2 (4.86e-4) − | 7.0899e-2 (1.14e-3) − | 1.9264e-2 (4.00e-4) |
| 1000 | 3.2863e-2 (1.66e-4) − | 2.5307e-2 (3.95e-4) − | 1.1443e-2 (1.84e-4) − | 3.8924e-2 (2.10e-3) − | 1.0443e-2 (4.51e-4) | ||
| 2000 | 1.7924e-2 (2.31e-4) − | 1.4030e-2 (2.81e-4) − | 8.5405e-3 (3.47e-4) − | 2.0717e-2 (1.51e-4) − | 1.0332e-2 (2.69e-4) | ||
| 2500 | 1.4934e-2 (3.85e-4) − | 1.1676e-2 (2.46e-4) − | 9.5457e-3 (3.15e-4) − | 1.6455e-2 (8.94e-5) − | 1.1486e-2 (4.12e-4) | ||
| LSMOP3 | 2 | 500 | 3.4226e+0 (4.93e-1) − | 2.2194e+1 (3.83e+0) − | 1.5714e+0 (3.77e-3) − | 2.7099e+1 (7.66e+0) − | 1.5654e+0 (8.68e-4) |
| 1000 | 1.7959e+0 (5.07e-2) − | 2.4727e+1 (6.10e+0) − | 1.5785e+0 (4.92e-3) − | 2.8951e+1 (6.71e+0) − | 1.5738e+0 (3.68e-4) | ||
| 2000 | 1.0804e+0 (1.40e-2) − | 2.8148e+1 (1.43e+0) − | 1.5773e+0 (1.44e-4) − | 3.0802e+1 (7.20e+0) − | 1.0723e+0 (1.00e-4) | ||
| 2500 | 9.2935e-1 (9.71e-3) = | 2.8682e+1 (4.76e+0) − | 1.5779e+0 (1.17e-4) − | 2.2149e+1 (7.33e+0) − | 9.2916e-1 (1.14e-2) | ||
| LSMOP4 | 2 | 500 | 4.8246e-2 (7.39e-4) − | 9.0366e-2 (1.35e-3) − | 5.0425e-2 (1.75e-3) − | 1.2402e-1 (3.68e-3) − | 4.0538e-2 (2.59e-4) |
| 1000 | 1.4908e-2 (2.93e-4) − | 5.2411e-2 (4.75e-4) − | 2.7831e-2 (6.40e-4) − | 7.3170e-2 (2.05e-3) − | 1.3411e-2 (9.96e-4) | ||
| 2000 | 6.1755e-3 (3.56e-4) − | 2.9962e-2 (2.16e-4) − | 1.6726e-2 (3.52e-4) − | 4.0805e-2 (5.30e-4) − | 1.5175e-2 (3.65e-4) | ||
| 2500 | 5.3751e-3 (3.54e-4) − | 2.5071e-2 (2.15e-4) − | 1.6530e-2 (7.54e-4) − | 3.0987e-2 (9.21e-4) − | 5.2445e-3 (4.85e-4) | ||
| LSMOP5 | 2 | 500 | 3.9520e-1 (1.36e-2) + | 2.8686e+0 (1.16e-1) − | 7.4195e-1 (2.71e-4) − | 1.1375e+1 (1.38e+0) − | 7.4209e-1 (0.00e+0) |
| 1000 | 1.2228e-1 (2.89e-3) + | 3.2203e+0 (1.68e-1) − | 7.4192e-1 (1.58e-4) − | 1.4864e+1 (1.59e+0) − | 7.4209e-1 (0.00e+0) | ||
| 2000 | 3.4879e-2 (6.22e-4) + | 3.2752e+0 (1.38e-1) − | 7.4209e-1 (0.00e+0) = | 1.5428e+1 (1.41e+0) − | 7.4209e-1 (0.00e+0) | ||
| 2500 | 2.3334e-2 (3.04e-4) − | 3.3334e+0 (1.23e-1) − | 7.4209e-1 (0.00e+0) − | 9.3920e+0 (1.11e+0) − | 2.3166e-2 (4.56e-4) | ||
| LSMOP6 | 2 | 500 | 2.6772e+0 (3.50e+0) − | 7.9260e-1 (8.17e-3) − | 7.0468e-1 (1.89e-1) − | 8.0800e-1 (8.71e-3) − | 3.2039e-1 (5.23e-4) |
| 1000 | 1.8657e+0 (2.76e+0) − | 7.7045e-1 (2.64e-3) − | 6.8490e-1 (7.28e-4) − | 7.7428e-1 (1.60e+0) − | 3.1252e-1 (2.94e-4) | ||
| 2000 | 7.0940e-1 (7.15e-1) − | 7.5721e-1 (6.56e-4) − | 3.0883e-1 (1.25e-4) − | 7.5703e-1 (9.28e-1) − | 3.0879e-1 (1.18e-4) | ||
| 2500 | 7.3782e-1 (2.08e+0) − | 7.5399e-1 (7.38e-4) − | 3.0768e-1 (1.30e-4)+ | 7.5374e-1 (5.09e-4) − | 6.2937e-1 (8.57e-1) | ||
| LSMOP7 | 2 | 500 | 8.0192e+1 (6.66e+0) − | 5.7964e+2 (1.06e+2) − | 1.5078e+0 (9.78e-4) − | 1.6902e+4 (4.51e+3) − | 1.5021e+0 (1.50e-3) |
| 1000 | 2.5410e+1 (1.09e+0) − | 9.4475e+2 (1.57e+2) − | 1.5137e+0 (7.44e-4) − | 3.1051e+4 (6.39e+3) − | 1.5103e+0 (3.34e-4) | ||
| 2000 | 1.0549e+1 (2.39e-1) + | 1.1627e+3 (9.92e+1) − | 1.5146e+0 (7.26e-4) − | 3.6112e+4 (4.40e+3) − | 1.5139e+0 (5.03e-4) | ||
| 2500 | 8.4641e+0 (2.36e-1) = | 1.7786e+3 (2.25e+2) − | 1.5170e+0 (9.95e-4) + | 4.9477e+4 (9.55e+3) − | 8.5032e+0 (1.25e-1) | ||
| LSMOP8 | 2 | 500 | 2.5023e-1 (7.95e-3) + | 1.8967e+0 (1.25e-1) − | 7.4188e-1 (2.39e-4) − | 7.5571e+0 (1.44e+0) − | 7.4209e-1 (0.00e+0) |
| 1000 | 7.3660e-2 (8.03e-4) − | 2.2786e+0 (1.60e-1) − | 7.4199e-1 (1.94e-4) − | 9.8467e+0 (6.17e-1) − | 7.2562e-1 (0.00e+0) | ||
| 2000 | 2.0770e-2 (3.35e-4) + | 2.5568e+0 (1.39e-1) − | 7.4209e-1 (0.00e+0) = | 1.0405e+1 (6.63e-1) − | 7.4209e-1 (0.00e+0) | ||
| 2500 | 1.4240e-2 (5.56e-4) + | 2.5419e+0 (2.24e-1) − | 7.4209e-1 (0.00e+0) − | 7.2183e+0 (8.03e-1) − | 1.4004e-2 (3.19e-4) | ||
| LSMOP9 | 2 | 500 | 4.5782e-1 (4.04e-2) + | 8.7112e-1 (1.77e-1) − | 8.0882e-1 (7.01e-4) − | 2.7666e+1 (3.48e+0) − | 8.1004e-1 (9.09e-4) |
| 1000 | 1.1718e-1 (4.95e-3) + | 2.8625e+0 (6.42e-1) − | 8.0576e-1 (1.19e-3) − | 3.9097e+1 (3.99e+0) − | 8.0695e-1 (2.28e-3) | ||
| 2000 | 3.4876e-2 (2.41e-3) + | 5.1625e+0 (2.44e+0) − | 8.0614e-1 (4.23e-3) = | 4.4518e+1 (2.45e+0) − | 8.0468e-1 (1.69e-3) | ||
| 2500 | 2.4722e-2 (1.32e-3) = | 5.8595e+0 (1.52e+0) − | 8.0475e-1 (2.79e-3) − | 2.9026e+1 (2.63e+0) − | 2.4707e-2 (2.31e-3) | ||
| +/−/= | 13/20/3 | 0/36/0 | 2/29/5 | 0/36/0 | 23/13/0 |
| Problem | M | D | MOEADVA | LMOCSO | LSMOF | MOEAD | LSMOEADPP |
|---|---|---|---|---|---|---|---|
| LSMOP1 | 3 | 500 | l1.5310e-1 (2.65e-3) + | 1.3713e+0 (8.01e-2) − | 5.7538e-1 (7.57e-3) = | 2.3318e+0 (3.84e-1) − | 5.7851e-1 (9.26e-3) |
| 1000 | 6.4418e-2 (1.89e-3) + | 1.4725e+0 (1.04e-1) − | 6.1096e-1 (1.99e-2) = | 4.3365e+0 (6.68e-1) − | 6.1067e-1 (1.38e-2) | ||
| 2000 | 4.7363e-2 (3.23e-3) + | 1.5188e+0 (1.15e-1) − | 6.4203e-1 (8.19e-3) = | 6.3107e+0 (5.36e-1) − | 6.3813e-1 (1.67e-2) | ||
| 2500 | 4.6129e-2 (3.72e-3) = | 1.5771e+0 (1.55e-1) − | 6.5703e-1 (1.77e-2) − | 6.7976e+0 (6.07e-1) − | 4.5164e-2 (2.41e-3) | ||
| LSMOP2 | 3 | 500 | 6.2848e-2 (3.37e-3) + | 5.1848e-2 (6.53e-4) − | 7.8036e-2 (3.42e-3) = | 5.9839e-2 (2.48e-4) + | 5.0355e-2 (2.94e-3) |
| 1000 | 4.9740e-2 (3.08e-3) + | 4.0786e-2 (3.87e-4) − | 6.0797e-2 (4.56e-3) − | 4.3205e-2 (7.26e-5) + | 4.0133e-2 (3.82e-3) | ||
| 2000 | 4.4343e-2 (2.79e-3) + | 3.5473e-2 (1.85e-4) − | 5.3458e-2 (2.66e-3) − | 3.6078e-2 (5.36e-5) + | 3.5363e-2 (4.04e-3) | ||
| 2500 | 4.5370e-2 (2.70e-3) = | 3.4513e-2 (1.02e-4) + | 5.0689e-2 (4.09e-3) − | 3.4834e-2 (5.53e-5) + | 3.3790e-2 (1.93e-3) | ||
| LSMOP3 | 3 | 500 | 2.5037e+0 (2.09e-1) − | 1.2837e+1 (2.72e+0) − | 8.6058e-1 (5.02e-4) = | 3.8781e+0 (2.96e+0) − | 8.6051e-1 (3.10e-3) |
| 1000 | 1.3333e+0 (5.76e-2) − | 1.3629e+1 (2.15e+0) − | 8.6070e-1 (1.10e-4) = | 8.1081e+0 (3.39e+0) − | 8.6066e-1 (1.41e-4) | ||
| 2000 | 7.9497e-1 (2.16e-2) − | 1.3567e+1 (1.77e+0) − | 8.6068e-1 (6.40e-5) = | 1.2424e+1 (5.81e+0) − | 6.8190e-1 (1.00e-4) | ||
| 2500 | 6.7546e-1 (1.11e-2) = | 1.3329e+1 (1.87e+0) − | 8.6072e-1 (1.02e-4) − | 1.4873e+1 (3.28e+0) − | 6.7537e-1 (1.54e-2) | ||
| LSMOP4 | 3 | 500 | 7.8148e-2 (2.64e-3) − | 1.5152e-1 (2.02e-3) + | 2.0536e-1 (6.26e-3) − | 1.7483e-1 (3.78e-3) + | 1.0144e-1 (6.63e-3) |
| 1000 | 5.1546e-2 (4.07e-3) + | 9.3167e-2 (8.04e-4) + | 1.3274e-1 (3.59e-3) = | 1.0617e-1 (1.89e-3) + | 1.3313e-1 (4.43e-3) | ||
| 2000 | 4.5686e-2 (3.88e-3) + | 5.9310e-2 (3.22e-4) + | 8.6618e-2 (2.88e-3) = | 6.5718e-2 (4.79e-4) + | 4.4963e-2 (2.94e-3) | ||
| 2500 | 4.4946e-2 (4.04e-3) − | 5.2303e-2 (3.45e-4) − | 7.5992e-2 (4.24e-3) − | 5.7264e-2 (3.02e-4) − | 4.3519e-2 (2.66e-3) | ||
| LSMOP5 | 3 | 500 | 4.1845e-1 (9.47e-3) + | 2.8865e+0 (2.51e-1) − | 5.4082e-1 (7.45e-2) = | 2.5322e+0 (8.39e-1) − | 1.8371e-1 (7.20e-2) |
| 1000 | 1.5005e-1 (3.61e-3) + | 3.1521e+0 (1.92e-1) − | 5.5421e-1 (9.51e-2) = | 5.8966e+0 (1.26e+0) − | 6.5262e-1 (1.37e-1) | ||
| 2000 | 7.2052e-2 (1.90e-3) + | 3.1823e+0 (2.35e-1) − | 5.9659e-1 (1.28e-1) = | 8.1210e+0 (1.33e+0) − | 3.1643e-1 (1.34e-1) | ||
| 2500 | 6.4266e-2 (3.43e-3) = | 3.3278e+0 (1.92e-1) − | 5.6857e-1 (1.02e-1) − | 9.2162e+0 (7.11e-1) − | 6.3560e-2 (3.13e-3) | ||
| LSMOP6 | 3 | 500 | 3.5414e+1 (5.39e+0) − | 2.2022e+2 (1.16e+2) − | 7.3389e-1 (1.50e-2) = | 3.3559e+0 (1.01e+0) − | 7.2039e-1 (2.58e-2) |
| 1000 | 1.2411e+1 (1.99e+0) − | 4.0659e+2 (1.55e+2) − | 7.4758e-1 (2.00e-2) = | 1.1591e+1 (1.11e+1) − | 7.4498e-1 (1.95e-2) | ||
| 2000 | 6.5737e+0 (6.95e-1) − | 5.4063e+2 (1.04e+2) − | 7.6323e-1 (2.73e-2) = | 1.2397e+3 (6.24e+2) − | 7.5841e-1 (1.88e-2) | ||
| 2500 | 5.6462e+0 (1.61e-1) = | 5.4280e+2 (1.25e+2) − | 7.5989e-1 (2.93e-2) + | 2.8405e+3 (1.45e+3) − | 5.8823e+0 (6.06e-1) | ||
| LSMOP7 | 3 | 500 | 1.2543e+0 (1.19e+0) − | 1.1624e+0 (6.81e-2) − | 8.9177e-1 (1.25e-2) + | 1.0184e+0 (8.44e-2) − | 8.7629e-1 (1.25e-2) |
| 1000 | 8.5598e-1 (2.24e-1) = | 1.0611e+0 (3.14e-2) − | 8.6669e-1 (3.76e-2) = | 8.8881e-1 (1.39e-1) = | 8.4505e-1 (5.03e-2) | ||
| 2000 | 6.1633e-1 (3.66e-2) = | 1.0035e+0 (9.59e-3) − | 8.5274e-1 (4.79e-2) − | 7.8850e-1 (2.45e-1) − | 6.1519e-1 (4.57e-2) | ||
| 2500 | 5.9231e-1 (2.84e-2) = | 9.8762e-1 (1.01e-2) − | 8.4802e-1 (4.90e-2) − | 7.5047e-1 (1.76e-1) − | 5.8876e-1 (2.44e-2) | ||
| LSMOP8 | 3 | 500 | 2.3658e-1 (5.80e-3) + | 6.0305e-1 (3.04e-2) − | 3.6026e-1 (8.19e-2) = | 6.6628e-1 (3.01e-2) − | 3.5960e-1 (1.11e-1) |
| 1000 | 9.8081e-2 (5.67e-3) + | 5.8513e-1 (2.81e-2) − | 3.9857e-1 (1.13e-1) = | 6.3332e-1 (1.20e-2) − | 3.7484e-1 (9.38e-2) | ||
| 2000 | 6.1872e-2 (4.50e-3) = | 5.8700e-1 (3.84e-2) − | 4.1896e-1 (9.96e-2) − | 6.2516e-1 (9.28e-3) − | 3.39805e-2 (2.57e-3) | ||
| 2500 | 5.9496e-2 (5.05e-3) = | 5.7760e-1 (2.55e-2) − | 3.6153e-1 (1.13e-1) − | 6.2011e-1 (2.33e-3) − | 5.9082e-2 (2.53e-3) | ||
| LSMOP9 | 3 | 500 | 7.9373e-1 (5.20e-2) + | 2.0633e+0 (2.11e+0) − | 1.5379e+0 (0.00e+0) = | 5.7809e-1 (8.90e-2) + | 1.5379e+0 (0.00e+0) |
| 1000 | 2.5031e-1 (1.76e-2) + | 5.5351e+1 (3.46e+1) − | 1.5379e+0 (3.93e-1) = | 4.2654e+0 (1.92e+0) − | 1.3415e+0 (3.93e-1) | ||
| 2000 | 1.1166e-1 (1.16e-2) = | 7.7855e+1 (2.88e+1) − | 1.1770e+0 (3.93e-1) − | 3.7867e+1 (3.32e+0) − | 1.1013e-1 (7.73e-3) | ||
| 2500 | 1.0570e-1 (1.06e-2) = | 9.1425e+1 (4.19e+1) − | 1.1537e+0 (2.21e-1) − | 5.2886e+1 (3.70e+0) − | 1.0438e-1 (1.42e-2) | ||
| +/−/= | 0/1/8 | 1/8/0 | 1/8/0 | 1/8/0 | 28/9/0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okoth, M.A.; Shang, R.; Jiao, L.; Arshad, J.; Rehman, A.U.; Hamam, H. A Large Scale Evolutionary Algorithm Based on Determinantal Point Processes for Large Scale Multi-Objective Optimization Problems. Electronics 2022, 11, 3317. https://doi.org/10.3390/electronics11203317
Okoth MA, Shang R, Jiao L, Arshad J, Rehman AU, Hamam H. A Large Scale Evolutionary Algorithm Based on Determinantal Point Processes for Large Scale Multi-Objective Optimization Problems. Electronics. 2022; 11(20):3317. https://doi.org/10.3390/electronics11203317
Chicago/Turabian StyleOkoth, Michael Aggrey, Ronghua Shang, Licheng Jiao, Jehangir Arshad, Ateeq Ur Rehman, and Habib Hamam. 2022. "A Large Scale Evolutionary Algorithm Based on Determinantal Point Processes for Large Scale Multi-Objective Optimization Problems" Electronics 11, no. 20: 3317. https://doi.org/10.3390/electronics11203317
APA StyleOkoth, M. A., Shang, R., Jiao, L., Arshad, J., Rehman, A. U., & Hamam, H. (2022). A Large Scale Evolutionary Algorithm Based on Determinantal Point Processes for Large Scale Multi-Objective Optimization Problems. Electronics, 11(20), 3317. https://doi.org/10.3390/electronics11203317










